Как найти корни тангенса по окружности

Отбор корней в тригонометрическом уравнение

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x — cosx = 0

cosx(sqrt(2)cosx — 1) = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx — 1 = 0

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

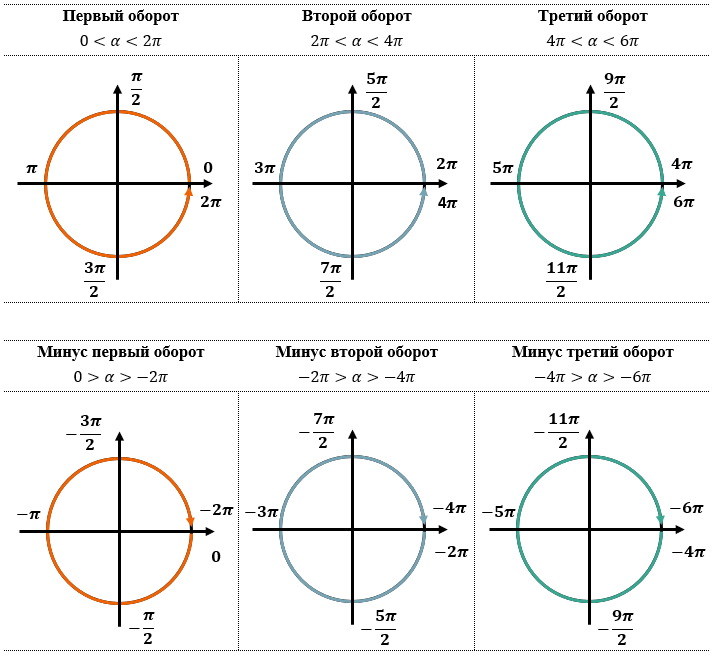
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

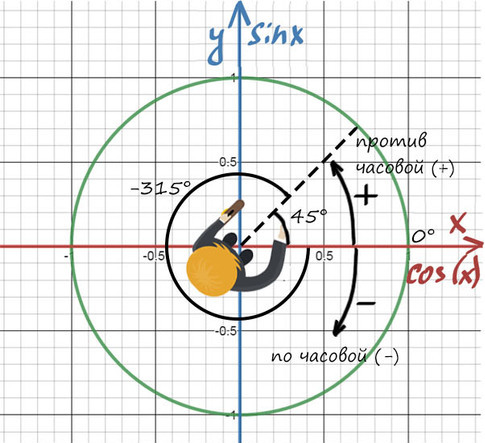
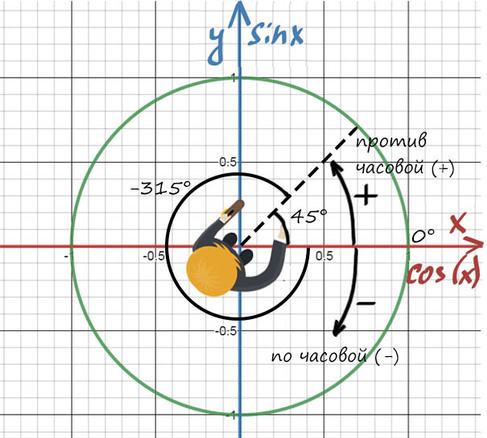
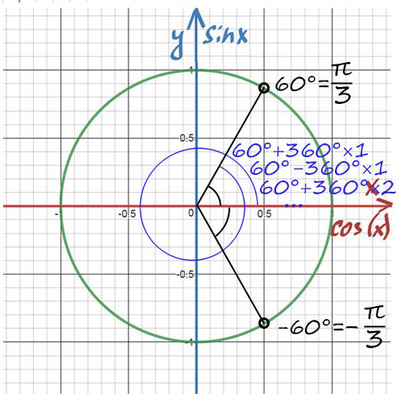
Обойдем раз против часовой стрелки

Обойдем 2 раза против часовой стрелки

Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

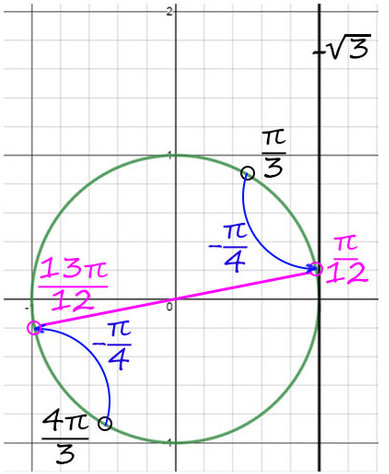
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

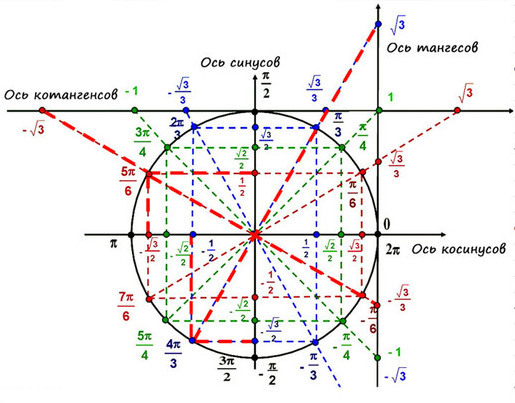
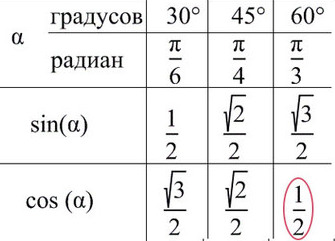
Значения тангенса и котангенса на тригонометрическом круге

В прошлой статье мы познакомились с тригонометрическим кругом и научились находить значения синуса и косинуса основных углов.

Как же быть с тангенсом и котангенсом ? Об этом и поговорим сегодня.

Где же на тригонометрическом круге оси тангенсов и котангенсов?

Ось тангенсов параллельна оси синусов (имеет тоже направление, что ось синусов) и проходит через точку (1; 0).

Ось котангенсов параллельна оси косинусов (имеет тоже направление, что ось косинусов) и проходит через точку (0; 1).

На каждой из осей располагается вот такая цепочка основных значений тангенса и котангенса: Почему так?

Я думаю, вы легко сообразите и сами. Можно по-разному рассуждать. Можете, например, использовать тот факт, что и

Собственно, картинка за себя сама говорит.

Если не очень все же понятно, разберем примеры:

Пример 1.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0;0) лучом (начало – точка (0;0)) и смотрим, где этот луч пересекает ось тангенсов. Видим, что

Ответ:

Пример 2.

Вычислить

Находим на круге . Точку (0;0) соединяем с указанной точкой лучом. И видим, что луч никогда не пересечет ось тангенсов.

не существует.

Ответ: не существует

Пример 3.

Вычислить

Находим на круге точку (это та же точка, что и ) и от нее по часовой стрелке (знак минус!) откладываем (). Куда попадаем? Мы окажемся в точке, что на круге у нас (см. рис.) названа как . Эту точку соединяем с точкой (0;0) лучом. Вышли на ось тангенсов в значение .

Так значит,

Ответ:

Пример 4.

Вычислить

Поэтому от точки (именно там будет ) откладываем против часовой стрелки .

Выходим на ось котангенсов, получаем, что

Ответ:

Пример 5.

Вычислить

Находим на круге . Эту точку соединяем с точкой (0; 0). Выходим на ось котангенсов. Видим, что

Ответ:

Теперь, умея находить по тригонометрическому кругу значения тригонометрических функций (а я надеюсь, что статья, где мы начинали знакомство с кругом и учились вычислять значения синусов и косинусов, вами прочитана…), вы можете пройт и тест по теме «Нахождение значений косинуса, синуса, тангенса и котангенса различных углов».

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Тригонометрический круг: вся тригонометрия на одном рисунке

Тригонометрический круг — это самый простой способ начать осваивать тригонометрию. Он легко запоминается, и на нём есть всё необходимое.
Тригонометрический круг заменяет десяток таблиц.

Вот что мы видим на этом рисунке:

Перевод градусов в радианы и наоборот. Полный круг содержит градусов, или радиан.

Значения синусов и косинусов основных углов. Помним, что значение косинуса угла мы находим на оси , а значение синуса — на оси .

И синус, и косинус принимают значения от до .

Значение тангенса угла тоже легко найти — поделив на . А чтобы найти котангенс — наоборот, косинус делим на синус.

Знаки синуса, косинуса, тангенса и котангенса.

Синус — функция нечётная, косинус — чётная.

Тригонометрический круг поможет увидеть, что синус и косинус — функции периодические. Период равен .

А теперь подробно о тригонометрическом круге:

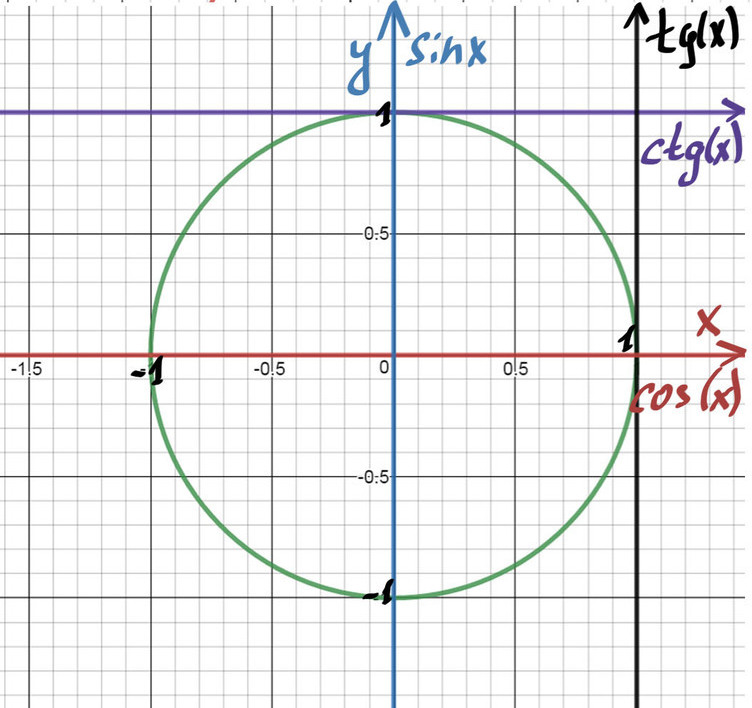
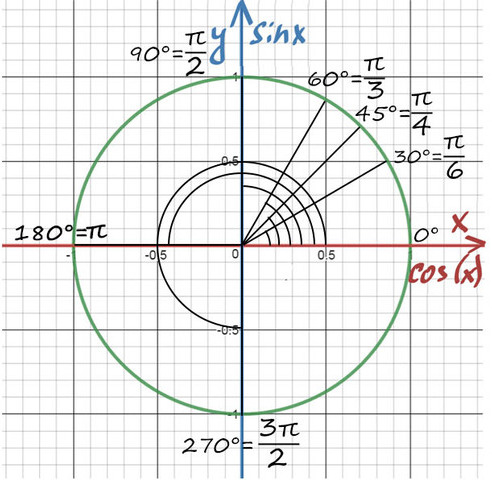
Нарисована единичная окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями и , в которой мы привыкли рисовать графики функций.

Мы отсчитываем углы от положительного направления оси против часовой стрелки.

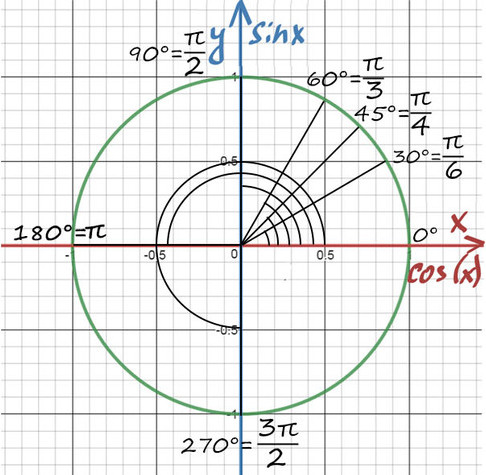
Полный круг — градусов.
Точка с координатами соответствует углу ноль градусов. Точка с координатами отвечает углу в , точка с координатами — углу в . Каждому углу от нуля до градусов соответствует точка на единичной окружности.

Косинусом угла называется абсцисса (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Синусом угла называется ордината (то есть координата по оси ) точки на единичной окружности, соответствущей данному углу .

Всё это легко увидеть на нашем рисунке.

Итак, косинус и синус — координаты точки на единичной окружности, соответствующей данному углу. Косинус — абсцисса , синус — ордината . Поскольку окружность единичная, для любого угла и синус, и косинус находятся в пределах от до :

Простым следствием теоремы Пифагора является основное тригонометрическое тождество:

Для того, чтобы узнать знаки синуса и косинуса какого-либо угла, не нужно рисовать отдельных таблиц. Всё уже нарисовано! Находим на нашей окружности точку, соответствующую данному углу , смотрим, положительны или отрицательны ее координаты по (это косинус угла ) и по (это синус угла ).

Принято использовать две единицы измерения углов: градусы и радианы. Перевести градусы в радианы просто: градусов, то есть полный круг, соответствует радиан. На нашем рисунке подписаны и градусы, и радианы.

Если отсчитывать угол от нуля против часовой стрелки — он положительный. Если отсчитывать по часовой стрелке — угол будет отрицательным. Например, угол — это угол величиной в , который отложили от положительного направления оси по часовой стрелке.

Легко заметить, что

Углы могут быть и больше градусов. Например, угол — это два полных оборота по часовой стрелке и еще . Поскольку, сделав несколько полных оборотов по окружности, мы возвращаемся в ту же точку с теми же координатами по и по , значения синуса и косинуса повторяются через . То есть:

где — целое число. То же самое можно записать в радианах:

Можно на том же рисунке изобразить ещё и оси тангенсов и котангенсов, но проще посчитать их значения. По определению,

Отбор корней с помощью тригонометрического круга

В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.

«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА

1. Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.

2. Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.

3. Определяем корни, попадающие в эту дугу.

4. Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.

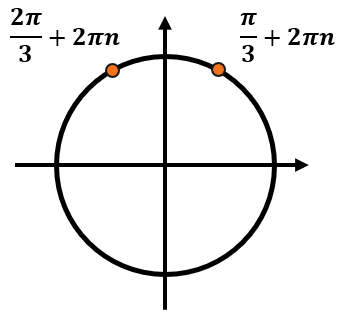
Пример:

Даны корни уравнения:

(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})

(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})

Найдите корни, принадлежащие отрезку (leftlbrack — pi, frac{3pi}{2} rightrbrack).

1. Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:

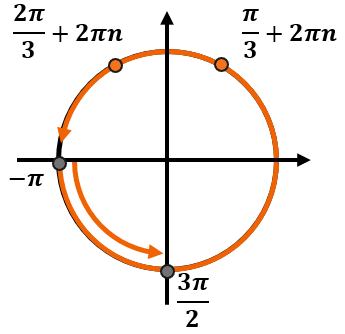
1. При этом мы знаем, что нужные корни должны находиться на промежутке (leftlbrack — pi, frac{3pi}{2} rightrbrack). Этот промежуток занимает больше, чем один оборот. Обозначим его так:

1. Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.

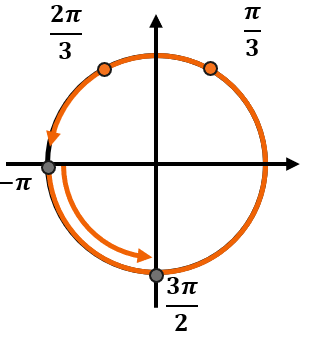
2. Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от (- pi) до (frac{3pi}{2}), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:

Запишем ответ.

Ответ: (frac{pi}{3});( frac{2pi}{3}).

Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.

Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте «Как запомнить тригонометрический круг»).

Эта статья состоит из двух частей:
Решение простейших уравнений с тангенсом
Решение простейших уравнений с котангенсом

Алгоритм решения простейших уравнений с тангенсом

Давайте с вами рассмотрим типичное уравнение, например, (tg⁡x=sqrt{3}).

Пример. Решить уравнение (tg⁡x=sqrt{3}).

Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…

…и обозначим то место на оси, куда мы должны попасть в итоге.

Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.

Точки найдены. Давайте подпишем значение одной из них…

…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: (x=frac{π}{3}+πn),    (n∈Z).

Задача решена.

Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом, здесь записывается только одна серия корней, причем в формуле добавляется (πn), а не (2πn). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии (π). Благодаря этому значение обеих точек можно записать одной формулой в виде (x=t_0+πn),    (n∈Z).

Пример. Решить уравнение (tg⁡x=-1).

Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:

Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.

Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.

Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn),  (n∈Z) (подробнее о формуле в видео), где (t_0) – как раз то значение, которые вы нашли в шаге 4.

Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.

Алгоритм решения простейших уравнений с котангенсом

Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.

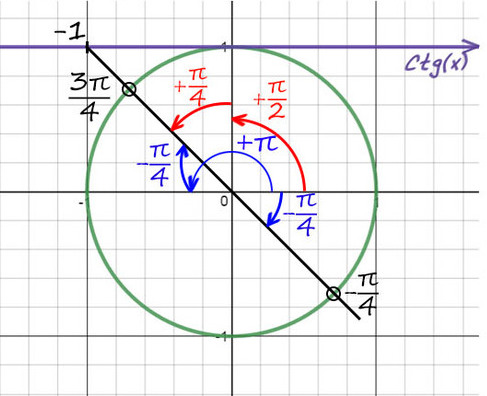
Пример. Решить уравнение (ctg⁡x=frac{1}{sqrt{3}})

Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в (frac{1}{sqrt{3}}) на оси котангенсов?
Строим круг, проводим нужные оси.

Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…

…и соединяем центр окружности и точку на оси котангенсов прямой линией.

По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…

…и записываем окончательный ответ по формуле (x=t_0+πn), (n∈Z), потому что у котангенса период такой же как у тангенса: (πn).

Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен (sqrt{3}), котангенс будет (frac{1}{sqrt{3}}).

Разберем еще пример, а потом подведем итог.

Пример. Решить уравнение (ctg⁡x=-1). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.

Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:

Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.

Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.

Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn),  (n∈Z), где (t_0) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.

Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции (arctg) и (arcctg). Если вы не знаете, что это – читайте эту статью.

Простейшие тригонометрические уравнения с тангенсом и котангенсом

Чтобы уверенно решать простейшие уравнения с тангенсом или котангенсом нужно знать значения стандартных точек на круге и стандартные значения на осях тангенсов и котангенсов (если в этом материале есть пробелы, читайте « Как запомнить тригонометрический круг »).

Алгоритм решения простейших уравнений с тангенсом

Давайте с вами рассмотрим типичное уравнение, например, (tg⁡x=sqrt<3>).

Пример. Решить уравнение (tg⁡x=sqrt<3>).

Чего от нас здесь хотят? Чтобы мы написали все такие значения угла в Пи, для которых тангенс равен корню из трех. Причем написать надо именно все такие углы. Давайте нарисуем тригонометрический круг и ось тангенсов…

…и обозначим то место на оси, куда мы должны попасть в итоге.

Теперь найдем через какие точки на окружности мы должны идти, чтобы попасть в этот самый корень из трех –проведем прямую через начало координат и найденную точку на оси тангенсов.

Точки найдены. Давайте подпишем значение одной из них…

…и запишем окончательный ответ – все возможные варианты значений в Пи, находящиеся в отмеченных точках: (x=frac<π><3>+πn), (n∈Z).

Замечание. Вы, наверно, обратили внимание, что в отличие от уравнений с синусом и косинусом , здесь записывается только одна серия корней, причем в формуле добавляется (πn), а не (2πn). Дело в том, что в любом уравнении с тангенсом решением получаются две точки на окружности, которые находятся друг от друга на расстоянии (π). Благодаря этому значение обеих точек можно записать одной формулой в виде (x=t_0+πn), (n∈Z).

Пример. Решить уравнение (tg⁡x=-1).

Итак, окончательный алгоритм решения подобных задач выглядит следующим образом:

Шаг 1. Построить окружность, оси синусов и косинусов, а также ось тангенсов.

Шаг 2. Отметить на оси тангенсов значение, которому тангенс должен быть равен.

Шаг 3. Соединить прямой линией центр окружности и отмеченную точку на оси тангенсов.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z) (подробнее о формуле в видео), где (t_0) – как раз то значение, которые вы нашли в шаге 4.

Специально для вас мы сделали удобную табличку со всеми шагами алгоритма и разными примерами к нему. Пользуйтесь на здоровье! Можете даже распечатать и повесить на стенку, чтоб больше никогда не ошибаться в этих уравнениях.

Алгоритм решения простейших уравнений с котангенсом

Сразу скажу, что алгоритм решения уравнений с котангенсом почти такой же, как и с тангенсом.

Шаг 1. Вопрос у нас практически тот же – из каких точек круга можно попасть в (frac<1><sqrt<3>>) на оси котангенсов?
Строим круг, проводим нужные оси.

Теперь отмечаем на оси котангенсов значение, которому котангенс должен быть равен…

…и соединяем центр окружности и точку на оси котангенсов прямой линией.

По сути точки найдены. Осталось записать их все. Вновь определяем значение в одной из них…

…и записываем окончательный ответ по формуле (x=t_0+πn), (n∈Z), потому что у котангенса период такой же как у тангенса: (πn).

Кстати, вы обратили внимание, что ответы в задачах совпали? Здесь нет ошибки, ведь для любой точки круга, тангенс которой равен (sqrt<3>), котангенс будет (frac<1><sqrt<3>>).

Разберем еще пример, а потом подведем итог.

Пример. Решить уравнение (ctg⁡x=-1). Здесь подробно расписывать не буду, так как логика полностью аналогична вышеизложенной.

Итак, алгоритм решения простейших тригонометрических уравнений с котангенсом:

Шаг 1. Построить окружность и оси синусов и косинусов, а также ось котангенсов.

Шаг 2. Отметить на оси котангенсов значение, которому котангенс должен быть равен.

Шаг 3. Соединить центр окружности и точку на оси котангенсов прямой линией.

Шаг 4. Найти значение одной из точек на круге.

Шаг 5. Записать ответ используя формулу (x=t_0+πn), (n∈Z), где (t_0) – как раз то значение, которые вы нашли в шаге 4. И табличка в награду всем дочитавшим до этого места.

Примечание. Возможно, вы обратили внимание, что при решении примеров 2 и 3 в обеих табличках мы использовали функции (arctg) и (arcctg). Если вы не знаете, что это – читайте эту статью.

Тригонометрические уравнения

Решение простейших тригонометрических уравнений

Градусы и радианы

Знакомство с тригонометрической окружностью

Повороты на тригонометрической окружности

Как много боли связано со словом тригонометрия. Эта тема появляется в 9 классе и уже никуда не исчезает. Тяжело приходится тем, кто чего-то не понял сразу. Попробуем это исправить, чтобы осветить ваше лицо улыбкой при слове тригонометрия или хотя бы добиться «poker face».

Начнем с того, что как длину можно выразить в метрах или милях, так и угол можно выразить в радианах или градусах .

1 радиан = 180/π ≈ 57,3 градусов

Но проще запомнить целые числа: 3,14 радиан = 180 градусов. Это все одно и то же значение числа π.

Вспомним, что если нас просят развернуться, то нам нужно повернуться на 180 градусов, а теперь можно так же сказать: Повернись на π!

О графиках синуса, косинуса и тангеса поговорим в другой статье.

А сейчас начем с декартовой (прямоугольной) системы координат.

Раньше она помогала строить графики, а теперь поможет с синусом и косинусом.

На пересечении оси Х и оси Y построим единичную (радиус равен 1) окружность:

Тогда ось косинусов будет совпадать с х, ось синусов с y. Оси тангенсов и котангенсов также показаны на рисунке.

А теперь отметим основные значения градусов и радиан на окружности.

Давай договоримся с тобой, как взрослые люди: на окружности мы будем отмечать угол в радианах, то есть через Пи.

Достаточно запомнить, что π = 180° (тогда π/6 = 180/6 = 30°; π/3 = 180/3 = 60°; π/4 = 180/4 = 45°).

А теперь давай покрутимся на окружности! За начало отчета принято брать крайнюю правую точку окружности (где 0°):

От нее задаем дальнейший поворот. Вращаться можем как в положительную сторону (против часовой), так и в отрицательную сторону (по часовой стрелке).

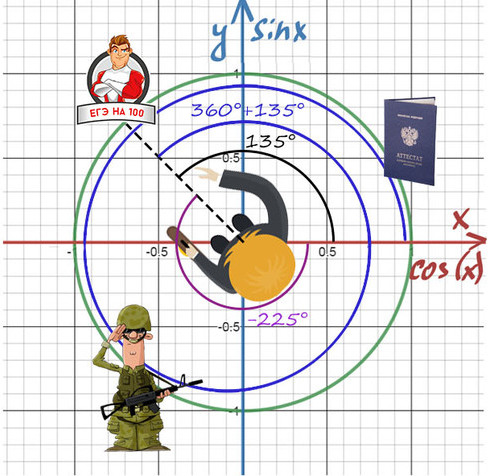
Повернуться на 45° можно двумя спобами: через левое плечо на 45° в (+) сторону, либо через правое плечо на 315° в (-).

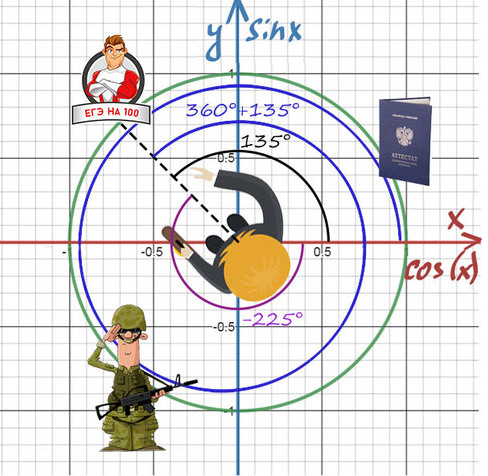
Главное — направление, куда мы будем смотреть, а не угол!

Нужно направить пунктир на 100 баллов, а сколько оборотов и в какую сторону вокруг себя мы сделаем — без разницы!

Получить 100 баллов можно поворотом на 135° или 360°+135°, или -225°, или -225°-360°.

А теперь у тебя есть два пути:

Выучить всю окружность (тригонометр). Неплохой вариант, если с памятью у тебя все отлично, и ничего не вылетит из головы в ответственный момент:

А можно запомнить несколько табличных углов и соответствующие им значения, а потом использовать их.

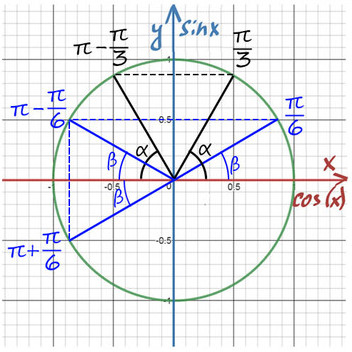
Находите равные углы (вертикальные, соответственные) на тригонометрической окружности. Попасть в любую точку можно с помощью суммы или разности двух табличных значений.

Сразу попробуем разобрать на примере:

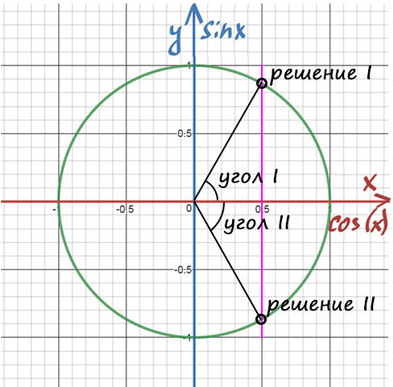
1) Помним, что ось cos(x) — это горизонтальная ось. На ней отмечаем значение ½ и проводим перпендикулярную (фиолетовую) прямую до пересечений с окружностью.

2) Получили две точки пересечения с окружностью, значение этих углов и будет решением уравнения.

Дело за малым — найти эти углы.

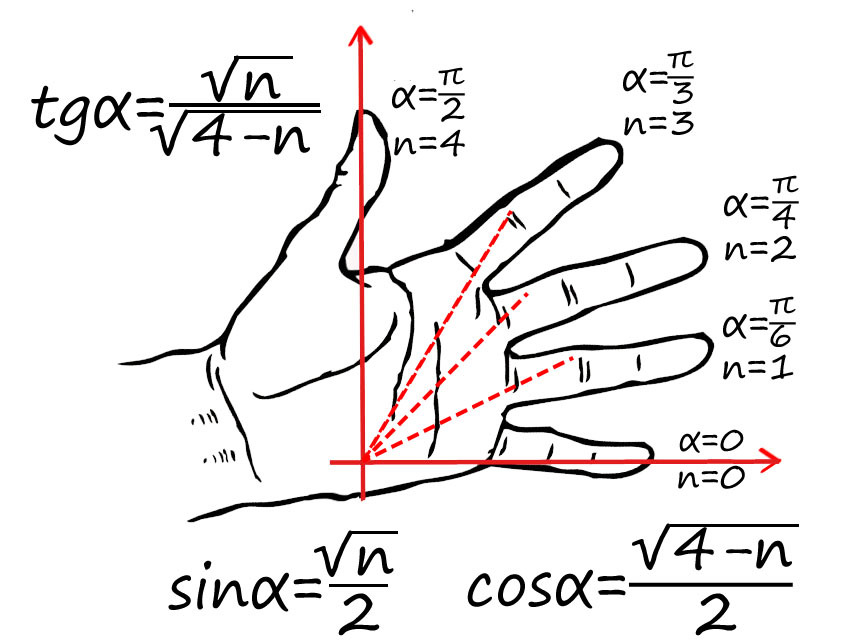
Лучше обойтись «малой кровью» и выучить значение синуса и косинуса для углов от 30° до 60°.

Или запомнить такой прием:

Пронумеруй пальцы от 0 до 4 от мизинца до большого. Угол задается между мизинцем и любым другим пальцем (от 0 до 90).

Например, требуется найти sin(π/2) : π/2 — это большой палец, n = 4 подставляем в формулу для синуса: sin(π/2) = √4/2 = 1 => sin(π/2) = 1.

cos(π/4) — ? π/4 соответсвует среднему пальцу (n = 2) => cos(π/4) = √2/2.

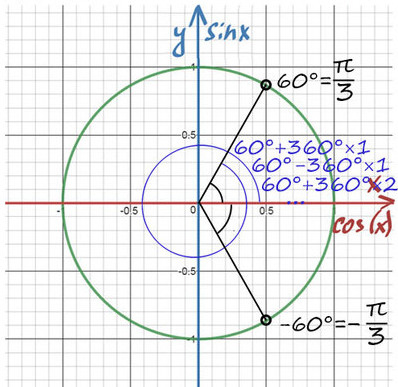
При значении cos(x) = ½ из таблицы или с помощью мнемонического правила находим x = 60° (первая точка x = +π/3 из-за того, что поворот происходил против часовой стерелки (+), угол показан черной дугой).

Вторая же точка соответствует точно такому же углу, только поворот будет по часовой стрелке (−). x = −π/3 (угол показан нижней черной дугой).

И последнее, прежде чем тебе, наконец, откроются тайные знания тригонометрии:

Когда требуется попасть в «100 баллов», мы можем в них попасть с помощью поворота на . =-225°=135°=495°=.

То же самое и здесь! Разные углы могут отражать одно и то же направление.

Абсолютно точно можно сказать, что нужно повернуться на требуемый угол, а дальше можно поворачиваться на 360° = 2π (синим цветом) сколько угодно раз и в любом направлении.

Таким образом, попасть в первое направление 60° можно: . 60°-360°, 60°, 60°+360°.

И как записать остальные углы, не записывать же бесконечное количество точек? (Хотел бы я на это посмотреть☻)

Поэтому правильно записать ответ: x = 60 + 360n, где n — целое число (n∈Ζ) (поворачиваемся на 60 градусов, а после кружимся сколько угодно раз, главное, чтобы направление осталось тем же). Аналогично x = −60 + 360n.

Но мы же договорились, что на окружности все записывают через π, поэтому cos(x) = ½ при x = π/3 + 2πn, n∈Ζ и x = −π/3 + 2πk, k∈Ζ.

Ответ: x = π/3 + 2πn, x= − π/3 + 2πk, (n, k) ∈Ζ.

Пример №2. 2sinx = √2

Первое, что следует сделать, это перенести 2-ку вправо => sinx=√2/2

1) sin(x) совпадает с осью Y. На оси sin(x) отмечаем √2/2 и проводим ⊥ фиолетовую прямую до пересечений с окружностью.

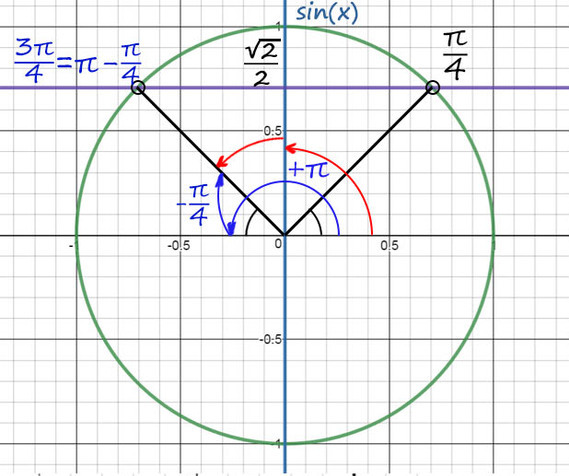
2) Из таблицы sinx = √2/2 при х = π/4, а вторую точку будем искать с помощью поворота до π, а затем нужно вернуться обратно на π/4.

Поэтому вторая точка будет x = π − π/4 = 3π/4, в нее также можно попасть и с помощью красных стрелочек или как-то по-другому.

И еще не забудем добавить +2πn, n∈Ζ.

Ответ: 3π/4 + 2πn и π/4 + 2πk, k и n − любые целые числа.

Пример №3. tg(x + π/4) = √3

Вроде все верно, тангенс равняется числу, но смущает π/4 в тангенсе. Тогда сделаем замену: y = x + π/4.

tg(y) = √3 выглядит уже не так страшно. Вспомним, где ось тангенсов.

1) А теперь на оси тангенсов отметим значение √3, это выше чем 1.

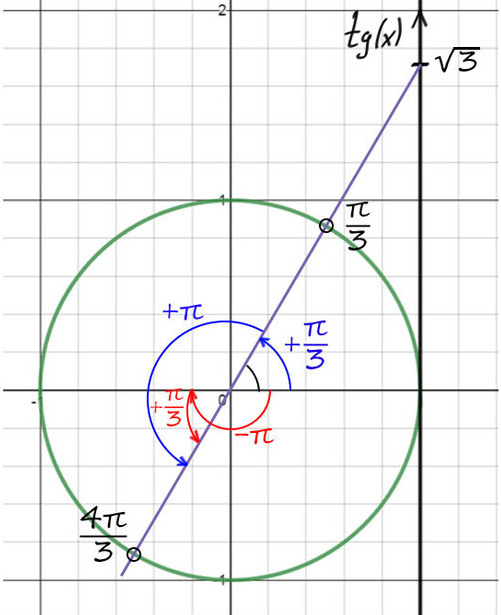
2) Проведем фиолетовую прямую через значение √3 и начало координат. Опять на пересечении с окружностью получается 2 точки.

По мнемоническому правилу при тангенсе √3 первое значение — это π/3.

3) Чтобы попасть во вторую точку, можно к первой точке (π/3) прибавить π => y = π/3 + π = 4π/3.

4) Но мы нашли только y , вернемся к х. y = π/3 + 2πn и y = x + π/4, тогда x + π/4 = π/3 + 2πn => x = π/12 + 2πn, n∈Ζ.

Второй корень: y = 4π/3 + 2πk и y = x + π/4, тогда x + π/4 = 4π/3 + 2πk => x = 13π/12 + 2πk, k∈Ζ.

Теперь корни на окружности будут здесь:

Ответ: π/12 + 2πn и 13π/12 + 2πk, k и n — любые целые числа.

Конечно, эти два ответа можно объединить в один. От 0 поворот на π/12, а дальше каждый корень будет повторяться через каждый π (180°).

Ответ можно записать и так: π/12 + πn, n∈Ζ.

Пример №4: −10ctg(x) = 10

Перенесем (−10) в другую часть: ctg(x) = −1. Отметим значение -1 на оси котангенсов.

1) Проведем прямую через эту точку и начало координат.

2) Придется опять вспомнить, когда деление косинуса на синус даст еденицу (это получается при π/4). Но здесь −1, поэтому одна точка будет −π/4. А вторую найдем поворотом до π, а потом назад на π/4 (π − π/4).

Можно это сделать по-другому (красным цветом), но мой вам совет: всегда отсчитывайте от целых значений пи (π, 2π, 3π. ) так намного меньше шансов запутаться.

Не забываем добавить к каждой точке 2πk.

Ответ: 3π/4 + 2πn и −π/4 + 2πk, k и n — любые целые числа.

Алгоритм решения тригонометрических уравнений (на примере cos(x) = − √ 3/2) :

1. Отмечаем значение (−√3/2) на оси тригонометрической функции (косинусов, это ось Х).
2. Проводим перпендикулярную прямую оси (косинусов) до пересечений с окружностью.
3. Точки пересечения с окружностью и будут являться корнями уравнения.
4. Значение одной точки (без разницы, как в нее попадете) +2πk.

Азов достаточно, прежде чем идти дальше закрепите полученные знания.

Простейшие тригонометрические уравнения. Часть 1

Простейшими называются тригонометрические уравнения следующих четырёх видов:

Любое тригонометрическое уравнение в конечном счёте сводится к решению одного или нескольких простейших. К сожалению, на этом заключительном стандартном шаге школьники часто допускают ошибки, что ведет к потере баллов на ЕГЭ. Именно поэтому так важна данная тема.

Существуют два подхода к решению простейших тригонометрических уравнений.
Первый подход — бессмысленный и тяжёлый. Следуя ему, надо выучить по шпаргалке общие формулы, а также все частные случаи. Польза от этого столь же невелика, как от зубрежки шестнадцати строк заклинаний на непонятном языке. Мы отказываемся от такого подхода раз и навсегда.

Второй подход — логический и наглядный. Для решения простейших тригонометрических уравнений мы пользуемся тригонометрическим кругом и определениями тригонометрических функций.

Уравнения и

Напомним, что — абсцисса точки на единичной окружности, соответствующей углу , а — её ордината.

Из определения синуса и косинуса следует, что уравнения и имеют решения только при условии .

Абитуриент, будь внимателен! Уравнения или решений не имеют!

Начнём с самых простых уравнений.

. .
Мы видим, что на единичной окружности имеется лишь одна точка с абсциссой 1:

Эта точка соответствует бесконечному множеству углов: . Все они получаются из нулевого угла прибавлением целого числа полных углов (т. е. нескольких полных оборотов как в одну, так и в другую сторону).

Следовательно, все эти углы могут быть записаны одной формулой:

Это и есть множество решений данного уравнения. Напоминаем, что — это множество целых чисел.

Снова видим, что на единичной окружности есть лишь одна точка с абсциссой :

Эта точка соответствует углу и всем углам, отличающихся от на несколько полных оборотов в обе стороны, т. е. на целое число полных углов. Следовательно, все решения данного уравнения записываются формулой:

. .
Отмечаем на тригонометрическом круге единственную точку с ординатой :

И записываем ответ:

Обсуждать тут уже нечего, не так ли? 🙂

Можете, кстати, записать ответ и в другом виде:

Это — дело исключительно вашего вкуса.
Заодно сделаем первое полезное наблюдение. Чтобы описать множество углов, отвечающих одной-единственной точке тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .

На тригонометрическом круге имеются две точки с ординатой 0:

Эти точки соответствуют углам Все эти углы получаются из нулевого угла прибавлением целого числа углов (т. е. с помощью нескольких полуоборотов в обе стороны). Таким образом,

Точки, лежащие на концах диаметра тригонометрического круга, мы будем называть диаметральной парой.

Точки с абсциссой 0 также образуют диаметральную пару, на сей раз вертикальную:

Все углы, отвечающие этим точкам, получаются из — прибавлением целого числа углов (полуоборотов):

Теперь мы можем сделать и второе полезное наблюдение.

Чтобы описать множество углов, отвечающих диаметральной паре точек тригонометрического круга, нужно взять какой-либо один угол из этого множества и прибавить .

Переходим к следующему этапу. Теперь в правой части будет стоять табличное значение синуса или косинуса (отличное от 0 или ). Начинаем с косинуса.

Имеем вертикальную пару точек с абсциссой :

Все углы, соответствующие верхней точке, описываются формулой (вспомните первое полезное наблюдение!):

Аналогично, все углы, соответствующие нижней точке, описываются формулой:

Обе серии решений можно описать одной формулой:

Остальные уравнения с косинусом решаются совершенно аналогично. Мы приводим лишь рисунок и ответ.

Теперь рассмотрим уравнения с синусом. Тут ситуация немного сложнее.

Имеем горизонтальную пару точек с ординатой :

Углы, отвечающие правой точке:

Углы, отвечающие левой точке:

Описывать эти две серии одной формулой никто не заставляет. Можно записать ответ в таком виде:

Тем не менее, объединяющая формула существует, и её надо знать. Выглядит она так:

На первый взгляд совершенно не ясно, каким образом она дает обе серии решений. Но давайте посмотрим, что получается при чётных . Если , то

Мы получили первую серию решений . А если — нечетно, , то

Это вторая серия .

Обратим внимание, что в качестве множителя при обычно ставится правая точка, в данном случае .

Остальные уравнения с синусом решаются точно так же. Мы приводим рисунок, запись ответа в виде совокупности двух серий и объединяющую формулу.

На этом с синусом и косинусом пока всё. Переходим к тангенсу.

Линия тангенсов.

Начнём с геометрической интерпретации тангенса — так называемой линии тангенсов. Это касательная к единичной окружности, параллельная оси ординат (см. рисунок).

Из подобия треугольников и имеем:

Мы рассмотрели случай, когда находится в первой четверти. Аналогично рассматриваются случаи, когда находится в остальных четвертях. В результате мы приходим к следующей геометрической интерпретации тангенса.

Тангенс угла равен ординате точки , которая является точкой пересечения линии тангенсов и прямой , соединяющей точку с началом координат.

Вот рисунок в случае, когда находится во второй четверти. Тангенс угла отрицателен.

Уравнение

Заметим, что тангенс может принимать любые действительные значения. Иными словами, уравнение имеет решения при любом .

.
Имеем диаметральную горизонтальную пару точек:

Эта пара, как мы уже знаем, описывается формулой:

Имеем диаметральную пару:

Вспоминаем второе полезное наблюдение и пишем ответ:

Остальные уравнения с тангенсом решаются аналогично. Мы приводим лишь рисунки и ответы.

На этом заканчиваем пока и с тангенсом.

Уравнение нет смысла рассматривать особо. Дело в том, что:
уравнение равносильно уравнению ;

при уравнение равносильно уравнению .

Впрочем, существует также и линия котангенсов, но. . . Об этом мы вам расскажем на занятиях 🙂

Итак, мы разобрали простейшие тригонометрические уравнения, содержащие в правой части табличные значения тригонометрических функций. Именно такие задачи встречаются в части В вариантов ЕГЭ.

А что делать, например, с уравнением ? Для этого надо сначала познакомиться с обратными тригонометрическими функциями. О них мы расскажем вам в следующей статье.

Всероссийский конкурс для школьных педагогов на лучшую образовательную статью «Просто о сложном»

Автор Лисицына Елена Федоровна.

учитель математики

МБОУ «Гимназия№11»

г. Бийска Алтайского кр.

Методы отбора корней в тригонометрических уравнениях

или

Ох уж эта тригонометрия!

Решение тригонометрических уравнений и отбор корней, принадлежащих заданному промежутку — это одна из сложнейших тем математики, которая выносится на Единый Государственный Экзамен в течение уже более 10лет. По результатам анкетирования многие учащиеся затрудняются или вообще не умеют решать тригонометрические уравнения и особенно затрудняются в отборе корней, принадлежащих промежутку. Необходимо также знать тригонометрические формулы, табличные значения тригонометрических функций для решения еще целого ряда заданий Единого Государственного Экзамена по математике. Постоянно работая в 10-11 классах, я регулярно сталкивалась с определенными проблемами при работе с вышеуказанным разделом тригонометрии: долго не могла установить баланс между доступностью изложения материала и достаточностью обоснований развернутого решения этой категории заданий. В моей практике были случаи, когда вполне успевающие по математике учащиеся начинали испытывать неуверенность и просто страх при решении тригонометрических уравнений с отбором корней, будь то принадлежность корней области допустимых значений переменной или указанному в задании промежутку. В результате целенаправленной многолетней работы в этом направлении у меня сложилась определенная методика работы с данным разделом, которая оказалась довольно успешной, что подтверждает следующая таблица результатов выполнения учащимися задания №13 профильного ЕГЭ по математике с 2015 по 2021 г.г. ( в % от общего количества учеников 11-х классов гимназии, сдающих профильный ЕГЭ по математике)

В тригонометрическом уравнении отбор корней можно осуществлять следующими способами: арифметическим, алгебраическим, геометрическим и функционально-графическим.

Арифметический способ отбора корней состоит в непосредственной подстановке полученных корней в уравнение, учитывая имеющиеся ограничения, при переборе значений целочисленного параметра.

Алгебраический способ предполагает составление неравенств, соответствующих дополнительным условиям, и их решение относительно целочисленного параметра.

Геометрический способ предполагает использование при отборе корней двух вариантов: тригонометрического круга или числовой прямой. Тригонометрический круг более удобен, когда речь идет об отборе корней на промежутке или в случае, когда значение обратных тригонометрических функций, входящих в решения, не являются табличными. Числовую прямую удобно использовать при отборе корней на промежутке, длина которого превосходит полный оборот или требуется найти наибольший отрицательный или наименьший положительный корень уравнения.

Функционально-графический способ предполагает отбор корней осуществлять с использование графиков тригонометрических функций. Чтобы использовать данный способ отбора корней, требуется умение схематичного построения графиков тригонометрических функций.

Моя практика показала, что чаще всего можно обойтись применением тригонометрического круга при отборе корней , а в случае, если промежуток превышает по длине полный оборот- алгебраическим способом. При этом, безусловно, следует познакомить учащихся и с остальными способами. Таким образом, работа над данным разделом разделилась у меня на следующие этапы:

1)Знакомство с устройством тригонометрического круга и отработка умений находить числа и промежутки на нем в ходе выполнения следующих упражнений:

2)Отработка навыков работы с тригонометрическим кругом при решении простейших тригонометрических уравнений с отбором корней , которая предполагает выполнение большого количества упражнений по типу приведенных ниже:

3)Отбор корней в одном и том же уравнении разными способами, чтобы учащиеся имели возможность выбора в соответствии со своими предпочтениями, например

Например,
а) Решить уравнение cos2x=sin(π/2+x).
б) Найдите все корни этого уравнения, принадлежащие промежутку [–7π/2; –2π].

Решим пункт а)Воспользуемся формулой приведения для синуса sin(π/2+x) = cos(x);cos2x = cosx ;
cos2x – cosx = 0; cosx(cosx – 1) = 0, т.е.

Решим пункт б).

I . Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [–7π/2; –2π], находим целые значения для n.
–7π/2 ≤ π/2 + πn ≤ –2π;

Сразу делим все на π или умножаем на 1/ π
–7/2 ≤ 1/2 + n ≤ –2;
–7/2 – 1/2 ≤ n ≤ –2 – 1/2 ;
–4 ≤ n ≤ –5/2.
Целые n в этом промежутке это: n=–4 n= –3.

Значит, корни, принадлежащие этому промежутку, будут следующие:

х= π/2 + π(–4) = –7π/2; х=π/2 + π(–3) = –5π/2.
Аналогично решаем еще два неравенства:
–7π/2 ≤ π/4 + 2πk ≤ –2π;
–15/8 ≤ k ≤ –9/8.
Получили, что целых k в этом промежутке нет.
–7π/2 ≤ –π/4 + 2πm ≤ –2π;
–13/8 ≤ m ≤ –7/8.
Получили одно целое n в этом промежутке, m =–1. Значит, отобранный корень на этом промежутке имеет вид: х= –π/4 + 2π·(–1) = –9π/4.
Ответ: –7π/2, –5π/2, –9π/4.

II. Отбор корней с помощью тригонометрической окружности.

Чтобы использовать этот способ надо понимать, как работать с окружностью. Так как функции синус, косинус, тангенс и котангенс периодичны, то окружность, можно обходить бесконечное число раз.

«Обойдем» окружность один раз против часовой стрелки (положительное направление, т.е. значения будут положительные)

«Обойдем» окружность два раза против часовой стрелки (положительное направление т.е. значения будут положительные)

«Обойдем» 1 раз по часовой стрелки (отрицательное направление, т.е. значения будут отрицательные)

Вернемся к вопросу об отборе корней на промежутке

[–7π/2; –2π].
Чтобы попасть к числам –7π/2 и –2π надо «обойти» окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = π/2 + πn. Какой приблизительно должен быть n, чтобы значение x было где–то в этом промежутке? Предположим n= –2, получаем х=π/2 – 2π = –3π/2, очевидно, это не входит в наш промежуток. Значит, берем меньше n=–3, то х= π/2 – 3π = –5π/2, это подходит. Попробуем еще n=–4, то х=π/2 – 4π = –7π/2, также подходит.
Рассуждая аналогично для х=π/4 + 2πk, k ∈ Z и х=–π/4 + 2πm, m ∈ Z находим еще один корень x=–9π/4.

После того, как отбор корней произвели разными способами, прошу проанализировать преимущества каждого из них, получились, в частности такие итоги: первый способ (с помощью неравенств) гораздо надежнее и намного проще для понимания, но нужно уметь решать простейшие неравенства. Если действительно серьезно разобраться с тригонометрической окружностью, то отбор корней по второму методу будет гораздо быстрее. Плюс экономия времени на экзамене.

4)Проведение смотра знаний по данной теме в форме математической игры «Своя игра»

(идея заимствована здесь https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia )

5)Рассмотрение реальных работ участников ЕГЭ прошлых лет, оцененных экспертами, с целью нахождения ошибок при выполнении отбора корней в тригонометрических уравнениях, например оценка эксперта-1 балл. Почему не засчитано решение п.б)?

Вывод: отбор корней нельзя назвать обоснованным, так как перебор остановлен на корне принадлежащем отрезку.

Вывод: при отборе корней отсутствует решение и ошибочно указано число, которое не является корнем тригонометрического уравнения.

В заключение отмечу, что поскольку задание № 13 (или №12 в модели профильного ЕГЭ 2022 года) является самым простым из заданий с развернутым решением, то целенаправленная работа над ним дает возможность большему числу выпускников успешно справиться с ним и получить высокий результат на экзамене.

Список используемых ресурсов:

1. Виленкин Н. Я. Алгебра и математический анализ 10 класс. Учебник для углубленного изучения математики в общеобразовательных учреждениях, Издательство Мнемозина, 13-е изд. стереотипное, 2006. — 336с.

2. Гельфанд И.М., Львовский С.М., Тоом А.Л. Тригонометрия, М. : МЦНМО, 2003.-7-16 с.

3. Захарова, И. Г. Информационные технологии в образовании: учебное пособие для студ. пед. учеб. заведений/ И. Г. Захарова,– М.: Издательский центр «Академия», 2003. – 192 с.

4. Звавич В.И., Пигарев Б.П. Тригонометрические уравнения (решение уравнений + варианты самостоятельных работ)//Математика в школе.№3, С.18-27.

5. А.Н. Колмагорова Алгебра и начала анализа. Учебник для 10-11 классов общеобразовательных учреждений, 17-е изд. – М. : Просвещение, 2008. — 384 с.

6. Королев С.В. Тригонометрия на экзамене по математике, изд. Экзамен, 2006. – 254 с.

7. Марасанов А.Н. О методологическом подходе в обучении тригонометрии/ Н.И. Попов, А.Н. Марасанов// Знание и понимание. Умение. -2008. — №4. — 139-141 с.

8. Марасанов А.Н. Тригонометрия: учебное пособие, 2-е изд., испр и доп. (Н.И. Попов, А.Н. Марасанов.-Йошкар-Ола; Мар. гос. Ун-т, 2009.-114с.)

9. Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И., Суворова С.Б. Тригонометрия. 10 класс, М. : Просвещение, 2008. – 61 с.

10. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 1.Учебник для учащихся общеобразовательных учреждений(базовый уровень). – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил.

11. Мордкович А.Г. Алгебра и начала анализа.10-11 классы. Часть 2. Задачник для учащихся общеобразовательных учреждений(базовый уровень), – 10-е изд., стер. – М. : Мнемозина, 2009. – 399 с.:ил. 69

12. Мирошин В. Отбор корней в тригонометрических уравнениях.//Математика. Приложение к газете «Первое сентября» №17, 2006г.

13. Просветов Г.И. Тригонометрия. Задачи и решения, Альфа-Пресс, 2010. – 72 с.

14. Решетников Н.Н. Тригонометрия в школе: М. Педагогический университет «Первое сентября», 2006, лк 1.

15. Смоляков А.Н., Севрюков П.Ф. Приемы решения тригонометрических уравнений//Математика в школе. 2004. №1. С.24-26.

16. Шабашова О.В. Приемы отбора корней в тригонометрических уравнениях//Математика в школе. 2004. №1. С.20-24.

17. https://ppt-online.org/491236

18. Методические материалы для председателей и членов предметных комиссий субъектов Российской Федерации по проверке выполнения заданий с развёрнутым ответом экзаменационных работ ЕГЭ 2022 года. МАТЕМАТИКА. Федеральный институт педагогических измерений, 2022

19. https://kopilkaurokov.ru/matematika/uroki/okh-uzh-eta-trighonomietriia