From Wikipedia, the free encyclopedia
John Herschel, Description of a machine for resolving by inspection certain important forms of transcendental equations, 1832
In applied mathematics, a transcendental equation is an equation over the real (or complex) numbers that is not algebraic, that is, if at least one of its sides describes a transcendental function.[1]
Examples include:
A transcendental equation need not be an equation between elementary functions, although most published examples are.
In some cases, a transcendental equation can be solved by transforming it into an equivalent algebraic equation.
Some such transformations are sketched below; computer algebra systems may provide more elaborated transformations.[2]
In general, however, only approximate solutions can be found.[3]
Transformation into an algebraic equation[edit]
Ad hoc methods exist for some classes of transcendental equations in one variable to transform them into algebraic equations which then might be solved.
Exponential equations[edit]
If the unknown, say x, occurs only in exponents:
- applying the natural logarithm to both sides may yield an algebraic equation,[4] e.g.
transforms to
, which simplifies to
, which has the solutions
- This will not work if addition occurs «at the base line», as in
- if all «base constants» can be written as integer or rational powers of some number q, then substituting y=qx may succeed, e.g.
transforms, using y=2x, to
which has the solutions
, hence
is the only real solution.[5]
- This will not work if squares or higher power of x occurs in an exponent, or if the «base constants» do not «share» a common q.
- sometimes, substituting y=xex may obtain an algebraic equation; after the solutions for y are known, those for x can be obtained by applying the Lambert W function,[citation needed] e.g.:
transforms to
which has the solutions
hence
, where
and
the denote the real-valued branches of the multivalued
function.
Logarithmic equations[edit]
If the unknown x occurs only in arguments of a logarithm function:
- applying exponentiation to both sides may yield an algebraic equation, e.g.
transforms, using exponentiation to base
to
which has the solutions
If only real numbers are considered,
is not a solution, as it leads to a non-real subexpression
in the given equation.
- This requires the original equation to consist of integer-coefficient linear combinations of logarithms w.r.t. a unique base, and the logarithm arguments to be polynomials in x.[6]
transforms, using
to
which is algebraic and can be solved.[clarification needed] After that, applying inverse operations to the substitution equation yields
Trigonometric equations[edit]
If the unknown x occurs only as argument of trigonometric functions:
transforms to
, and, after substitution, to
which is algebraic[9] and can be solved. After that, applying
obtains the solutions.
Hyperbolic equations[edit]
If the unknown x occurs only in linear expressions inside arguments of hyperbolic functions,
- unfolding them by their defining exponential expressions and substituting
yields an algebraic equation,[10] e.g.
unfolds to
which transforms to the equation
which is algebraic[11] and can be solved. Applying
obtains the solutions of the original equation.
Approximate solutions[edit]
Graphical solution of sin(x)=ln(x)
Approximate numerical solutions to transcendental equations can be found using numerical, analytical approximations, or graphical methods.
Numerical methods for solving arbitrary equations are called root-finding algorithms.
In some cases, the equation can be well approximated using Taylor series near the zero. For example, for 




For a graphical solution, one method is to set each side of a single-variable transcendental equation equal to a dependent variable and plot the two graphs, using their intersecting points to find solutions (see picture).
Other solutions[edit]
See also[edit]
- Mrs. Miniver’s problem – Problem on areas of intersecting circles
References[edit]
- ^ I.N. Bronstein and K.A. Semendjajew and G. Musiol and H. Mühlig (2005). Taschenbuch der Mathematik (in German). Frankfurt/Main: Harri Deutsch. Here: Sect.1.6.4.1, p.45. The domain of equations is left implicit throughout the book.
- ^ For example, according to the Wolfram Mathematica tutorial page on equation solving, both
and
can be solved by symbolic expressions, while
can only be solved approximatively.
- ^ Bronstein et al., p.45-46
- ^ Bronstein et al., Sect.1.6.4.2.a, p.46
- ^ Bronstein et al., Sect.1.6.4.2.b, p.46
- ^ Bronstein et al., Sect.1.6.4.3.b, p.46
- ^ Bronstein et al., Sect.1.6.4.3.a, p.46
- ^ Bronstein et al., Sect.1.6.4.4, p.46-47
- ^ over an appropriate field, containing
and
- ^ Bronstein et al., Sect.1.6.4.5, p.47
- ^ over an appropriate field, containing
- ^ V. A. Varyuhin, S. A. Kas’yanyuk, “On a certain method for solving nonlinear systems of a special type”, Zh. Vychisl. Mat. Mat. Fiz., 6:2 (1966), 347–352; U.S.S.R. Comput. Math. Math. Phys., 6:2 (1966), 214–221
- ^ V.A. Varyukhin, Fundamental Theory of Multichannel Analysis (VA PVO SV, Kyiv, 1993) [in Russian]
- John P. Boyd (2014). Solving Transcendental Equations: The Chebyshev Polynomial Proxy and Other Numerical Rootfinders, Perturbation Series, and Oracles. Other Titles in Applied Mathematics. Philadelphia: Society for Industrial and Applied Mathematics (SIAM). doi:10.1137/1.9781611973525. ISBN 978-1-61197-351-8.
Постановка задачи. Основные определения из алгебры нелинейных и трансцендентных уравнений.
Уравнение, не сводящееся к алгебраическому уравнению с помощью алгебраических преобразований, называется трансцендентным уравнением.
Простейшими трансцендентными уравнениями являются показательные, логарифмические и тригонометрические уравнения.
Под алгебраическими преобразованиями уравнения F=0 понимают следующие преобразования:
1) прибавление к обеим частям уравнения одного и того же алгебраического выражения;
2) умножение обеих частей уравнения на одно и то же алгебраическое выражение;
3) возведение обеих частей уравнения в рациональную степень.
Алгебраическим уравнением называется уравнение вида
где Рn – многочлен n-ой степени от одной или нескольких переменных.
Трансцендентная функция– функция, не являющаяся алгебраической функцией.
Трансцендентное уравнение – уравнение, содержащее неизвестное в аргументе некоторой трансцендентной функции, например: 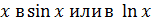
Алгебраическая функция – : 1. Функция от одного переменного 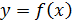
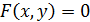
2.Функция от n переменных 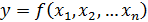
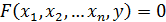
Рассмотрим нелинейное уравнение одной независимой переменной x,
f(x)=0, x 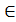
где f(x) – любая нелинейная или трансцендентная функция, например, 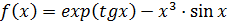
Нахождение корней уравнения (1) производится в два этапа:
1. Отделение корней – это нахождение таких интервалов по аргументу x, внутри каждого из которых существует только один корень уравнения (1).
2. Уточнение корней заключается в применении некоторого итерационного метода, в результате которого корень уравнения (1) может быть получен с любой наперед заданной точностью ε.
Уравнения. Системы уравнений
Цель лекции: познакомиться с основными возможностями, принципами и средствами Mathematica для решения алгебраических и дифференциальных уравнений, систем уравнений.
8.0. Введение
Доступ к множеству оригинальных алгоритмов при помощи встроенных функций, широчайшие возможности символьного и графического представления результатов делают Mathematica эффективным инструментом аналитического и численного решения уравнений. В данной лекции мы познакомимся с основными функциями Mathematica, применяемыми для нахождения решений алгебраических, трансцендентных и дифференциальных уравнений, а также систем уравнений. В этом нам помогут книги Е. М. Воробьёва [1] и А.Н. Прокопени [5].
8.1. Нахождение символьных решений алгебраических и трансцендентных уравнений
Наиболее часто используемая функция для решений уравнений — Solve . Она позволяет находить решения полиномиальных уравнений вплоть до чётвёртого порядка, некоторых полиномиальных уравнений высших порядков, а также неполиномииальных уравнений (А. Н. Прокопеня и А. В. Чичурин [5, с. 28]). В простейшем случае для решения одного уравнения lhs==rhs ( lhs и rhs — левая и правая части уравнения, соответственно) с одной неизвестной var функция задаётся в виде Solve[lhs==rhs,var] (пример In[1] на рис. 8.1). Корни уравнения выдаются в виде вложенного списка правил замены в виде подстановок (см. Out[1] )
Для того чтобы решить при помощи этой функции систему уравнений, нужно задать оба обязательных аргумента в виде списков уравнений и переменных, т. е., записать функцию как Solve[,] . Уравнения также можно отделять друг от друга логическим оператором && (логическим умножением).
В примере In[2] на рис. 8.1 мы решили систему уравнений. Обратим внимание на то, в каком виде мы получаем корни системы. В Out[2] мы получаем вложенный список , элементами которого являются одномерные списки. Каждый одномерный список в качестве элементов содержит пару корней системы уравнений.
Для того чтобы была возможность в дальнейшем производить манипуляции с корнями уравнения или системы уравнений, следует от вложенного списка правил преобразований перейти к одномерному списку корней уравнения или системы уравнений. Делается это при помощи уже известного нам оператора » /. «. Так в примере In[3] на рис. 8.1 мы присвоили выражению xroots список корней системы уравнений в In[2] для переменной x .
Обратиться к конкретному корню уравнения или системы уравнений теперь можно, пользуясь навыками работы со списками. Так в примере In[4] на рис. 8.1 мы вывели на экран первое правило подстановки из списка, полученного в результате решения уравнения In[2] , а в In[5] — второй в списке набор корней этого же уравнения с учётом преобразования In[3] .
Если Mathematica не может представить решение полиномиального уравнения в аналитическом виде, например, в случае, если полином в уравнении имеет степень выше четвёртой, то корни таких уравнений представляются программой при помощи Root -объектов (А. Н. Прокопеня и А. В. Чичурин [5, с. 29]). Такой объект в виде Root[f,k] представляет точное значении корня с номером k полиномиального уравнения f[x]==0 . Пример полученных в таком виде решений — Out[1] на рис. 8.2.
В примере In[1] на рис. 8.2 мы находили решение уравнения, заданного в общем виде. Если все коэффициенты уравнения имеют численные значения (как в примере In[2] ), то получить численные значения корней не составляет труда при помощи функции N — пример In[3] .
В предыдущих примерах обсуждались возможности функции Solve применительно к алгебраическим уравнениям. В примере In[1] на рис. 8.3 мы попробовали решить с её помощью трансцендентное уравнение 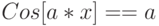
Как мы видим в Out[1] на рис. 8.3, для нашего трансцендентного уравнения Mathematica также сумела найти корень. Мы знаем, что на самом деле такое уравнение имеет бесконечное число корней, отличающихся на 
Однако в ряде случаев Mathematica оказывается бессильной найти корни трансцендентного уравнения в символьном виде. Тогда она выдаёт сообщение, в котором честно признаётся в своём бессилии и рекомендует попробовать решить уравнение неалгебраическими (численными) методами (см. пример In[2] на рис. 8.3).
Что такое Трансцендентность
Значение трансцендентности
Трансцендентность (от лат. transcendens – превосходящий, выходящий за пределы) — это всё то, что выходит за пределы познания мира через органы чувств; предмет метафизического и религиозного учения.
Антонимы слова трансцендентный — эмпирический, познаваемый, опытный. Синонимы слова трансцендентный — непознаваемый, запредельный.
Различия между трансцендентальный и трансцендентный
Трансцендентальное — по мнению философа Иммануила Канта, это касается предшествующих форм изучения (до опыта), не относится к предмету или содержанию познания. Например: время, пространство, причинность.
Трансцендентным, по мнению Канта, было всё то, что выходило за грань познания опытом.
Например, в системе Канта трансцендентными называются «вещи в себе» (или «вещь сама по себе»). Так Иммануил Кант обозначал вещи непознаваемыми — они существуют сами по себе, независимо от того, чем они являются для нас.
Трансцендентальным Кант называет всё то, что относится к априорным условиям опыта, вдобавок те знания, которые могут выйти из этого опыта.
В своих трудах Кант называет трансцендентальным всякое познание, которое появляется больше из изучения видов познания предметов, чем самих предметов. И это познание возможно лишь до опыта.
Трансцендентально — всё то, что является частью опыта и делает возможным его эмпирическое познание. Трансцендентно — всё то, что выходит за рамки опыта.
Трансцендентальное — это как противоположность трансцендентному.
Трансцендентные и имманентные причины и действия
В схоластике (средневековая христианская философия, которая стремилась обосновать религиозные догматы) различали имманентные и трансцендентные причины и действия. Имманентные случаются в самих объектах, трансцендентные существуют за гранью их реального бытия.
Трансцендентность и имманентность Бога
На первый взгляд трансцендентность и имманентность противоречат друг другу. Однако, если вдуматься в оба понятия и идею Бога, можно понять смысл этого выражения.
Трансцендентное — это то, что находится за пределами восприятия, независимо от Вселенной. И если сравнивать, это совершенно от нас отличается. В противовес этому существует понятие «имманентный Бог» — это тот, который существует внутри нас, внутри Вселенной и т. д. Что означает, что Он является частью нашего существования.
Что такое трансценденция?
Трансценденция — это философский термин, который означает «переступать через сущее»; это основная структура субъективности. Трансценденция превосходит всё, что означает, что она не имеет сущности.
Трансцендентное состояние
В медитации существует такое понятие как «Трансцендентное состояние». Это когда сознание выходит за рамки нормальных трёх состояний сознания, которые известны нам в обычной жизни (бодрствование, сон со снами, крепкий сон).
Эти считаются уровнями возбуждённого состояния, и когда человек их трансцендирует, его разум переходит стесняющие его границы. Таким образом он проникает на более углублённые, безмятежные и мощные ступени познания.
Трансцендентность в математике
Это понятие также существует в математике.
Трансцендентное уравнение
Уравнения, которые не попадают в категорию алгебраических уравнений называются трансцендентными уравнениями. Это уравнение, где есть трансцендентные функции. Например: tan x – e× = 0.
Трансцендентная функция
Это элементарная функция (аналитическая), которая не является алгебраической функцией. Например, функция sin(x).
Трансцендентное число
Это (возможно, комплексное) число, которое не является корнем любого целочисленного полинома. Это означает, что это число не является алгебраическим (ни в какой степени).
Любое трансцендентное число также является иррациональным (т. к. рациональное число — это алгебраическое число в первой степени, а этого быть не может).
Примеры трансцендентных чисел включают π (Пи) и e (число Эйлера).
Узнайте также, что такое Экспонента и Число Пи.
http://intuit.ru/studies/courses/4765/1039/lecture/15749
http://www.uznaychtotakoe.ru/transcendentnost/
Уравнение
F(x)=0
называется трансцендентным, если хотя
бы одна из функций в нем не является
алгебраической.
Пример
(6.4)
Регулярных
аналитических методов решения
трансцендентных уравнений не существует.
В каждом конкретном случае ищется свой
индивидуальный прием.
Общим
является только графический метод,
состоящий в построении графика функций
F(x).
Точки
пересечения построенного графика с
осью абсцисс и есть искомые действительные
корни уравнения.
В
среде MathCAD
возможны два способа нахождения корней
уравнения (6.4)
-
с
помощью методов символьной математики
согласно правилу 6; -
с
помощью встроенной функции root
в подменю f(x)
меню «Вставка» согласно правилу 2.
Рассмотрим
применение обоих методов на примере
нахождения корней уравнения (6.4).
Поскольку
неизвестно решение (значения х,
при которых F(x)=0),
то строим его график с целью приблизительного
определения искомого действительного
решения.
х
:= -10 … +10
Рис.
6.35
Графическое решение
Из
графика видно, что это решение, определяемое
как точка пересечения графика с осью
абсцисс, лежит в промежутке значений
х
= 2…3.
Решение
по правилу 6
Записываем
многочлен из уравнения (6.4):
Выделяем
(затемняем ■) в этом многочлене в любом
месте символ переменной х
– путем протаскивания курсора.
Открываем
меню «Символ», подменю «Переменные» и
делаем щелчок по опции «Вычислить».
На
рабочем листе получается результат:
Решение
по правилу 2:
Записываем
уравнение:
Вводим
любое имя искомого решения и знак
присвоения, например:
r
:= ,
после
которого размещаем красный визир ±.
Обращаемся
к пиктограмме «Встроенная функция f(x)»
на 2-ой строке текстового окна –
стандартной линейке.
На
появившемся после щелчка диалоговом
окне в разделе «Категория функций»
выбираем строку с надписью «Решение»,
а в разделе «Название функций» — root
(корни). После нажатия на кнопку «ок»
или «Вставить» на рабочем листе появляется
название данной функции с четырьмя
черными прямоугольниками, которые
следует заполнить:
r
:=
root
(■, ■, ■, ■)
В
первое окошко вписываем имя функций
F(x),
во второе – переменную х,
в третье и четвертое – (а) нижний и (в)
верхний пределы, внутри которых ищется
решение. Запись приобретает вид:
r:
= root
(F(x),
x,
a,
в)
,
(пределы
согласно рисунку 6.1 установлены 0 и 3).
Вновь
вводим искомое решение, но теперь со
знаком равенства:
r
=
,
и
сразу получаем результат.
r
= 2,8267802
Точность
полученного результата устанавливаем
путем открытия меню «Формат», подменю
«Результат» и выбора требуемого числа
десятичных знаков в открывшемся окне.
Проводим
проверку полученного результата, для
чего вычисляем значение функции F(x)
при найденном значении корня.
x
:= 2.8267802
F(x)
= 2.287 · 10-7
Близость
к нулю функции F(x)
указывает на правильность полученного
результата.
6.
Вычисления по циклу
При
решении самых разнообразных
научно-технических задач возникает
необходимость в определении зависимости
функции от одного или нескольких
аргументов. Например, необходимо
рассчитать мощность радиосигнала в
зависимости от расстояния или колебательный
процесс в электрическом контуре.
При
этом результаты расчета следует
представить в виде массива чисел,
заключив их в определенную таблицу.
При
подобных многократных расчетах по одной
и той же формуле или алгоритму следует:
-
во-первых,
выбрать «шаг» или дискрет изменения
аргумента; -
во-вторых,
определить точность, с которой требуется
рассчитывать значение того или иного
параметра.
Иногда
требуется рассчитать десятки, сотни и
даже тысячи значений одной и той же
функции в зависимости от значения
аргумента.
В
подобных случаях экономный путь решения
задачи состоит в организации расчета
в рамках определенного цикла.
В
таком цикле автоматическое обращение
к функции производится согласно зашитому
в программу алгоритму.
При
этом пользователь указывает только
шаг, точность и количество вариантов
расчета.
Самый
простой способ организации циклического
расчета состоит в использовании оператора
цикла «m…n»,
пиктограмма которого расположена на
математической панели инструментов
«Матрица».
После
вызова щелчком этого оператора в него
следует ввести значения нижнего и
верхнего пределов:
k
:= M…N,
где
k
– дискретно на 1 изменяемый параметр,
последовательно принимающий целые
значения от M≥0
до N.
Причем при M<0
все значения функции при 0≤k<M
принимают значения, равные 0.
Аргумент
при циклическом расчете изменяется с
«шагом» (дискретом) ∆, значение которого
может быть выбрано любым.
Пример
циклического расчета
Рассчитать
с «шагом»

описываемый функцией:

при
А = 10, α = 0,5, F
= 10 и N
= 1000.
Организуем
цикл расчета с помощью записи k
:= 0…N
и выражений для аргумента tk
и дискретной функции Yk(tk),
полученной из непрерывной
функции Y(t).
Строим
график дискретной функции
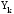
Рис.6.36
График дискретной функции
Вывод
в виде таблицы дискретных значений

или

По
умолчанию на рабочий лист выводится 16
значений функции.
Щелкнув
по графику функции, обрамляют ее рамкой
и путем протаскивания вниз курсора
расширяют таблицу до любого требуемого
значения k≤N.
При
протаскивании курсора вверх таблица
наоборот сжимается.
Таким
же образом можно вывести и таблицу
значений аргумента, сделав в рассматриваемом
случае запись

7.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нахождение точных корней алгебраического или трансцендентного уравнения (т.е. уравнения неалгебраического, например, тригонометрического, логарифмического или иррационального) является зачастую достаточно сложной задачей, не решаемой аналитически с помощью конечных формул. Кроме того, иногда на практике уравнение содержит коэффициенты, значения которых заданы приблизительно, так что говорить о точном решении уравнений в таких случаях вообще не имеет смысла. Поэтому задачи приближенного определения корней уравнения и соответствующей оценки их точности имеют важное значение и в наши дни.
Приближенные методы решения уравнений можно условно разделить на графические и численные. Мы ограничимся рассмотрением численных методов решения.
Рассмотрим уравнение:
(1)
где функция F( x ) – непрерывна и определена на некотором интервале
В ряде случаев потребуется существование и непрерывность первой и второй производных этой функции: , что каждый раз будет оговариваться особо.
Всякое значение , при котором F( x ) обращается в нуль:
(2)
называется корнем уравнения (1) или нулем функции F( x ).
Будем считать, что уравнение (1) имеет только изолированные корни, т.е. для каждого корня уравнения (1) существует окрестность, не содержащая других корней этого уравнения. Процесс отделения корней подробно описан в литературе [1, 2] и здесь не рассматривается.
Приближенное нахождение изолированных действительных корней выполняется в два этапа:
1) Нахождение приближенного значения корня – так называемого нулевого приближения.
2) Уточнение приближенного значения корня до тех пор, пока не будет достигнута заданная точность решения, путем итераций или последовательных приближений.
Остановимся подробно на втором этапе, так как нахождение нулевого приближения является специфической задачей, решаемой обычно либо на основе физических соображений или конструктивных особенностей, либо путем графического решения уравнения.
Трансцендентное уравнение — уравнение, не являющееся алгебраическим. Обычно это
уравнения, содержащие показательные, логарифмические, тригонометрические, обратные
тригонометрические функцииcos x = x {displaystyle cos x=x}
-
lg x = x − 5 {displaystyle lg x=x-5} 2 x = lg x + x 5 + 40 {displaystyle 2^{x}=lg x+x^{5}+40}
7.2 Решение трансцендентных уравнений
Уравнение, в котором неизвестное входит в аргумент трансцендентных функций, называется трансцендентным уравнением. К трансцендентным уравнениям принадлежат показательные, логарифмические, тригонометрические.
Для решения трансцендентных уравнений вида 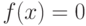

![fzero(name, [a, b])](https://intuit.ru/sites/default/files/tex_cache/5fff2a3e9373b95b078fec50acd24f67.png)
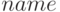
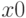
![[a, b]](https://intuit.ru/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png)
Если функция вызывается в формате: ![[x, y] = fzero(name, x0)](https://intuit.ru/sites/default/files/tex_cache/2562efaafed3bb64258ee94f5d6ac5c0.png)



Пример 7.14. Найти решение уравнения:
Начнём решение данного трансцендентного уравнения с определения интервала изоляции корня. Воспользуемся для этого графическим методом. Построим график функции, указанной в левой части уравнения (листинг 7.15), создав предварительно функцию для её определения.
% Функция для вычисления левой части уравнения f(x)=0
function y=f1(x)
y=((2-x-3).^2).^(1/3)-((x-1).^2).^(1/3);
end;
% Построение графика функции f(x)
cla; okno1=figure();
x = -1:0.1:3;
y=f1(x);
pol=plot(x, y);
set(pol, ’LineWidth’, 3, ’Color’, ’k’)
set(gca, ’xlim’, [-1, 3]); set(gca, ’ylim’, [-1,1.5]);
set(gca, ’xtick’, [-1:0.5:3]); set(gca, ’ytick’,[-1:0.5:1.5]);
grid on; xlabel(’x’); ylabel(’y’);
title(’Plot y=(2x-3)^{2/3}-(x-1)^{2/3}’);
Листинг
7.15.
Графическое отделение корней (пример 7.14).
На графике (рис. 7.3) видно, что функция 
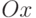
Уточним корни, полученные графическим методом. Воспользуемся функцией, вычисляющей левую часть заданного уравнения из листинга 7.15 и обратимся к функции 
>>> x1=fzero(’f1’, 1.5) x1 = 1.3333
Теперь применим функцию 
>>> x2=fzero(’f1’, [1.52.5]) x1= 2
Не трудно заметить, что и в первом и во втором случае функция 
Рис.
7.3.
Графическое решение примера 7.14
Ниже приведён пример некорректного обращения к функции 
>>>fzero(’f1’, [1 3]) error: fzero: not a valid initial bracketing error: called from: error: /usr/share/octave/3.4.0/m/optimization/fzero.m at line 170, column 5
В следующем листинге приведён пример обращения к функции 
>>> [X(1),Y(1)]= fzero(’f1’, [1 1.5]); >>> [X(2),Y(2) ]= fzero(’f1’, [1.5 2.5]); >>> X % Решение уравнения X = 1.3333 2.0000 >>> Y % Значения функции в точке Х Y = -2.3870e-15 0.0000e+00
Пример 7.15. Найти решение уравнения 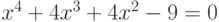
Как видим, левая часть уравнения представляет собой полином. В примере 7.13 было показано, что данное уравнение имеет четыре корня: два действительных и два мнимых (листинг 7.14).
Листинг 7.16 демонстрирует решение алгебраического уравнения при помощи функции 
function y=f2(x) y=x.^4+4-x.^3+4-x.^2-9; end; >>> [X(1),Y(1)]= fzero(’f2’, [-4 -2]); >>> [X(2),Y(2)]= fzero(’f2’, [0 2]); >>> X >>> Y X = -3 1 Y = 0 0
Листинг
7.16.
Решение уравнения с помощью fzero (пример 7.15).























































![sqrt[3]{(2x-3)^2}- sqrt[3]{(x-1)^2}=0.](https://intuit.ru/sites/default/files/tex_cache/2797184839ebd07b7f8e224ba3830f7f.png)
