Как найти корни уравнение через неравенство

Отбор корней с помощью двойного неравенства

Для того, чтобы отобрать корни при решении тригонометрических уравнений использую двойные неравенства. Мы ставим серию ответов в двойное неравенство, которое определяется заданным промежутком и ищем подходящие корни. Этот метод максимально прост. Все, что требует при отборе корней данным методом – уметь решать двойные неравенства. Но у этого есть и обратная сторона. При работе с двойными неравенствами можно совершить ошибку по невнимательности.

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ДВОЙНОГО НЕРАВЕНСТВА:

1. Полученное решение записываем в двойное неравенство, определяющее заданный промежуток.

2. Решаем неравенство относительно n. Мы знаем, что n – количество периодов, которое может быть только целым числом. Если n попадает в промежуток, где нет целых чисел, тогда данная серия ответов не подходит.

3. Подставляем полученное n в серию ответов и находим нужные углы.

Пример:

Даны корни уравнения:

(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})

(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})

Найдите корни, принадлежащие отрезку(leftlbrack — pi, frac{3pi}{2} rightrbrack)

1. Составим двойное неравенство с первой серией ответов:

(- pi leq frac{pi}{3} + 2pi n leq frac{3pi}{2})

1. Решим двойное неравенство. Так как нам нужно выразить n, которое находится в середине двойного неравенства, будет постепенно убирать из этой части слагаемые и множители. Вычтем из каждой части неравенства слагаемое (frac{pi}{3}):

(- pi — frac{pi}{3} leq 2pi n leq frac{3pi}{2} — frac{pi}{3})

(- frac{4pi}{3} leq 2pi n leq frac{8pi}{6})

1. Теперь избавимся от лишнего множителя посередине. Поделим каждую часть неравенства на (2pi):

(- frac{4pi}{3 bullet 2pi} leq n leq frac{8pi}{6 bullet 2pi})

(- frac{2}{3} leq n leq frac{2}{3})

1. Таким образом единственное целое значение (n), которое попадает в данный промежуток – это (n = 0). Подставим в серию ответом это значение n и найдем угол:

(x_{1} = frac{pi}{3} + 2pi n = frac{pi}{3})

1. Аналогично составим и решим двойное неравенство со второй серией ответов:

(- pi leq frac{2pi}{3} + 2pi n leq frac{3pi}{2})

1. Вычтем слагаемое (frac{2pi}{3}) из каждой части уравнения:

(- pi — frac{2pi}{3} leq 2pi n leq frac{3pi}{2} — frac{2pi}{3})

(- frac{5pi}{3} leq 2pi n leq frac{5pi}{6})

1. Поделим каждую часть уравнения на (2pi)

(- frac{5pi}{3 bullet 2pi} leq n leq frac{5pi}{6 bullet 2pi})

(- frac{5}{6} leq n leq frac{5}{12})

1. Мы получили промежуток, в котором n также принимает единственное целое значение, когда (n = 0.) Найдем угол, зная, чему равно n:

(x_{2} = frac{2pi}{3} + 2pi n = frac{2pi}{3})

Ответ: (frac{pi}{3};frac{2pi}{3}).

В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.

а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]

Решим пункт а.

Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)

sqrt(2)cos^2x = cosx

sqrt(2)cos^2x — cosx = 0

cosx(sqrt(2)cosx — 1) = 0

cosx = 0

x1 = Pi/2 + Pin, n ∈ Z

sqrt(2)cosx — 1 = 0

cosx = 1/sqrt(2)

cosx = sqrt(2)/2

x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Z

x2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ Z

Решим пункт б.

1) Отбор корней с помощью неравенств

Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.

-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi

Сразу делим все на Pi

-7/2 меньше или равно 1/2 + n меньше или равно -2

-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2

-4 меньше или равно n меньше или равно -5/2

Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2

Аналогично делаем еще два неравенства

-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8

Целых n в этом промежутке нет

-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8

Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.

Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4

2) Отбор корней с помощью тригонометрической окружности

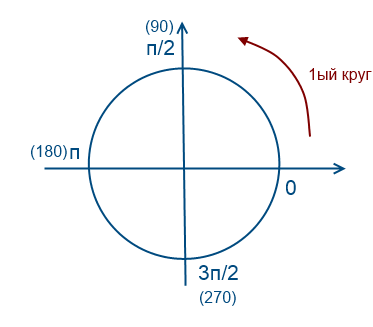
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.

Обойдем раз против часовой стрелки

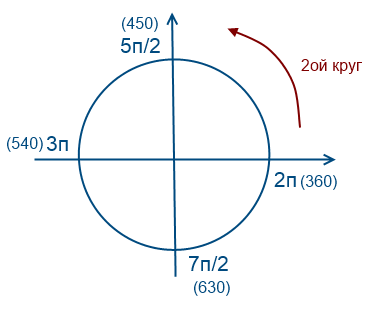
Обойдем 2 раза против часовой стрелки

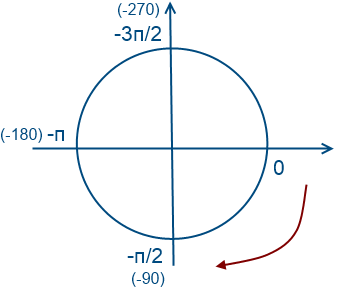
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)

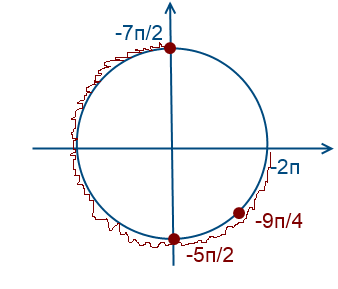
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]

Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.

Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.

Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.

Сравнение двух методов.

Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.

Просмотры: 158975 |
Статью добавил: slava191 |
Категория: математика

Одно из заданий второй части ЕГЭ по математике — решение тригонометрических уравнений с корнем. Основная его сложность в том, что нужно уметь не только упрощать выражения и находить ответ, но и проводить отбор корней. Как это сделать, мы разберем в статье. 

Что такое тригонометрическое уравнение

Тригонометрическое уравнение содержит в себе функцию синуса, косинуса, тангенса или котангенса. Решение без отбора корней происходит по следующим формулам: 

• sinx = a при |a| ≤ 1 → x = (-1)narcsina + πn;

• cosx = a при |a| ≤ 1 → x = ± arccosa + 2πn;

• tgx = b при b — любое число → x = arctgb + πn;

• сtgx = b при b — любое число → x = arcсtgb + πn.

Многие корни тригонометрических уравнений имеют конечные значения. Например, при sinx = -1 ответ следующий: x = π/2 + 2πn. Полная таблица достаточно большая, поэтому ее мы приводить тут не будем. 

Отбор 

Прежде чем изучить методы отбора корней, решим один несложный пример. 

Задание. 

а) Решите cos2x — 3cosx + 2 = 0

б) Найдите все ответы, принадлежащие отрезку -4; —52

Решение. 

Первое слагаемое распишем по формуле косинуса двойного угла: 

2cos2x — 1 — 3cosx + 2 = 0

Приведем однородные слагаемые: 

2cos2x — 3cosx + 1 = 0

Произведем замену: 

Пусть cosx = t, где |t| ≤ 1

Получаем: 

2t2 — 3t + 1 = 0

Находим дискриминант: 

D = (-3)2 — 4 • 2 • 1 = 9 — 8 = 1

Решаем:

x1=3+122=44=1

x2=3-122=24=12

Возвращаемся к исходной переменной и получаем: 

cosx = 1 → x = 2πn, n ∈ Z

cosx = ½ → x = ± π/3 + 2πk, k ∈ Z

Области допустимых значений нет, поэтому оба значения используем при решении пункта «б».

Теперь проведем отбор корней разными способами.

Арифметический

Для решения нужно перебирать все значения целочисленного параметра и считать корни. Разберем на примере cosx = 1.

Решение. x = 2πn

При n = -1 получаем x = 2 • (-1)π = -2π = -4π/2. Это больше, чем -5π/2, следовательно, ответ: не принадлежит отрезку.

При n = -2 получаем x = 2 • (-2)π = -4π. Число принадлежит отрезку.

При n = -3 получаем x = 2 • (-3)π = -6π. Это меньше, чем -4π, следовательно, значение не принадлежит отрезку. 

Далее то же самое нужно сделать с остальными корнями. Тогда вы получите ответ. 

Алгебраический

Чтобы отобрать корни, нужно решить неравенства относительно известного целочисленного параметра. Рассмотрим на примере первого значения. 

Решение. -4π ≤ 2πn ≤ -5π/2

Делим все части неравенства на «2π»: 

-2 ≤ n ≤ -5/4

Согласно условию, n ∈ Z. Рассматриваем только ответ n = -2. Получаем x = -4π.

Геометрический

Рисуем единичную окружность, наносим на нее числа из области и корни. После определяем, попадают ли они в промежуток. Отсчет промежутка происходит против часовой стрелки!

По рисунку видно, что в указанный промежуток попадает два корня. Первый: -4π. Второй нужно посчитать. Для этого к «-4π» мы прибавляем «π/3». Получаем: -11π/3. 

Функционально-графический

Для решения нарисуем функцию косинуса на области от y = -1 до y = 0,5. Зная значения промежутка, найдем абсциссы точек пересечения на заданном отрезке. 

Как видно по рисунку, у нас получаются те же корни, что и в предыдущем методе. 

Теперь вы знаете основные способы отбора корней в тригонометрических уравнениях. Это поможет вам правильно решать задания из второй части. Дома вам сложно практиковаться, не хватает помощи учителя? Тогда записывайтесь на курсы подготовки к ЕГЭ в центре «Уникум» при Российском университете дружбы народов. Центр предлагает не только полезные уроки с экспертами ЕГЭ, но и доступ к учебному порталу. На нем вы сможете делать домашние задания, решать пробные варианты экзамена и изучать полезные материалы. Форматы курсов разные  — очный и дистанционный. 

Содержание данной статьи носит ознакомительный характер. Для подготовки к сдаче ЕГЭ пользуйтесь дополнительными источниками информации!