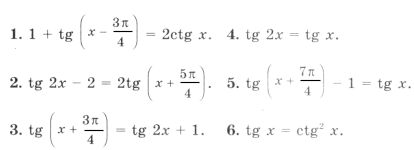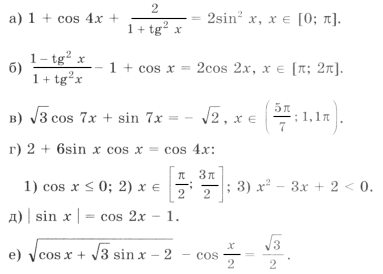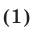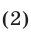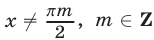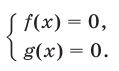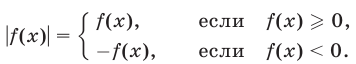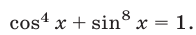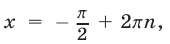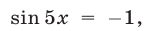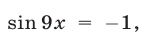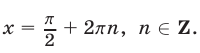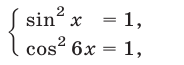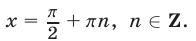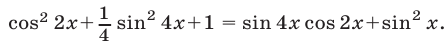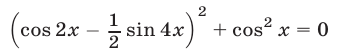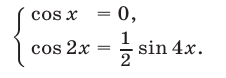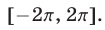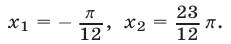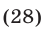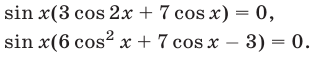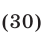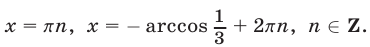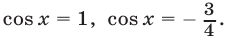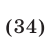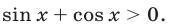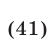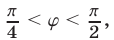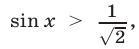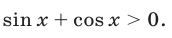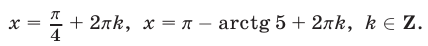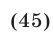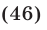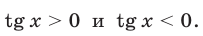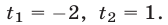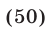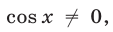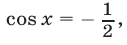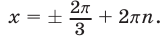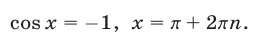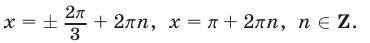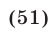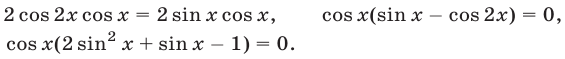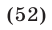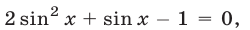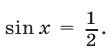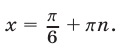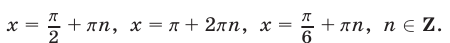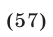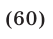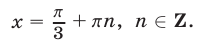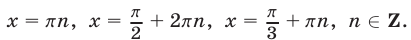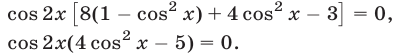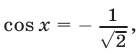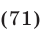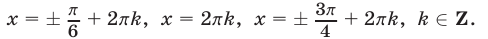Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравнениях
Практика приемных экзаменов в вузы показывает, что при решении тригонометрических уравнений абитуриенты нередко затрудняются как в выборе способа решения уравнения, так и при отборе его корней.
Проблема отбора корней, отсеивания лишних корней при решении тригонометрических уравнений специфична. Лишние корни могут появиться вследствие того, что в процессе решения произошло расширение области определения уравнения. Запись ответа тригонометрического уравнения часто связана с понятиями объединения и пересечения множеств. Обычно при решении таких уравнений получают серии корней, и в окончательном варианте ответ записывают в виде объединения этих серий. Но как быть, если эти серии пересекаются? Надо ли исключать повторяющиеся корни решения или этого можно не делать?
С понятием пересечения множеств связан и еще один важный вопрос: в ответе не должно быть значений переменной, при которых выражения в левой или правой частях уравнения не определены. Такие значения надо исключить. Для этого надо уметь находить пересечение различных серий.
В предлагаемой работе на конкретных примерах рассматриваются различные способы и приемы при выборе ответа. Надеемся, что данная работа поможет учителям старших классов и самим учащимся при подготовке к вступительным экзаменам в вузы.
1. Отбор чисел на тригонометрическом круге
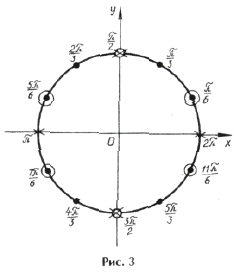
Проблему отбора корней, отсеивания лишних корней при решении тригонометрических уравнений часто можно решить с помощью изображения чисел на тригонометрическом круге. В ряде случаев этот прием, на наш взгляд, более наглядный и убедительный.
Пример 1. cos x + cos 2x – cos 3x = 1.
2sin x sin 2x – 2sin 2 x = 0,

Из рис. 1 видно, что серия x3(*) включает в себя один из корней серии x1( · ).
Ответ:
Пример 2. tg x + tg 2x – tg 3x = 0.
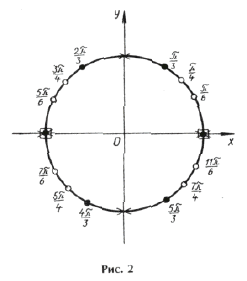
Серия x2(*) не удовлетворяет ОДЗ (рис. 2). Серия x1( o ) входит в серию x3( · ), поэтому ответ можно записать одной формулой:
Пример 3.
sin 2x (2cos 2x cos x + cos 7x) = 0,
sin 2x (cos 3x + cos x + cos 7x) = 0,
sin 2x (cos 3x + 2cos 4x cos 3x) = 0,
sin 2x cos 3x (1 + 2cos 4x) = 0,
Объединяя все три серии корней, ответ можно записать так:
Пример 4. sin 2 x + sin 2 2x = sin 2 3x.
– (cos 2x + cos 4x) + 1 + cos 6x = 0,
– 2cos 3x cos x + 2cos2 3x = 0,
cos 3x (cos 3x – cos x) = 0,
cos 3x sin 2x sin x = 0,
Серия корней x2 содержится в серии x1 и x3, в чем легко убедиться, изобразив их различными точками на круге, поэтому
ответ:
Пример 5. sin x + sin 7x – cos 5x + cos (3x – 2 p ) = 0.
2sin 4x cos 3x + 2sin 4x sin x = 0,
sin 4x (cos 3x + sin x) = 0,
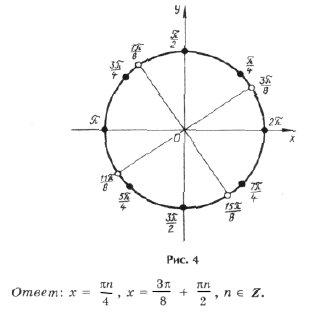
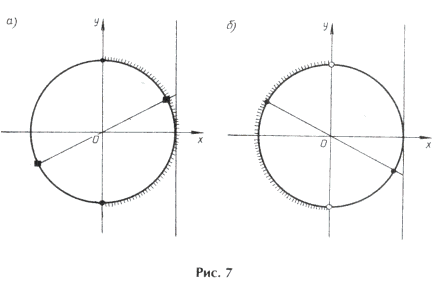
Серия x2 содержится в серии корней x1, а на круге (рис. 4) изобразим точками серии x1( · ) и x3(О), которые не совпадают.
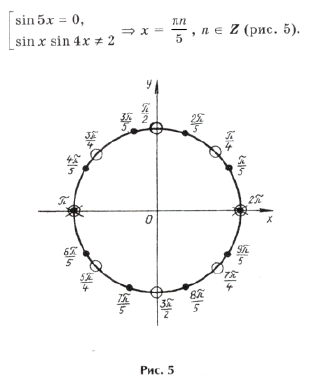
Пример 6. ctg 2x + 2ctg x – tg 2x = sin 5x.
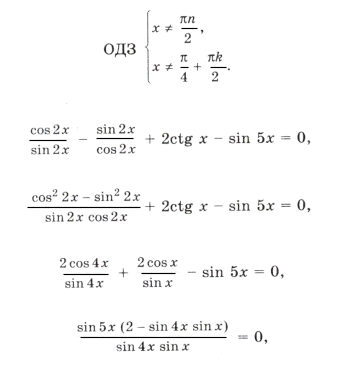
Учитывая ОДЗ, получим
Пример 7.
Иногда случается, что часть серии входит в ответ, а часть нет.
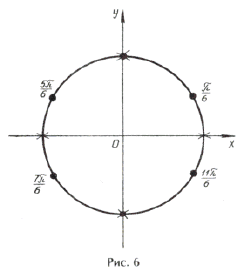
Нанесем на тригонометрический круг (рис. 6) все числа серии 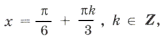
и выбросим корни, удовлетворяющие условию
Оставшиеся решения из серии x1 можно объединить в формулу
2. Отбор корней в тригонометрическом уравнении алгебраическим способом
Изображение корней на тригонометрическом круге не всегда удобно, когда период меньше 2 p .
Пример 8. sin 2 2x + sin 2 3x + sin 2 4x + sin 2 5x = 2.
cos 4x + cos 6x + cos 8x + cos 10x = 0,
2cos 5x cos x + 2cos 9x cos x = 0,
cos x cos 2x cos 7x = 0.
«Период» серий равен p. Рассмотрим те корни из серий x1, x2, x3, которые попадают в промежуток [0; p ]. Это будут:
Сразу видно, что серия x1 содержится в серии x3, а серии x2 и x3 не пересекаются. Значит, ответ можно записать в виде .
Способ алгебраический. Общим знаменателем в сериях x1 и x2 будет 4:
Если x1 = x2, то 2 + 4k = 1 + 2l, но слева – четное число, а справа – нечетное. Равенство невозможно, серии x1 и x2 не пересекаются. Аналогично получаем, что серии х3 и х2 тоже не пересекаются, а вот для серий x1 и x3 получаются формулы
Из равенства 7 + 14k = 1 + 2m получаем m = 7k + 3. Это означает, что для всякого k найдется целое m такое, что будет выполняться равенство 7 + 14k = 1 + 2m, т. е. всякий корень из серии x1 встретится и в серии x3, поэтому серия x1 содержится в серии x3, и в ответе писать ее не надо.
При решении некоторых тригонометрических уравнений их заменяют эквивалентной системой уравнений, а затем находят пересечение множеств решений. Эти пересечения часто найти легко. Но иногда для нахождения решений необходимо решать диафантово уравнение (ax + by = c).
Пример 9.
В данном случае сделать отбор решений на тригонометрическом круге неудобно, так как периоды серий разные. Найдем такие целые k, при которых x = p + 2 p k имеет посторонние корни, удовлетворяющие условию x № 3 p n, n О Z. Пусть p + 2 p k = 3 p n; 1 + 2k = 3n. Отсюда n = 2m + 1 Ю k = 3m + 1. Итак, посторонние корни в серии x = p + 2 p k будет при k = 3m + 1, m О Z.
Пример 10. cos 7x (sin 5x – 1) = 0.
Пересекаются ли эти серии? Из равенства
следует 5k = 14n + 1. Выразим ту неизвестную, коэффициент при которой меньше по абсолютной величине:
– целое число.
Ответ можно записать в виде
.
Пример 11.
Поскольку наибольшее значение функции y = cos t равно 1, уравнение равносильно системе
Решением уравнения является пересечение серий x1 и x2, т. е. нам надо решить уравнение
Из него получаем уравнение, имеющее решение k = 8t, n = 3t.
Пример 12.
Решением уравнения является пересечение серий x1 и x2;
,
где
– целое число;
Пример 13.
sin 2x sin 4x = 2sin x sin 3x cos x,
sin 2x sin 4x = sin 2x sin 3x,
sin 2x (sin 4x – sin 3x) = 0,
Остается проверить, лежат ли они в области x О R,
Серию x1 проверить легко: поскольку
,
а при n, кратных 8, n = 8l (l О Z), получается как раз x № 2 p l, вся серия x1 исключается. Сложнее обстоит дело с серией x2. Здесь надо выяснить, при каких целых k найдется такое n, что выполняется равенство
,
и исключить такие k. Последнее уравнение приводится к виду 8k + 4 = 7n, причем решать это уравнение надо в целых числах. Из него следует, что n = 4l, поскольку левая часть уравнения делится на 4. Подставляя n = 4l в уравнение, получаем 8k + 4 = 28l, откуда 2k + 1 = 7l. Далее, l должно быть нечетно, l = 2t + 1; поэтому 2k + 1 = 14t + 7, k = 7t + 3. Вот решение и получилось:
Ответ:
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями
Изложенные выше способы отбора корней в тригонометрических уравнениях не всегда применяются в чистом виде: выбор способа зависит от конкретных условий, но иногда эти способы комбинируются.
Пример 14. Найти корни уравнения sin 2x = cos x | cos x |,
удовлетворяющие условию x О [0; 2 p ].
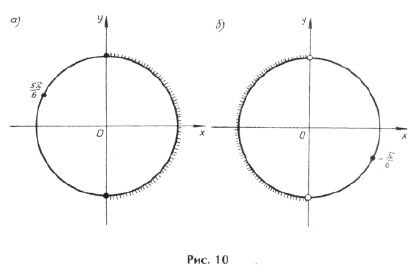
Условию cos x і 0 удовлетворяют
из серии
из серии
Наконец,
Пример 15. Найти все решения уравнения
удовлетворяющие условию
так как
то
Пример 16. Найти все решения уравнения
принадлежащие отрезку
.
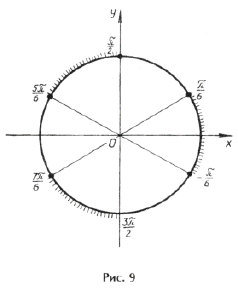
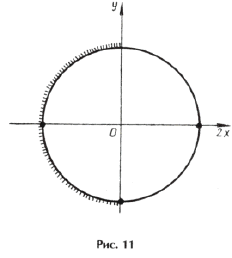
Отметим ОДЗ на тригонометрическом круге (рис. 9):
Отрезку
принадлежит только один промежуток из ОДЗ, а именно
.
Решим уравнение и выберем корни, принадлежащие этому промежутку:
1 + sin 2x = 2cos 2 3x Ю sin 2x = cos 6x,
Из серии
при n = 2 имеем
Из серии
при n = 5 имеем
Пример 17.
Ответ:
Пример 18. Найти все корни уравнения
которые удовлетворяют условию
.
10sin 2 x = – cos 2x + 3 Ю 10sin 2 x = 2sin 2 x – 1 + 3,
Выберем корни, удовлетворяющие условию задачи. Из серии
При
при
.
Аналогично выберем корни, удовлетворяющие условию задачи, из второй серии. Это будут
.
Пример 19.
sin x и cos x должны быть одинакового знака, а, учитывая первое неравенство, только при sin x > 0 и cos x > 0 система совместна. Значит, x оканчивается в первой четверти. Имеем
1 + 2sin x cos x = 4sin x cos x Ю sin 2x = 1,
Ответ:
Пример 20.
Ответ:
Пример 21.
а)
Но ctg x 0. Решений нет.
б)
Ответ:
.
Примеры для самостоятельного решения
7. Найти все решения уравнения, принадлежащие указанным промежуткам:

Л. Максименко,
Р. Зинченко,
г. АнгарскОтбор корней в тригонометрическом уравнение
В этой статье и постараюсь объяснить 2 способа отбора корней в тригонометрическом уравнение: с помощью неравенств и с помощью тригонометрической окружности. Перейдем сразу к наглядному примеру и походу дела будем разбираться.
а) Решить уравнение sqrt(2)cos^2x=sin(Pi/2+x)
б) Найдите все корни этого уравнения, принадлежащие промежутку [-7Pi/2; -2Pi]Решим пункт а.
Воспользуемся формулой приведения для синуса sin(Pi/2+x) = cos(x)
sqrt(2)cos^2x — cosx = 0
cosx(sqrt(2)cosx — 1) = 0
x1 = Pi/2 + Pin, n ∈ Z
sqrt(2)cosx — 1 = 0
x2 = arccos(sqrt(2)/2) + 2Pin, n ∈ Z
x3 = -arccos(sqrt(2)/2) + 2Pin, n ∈ Zx2 = Pi/4 + 2Pin, n ∈ Z
x3 = -Pi/4 + 2Pin, n ∈ ZРешим пункт б.
1) Отбор корней с помощью неравенств
Здесь все делается просто, полученные корни подставляем в заданный нам промежуток [-7Pi/2; -2Pi], находим целые значения для n.
-7Pi/2 меньше или равно Pi/2 + Pin меньше или равно -2Pi
Сразу делим все на Pi
-7/2 меньше или равно 1/2 + n меньше или равно -2
-7/2 — 1/2 меньше или равно n меньше или равно -2 — 1/2
-4 меньше или равно n меньше или равно -5/2
Целые n в этом промежутку это -4 и -3. Значит корни принадлежащие этому промежутку буду Pi/2 + Pi(-4) = -7Pi/2, Pi/2 + Pi(-3) = -5Pi/2
Аналогично делаем еще два неравенства
-7Pi/2 меньше или равно Pi/4 + 2Pin меньше или равно -2Pi
-15/8 меньше или равно n меньше или равно -9/8Целых n в этом промежутке нет
-7Pi/2 меньше или равно -Pi/4 + 2Pin меньше или равно -2Pi
-13/8 меньше или равно n меньше или равно -7/8Одно целое n в этом промежутку это -1. Значит отобранный корень на этом промежутку -Pi/4 + 2Pi*(-1) = -9Pi/4.
Значит ответ в пункте б: -7Pi/2, -5Pi/2, -9Pi/4
2) Отбор корней с помощью тригонометрической окружности
Чтобы пользоваться этим способом надо понимать как работает эта окружность. Постараюсь простым языком объяснить как это понимаю я. Думаю в школах на уроках алгебры эта тема объяснялась много раз умными словами учителя, в учебниках сложные формулировки. Лично я понимаю это как окружность, которую можно обходить бесконечное число раз, объясняется это тем, что функции синус и косинус периодичны.
Обойдем раз против часовой стрелки
Обойдем 2 раза против часовой стрелки
Обойдем 1 раз по часовой стрелки (значения будут отрицательные)
Вернемся к нашем вопросу, нам надо отобрать корни на промежутке [-7Pi/2; -2Pi]
Чтобы попасть к числам -7Pi/2 и -2Pi надо обойти окружность против часовой стрелки два раза. Для того, чтобы найти корни уравнения на этом промежутке надо прикидывать и подставлять.
Рассмотри x = Pi/2 + Pin. Какой приблизительно должен быть n, чтобы значение x было где-то в этом промежутке? Подставляем, допустим -2, получаем Pi/2 — 2Pi = -3Pi/2, очевидно это не входит в наш промежуток, значит берем меньше -3, Pi/2 — 3Pi = -5Pi/2, это подходит, попробуем еще -4, Pi/2 — 4Pi = -7Pi/2, также подходит.
Рассуждая аналогично для Pi/4 + 2Pin и -Pi/4 + 2Pin, находим еще один корень -9Pi/4.
Сравнение двух методов.
Первый способ (с помощью неравенств) гораздо надежнее и намного проще для пониманию, но если действительно серьезно разобраться с тригонометрической окружностью и со вторым методом отбора, то отбор корней будет гораздо быстрее, можно сэкономить около 15 минут на экзамене.
Отбор корней при решении тригонометрических уравнений
материал для подготовки к егэ (гиа) по алгебре (11 класс) на тему
Методы отбора корней тригонометрических уравнений
Скачать:
Вложение Размер Методы отбора корней в тригонометрических уравнениях 1.25 МБ Предварительный просмотр:
Подписи к слайдам:
Отбор корней при решении тригонометрических уравнений
1. Вычислите: б) arccos в) arcsin 2 д) arccos е) ar с ctg а) arcsin (-1) г) arctg (не существует); (не существует);
2. Решить уравнения: б) sin х = в) cos х = 0; г) tg x = а) cos x = — 1;
1. Отбор корней в тригонометрическом уравнении с помощью числовой окружности. Пример 1 . cos x + cos 2 x – cos 3 x = 1. Решение . cos x – cos 3 x – (1 – cos 2 x ) = 0, 2sin x sin 2 x – 2sin 2 x = 0, 2sin x (sin 2 x – sin x ) = 0,
Изобразим серии корней на тригонометрическом круге. 0 x y Видим, что первая серия ( ) включает в себя корни второй серии ( ), а третья серия ( ) включает в себя числа вида из корней первой серии ( ). 0
Пример 2. tg x + tg 2 x – tg 3 x = 0. Решение.
tg x · tg 2 x · tg 3 x = 0; Изобразим ОДЗ и серии корней на числовой окружности. 0 x y 0 Из второй серии корней ( ) числа вида не удовлетворяют ОДЗ, а числа вида . входят в третью серию ( ) Первая серия ( ) так же входит в третью серию корней ( ), поэтому ответ можно записать одной формулой.
Пример 3. Решение. Иногда случается, что часть серии входит в ответ, а часть нет. Нанесем на числовую окружность все числа серии и исключим корни, удовлетворяющие Оставшиеся решения из серии корней можно объединить в формулу 0 x y 0 условию
2. Отбор корней в тригонометрическом уравнении алгебраическим способом Пример 1. Решение. Поскольку наибольшее значение функции y = cos t равно 1, то уравнение равносильно системе Решением уравнения является пересечение серий, то есть нам надо решить уравнение Получаем Итак,
Пример 2. Решение . Решением уравнения является пересечение серий, то есть нам надо решить уравнение где целое число. тогда Пусть Итак,
3. Отбор корней в тригонометрическом уравнении с некоторыми условиями Пример 1. Найти корни уравнения sin 2 x = cos x | cos x |, удовлетворяющие условию x [0; 2 π ]. cos x (2sin x — | cos x |)=0; Решение. sin 2 x = cos x | cos x |; 2sin x · cos x — cos x | cos x |=0;
0 y x 0 y x cos x ≥ 0 cos x Мне нравится
источники:
http://reshimvse.com/article.php?id=100
http://nsportal.ru/shkola/algebra/library/2015/07/21/otbor-korney-pri-reshenii-trigonometricheskih-uravneniy
Найдите корни уравнения: 1) х2 + х + √7 -7 = 0, удовлетворяющие условию х √5.
Ваш ответ
решение вопроса
Похожие вопросы
- Все категории
- экономические 43,299
- гуманитарные 33,630
- юридические 17,900
- школьный раздел 607,256
- разное 16,836
Популярное на сайте:
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как быстро и эффективно исправить почерк? Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Пример частного решения линейного дифференциального уравнения
Рассмотрим тоже самое уравнение, но решим методом вариации произвольной постоянной.
Для нахождения производных C’i составляем систему уравнений:
C’1·e -3x ·cos(2x)+C’2·e -3x ·sin(2x)=0
C’1(-2·e -3x ·sin(2x)-3·cos(2x)·e -3x ) + C’2(-3·e -3x ·sin(2x)+2·cos(2x)·e -3x ) = 8*exp(-x)
Выразим C’1 из первого уравнения:
C’1 = -c2·sin(2x)/(cos(2x))
и подставим во второе. В итоге получаем:
C’1 = -4·e 2x ·sin(2x)
C’2 = 4·cos(2x)·e 2x
Интегрируем полученные функции C’i:
C1 = -e 2x ·sin(2x)+cos(2x)·e 2x + C * 1
C2 = e 2x ·sin(2x)+cos(2x)·e 2x + C * 2
Записываем полученные выражения в виде:
C1 = (-e 2x ·sin(2x)+cos(2x)·e 2x )·cos(2x)·e -3x + C * 1e -3x ·cos(2x)
C2 = (e 2x ·sin(2x)+cos(2x)·e 2x )·e -3x ·sin(2x) + C * 2e -3x ·sin(2x)
или
C1 = -cos(2x)·e -x ·sin(2x)+cos 2 (2x)·e -x + C * 1e -3x ·cos(2x)
C2 = cos(2x)·e -x ·sin(2x)+sin 2 (2x)·e -x + C * 2e -3x ·sin(2x)
y = C1 + C2
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример . y″ + 5y’ + 6 = 12cos(2x)
Cоставляем характеристическое уравнение дифференциального уравнения: r 2 +5 r + 6 = 0
Находим дискриминант: D = 5 2 — 4·1·6 = 1
Корни характеристического уравнения: r1 = -2, r2 = -3. Следовательно, фундаментальную систему решений составляют функции: y1 = e -2x , y2 = e -3x
Общее решение однородного уравнения имеет вид: y =C1·e -2x +C2·e -3x
Найдем частное решение при условии:y(0) = 1, y'(0) = 3
Поскольку y(0) = c1+c2, то получаем первое уравнение:
c1+c2 = 1
Находим первую производную: y’ = -3·c2·e -3·x -2·c1·e -2·x
Поскольку y'(0) = -3·c2-2·c2, то получаем второе уравнение:
-3·c2-2·c2 = 3
В итоге получаем систему из двух уравнений:
c1+c2 = 1
-3·c2-2·c2 = 3
которую решаем или методом обратной матрицы или методом исключения переменных.
c1 = 6, c2 = -5
Тогда частное решение при заданных начальных условиях можно записать в виде: y =6·e -2x -5·e -3x
Рассмотрим правую часть: f(x) = 12·cos(2·x)
Уравнение имеет частное решение вида: y * = Acos(2x) + Bsin(2x)
Вычисляем производные: y’ = -2·A·sin(2x)+2·B·cos(2x); y″ = -4·A·cos(2x)-4·B·sin(2x)
которые подставляем в исходное дифференциальное уравнение: y″ + 5y’ + 6y = (-4·A·cos(2x)-4·B·sin(2x)) + 5(-2·A·sin(2x)+2·B·cos(2x)) + 6(Acos(2x) + Bsin(2x)) = 12·cos(2·x) или -10·A·sin(2x)+2·A·cos(2x)+2·B·sin(2x)+10·B·cos(2x) = 12·cos(2·x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему линейных уравнений:
-10A + 2B = 0
2A + 10B = 12
СЛАУ решаем методом Крамера:
A = 3 /13;B = 15 /13;
Частное решение имеет вид:
y * = 3 /13cos(2x) + 15 /13sin(2x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Пример 2 . y’’ + y = cos(x)
Данное дифференциальное уравнение относится к линейным дифференциальным уравнениям с постоянными коэффициентами. Решение уравнения будем искать в виде y = e rx . Для этого составляем характеристическое уравнение линейного однородного дифференциального уравнения с постоянными коэффициентами:
r 2 + 1 = 0
D = 0 2 — 4·1·1 = -4

Корни характеристического уравнения:
(комплексные корни):
r1 = i, r2 = -i
Следовательно, фундаментальную систему решений составляют функции:
y1 = e 0 x cos(x) = cos(x)
y2 = e 0 x sin(x) = sin(x)
Общее решение однородного уравнения имеет вид: y =C1·cos(x)+C2·sin(x)
Рассмотрим правую часть: f(x) = cos(x)
Найдем частное решение. Линейное дифференциальное уравнение с постоянными коэффициентами и правой частью вида:
R(x) = e αx (P(x)cos(βx) + Q(x)sin(βx)), где P(x), Q(x) — некоторые полиномы
имеет частное решение
y(x) = x k e αx (R(x)cos(βx) + S(x)sin(βx))
где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x), S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x), Q(x).
Здесь P(x) = 0, Q(x) = 0, α = 0, β = 1.
Следовательно, число α + βi = 0 + 1i является корнем характеристического уравнения кратности k = 1(r1).
Уравнение имеет частное решение вида:
y * = x (Acos(x) + Bsin(x))
Вычисляем производные:
y’ = sin(x)(B-A·x)+cos(x)(A+B·x)
y″ = cos(x)(2·B-A·x)-sin(x)(2·A+B·x)
которые подставляем в исходное дифференциальное уравнение:
y″ + y = (cos(x)(2·B-A·x)-sin(x)(2·A+B·x)) + (x (Acos(x) + Bsin(x))) = cos(x)
или
2·B·cos(x)-2·A·sin(x) = cos(x)
Приравнивая коэффициенты при одинаковых степенях х, получаем систему уравнений:
2B = 1
-2A = 0
Следовательно:
A = 0; B = 1 /2;
Частное решение имеет вид: y * = x (0cos(x) + ½ sin(x)) = ½ x sin(x)
Таким образом, общее решение дифференциального уравнения имеет вид:
Задача Коши онлайн
Данная задача возникает при поиске частного решения дифференциального уравнения. Наш онлайн калькулятор, построенные на основе системы Wolfram Alpha, позволяет найти решение задачи Коши для различных типов дифференциальных уравнений. Чтобы начать работу, необходимо ввести данные своей задачи (дифференциальное уравнение и начальные условия) в калькулятор.
Найти решение задачи Коши для дифференциального уравнения:
при заданных начальных условиях:
При постановке задачи Коши, указываются так называемые начальные условия, позволяющие однозначно выделить искомое частное решение из общего. Эти условия включают в себя значения функции и всех её производных до включительно (где -порядок дифференциального уравнения), заданные в одной и той же точке .
Поясним вышесказанное на конкретном примере. Пусть нам требуется найти частное решение дифференциального уравнения:
удовлетворяющее начальным условиям:
Первым делом, используя различные методы (Бернули, вариации произвольной постоянной Лагранжа), сначала находим общее решение данного дифференциального уравнения:
Теперь, для поиска частного решения, нам необходимо использовать заданные начальные условия. Для этого, находим производную функции полученной ранее:
Далее, поставляем начальные условия в функцию и её производную :
Решая полученную систему уравнений получаем значения произвольных постоянных и :
Подставляем полученные результаты в общее решение дифференциального уравнения, в результате получаем искомое частное решение:
Другие полезные разделы:
Оставить свой комментарий:
Мы в социальных сетях:
Группа ВКонтакте | Бот в Телеграмме
http://math.semestr.ru/math/example-differential.php
http://mathforyou.net/online/calculus/cauchy/

Экспресс-тренинг
Подготовка к ЕГЭ-2023 по профильной математике в кратчайшие сроки!
До экзамена осталось совсем немного времени! Закрепите свои знания! Понятная теория и эффективные тренажеры с объяснением! Ваш ребенок успеет подготовиться к экзамену!

Способы отбора корней тригонометрического уравнения по различным условиям
Способы отбора корней тригонометрического уравнения по различным условиям
Здравствуйте!
Посмотрим, какими способами можно решать вторую часть задачи №13 варианта КИМ ЕГЭ — отобрать корни тригонометрического уравнения по разным условиям.
1. Отбор при помощи тригонометрической окружности
Есть два случая, когда удобно проводить отбор корней с помощью тригонометрического круга.
2. Отбор на графике тригонометрической функции
При использовании этого способа важно не забыть выписать период решения!
3. Отбор корней на основе решения неравенства
Отобрать корни, удовлетворяющие заданному условию, можно поместив полученные серии корней в неравенства и найдя удовлетворяющие ему значения
4. Метод перебора
Основные методы отбора корней тригонометрического уравнения мы систематизировали на слайдах. Рекомендуем еще раз повторить эти методы.
Следите за обновлениями на сайте и подписывайтесь на наш канал в Ютьюбе и группу Вконтакте!
На этой странице вы узнаете
- Игра в прятки: как значение одной переменной может помочь найти другую?
- Парадокс: как стоять на месте и бежать с любой скоростью одновременно?
- Решаем параметры осторожно: как не совершить ошибку в квадратном уравнении с параметром?
Мы привыкли, что в уравнении коэффициенты не меняются. Но возможно ли из одного уравнения составить бесконечное множество различных его вариантов? Узнаем об этом в статье.
Что такое параметр
Утром на термометре было некоторое количество градусов, которое мы обозначим за х. В обед температура воздуха изменилась в несколько раз. Во сколько раз должна была измениться температура воздуха, чтобы на термометре было 20 градусов?
Такие задачи достаточно легко решаются. Если бы изначально было пять градусов, то искомое число было бы равно (frac{20}{5} = 4). А если было 10 градусов, то искомое число было бы равно (frac{20}{10} = 2).
Но не все так просто. Мы не знаем, какой изначально была температура. Также мы не знаем, во сколько раз она изменилась. То есть мы получили уравнение с двумя неизвестными переменными.
Обозначим вторую переменную a, у нас получится уравнение вида ax=20. Только что введенная нами переменная “a” называется параметр.
Параметр — это условная буква, вместо которой можно подставить число.
То есть параметр — это еще одна переменная, которая может принять несколько значений.
Как решать уравнения с параметром, если у нас целых две (а то и больше) неизвестных переменных? Нужен иной подход, чем при решении обычного уравнения.
Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
Мы ищем не единственное значение параметра, а все возможные его значения для заданного условия.
Поскольку параметр — переменная в уравнении, которая является коэффициентом, его значение задает и корни уравнения. То есть переменные а и х зависят друг от друга так же, как и зависят корни обычного уравнения от его коэффициентов.
Линейные уравнения с параметром
Вернемся к нашей погоде. У нас получилось уравнение ax = 20. Как найти, сколько градусов было изначально? Разделить все уравнение на число a.
(x = frac{20}{a})
Какие значения может принимать параметр? Любые. Например, при a = 1 x = 20.
При a = 2 x = 10.
При a = 40 x = 0,5
Что, если a=0? Мы получаем уравнение (x = frac{20}{0}), у которого нет решения, поскольку на 0 делить нельзя.
Если мы не будем преобразовывать изначальное уравнение, то получится 0*x=20, то есть уравнение не будет выполняться: какое бы число мы ни умножили на 0, получится 0.
Получается, решение есть при любых значениях a, кроме 0. Таким образом, мы и нашли ответ: при a = 0 решений нет, при a (neq) 0 — x = 20a.
Добавим немного теории. Представим наше уравнение в виде ax = b, где a, b — действительные числа. Рассмотрим несколько случаев.
1) b (neq) 0.
Предположим, Пете необходимо в несколько раз увеличить скорость х, пробежать дистанцию и поставить рекорд. Чтобы поставить рекорд, он должен бежать со скоростью 15 км/ч — это и будет коэффициент b.
Получаем уравнение ax = 15. Как найти начальную скорость Пети? (x = frac{15}{a}).
Такое уравнение мы уже решали выше. Получаем два случая:
- Если a = 0 — решений нет.
- Если a (neq) 0, то изначальная скорость Пети была равна (x = frac{15}{a}).
Когда Пете нужно увеличить скорость в 0 раз, получается парадокс.
С какой бы скоростью ни бежал Петя, он все равно будет стоять на месте, поскольку 0 * x = 0. Даже если он изначально бегал со скоростью света, его скорость останется равна 0, а не 15 км/ч.
2) b = 0.
Мы получаем уравнение ax = 0. Также разберем два случая значений параметра:
- a = 0. Мы получаем уравнение 0 * x = 0. Какое значение х нужно подставить, чтобы уравнение выполнялось?
Какое бы число мы ни умножили на 0, получим 0. Получаем бесконечное множество решений.
- a (neq) 0. Здесь получается, что равен 0 уже х: (x = frac{0}{a} = 0).
Подведем итог. Как можно решить уравнение вида ax = b?
- Если a = 0, b = 0 — бесконечное множество решений.
- Если a = 0, b (neq) 0 — решений нет.
- Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}).
Квадратные уравнения с параметром
Прежде чем приступать к изучению следующего материала, рекомендуем ознакомиться с понятием квадратного уравнения в статье «Линейные, квадратные и кубические уравнения». Также важно ориентироваться в графиках параболы из статьи «Основные элементарные функции».
Квадратное уравнение имеет вид ax2 + bx + c = 0, а графиком функции y = ax2 + bx + c будет парабола.
Как работать с такими уравнениями, если в них присутствует параметр? В первую очередь, важны рассуждения. Любое задание с параметром можно решить, проанализировав функцию.
Решение квадратного уравнения опирается на понятие дискриминанта. В зависимости от его значений может получиться разное количество корней:
- При D > 0 уравнение имеет два корня.
- При D = 0 уравнение имеет один корень.
- При D < 0 уравнение не имеет корней.
Как это проверить на графике? Корни уравнения — это точки, в которых парабола пересекает ось абсцисс, то есть ось х.
Рассмотрим три уравнения.
1) x2 — x — 2 = 0
Решим уравнение с помощью дискриминанта.
D = 12 — 4 * 1 * (-2) = 1 + 8 = 9
Поскольку дискриминант больше 0, то уравнение имеет два корня.
(x_1 = frac{1 + 3}{2} = 2)
(x_2 = frac{1 — 3}{2} = -1)
Проверим с помощью графика функции. Построим параболу и заметим, что она действительно дважды пересекает ось абсцисс, а координаты этих точек равны (−1; 0) и (2; 0) .

2) x2 -4x + 4 = 0
Решим уравнение с помощью дискриминанта.
D = 16 — 4 * 1 * 4 = 16 — 16 = 0
Поскольку дискриминант равен 0, у уравнения всего один корень.
(x = frac{4}{2} = 2)
Проверим на графике. И действительно, парабола касается оси х только один раз в вершине, координаты которой (2; 0).

3) x2 — 5x + 7 = 0
Решим уравнение с помощью дискриминанта.
D = 25 — 4 * 1 * 7 = 25 — 28 = -3
Поскольку дискриминант отрицательный, у уравнения нет корней. И это отлично видно, если посмотреть на график функции: парабола лежит выше оси х и никогда ее не пересечет.
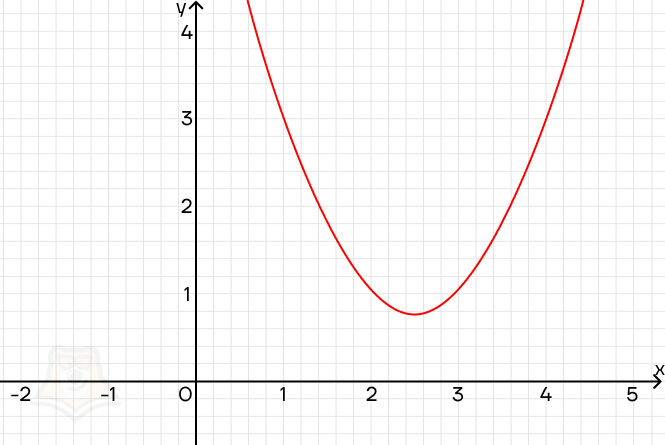
Где можно применить эти знания, решая параметры?
Пример 1. Найдите все значения параметра a, при которых уравнение x2 + (3a + 11)x + 18,25 + a = 0 имеет два различных решения.
Решение. Перед нами квадратное уравнение с коэффициентами b = 3a + 11, c = a + 18,25. В каких случаях это уравнение будет иметь два различных корня?
Квадратное уравнение имеет два корня, если D > 0. Нужно найти все значения параметра, при которых дискриминант будет положительным.
1. Для начала найдем сам дискриминант.
D = (3a + 11)2 — 4 * 1 * (a + 18,25) = 9a2 + 66a + 121 — 4a — 73 = 9a2 + 62a + 48
2. Поскольку дискриминант должен быть больше 0, то получаем неравенство 9a2 + 62a + 48 > 0
3. Решим его «Методом интервалов».
9a2 + 62a + 48 = 0
D = 3844 — 1728 = 2116
(a_1 = frac{-62 + 46}{18} = -frac{16}{18} = -89)
(a_2 = frac{-62 — 46}{18} = -frac{108}{18} = -6)

4. Дискриминант будет положительным при (a in (-infty; -6) cup (-frac{8}{9}; +infty)). Это и будет ответ.
Ответ: (a in (-infty; -6) cup (-frac{8}{9}; +infty)).
Важно: в уравнении мы указываем не сами решения уравнения, а значения параметра, при которых уравнение имеет два решения.
Пример 2. При каких значениях параметра a уравнение (2a + 1)x2 — ax + 3a + 1 = 0 имеет два различных решения?
Решение. Этот пример похож на предыдущий, однако здесь есть одна важная особенность. Что произойдет с уравнением, если 2a+1 = 0?
Мы получим уравнение 0,5x — 0,5 = 0, то есть линейное уравнение. У уравнения будет всего одно решение, что уже не подходит под условие задачи.
Если перед x2 стоит коэффициент, обязательно проверить, чтобы он не был равен 0. В противном случае уравнение из квадратного превращается в линейное, а это уже совершенно другой алгоритм решений уравнений.
1. Поскольку по условию должно быть 2 решения, мы получаем, что a (neq) -0,5.
2. Найдем дискриминант уравнения. Он должен быть строго больше 0, чтобы у уравнения было два решения.
D = a2 — 4 * (2a + 1) * (3a + 1) = a2 — 24a2 — 20a -4 = -23a2 — 20a — 4
3. Составим неравенство и решим его:
-23a2 — 20a — 4 > 0
23a2 + 20a + 4 < 0
23a2 + 20a + 4 = 0
D = 400 — 4 * 23 * 4 = 400 — 368 = 32
(a_1 = frac{-20 + 4 sqrt{2}}{46} = frac{2sqrt{2} — 10}{23})
(a_2 = frac{-20 — 4sqrt{2}}{46} = frac{-2sqrt{2} — 10}{23})
4. Разложим уравнение на множители:
(23a^2 + 20a + 4 = 23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23}))
5. Получаем неравенство:
(23(a — frac{2sqrt{2} — 10}{23})(a — frac{-2sqrt{2} — 10}{23} < 0)
6.Тогда (a in (frac{-2sqrt{2} — 10}{23}; frac{2sqrt{2} — 10}{23})). Вспомним, что a (neq) -0,5, следовательно, мы получаем ответ (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23})).

Ответ: (a in (frac{-2sqrt{2} — 10}{23}; -0,5) cup (-0,5; frac{2sqrt{2} — 10}{23}))
Теорема Виета
Дискриминант — не единственный способ решить квадратное уравнение. Обратимся к теореме Виета. Если нам дано уравнение ax2 + bx + c = 0, то его корни можно найти с помощью следующей системы:

Теорему Виета удобно использовать, если на корни уравнения наложены дополнительные ограничения.
Пример 3. При каких значениях параметра a корни уравнения x2 — 3ax — a(a — 1) = 0 удовлетворяют условию x1 = 5x2.
Решение. 1. Корни уравнения — это два различных числа. Значит, дискриминант должен быть строго больше 0:
D = 9a2 — 4 * 1 * (-a2 + a) = 9a2 + 4a2 — 4a = 13a2 — 4a = a(13a — 4)
Получаем неравенство a(13a — 4) > 0, следовательно, (a in (-infty; 0) cup (frac{4}{13}; +infty)).
2. По теореме Виета найдем корни уравнения:

3. По условию x1 = 5x2, тогда 5x2 + x2 = 6x2 = 3a, откуда получаем:
(x_2 = frac{3a}{6} = frac{a}{2})
(x_1 = 5 * a_2 = frac{5a}{2})
4. Подставим во второе уравнение системы:
(frac{a}{2} * frac{5a}{2} = a — a^2)
(frac{5a^2}{4} = a — a^2 | * 4)
5a2 = 4a — 4a2
(9a^2 — 4a = 0 rightarrow a(9a — 4) = 0 rightarrow a = 0, a = frac{4}{9})
5. Мы нашли значения параметра, при которых выполняется условие. Осталось проверить, чтобы при этих значениях у уравнения было два корня.
a = 0 не подходит, поскольку ограничение (a in (-infty; 0) cup (frac{4}{13}; +infty)) не включает точку 0.
(a = frac{4}{9}) подходит, поскольку (frac{4}{9} > frac{4}{13}).
Ответ: (a = frac{4}{9})
Условия на корни квадратного трехчлена
Однако могут встретиться еще более сложные задания с параметрами. Рассмотрим каждый из этих случаев.
1. Корни квадратного трехчлена меньше, чем число N.
Построим параболу. Вспомним, что ветви параболы могут быть направлены или вверх, или вниз.
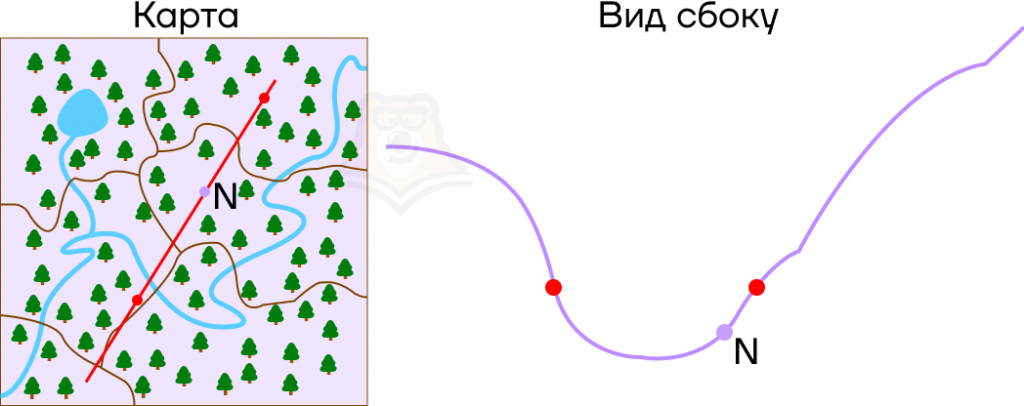
Если ветви параболы направлены вверх. Отметим на оси х точку N так, чтобы она лежала правее обоих корней уравнения. Так мы зададим условие, что корни уравнения меньше, чем число N.

Представим, что мы идем по холмистой местности, и у нас есть ее карта. Имея перед собой плоскую картинку, мы понимаем, как относительно друг друга располагаются точки в пространстве. Но посмотрев на рельеф сбоку, заметим, что точки имеют разную высоту.
Пусть в точках, где парабола пересекает ось х, будут привалы на экскурсионном маршруте, а в точке N будет смотровая площадка.

Что можно сказать про смотровую площадку на этой карте? Она находится выше, чем привалы, и лежит правее, чем самая низкая точка рельефа.
Рассмотрим эти условия на графике. В точке N значение функции f(x) больше, чем в корнях уравнения. Более того, она лежит правее, чем вершина параболы, то есть ее абсцисса больше абсциссы параболы.
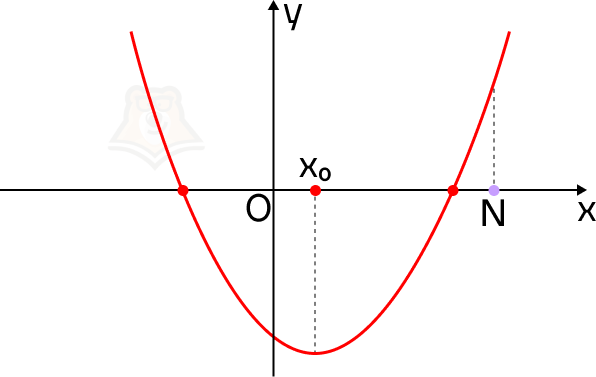
Почему эти условия так важны? Пусть точка N будет лежать левее вершины параболы. Тогда не выполняется условие, что корни меньше, чем N.
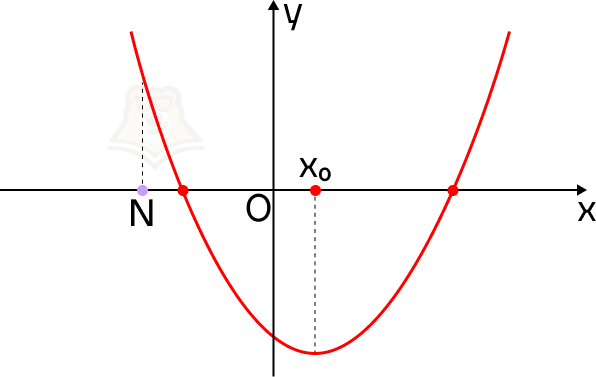
В этом случае на нашем экскурсионном маршруте смотровая площадка будет лежать до привалов.

А если значение функции в точке N будет меньше, чем в корнях уравнения? Точка N будет лежать между ними.

В этом случае смотровая площадка окажется между привалами.
Аналогичным способом можно проследить изменение условий при любом положении точки N на графике.
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:

Что произойдет, если ветви параболы будут направлены вниз? Наш экскурсионный маршрут немного поменяется: появится гора, а не овраг.
Где теперь располагается смотровая площадка? Она будет ниже, чем привалы, и дальше, чем самая высокая точка горы.

Мы можем сделать вывод, что точка N на графике будет лежать правее вершины параболы, а значение функции в ней будет меньше, чем значение функции в корнях уравнения.
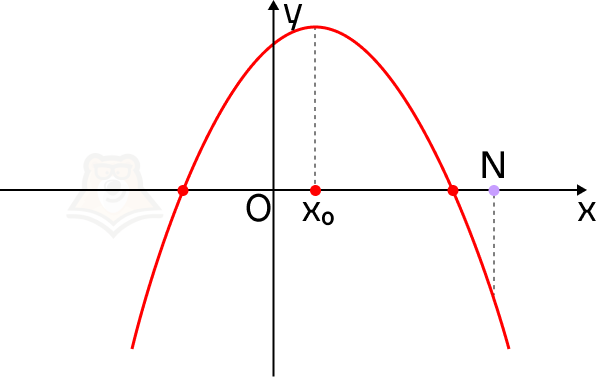
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были меньше, чем число N, необходимо и достаточно выполнение следующих условий:

2. Корни квадратного трехчлена больше, чем число N.
Рассуждаем так же, как и в предыдущей функции, однако теперь точка N перемещается левее параболы.
Если ветви параболы направлены вверх, то функция в точке N принимает большее значение, чем в корнях уравнения, а сама точка N будет лежать левее параболы.
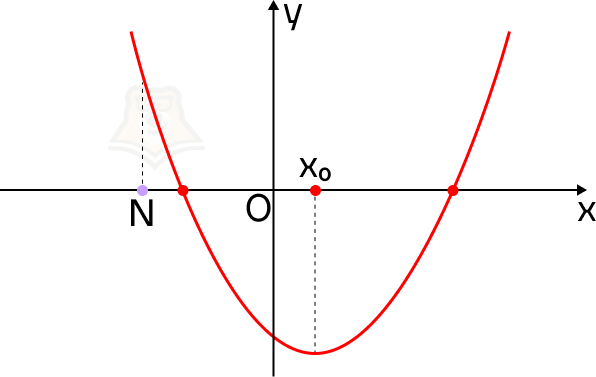
Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:

Теперь направим ветви параболы вниз. Значение функции в точке N будет меньше, чем в корнях уравнения.

Для того чтобы оба корня квадратного трехчлена ax2 + bx + c были больше, чем число N, необходимо и достаточно выполнение следующих условий:

С помощью анализа расположения точек на графике функций можно задать условия для любой ситуации, даже если точек будет несколько.
Достаточно начертить примерный график функции и расставить на оси х нужные точки. Чтобы составить систему, необходимо:
1. Определить, куда направлены ветви параболы и задать условие для коэффициента перед x2.
2. Определить, сколько корней имеет уравнение и задать условие для дискриминанта.
3. Определить расположение вершины параболы относительно точек на графике и задать условие для их абсцисс.
4. Определить, какое значение принимает функция в данных точках относительно корней уравнения.
В итоге должна получиться система, с помощью которой можно решить задачу.
Фактчек
- Параметр — это буква a, вместо которой можно подставить число. Решить уравнение с параметром — это найти такие числовые значения параметра, при которых условие выполняется.
- При решении линейного уравнения ax=b в зависимости от значения коэффициентов может получиться несколько вариантов решений. Если a = 0, b = 0 — бесконечное множество решений. Если a = 0, b (neq) 0 — решений нет. Если a (neq) 0, b (neq) 0 — решением будет (x = frac{b}{a}).
- При решении квадратного уравнения обязательно проверять коэффициент перед x2. Если коэффициент будет равен 0, то уравнение станет линейным.
- При решении квадратного уравнения важно учитывать значение дискриминанта: если он строго больше 0, то корней у уравнения два, если дискриминант равен 0, то у уравнения один корень, если дискриминант меньше 0, то у уравнения нет корней.
- Решить квадратное уравнение можно и с помощью теоремы Виета.
- Если в задаче даны дополнительные условия на корни уравнения (например, они должны быть больше или меньше определенного числа), то задать их можно с помощью системы. Неравенства в системе можно составить с помощью анализа примерного графика функций.
Проверь себя
Задание 1.
Что такое параметр?
- Это буква a, вместо которой можно подставить число.
- Это коэффициент перед x2 в квадратном уравнении.
- Это переменная х.
- Это значение функции в определенной точке.
Задание 2.
Дано уравнение ax = b. Сколько решений оно имеет, если a = 0 и b = 0?
- Решений нет.
- Одно решение.
- Бесконечное множество решений.
- Невозможно определить количество решений.
Задание 3.
При каких значениях дискриминанта уравнение будет иметь корни?
- D > 0
- D = 0
- D < 0
- D (neq) 0
Задание 4.
Корни квадратного уравнения меньше числа А. Где будет лежать вершина параболы относительно точки А?
- Справа.
- Слева.
- Совпадать с точкой А.
- Невозможно определить расположение вершины.
Задание 5.
Меньший корень квадратного уравнения больше числа А, но меньше числа В. Ветви параболы направлены вниз. Чему будет равно значение функции в точке В?
- Значение функции в точке В будет меньше 0.
- Значение функции в точке В будет равно 0.
- Значение функции в точке В будет больше 0.
- Невозможно определить значение функции.
Ответы: 1. — 1 2. — 3 3. — 4 4. — 2 5. — 3.
Уравнения, решаемые с помощью оценки их левой и правой частей. Уравнения, содержащие знаки корня и модуля
Справочные сведения
Оценка левой и правой части уравнения.
Решение некоторых тригонометрических уравнений основывается на неравенствах
Кроме этих неравенств могут оказаться полезными неравенства

справедливые для любых 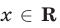
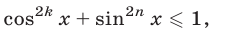
причем неравенство (2) является строгим при
Если 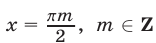
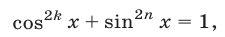
т. е. числа 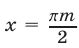
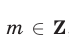
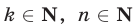
или преобразуется к такому виду, то оно равносильно системе уравнений
Уравнения, содержащие знак корня.
Если тригонометрическое уравнение имеет вид
то, как было отмечено в §8, такое уравнение равносильно системе
При решении тригонометрических уравнений вида
следует иметь в виду, что такое уравнение равносильно каждой из следующих систем:
Уравнения, содержащие знак модуля.
При решении тригонометрических уравнений, содержащих знак модуля, следует иметь в виду, что
Примеры с решениями
Пример №137.
Решить уравнение
Решение:
В § 12 (см. пример 
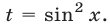
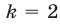
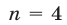
Ответ.
Пример №138.
Решить уравнение
Решение:
Так как 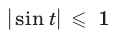
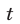
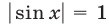
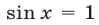
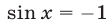
Если 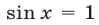
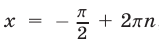
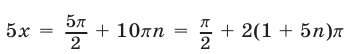
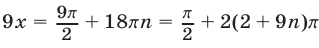
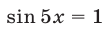
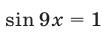
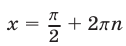
Если 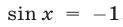
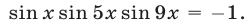

Ответ.
Пример №139.
Решить уравнение
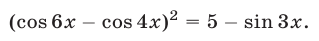
Решение:
Левая часть уравнения (4) не превосходит четырех, так как 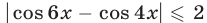
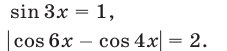
Если справедливо равенство (5), то
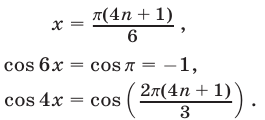
Из (8) и (9) следует, что равенство (6) верно только тогда, когда 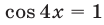
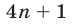
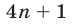
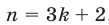
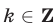
Ответ.
Пример №140.
Решить уравнение
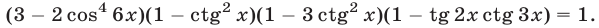
Решение:
Допустимые значения 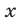

Воспользуемся равенствами
справедливыми при условиях (11).
Тогда уравнение (10) равносильно уравнению
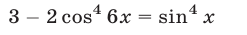
при выполнении условий (11).
Так как 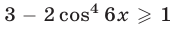
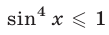
которая, в свою очередь, равносильна системе
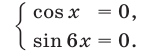
Поскольку каждый корень уравнения (13) является корнем уравнения (14), а для значений 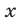
Ответ.
Пример №141.
Решить уравнение
Решение:
Уравнение можно записать в виде
и поэтому оно равносильно системе
Уравнение 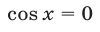
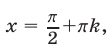
Пример №142.
Найти все корни уравнения
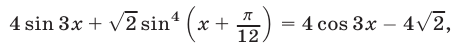
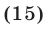
принадлежащие отрезку
Решение:
Уравнение (15) равносильно каждому из следующих уравнений:
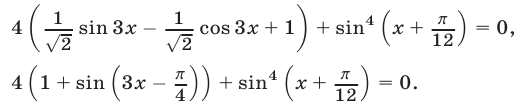
Уравнение (16) равносильно системе уравнений
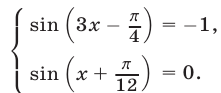
Из (18) следует, что
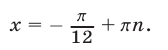
Подставляя найденное значение 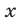
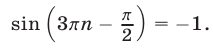
Равенство (20) является верным в том и только в том случае, когда 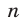
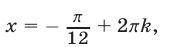
а отрезку 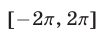
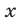
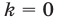
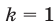
Ответ.
Пример №143.
Решить уравнение
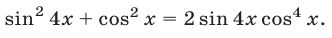
Решение:
Первый способ. Запишем уравнение в виде
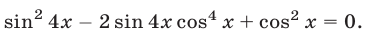
Прибавляя и вычитая в левой части уравнения (23) 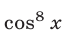
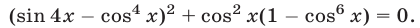
Равенство (24) является верным тогда и только тогда, когда верны равенства
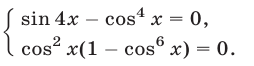
Система (25) равносильна совокупности двух систем
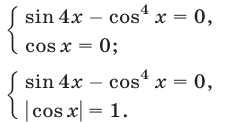
Если 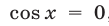
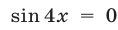
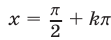
Система (27) не имеет решений, так как из равенства 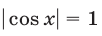
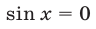
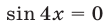
Ответ.
Второй способ. Решив уравнение (22) как квадратное относительно 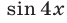
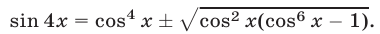
Из (28) следует, что уравнение (22) может иметь решение лишь тогда, когда 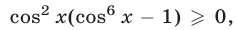
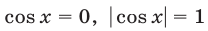
Если 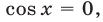
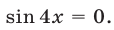
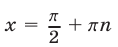
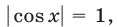
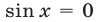
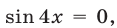
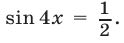
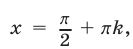
Пример №144.
Решить уравнение
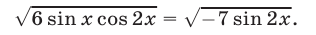
Решение:
Возведя обе части уравнения (29) в квадрат, получаем уравнение 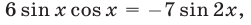
Уравнение 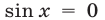
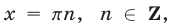
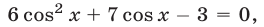
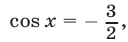
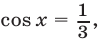
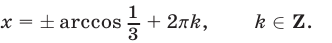
Из чисел, определяемых формулой (30), уравнению (29) удовлетворяют лишь те значения 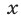
Так как 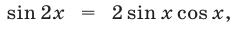
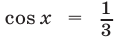
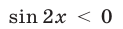
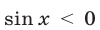
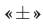
Ответ.
Пример №145.
Решить уравнение
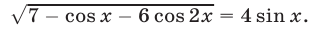
Решение:
Левая часть уравнения определена при всех значениях 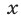
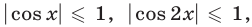
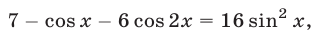
являющееся следствием уравнения (31).
Корнями уравнения (31) являются все те и только те корни уравнения (32), которые удовлетворяют условию
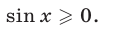
Иначе говоря, уравнение (31) равносильно системе, состоящей из уравнения (32) и неравенства (33).
Уравнение (32) сводится к квадратному относительно 
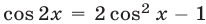
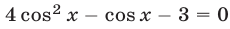
Если 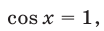
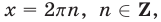
Если 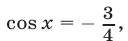
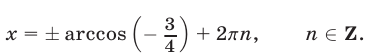
В том случае, когда в формуле (34) взят знак 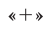
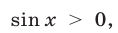
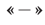
Отметим еще, что
Ответ.
Замечание. Многие абитуриенты допустили ошибку, решая уравнение (32) без учета условия (33). Это привело к появлению посторонних для уравнения (31) корней.
Пример №146.
Решить уравнение
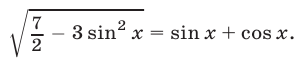
Решение:
Возведя обе части уравнения (35) в квадрат, получим уравнение
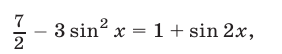
являющееся следствием уравнения (35). Уравнение (36) равносильно каждому из следующих уравнений:
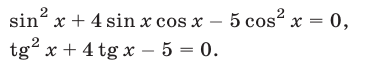
Решив уравнение (37), находим
1) Если 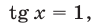
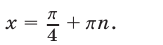
Пусть в формуле (38) 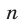
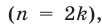
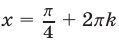
Пусть 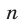
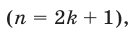
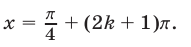
Из (39) следует, что 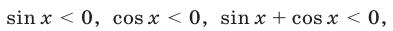
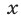
2) Если 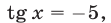
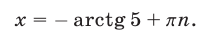
Пусть в формуле (40) 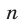
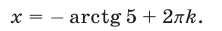
Положим 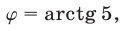
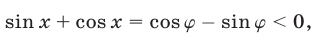
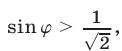
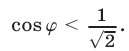
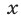
Пусть 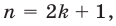
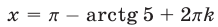
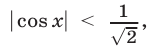
Ответ.
Пример №147.
Решить уравнение
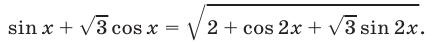
Решение:
Так как правая часть уравнения (42) неотрицательна, то уравнение может иметь решения только в том случае, когда
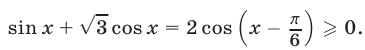
Если освободиться от радикала возведением обеих частей уравнения (42) в квадрат, то получается уравнение
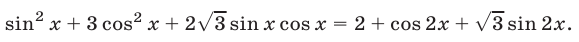
Уравнение (44) является тождеством. Однако это не означает, что уравнению (42) удовлетворяют все значения 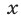
Ответ. Объединение всех отрезков вида
Замечание. Так как
то уравнение (42) равносильно уравнению
решениями которого являются те и только те значения х, которые удовлетворяют неравенству
Пример №148.
Решить уравнение
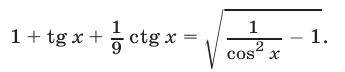
Решение:
Допустимые значения 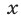
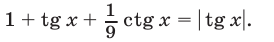
Рассмотрим два случая:
1) Если 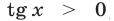
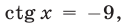
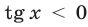
2) Если 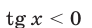
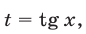
откуда
Ответ.
Пример №149.
Решить уравнение
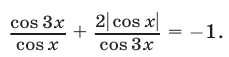
Решение:
Положим 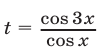
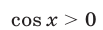
а) Пусть 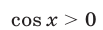
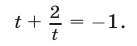
Уравнение (48), равносильное уравнению (47), не имеет действительных корней.
б) Пусть 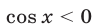
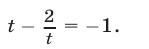
Так как 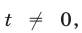
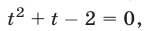
Если 
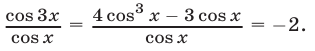
Так как
, то уравнение (50) равносильно уравнению 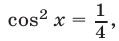
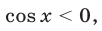
Если 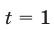
Ответ.
Пример 150.
Решить уравнение
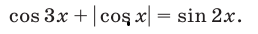
Решение:
Возможны два случая: 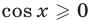
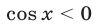
1) Пусть 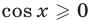
Преобразуя это уравнение, получаем
Если 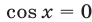
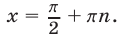
Если 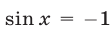
Корни уравнения 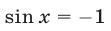
Решив уравнение 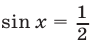
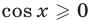
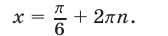
2) Пусть 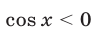
Решив уравнения 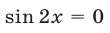
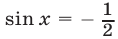
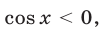
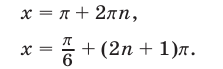
Серии (53) и (55) можно объединить в одну:
Ответ.
Пример №151.
Решить уравнение
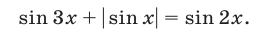
Решение:
Рассмотрим два случая: 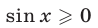
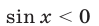
1) Если 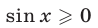
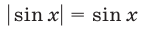
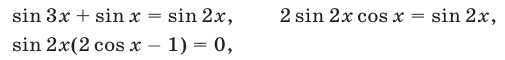
а уравнение (57) равносильно совокупности уравнений
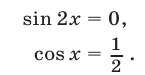
Условию 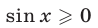
а также корни уравнения (59) такие, что
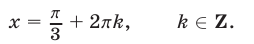
2) Если 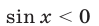
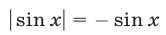
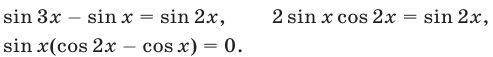
Так как 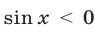
откуда получаем 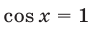
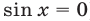
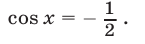
Таким образом, если 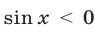
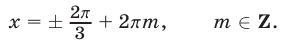
Условию 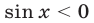
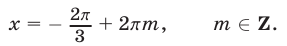
Заметим, что серии (64) и (60) можно объединить в одну:
Ответ.
Пример №152.
Решить уравнение
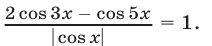
Решение:
Здесь ОДЗ уравнения (65) определяется условием 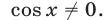
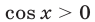
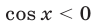
1) Если 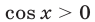
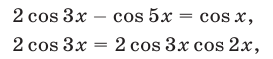
а уравнение (66) равносильно совокупности уравнений
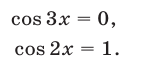
Чтобы найти корни уравнения (67), удовлетворяющие условию 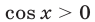
Отсюда следует, что уравнению (67) и условию 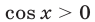
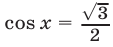
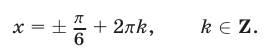
Корнями уравнения (68), удовлетворяющими условию 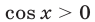
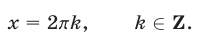
2) Если 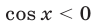
Уравнение 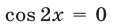
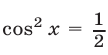
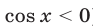
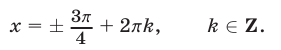
Уравнение 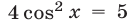
Ответ.
Этот материал взят со страницы решения задач с примерами по всем темам предмета математика:
Решение задач по математике
Возможно вам будут полезны эти страницы:

 Отбор корней в тригонометрических уравнениях
Отбор корней в тригонометрических уравнениях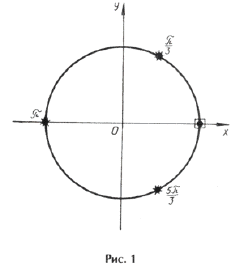
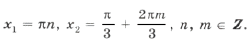
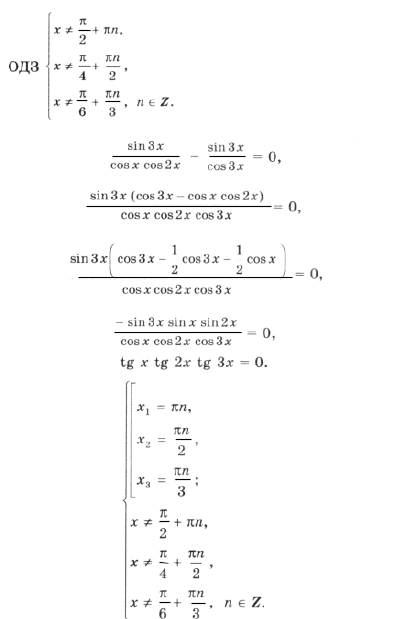
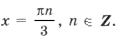
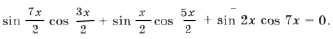
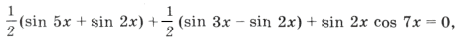
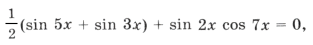
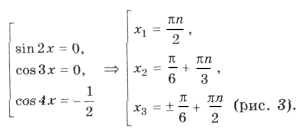
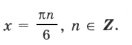
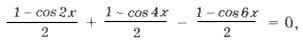
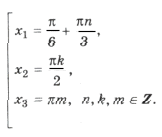
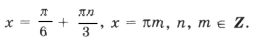
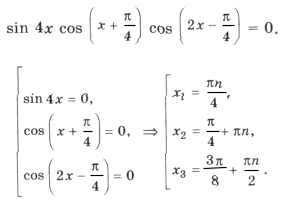
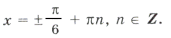
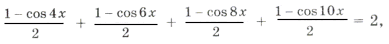
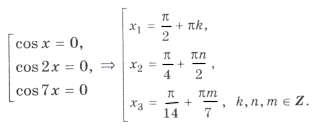
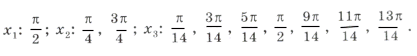
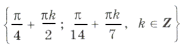
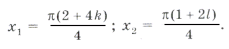
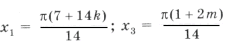
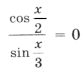
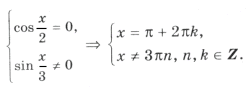
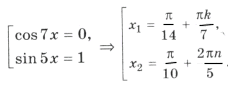
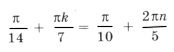
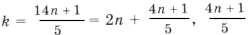 – целое число.
– целое число.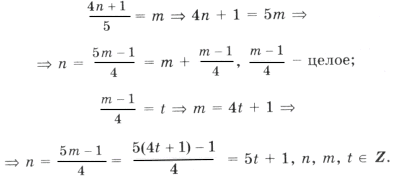
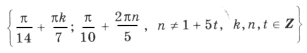 .
.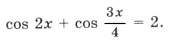
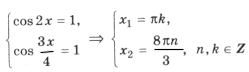
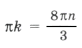
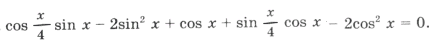
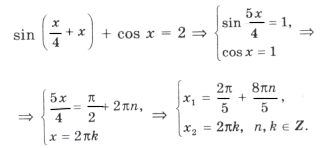
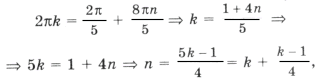 ,
,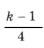 – целое число;
– целое число;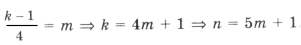
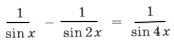
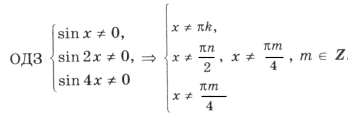
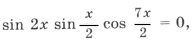
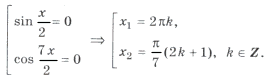
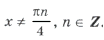
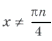 ,
,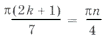 ,
,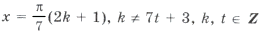
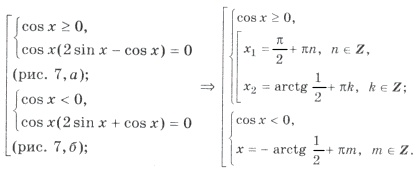
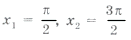
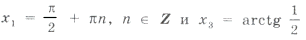
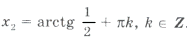

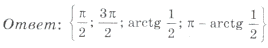
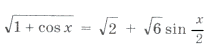
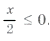
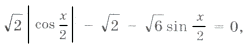
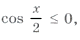 то
то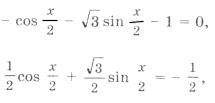
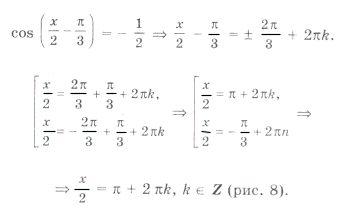
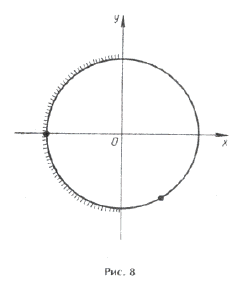
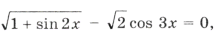
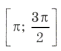 .
.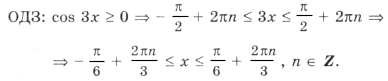
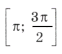 принадлежит только один промежуток из ОДЗ, а именно
принадлежит только один промежуток из ОДЗ, а именно 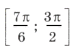 .
.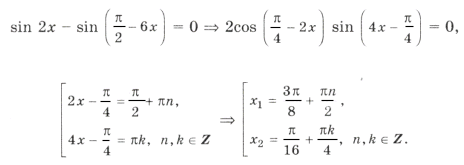
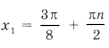 при n = 2 имеем
при n = 2 имеем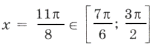
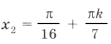 при n = 5 имеем
при n = 5 имеем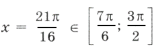
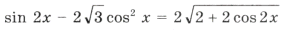
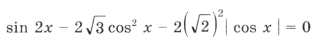
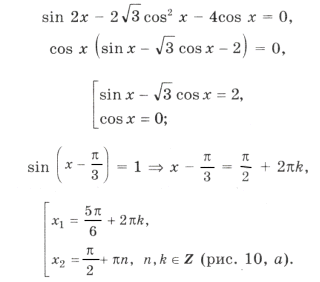
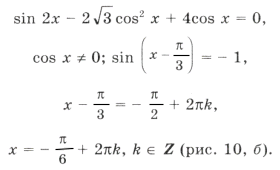
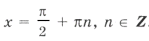
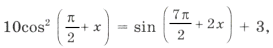
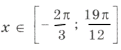 .
.
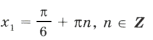
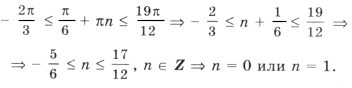
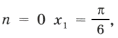
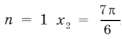 .
.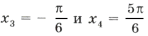 .
.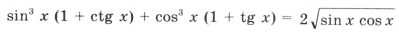
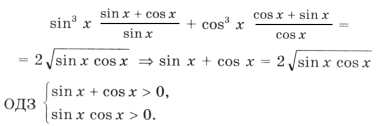
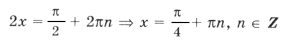
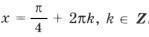
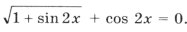
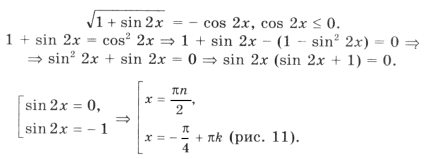
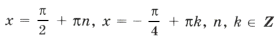
 .
.