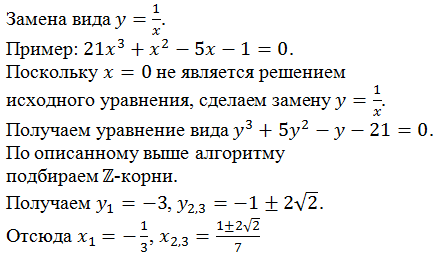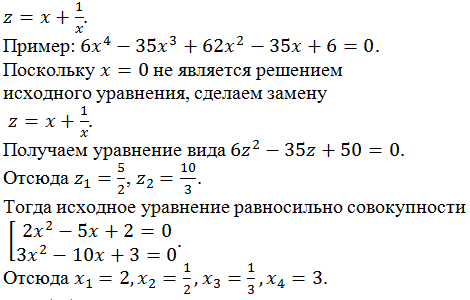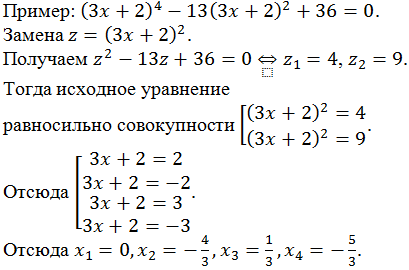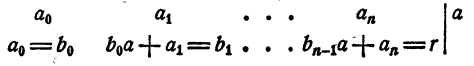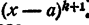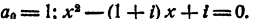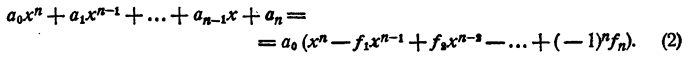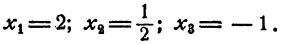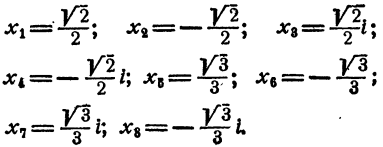Рассмотрим решения уравнений с одной переменной степени выше второй.
Степенью уравнения Р(х) = 0 называется степень многочлена Р(х), т.е. наибольшая из степеней его членов с коэффициентом, не равным нулю.
Так, например, уравнение (х3 – 1)2 + х5 = х6 – 2 имеет пятую степень, т.к. после операций раскрытия скобок и приведения подобных получим равносильное уравнение х5 – 2х3 + 3 = 0 пятой степени.
Вспомним правила, которые понадобятся для решения уравнений степени выше второй.
Утверждения о корнях многочлена и его делителях:
1. Многочлен n-й степени имеет число корней не превышающее число n, причем корни кратности m встречаются ровно m раз.
2. Многочлен нечетной степени имеет хотя бы один действительный корень.
3. Если α – корень Р(х), то Рn(х) = (х – α) · Qn – 1(x), где Qn – 1(x) – многочлен степени (n – 1).
4. Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
5. Приведенный многочлен с целыми коэффициентами не может иметь дробных рациональных корней.
6. Для многочлена третьей степени
Р3(х) = ах3 + bx2 + cx + d возможно одно из двух: либо он разлагается в произведение трех двучленов
Р3(x) = а(х – α)(х – β)(х – γ), либо разлагается в произведение двучлена и квадратного трехчлена Р3(x) = а(х – α)(х2 + βх + γ).
7. Любой многочлен четвертой степени раскладывается в произведение двух квадратных трехчленов.
8. Многочлен f(x) делится на многочлен g(х) без остатка, если существует многочлен q(x), что f(x) = g(x) · q(x). Для деления многочленов применяется правило «деления уголком».
9. Для делимости многочлена P(x) на двучлен (x – c) необходимо и достаточно, чтобы число с было корнем P(x) (Следствие теоремы Безу).
10. Теорема Виета: Если х1, х2, …, хn – действительные корни многочлена
Р(х) = а0хn + а1хn — 1 + … + аn, то имеют место следующие равенства:
х1 + х2 + … + хn = -а1/а0,
х1 · х2 + х1 · х3 + … + хn – 1 · хn = a2/а0,
х1 · х2 · х3 + … + хn – 2 · хn – 1 · хn = -a3 / а0,
…
х1 · х2 · х3 · хn = (-1)nan / а0.
Решение примеров
Пример 1.
Найти остаток от деления Р(х) = х3 + 2/3 x2 – 1/9 на (х – 1/3).
Решение.
По следствию из теоремы Безу: «Остаток от деления многочлена на двучлен (х – с) равен значению многочлена от с». Найдем Р(1/3) = 0. Следовательно, остаток равен 0 и число 1/3 – корень многочлена.
Ответ: R = 0.
Пример 2.
Разделить «уголком» 2х3 + 3x2 – 2х + 3 на (х + 2). Найти остаток и неполное частное.
Решение:
2х3 + 3x2 – 2х + 3| х + 2
2х3 + 4x2 2x2 – x
-x2 – 2x
—x2 – 2x
3
Ответ: R = 3; частное: 2х2 – х.
Основные методы решения уравнений высших степеней
1. Введение новой переменной
Метод введения новой переменной уже знаком на примере биквадратных уравнений. Он заключается в том, что для решения уравнения f(x) = 0 вводят новую переменную (подстановку) t = xn или t = g(х) и выражают f(x) через t, получая новое уравнение r(t). Решая затем уравнение r(t), находят корни:
(t1, t2, …, tn). После этого получают совокупность n уравнений q(x) = t1, q(x) = t2, … , q(x) = tn, из которых находят корни исходного уравнения.
Пример 1.
(х2 + х + 1)2 – 3х2 – 3x – 1 = 0.
Решение:
(х2 + х + 1)2 – 3(х2 + x) – 1 = 0.
(х2 + х + 1)2 – 3(х2 + x + 1) + 3 – 1 = 0.
Замена (х2 + х + 1) = t.
t2 – 3t + 2 = 0.
t1 = 2, t2 = 1. Обратная замена:
х2 + х + 1 = 2 или х2 + х + 1 = 1;
х2 + х — 1 = 0 или х2 + х = 0;
Ответ: Из первого уравнения: х1, 2 = (-1 ± √5)/2, из второго: 0 и -1.
2. Разложение на множители методом группировки и формул сокращенного умножения
Основа данного метода также не нова и заключается в группировке слагаемых таким образом, чтобы каждая группа содержала общий множитель. Для этого иногда приходится применять некоторые искусственные приемы.
Пример 1.
х4 – 3x2 + 4х – 3 = 0.
Решение.
Представим — 3x2 = -2x2 – x2 и сгруппируем:
(х4 – 2x2) – (x2 – 4х + 3) = 0.
(х4 – 2x2 +1 – 1) – (x2 – 4х + 3 + 1 – 1) = 0.
(х2 – 1)2 – 1 – (x – 2)2 + 1 = 0.
(х2 – 1)2 – (x – 2)2 = 0.
(х2 – 1 – х + 2)(х2 – 1 + х — 2) = 0.
(х2 – х + 1)(х2 + х – 3) = 0.
х2 – х + 1 = 0 или х2 + х – 3 = 0.
Ответ: В первом уравнении нет корней, из второго: х1, 2 = (-1 ± √13)/2.
3. Разложение на множитель методом неопределенных коэффициентов
Суть метода состоит в том, что исходный многочлен раскладывается на множители с неизвестными коэффициентами. Используя свойство, что многочлены равны, если равны их коэффициенты при одинаковых степенях, находят неизвестные коэффициенты разложения.
Пример 1.
х3 + 4x2 + 5х + 2 = 0.
Решение.
Многочлен 3-й степени можно разложить в произведение линейного и квадратного множителей.
х3 + 4x2 + 5х + 2 = (х – а)(x2 + bх + c),
х3 + 4x2 + 5х + 2 = х3 +bx2 + cх – ax2 – abх – ac,
х3 + 4x2 + 5х + 2 = х3 + (b – a)x2 + (cх – ab)х – ac.
Решив систему:
{b – a = 4,
{c – ab = 5,
{-ac = 2,
получим
{a = -1,
{b = 3,
{c = 2, т.е.
х3 + 4x2 + 5х + 2 = (х + 1)(x2 + 3х + 2).
Корни уравнения (х + 1)(x2 + 3х + 2) = 0 находятся легко.
Ответ: -1; -2.
4. Метод подбора корня по старшему и свободному коэффициенту
Метод опирается на применение теорем:
1) Всякий целый корень многочлена с целыми коэффициентами является делителем свободного члена.
2) Для того, чтобы несократимая дробь p/q (p – целое, q – натуральное) была корнем уравнения с целыми коэффициентами, необходимо, чтобы число p было целым делителем свободного члена а0, а q – натуральным делителем старшего коэффициента.
Пример 1.
6х3 + 7x2 – 9х + 2 = 0.
Решение:
2 : p = ±1, ±2
6 : q = 1, 2, 3, 6.
Следовательно, p/q = ±1, ±2, ±1/2, ±1/3, ±2/3, ±1/6.
Найдя один корень, например – 2, другие корни найдем, используя деление уголком, метод неопределенных коэффициентов или схему Горнера.
Ответ: -2; 1/2; 1/3.
Остались вопросы? Не знаете, как решать уравнения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!
Зарегистрироваться
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Вид уравнений высших степеней
Уравнения высших степеней имеют вид:
(P(x)=0,)
где( p(x)=a_0x^n+a_1x^{n-1}+…+a_{n-1}x+a_n.)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На практике коэффициенты (a_0, a_1, a_{0-1}), an всегда являются целыми числами.
(a_0) является старшим коэффициентом, который никогда не равен 0.
(a_n )— свободный член.
В таких уравнениях степень больше 2.
Чтобы решить уравнение высшей степени надо найти его корни, или обнаружить, что их нет. Корни представляют собой все значения переменной х, которые приводят многочлен к нулю или верному равенству.
Виды уравнений высших степеней:
- Приведенные целые рациональные уравнения n-й степени.
- Неприведенные.
- Дробные рациональные.
- Кубические.
- Четвертой степени.
- Биквадратные.
- Симметричные. Признаком симметричных уравнений являются равные коэффициенты у одночленов, которые равноудалены от начала и конца многочлена, записанного в стандартном виде и стоящего в левой части уравнения.
- Сводящиеся к возвратному.
На сегодняшний день в математике нет общих формул, которые бы подходили для решения уравнений высших степеней разных видов. Существуют различные системы для решения разных видов таких уравнений.
Методы решения уравнений высших степеней подразделяются на: стандартные и специальные.
Стандартные:
- разложение на множители;
- введение новой переменной.
Специальные:
- деление на подходящее выражение с переменной;
- выделение полного квадрата;
- схема Горнера;
- деление уголком;
- группировка скобок;
- специальная замена;
- представление дроби в виде двух дробей;
- через построение графика функции;
- метод введения параметра.
Теорема Виета
Теорема Виета применяется для решения приведенных квадратных уравнений.
Первый коэффициент в таких уравнениях равен единице.
Теорема
Правило теоремы Виета: Если (x_1) и (x_2) — корни приведенного квадратного уравнения ( x^2+px+q=0,) то
(x_1+x_2=-p,)
(x_1x_2=q.)
Чтобы решить уравнения высших степеней по данной системе, их сначала приводят к квадратным уравнениям.
Теорема Безу
Теорема
Теорема Безу — остаток при делении многочлена (Р(х)) на линейный многочлен (х-α) будет равен (Р(α):)
(q= Р(α).)
Схема решения:
Пусть (α) — корень уравнения (Р(х)=0.)
Тогда при замене вместо х на α, получим
(Р(α)=0.)
Это означает, что остаток при делении( Р(х)) на (х-α):
(Р(α)=0=q.)
Таким образом, если удалось подобрать корень α, то, в соответствии с теоремой Безу, многочлен (Р(х)) нацело разделится на (х-α).
Таким образом, данный метод решения уравнения высших степеней предполагает, что мы подбираем корень α.
В соответствии с теоремой Безу, остаток (q) при делении многочлена на (х-α) будет равен нулю, и мы получим уравнение уже на порядок ниже.
Затем, если оно по-прежнему не квадратное, повторяем процедуры, подбираем новый корень (alpha_1). Снова делим на (х-alpha_1.)
Снова получаем целое число, так как, по теореме Безу, остаток (q=P(α)). А если α — это корень, то остаток q равен нулю.
То есть, если корень подходит, то деление будет осуществляться нацело.
Как подобрать корень
Правило 1
Если (a_0=1, ) (a_iin Z, forall i.)
Такое уравнение называется приведенным, когда старшая степень входит с коэффициентом, равным единице. Если уравнение приведенное, и (α) — целый корень, то (α) содержится в множестве делителей свободного члена:
(alphainleft{da_nright}.)
Корень уравнения находится среди делителей свободного члена (a_n.)
Правило 2
Если (a_0≠1), это неприведенное уравнение.
В этом случае необязательно, что корень будет лежать среди делителей свободного члена. Корень может быть нецелым. Если α рациональна, то корень содержится среди дробей вида, где в числителе стоят делители свободного члена, а в знаменателе стоят делители старшего коэффициента:
(alphainleft{frac{dan}{da_n}right}.)
Схема Горнера
По данной схеме корень уравнения находят через делители свободного члена. Метод заключается в составлении таблицы, в которой отображаются в верхней строке все коэффициенты уравнения. А в первый столбик заносятся потенциальные варианты решения, то есть делители свободного члена.
Принцип заполнения таблицы:
- Во втором столбце во вторую и последующие строчки сносится то, что находится в самом верхнем элементе второго столбика.
- Чтобы найти число для второй строки третьего столбца, перемножают делитель, стоящий на второй строке, с соответствующим ему числом, находящемся во втором столбце и второй строчке, а затем к этому произведению прибавляют следующий коэффициент, стоящий наискосок.
- Далее схема повторяется.
- Продолжаем до тех пор, пока в какой-либо строке не получим нуль.
- Для каждой новой строки прибавляем коэффициенты, а не числа, полученные в предыдущей строке.
Такая таблица позволяет не только проверять, является ли число корнем этого уравнения, но и параллельно осуществляет деление.
Метод Феррари для уравнений 4-ой степени
Уравнение четвертой степени имеет вид: (a_0x^4+a_1x^3+a_2x^2+a_3x+a_4=0).
При этом ( a_0≠0.)
Метод Феррари позволяет решить уравнения четвертой степени через их приведение к кубическому виду. Далее они решаются по формуле Кардано. То есть используется алгоритм решения кубических уравнений.
Находят (y_0) — любой из корней кубического уравнения:
(y^3-By^2+(AC-4D)y-A^2D+4BD-C^2=0.)
Затем решают два квадратных уравнения:
(x^2+frac A2x+frac{y_0}2pmsqrt{left(frac{A^2}4-B+y_0right)x^2+left(frac A2y_0-Cright)x+frac{y_0^2}4-D}=0.)
Полный квадрат является подкоренным выражением.
Корни этих уравнений являются корнями исходного уравнения четвертой степени.
Примеры применения способов на практике
Решение заданий с помощью теоремы Безу
Задача
Рассмотрим два многочлена:
(Р(х) = x^3+3x^2-2x+2;)
(Q(x) = x-1;)
Необходимо найти остаток от деления (Р(х)) на (Q(x)). Используем деление столбиком.
Получим (q=4.)
В нашем примере число (α = 1.)
(P(α)) означает, что в многочлен (Р(x)) вместо х нужно подставить (α).
Тогда многочлен примет вид:
(P(x)= 1^3+3cdot1^2-2cdot1+2.)
(P(x)=4.)
Решение заданий при помощи схемы Горнера
Решим уравнение:
(x^3+4x^2-6x-3=0.)
Сначала выписываем делители свободного члена:
(d{-3}:pm1; pm3.)
Коэффициенты: 1, -4, 6, -3. Их заносим в верхнюю строчку таблицы.
В первый столбец занесем потенциальные кандидаты в решения, например, -1 и 1.
В первый столбец запишем единицу. Она просто носится по строкам.
Чтобы записать ответ во второй строке третьего столбца, умножим единицу на минус единицу и прибавим минус 4:
(-1*1+4=-5.)
По этому принципу заполняем всю таблицу.
|
1 |
-4 |
6 |
-3 |
|
|
-1 |
1 |
-5 |
11 |
-14 |
|
1 |
1 |
-3 |
3 |
0 |
В соответствии с таблицей, мы видим, что корень (х=1) подходит.
Далее находим корни в полученном квадратном уравнении (x^2-3x+3=0.)
Единственным корнем уравнения будет (х=1.)
Решение уравнений четвертой степени через разложение на множители и теорему Безу
Задача
Дано уравнение четвертой степени:
(3x^4-3x^3+2x^2+x+1=0.)
(P4(х) = 0.)
Первый корень находим подбором среди делителей свободного члена.
Делители числа 1 — 1; -1.
Возьмем первое значение х=1 и подставим в уравнение вместо х.
Получим:
(3cdot1^4-3cdot1^3+2cdot1^2+1+1=0.)
Получилось верное равенство, а, значит, единица является корнем.
Значит многочлен (P4(х)) делится без остатка на ((х-1).)
Разделим столбиком и получим кубическое уравнение:
(3x^3-2x-1=0.)
Тогда запишем многочлен в виде множителей:
((х-1)(3x^3-2x-1=0)=0.)
Произведение равно нулю, если хотя бы один из множителей равен нулю.
Тогда ((х-1)=0) или ((3 *(3x^3-2x-1=0)=0.)
Чтобы решить уравнение третьей степени так же находим корень подбором среди делителей свободного члена.
Повторяем деление столбиком многочлена на (х-корень).
Получаем квадратное уравнение.
Разложим многочлен четвертого уровня на множители:
((х-1)(х-1)(3x^2-3x+1=0)=0.)
Получим:
(left(x-1right)^2(3x^2-3x+1=0)=0.)
(left(x-1right)^2=0) или ((3x^2-3x+1=0)=0.)
Из (left(x-1right)^2=0) получим: (х=1). Это корень второй кратности.
У квадратного уравнения (3x^2-3x+1=0=0) нет корней.
Ответ: (x_1=x_2=1.)
Решение уравнений четвертой степени по методу Феррари
Задача
Дано уравнение (x^4+3x^3+3x^2-x-6=0.)
Необходимо найти его корни.
Коэффициенты уравнения: (a=3), (b=3), (c=-1), (d=-6.)
Сначала составим кубическое уравнение:
(y^3-By^2+(AC-4D)y-A^2D+4BD-C^2=0;)
(y^3-3y^2+21y-19=0.)
Корень полученного кубического уравнения — (y_0=1,)
так как (1^3-3cdot1^2+21cdot1-19=0.)
Получим два квадратных уравнения и найдем их корни.
(x^2+frac A2x+frac{y_0}2pmsqrt{left(frac{A^2}4-B+y_0right)x^2+left(frac A2y_0-Cright)x+frac{y_0^2}4-D}=0;)
(x^2+frac32x+frac12pmsqrt{frac14x^2+frac52x+frac{25}4}=0;)
(x^2+frac32x+frac12+frac12x+frac52=0) или (x^2+frac32x+frac12-frac12x-frac52=0.)
(x^2+2x+3=0) или (x^2+x-2=0.)
Корнями первого уравнения являются (x=-1pm isqrt2), корнями второго — (х = 1) и (х = -2.)
Ответ: (x_{1,2}=x=-1pm isqrt2), (x_3=1, x_4=-2.)
Основные цели:
- Закрепить понятие целого рационального уравнения -й степени.
- Сформулировать основные методы решения уравнений высших степеней (n >
3). - Обучить основным методам решения уравнений высших степеней.
- Научить по виду уравнения определять наиболее эффективный способ его
решения.
Формы, методы и педагогические приемы, которые используются учителем на
уроке:
- Лекционно-семинарская система обучения (лекции – объяснение нового
материала, семинары – решение задач). - Информационно-коммуникационные технологии (фронтальный опрос, устная
работа с классом). - Дифференцированное обучение, групповые и индивидуальные формы.
- Использование исследовательского метода в обучении, направленного на
развитие математического аппарата и мыслительных способностей каждого
конкретного ученика. - Печатный материал – индивидуальный краткий конспект урока (основные
понятия, формулы, утверждения, материал лекций сжато в виде схем или таблиц).
План урока:
- Организационный момент.
Цель этапа: включить учащихся в учебную деятельность, определить
содержательные рамки урока. - Актуализация знаний учащихся.
Цель этапа: актуализировать знания учащихся по изученным ранее смежным темам - Изучение новой темы (лекция). Цель этапа: сформулировать основные методы
решения уравнений высших степеней (n > 3) - Подведение итогов.
Цель этапа: еще раз выделить ключевые моменты в материале, изученном на
уроке. - Домашнее задание.
Цель этапа: сформулировать домашнее задание для учащихся.
Конспект урока
1. Организационный момент.
Формулировка темы урока: “Уравнения высших степеней. Методы их решения”.
2. Актуализация знаний учащихся.
Теоретический опрос – беседа. Повторение некоторых ранее изученных сведений
из теории. Учащиеся формулируют основные определения и дают формулировки
необходимых теорем. Приводят примеры, демонстрируя уровень полученных ранее
знаний.
- Понятие уравнения с одной переменной.
- Понятие корня уравнения, решения уравнения.
- Понятие линейного уравнения с одной переменной, понятие квадратного
уравнения с одной переменной. - Понятие равносильности уравнений, уравнения-следствия (понятие
посторонних корней), переход не по следствию (случай потери корней). - Понятие целого рационального выражения с одной переменной.
- Понятие целого рационального уравнения n-й степени. Стандартный
вид целого рационального уравнения. Приведенное целое рациональное уравнение. - Переход к совокупности уравнений более низких степеней путем разложения
исходного уравнения на множители. - Понятие многочлена n-й степени от x. Теорема Безу.
Следствия из теоремы Безу. Теоремы о корнях (Z-корни и Q-корни)
целого рационального уравнения с целыми коэффициентами (соответственно
приведенного и неприведенного). - Схема Горнера.
3. Изучение новой темы.
Будем рассматривать целое рациональное уравнение n-й степени
стандартного вида с одной неизвестной переменной x : Pn(x) = 0
, где Pn(x) = anxn + an-1xn-1
+ a1x + a0 – многочлен n-й степени от x,
an ≠ 0. Если an
= 1 то такое уравнение называют приведенным целым рациональным уравнением
n-й степени. Рассмотрим такие уравнения при различных значениях n
и перечислим основные методы их решения.
n = 1 – линейное уравнение.
n = 2 – квадратное уравнение. Формула дискриминанта. Формула
для вычисления корней. Теорема Виета. Выделение полного квадрата.
n = 3 – кубическое уравнение.
Метод группировки.
Пример: x3 – 4x2 – x + 4 = 0
(x – 4)(x2 – 1) = 0
x1 = 4 , x2 = 1, x3 = -1.
Возвратное кубическое уравнение вида ax3 + bx2
+ bx + a = 0. Решаем, объединяя члены с одинаковыми
коэффициентами.
Пример: x3 – 5x2 – 5x + 1 = 0
(x + 1)(x2 – 6x + 1) = 0
x1 = -1, x2 = 3 + 2,
x3 = 3 – 2.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы.
Схема Горнера. При применении этого метода необходимо сделать акцент на том, что
перебор в данном случае конечный, и корни мы подбираем по определенному
алгоритму в соответствии с теоремой о Z-корнях приведенного целого
рационального уравнения с целыми коэффициентами.
Пример: x3 – 9x2 + 23x – 15 = 0.
Уравнение приведенное. Выпишем делители свободного члена {+1; +3;
+5; +15}. Применим схему Горнера:
| x3 | x2 | x1 | x0 | вывод | |
| 1 | -9 | 23 | -15 | ||
| 1 | 1 | 1 х 1 – 9 = -8 | 1 х (-8) + 23 = 15 | 1 х 15 – 15 = 0 | 1 – корень |
| x2 | x1 | x0 |
Получаем
(x – 1)(x2 – 8x + 15) = 0
x1 = 1, x2 = 3, x3 = 5.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании теоремы.
Схема Горнера. При применении этого метода необходимо сделать акцент на том, что
перебор в данном случае конечный и корни мы подбираем по определенному алгоритму
в соответствии с теоремой о Q-корнях неприведенного целого рационального
уравнения с целыми коэффициентами.
Пример: 9x3 + 27x2 – x – 3 = 0.
Уравнение неприведенное. Выпишем делители свободного члена {+1; +3}.
Выпишем делители коэффициента при старшей степени неизвестного. {+1; +3;
+9} Следовательно, корни будем искать среди значений {+1; +;
+;
+3}. Применим схему Горнера:
| x3 | x2 | x1 | x0 | вывод | |
| 9 | 27 | -1 | -3 | ||
| 1 | 9 | 1 x 9 + 27 = 36 | 1 x 36 – 1 = 35 | 1 x 35 – 3 = 32 ≠ 0 | 1 – не корень |
| -1 | 9 | -1 x 9 + 27 = 18 | -1 x 18 – 1 = -19 | -1 x (-19) – 3 = 16 ≠ 0 |
-1 – не корень |
|
|
9 |
x 9 + 27 = 30 |
x 30 – 1 = 9 |
x 9 – 3 = 0 |
корень |
| x2 | x1 | x0 |
Получаем
(x –
)(9x2
+ 30x + 9) = 0
x1 =
,
x2 = —
, x3 = -3.
Для удобства подсчета при подборе Q-корней бывает удобно сделать
замену переменной, перейти к приведенному уравнению и подбирать Z-корни.
- Если свободный член равен 1.
- Если можно воспользоваться заменой вида y = kx .
Формула Кардано. Существует универсальный метод решения кубических
уравнений – это формула Кардано. Эту формулу связывают с именами итальянских
математиков Джероламо Кардано (1501–1576), Николо Тарталья (1500–1557), Сципиона
дель Ферро (1465–1526). Эта формула лежит за рамками нашего курса.
n = 4 – уравнение четвертой степени.
Метод группировки.
Пример: x4 + 2x3 + 5x2
+ 4x – 12 = 0
(x4 + 2x3) + (5x2 + 10x)
– (6x + 12 ) = 0
(x + 2)(x3 + 5x – 6) = 0
(x + 2)(x – 1)(x2 + x + 6) = 0
x1 = -2, x2 = 1.
Метод замены переменной.
- Биквадратное уравнение вида ax4 + bx2
+ с = 0.
Пример: x4 + 5x2
– 36 = 0. Замена y = x2. Отсюда y1 =
4, y2 = -9. Поэтому x1,2 = +2 .
- Возвратное уравнение четвертой степени вида ax4 +
bx3 + cx2 + bx + a = 0.
Решаем, объединяя члены с одинаковыми коэффициентами, путем замены вида
- Обобщенное возвратное уравнение четвертой степени вида ax4
+ bx3 + cx2 – bx + a = 0.
- Обобщенное возвратное уравнение четвертой степени вида ax4
+ bx3 + cx2 + kbx
+ k2a = 0.
- Замена общего вида. Некоторые стандартные замены.
Пример 1:
Пример 3. Замена общего вида (вытекает из вида конкретного
уравнения).
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы.
Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании
теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n =
3.
Формула общего вида. Существует универсальный метод решения уравнений
четвертой степени. Эту формулу связывают с именем Людовико Феррари (1522–1565).
Эта формула лежит за рамками нашего курса.
n > 5 – уравнения пятой и более высоких степеней.
Уравнение с целыми коэффициентами. Подбор Z-корней на основании теоремы.
Схема Горнера. Алгоритм аналогичен рассмотренному выше для n = 3.
Уравнение с целыми коэффициентами. Подбор Q-корней на основании
теоремы. Схема Горнера. Алгоритм аналогичен рассмотренному выше для n =
3.
Симметрические уравнения. Любое возвратное уравнение нечетной степени
имеет корень x = -1 и после разложения его на множители получаем, что
один сомножитель имеет вид (x + 1), а второй сомножитель – возвратное
уравнение четной степени (его степень на единицу меньше, чем степень исходного
уравнения). Любое возвратное уравнение четной степени вместе с корнем вида x
= φ содержит и корень вида
.
Используя эти утверждения, решаем задачу, понижая степень исследуемого уравнения.
Метод замены переменной. Использование однородности.
Не существует формулы общего вида для решения целых уравнений пятой
степени (это показали итальянский математик Паоло Руффини (1765–1822) и
норвежский математик Нильс Хенрик Абель (1802–1829)) и более высоких степеней (это
показал французский математик Эварист Галуа (1811–1832)).
- Напомним еще раз, что на практике возможно использование комбинации
перечисленных выше методов. Удобно переходить к совокупности уравнений более
низких степеней путем разложения исходного уравнения на множители.
- За рамками нашего сегодняшнего обсуждения остались широко используемые
на практике графические методы решения уравнений и методы
приближенного решения уравнений высших степеней. - Бывают ситуации, когда у уравнения нет R-корней. Тогда решение
сводится к тому, чтобы показать, что уравнение корней не имеет. Для
доказательства анализируем поведение рассматриваемых функций на промежутках
монотонности. Пример: уравнение x8 – x3
+ 1 = 0 не имеет корней. - Использование свойства монотонности функций. Бывают ситуации, когда
использование различных свойств функций позволяет упростить поставленную
задачу.
Пример 1: уравнение x5 + 3x – 4 = 0 имеет
один корень x = 1. По свойству монотонности анализируемых функций
других корней нет.
Пример 2: уравнение x4 + (x – 1)4
= 97 имеет корни x1 = -2 и x2 = 3.
Проанализировав поведение соответствующих функций на промежутках
монотонности, заключаем, что других корней нет.
4. Подведение итогов.
Резюме: Теперь мы овладели основными методами решения различных уравнений
высших степеней (для n > 3).
Наша задача научиться эффективно использовать перечисленные выше алгоритмы. В
зависимости от вида уравнения мы должны будем научиться определять, какой способ
решения в данном случае является наиболее эффективным, а также правильно
применять выбранный метод.
5. Домашнее задание.
[1]: п.7, стр. 164–174, №№ 33–36,
39–44, 46,47.
[4]: №№ 9.1–9.4, 9.6–9.8, 9.12,
9.14–9.16, 9.24–9.27.
Возможные темы докладов или рефератов по данной тематике:
- Формула Кардано
- Графический метод решения уравнений. Примеры решения.
- Методы приближенного решения уравнений.
Анализ усвоения материала и интереса учащихся к теме:
Опыт показывает, что интерес учащихся в первую очередь вызывает возможность
подбора Z-корней и Q-корней уравнений при помощи достаточно
простого алгоритма с использованием схемы Горнера. Также учащиеся интересуются
различными стандартными типами замены переменных, которые позволяют существенно
упрощать вид задачи. Особый интерес обычно вызывают графические методы решения.
В этом случае дополнительно можно разобрать задачи на графический метод решения
уравнений; обсудить общий вид графика для многочлена 3, 4, 5 степени;
проанализировать, как связано число корней уравнений 3, 4, 5 степени с видом
соответствующего графика. Ниже приведен список книг, в которых можно найти
дополнительную информацию по данной тематике.
Список литературы:
- Виленкин Н.Я. и др. “Алгебра. Учебник для учащихся 9 классов с
углубленным изучением математики” – М., Просвещение, 2007 – 367 с. - Виленкин Н.Я., Шибасов Л.П., Шибасова З.Ф. “За страницами
учебника математики. Арифметика. Алгебра. 10-11 класс” – М., Просвещение,
2008 – 192 с. - Выгодский М.Я. “Справочник по математике” – М., АСТ, 2010 – 1055
с. - Галицкий М.Л. “Сборник задач по алгебре. Учебное пособие для 8-9
классов с углубленным изучением математики” – М., Просвещение, 2008 – 301 с. - Звавич Л.И. и др. “Алгебра и начала анализа. 8–11
кл. Пособие для школ и классов с углубленным изучением математики” – М.,
Дрофа, 1999 – 352 с. - Звавич Л.И., Аверьянов Д.И., Пигарев Б.П., Трушанина Т.Н.
“Задания по математике для подготовки к письменному экзамену в 9 классе” –
М., Просвещение, 2007 – 112 с. - Иванов А.А., Иванов А.П. “Тематические тесты для систематизации
знаний по математике” ч.1 – М., Физматкнига, 2006 – 176 с. - Иванов А.А., Иванов А.П. “Тематические тесты для систематизации
знаний по математике” ч.2 – М., Физматкнига, 2006 – 176 с. - Иванов А.П. “Тесты и контрольные работы по математике. Учебное
пособие”. – М., Физматкнига, 2008 – 304 с. - Лейбсон К.Л. “Сборник практических заданий по математике. Часть
2–9 класс” – М., МЦНМО, 2009 – 184 с. - Макарычев Ю.Н., Миндюк Н.Г. “Алгебра. Дополнительные главы к
школьному учебнику 9 класса. Учебное пособие для учащихся школ и классов с
углубленным изучением математики.” – М., Просвещение, 2006 – 224 с. - Мордкович А.Г. “Алгебра. Углубленное изучение. 8 класс. Учебник”
– М., Мнемозина, 2006 – 296 с. - Савин А.П. “Энциклопедический словарь юного математика” – М.,
Педагогика, 1985 – 352 с. - Сурвилло Г.С., Симонов А.С. “Дидактические материалы по алгебре
для 9 класса с углубленным изучением математики” – М., Просвещение, 2006 –
95 с. - Чулков П.В. “Уравнения и неравенства в школьном курсе математик.
Лекции 1–4” – М., Первое сентября, 2006 – 88 с. - Чулков П.В. “Уравнения и неравенства в школьном курсе математик.
Лекции 5–8” – М., Первое сентября, 2009 – 84 с.
Елена Борисовна Калюжная
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Замечание 1
Уравнения высших степеней — это уравнения, в которых старшая степень при переменной больше либо равна трём. На данный момент не существует какой-либо единой схемы для решения уравнений высших степеней.
Наиболее известными схемами для решения являются:
- Формула Кардано, он подходит только для уравнений 3-ьей степени;
- Метод Феррари для уравнений 4-ой степени;
- Теорема Виета для степени больше двух;
- Теорема Безу;
- Схема Горнера.
Ниже рассмотрены основные методы решения уравнений высших степеней с целыми и рациональными коэффициентами, справедливые для разных степеней.
Теорема Виета
Рассмотрим уравнение вида $ax^3+bx^2+cx+d=0$.
Данное уравнение обладает тремя корнями и для того чтобы его решить в общем виде, необходимо решить следующую систему:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
$begin{cases} x_1 + x_2+x_3=-frac{b}{a} \ x_1x_2 + x_2x_3+x_3x_1=frac{c}{a} \ x_1x_2x_3=-frac{d}{a} \ end{cases}$
Иначе эти системы уравнений также называют формулами Виета.
Пример 1
Решите уравнение: $x^3+x^2-4x-4=0$.
Решение:
Составим систему уравнений:
$begin{cases} x_1+ x_2+x_3=-frac{1}{1} \ x_1 cdot x_2 + x_2 cdot x_3 + x_1 cdot x_3=-frac{4}{1}=-4 \ x_1 cdot x_2 cdot x_3= -frac{4}{1}\ end{cases}$
Решив её, получим следующие корни:
$begin{cases} x_1=-2 \ x_2=2 \ x_3=-1 \ end{cases}$
Теорема Безу
Суть этой теоремы в том, что если уравнение вида $a_0x^n + a_1x^{n-1}+a_2x^{n-2]}+…+a_{n-1}x+a_n=0$ с ненулевым свободным членом имеет некий корень $α$, принадлежащий к множеству целых чисел, то этот корень будет делителем свободного члена.
Алгоритм при решении уравнения с использованием теоремы Безу следующий:
- Найти и выписать все делители свободного члена.
- Проверять эти делители до тех пор, пока не будет найден хотя бы один, являющийся корнем уравнения.
- Разделить всё уравнение на $(x-α)$ и записать само уравнение как произведение $(x-α)$ и результата выполненного деления.
- Решить полученное после разложения уравнение.
«Уравнения высших степеней» 👇
Пример 2
Решите: $x^3+4x^2+x-6=0$
Решение:
Делители члена не при переменной: $±1;±2;±3;±6$
Подставим $1$ в корень уравнения и получим, что наше равенство выполняется:
$1^3+4 cdot 1^2+1-6=0$
Следовательно, $x_1=1$ — один из корней уравнения.
Теперь необходимо выполнить деление многочлена столбиком:
Рисунок 1. Схема деления многочлена столбиком. Автор24 — интернет-биржа студенческих работ
После этого исходное уравнение можно записать разложив на множители:
$(x-1)(x^2+5x+6)=0$
Решаем полученное квадратное уравнение и получаем ещё 2 корня: $x_{2,3}=-3;-2$.
Схема Горнера
Схема Горнера состоит в том, чтобы также сначала найти какой-либо корень уравнения вида $a_0x^n + a_1x^{n-1}+a_2x^{n-2]}+…+a_{n-1}x+a_n=0$ через делители свободного члена.
После этого составляется специальная таблица с результатами деления на $(x-α)$, в которой каждый член зависим от предыдущего. Коэффициенты из данной таблицы используются как коэффициенты в полученном от деления частного многочлене, они вычисляются по формулам:
$b_0=a_0; b_1=αb_0+a_1; b_2=αb_1+a_2…b_{n-1}= αb_{n-2}+a_{n-1};b_n=αb_{n-1}+a_n$.
Рисунок 2. Таблица для вычисления коэффициентов по схеме Горнера. Автор24 — интернет-биржа студенческих работ
Пример 3
Решить: $x^3+4x^2+x-6=0$.
Решение:
Делители свободного члена — $±1;±2;±3;±6$
Запишем таблицу со коэффициентами:
Рисунок 3. Схема Горнера: пример. Автор24 — интернет-биржа студенческих работ
Отсюда получаем, что многочлен, полученный от деления на $(x-α)$ при $α=1$, равен $x^2+5x+6$.Получается, что исходное уравнение принимает вид:
$(x-1) cdot ( x^2+5x+6)=0$.
Корни же второго многочлена будут $x_{2,3}=-2;-3$.
Метод одновременного подбора по коэффициенту при старшей степени и при свободном члене
Данный метод основан на следующем условии:
Определение 1
Несократимая дробь $frac{p}{q}$ будет корнем уравнения, если числитель этой дроби является делителем свободного члена, а знаменатель — делителем коэффициента, стоящего при члене со старшей степенью.
Алгоритм этого метода:
- Поиск делителей свободного члена.
- Поиск делителей коэффициента, стоящего при члене со старшей степенью.
- Составление дробей и подбор решения.
Пример 4
Решите: $2x^4+17x^3-17x^2-8x+6=0$.
Решение:
Делители свободного члена: $±1; ±2; ±3; ±6$.
Делители коэффициента при старшем члене: $1; 2$.
Следовательно, как корни нужно проверить следующие значения: $1;-1;2;-2;3;-3;6;-6;frac{1}{2}; -frac{1}{2}; frac{3}{2}; -frac{3}{2}$.
Подставив эти числа в уравнения, получим, что корнями уравнения являются $x_1=1;x_2= frac{1}{2}$.
Это значит, что многочлен можно разделить на $2(x-1)(x-frac{1}{2})=2x^2-3x+1$. При выполнении деления получаем частное $x^2+10x+6$.
Приравниваем этот многочлен к нулю и находим его корни через дискриминант, они равны $x_{3,4}=-5±sqrt{19}$.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Уравнение n-й степени с одним неизвестным:
Определение:
Уравнением n-й степени с одним неизвестным х называется уравнение
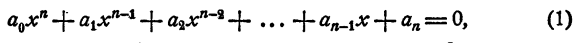
где 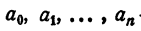
Изучение уравнения (1) в общем виде выходит за рамки школьного курса алгебры. В этой главе рассматриваются лишь некоторые свойства уравнения (1) и, кроме того, изучаются некоторые его частные виды.
Деление многочлена относительно х на х—а
Теорема:
Остаток от деления многочлена относительно х на двучлен х — а равен значению этого многочлена при х, равном а.
Доказательство:
Разделим многочлен n-й степени
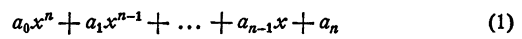
на двучлен х — а. Как известно, частным (неполным) в этом случае будет многочлен n— 1 степени
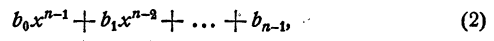
а остатком — некоторое число r. Так как делимое равно делителю, умноженному на частное, плюс остаток, то
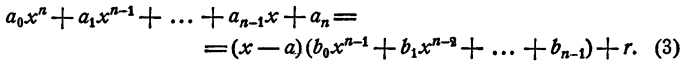
Равенство (3) есть тождество, оно справедливо при любых значениях х. В частности, оно справедливо и при х = а. При х = а. первое слагаемое правой части равенства (3) обращается в нуль, а потому
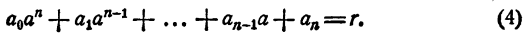
Следствие:
Для того чтобы многочлен относительно х делился на двучлен х — а, необходимо и достаточно, чтобы число а было корнем этого многочлена, т. е. чтобы при х = а многочлен обращался в нуль.
Доказательство:
Необходимость:
Пусть многочлен (1) делится на х — а, т. е. остаток r равен нулю. Тогда на основании равенства (4)
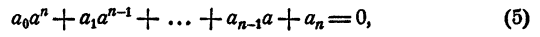
т. е. а — корень многочлена (1).
Достаточность:
Пусть а — корень многочлена (1), т. е. имеет место равенство (5). Тогда на основании равенства (4) r = 0, т. е. многочлен (1) делится на двучлен х — а.
Рассмотрим вновь тождество (3). Если в правой части его раскрыть скобки и сделать приведение подобных членов, в результате должен получиться тот же многочлен, что и в левой части. На этом основании, приравнивая коэффициенты при одинаковых степенях х, получаем
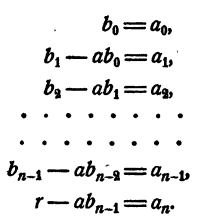
Перепишем эти равенства так:
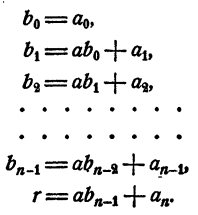
Полученные равенства показывают, что коэффициенты частного и остаток, т. е. 
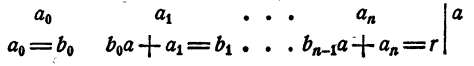
Пример:
Разделить многочлен
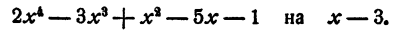
Решение:
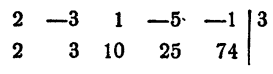
Первый коэффициент 2 второй строки просто сносится (b₀ = а₀). Второй коэффициент 3 получен так:
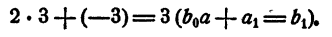
Третий коэффициент 10 получен так:
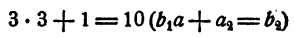
и т. д. Неполное частное равно
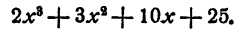
Остаток 74.
Пример:
Найти значение многочлена
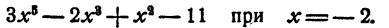
Решение:
Искомое значение многочлена равно остатку от деления многочлена на x + 2
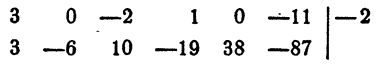
В двух местах первой строки потребовалось вписать 0. Объясняется это тем, что делимое имеет следующий вид:
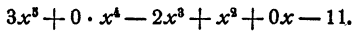
Обычно члены, коэффициенты которых равны нулю, пропускаются. Здесь их пропускать нельзя.
Ответ. —87.
Составление уравнения n-й степени по его корням
Теорема:
Каковы бы ни были числа 
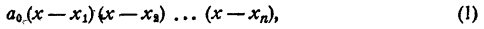
где a₀ — любое число, отличное от нуля. При x = x₁ двучлен x — x₁ обращается в нуль, значит, при этом значении х обращается в нуль и произведение (1). При х = х₂ обращается в нуль двучлен х — x₂, и опять произведение (1) обращается в нуль. То же самое происходит при х =x₃; х = хₙ.
Пусть теперь х = а, где a — число, отличное от x₁ x₂ , …., хₙ . Ни одна из разностей а— x₁ а— x₂ ,…..о— хₙ „ не равна нулю. Число а₀ тоже отлично от нуля. Значит, и произведение
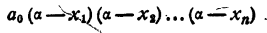
отлично от нуля.
Таким образом, уравнение
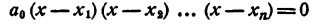
имеет корнями x₁ x₂ , …., хₙ и только эти числа.
Раскрыв скобки и выполнив приведение подобных членов, получим в левой части уравнения многочлен n-й степени относительно х, т. е.
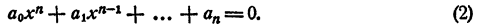
Корнями уравнения (2) являются числа x₁ x₂ , …., хₙ и только эти числа.
Возможно, что корни x₁ x₂ , …., хₙ уравнения (2) не все различны между собой. В этих случаях говорят, что уравнение (2) имеет кратные корни. Так, например, если x₁ = x₂ и отлично от других корней уравнения (2), число является корнем второй кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (x — x₁ )³ и не делится на (х — x₁)³. Если x₁ = x₂ = x₃ и отлично от других корней уравнения (2), число x₁ является корнем третьей кратности уравнения (2). Левая часть уравнения (2) делится в этом случае на (х — x₁ )³ и не делится на (х— x₁ )⁴.
Вообще корнем кратности k уравнения (2) называется такое число а, что левая часть уравнения (2) делится на (х — а)ᵏ и не делится на
Пример:
Составить уравнение второй степени, корни которого
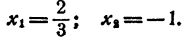
Решение:
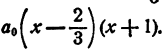
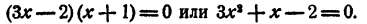
Пример:
Составить уравнение второй степени, корни которого x₁ = 1; х₂ =i.
Решение:
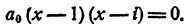
Пример:
Составить уравнение четвертой степени, корни которого i; —i; 1+i; 1-i
Решение:
Имеем
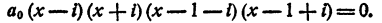
Положим а₀ = 1.
Пример:
Составить уравнение третьей степени, корни которого x₁ = 1; х₂ = 1; х₃ = — 1.
Решение:
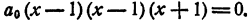
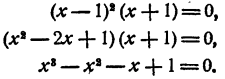
Число единица является здесь корнем второй кратности,
Основная теорема алгебры и некоторые следствия из нее
Мы видели, что, выбрав произвольные п комплексных чисел, можно составить уравнение п-й степени, корнями которого будут выбранные числа. Коэффициенты этого уравнения могут при -этом оказаться как вещественными, так и мнимыми. Возникает следующий весьма важный вопрос.
Дано уравнение n-й степени с комплексными коэффициентами
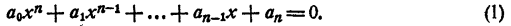
Можно ли утверждать, что среди комплексных чисел найдется хоть одно число, являющееся корнем этого уравнения?
В свое время мы видели, что среди целых чисел нет числа, являющегося корнем уравнения 2х— 3 = 0 с целыми коэффициентами. Среди положительных чисел нет числа, являющегося корнем уравнения x+ 1 = 0 с положительными коэффициентами.
Среди рациональных чисел нет числа, являющегося корнем уравнения x² — 2 = 0 с рациональными коэффициентами. Среди действительных чисел нет числа, являющегося корнем уравнения x²+ 1 = 0 с действительными коэффициентами.
Понятно поэтому, сколь важное значение имеет поставленный вопрос. Ответ на него дает основная теорема алгебры.
Всякое уравнение n-й степени с любыми комплексными коэффициентами имеет комплексный корень.
Доказательство этой теоремы выходит за рамки школьной программы.
Теорема:
Всякий многочлен n-й степени с любыми комплексными коэффициентами может быть представлен и притом единственным образом в виде произведения п двучленов первой степени, т. е.
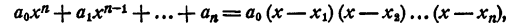
где a ≠ 0, n ≥ 1. (Два таких разложения, отличающиеся только порядком расположения множителей, не считаются различными.)
Доказательство:
Доказательство разбивается на две части. В первой части доказывается возможность представления многочлена n-й степени в виде произведения п двучленов первой степени, во второй—единственность такого представления.
Для n = 1 теорема верна, так как
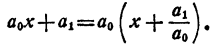
Предположим, что теорема справедлива для многочленов степени n—1.
Согласно основной теореме алгебры многочлен 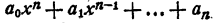
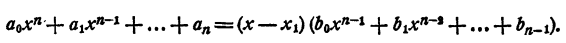
Здесь b₀ = a₀ (см. § 2).
Для многочлена 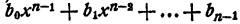
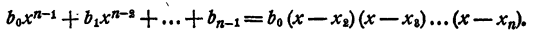
Следовательно,
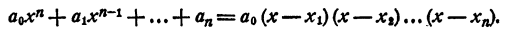
Допустим, что имеется два таких разложения:
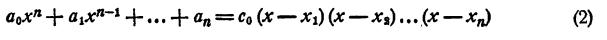
и
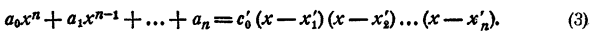
Так как коэффициенты при хⁿ в правой и левой частях равенств (2) и (3) должны быть равны, то
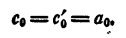
Приравниваем правые части равенств (2) и (3). После сокращения на а₀ имеем
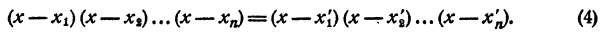
Методом математической индукции докажем, что правая и левая части равенства (4) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке.
Для n= 1 утверждение, очевидно, справедливо.
Пусть утверждение справедливо для произведений, состоящих из n—1 множителей. Докажем, что утверждение справедливо и для произведений, состоящих из n множителей.
Левая часть равенства (4) при x = x₁ обращается в нуль. Значит, при x = x₁ обращается в нуль и правая часть этого равенства, т. е.
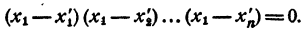
Произведение равно нулю. Значит, хоть один из сомножителей равен нулю. Допустим, что 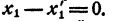
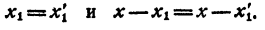
Сократим равенство (4) на х— x₁ получим
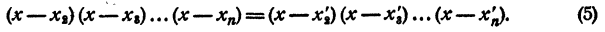
По допущению правая и левая части равенства (5) состоят из соответственно равных множителей, но, быть может, записанных в другом порядке. Приписав в каждую часть равенства (5) по одинаковому множителю х— x₁ получим, что правая и левая части равенства (4) состоят из соответственно равных сомножителей.
Теорема доказана полностью.
В разложении
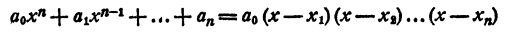
некоторые из сомножителей правой части могут быть одинаковы. Обозначив 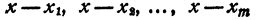
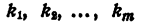
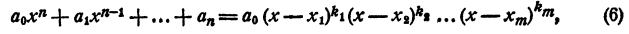
где 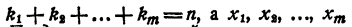
Представление левой части уравнения в виде (6) называется представлением левой части уравнения в канонической форме.
Теорема:
Всякое уравнение п-й степени с любыми комплексными коэффициентами имеет ровно п корней, среди которых могут быть и равные друг другу.
Доказательство:
Дано уравнение
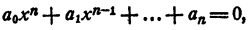
где a₀ ≠ 0, n ≥ 0 Как доказано, левая часть может быть представлена в виде произведения n множителей первой степени. Таким образом, имеем
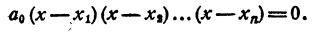
При x=x₁; х = х₂; х=хₙ левая часть уравнения превращается в нуль и, следовательно, х₁, х₂, …,xₙ— корни уравнения. Покажем, что никакое число а, отличное от х₁ х₂,…..хₙ, не может быть корнем этого уравнения.
Действительно, произведение а₀ (а — x₁) (а — х ₂ ,)… (а — x ₙ )не равно нулю, так как ни один из множителей его не равен нулю. Таким образом, корнями рассматриваемого уравнения являются числа x₁; х ₂ ;…; x ₙ и других корней нет.
Следствие:
Уравнение n-й степени имеет n корней, если каждый корень считать столько раз, какова его кратность.
Теорема:
Если уравнение n-й степени имеет действительные коэффициенты и мнимое число а + bi является корнем этого уравнения, то и сопряженное число а — bi является также корнем этого уравнения.
Доказательство:
Пусть мнимое число а + bi является корнем уравнения
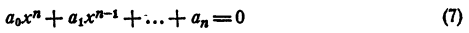
с действительными коэффициентами. Требуется доказать, что сопряженное число а — bi также является корнем уравнения (7). Составим многочлен
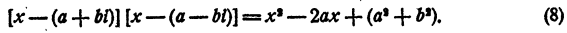
Этот многочлен имеет действительные коэффициенты. Разделим левую часть уравнения (7) на многочлен (8). В частном получим многочлен n— 2 степени с действительными коэффициентами, в остатке многочлен степени не выше первой и тоже с действительными коэффициентами.
Так как делимое равно делителю, умноженному на частное плюс остаток, то
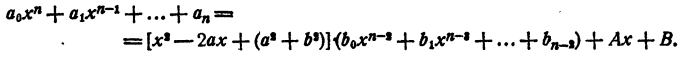
Положим в этом равенстве х = а + bi . Получим
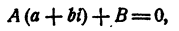
так как и левая часть равенства и трехчлен 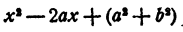
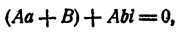
следовательно,

Так как b ≠ 0, то A = 0. Из первого уравнения системы (9) имеем В = 0. Выходит, что остаток Ах + В равен нулю, т. е.
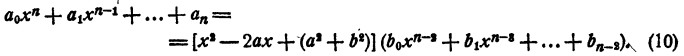
При х = а — bi первый сомножитель правой части равенства (10) превращается в нуль, значит, и левая часть равенства тоже обращается в нуль. Значит, число а — bi является корнем уравнения (7).
Теорема:
Всякий многочлен n-й степени с действительными коэффициентами может быть представлен в виде произведения многочленов первой или второй степени с действительными коэффициентами.
Доказательство этой теоремы проводится методом математической индукции. Теорема, очевидно, справедлива для многочленов первой и второй степени. При этом многочлен второй степени либо имеет действительные корни и тогда разлагается на множители первой степени с действительными коэффициентами, либо он имеет два мнимых сопряженных корня, и тогда он на множители с действительными коэффициентами не разлагается.
Допустим, что теорема справедлива для многочленов n— 2 степени и многочленов n—1 степени. Докажем, что тогда она справедлива и для многочленов n-й степени.
Пусть 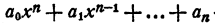
Если этот многочлен имеет действительный корень x₁ то он представляется в виде произведения многочлена первой степени на многочлен n—1 степени с действительными коэффициентами, т. е.
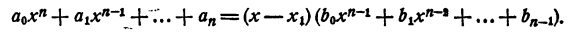
Если же многочлен действительных корней не имеет, то он имеет мнимый корень а + bi и сопряженный с ним корень а — bi. В этом случае многочлен представляется в виде произведения трехчлена второй степени на многочлен n— 2 степени с действительными коэффициентами, т. е.
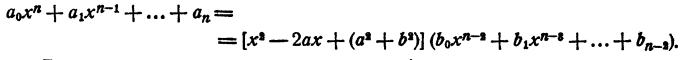
Так как теорема для многочленов п—1 степени и многочленов n— 2 степени справедлива, то она справедлива и для многочленов степени n.
Теорема Виета
Из равенства
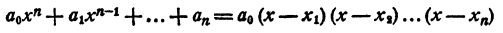
легко получить теорему Виета для уравнений любой степени. Перепишем это равенство так:
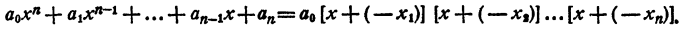
К правой части этого равенства применим правило умножения двучленов, первые члены которых одинаковы (см. гл. VIII, § 5). Получаем
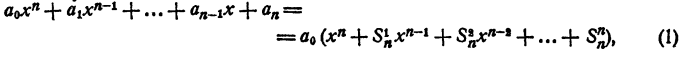
где 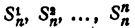
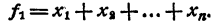
Знаком f₂ обозначим сумму всевозможных произведений корней, взятых по два. Подобный же смысл имеют знаки f₃, f₄, …, f ₙ . Тогда
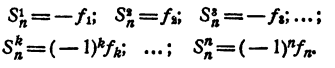
Равенство (1) теперь можно переписать так:
Приравнивая коэффициенты при одинаковых степенях х в правой и левой частях равенства (2), получим
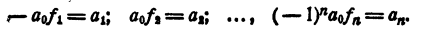
Теперь имеем
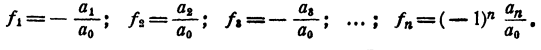
Последние равенства и выражают теорему Виета для уравнения любой степени. При n= 2, т. е. для уравнения 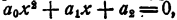
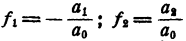
Пример:
Не решая уравнения 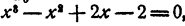
Решение:
Пусть х₁ x₂, х₃, — корни данного уравнения. Рассмотрим равенство
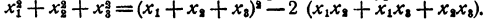
По теореме Виета
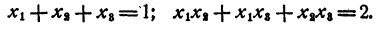
Значит,
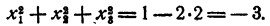
Полученный результат означает, что среди чисел х₁ x₂, х₃, имеются мнимые, иначе сумма квадратов их не могла бы быть отрицательной.
Предложенное уравнение нетрудно решить и подсчитать сумму квадратов корней непосредственно:
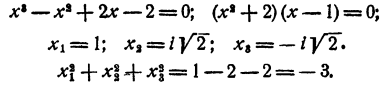
О решении уравнений высших степеней
Прежде всего возникает такой вопрос: можно ли для уравнений любой степени составить формулы для выражения корней уравнения через его коэффициенты, подобно известной формуле для квадратного уравнения? Оказывается, что это можно сделать для уравнений 3-й и 4-й степени, при этом формулы эти содержат столь сложные радикалы, что на практике ими предпочитают не пользоваться.
Что же касается уравнений выше 4-й степени, то доказано, что для них при помощи радикалов такие формулы составить нельзя.
В математике разработан ряд способов, дающих возможность вычислить любой корень любого уравнения с любой точностью. Один из таких способов разработан великим русским математиком, творцом неевклидовой геометрии Н. И. Лобачевским.
Ограничимся рассмотрением графического способа. Этот способ может применяться для вычисления действительных корней уравнений с действительными коэффициентами.
Пример:
Вычислить вещественные корни уравнения
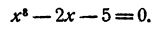
Решение:
Построим график функции у = х³ — 2х— 5 (рис. 107). Имеем
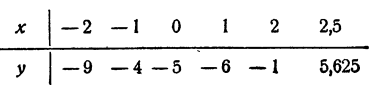
Нетрудно видеть, что при x > 2,5 первое слагаемое х³ будет столь большим сравнительно с остальными, что у будет положительным числом.
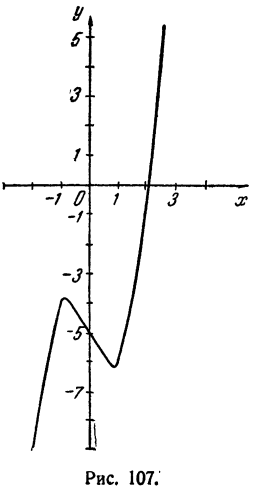
По мере продвижения направо от х = 2,5 график будет подниматься кверху и, следовательно, больше пересекать ось Ох не будет.
Точно так же при х < — 2 первое слагаемое х³ будет столь большим по абсолютной величине, что у будет отрицательным числом. По мере продвижения влево от х = — 2 график будет опускаться книзу и больше пересекать ось Ох не будет.
График пересекает ось Ох в одной точке, и это означает, что уравнение имеет один действительный корень два других корня уравнения — мнимые сопряженные).
Как видно из таблицы, действительный корень заключен между 2 и 2,5. По графику видно, что он ближе к 2, чем к 2,5. Определим знак у при x = 2,1. Имеем
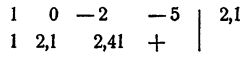
Это означает, что точка 2,1 лежит правее корня, так как соответствующая ордината положительна (см. график).
Таким образом, 2 < x < 2,1. Корень вычислен с точностью до 0,1. Для получения более точного результата можно воспользоваться приемом, указанным в гл. IV, § 7. Можно показать, что с точностью до 0,000001 x = 2,094551.
Вычисление рациональных корней уравнений с целыми коэффициентами
Теорема:
Для того чтобы несократимая дробь 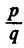
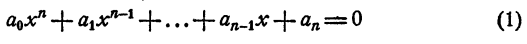
с целыми коэффициентами, необходимо, чтобы р было делителем свободного члена аₙ, a q было делителем старшего коэффициента а₀.
Доказательство:
Пусть 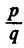
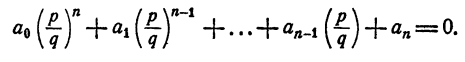
Умножим обе части тождества на qⁿ, получим
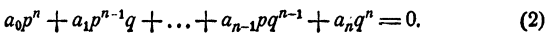
Из тождества (2) имеем
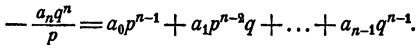
Правая часть равенства — целое число. Значит,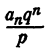
По условию, дробь 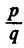
Из тождества (2) имеем
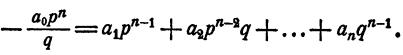
Так как ни одно простое число, входящее в q, не входит в р, число 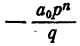
Следствие:
Если уравнение имеет целые коэффициенты и старший из них равен единице, то рациональными корнями такого уравнения могут быть только целые числа.
Действительно, а₀ = 1, a q — делитель а₀ . Значит, q = ± 1, а тогда 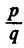
Следствие:
Целые корни уравнения с целыми коэффициент тами являются делителями свободного члена.
Пример:
Вычислить рациональные корни уравнения
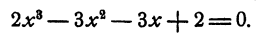
Решение:
Свободный член равен 2. Поэтому для р возможны только следующие значения: 1, —1, 2 и —2.
Старший коэффициент равен 2. Поэтому для q возможны только следующие значения: 1, —1, 2, —2.
Составляя всевозможными способами несократимые дроби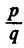
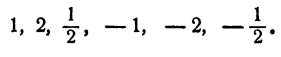
Подстановкой в уравнение легко выяснить, что из этих шести
чисел удовлетворяют уравнению 2, 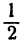
Таким образом, уравнение имеет три рациональных корня:
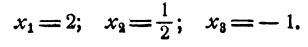
Для испытания, является ли данное число корнем уравнения, удобно пользоваться правилом сокращенного деления многочлена на двучлен х — а. Для данного примера эти испытания проводятся так:
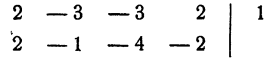
1 не является корнем уравнения, так как при делении левой части уравнения на х — 1 в остатке получилось — 2.
Испытываем число 2
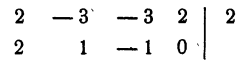
2 — корень уравнения. В результате деления оказалось, что
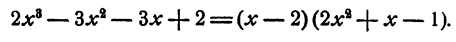
Поэтому для отыскания остальных корней данного уравнения достаточно решить уравнение
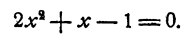
Ответ.
Пример:
Найти рациональные корни уравнения
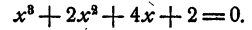
Решение:
Старший коэффициент уравнения равен единице, поэтому рациональными корнями уравнения могут быть только целые числа.
Делители свободного члена суть: 1,2, — 1, — 2. Сразу видно,-что никакое положительное число не может быть корнем данного уравнения, так как при любом положительном значении х левая часть уравнения положительна. Остается испытать — 1 и — 2:
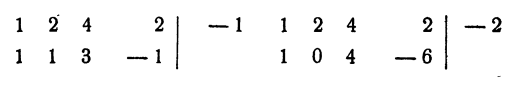
Ответ. Уравнение рациональных корней не имеет.
Полученный в последнем примере результат означает, что корни рассматриваемого уравнения иррациональные или мнимые.
Пример:
Решить уравнение
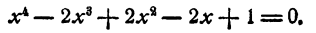
Решение:
Выясним прежде всего, не имеет ли уравнение рациональных корней. Испытанию подлежат два числа 1 и — 1:
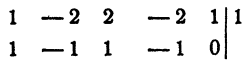
x₁² = 1. Остальные корни данного уравнения являются корнями уравнения третьей степени х³ — х² + х —1=0:
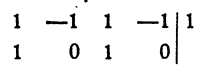
x₂ = 1. Остальные корни данного уравнения являются корнями квадратного уравнения х² + 1 = 0.
Ответ. x₁ = x₂ = 1; х₃ = i; x₄= — 1.
Решение двучленных уравнений 3-й, 4-й и 6-й степени
Определение. Двучленным уравнением n-й степени называется уравнение вида 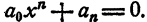
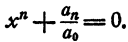
В этом параграфе излагается решение двучленных уравнений с действительными коэффициентами при n= 3, 4 и 6.
а) n = 3.
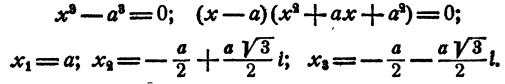
Уравнение имеет один действительный и два мнимых сопряженных корня.
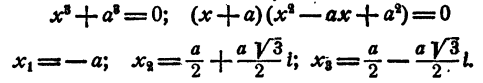
Уравнение имеет один действительный и два мнимых сопряженных корня.
б) n = 4.
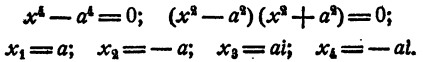
Уравнение имеет два действительных и два мнимых сопряженных корня.
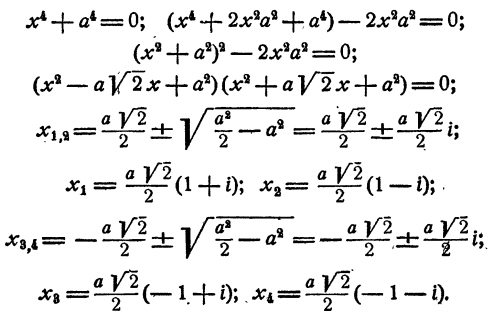
Уравнение имеет две пары мнимых сопряженных корней.
в) n = 6.
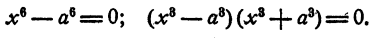
Уравнение распадается на два кубических двучленных уравнения. На основании рассмотренного в п. а)
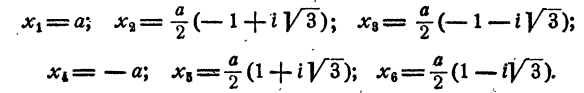
Уравнение имеет два действительных и две пары мнимых сопряженных корней
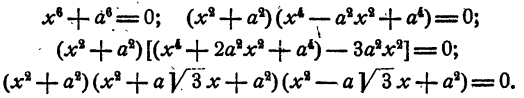
Уравнение распадается на три квадратных уравнения. Решая их, получаем
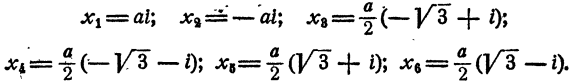
Уравнение имеет три пары мнимых сопряженных корней.
Замечание. Пользуясь извлечением корня n-й степени из комплексного числа, можно решить двучленное уравнение хⁿ = а любой степени n при любой правой части а.
Корнями уравнения хⁿ = а являются все значения корня n-й степени из а.
Пример:
Решить уравнение
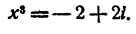
Решение:
Запишем правую часть уравнения в тригонометрической форме
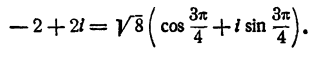
Пусть кубический корень из —2 + 2i равен р (cos 0 +isin 0). Тогда имеем
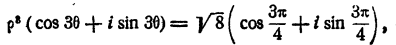
отсюда (§ 9 гл. IX) имеем
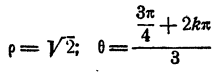
Для получения всех значений корня достаточно k положить равным 0, 1, 2. При k = 0 имеем
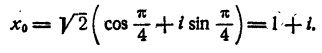
При k= 1 имеем
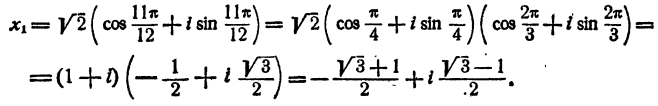
При к = 2 имеем
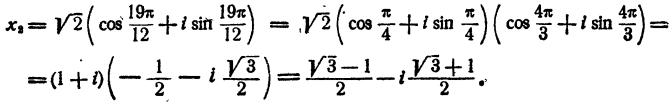
Ответ.
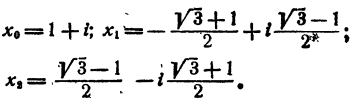
Решение трехчленных уравнений
Определение:
Трехчленным уравнением называется уравнение вида
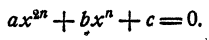
При n= 2 уравнение является биквадратным.
Решение трехчленного уравнения подстановкой хⁿ = у сводятся к квадратному уравнению ay² + by + с = 0 и двучленному уравнению n-й степени.
Пример:
Решить уравнение
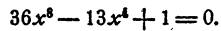
Решение:
Положим x⁴ = у. Имеем
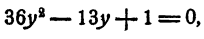
отсюда
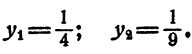
Теперь имеем
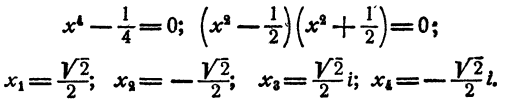
Далее,
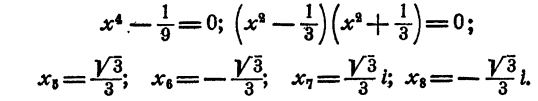
Ответ.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Теория устойчивости дифференциальных уравнений
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат