Как найти корни уравнения на определенном отрезке

в) arcsin + arcsin . Ответ: .

г) 5 arctg (-) – arccos (-). Ответ:– .

– Проверим домашнее задание, откройте свои тетради с домашними работами.

Некоторые из вас нашли решение методом подбора, а некоторые с помощью графика.

2. Вывод о способах решения данных заданий и постановка проблемы, т. е. сообщение темы и цели урока.

– а) С помощью подбора решать сложно, если задан большой промежуток.

– б) Графический способ не даёт точных результатов, требует проверку, и занимает много времени.

– Поэтому должен быть ещё как минимум один способ, наиболее универсальный -попробуем его найти. Итак, чем мы будем заниматься сегодня на уроке? (Учиться выбирать корни тригонометрического уравнения на заданном промежутке.)

– Пример 1. (Ученик выходит к доске)

cos x = -0,5, где хI [- ].

Вопрос: Отчего зависит ответ на данное задание? (От общего решения уравнения. Запишем решение в общем виде). Решение записывается на доске

х = + 2?k, где k R.

– Запишем это решение в виде совокупности:

– Как вы считаете, при какой записи решения удобно выбирать корни на промежутке? (из второй записи). Но это ведь опять способ подбора. Что нам необходимо знать, чтобы получить верный ответ? (Надо знать значения k).

(Составим математическую модель для нахождения k).

1 уровень: № 295 (а,б), № 317 (а,б)

2 уровень: № 307 (в), № 308 (б), № 326(б), № 327(б).

С1 (№15) с отбором корней на отрезке

В рамках подготовки к ЕГЭ по математике рассмотрим задачу С1 ( В новом формате ЕГЭ по математике – «Задание №13» ) , которая предлагалась в Тренировочной работе №60 А. Ларина.

а) Решите уравнение

б) Найдите все корни на промежутке

a)

Применяем формулу двойного угла для :

(1) или (2) ;

Уравнение (2) равносильно уравнению (произвели деление на ).

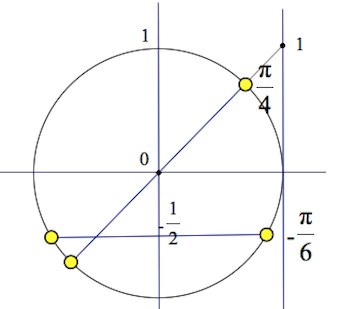
Откладываем на оси синусов , на оси тангенсов . Выходим на четыре серии точек:

Ответ:

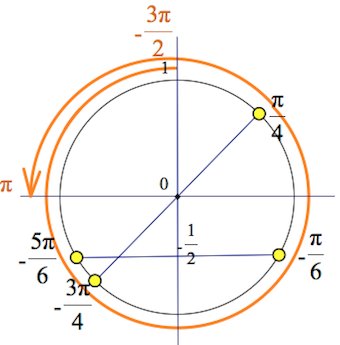
б) Произведем отбор корней из отрезка при помощи тригонометрического круга:

Ответ:

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Можете подробно объяснить, как проводится отбор корней?

Следует хорошо ориентироваться в тригонометрическом круге.
Долго объяснять на словах…
Если никак с кругом, то
решаем сначала неравенство:

Так как , то
При , при .
Потом
И так далее..

Помогите мне! Пn/2 на отрезке [0,1]

При n=0 x=0, 0 входит в [0;1].
При n=1 x=pi2, pi2>1.
Только 0.

Объясните по-подробнее какие страницы в какой последовательности надо читать, чтобы научиться отбирать корни тригонометрического уравнения в задании 13 профильного уровня!
А то я в приведённой вами ссылке в сообщении прочитал статью, на ней переход к странице: https://egemaximum.ru/trigonometricheskij-krug-ii/
А после этой страницы не написано куда дальше идти!
Спасибо большое!

Спасибо огромное вам!
Выручаете!=)
А подскажите, чтобы научиться правильно отбирать корни в 13ом задании нужно знать формулы приведения, суммы синусов и т. п?
И отличается ли отбор корней когда один оборот и когда несколько?!
Спасибо!

Для отбора корней не нужны формулы приведения, суммы синусов и т.п.
Принцип отбора – один, не важно полтора оборота, два или один…
Полезно хотя бы раз развернуть тригонометрический круг в ось. И увидеть, что, например, точки на круге отображаются одной точкой, а на оси – разными. Или, например, изобразите точки на круге, затем на оси…

Спасибо!
А при отборе корней с помощью окружности нужно что-то вычислять? Не понимаю когда находят серию корней как они определяют что будет корнем и отмечают это на окружности а что нет?

Не очень понятен вопрос…
Вам следует сперва научиться видеть серии корней на окружности. Только потом осваивайте отбор (при помощи тригонометрической окр.).
Например, если вас просят отметить на окружности точки а вы не понимаете, – как это. то до отбора далеко…
Начинайте перебирать различные значения смотрите, что получается…

Я про то, например, нашли серию корней: x=+_pi/6+pi n, n принадлежит Z.
Просят отобрать (в этапе б) корни на промежутке [2pi;3pi], я нахожу этот помежуток и выделяю его (это очень легко!).
А как вычислить корни, которые попадут на окружность на выделенный промежуток?!
Например, дано уравнение: 16cos^4x-24cos^2x+9=0
Его решить а.
Отобрать корни на промежутке [2pi; 3pi] б.
Нашел серию корней: x=+_pi/6+2pi n, n принадлежит Z.
Далее – черчу окружность, выделяю жирным промежуток, указанный в условии.
Мне не ясно, как туда попали корни 13 pi/6 и 17 pi/6.
Откуда они?
Спасибо огромное за объяснение!

Пока вы не выучите основные углы от нуля до 2пи на тригонометрическом круге, вы не сдвинетесь с места. Я вам много чего сказала по делу, но вы меня не слышите…

Я знаю эти углы! И как их отмечать на окружности! И формулы приведения!
Но я задал вопрос?

Некоторые
приемы отделения корней уравнения.

Определение

Корень
уравнения F(x) = 0 считается отделенным
на отрезке [a,
b],
если на этом отрезке нет других корней.

Существует большой
набор приемов и теорем, помогающие это
сделать, но единой теории не существует.

Корни
отделяются просто, если можно построить
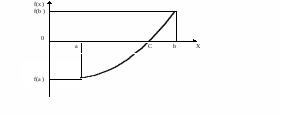
график функции f(x).
Точки пересечения графика с осью
Оx дают
значения корней, и по графику легко
определить два числа a
и b,
между которыми заключен только один
корень.

Пример
1. Отделить корни уравнения x³-3x-1=0.

 Построим график функции y = x3-3x-1 (рис.1). Кривая пересекает ось Оx в трех точках. Следовательно, уравнение имеет три действительных корня с1 , с2 , с3. Из чертежа видно, что с1[-2,1], с2[-1,0], с3[1,2] 
	Рис.1.

Если
построение графика y
= f(x) вызывает
затруднение, то уравнение (1) преобразовывают
к виду f₁(x)
= f₂(x)
так, чтобы
графики функций f₁(x)
и f₂(x)
было легко построить. Абсциссы точек
пересечения этих графиков и являются
корнями уравнения. По графику определяют
два числа a
и b,
между которыми заключен корень.

Пример
2. Отделить корни уравнения x
— cos x = 0 .

 Перепишем уравнение в виде: x = cos x и построим графики функций y = x и y = cos x в промежутке [-,] (рис.2). Графики функций пересекаются в одной точке. Учитывая свойства функ-ций можно утверждать, что вне этого промежутка данное уравнение корней не имеет. Таким образом, c [ 0,/2].
	Рис.2.

Рассмотренный способ
отделения корней будем называть
графическим.

Корни
уравнения (1) можно отделить, используя
приемы анализа функций, известные из
курса математического анализа. Ниже
приведены некоторые теоремы, знание
которых необходимо при отделении корней.

Теорема 1 (о существовании нуля функции)
	Если функция f(x) непрерывна на отрезке [a,b] и на его концах принимает значения разного знака, то есть f(a)f(b)<0, то внутри отрезка существует хотя бы одна точка, в которой функция f(x) обращается в нуль.

Проиллюстрируем
теорему графически:

f(a)>0; f(b)<0. Рис.3.

Теорема 2 (о существовании и единственности нуля функции).
	Если функция f(x) непрерывна на отрезке [a,b], принимает на его концах значения разного знака, то есть f(a) f(b) < 0, и первая производная f(x) сохраняет постоянный знак на интервале (a,b), то на этом интервале существует точка — и при том единственная — в которой функция f(x) обращается в нуль.

Проиллюстрируем
теорему графически:

Рис.4. f(a)<0, f(b)>0; f(x)>0.	Рис.5. f(a)>0, f(b)<0; f(x)<0.

Пример
3. Отделить корни уравнения 5^x
— 6x — 3 =
0.


Проведем
аналитическое исследование заданной
функции.

Функция
f(x) = 5^x
— 6x — 3
определена и непрерывна на всей числовой
прямой. Находим первую производную
f(x)=
5^x ln
5- 6 и выделяем
промежутки, внутри которых первая
производная сохраняет знак. Для этого
находим точки, в которых производная
обращается в нуль:

5^x
ln
5 — 6 = 0;

5^x
=
6 / ln 5;

x
ln 5 = ln 6 — ln(ln 5);

x
= (ln 6 — ln(ln 5))/ ln 5 
(1.7918- 0.4759)/1.6094 
0.8176;

Найденная точка делит числовую ось на
два промежутка. Если значения функции
на концах этих промежутков имеют
противоположные знаки, то по теореме 2
каждый из них содержит корень уравнения
и при том только один. Составим таблицу
знаков функции на концах выделенных
промежутков:

x	— 	0.8176	+ 
знак f(x)	+		+

Следовательно, уравнение
имеет два действительных корня,
заключенных в промежутках: (- ,
0.8176) , (0.8176, + ).

Сузим каждый промежуток так, чтобы его
границы были конечными:

x	— 1	0	0.8176	1	2
знак f(x)	+				+

Итак,
уравнение имеет два действительных
корня: с₁
[-1,
0 ],
с₂
[1,
2].

Рассмотренный
способ отделения корней будем называть
аналитическим.

Замечание.
 Если оказалось,
что функция f(x) в области определения
не меняет знак, то это значит, что
уравнение либо не имеет корней, либо
имеет корень четной кратности, либо
имеет четное число близлежащих корней.


Для
полиномов, т.е. когда F(x) = P_n(x)=
a_nxⁿ + a_n
-1 x^n-1 + 
+ a₁x + a₀
, таких вспомогательных теорем
гораздо больше.

Теорема 3 (Основная теорема алгебры).
	У всякого многочлена Pn(x) степени не ниже первой с произвольными коэффициентами (действительными или комплексными) число корней — с учетом их кратности — равно степени многочлена.

В данном
случае учитываются все корни — как
действительные, так и комплексные.
Поэтому следует не забывать, что
комплексные корни всегда попарно
сопряженные.

Теорема 4 (теорема Декарта).

Количество действительных положительных корней уравнения Pn(x)= 0 — с учетом их кратности — либо равно числу перемен знака в последовательности коэффициентов полинома Pn(x) уравнения, либо на четное число меньше. Количество действительных отрицательных корней уравнения — с учетом их кратности — либо равно числу перемен знака в последовательности коэффициентов полинома Pn(-x), либо на четное число меньше.

При
составлении последовательности
коэффициентов, свободный член учитывается,
а равные нулю коэффициенты не
учитываются.

Пример
4. Отделить корни уравнения x³
— 6x²
+20 = 0.

 По
основной теореме алгебры уравнение
может иметь не более трех действительных
корней. Для их отделения воспользуемся
теоремой Декарта.

Выпишем последовательность коэффициентов
заданного полинома:

коэффициент	1	6	+20
знак коэффициента	+		+	две смены знака

Следовательно,
положительных действительных корней
не более двух.

Теперь
выпишем последовательность коэффициентов
полинома

P₃
(-x)= — x³
—
6x²
+20:

коэффициент	1	6	+20
знак коэффициента			+	одна смена знака

Следовательно,
отрицательных действительных корней
не более одного.

Полином
P₃
(x)= x³ —
6x²+
20 определен
и непрерывен на всей числовой прямой.
Находим первую производную P₃(x)
= 3x²—
2x=3x(x-4) и
выделяем промежутки, внутри которых
первая производная сохраняет знак:

x	(- , 0)	(0, 4)	(4, + )
знак P3(x)	+		+

Сузим промежутки так, чтобы их границы
были конечными и найдем значение полинома
на концах промежутков:

x	— 2	(-2, 0)	0	(0, 4)	4	(4, 6)	6
P3(x)	-12		20		-12		20
знак P3(x)	+	+	0		0	+	+

Итак, уравнение имеет
три действительных корня:

с₁(-2,
0 ),
с₂(
0, 4),
с₃(4,
6).

Пример
5. Отделить корни уравнения x⁵
+ 3x⁴
— x³
-1 = 0.

 По основной теореме алгебры уравнение
может иметь не более пяти действительных
корней. Для их отделения воспользуемся
теоремой Декарта.

Выпишем последовательность коэффициентов
заданного полинома:

коэффициент	1	+3	1	1
знак коэффициента	+	+			одна смена знака

Следовательно,
положительных действительных корней
не более одного.

Теперь
выпишем последовательность коэффициентов
полинома

P₅(-x)=
— x⁵
+
3x⁴
+ x³
-1:

коэффициент	1	+3	+1	1
знак коэффициента		+	+		две смены знака

Следовательно,
отрицательных действительных корней
не более двух.

Значит данное
уравнение может иметь не более трех
действительных корней. Определим, где
они находятся.

Полином
P₅(x)=
x⁵ +
3x⁴
— x³
-1 определен
и непрерывен на всей числовой прямой.

Перепишем
уравнение в виде:
x² +
3x- 1= 1/x³
и построим графики функций

f₁
=x²
+ 3x
—
1=(x+3/2)²
— 13/4
и f₂
= 1/
x³.
Графики функций пересекаются в трех
точках.

Рис.6.

По
графику определяем, что корни уравнения
заключены в промежутках:

с₁(-4,-3),
с₂(-1,
0 ),
с₃(
0, 1).

Соседние файлы в папке Самостоятельно

• #
• #
• #
• #
• #
• #

Отбор корней с помощью тригонометрического круга

В заданиях, где требуется отобрать корни тригонометрического уравнения, принадлежащие определенному числовому промежутку, можно использовать тригокруг. Этот метод отбора корней является наиболее распространенным. Его плюсы заключаются в том, что это визуальный метод, т. е. отбор корней происходит наглядно, но у этого есть и свои недостатки – углов бесконечное множество, из которых только 360° можно визуализировать на тригокруге, поэтому может возникнуть путаница с количеством оборотов по нему.

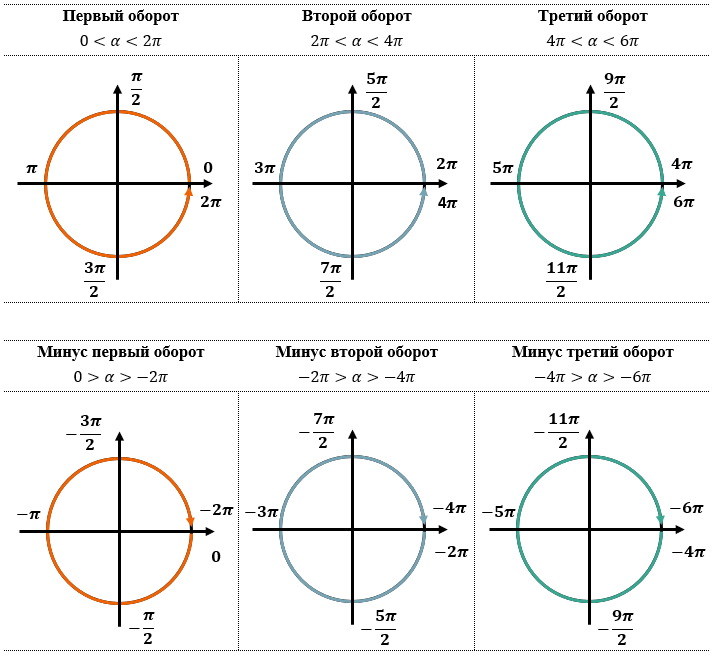
«ОБОРОТЫ» ПО ТРИГОКРУГУ И СООТВЕТВЕТСТВУЮЩИЕ ИМ УГЛЫ:

АЛГОРИТМ ОТБОРА КОРНЕЙ С ПОМОЩЬЮ ТРИГОКРУГА

1. Отмечаем получившийся угол на тригокруге. Это будет серия ответов – бесконечное количество углов, визуально находящееся на тригокруге в одной точке.

2. Отмечаем нужную дугу, т. е. обозначаем указанный промежуток, в котором нужно отобрать корни.

3. Определяем корни, попадающие в эту дугу.

4. Находим искомые углы учитывая обороты – прибавляем соответствующее количество периодов к отмеченному на окружности углу.

Пример:

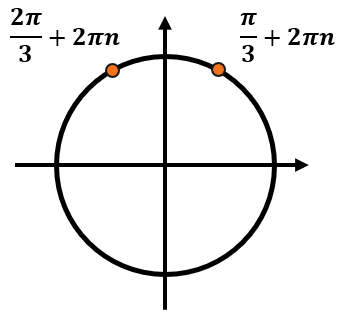
Даны корни уравнения:

(x_{1} = frac{pi}{3} + 2pi n, nmathbb{in Z})

(x_{2} = frac{2pi}{3} + 2pi n, nmathbb{in Z})

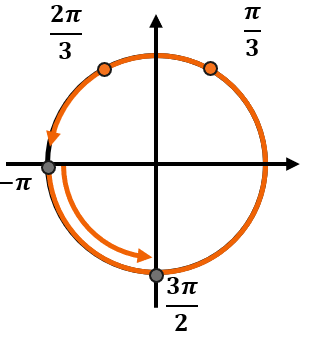
Найдите корни, принадлежащие отрезку (leftlbrack — pi, frac{3pi}{2} rightrbrack).

1. Каждый из этих корней включает в себя бесконечное количество углов. Отметим эти серии ответов на тригокруге:

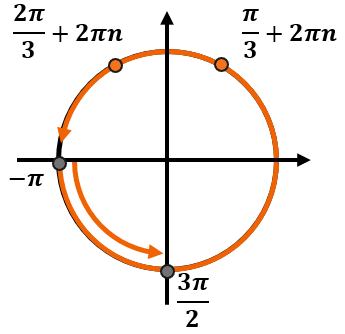
1. При этом мы знаем, что нужные корни должны находиться на промежутке (leftlbrack — pi, frac{3pi}{2} rightrbrack). Этот промежуток занимает больше, чем один оборот. Обозначим его так:

1. Так как промежуток занимает больше одного круга, каждая серия ответов так или иначе попадет в этот него.

2. Теперь определим, на каком обороте серии ответов попадут именно в этот промежуток. Если мы будем идти по тригокругу от (- pi) до (frac{3pi}{2}), то попадем в точки с сериями ответов по одному разу – в первом обороте после нуля. Тогда получим следующие углы:

Запишем ответ.

Ответ: (frac{pi}{3});( frac{2pi}{3}).

Важно! Чтобы решение было обоснованным, очень важно отметить всё на круге: и точки, и углы, и промежуток.

22
Янв 2014

Категория: 12 (С1) УравненияТ/P A. ЛаринаТригонометрические выражения, уравнения и неравенства

С1 (№15) с отбором корней на отрезке

2014-01-22
2015-09-04

Автор: egeMax |

комментария 22