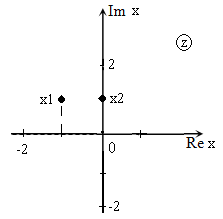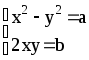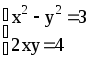Как найти корни уравнения с комплексными числами

Числа. Извлечение корней из комплексных чисел. Квадратное уравнение с комплексными корнями.

Рассматривать будем на таком примере:

Если говорить о действительных числах, то, вы знаете, что корень из отрицательного числа нельзя извлекать. Однако в комплексных числах можно. Если конкретнее, 2 корня:

Выполним проверку того, что эти корни и права оказываются решением уравнения:

Что и требовалось доказать.

Зачастую используют сокращенную запись, корни записывают в одну строчку в таком виде: .

Такие корни являются сопряженными комплексными корнями.

Теперь вы знаете как можно извлечь квадратный корень из отрицательного числа. Приведем еще несколько примеров:

, ,

,

,

В каждом случае получаем 2 сопряженных комплексных корня.

Решим квадратное уравнение .

Первым шагом определим дискриминант уравнения:

В нашем случае дискриминант оказался отрицательным, и в случае с действительными числами у уравнения нет решений, но у нас вариант с комплексными числами, поэтому можем продолжать решение:

Как известно из формул дискриминанта у нас образуется 2 корня:

– сопряженные комплексные корни

Т.о., у уравнения есть 2 сопряженных комплексных корня:

,

Теперь можно решить любое квадратное уравнение!

У любого уравнения с многочленом n-ой степени есть ровно n корней, некоторые из них могут быть комплексными.

Как извлечь корень из произвольного комплексного числа?

Рассмотрим уравнение z n = w, либо, записав в другом виде: . Здесь n может принимать всякое натуральное значение, которое больше 1-цы.

В частности, при n = 2 получаем квадратный корень .

У уравнения типа есть ровно n корней ­z₀, z₁, z₂, … z_n-1, которые можно вычислить с помощью формулы:

,

где – это модуль комплексного числа w,

φ – его аргумент,

а параметр k принимает значения: .

Найдем корни уравнения: .

Перепишем уравнение как: .

В этом примере , , поэтому у уравнения будет 2 корня: z₀ и z₁. Детализируем общую формулу:

, .

Далее найдем модуль и аргумент комплексного числа :

Число w находится в 1-ой четверти, значит:

Помним, что определяя тригонометрическую форму комплексного числа лучше делать чертеж.

Детализируем еще немного общую формулу:

, .

Так подобно расписывать не обязательно. Здесь мы это сделали, что бы было ясно откуда что образовалось.

Подставляем в формулу значение k = 0 и получаем 1-й корень:

.

Подставляем в формулу значение k = 1 и получаем 2-й корень:

.

Ответ: ,

Если необходимо, корни, которые мы получили можно перевести обратно в алгебраическую форму.

Часто вычисленные корни нужно изобразить геометрически:

Как выполнить чертеж?

Для начала на калькуляторе вычисляем, чему равен модуль корней и чертим с помощью циркуля окружность этого радиуса. Все корни будем откладывать на данной окружности.

Далее берем аргумент 1-го корня и вычисляем, чему равен угол в градусах:

.

Отмеряем транспортиром 45° и ставим на чертеже точку z₀.

Берем аргумент 2-го корня и переводим его тоже в градусы: . Отмеряем транспортиром 165° и ставим на чертеже точку z₁.

По этому же алгоритму ставим точку z₂.

Видно, что корни располагаются геометрически правильно с интервалом между радиус-векторами. Чертеж обязательно делать при помощи транспортира.

Квадратное уравнение с комплексными корнями

Всем известно из школы квадратное уравнение:

,

поиск дискриминанта и решение вопроса: имеет ли квадратное уравнение корни или корень или нет. Как следует из основной теоремы алгебры, любое уравнение — ой степени имеет ровно корней с учетом кратности этих корней. Таким образом, любое квадратное уравнение с действительными или комплексными коэффициентами имеет ровно два корня. При этом кратные корни в комплексном анализе считаются ровно столько раз, какая у них кратность.

Утверждение. Пусть коэффициенты многочлена — ой степени

– действительные и его комплексный корень, тогда тоже является корнем этого многочлена.

Доказательство. Перейдем к комплексному сопряжению в равенстве : , так как . Поскольку коэффициенты многочлена действительны, то: .

Получили , следовательно, — также корень многочлена .

Если коэффициенты квадратного трехчлена действительны, а дискриминант отрицательный, то пару сопряженных корней можно найти через дискриминант.

При этом в формуле

нужно учесть что .

Решить квадратное уравнение с действительными коэффициентами: .

Решаем по «половинной» формуле: .

Если квадратный трехчлен имеет хотя бы один не действительный коэффициент, то корни не будут комплексно сопряженными.

Рассмотрим уравнение с комплексными коэффициентами:

Решаем через дискриминант. .

Таким образом, — корни нашего уравнения.

Пример 3

Решить квадратное уравнение:

Опять используем школьную формулу решения. Находим дискриминант:

Чтобы извлечь корень из дискриминанта обратимся к формуле извлечения корня ой степени из комплексного числа. Если , то корни ой степени из имеют вид:

В нашем случае .

Так что корни такие:

Теперь запишем корни исходного квадратного уравнения: .

Длины волн инфракрасного света достаточно велики, чтобы перемещаться сквозь облака, которые в противном случае блокировали бы наш обзор. Используя большие инфракра сные телескопы, астрономы смогли заглянуть в ядро нашей галактики. Большое количество звезд излучают часть своей электромагнитной энергии в виде видимого света, крошечной части спектра, к которой чувствительны наши глаза.

Так как длина волны коррелирует с энергией, цвет звезды говорит нам, насколько она горячая. Используя телескопы, чувствительные к различным диапазонам длин волн спектра, астрономы получают представление о широком круге объектов и явлений во вселенной.

Пример №1 Постройте центральную симметрию тетраэдра, относительно точки O, изображенных на рисунке 3.

Для построения такой центральной симметрии сначала проведем через все точки тетраэдра прямые, каждая из которых будет проходить через точку O. На них построим отрезки, удовлетворяющие условиям |AO|=|A?O|, |BO|=|B?O|, |CO|=|C?O|, |DO|=|D?O| Таким образом, и получим искомую симметрию (рис. 4).

В ряду разных механических движений особенным значением обладают колебания. Это движения и процессы, имеющие периодичность во времени.

В среде электромагнитных явлений также значительное место заняли электромагнитные колебания. В этих колебаниях заряды, токи, электрические и магнитные поля изменяются согласно периодическим законам.

Совет №1 Велосипедист, имеющий скорость 300 м/с, или идеальный газ, оказывающий давление 100 паскалей в большой тепловой машине — это странно.

Нужна помощь с курсовой или дипломной работой?

Квадратное уравнение с комплексными корнями

Вы будете перенаправлены на Автор24

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

Двучленным называется уравнение вида $x^ =A$.

Рассмотрим три случая:

Решить уравнение: $x^ <3>=8$.

Так как $A>0$, то $x_ =sqrt[<3>] <8>cdot left(cos frac<2kpi > <3>+icdot sin frac<2kpi > <3>right),, , , k=0. 2$.

При $k=0$ получаем $x_ <0>=sqrt[<3>] <8>cdot left(cos 0+icdot sin 0right)=sqrt[<3>] <8>=2$.

При $k=1$ получаем

[x_ <1>=sqrt[<3>] <8>cdot left(cos frac<2pi > <3>+icdot sin frac<2pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>+frac <sqrt<3>> <2>cdot i)=-1+sqrt <3>cdot i.]

При $k=2$ получаем

[x_ <2>=sqrt[<3>] <8>cdot left(cos frac<4pi > <3>+icdot sin frac<4pi > <3>right)=sqrt[<3>] <8>cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=2cdot (-frac<1> <2>-frac <sqrt<3>> <2>cdot i)=-1-sqrt <3>cdot i.]

Решить уравнение: $x^ <3>=1+i$.

Готовые работы на аналогичную тему

Так как $A$ — комплексное число, то

Тригонометрическая форма записи некоторого комплексного числа имеет вид $z=r(cos varphi +icdot sin varphi )$.

По условию $a=1,b=1$.

Вычислим модуль исходного комплексного числа:

Вычислим аргумент исходного комплексного числа:

[varphi =arg z=arctgfrac<1> <1>=arctg1=frac<pi > <4>]

Подставим полученные значения и получим:

Уравнение перепишем в виде:

При $k=0$ получаем $x_ <0>=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi /4> <3>+icdot sin frac<pi /4> <3>right)=sqrt[<3>] <sqrt<2>> cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)=sqrt[<6>] <2>cdot left(cos frac<pi > <12>+icdot sin frac<pi > <12>right)$.

При $k=1$ получаем

При $k=2$ получаем

Квадратным называется уравнение вида $ax^ <2>+bx+c=0$, где коэффициенты $a,b,c$ в общем случае являются некоторыми комплексными числами.

Решение квадратного уравнения находится с помощью дискриминанта $D=b^ <2>-4ac$, при этом

В случае, когда дискриминант является отрицательным числом, корни данного уравнения являются комплексными числами.

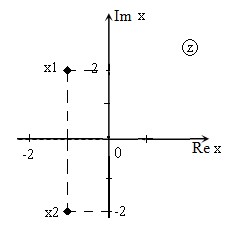
Решить уравнение $x^ <2>+2x+5=0$ и изобразить корни на плоскости.

[D=2^ <2>-4cdot 1cdot 5=4-20=-16.]

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 1.

В случае, когда уравнение имеет комплексные корни, они являются комплексно-сопряженными числами.

Комплексное число вида $overline=a-bi$ называется числом комплексно-сопряженным для $z=a+bi$.

Известно, что если $x_ <1,2>$ являются корнями квадратного уравнения $ax^ <2>+bx+c=0$, то данное уравнение можно переписать в виде $(x-x_ <1>)(x-x_ <2>)=0$. В общем случае $x_ <1,2>$ являются комплексными корнями.

Зная корни уравнения $x_ <1,2>=1pm 2i$, записать исходное уравнение.

Запишем уравнение следующим образом:

[x^ <2>-(1-2i)cdot x-xcdot (1+2i)+(1-2i)cdot (1+2i)=0] [x^ <2>-x+2icdot x-x-2icdot x+1-4i^ <2>=0] [x^ <2>-2x+1+4=0] [x^ <2>-2x+5=0]

Следовательно, $x^ <2>-2x+5=0$ — искомое уравнение.

Рассмотрим квадратное уравнение с комплексными коэффициентами.

Решить уравнение: $z^ <2>+(1-2i)cdot z-(1+i)=0$ и изобразить корни на плоскости.

Так как $D>0$, уравнение имеет два корня:

Изображение корней уравнения на комплексной плоскости (так как корни комплексные) приведено на рис. 2.

В случае, когда уравнение имеет комплексные коэффициенты, его корни не обязательно являются комплексно-сопряженными числами.

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 13 11 2021

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Работаем по будням с 10:00 до 20:00 по Мск

Регистрация прошла успешно!

На email мы отправили пароль для доступа ко всем сервисам

Не пропусти промокод на скидку в ближайших письмах

Пусть задано квадратное уравнение $ax^2+bx+c=0$, где коэффициенты
$a$,
$b$ и
$c$ — в общем случае являются комплексными.
Его решение находим с помощью дискриминанта

$$D=b^{2}-4 a c$$

тогда

$$x_{1,2}=frac{-b pm sqrt{D}}{2 a}$$

В общем случае и дискриминант, и корни уравнения являются
комплексными числами.

Читать дальше: элементарные функции комплексного аргумента.

Рассмотрим решение уравнений с комплексными корнями и коэффициентами.

«Квадратное уравнение с комплексными корнями» 👇

Множество
всевозможных пар действительных чисел
называется множеством комплексных
чисел, если выполняются условия:

1) определено
сравнение (a,b)=(c,d)
Û
a=c Ù
b=d

2) определено
cложение
(a,b)+(c,d)=(a+c,b+d)

3) определено
умножение (a,b)(c,d)=(ac-bd,ad+bc)

При этом число
(0,0) называется нулём и обозначается 0,
число (1,0) называется единицей и
обозначается 1, число (0,1) называется
мнимой единицей и обозначается i.
Комплексные числа (a,b)
можно
обозначать в виде
a+ib. При
таких обозначениях арифметические
операции над комплексными числами
выполняются по обычным алгебраическим
правилам, но при этом i²
заменяется
на -1. Число a-ib
называется
комплексно сопряжённым к числу a+ib.

Модулем комплексного
числа u=a+ib
называется
действительное число
.
При этом можно записатьu=|u|(cosj+isinj)
(тригонометрическая форма записи), где
j
— некоторый угол из промежутка [0;2p)
называемый
аргументом числа u.
Справедливы свойства:

|u|³0

|-u|=|u|

|uv|=|u||v|

|u+v|£|u|+|v|
(неравенство
треугольника
для
модуля)

|u-v|³|u|-|v|
(следствие
из неравенства треугольника)

uⁿ=|u|ⁿ(cosnj+isinnj) (формула
возведения в степень)

(формула
извлечения корня n-ой
степени)

Для вычисления
квадратного
корня
кроме общего способа можно использовать
специальный приём.
Пусть
требуется вычислить квадратный корень
из числа a+ib.
Обозначим
этот корень через x+iy.
По
определению квадратного корня a+ib
= (x+iy)².
Раскрывая
скобки и сравнивая получаем систему

Её решения дадут
нам два значения квадратного корня.

Пример 1.

(1+i)(5-i)=5+5i-i-i²=5+5i-i+1=6+4i
(i²
заменили
на -1)

Ответ:
6+4i

Пример 2.

(домножили
числитель и знаменатель на 1-i
(сопряжённое
к 1+i)
и затем i²
заменили
на -1)

Ответ:
1+i

Пример
3.

(1-i)⁵
=
((cos(7p/4)+isin(7p/4))⁵
=
4(cos(35p/4)+isin(35p/4))
=

=
4(-/2+i/2)
= -4+4i (перешли
к тригонометрической форме записи и
воспользовались формулой возведения
в степень)

Ответ:
-4+4i

Пример 4.

Вычислить
.
Решение: ,обозначим
значения корня (их четыре) через u₀,
u₁,
u₂,
u₃.
По
формуле извлечения корня
.

При к=0 получаем
u₀=cos(p/8)+isin(p/8)

При к=1 получаем
u₁=cos(5p/8)+isin(5p/8)

При к=2 получаем
u₂=cos(9p/8)+isin(9p/8)

При к=3 получаем
u₃=cos(13p/8)+isin(13p/8)

Ответ:
{ cos(p/8)+isin(p/8);
cos(5p/8)+isin(5p/8);
cos(9p/8)+isin(9p/8);
cos(13p/8)+isin(13p/8)
}

Пример 5.

Вычислить
.

Составим систему

Û
Þ
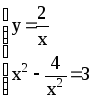
x⁴-3x²-4=0.

Обозначим t=x²
Þ
t²-3t-4=0
Þ
t₁=-1,
t₂=4
Þ
x²=4
Þ
x₁=-2,
y₁=-1
и
x₂=2,
y₂=1

Ответ:
{ -2-i; 2+i }

Пример
6.

Решить уравнение
x²
+ 4x + 5 = 0. Находим
D
= 16 — 4×5
= -4 < 0 Þ
корни
комплексные:

Ответ:
{ -2-i ; -2+i }

666

Вычислить:

1. (1+2i)(2+i) 2.
(1+2i):(2+i) 3.

4.

5.

Решить уравнения:

6. x²
— 16x + 65 = 0 7. 9x²
+ 6x + 5 = 0

8.
x⁴
+ 2x²
— 3 = 0 9. x⁴
+ 6x²
+ 25 = 0

Вычислить:

10. (2+i)(3-i) 11.
(4+2i):(3-i) 12.

13.

Решить уравнения:

14. x²
+ 12x + 40
= 0 15.
x⁴
— 4x²
— 5
= 0

16. x⁴
—
6x²
+
25
= 0

555 Решение алгебраических уравнений.

Поиск рациональных
корней алгебраических уравнений с
целыми коэффициентами основан на
теореме:
если рациональное число —
корень такого уравнения, то его числитель
— множитель свободного члена, а знаменатель
— множитель коэффициента при старшей
степени. Для подстановки чисел в уравнение
можно применять схему Горнера. В
комплексной области любое алгебраическое
уравнение n-ой
степени имеет ровно n
корней.

Схема Горнера.

Вычисления по
схеме Горнера заносим в таблицу из двух
строк. Слева от таблицы пишем проверяемое
число. В первой строке записываем
коэффициенты исходного уравнения,
включая нулевые. Затем в первую ячейку
второй строки переписываем число из
верхней ячейки, во вторую ячейку второй
строки записываем сумму верхнего числа
и предыдущего, умноженного на проверяемое
число и т.д. Если в последней ячейке
получится 0, то проверяемое число —
корень, а остальные числа — коэффициенты
алгебраического уравнения с уменьшенной
на один степенью. Решая это уравнение
получим остальные корни.

Пример 7.

Решить уравнение
x³
+ x — 2 = 0. Рациональные
корни этого уравнения ищем среди чисел
±1,
±2.
Проверяем число 1:

1	1	0	1	-2
	1	1	2	0

Так как в последней
ячейке ноль, то x₁=1.
Остальные
корни ищем из уравнения x²
+ x + 2 = 0
(его коэффициенты берём из второй
строки).
D = 1 — 8 = — 7 < 0 Þ

Ответ:

666

Решить уравнения:

17. x³
— x²
— 2x + 2 = 0 18. x³
+ x²
— 2 = 0

19.
x⁵
— 4x³
— 8x²
+ 32 = 0 20. x³
— 12x²
+ 47x -60 = 0

21.
x⁴
— 10x³
+ 35x²
— 50x + 24 = 0

555

Выучить наизусть

|u+v|£|u|+|v| |u-v|³|u|-|v| u=|u|(cosj+isinj) un=|u|n(cosnj+isinnj)

Ответы.

1. 5i
2. 0,8+0,6i 3. 3+i; -3-i

4.
2(cos(p/10+2kp/5)+isin(p/10+2kp/5)),
k=0,1,2,3,4

5.
Ö2(cos(p/36+2kp/3)+isin(p/36+2kp/3)),
k=0,1,2 6. 8±i
7. -1/3±2i/3

8.
±1;
±iÖ3
9. 1±2i;
-1±2i
10. 7+i 11. 1+i 12. ±(3-i)

13.
2(cos(3p/8+kp/2)+isin(3p/8+kp/2)),
k=0,1,2,3 14. -6±2i
15. ±i;
±Ö5
16. 2±i;
-2±i

17. 1;
±Ö2
18. 1; -1±i
19. ±2;
-1±iÖ3
20. 3; 4; 5 21. 1;2;3;4

Вычислить u+v,
u-v, uv,
,

3.1
u=3-4i

v=8+6i 3.2
u=21+20i
v=9-40i

3.3

u=-16+30i v=-21-20i 3.4
u=-9-40i

v=21-20i

3.5
u=24+10i
v=-15+8i 3.6
u=-21+20i
v=-8-6i

3.7
u=24-10i

v=-21-20i 3.8
u=3+4i

v=-5+12i

3.9
u=21-20i

v=7+24i 3.10 u=-7+24i

v=24-10i

3.11 u=-7+24i

v=-16+30i 3.12 u=7+24i

v=-5+12i

3.13 u=-7-24i
v=5+12i 3.14
u=21-20i

v=-16-30i

3.15 u=-16-30i

v=16+30i 3.16 u=3-4i

v=7-24i

3.17 u=16+30i

v=-15+8i 3.18 u=-8-6i

v=16-30i

3.19 u=24+10i
v=8+6i 3.20 u=-3+4i

v=7-24i

3.21 u=21+20i
v=16+30i 3.22 u=5-12i
v=9-40i

3.23 u=5-12i

v=8+6i 3.24 u=-9+40i
v=-16+30i

3.25 u=5-12i
v=-7-24i 3.26
u=-16-30i

v=21+20i

3.27 u=-16+30i
v=15-8i 3.28 u=-7-24i

v=-8-6i

3.29 u=21-20i
v=-5-12i 3.30
u=-8-6i

v=-15-8i

3.31 u=-16-30i
v=-3+4i 3.32
u=7+24i v=-9+40i

3.33 u=-24-10i
v=21-20i 3.34
u=-7-24i v=8+6i

3.35 u=15-8i

v=8-6i

Возвести в степень,
преобразовав в тригонометрическую
форму
и
вычислить корень этой же степени:

4.1

(-Ö3+i)³ 4.2

(-1+iÖ3)⁷ 4.3
(-1+i)⁷

4.4

(1-iÖ3)⁵ 4.5

(1+iÖ3)³ 4.6
(Ö3-i)³

4.7
(Ö3+i)³ 4.8

(-1+i)³ 4.9
(-Ö3-i)³

4.10 (-Ö3+i)⁷ 4.11
(-Ö3+i)³ 4.12
(1-i)⁵

4.13 (1+iÖ3)⁵ 4.14
(1-iÖ3)³ 4.15
(1-iÖ3)⁷

4.16 (-Ö3-i)³ 4.17
(-1+iÖ3)³ 4.18
(-1+i)⁷

4.19 (1-i)⁷ 4.20
(1-iÖ3)³ 4.21
(1-i)³

4.22 (-1+iÖ3)⁵ 4.23
(-1-i)⁵ 4.24
(-Ö3-i)³

4.25 (Ö3-i)⁵ 4.26
(1+i)⁷ 4.27
(1-i)⁷

4.28 (-Ö3+i)³ 4.29
(-1-i)⁷ 4.30
(1+i)³

4.31 (-1+iÖ3)³ 4.32
(-Ö3-i)³ 4.33
(-1-iÖ3)⁵

4.34 (-1+i)⁵ 4.35
(-1-iÖ3)⁷

Найти действительные
и комплексные корни уравнений:

5.1 x⁴+10x³+37x²+58x+30=0
75x³-35x²-8x+4=0

5.2
x⁴-5x³-6x²+84x-144=0 12x³-68x²+115x-50=0

5.3
x⁴-9x³+30x²-52x+48=0 18x³-15x²-100x+125=0

5.4
x⁴-2x³-7x²+18x-18=0 18x³-33x²-28x-5=0

5.5
x⁴+8x³+22x²+28x+16=0 75x³-140x²+87x-18=0

5.6
x⁴-9x³+30x²-46x+24=0 12x³+40x²+39x+9=0

5.7
x⁴-9x³+25x²-9x-44=0 12x³+20x²+4x-4=0

5.8
x⁴+5x³+x²-3x+36=0 20x³+60x²+60x+20=0

5.9
x⁴-5x³-8x²+82x-120=0 20x³+76x²+64x-16=0

5.10 x⁴-7x³+16x²
— 24=0 75x³+40x²-33x-18=0

5.11
x⁴+7x³+11x²-25x-66=0 12x³-56x²+80x-32=0

5.12
x⁴-6x³+10x²+6x-11=0 12x³+4x²-5x-2=0

5.13
x⁴-3x³-11x²+13x+60=0 75x³+35x²-123x+45=0

5.14
x⁴-3x³-10x²+6x+72=0 45x³+57x²+23x+3=0

5.15
x⁴-3x³-8x²+22x-24=0 18x³+33x²-28x+5=0

5.16
x⁴-7x³+20x²-32x+24=0 12x³+8x²-20x-16=0

5.17
x⁴+5x³-2x²-42x-72=0 45x³+42x²-4x-8=0

5.18
x⁴-6x³+14x²-18x+9=0 12x³+32x²+23x+5=0

5.19
x⁴-11x³+46x²-90x+72=0 45x³-141x²+95x+25=0

5.20
x⁴+2x³-14x²-32x-32=0 20x³-104x²+145x-25=0

5.21
x⁴-10x³+37x²-62x+40=0 20x³-76x²+64x+16=0

5.22
x⁴-11x³+48x²-96x+72=0 50x³-85x²-92x-20=0

5.23 x⁴
— 3x²+14x-12=0 12x³-80x²+175x-125=0

5.24
x⁴+7x³+18x²+28x+16=0 12x³-76x²+155x-100=0

5.25
x⁴+2x³-10x²-44x-48=0 20x³+44x²+28x+4=0

5.26
x⁴+8x³+25x²+36x+18=0 20x³+68x²+69x+18=0

5.27
x⁴-7x³+16x²-18x+8=0 18x³+27x²
— 9=0

5.28
x⁴-5x³-2x²+42x-72=0 50x³+55x²-28x+3=0

5.29
x⁴-3x³-3x²+31x-42=0 18x³+60x²+56x+16=0

5.30
x⁴-4x³-8x²+72x-96=0 75x³+170x²+128x+32=0

5.31 x⁴
— 10x²-20x-16=0 75x³-20x²-17x-2=0

5.32
x⁴+13x³+66x²+156x+144=0 20x³+104x²+145x+25=0

5.33 x⁴-4x³
+ 8x-32=0 50x³+110x²+78x+18=0

5.34
x⁴-8x³+23x²-34x+24=0 18x³-93x²+152x-80=0

5.35
x⁴-8x³+24x²-32x+15=0 20x³+44x²+28x+4=0

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #