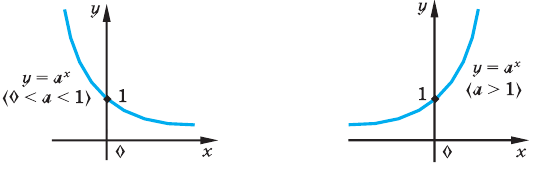
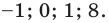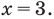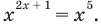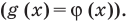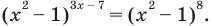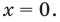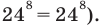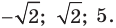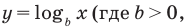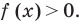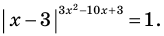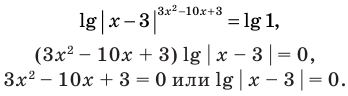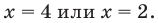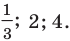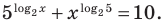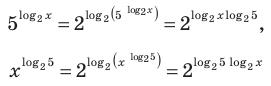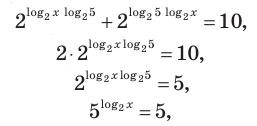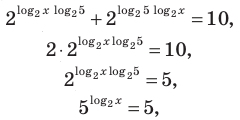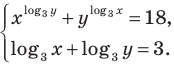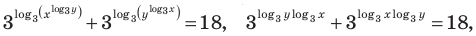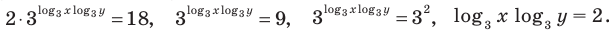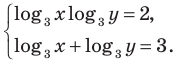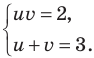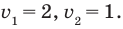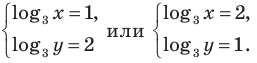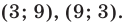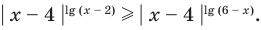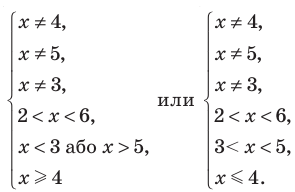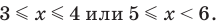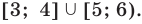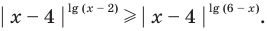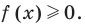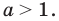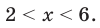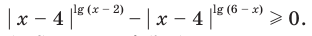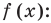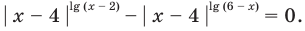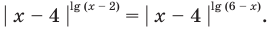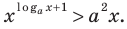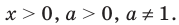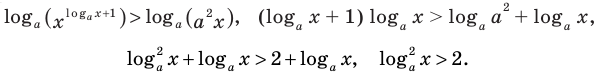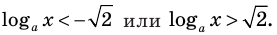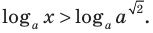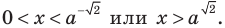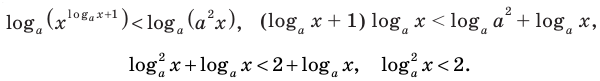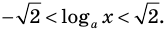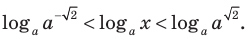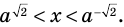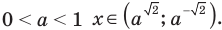Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Он поможет решить задания №4, 12 и 14 из профильного уровня математики.
Одна из их разновидностей уравнений – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие степеней и переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
$$ a^{f(x)}=b^{g(x)}; $$
Где (a) и (b) — некоторые числа, а (f(x)) и (g(x)) — какие-то выражения, зависящие от (x). Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
$$2^x=8;$$
$$ 2^x=2^{2x+1};$$
$$3^{x^2}=2^{x^2-2x+3};$$
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
$$ 7x+2=16;$$
$$x^2-4x+5=0;$$
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Пример 1
$$ 2^x=8;$$
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
$$ 2^3=2*2*2=8; $$
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь по-сложнее.
Пример 2
$$ 3^{4x-1}=frac{1}{9};$$
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
$$frac{1}{9}=frac{1}{3^2}=3^{-2};$$
Мы применили свойство отрицательной степени по формуле:
$$ a^{-n}=frac{1}{a^n};$$
Теперь наше уравнение будет выглядеть так:
$$ 3^{4x-1}=3^{-2};$$
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
$$ 4x-1=-2;$$
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
$$4х=-2+1;$$
$$4x=-1;$$
$$x=-frac{1}{4}.$$
Поздравляю, мы нашли корень нашего показательного уравнения.
Пример 3
$$125^x=25;$$
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
$$ (5^3)^x=5^2;$$
Воспользуемся одним из свойств степеней ((a^n)^m=a^{n*m}):
$$ 5^{3*x}=5^2;$$
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
$$ 3*x=2;$$
$$ x=frac{2}{3};$$
И еще один пример:
Пример 4
$$2^x=-4;$$
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
$$ a^x=b;$$
Где (a,b) какие-то положительные числа. ((a>0, ; b>0)).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
$$ a^x=a^m;$$
Раз основания одинаковые, то мы можем просто приравнять степени:
$$x=m.$$
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Пример 5
$$2^x=16;$$
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
$$2^x=2^4$$
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6
$$5^{-x}=125 Rightarrow 5^{-x}=5*5*5 Rightarrow 5^{-x}=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7
$$9^{4x}=81 Rightarrow (3*3)^{4x}=3*3*3*3 Rightarrow(3^2)^{4x}=3^4 Rightarrow 3^{8x}=3^4 Rightarrow 8x=4 Rightarrow x=frac{1}{2}.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
Пример 8
$$ 3^x=2;$$
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
$$ b=a^{log_{a}(b)};$$
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
$$ 2=3^{log_{3}(2)};$$
Подставим данное преобразование в наш пример:
$$3^x=3^{log_{3}(2)};$$
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
$$x=log_{3}(2).$$
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Пример 9
$$ 7^{2x}=5;$$
$$ 7^{2x}=7^{log_{7}(5)};$$
$$2x=log_{7}(5);$$
$$x=frac{1}{2}*log_{7}(5).$$
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
$$ x=frac{1}{2}*log_{7}(5)=log_{7}(5^{frac{1}{2}})=log_{7}(sqrt{5});$$
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Рассмотрим уравнение:
Пример 10
$$ 9^x-5*3^x+6=0;$$
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^{2x}=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^{n*m}). Подставим:
$$(3^x)^2-5*3^x+6=0;$$
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
$$t^2-5t+6=0;$$
Квадратное уравнение, которое решается через дискриминант:
$$D=5^2-4*6=25-24=1; Rightarrow t_{1}=frac{5+sqrt{1}}{2}=3; Rightarrow t_{2}=frac{5-sqrt{1}}{2}=2;$$
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
$$ 3^x=3;$$
$$3^x=3^1;$$
$$x=1.$$
И второй корень:
$$ 3^x=2;$$
$$3^x=3^{log_{3}(2)};$$
$$x=log_{3}(2).$$
Ответ: (x_{1}=1; ; x_{2}=log_{3}(2).)
И еще один пример на замену:
Пример 11
$$3^{4x^2-6x+3}-10*3^{2x^2-3x+1}+3=0;$$
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Преобразуем первое слагаемое. Если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
$$ 3^{4x^2-6x+3}=3^{4x^2-6x+2+1}=3^{2(2x^2-3x+1)+1}=3^{2*(2x^2-3x+1)}*3^1=3*(3^{2x^2-3x+1})^2;$$
Подставим в исходное уравнение:
$$3*(3^{2x^2-3x+1})^2-10*3^{2x^2-3x+1}+3=0;$$
Теперь показательные функции одинаковы и можно сделать замену:
$$t=3^{2x^2-3x+1}; ; t>0;$$
$$3*t^2-10t+3=0;$$
$$D=100-36=64; Rightarrow t_{1}=3; t_{2}=frac{1}{3};$$
Обратная замена, и наше уравнение сводится к простейшему:
$$ 3^{2x^2-3x+1}=3;$$
$$ 2x^2-3x+1=1;$$
$$x(2x-3)=0;$$
$$x=0; ; x=frac{3}{2}.$$
И второе значение (t):
$$3^{2x^2-3x+1}=frac{1}{3};$$
$$3^{2x^2-3x+1}=3^{-1};$$
$$2x^2-3x+1=-1;$$
$$2x^2-3x+2=0;$$
$$D=9-16=-7<0;$$
Раз дискриминант получился меньше нуля, то вторая ветка решений нам корней не дает.
Ответ: (x_{1}=0; ; x_{2}=frac{3}{2}.)
Однородные показательные уравнения
Иногда встречаются такие показательные уравнения, в которых не сразу видно, как сделать одинаковые функции, а именно одинаковые основания, чтобы произвести замену. Посмотрим на такой пример:
Пример 12
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x};$$
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
$$ 7^{x+1}+3*7^{x}=3^{x+2}+3^{x} ; ; :3^x$$
$$ frac{7^{x+1}}{3^x}+frac{3*7^{x}}{3^x}=frac{3^{x+2}}{3^x}+frac{3^{x}}{3^x};$$
Здесь нам придется воспользоваться свойствами степеней:
$$frac{a^n}{a^m}=a^{n-m};$$
$$ a^n*a^m=a^{n+m};$$
$$ frac{a^n}{b^n}=(frac{a}{b})^n;$$
Разберем каждое слагаемое:
$$ frac{7^{x+1}}{3^x}=frac{7*7^x}{3^x}=7*frac{7^x}{3^x}=7*(frac{7}{3})^x;$$
$$ frac{3*7^{x}}{3^x}=3*frac{7^x}{3^x}=3*(frac{7}{3})^x;$$
$$ frac{3^{x+2}}{3^x}=3^2*frac{3^x}{3^x}=3^2*1=9;$$
$$ frac{3^{x}}{3^x}=1;$$
Теперь подставим получившееся преобразования в исходное уравнение:
$$ 7*(frac{7}{3})^x+3*(frac{7}{3})^x=9+1;$$
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac{7}{3})^x):
$$7t+3t=10;$$
$$10t=10;$$
$$t=1;$$
Сделаем обратную замену:
$$(frac{7}{3})^x=1;$$
Вспоминаем, что (1=(frac{7}{3})^0):
$$(frac{7}{3})^x=(frac{7}{3})^0;$$
$$x=0.$$
Ответ: (x=0).
И последний пример на замену:
Пример 13
$$2^{x+2}+0,5^{-x-1}+4*2^{x+1}=28;$$
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
$$ a^n*a^m=a^{n+m};$$
$$a^{-n}=frac{1}{a^n};$$
$${(a^n)}^m=a^{n*m};$$
Разберем каждое слагаемое нашего уравнения:
$$2^{x+2}=2^x*2^2=4*2^x;$$
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
$$0,5^{-x-1}=0,5^{-(x+1)}={(frac{1}{2})}^{-(x+1)}={(2^{-1})}^{-(x+1)}=2^{x+1}=2^x*2^1=2*2^x;$$
И последнее слагаемое со степенью:
$$ 4*2^{x+1}=4*2^x*2^1=8*2^x;$$
Подставим все наши преобразования в исходное уравнение:
$$4*2^x+2*2^x+8*2^x=28;$$
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
$$2^x*(4+2+8)=28;$$
$$14*2^x=28;$$
$$2^x=frac{28}{14}=2;$$
$$2^x=2^1;$$
$$x=1.$$
Ответ: (x=1.)
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера.
Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Пример 14
$$2^{x+1}*5^x=10^{x+1}*5^{x+2};$$
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
$$2^{x+1}*5^x=(2*5)^{x+1}*5^{x+2};$$
Воспользуемся формулой ((a*b)^n=a^n*b^n):
$$ 2^{x+1}*5^x=2^{x+1}*5^{x+1}*5^{x+2};$$
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
$$frac{2^{x+1}}{2^{x+1}}=frac{5^{x+1}*5^{x+2}}{5^x};$$
Сокращаем и воспользуемся формулами (a^n*a^m=a^{n+m}) и (frac{a^n}{a^m}=a^{n-m}):
$$1=frac{5^{x+1+x+2}}{5^x};$$
$$1=frac{5^{2x+3}}{5^x};$$
$$1=5^{2x+3-x};$$
$$1=5^{x+3};$$
$$5^0=5^{x+3};$$
$$x+3=0;$$
$$x=-3.$$
Ответ: (x=-3).
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Содержание:
Показательно-степенные уравнения:
Показательно степенными уравнениями обычно называют уравнения, содержащие выражения вида
Основные способы решения уравнения вида
Ориентир
Используем (если возможно) основное логарифмическое тождество в виде
Логарифмируем (если возможно) обе части уравнения по числовому основанию или представляем все степени как степени с одним и тем же числовым основанием по формуле
Пример:
На ОДЗ (х > 0) обе части уравнения положительны, поэтому после логарифмирования по основанию 10 получаем уравнение, равносильное данному:
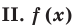
Ориентир:
Две степени с одинаковыми основаниям и 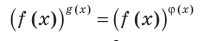
для корней, этого уравнения
— целые, числа одинаковой четности;
для корней этого уравнения
для корней этого уравнения
существуют;
для корней этого уравнения существуют
и
Пример:
Если предположить, что основание степени 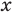
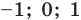
- при
получаем верное равенство
- при
то
— верное равенство;
- при
то
— верное равенство;
- при
то есть
то
— верное равенство.
Ответ:
Замечание. Если предположить, что основание 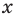
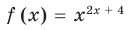
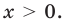
Таким образом, ответ к такому уравнению нельзя записать однозначно.
Объяснение и обоснование
Показательно степенными уравнениями и неравенствами обычно называют уравнения и неравенства, содержащие выражения вида 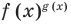
Анализируя показательно-степенные уравнения, представленные в табл. 26, следует помнить, что в школьном курсе математики понятие уравнения на разных этапах вводилось по-разному. В 4 -5 классах уравнением называлось числовое равенство, содержащее неизвестное число, обозначенное буквой. Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называлось корнем, или решением этого уравнения. Например, для уравнения 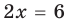
С точки зрения приведенного определения, в уравнении 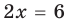
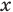
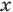
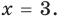
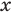
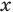
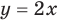
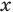
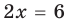
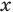
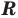
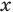
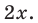
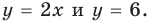
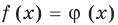
Для всех видов уравнений, которые рассматривались в курсе алгебры или алгебры и начал анализа, приведенные два определения уравнения приводят к одному и тому же результату при решении уравнений. Но в случае показательно-степенного уравнения иногда можно получить разные ответы, используя разные подходы к определению уравнения. Например, решим уравнение
Если рассматривать такое уравнение как числовое равенство, то две степени с одинаковым основанием 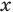
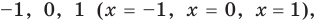
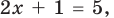
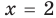
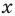
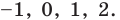
Если же рассматривать это уравнение как равенство с переменной и встать на функциональную точку зрения, то функция 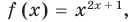
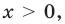
Таким образом, в рассмотренном уравнении ответ нельзя записать однозначно (поскольку каждый из указанных подходов к определению уравнения имеет право на существование и реально используется в математике). Поэтому в подобных ситуациях приходится приводить оба варианта ответа. Аналогичный пример приведен в табл. 26.
Обобщая приведенные выше рассуждения, заметим, что в том слу чае, когда при решении уравнения вида 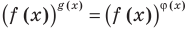
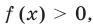
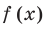
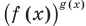
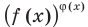
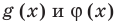
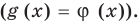
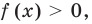
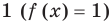
Например, решим уравнение
Из условия не следует, что основание степени 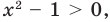
Объединяя полученные результаты, получаем ответ.
Ответ:
Замечание. При 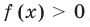
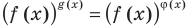
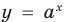
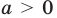
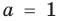
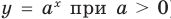
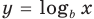
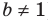
Также отметим, что при решении неравенств вида 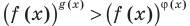
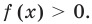
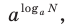
Достаточно часто при решении показательно-степенных уравнений логарифмируют обе его части. Это можно сделать только тогда, когда обе части уравнения положительны на его ОДЗ (см. пример 2 в табл. 26). Приведем еще несколько примеров решения показательно-степенных уравнений и неравенств.
Примеры с решениями
Пример №1
Решите уравнение
Решение:
Поскольку 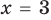
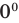
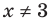
Из первого полученного уравнения имеем 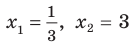
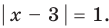
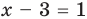
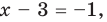
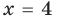
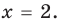
Комментарий:
Поскольку 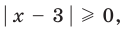
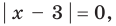
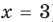
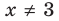
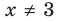
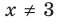
Пример №2
Решите уравнение
Комментарий:
Прологарифмировать обе части данного уравнения не удается (в левой части стоит сумма), поэтому попытаемся представить все степени в виде степеней с одним и тем же числовым основанием. Так как в уравнении есть логарифм по основанию 2, представим все данные степени в виде степеней с основанием 2 по формуле 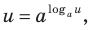
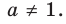
(то есть слагаемые, стоящие в левой части данного уравнения, одинаковы). После получения уравнения (2) (см. решение) можно использовать равенство (1) справа налево, а также записать правую часть уравнения (2) как степень числа 2 или прологарифмировать обе его части по основанию 2.
Решение:
ОДЗ: 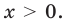
Ответ: 2.
Пример №3
Решите систему уравнений:
Комментарий :
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим, чтобы на этой ОДЗ преобразования уравнений как в прямом, так и в обратном направлениях сохраняли верные равенства. В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 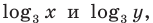
Решение:
ОДЗ: 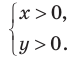
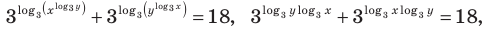
Тогда данная система уравнений равносильна системе
Замена 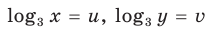
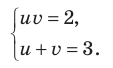
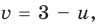
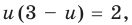
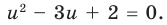
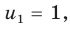
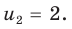
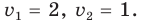
Тогда
(найденные решения входят в ОДЗ). Ответ:
Пример №4
Решите неравенство
I способ
Комментарий:
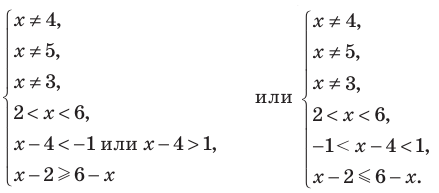
Попытаемся выполнить равносильные преобразования данного неравенства, применив рассуждения, аналогичные тем, что приводились при решении показательно-степенных уравнений (см. пункт II табл. 60). Поскольку 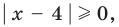
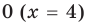
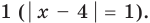
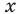
Рассмотрим два случая:
- 1) основание больше 1 (при переходе от степеней к показателям в данном неравенстве знак неравенства не меняется);
- 2) основание меньше 1, но больше 0 (при переходе от степеней к показателям знак неравенства меняется на противоположный). При таких преобразованиях получаем неравенства, равносильные данному (на его ОДЗ), поскольку можем гарантировать правильность не только прямых, но и обратных переходов.
При решении полученных простейших логарифмических неравенств учитываем, что функция 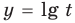
Решение:
При 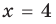
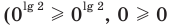
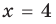
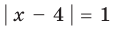
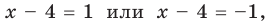
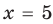
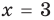
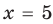
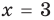

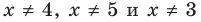
Таким образом, 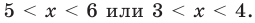
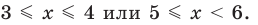
II способ
Комментарий:
Решим данное неравенство методом интервалов, для этого приведем его к виду 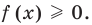
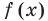
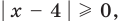
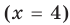
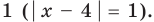
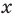
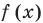
Решение:
На этой ОДЗ данное неравенство равносильно неравенству
2. Пусть
На ОДЗ уравнение (2) равносильно уравнению
При 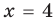
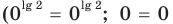
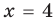
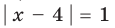
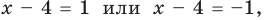
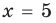
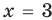
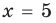
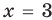
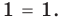
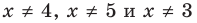
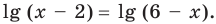
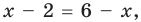
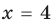
3. Отмечаем нули функции на ОДЗ и находим знак 
Ответ:
Пример №5
Решите неравенство
Комментарий:
На ОДЗ обе части неравенства положительны, поэтому попытаемся прологарифмировать обе его части. Поскольку в данное неравенство уже входит 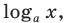
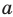
Решение:
Прологарифмируем обе части неравенства.
1) При 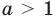
Учитывая ОДЗ 

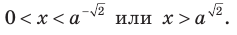
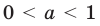
Ответ:
Показательно-степенные уравнения
Показательно-степенные уравнения:
Показательно-степенными уравнениями обычно называют уравнения, содержащие выражения вида 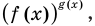
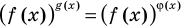
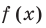
Основные способы решения уравнения вида
Используем (если возможно) основное логарифмическое тождество в виде
Ответ: 2
Логарифмируем (если возможно) обе части уравнения по числовому основанию или представляем все степени как степени с одним и тем же числовым основанием по формуле
На ОДЗ 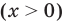
Отсюда
Замена: 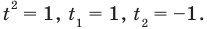
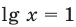
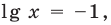
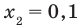
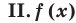
Две степени с одинаковыми основаниями 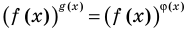
и для корней этого уравнения
— целые числа одинаковой четности.
-
и для корней этого уравнения
-
и для корней этого уравнения
существуют.
-
и для корней этого уравнения существуют
Пример:
Если предположить, что основание степени 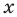
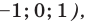
- при
получаем верное равенство
- при
— верное равенство;
- при
— верное равенство;
- при
— верное равенство.
Ответ:
Замечание. Если предположить, что основание 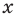
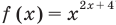
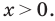
Объяснение и обоснование:
Показательно-степенными уравнениями и неравенствами обычно называют уравнения и неравенства, содержащие выражения вида 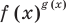
Анализируя показательно-степенные уравнения, представленные в таблице 57, следует помнить, что в школьном курсе математики понятие уравнения на разных этапах вводилось по-разному. А именно: в 4-5 классах уравнением называлось числовое равенство, содержащее неизвестное число, обозначенное буквой. Значение неизвестного, при котором уравнение обращается в верное числовое равенство, называлось корнем или решением этого уравнения. Например, для уравнения 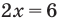
С точки зрения приведенного определения в уравнении 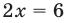
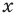
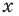
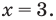
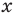
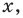
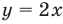
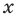
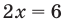
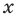
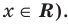
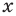
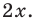
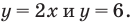
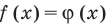
Для всех видов уравнений, которые рассматривались в курсе алгебры или алгебры и начал анализа, приведенные два определения уравнения приводят к одному тому же результату при решении уравнений. Но в случае показательно-степенного уравнения иногда можно получить разные ответы, используя разные подходы к определению уравнения.
Например, решим уравнение
Если рассматривать такое уравнение как числовое равенство, то две степени с одинаковым основанием 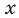
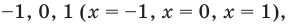
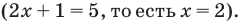
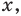
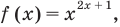
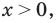
Таким образом, в рассмотренном уравнении ответ нельзя записать однозначно (поскольку каждый из указанных подходов к определению уравнения имеет право на существование и реально используется в математике). Поэтому в подобных ситуациях приходится приводить оба варианта ответа. Аналогичный пример приведен в таблице 57.
Обобщая приведенные выше рассуждения, заметим, что в том случае, когда при решении уравнения вида 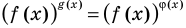
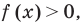
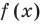
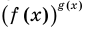
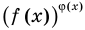
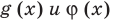
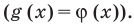
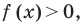
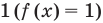
Например, решим уравнение
Из условия не следует, что основание степени 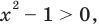
1) Если 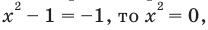
Подставляя это значение в данное уравнение, имеем 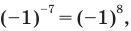
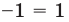
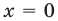
2) Если 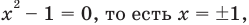
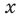
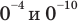
3) Если 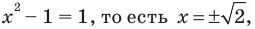
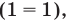
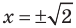
4) Приравняем показатели степеней данного уравнения (основания степеней в левой и правой частях уравнения одинаковые): 
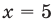
Объединяя полученные результаты, получаем ответ.
Ответ:
Замечание. При 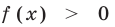
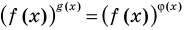
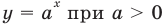
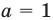
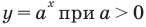
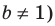
Также отметим, что при решении неравенств вида 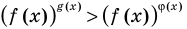
Заметим, что в тех случаях, когда в показательно-степенное уравнение входят выражения вида 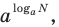
Достаточно часто для решения показательно-степенных уравнений используется логарифмирование обеих частей. Конечно, это можно сделать только тогда, когда на ОДЗ данного уравнения обе части уравнения положительны (см. пример 2 в табл. 57).
Приведем еще несколько примеров решения показательно-степенных уравнений и неравенств.
- Заказать решение задач по высшей математике
Пример №6
Решите уравнение
Решение:
Поскольку 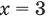
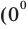
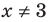
Из первого полученного уравнения имеем 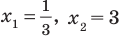
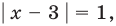
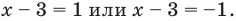
Ответ:
Комментарий:
Поскольку 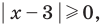
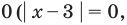
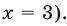
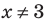
При 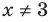
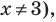
Пример №7
Решите уравнение
Комментарий:
Прологарифмировать обе части данного уравнения не удается (в левой части стоит сумма), поэтому попытаемся все степени представить в виде степеней с одним и тем же числовым основанием. Учитывая, что в данном уравнении есть логарифм по основанию 2, представим все данные степени как степени с основанием 2 по формуле 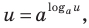
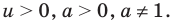
(то есть слагаемые, стоящие в левой части данного уравнения, одинаковы). После получения уравнения (2) (см. решение) можно использовать равенство (1) справа налево. Можно также записать правую часть уравнения (2) как степень числа 2 или прологарифмировать обе его части по основанию 2.
Решение:
► ОДЗ: х > 0. На этой ОДЗ данное уравнение равносильно уравнениям:
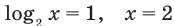
Ответ: 2.
Комментарий:
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим за тем, чтобы на этой ОДЗ все преобразования уравнений как в прямом, так и в обратном направлении сохраняли верные равенства.
В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. выше комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 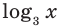
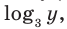
Решение:
ОДЗ: 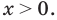
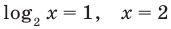
Пример №8
Решите систему уравнений
Комментарий:
Используем равносильные преобразования системы. Для этого учтем ОДЗ и проследим за тем, чтобы на этой ОДЗ все преобразования уравнений как в прямом, так и в обратном направлении сохраняли верные равенства.
В первом уравнении данной системы запишем все степени как степени с основанием 3 (см. выше комментарий к задаче 2). После равносильных (на ОДЗ) преобразований первого уравнения получаем систему (1) (см. решение), в которую переменные входят только в виде 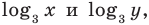
Решение:
ОДЗ: 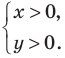
Тогда заданная система равносильна системе
Замена 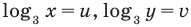
Из второго уравнения последней системы 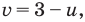
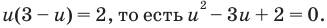
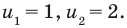
Обратная замена дает
Тогда 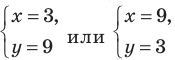
Ответ:
Пример №9
Решите неравенство
I способ
Комментарий:
Попытаемся выполнить равносильные преобразования данного неравенства, применив рассуждения, аналогичные тем, что приводились при решении показательно-степенных уравнений (см. пункт II табл. 57). Поскольку 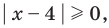
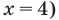
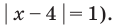
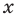
При решении полученных простейших логарифмических неравенств учитываем, что функция 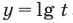
В ответ следует включить все решения полученных систем неравенств и все особые значения, которые являются решениями данного неравенства.
Решение:
ОДЗ: 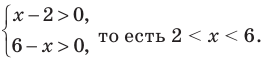
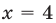
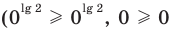
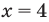
Если 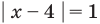
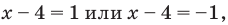
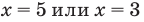
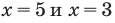
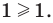
При 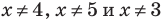
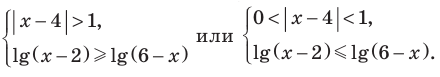
Тогда:
Таким образом, 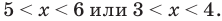
Ответ:
II способ решения неравенства
Комментарий:
Решим данное неравенство методом интервалов, для этого приведем его к виду
Для нахождения нулей 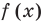
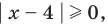
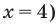
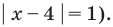
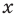
Для нахождения знаков 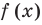
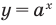
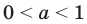
Решение:
1. ОДЗ 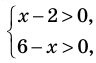
На этой ОДЗ данное неравенство равносильно неравенству
2. Пусть 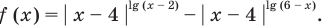
На ОДЗ уравнение (2) равносильно уравнению
При 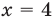
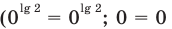
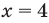
Если 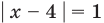
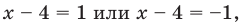
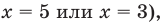
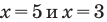
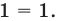
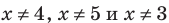
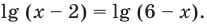
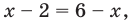
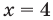
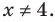
3. Отмечаем нули функции на ОДЗ и находим знак 
Ответ:
Пример №10
Решите неравенство
Комментарий:
На ОДЗ обе части неравенства положительны, поэтому попытаемся прологарифмировать обе части неравенства. Поскольку в данное неравенство уже входит 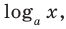
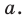
Решение:
ОДЗ:
Прологарифмируем обе части неравенства.
1) При 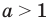
Таким образом,
To есть 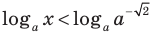
Учитывая ОДЗ 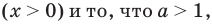
2) При 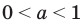
Таким образом,
То есть
Учитывая ОДЗ 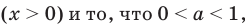
Ответ: 1)при 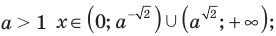
- Показательные уравнения и неравенства
- Логарифмические уравнения и неравенства
- Степенная функция — определение и вычисление
- Степень с целым показателем
- Логарифмическая функция, её свойства и график
- Логарифмические выражения
- Показательная функция, её график и свойства
- Производные показательной и логарифмической функций
План урока:
Простейшие показательные уравнения ах = b
Уравнения вида аf(x) = ag(x)
Задачи, сводящиеся к показательным уравнениям
Уравнения с заменой переменных
Графическое решение показательных уравнений
Показательные неравенства
Простейшие показательные уравнения ах = b
Рассмотрим уравнение
2х = 8
Его называют показательным уравнением, ведь переменная находится в показателе степени. Для его решения представим правую часть как степень числа 2:
8 = 23
Тогда уравнение будет выглядеть так:
2х = 23
Теперь и справа, и слева стоят степени двойки. Очевидно, что число 3 будет являться его корнем:
23 = 23
Является ли этот корень единственным? Да, в этом можно убедиться, если построить в координатной плоскости одновременно графики у = 2х и у = 8. Второй график представляет собой горизонтальную линию.
Пересекаются эти графики только в одной точке, а потому найденное нами решение х = 3 является единственным.
Так как любая показательная функция является монотонной, то есть либо только возрастает (при основании, большем единицы), либо только убывает (при основании, меньшем единицы), то в общем случае ур-ние ах = b может иметь не более одного решения. Это является следствием известного свойства монотонных функций – горизонтальная линия пересекает их не более чем в одной точке.
Сразу отметим, что если в ур-нии вида ах = b число b не является положительным, то корней у ур-ния не будет вовсе. Это следует из того факта, что область значений показательной функции – промежуток (0; + ∞), ведь при возведении в степень любого положительного числа результат всё равно остается положительным. Можно проиллюстрировать это и графически:
Решая простейшее показательное уравнение
2х = 8
мы специально представляли правую часть как степень двойки:
2х = 23
После этого мы делали вывод, что если в обеих частях ур-ния стоят степени с равными основаниями (2 = 2), то у них должны быть равны и показатели. Это утверждение верно и в более общем случае. Если есть ур-ние вида
ах = ас
то его единственным решением является х = с.
Задание. Найдите решение показательного уравнения
8х = 8– 9
Решение. У обоих частей равны основания, значит, равны и показатели:
х = – 9
Ответ: – 9.
Задание. Найдите корень уравнения
Решение. Заметим, что число 625 = 54. Тогда ур-ние можно представить так:
Отсюда получаем, что х = 4.
Ответ: 4.
Видно, что основной метод решения показательных уравнений основан на его преобразовании, при котором и в правой, и в левой части стоят степени с совпадающими основаниями.
Задание. При каком х справедливо равенство
Решение. Преобразуем число справа:
Теперь ур-ние можно решить:
Ответ: – 3.
Задание. Решите ур-ние
Решение. Любое число при возведении в нулевую степень дает единицу, а потому можно записать, что 1 = 1270. Заменим с учетом этого правую часть равенства:
Ответ: 0.
Уравнения вида аf(x) = ag(x)
Рассмотрим чуть более сложное показательное ур-ние
Для его решения заменим показатели степеней другими величинами:
Теперь наше ур-ние принимает вид
Такие ур-ния мы решать умеем. Надо лишь приравнять показатели степеней:
При решении подобных ур-ний введение новых переменных опускают. Можно сразу приравнять показатели степеней, если равны их основания:
В общем случае использованное правило можно сформулировать так:
Задание. Найдите корень ур-ния
Решение. Представим правую часть как степень двойки:
Тогда ур-ние примет вид
Теперь мы имеем право приравнять показатели:
Ответ: – 1
Задание. Укажите значение х, для которого выполняется условие
Решение. Здесь удобнее преобразовать не правую, а левую часть. Заметим, что
С учетом этого можно записать
Основания у выражений слева и справа совпадают, а потому можно приравнять показатели:
Ответ: 12,5
Задание. Укажите корень показательного уравнения
Решение. Для перехода к одному основанию представим число 64 как квадрат восьми:
Тогда ур-ние примет вид:
Ответ: х = 3
Задание. Найдите корень ур-ния
Решение. Здесь ситуация чуть более сложная, ведь число 2 невозможно представить как степень пятерки, а пятерки не получится выразить как степень двойки. Однако у обеих степеней в ур-нии совпадают показатели. Напомним, что справедливы следующие правила работы со степенями:
С учетом этого поделим обе части ур-ния на выражения 53+х:
Ответ: – 2.
Задание. При каких х справедлива запись
Решение.
Можно сделать преобразования, после которых в ур-нии останется только показательная функция 5х. Для этого произведем следующие замены:
Перепишем исходное ур-ние с учетом этих замен:
Теперь множитель 5х можно вынести за скобки:
Ответ: 2
Рассмотрим чуть более сложное ур-ние, которое может встретиться на ЕГЭ в задании повышенной сложности №13.
Задание. Найдите решение уравнения
Решение. Преобразуем левое слагаемое:
Перепишем начальное ур-ние, используя это преобразование
Теперь мы можем спокойно вынести множитель за скобки:
Получили одинаковые основания слева и справа. Значит, можно приравнять и показатели:
Это квадратное уравнение, решение которого не должно вызывать у десятиклассника проблем:
Задачи, сводящиеся к показательным уравнениям
Рассмотрим одну прикладную задачу, встречающуюся в ЕГЭ по математике.
Задание. Из-за радиоактивного распада масса слитка из изотопа уменьшается, причем изменение его массы описывается зависимостью m(t) = m0 • 2–t/T, где m0 – исходная масса слитка, Т – период полураспада, t – время. В начальный момент времени изотоп, чей период полураспада составляет 10 минут, весит 40 миллиграмм. Сколько времени нужно подождать, чтобы масса слитка уменьшилась до 5 миллиграмм.
Решение. Подставим в заданную формулу значения из условия:
m0 = 40 миллиграмм;
T = 10 минут;
m(t) = 5 миллиграмм.
В результате мы получим ур-ние
из которого надо найти значение t. Поделим обе части на 40:
Ответ: 30 минут.
Далее решим чуть более сложную задачу, в которой фигурирует сразу 2 радиоактивных вещества.
Задание. На особо точных рычажных весах в лаборатории лежат два слитка из радиоактивных элементов. Первый из них весит в начале эксперимента 80 миллиграмм и имеет период полураспада, равный 10 минутам. Второй слиток весит 40 миллиграмм, и его период полураспада составляет 15 минут. Изначально весы наклонены в сторону более тяжелого слитка. Через сколько минут после начала эксперимента весы выровняются? Масса слитков меняется по закону m(t) = m0 • 2–t/T, где m0 и Т – это начальная масса слитка и период его полураспада соответственно.
Решение. Весы выровняются тогда, когда массы слитков будут равны. Если подставить в данную в задаче формулу условия, то получится, что масса первого слитка меняется по закону
а масса второго слитка описывается зависимостью
Приравняем обе формулы, чтобы найти момент времени, когда массы слитков совпадут (m1 = m2):
Делим обе части на 40:
Основания равны, а потому приравниваем показатели:
Ответ: 30 минут.
Уравнения с заменой переменных
В ряде случаев для решения показательного уравнения следует ввести новую переменную. В учебных заданиях такая замена чаще всего (но не всегда) приводит к квадратному ур-нию.
Задание. Решите уравнение методом замены переменной
Заметим, что в уравнении стоят степени тройки и девятки, но 32 = 9. Тогда введем новую переменную t = 3x. Если возвести ее в квадрат, то получим, что
C учетом этого изначальное ур-ние можно переписать:
Получили обычное квадратное ур-ние. Решим его:
Мы нашли два значения t. Далее необходимо вернуться к прежней переменной, то есть к х:
Первое ур-ние не имеет решений, ведь показательная функция может принимать лишь положительные значения. Поэтому остается рассмотреть только второе ур-ние:
Ответ: 2.
Задание. Найдите корни ур-ния
Решение. Здесь в одном ур-нии стоит сразу три показательных функции. Попытаемся упростить ситуацию и избавиться от одной из них. Для этого поделим ур-ние на выражение 44х+1:
Так как 14х+1 = 1, мы можем записать:
Обратим внимание, что делить ур-ние на выражение с переменной можно лишь в том случае, если мы уверены, что оно не обращается в ноль ни при каких значениях х. В данном случае мы действительно можем быть в этом уверены, ведь величина 44х+1 строго положительна при любом х.
Вернемся к ур-нию. В нем стоят величины (9/4)4х+1 и (3/2)4х+1. У них одинаковые показатели, но разные степени. Однако можно заметить, что
9/4 = (3/2)2, поэтому и (9/4)4х+1 = ((3/2)4х+1)2. Это значит, что перед нами уравнение с заменой переменных.
Произведем замену t = (3/2)4х+1, тогда (9/4)4х+1 = ((3/2)4х+1)2 = t2. Далее перепишем ур-ние с новой переменной t:
Снова получили квадратное ур-ние.
Возвращаемся к переменной х:
И снова первое ур-ние не имеет корней, так как при возведении положительного числа в степень не может получится отрицательное число. Остается решить второе ур-ние:
Ответ: – 0,25.
Графическое решение показательных уравнений
Не всякое показательное уравнение легко или вообще возможно решить аналитическим способом. В таких случаях выручает графическое решение уравнений.
Задание. Найдите графическим способом значение х, для которого справедливо равенство
Решение. Построим в одной системе координат графики у = 3х и у = 4 – х:
Видно, что графики пересекаются в одной точке с примерными координатами (1; 3). Так как графический метод не вполне точный, следует подставить х = 1 в ур-ние и убедиться, что это действительно корень ур-ния:
Получили верное равенство, значит, х = 1 – это действительно корень ур-ния.
Ответ: 1
Задание. Решите графически ур-ние
Решение. Перенесем вправо все слагаемые, кроме 2х:
Слева стоит показательная функция, а справа – квадратичная. Построим их графики и найдем точки пересечения:
Видно, что у графиков есть две общие точки – это (0;1) и (1; 2). На всякий случай проверим себя, подставив х = 0 и х = 1 в исходное ур-ние:
Ноль подходит. Проверяем единицу:
И единица тоже подошла. В итоге имеем два корня, 0 и 1.
Ответ: 0; 1.
Показательные неравенства
Рассмотрим координатную плоскость, в которой построен график некоторой показательной ф-ции у = ах, причем а > 0. Пусть на оси Ох отложены значения s и t, и t < s. То есть точка t располагается левее на оси Ох.
Ясно, что точкам t и s оси Ох соответствуют точки at и as на оси Оу. Так как
у = ах
является возрастающей функцией, то и величина at окажется меньше, чем as. Другими словами, точка at на оси Оу будет лежать ниже точки аs (это наглядно видно на рисунке). Получается, что из условия t < s следует неравенство at < as. Это значит, что эти два нер-ва являются равносильными.
С помощью этого правила можно решать некоторые простейшие показательные неравенства. Например, пусть дано нер-во
Представим восьмерку как степень двойки:
По только что сформулированному правилу можно заменить это нер-во на другое, которое ему равносильно:
Решением же этого линейного неравенства является промежуток (– ∞; 3).
Однако сформулированное нами правило работает тогда, когда основание показательной ф-ции больше единицы. А что же делать в том случае, если оно меньше единицы? Построим график такой ф-ции и снова отложим на оси Ох точки t и s, причем снова t будет меньше s, то есть эта точка будет лежать левее.
Так как показательная ф-ция у = ах при основании, меньшем единицы, является убывающей, то окажется, что на оси Оу точка as лежит ниже, чем at. То есть из условия t < s следует, что at > as. Получается, что эти нер-ва равносильны.
Например, пусть надо решить показательное неравенство
Выразим число слева как степень 0,5:
Тогда нер-во примет вид
По рассмотренному нами правилу его можно заменить на равносильное нер-во
В более привычном виде, когда выражение с переменной стоит слева, нер-во будет выглядеть так:
а его решением будет промежуток (3; + ∞).
В общем случае мы видим, что если в показательном нер-ве вида
основание a больше единицы, то его можно заменить равносильным нер-вом
Грубо говоря, мы просто убираем основание степеней, а знак нер-ва остается неизменным. Если же основание а меньше единицы, то знак неравенства необходимо поменять на противоположный:
Это правило остается верным и в том случае, когда вместо чисел или переменных t и s используются произвольные функции f(x) и g(x). Сформулируем это правило:
Таким образом, для решения показательных неравенств их следует преобразовать к тому виду, при котором и справа, и слева стоят показательные ф-ции с одинаковыми показателями, после чего этот показатель можно просто отбросить. Однако надо помнить, что при таком отбрасывании знак нер-ва изменится на противоположный, если показатель меньше единицы.
Задание. Решите простейшее неравенство
Решение.
Представим число 64 как степень двойки:
теперь и справа, и слева число 2 стоит в основании. Значит, его можно отбросить, причем знак нер-ва останется неизменным (ведь 2 > 1):
Задание. Найдите промежуток, на котором выполняется нер-во
Решение. Так как основание степеней, то есть число 0,345, меньше единицы, то при его «отбрасывании» знак нер-ва должен измениться на противоположный:
Это самое обычное квадратное неравенство. Для его решения нужно найти нули квадратичной функции, стоящей слева, после чего отметить их на числовой прямой и определить промежутки, на которых ф-ция будет положительна.
Нашли нули ф-ции. Далее отмечаем их на прямой, схематично показываем параболу и расставляем знаки промежутков:
Естественно, что в более сложных случаях могут использоваться всё те же методы решения нер-ва, которые применяются и в показательных ур-ниях. В частности, иногда приходится вводить новую переменную.
Задание. Найдите решение нер-ва
Решение. Для начала представим число 3х+1 как произведение:
Теперь перепишем с учетом этого исходное нер-во:
Получили дробь, в которой есть одна показательная ф-ция 3х. Заменим её новой переменной t = 3x:
Это дробно-рациональное неравенство, которое можно заменить равносильным ему целым нер-вом:
которое, в свою очередь, решается методом интервалов. Для этого найдем нули выражения, стоящего слева
Отмечаем найденные нули на прямой и расставляем знаки:
Итак, мы видим, что переменная t должна принадлежать промежутку (1/3; 9), то есть
Теперь произведем обратную замену t = 3x:
Так как основание 3 больше единицы, просто откидываем его:
Итак, мы узнали о показательных уравнениях и неравенствах и способах их решения. В большинстве случаев необходимо представить обе части равенства или неравенства в виде показательных степеней с одинаковыми основаниями. Данное действие иногда называют методом уравнивания показателей. Также в отдельных случаях может помочь графический способ решения ур-ний и замена переменной.
Приветствую вас дорогие учащиеся!
Рекомендуем подписаться на канал на youtube нашего сайта TutoMath.ru, чтобы быть в курсе всех новых видео уроков.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=an
1. a0 = 1 (a ≠ 0)
2. a1 = a
3. an • am = an + m
4. (an)m = anm
5. anbn = (ab)n
6. a-n= 1/an
7. an/am= an — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
6x=36
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2x*5=10
16x — 4x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
2х = 23
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
2х = 23
х = 3
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
2х+2 = 24
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
33х — 9х+8 = 0
Для начала переносим девятку в правую сторону, получаем:
33х = 9х+8
Теперь нужно сделать одинаковые основания. Мы знаем что 9=32 . Воспользуемся формулой степеней (an)m = anm.
33х = (32)х+8
Получим 9х+8 =(32)х+8 =3 2х+16
33х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
22х+4 — 10•4х = 24
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (an)m = anm.
4х = (22)х = 22х
И еще используем одну формулу an • am = an + m:
22х+4 = 22х•24
Добавляем в уравнение:
22х•24 — 10•22х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 22х ,вот и ответ — 22х мы можем вынести за скобки:
22х(24 — 10) = 24
Посчитаем выражение в скобках:
24 — 10 = 16 — 10 = 6
6•22х = 24
Все уравнение делим на 6:
22х = 4
Представим 4=22:
22х = 22 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
Решим уравнение:
9х – 12*3х +27= 0
Преобразуем:
9х = (32)х = 32х
Получаем уравнение:
32х — 12•3х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
3х = t
Тогда 32х = (3х)2 = t2
Заменяем в уравнении все степени с иксами на t:
t2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
Берем t1:
t1 = 9 = 3х
Стало быть,
3х = 9
3х = 32
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3х
3х = 31
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
Вступайте в группу ВКОНТАКТЕ
Как решать
показательные уравнения?
Решение уравнений – навык, который необходим каждому нацеленному на успешную сдачу ЕГЭ и ОГЭ школьнику. Это поможет решить задания №5, 13 и 15 из профильного уровня математики.
Одна из их разновидностей – степенные уравнения, которые иногда также называют показательными. Основная отличительная особенность – наличие переменной (х) не в основании степени, а в самом показателе. Как это выглядит:
Не бойтесь – это самый общий вид показательных уравнений. Реальные примеры выглядят как-то так:
Внимательно посмотрите на приведенные уравнения. В каждом из них присутствует, так называемая, показательная (степенная) функция. При решении необходимо помнить об основных свойствах степени, а также использовать особые правила, помогающие вычислить значение (х). Познакомиться с понятием степени и ее свойствами можно тут и тут.
И вам понадобится умение решать обыкновенные линейные и квадратные уравнения, те, что вы проходили в 7-8 классе. Вот такие:
И так, любое уравнение, в котором вы увидите показательную (степенную) функцию, называется показательным уравнением. Кроме самой показательной функции в уравнении могут быть любые другие математические конструкции – тригонометрические функции, логарифмы, корни, дроби и т.д. Если вы видите степень, значит перед вам показательное уравнение.
Ура! Теперь знаем, как выглядят показательные уравнения, но толку от этого не очень много. Было бы неплохо научиться их решать. Отличная новость – на наш взгляд показательные уравнения одни из самых простых типов уравнений, по сравнению с логарифмическими, тригонометрическими или иррациональными.
Простейшие показательные уравнения
Давайте начнем с самых простых типов уравнений и разберем сразу несколько примеров:
Что такое решить уравнение? Это значит, что нужно найти такое число, которое при подстановке в исходное уравнение вместо (х) даст верное равенство. В нашем примере нужно найти такое число, в которое нужно возвести двойку, чтобы получить восемь. Ну это просто:
Значит, если (х=3), то мы получим верное равенство, а значит мы решили уравнение.
Решим что-нибудь посложнее.
Такое уравнение выглядит сложнее. Попробуем преобразовать правую часть уравнения:
Мы применили свойство отрицательной степени по формуле:
Теперь наше уравнение будет выглядеть так:
Заметим, что слева и справа у нас стоят показательные функции, и там, и там основания одинаковые и равны (3), только вот степени разные – слева степень ((4х-1)), а справа ((-2)). Логично предположить, что если степени у такой конструкции будут равны, при условии, что основания одинаковые, то мы получим верное равенство. Так и поступим:
Такое мы решать умеем, ведь это обыкновенное линейное уравнение.
Поздравляю, мы нашли корень нашего показательного уравнения.
Попробуем поступить так, как в предыдущем примере – преобразуем левую и правую часть, чтобы слева и справа была показательная функция с одинаковым основанием. Как это сделать? Обращаем внимание, что (125=5*5*5=5^3), а (25=5*5=5^2), подставим:
Воспользуемся одним из свойств степеней ((a^n)^m=a^):
И опять мы получили две показательные функции, у которых одинаковые основания и для того, чтобы равенство выполнялось, необходимо приравнять из степени:
И еще один пример:
Те, кто хорошо знает свойства степеней, знают, что показательная функция не может быть отрицательной. Действительно, попробуйте возводить (2) в различную степень, вы никогда не сможете получить отрицательное число.
Внимание! Показательная функция не может быть отрицательной, поэтому, когда вы встречаете примеры на подобии примера 4, то знайте, что такого быть не может. Здесь корней нет, потому что показательная функция всегда положительна.
Теперь давайте разработаем общий метод решения показательных уравнений. И научимся решать более сложные примеры.
Общий метод решения показательных уравнений
Пусть у нас есть вот такой пример:
Где (a,b) какие-то положительные числа. ((a>0, ; b>0).
Согласно разобранным выше примерам, логично предположить, что для того, чтобы решить данное уравнение, нужно его преобразовать к виду, где слева и справа стоят показательные функции с одинаковым основанием. Так и поступим.
Слева у нас уже стоит (a^x), с этим ничего делать не будем, а вот справа у нас стоит загадочное число (b), которое нужно попытаться представить в виде (b=a^m). Тогда уравнение принимает вид:
Раз основания одинаковые, то мы можем просто приравнять степени:
Вот и весь алгоритм решения. Просто нужно преобразовать исходное уравнение таким образом, чтобы слева и справа стояли показательные функции с одинаковыми основаниями, тогда приравниваем степени и вуаля – сложное показательное уравнение решено. Осталось только разобраться, как так преобразовывать. Опять разберем на примерах:
Замечаем, что (16=2*2*2*2=2^4) это степень двойки:
Основания одинаковые, значит можно приравнять степени:
$$x=4.$$
Пример 6 $$5^<-x>=125 Rightarrow 5^<-x>=5*5*5 Rightarrow 5^<-x>=5^3 Rightarrow –x=3 Rightarrow x=-3.$$
Пример 7 $$9^<4x>=81 Rightarrow (3*3)^<4x>=3*3*3*3 Rightarrow(3^2)^<4x>=3^4 Rightarrow 3^<8x>=3^4 Rightarrow 8x=4 Rightarrow x=frac<1><2>.$$
Здесь мы заметили, что (9=3^2) и (81=3^4) являются степенями (3).
Все здорово, но проблема в том, что такая схема решения показательных уравнений работает не всегда. Что делать, если привести к одинаковому основанию не получается. Например:
(3) и (2) привести к одинаковому основанию затруднительно. Но тем не менее мы должны это сделать. Воспользуемся следующей схемой преобразований: пусть есть некоторое положительное число (b>0), тогда его можно представить в виде степени любого, нужного вам, положительного числа не равного единице (a>0, ; a neq 1):
Эта очень важная формула, рекомендуем ее выучить. Вернемся к нашему примеру и по формуле представим (2) в виде (3) в какой-то степени, где (a=3), а (b=2):
Подставим данное преобразование в наш пример:
Получили равенство двух показательных функций с одинаковым основанием, значит можем приравнять их степени:
Так в ответ и запишем. Никакой ошибки здесь нет, дело в том, что такие логарифмы можно посчитать только на калькуляторе, поэтому на ЕГЭ или в контрольной работе вы просто оставляете ответ в таком виде.
Кто забыл, что такое логарифм, можно посмотреть здесь.
Рассмотрим еще несколько аналогичных примеров.
Те, кто хорошо знает свойства логарифмов, могут поиграться с последней формулой и получить ответ в разном виде:
Все эти варианты ответа верные, их можно смело писать в ответ.
И так, мы с вами научились решать любые показательные уравнения вот такого вида: (a^x=b), где (a>0; ; b>0).
Но это еще далеко не все. Часто вы будете встречать показательные уравнения гораздо более сложного типа. В ЕГЭ по профильной математике это номер 15 из 2й части. Но бояться тут не нужно, все на первый взгляд сложные уравнения при помощи обычно не самых сложных преобразований сводятся к уравнениям типа (a^x=b), где (a>0; ; b>0). Рассмотрим типы сложных уравнений, которые могут попасться:
Решение показательных уравнений при помощи замены
Самое первое, что вы должны всегда делать, это пытаться привести все имеющиеся показательные функции к одинаковому основанию.
Здесь это сделать легко, замечаем, что (9=3^2), тогда (9^x=(3^2)^x=3^<2x>=(3^x)^2). Здесь мы воспользовались свойством степеней: ((a^n)^m=a^). Подставим:
Обратим внимание, что во всем уравнении все (х) «входят» в одинаковую функцию — (3^x). Сделаем замену (t=3^x, ; t>0), так как показательная функция всегда положительна.
Квадратное уравнение, которое решается через дискриминант:
Оба корня больше нуля, значит оба нам подходят. Сделаем обратную замену и уравнение сводится к решению двух простых показательных уравнений:
И второй корень:
И еще один пример на замену:
Воспользуемся нашим правилом, что все нужно приводить к одинаковому основанию – а стоп, тут и так у всех показательных функций основание (3). Давайте еще внимательно посмотрим на наш пример, очень похоже на то, что он тоже делается через замену. Но у нас тут нет одинаковых показательных функций, основания то одинаковые, а вот степени отличаются. Но если быть внимательным, то можно заметить, что в первой степени можно разбить свободный член (3=2+1) и вынести общий множитель (2):
Подставим в исходное уравнение:
Теперь показательные функции одинаковы и можно сделать замену:
Обратная замена, и наше уравнение сводится к простейшему:
И второе значение (t):
Тут у нас две показательные функции с основаниями (7) и (3), и как сделать из них одинаковые основания непонятно. Этот пример решается при помощи деления. Давайте поделим все наша уравнение на (3^x):
Здесь нам придется воспользоваться свойствами степеней:
Разберем каждое слагаемое:
Теперь подставим получившееся преобразования в исходное уравнение:
Теперь видно, что в нашем уравнении есть одинаковая функция, которую можно убрать в замену (t=(frac<7><3>)^x):
Сделаем обратную замену:
И последний пример на замену:
Первым делом нужно сделать так, чтобы все показательные функции были с одинаковым основанием и в идеале с одинаковой степенью. Для этого нам понадобятся формулы для степеней:
Разберем каждое слагаемое нашего уравнения:
Все десятичные дроби всегда разумно представить в виде обыкновенных дробей. И будьте внимательны — отрицательная степень не имеет никакого отношения к знаку показательной функции!
И последнее слагаемое со степенью:
Подставим все наши преобразования в исходное уравнение:
Теперь можно сделать замену (t=2^x) или можно обойтись без замены, просто приведя подобные слагаемые (вынести общий множитель (2^x)):
Особенно стоит подчеркнуть прием, который мы использовали при решении 13-го примера. Всегда старайтесь избавляться от десятичных дробей. Переводите их в обыкновенные дроби.
И другой тип степенных уравнений, где обычно не нужно делать замену, а необходимо отлично знать все свойства степеней, некоторые из них мы уже обсудили выше. Все про свойства степеней можно посмотреть тут
Вот такое уравнение, в котором у нас, во-первых, показательных функции перемножаются, а еще хуже то, что у них у всех разные основания. Катастрофа, а не пример. Но ничего, все не так страшно, как кажется. Внимательно посмотрите на основания: у нас есть в основании (2), (5) и (10). Очевидно, что (10=2*5). Воспользуемся этим и подставим в наше уравнение:
Воспользуемся формулой ((a*b)^n=a^n*b^n):
И перекинем все показательные функции с основанием (2) влево, а с основанием (5) вправо:
Сокращаем и воспользуемся формулами (a^n*a^m=a^) и (frac=a^):
Самая главная идея при решении показательных уравнений – это любыми доступными способами свести все имеющиеся степенные функции к одинаковому основанию. А еще лучше и к одинаковой степени. Вот почему необходимо знать все свойства степеней, без этого решить уравнения будет проблематично.
Как же понять, где какие преобразования использовать? Не бойтесь, это придет с опытом, чем больше примеров решите, тем увереннее будете себя чувствовать на контрольных в школе или на ЕГЭ по профильной математике. Сначала потренируйтесь на простых примерах и постепенно повышайте уровень сложности. Успехов в изучении математики!
Показательные уравнения
О чем эта статья:
6 класс, 7 класс
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Определение показательного уравнения
Показательными называются уравнения с показательной функцией f(x) = a х . Другими словами, неизвестная переменная в них может содержаться как в основании степени, так и в ее показателе. Простейшее уравнение такого вида: a х = b, где a > 0, a ≠ 1.
Конечно, далеко не все задачи выглядят так просто, некоторые из них включают тригонометрические, логарифмические и другие конструкции. Но для решения даже простых показательных уравнений нужно вспомнить из курса алгебры за 6–7 класс следующие темы:
Если что-то успело забыться, советуем повторить эти темы перед тем, как читать дальнейший материал.
С точки зрения геометрии показательной функцией называют такую: y = a x , где a > 0 и a ≠ 1. У нее есть одно важное для решения показательных уравнений свойство — это монотонность. При a > 1 такая функция непрерывно возрастает, а при a
Иногда в результате решения будет получаться несколько вариантов ответа, и в таком случае мы должны выбрать тот корень, при котором показательная функция больше нуля.
Свойства степеней
Мы недаром просили повторить свойства степенной функции — на них будет основано решение большей части примеров. Держите небольшую шпаргалку по формулам, которые помогут упрощать сложные показательные уравнения.
Степенные или показательные уравнения.
Для начала вспомним основные формулы степеней и их свойства.
Произведение числа a само на себя происходит n раз, это выражение мы можем записать как a•a•…•a=a n
3. a n • a m = a n + m
5. a n b n = (ab) n
7. a n /a m = a n — m
Степенные или показательные уравнения – это уравнения в которых переменные находятся в степенях (или показателях), а основанием является число.
Примеры показательных уравнений:
В данном примере число 6 является основанием оно всегда стоит внизу, а переменная x степенью или показателем.
Приведем еще примеры показательных уравнений.
2 x *5=10
16 x — 4 x — 6=0
Теперь разберем как решаются показательные уравнения?
Возьмем простое уравнение:
Такой пример можно решить даже в уме. Видно, что x=3. Ведь чтобы левая и правая часть были равны нужно вместо x поставить число 3.
А теперь посмотрим как нужно это решение оформить:
Для того, чтобы решить такое уравнение, мы убрали одинаковые основания (то есть двойки) и записали то что осталось, это степени. Получили искомый ответ.
Теперь подведем итоги нашего решения.
Алгоритм решения показательного уравнения:
1. Нужно проверить одинаковые ли основания у уравнения справа и слева. Если основания не одинаковые ищем варианты для решения данного примера.
2. После того как основания станут одинаковыми, приравниваем степени и решаем полученное новое уравнение.
Теперь прорешаем несколько примеров:
Начнем с простого.
Основания в левой и правой части равны числу 2, значит мы можем основание отбросить и приравнять их степени.
x+2=4 Получилось простейшее уравнение.
x=4 — 2
x=2
Ответ: x=2
В следующем примере видно, что основания разные это 3 и 9.
Для начала переносим девятку в правую сторону, получаем:
Теперь нужно сделать одинаковые основания. Мы знаем что 9=3 2 . Воспользуемся формулой степеней (a n ) m = a nm .
Получим 9 х+8 =(3 2 ) х+8 =3 2х+16
3 3х = 3 2х+16 теперь видно что в левой и правой стороне основания одинаковые и равные тройке, значит мы их можем отбросить и приравнять степени.
3x=2x+16 получили простейшее уравнение
3x — 2x=16
x=16
Ответ: x=16.
Смотрим следующий пример:
2 2х+4 — 10•4 х = 2 4
В первую очередь смотрим на основания, основания разные два и четыре. А нам нужно, чтобы были — одинаковые. Преобразовываем четверку по формуле (a n ) m = a nm .
4 х = (2 2 ) х = 2 2х
И еще используем одну формулу a n • a m = a n + m :
2 2х+4 = 2 2х •2 4
Добавляем в уравнение:
2 2х •2 4 — 10•2 2х = 24
Мы привели пример к одинаковым основаниям. Но нам мешают другие числа 10 и 24. Что с ними делать? Если приглядеться видно, что в левой части у нас повторяется 2 2х ,вот и ответ — 2 2х мы можем вынести за скобки:
2 2х (2 4 — 10) = 24
Посчитаем выражение в скобках:
2 4 — 10 = 16 — 10 = 6
Все уравнение делим на 6:
Представим 4=2 2 :
2 2х = 2 2 основания одинаковые, отбрасываем их и приравниваем степени.
2х = 2 получилось простейшее уравнение. Делим его на 2 получаем
х = 1
Ответ: х = 1.
9 х – 12*3 х +27= 0
Преобразуем:
9 х = (3 2 ) х = 3 2х
Получаем уравнение:
3 2х — 12•3 х +27 = 0
Основания у нас одинаковы равны трем.В данном примере видно, что у первой тройки степень в два раза (2x) больше, чем у второй (просто x). В таком случаем можно решить методом замены. Число с наименьшей степенью заменяем:
Тогда 3 2х = (3 х ) 2 = t 2
Заменяем в уравнении все степени с иксами на t:
t 2 — 12t+27 = 0
Получаем квадратное уравнение. Решаем через дискриминант, получаем:
D=144-108=36
t1 = 9
t2 = 3
Возвращаемся к переменной x.
3 х = 9
3 х = 3 2
х1 = 2
Один корень нашли. Ищем второй, из t2:
t2 = 3 = 3 х
3 х = 3 1
х2 = 1
Ответ: х1 = 2; х2 = 1.
На сайте Вы можете в разделе ПОМОГИТЕ РЕШИТЬ задавать интересующие вопросы мы Вам обязательно ответим.
http://skysmart.ru/articles/mathematic/pokazatelnye-uravneniya
http://tutomath.ru/uroki/stepennye-pokazatelnye-uravneniya.html

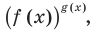
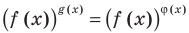
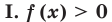
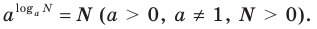
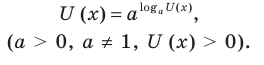
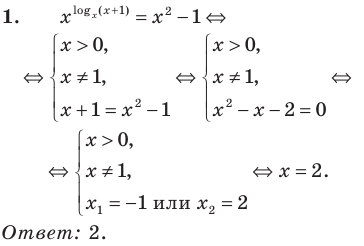
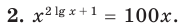
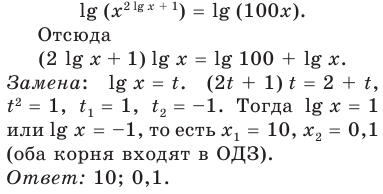
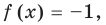 для корней, этого уравнения
для корней, этого уравнения 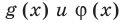 — целые, числа одинаковой четности;
— целые, числа одинаковой четности;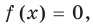 для корней этого уравнения
для корней этого уравнения 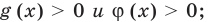
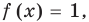 для корней этого уравнения
для корней этого уравнения 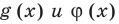 существуют;
существуют;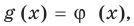 для корней этого уравнения существуют
для корней этого уравнения существуют 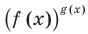 и
и 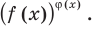
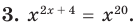
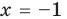 получаем верное равенство
получаем верное равенство 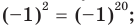
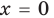 то
то 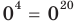 — верное равенство;
— верное равенство;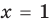 то
то 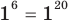 — верное равенство;
— верное равенство;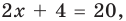 то есть
то есть 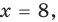 то
то 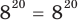 — верное равенство.
— верное равенство.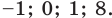
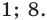
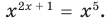
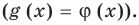
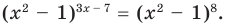
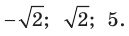
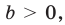
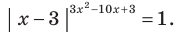
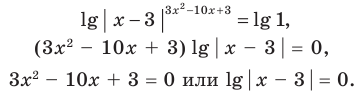
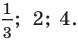
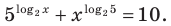
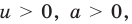
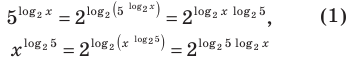
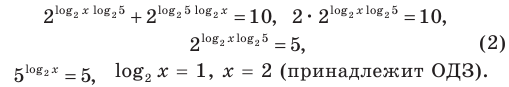
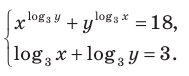
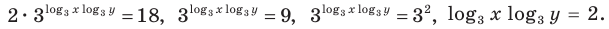
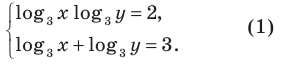
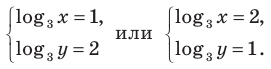

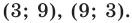
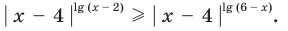
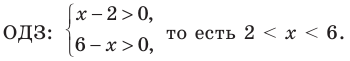
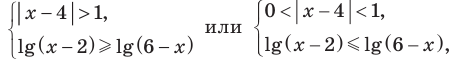
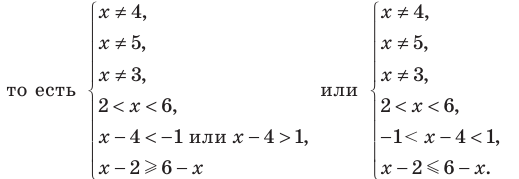
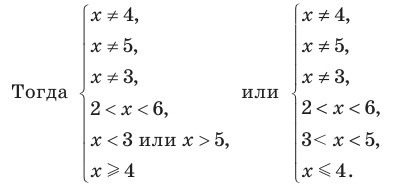
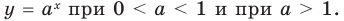
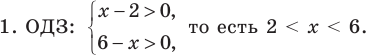
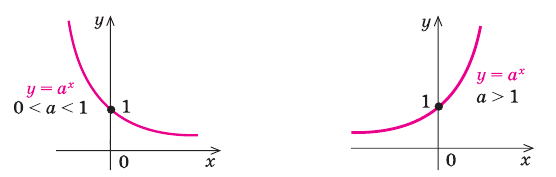
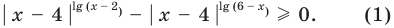
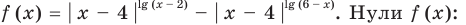
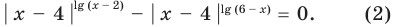
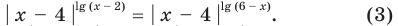

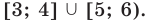
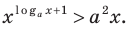
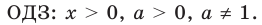
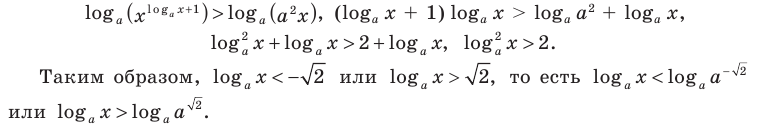
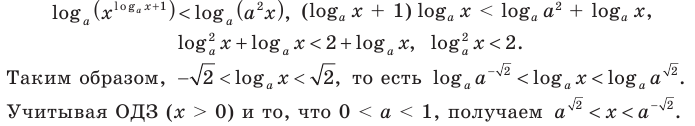
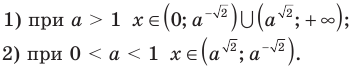
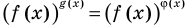
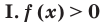
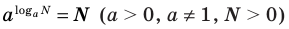
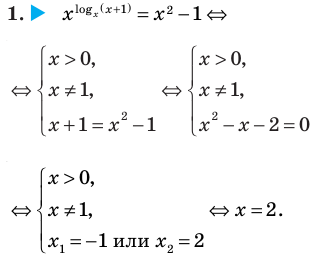
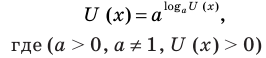
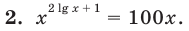
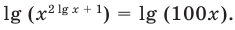
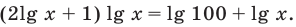
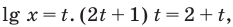
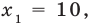
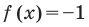 и для корней этого уравнения
и для корней этого уравнения 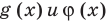 — целые числа одинаковой четности.
— целые числа одинаковой четности.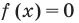 и для корней этого уравнения
и для корней этого уравнения 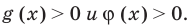
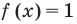 и для корней этого уравнения
и для корней этого уравнения 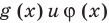 существуют.
существуют. 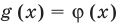 и для корней этого уравнения существуют
и для корней этого уравнения существуют 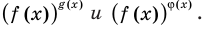
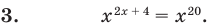
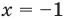 получаем верное равенство
получаем верное равенство 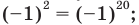
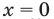
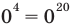 — верное равенство;
— верное равенство;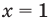
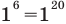 — верное равенство;
— верное равенство;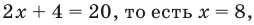 — верное равенство.
— верное равенство.