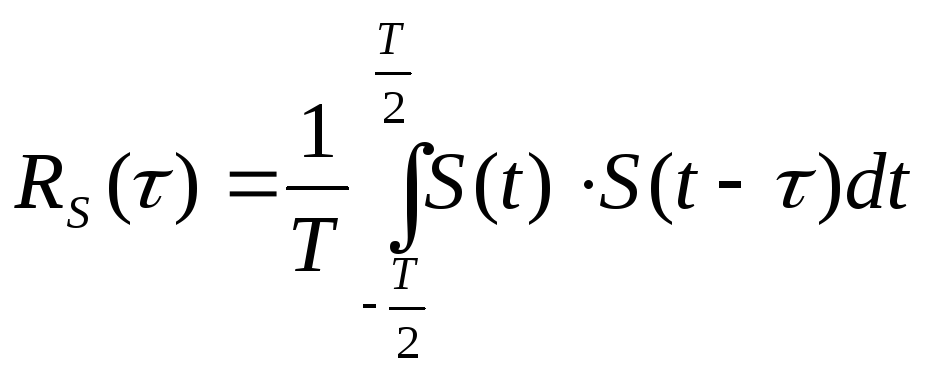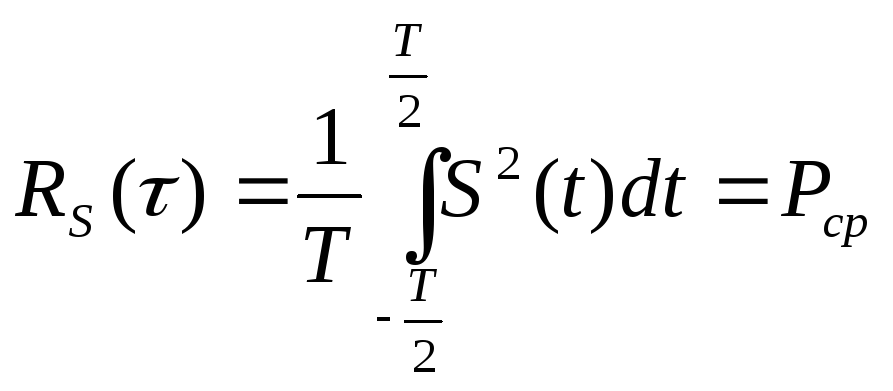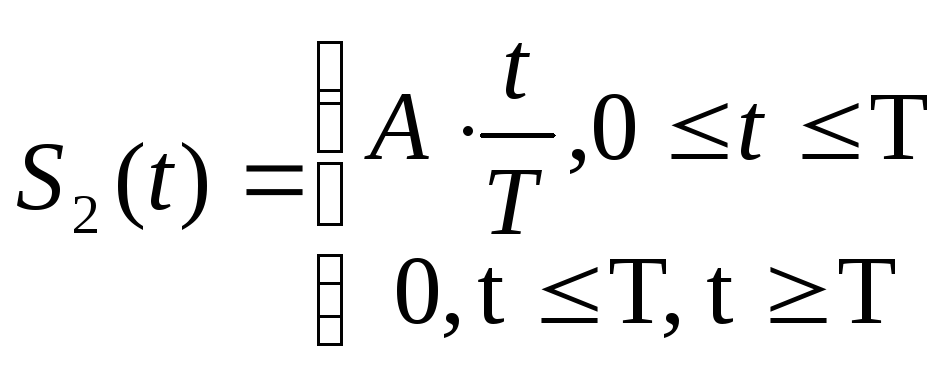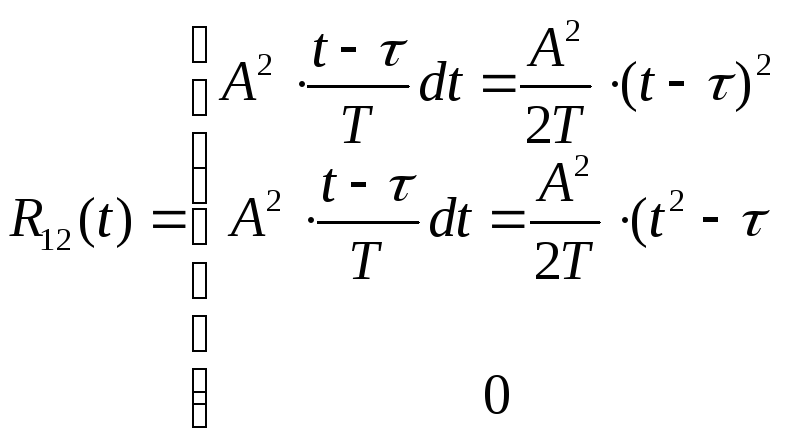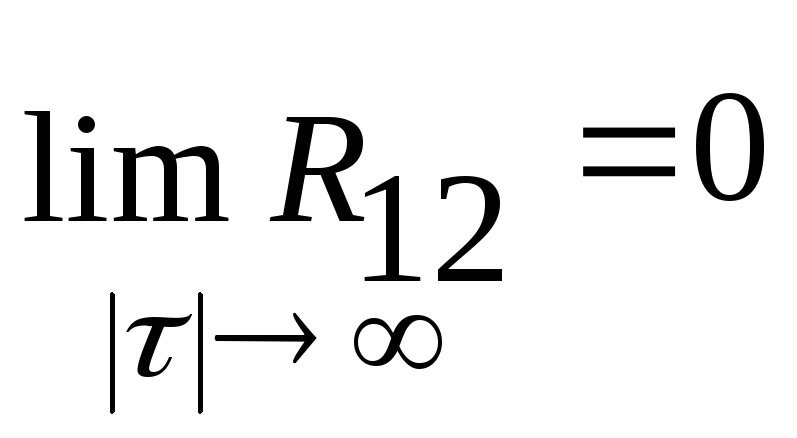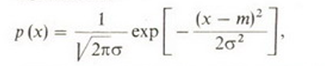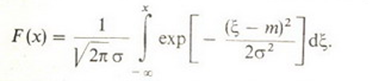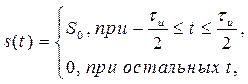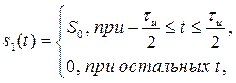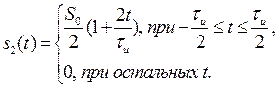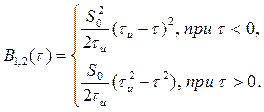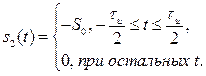Как найти корреляционную функцию сигнала

3 Корреляционный анализ сигналов

Смысл спектрального анализа сигналов заключается в изучении того, как сигнал может быть представлен в виде суммы (или интеграла) простых гармонических колебаний и как форма сигнала определяет структуру распределения по частотам амплитуд и фаз этих колебаний. В противоположность этому задачей корреляционного анализа сигналов является определение меры степени сходства и различия сигналов или сдвинутых по времени копий одного сигнала. Введение меры открывает пути к проведению количественных измерений степени схожести сигналов. Будет показано, что существует определенная взаимосвязь между спектральными и корреляционными характеристиками сигналов.

3.1 Автокорреляционная функция (АКФ)

Автокорреляционная функция сигнала с конечной энергией – это значение интеграла от произведения двух копий этого сигнала, сдвинутых относительно друг друга на время τ, рассматриваемое в функции этого временного сдвига τ:

.

Если сигнал определен на конечном интервале времени , то его АКФ находится как:

,

где  — интервал перекрытия сдвинутых копий сигнала.

Считается, что чем больше значение автокорреляционной функции  при данном значении , тем в большей степени две копии сигнала, сдвинутые на промежуток времени , похожи друг на друга. Поэтому корреляционная функция  и является мерой сходства для сдвинутых копий сигнала.

Рекомендуемые материалы

Вводимая таким образом мера сходства для сигналов, имеющих форму случайных колебаний вокруг нулевого значения, обладает следующими характерными свойствами.

Если сдвинутые копии сигнала колеблются примерно в такт друг к другу, то это является признаком их схожести и АКФ принимает большие положительные значения (большая положительная корреляция). Если копии колеблются почти в противофазе, АКФ принимает большие отрицательные значения (антисходство копий сигнала, большая отрицательная корреляция).

Максимум АКФ достигается при совпадении копий, то есть при отсутствии сдвига. Нулевые значения АКФ достигаются при сдвигах, при которых не заметно ни сходства, ни антисходства копий сигнала (нулевая корреляция,

отсутствие корреляции).

На рис.3.1 изображен фрагмент реализации некоторого сигнала на интервале времени от 0 до 1 с. Сигнал случайным образом колеблется вокруг нулевого значения. Поскольку интервал существования сигнала конечен, то конечна и его энергия. Его АКФ можно вычислить в соответствии с уравнением:

.

Автокорреляционная функция сигнала, вычисленная в MathCad в соответствии с этим уравнением, представлена на рис. 3.2. Корреляционная функция показывает не только то, что сигнал похож сам на себя (сдвиг τ=0), но и то, что некоторой схожестью обладают и копии сигнала, сдвинутые друг относительно друга приблизительно на 0.063 с (боковой максимум автокорреляционной функции). В противоположность этому копии сигнала сдвинутые на 0.032 с, должны быть антипохожи дуг на друга, то есть быть в некотором смысле противоположными друг другу.

На рис.33 показаны пары этих двух копий. По рисунку можно проследить, что понимается под похожестью и антипохожестью копий сигнала.

Корреляционная функция обладает следующими свойствами:

1. При τ = 0 автокорреляционная функция принимает наибольшее значение, равное энергии сигнала

2. Автокорреляционная функция является четной функцией временного сдвига .

3. С ростом τ автокорреляционная функция убывает до нуля

4. Если сигнал не содержит разрывов типа δ — функций, то  — непрерывная функция.

5. Если сигнал является электрическим напряжением, то корреляционная функция имеет размерность .

Для периодических сигналов в определении автокорреляционной функции тот же самый интеграл делят еще на период повторения сигнала:

.

Так введенная корреляционная функция отличается следующими свойствами:

— значение корреляционной функции в нуле равно мощности сигнала ,

— размерность корреляционной функции равна квадрату размерности сигнала, например .

Для примера вычислим корреляционную функцию гармонического колебания :

Используя ряд тригонометрических преобразований, получим окончательно:

Таким образом, автокорреляционная функция гармонического колебания является косинусоидой с тем же периодом изменения, что и сам сигнал. При сдвигах, кратных периоду колебания, гармоника преобразуется в себя и АКФ принимает наибольшие значения, равные половине квадрата амплитуды. Сдвиги по времени, кратные половине периода колебания, равносильны смещению фазы на угол , при этом меняется знак колебаний, а АКФ принимает минимальное значение, отрицательное и равное половине квадрата амплитуды. Сдвиги, кратные четверти периода, переводят, например, синусоидальное колебание в косинусоидальное и наоборот. При этом АКФ обращается в нуль. Такие сигналы, находящиеся в квадратуре друг относительно друга, с точки зрения автокорреляционной функции оказываются совершенно не похожими друг на друга.

Важным является то, что в выражение для корреляционной функции сигнала не вошла его начальная фаза. Информация о фазе потерялась. Это означает, что по корреляционной функции сигнала нельзя восстановить сам сигнал. Отображение  в противоположность отображению  не является взаимно однозначным.

Если под механизмом генерирования сигналов понимать некоего демиурга, создающего сигнал по выбранной им корреляционной функции, то он смог бы создать целую совокупность сигналов (ансамбль сигналов), имеющих действительно одну и ту же корреляционную функцию, но отличающихся друг от друга фазовыми соотношениями.

Акт выбора начальной фазы можно считать:

— актом проявления сигналом своей свободной воли, независимой от воли создателя (возникновение отдельных реализаций некоторого случайного процесса),

— результатом постороннего насилия над сигналом (введение в сигнал измерительной информации, получаемой при проведении измерений какой либо физической величины).

Аналогичным образом обстоит дело с любым периодическим сигналом. Если периодический сигнал с основным периодом Т имеет амплитудный спектр  и фазовый спектр , то корреляционная функция сигнала принимает следующий вид:

.

Уже в этих примерах проявляется некоторая связь между корреляционной функцией и спектральными свойствами сигнала. Подробнее об этих соотношениях речь пойдет в дальнейшем.

3.2 Взаимнокорреляционная функция (ВКФ).

В отличие от автокорреляционной функции взаимнокорреляционная функция определяет степень схожести копий двух различных сигналов x(t) и y(t), сдвинутых на время τ друг относительно друга:

Взаимнокорреляционная функция обладает следующими свойствами:

1. При τ = 0 взаимнокорреляционная функция принимает значение, равное взаимной энергии сигналов, то есть энергии их взаимодействия

.

2. При любом τ имеет место соотношение:

,

где  — энергии сигналов.

3. Изменение знака временного сдвига равносильно взаимной перестановке сигналов:

.

4. С ростом τ взаимнокорреляционная функция хотя и не монотонно, но убывает до нуля

5. Значение взаимнокорреляционной функции в нуле  ничем не выделяется среди других значений.

Для периодических сигналов понятие взаимнокорреляционной функции, как правило, вообще не используется.

Приборы для измерения значений автокорреляционной и взаимнокорреляционной функций называются коррелометрами или корреляторами. Коррелометры применяются, например, для решения следующих информационно-измерительных задач:

— статистический анализ электроэнцефалограмм и других результатов регистрации биопотенциалов,

— определение пространственных координат источника сигнала по величине временного сдвига, при котором достигается максимум ВКФ,

— выделение слабого сигнала на фоне сильных статических несвязанных помех,

— обнаружение и локализация каналов утечки информации путем определения корреляции между сигналами радиоэфира в помещении и за его пределами,

— автоматизированное обнаружение в ближней зоне, распознавание и поиск работающих радиоизлучающих подслушивающих устройств, включая мобильные телефоны, используемые как подслушивающие устройства,

— локализация мест утечек в трубопроводах на основании определения ВКФ двух сигналов акустического шума, вызываемого утечкой, в двух точках измерения, в которых расположены датчики на трубе.

3.3 Соотношения между корреляционными и спектральными функциями.

Как корреляционные, так и спектральные функции описывают внутреннюю структуру сигналов, их внутреннее строение. Поэтому можно ожидать, что между этими двумя способами описания сигналов существует некоторая взаимозависимость. Наличие такой связи Вы уже видели на примере периодических сигналов.

Взаимная корреляционная функция, как и любая другая функция времени, может быть подвергнута преобразованию Фурье:

.

Изменим порядок интегрирования:

Выражение в квадратных скобках можно было бы рассматривать как преобразование Фурье для сигнала y(t), но в показателе экспоненты не стоит знак минус. Это говорит о том, что внутренний интеграл дает нам выражение , комплексно сопряженное со спектральной функцией .

Но выражение  не зависит от времени, поэтому его можно вынести за знак внешнего интеграла. Тогда внешний интеграл просто даст нам определение спектральной функции  сигнала x(t). Окончательно имеем:

.

Это означает, что преобразование Фурье для взаимной корреляционной функции двух сигналов равно произведению их спектральных функций, одна из которых подвергнута комплексному сопряжению. Это произведение называется взаимным спектром сигналов:

.

Из полученного выражения следует важный вывод: если спектры сигналов x(t) и y(t) не перекрывают друг друга, то есть располагаются в различных диапазонах частот, то такие сигналы являются некоррелированными, независимыми друг от друга.

Если положить в приведенных формулах: x(t) = y(t), то получим выражение для преобразования Фурье автокорреляционной функции

.

Это означает, что автокорреляционная функция сигнала и квадрат модуля его спектральной функции связаны друг с другом посредством преобразования Фурье.

Функция  называется энергетическим спектром сигнала . Энергетический спектр показывает, как общая энергия сигнала распределяется по частотам его отдельных гармонических составляющих.

3.4 Энергетические характеристики сигналов с частотной области

Взаимная корреляционная функция двух сигналов связана преобразованием Фурье с взаимным спектром сигналов, поэтому ее можно выразить в виде обратного преобразования Фурье от взаимного спектра:

.

Теперь подставим в эту цепочку равенств значение временного сдвига . В результате получим соотношение, которое определяет смысл равенства Релея:

,

то есть интеграл от произведения двух сигналов равен интегралу от произведения спектров этих сигналов, один из которых подвергнут операции комплексного сопряжения.

Ещё посмотрите лекцию «14 Подготовка России к войне» по этой теме.

Если считать сигналы одинаковыми x(t)=y(t), получится соотношение, позволяющее фактически по одной формуле вычислять энергию сигнала, как во временной, так и в частотной области:

.

Это соотношение называется равенством Парсеваля.

Периодические сигналы обладают бесконечной энергией, но конечной мощностью. При их рассмотрении мы уже сталкивались с возможностью вычисления мощности периодического сигнала через сумму квадратов модулей коэффициентов его комплексного спектра:

.

Это соотношение обладает полной аналогией с равенством Парсеваля.

Наряду со спектральным
анализом корреляционный анализ играет
большую роль в теории сигналов. Его
смысл состоит в измерении степени
сходства (различия) сигналов. Для этого
служит корреляционная ф-ция.

КФ представляет
собой интеграл от произведения двух
копий сигнала, сдвинутых друг отн. друга
на время
.

Чем больше значение
КФ, тем сильнее сходство. КФ обладает
следующими свойствами:

1. Значение КФ при
равно энергии сигнала (интегралу от его
квадрата)

2. Является четной
функцией

3. Значение КФ при
является максимально возможным.

4. С ростом абс.
значения
КФ сигнала с конечной энергией затухает

5. Если сигнал
является ф-цией напряжения от времени,
то размерность его КФ []

В случае периодического
сигнала (с периодом Т) КФ вычисляют,
усредняя произведение сдвинутых копий
в пределах одного периода:

Набор свойств
такой КФ изменяется:

1. Значение КФ при
равно средней мощности сигнала

2. Свойство четности
сохраняется.

3. Значение КФ при
является максимально возможным.

4. КФ является
периодической ф-цией (с тем же периодом,
что и сигнал)

5. Если сигнал не
содержит дельта-функций, то его КФ
непрерывна.

6. Если сигнал
является зависимостью U(t),
то размерность КФ []

КФ гармонического
сигнала является гармонической ф-цией,
которая не зависит от начальной фазы
сигнала.

10 Взаимная корреляционная функция, ее свойства. Вычисление взаимной корреляционной функции сигналов

Взаимная
корреляционная функция (ВКФ)- функция,
показывающая степень сходства для
сдвинутых во времени 2-ух различных
сигналов.

Общий вид:

Для примера вычислим
ВКФ 2-ух функций:

При

При

При

Объединяя результаты,
можно записать:

Свойства ВКФ:

1)

2)

3)

4) Если функции
S₁(t)
и S₂(t)
не содержат дельта-функций, то их ВКФ
не может иметь разрывов.

5) Если в качестве
сигнала выступает функция U(t),
то размерность ВКФ

11 Случайные процессы. Реализация случайного процесса. Законы распределения случайных процессов

_{Иногда
на практике приходится иметь дело с
явлениями, протекание которых во времени
непредсказуемо и в каждый момент времени
описывается случайной величиной. Такие
явления называются случайными процессами.
Случайным
процессом называется
функция ζ(t)
неслучайного аргумента t
(как
правило, времени), которая при каждом
фиксированном значении аргумента
является случайной величиной. Например,
температура в течение суток, регистрируемая
самописцем. Значения, принимаемые
процессом ζ(t)
в определенные моменты времени называются
состояниями,
а множество всех состояний – фазовым
пространством случайного
процесса. В зависимости от количества
возможных состояний случайного процесса
его фазовое пространство может быть
дискретным
или
непрерывным.
Если
случайный процесс может изменять свое
состояние лишь в определенные моменты
времени, то такой процесс называется
случайным
процессом с дискретным временем;
а если в произвольные, то – процессом
с непрерывным временем.}

Случайный
процесс ζ(t)
называется стационарным,
если распределение вероятностей его
возможных состояний не изменяется во
времени. Например, при ежесекундном
подбрасывании игральной кости
распределение вероятностей состояний
соответствующего случайного процесса
(рис.44, б)
не зависит (не изменяется) от времени
(при этом все состояния ζ(t)
равновозможны). В противоположность
этому, случайный процесс, характеризующий
температуру окружающей среды, не является
стационарным, т.к. для лета характерны
более высокие температуры, чем для зимы.

Распределение
вероятностей состояний стационарного
случайного процесса называется
стационарным
распределением.

Существуют различные
законы распределения среди них
Равномерное, Гаусовское (нормальное)

Равномерное:
пусть некторая случ величина х может
принимать значения х₁<=x<=x₂
тогда плотность вероятности

P(x)=система(0
при x<x₁;1/(x₂-x₁)
при х1<=x<=x₂;
0 при х>х₂)

Функцию распределения
найдем путем интегрирования

F(x)=
система(0 при x<x₁;(x-x₁)/(x₂-x₁)
при х1<=x<=x₂;
1 при x>x₂)

Гауссово
(нормальное) распределение.
В теории случайных сигналов фундаментальное
значение имеет гауссова плотность
вероятности

содержащая два
числовых параметра
.
График данной функции представляет
собой колоколообразную кривую с
единственным максимумом в точке.

Непосредственным
вычислением можно убедиться, что
параметры гауссова распределения имеют
смысл соответственно математического
ожидания и дисперсии:

Функция распределения
гауссовой случайной величины

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Во многих радиотехнических задачах часто возникает необходимость сравнения сигнала и его копии, сдвинутой на некоторое время . В частности такая ситуация имеет место в радиолокации, где отраженный от цели импульс поступает на вход приемника с задержкой во времени. Сравнение этих сигналов между собой, т.е. установление их взаимосвязи, при обработке позволяет определять параметры движения цели.

Для количественной оценки взаимосвязи сигнала и его сдвинутой во времени копии вводится характеристика

, (2.57)

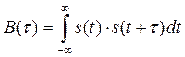
Которая называется автокорреляционной функцией (АКФ).

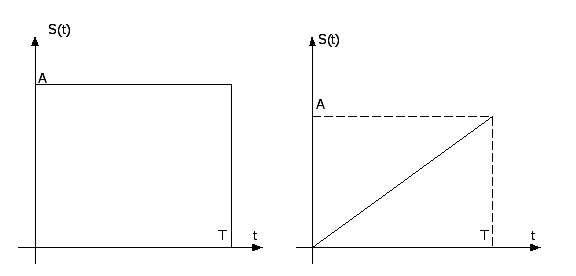
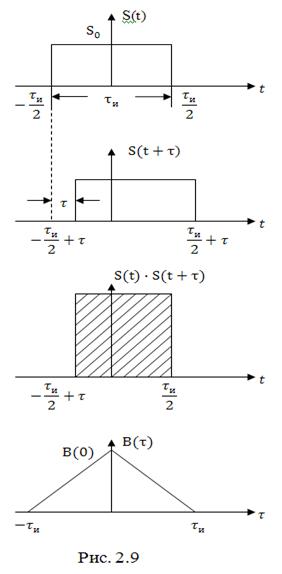
Для пояснения физического смысла АКФ приведем пример, где в качестве сигнала выступает прямоугольный импульс длительностью и амплитудой . На рис. 2.9 изображены импульс, его копия, сдвинутая на интервал времени и произведение . Очевидно, интегрирование произведения дает значение площади импульса, являющегося произведением . Это значение при фиксированном можно изобразить точкой в координатах . При изменении мы получим график автокорреляционной функции.

Найдем аналитическое выражение . Так как

то подставляя это выражение в (2.57), получим

. (2.58)

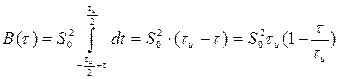
Если осуществлять сдвижку сигнала влево, то аналогичными вычислениями нетрудно показать, что

. (2.59)

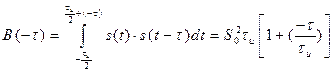
Тогда объединяя (2.58) и (2.59), получим

. (2.60)

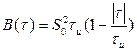
Из рассмотренного примера можно сделать следующие важные выводы, распространяющиеся на сигналы произвольной формы:

1. Автокорреляционная функция непериодического сигнала с ростом убывает (необязательно монотонно для других видов сигналов). Очевидно, при АКФ также стремиться к нулю.

2. Своего максимального значения АКФ достигает при . При этом, равна энергии сигнала. Таким образом, АКФ является энергетической характеристикой сигнала. Как и следовало ожидать при сигнал и его копия полностью коррелированны (взаимосвязаны).

3. Из сравнения (2.58) и (2.59) следует, что АКФ является четной функцией аргумента , т.е.

.

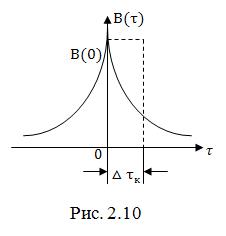
Важной характеристикой сигнала является интервал корреляции. Под интервалом корреляции понимают интервал времени , при сдвижке на который сигнал и его копия становятся некоррелированными.

Математически интервал корреляции определяется следующим выражением

,

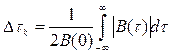
или поскольку – четная функция

. (2.61)

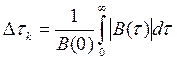
На рис. 2.10 изображена АКФ сигнала произвольной формы. Если построить прямоугольник, по площади равный площади под кривой при положительных значениях (правая ветвь кривой), одна сторона которого равна , то вторая сторона будет соответствовать .

Найдем интервал корреляции для прямоугольного импульса. Подставляя (2.58) в (2.60) после несложных преобразований, получим:

,

что и следует из рис. 2.9.

По аналогии с автокорреляционной функцией степень взаимосвязи двух сигналов и оценивается взаимной корреляционной функцией (ВКФ)

. (2.62)

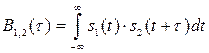
Найдем взаимную корреляционную функцию двух сигналов: прямоугольного импульса с амплитудой и длительностью

и треугольного импульса той же амплитуды и длительности

Воспользовавшись (2.61) и вычисляя интегралы отдельно для и , получим:

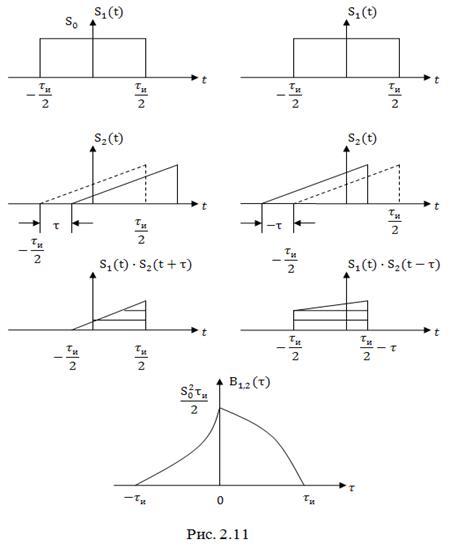
Графические построения, иллюстрирующие вычисления ВКФ, приведены на рис. 2.11

Здесь пунктирными линиями показано исходное (при ) положение треугольного импульса.

При выражение (2.61) преобразуется в (2.57). Отсюда следует, что АКФ является частным случаем ВКФ при полностью совпадающих сигналах.

Отметим основные свойства ВКФ.

1. Так же, как и автокорреляционная функция, ВКФ является убывающей функцией аргумента . При ВКФ стремиться к нулю.

2. Значения взаимной корреляционной функции при произвольных представляют собой значения взаимной энергии (энергии взаимодействия) сигналов и .

3. При взаимная корреляционная функция (в отличие от автокорреляционной) не всегда достигает максимума.

4. Если сигналы и описываются четными функциями времени, то ВКФ тоже четна. Если же хотя бы один из сигналов описывается нечетной функцией, то ВКФ так же нечетна. Первое утверждение легко доказать, если вычислить ВКФ двух прямоугольных импульсов противоположной полярности

и

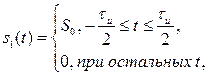
Взаимная корреляционная функция таких сигналов

, (2.63)

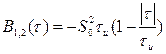
является четной функцией аргумента .

Что же касается второго утверждения рассмотренный пример вычисления ВКФ прямоугольного и треугольного импульсов доказывает его.

В некоторых прикладных задачах радиотехники используют нормированную АКФ

, (2.64)

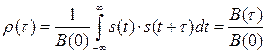
и нормированную ВКФ

, (2.65)

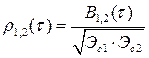
где и – собственные энергии сигналов и . При значение нормированной ВКФ называют коэффициентом взаимной корреляции. Если , то коэффициент взаимной корреляции

.

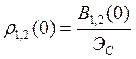
Очевидно, значения лежат в пределах от -1 до +1. Если сравнить (2.65) с (1.32), то можно убедиться, что коэффициент взаимной корреляции соответствует значению косинуса угла между векторами и при геометрическом представлении сигналов.

Рассчитаем коэффициент взаимной корреляции для рассмотренных выше примеров. Так как энергия сигнала прямоугольного импульса составляет

,

а треугольного импульса

,

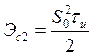
то коэффициент взаимной корреляции в соответствии с (2.62) и (2.65) будет равен . Что же касается второго примера, то для двух прямоугольных импульсов одинаковой амплитуды и длительности, но противоположной полярности, .

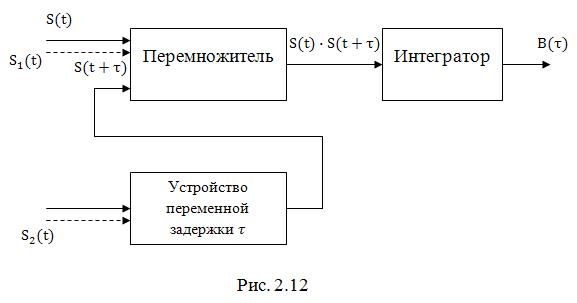
Экспериментально АКФ и ВКФ могут быть получены с помощью устройства, структурная схема которого изображена на рис. 2.12

При снятии АКФ на один из входов перемножителя поступает сигнал , а на второй – этот же сигнал, но задержанный на время . Сигнал, пропорциональный произведению , подвергается операции интегрирования. На выходе интегратора формируется напряжение, пропорциональное значению АКФ при фиксированном . Изменяя время задержки, можно построить АКФ сигнала.

Для экспериментального построения ВКФ сигнал подается на один из входов перемножителя, а сигнал – на устройство задержки (входящие цепи показаны пунктиром). В остальном, устройство работает аналогичным образом. Отметим, что описанное устройство называется коррелятором и широко используется в различных радиотехнических системах для приема и обработки сигналов.

До сих пор мы проводили корреляционный анализ непериодических сигналов, обладающих конечной энергией. Вместе с тем, необходимость подобного анализа часто возникает и для периодических сигналов, которые теоретически обладают бесконечной энергией, но конечной средней мощностью. В этом случае АКФ и ВКФ вычисляются усреднением по периоду и имеют смысл средней мощности (собственной или взаимной соответственно). Таким образом, АКФ периодического сигнала:

, (2.66)

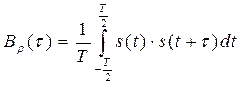
а взаимная корреляционная функция двух периодических сигналов с кратными периодами:

, (2.67)

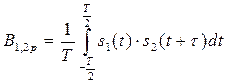
где – наибольшее значение периода.

Найдем автокорреляционную функцию гармонического сигнала

,

где 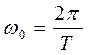– круговая частота, – начальная фаза.

Подставляя это выражение в (2.66) и вычисляя интеграл с использованием известного тригонометрического соотношения:

,

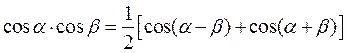
получим:

.

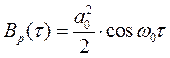
Из рассмотренного примера можно сделать следующие выводы, справедливые для любого периодического сигнала.

1. АКФ периодического сигнала является периодической функцией с тем же периодом.

2. АКФ периодического сигнала является четной функцией аргумента .

3. При значение представляет собой среднюю мощность, которая выделяется на сопротивлении в 1 Ом и имеет размеренность .

4. АКФ периодического сигнала не содержит информации о начальной фазе сигнала.

Следует также отметить, что интервал корреляции периодического сигнала .

А теперь вычислим взаимную корреляционную функцию двух гармонических сигналов одинаковой частоты, но отличающихся амплитудами и начальными фазами

и .

Воспользовавшись (2.67) и проводя несложные вычисления, получим

,

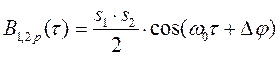
где – разность начальных фаз сигналов и .

Таким образом, взаимная корреляционная функция двух рассматриваемых сигналов содержит информацию о разности начальных фаз. Это важное свойство широко используется при построении различных радиотехнических устройств, в частности, устройств синхронизации некоторых систем радиоавтоматики и других.

В заключение установим связь между АКФ непериодического сигнала и его энергетическим спектром, определение которого [см. (2.51)] было дано выше. Для этого воспользуемся (2.49) при . Тогда получим соотношение

, (2.68)

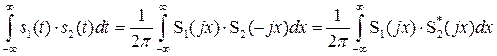
где – функция, комплексно сопряженная с .

Положим теперь и . В соответствии с (2.45) преобразование Фурье имеет вид

.

С другой стороны

.

Подставляя эти выражения в (2.68), получим

.

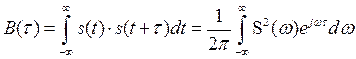
Но в соответствие с (2.51) есть энергетический спектр. Тогда окончательно

. (2.69)

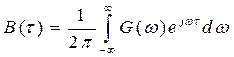
Применяя к прямое преобразование Фурье, приходим к соотношению

. (2.70)

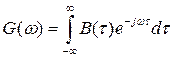
Таким образом, АКФ и энергетический спектр сигнала связаны парой преобразований Фурье.

Так как и – вещественные и четные функции, выражения (2.69) и (2.70) можно записать соответственно в виде

, (2.71)

. (2.72)

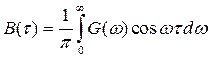
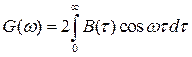
Рассмотренный корреляционно-спектральный анализ позволяет дать еще одну трактовку эффективной ширины спектра. Если известен энергетический спектр, то эффективная ширина спектра определяется так:

. (2.73)

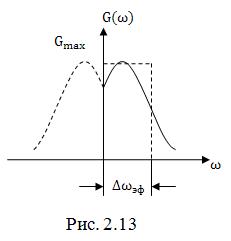
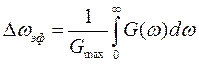
Иными словами представляет собой сторону прямоугольника по площади равного площади под кривой одностороннего спектра, вторая сторона которого равна (рис.2.13). Очевидно, произведение эффективной ширины энергетического спектра на величину интервала корреляции есть величина постоянная

.

Таким образом, и в этом случае мы сталкиваемся с проявлением принципа неопределенности: чем больше интервал корреляции, тем меньше ширина энергетического спектра, и наоборот.

В данном посте освещены 3 темы по основам цифровой обработки сигналов:

• Виды шумов, отношение сигнал/шум,
• Статистическая обработка сигнала,
• Корреляционная функция.

Виды шумов, отношение сигнал/шум.

В данной публикации мы поговорим о характеристиках случайных процессов, познакомимся с разными видами шумов, и узнаем о важном определении – отношение сигнал/шум. Начнём с характеристик.

Случайный процесс колеблется вокруг какого-то среднего значения, и значение это называется математическим ожиданием.

Насколько сильно значения случайного процесса могут отличаться от матожидания описывает параметр дисперсия, мера разброса случайной величины.

Также в качестве меры разброса употребляется среднеквадратичное отклонение, также именуемое стандартным отклонением. Значение его — квадратный корень из дисперсии.

На рисунке представлены нормальные распределения 4-х случайных процессов с разными значениями матожидания и дисперсии. В случае большего значения дисперсии колокол гауссовского распределения более широкий и низкий, что говорит о большей вероятности выпадения экстремальных значений, и меньшей вероятности значений, близких к матожиданию.

В качестве меры скорости изменения случайного процесса может использоваться авто-корреляционная функция или просто корреляционная функция. Она описывает зависимость взаимосвязи сигнала с его сдвинутой во времени копией от величины временного сдвига.

В случае нулевого сдвига сигналы полностью совпадают, и значение авто-корреляционной функции максимально. При увеличении расхождения это значение уменьшается, причём для слабо изменяющихся во времени сигналов спад функции происходит медленнее, чем для быстро изменяющихся.

Математическое ожидание, дисперсия, авто-корреляционная функция – это примеры численных характеристик, которыми можно описать случайный процесс.

Законы изменения реальных физических величин весьма сложны, и для того, чтобы могли описывать их доступным нам математическим аппаратом, нам часто приходится делать определённые допущения. При описании сигналов случайными процессами мы часто оговариваем свойства стационарности и эргодичности.

Стационарым процесс называется в том случае, когда его плотность вероятности не зависит от временного сечения. То есть его статистические характеристики – матожидание, дисперсия, коореляционная функция – не будут зависеть от времени.

Стационарный процесс считается эргодическим, если для определения его характеристик вместо усреднения по ансамблю реализаций мы можем использовать усреднение по времени одной реализации. На практике нам обычна доступна только одна реализация случайного процесса.

Ещё одна важная характеристика случайного процесса – спектральная плотность мощности. По определению, это распределение мощности сигнала в зависимости от частоты, то есть мощность, приходящаяся на единичный интервал частоты.

Мы можем рассматривать спектральную плотность мощности как ещё одну меру скорости изменения случайного процесса. Она связана с корреляционной функцией случайного процесса теоремой Винера-Хинчина-Колмогорова, и с ней я советую познакомиться самостоятельно.

А мы пока что рассмотрим два синусоидальных сигнала разной частоты. В частотной области эти сигналы будут представлены двумя линиями. Положение линии на оси Х говорит о величине частоты синусоиды, а длина линии – о её мощности или амплитуде.

Случайные процессы мы также можем рассматривать как кусочки и отрезки различных синусоид, разной амплитуды и фазы, меняющихся быстро или медленно. Спектр медленно изменяющегося случайного процесса содержит больше синусоид, или спектральных компонент, в левой части оси f – то есть в зоне низких частот. В то время как спектр быстро меняющегося процесса содержит больше компонент большей амплитуды в левой части частотной оси.

Слуйчайный процесс, у которого область частот заполнена равномерно, называется белым шумом.

Белый шум – это стационарный слуйчайный процесс с равномерно распределённой спектральной плотностью мощности. В таком процессе присутствуют компоненты, изменяющиеся быстро, медленно, средне, и ни одна из них не преобладает над другими.

Белый шум получил свой название по аналогии со спектром белого света. Нам известно, что белый цвет получается в результате сложения всех других цветов видимого диапазона. Если в качестве аналогии и далее использовать видимый диапазон длин волн, то определённым цветом можно обозначить преобладание в спектре сигнала определённых компонент. Если наложить красный светофильтр, то мы пропустим только более длинные волны, или более низкие частоты. Если наложим синий фильтр – получим сигнал с относительно высокими частотами в спектре.

Цветовое обозначение частотного состава используется для описания так называемых цветных шумов. Они никак не привязаны к какому-либо конкретному частотному диапазону, и различаются только видом их спектральной плотностью мощности. Сразу оговорюсь, что цветные шумы, в том числе и белый шум – это модели шумов, приближающие некоторые физические явления. К примеру, процессы генерации и рекомбинации носителей заряда в цепях постоянного тока приводят к так называемому фликкер-шуму, который достаточно успешно описывается моделью розового шума. Красный шум описывает броуновское движение, модель серого шума используется в психоакустике и так далее.

Какая же модель шума чаще всего используется в цифровой обработке сигналов? Это аддитивный белый гауссовский шум.

• У него равномерная спектральная плотность мощности, поэтому он белый.
• Нормальное распределение, поэтому он Гауссовский.
• С полезным сигналом он суммируется, поэтому он аддитивный.
• И  статистически он от сигнала независим.

На системы беспроводной связи и обработки сигналов воздействуют множество разнообразных широкополосных шумов, не связанных друг с другом. По центральной предельной теореме распределение их суммарного воздействия будет близко к нормальному.

Именно поэтому данная модель наиболее распространена в системах ЦОС и системах связи, и используется как модель канала передачи данных. Шум в подобных системах, конечно же, является нежелательным явлением.

Одной из мер качества системы является отношение сигнал/шум. Это безразмерная величина, равная отношению мощности полезного сигнала к мощности шума. Отношение сигнал/шум часто измеряется в децибелах, для разных систем приемлемые значения этого отношения могут сильно отличаться. Но в любом случае, чес выше этот показатель, тем лучше.

Одна из задач цифровой обработки сигналов – повышение отношения сигнал/шум. Существуют разные способы повышения. О фильтрации мы поговорим в дальнейших публикациях, а сейчас давайте познакомимся с усреднением, или когерентным накоплением.

Если мы сложим два одинаковых сигнала в фазе, то амплитуда результирующего сигнала будет вдвое больше. Положительные отсчёты сложатся с положительными, отрицательные – с отрицательными. Но сложить две реализации случайного процесса в фазе не получится. В каких-то точках произойдёт усиление, в каких-то – ослабление шума. Проще говоря, при усреднении амплитуда шума не растёт.

Давайте рассмотрим пример накопления сигнала с шумом в MATLAB.

Мы генерируем синусоиду, и добавляем к ней аддитивный белый Гауссовский шум при помощи функции awgn. Функция эта содержится в расширении MATLAB Communications Toolbox. На её вход мы подаём исходный незашумлённый сигнал, и параметр отношения сигнал/шум в децибелах. Строим на графике сигнал с шумом и без шума.

Затем мы выделим только шумовую компоненту, вычитаем из смеcи сигнал/шум исходный сигнал. Визуализируем его отсчёты командой stem. Функция периодограм позволит нам оценить спектральную плотность мощности нашего шума. Мы видим, то что распределение действительно равномерное, это белый шум.

Гистрограмма показывает нам, что распределение значений вектора noise близко к нормальному. 

Теперь мы генерируем большое число зашумлённых сигналов.  Несмотря на то, что мы вызываем одну и ту же команду, реализации шума в каждом из векторов будут отличаться. Можем убедиться в этом, отразив четыре первых вектора на графике.

Если мы будем складывать эти вектора между собой, то их синусоидальная компонента будет всегда складываться в фазе, в то время как шумовые компоненты будут складываться случайным образом. Убедимся в том, что амплитуда шума в результирующей сумме заметно ниже.

В завершении давайте поговорим о ещё двух хар-ках системы, которые непосредственно связаны с шумом.

Динамический диапазон – это характеристика системы, представляющая логарифм отношения максимального и минимального возможных значений величины входного параметра. Сверху этот диапазон обычно ограничен порогом искажений, а снизу – так называемым шумовым дном, или чувствительностью.

Чувствительность – это численный параметр, равный уровню сигнала, различимого системой над шумами. Если у системы хорошая чувствительность, значит она меньше восприимчива к внешним помехам, имеет меньший уровень собственных шумов, и за счёт этого способна различать сигналы малой энергетики.

В следующей публикации мы подробнее поговорим о статистических параметрах сигнала.

Наверх

Статистическая обработка сигнала.

В этой публикации мы под робнее поговорим о статистической обработке сигналов. Давайте вспомним, какие статистические параметры мы рассматривали, когда говорили о случайных процессах. Когда мы рассматривали случайный процесс с нормальным распределением мы оперировали понятиями математического ожидания  и дисперсии. Когда мы рассматриваем сигналы в общем виде, то у них так же есть статистические показатели со схожим смыслом.

У любого сигнала, непрерывного и дискретного, можно определить среднее значение. Оно может вычисляться по-разному.

Если мы ищем среднее арифметическое, то для этого мы складываем все отсчёты сигнала и делим сумму на количество отсчётов.

Но также в качестве среднего значения для дискретной последовательности может применяться медианное значение. При его вычислении все элементы дискретного сигнала выстраиваются по возрастанию, и находится центральный элемент упорядоченной последовательности.

То, что мы называли дисперсией случайного процесса, у произвольного сигнала может именоваться отклонением от среднего значения. Для колебательных процессов отклонение по сути – это амплитуда колебаний.

Для любого сигнала мы можем определить минимальное и максимальное значение на отрезке наблюдения. Минимум и максимум сигнала определяют его размах, или динамический диапазон.

Ну и скорость изменения сигнала может характеризоваться корреляционной функцией. Её мы подробно рассмотрим в следующей публикации.

Статистические показатели реальных сигналов часто изменяются во времени. К примеру, при относительной стабильности амплитуды колебаний во времени, среднее значение, вокруг которого изменяется сигнал, может «плавать».

При обработке зачастую выбирают некоторые временные рамки относительной стабильности статистических характеристик, и подсчитывают эти характеристики для коротких отрезков исходного сигнала. Временной интервал, на котором рассматривается сигнал, называется окном. И окно это обычно перемещается или скользит по исходному сигналу.

Подобным образом мы можем находить локальные статистические характеристики, такие как, например, локальные средние значения, или локальные минимумы и максимумы. Подобная обработка позволяет отслеживать постоянную составляющую сигнала, которую мы также называем трендом, и находить пики или спады на графике сигнала.

Рассмотрим пример нахождения тренда или меняющейся во времени постоянной составляющей сигнала методом скользящего среднего. Как вы поняли из названия, этот метод подразумевает нахождение локального среднего арифметического. Окно перемещается по сигналу, и в результате обработки формируется выходной вектор, в отсчёты которого записываются значения среднего арифметического для каждого шага.

Результирующий вектор становится сглаженным, по сравнению с исходным. И чем больше размер окна – тем больше степень сглаживания. Можно использовать небольшие окна для сглаживания формы сигнала и избавления от нежелательных высокочастотных колебаний, либо можно взять большое окно для выделения постоянной составляющей.

Если рассматривать процесс вычисления среднего значения, как набор арифметических операций над каждым из отсчётов, попавших в окно, то в случае со скользящим средним каждый отсчёт умножается на величину, обратную размеру окна, и затем все результаты произведения складываются.

Если мы берём окно не из трёх, а из пяти элементов, то и коэффициент становится равным одной пятой. Но коэффициенты не обязательно должны быть одинаковыми. В общем случае мы рассматриваем операцию нахождения взвешенного среднего. Окна с разнообразными коэффициентами могут усиливать или ослаблять различные частотные компоненты сигнала. Процесс взвешенного усреднения – одна из форм цифровой фильтрации. О цифровых фильтрах мы будем подробно говорить в других публикациях. А пока что давайте осуществим статистическую обработку сигнала в MATLAB.

 

Мы вновь проанализируем сигнал ЭКГ, но в этот раз мы попробуем выделить из него так называемый Q-R-S комплекс, то есть определить положение Q-, R-, S-зубцов в наших данных. Но наши данные зашумлены и постоянная составляющая у сигнала изменяется во времени, что может помешать нам выделить искомое зубцы. Поэтому нам необходимо отфильтровать наши данные, избавиться от постоянной составляющей и выделить локальные экстремумы. Для фильтрации и удаления тренда мы можем воспользоваться одной и той же функцией movmean из состава Signal Processing Toolbox. Она у нас выполняет операцию скользящего среднего. Если мы возьмём маленькое кошка из 10 отсчётов, то мы сгладим форму нашего сигнала. А если мы возьмём большое окно из 300 отсчётов, то мы выделим постоянную составляющую. Отразим её на том же графике.

Для выделения пиков наших Q-, R-, S-зубцов воспользуемся встроенной функцией findpeaks. Выделение R-, S-зубцов происходит достаточно просто, мы просто берём выбросы величины, которые больше чем 0,5 или меньше чем –0,5 и отображаем их на том же графике.

А вот для выделения Q-зубцов нам придется воспользоваться логической индексацией. Мы знаем то, что Q-выброс лежит в пределах от –0,2 мВ до –0,5 мВ, поэтому мы выделяем только те минимальные, скажем так экстремумы, минимальные значение сигнала, которые лежат в этих пределах. Также можно построить Q-зубцы на том же самом графике.

Как видите воспользовавшись двумя встроенными функциями мы успешно выделили Q-R-S комплекс из наших зашумленных и нестабильных по времени данных ЭКГ. В следующей публикации мы поговорим о корреляционной функции и корреляционной обработке.

Наверх

Корреляционная функция.

Когда мы рассматривали случайные процессы, мы упоминали корреляционную функцию, как меру изменения скорости процесса. КФ измерялась для одного сигнала, а значит происходило сравнение сигнала с самим собой, сдвинутым во времени. По факту мы рассматривали так называемую автокорреляционную функцию. Но в предыдущих видео мы не рассказали, как эта функция вычисляется. Для того, чтобы понять, как мы находим корреляционную функцию сигнала, надо вспомнить понятие корреляции.

Корреляция – это мера зависимости двух величин. Для численной оценки используется коэффициент корреляции. Он не может быть больше единицы, и меньше минус единицы. Когда коэффициент корреляции +1, говорят, что две величины идеально коррелированы друг с другом, а значит что при изменении первой величины на какой-то значение вторая изменяется на такое-же значение. Если коэффициент –1 , то росту первой величины соответствует уменьшение второй величины на такое же значение.

Проиллюстрируем зависимость коэффициента корреляции от временного сдвига двух идентичных сигналов.

В начальный момент времени сигналы выровнены, и коэффициент корреляции равен +1. При равном приращении первая и вторая функции изменяются одинаково. Теперь сдвинем вторую зависимость по времени.

При равном приращении она изменяется на меньшую величину. А значит, коэффициент корреляции между двумя зависимостями становится меньше. Увеличивая временной сдвиг мы доходим до момента, когда умен ьшение значения первой величины соответствует увеличению значения второй, а значит коэффициент корреляции становится отрицательным.

Зависимость коэффициента корреляции от временного сдвига между сигналами – по сути есть корреляционная функция. Но давайте рассмотрим формулу.

В общем случае мы рассматриваем взаимно-корреляционную функцию и оцениваем зависимость между двумя сигналами. Частным случаем взаимно-корреляционной функции является автокорреляционная функция, когда мы сравниваем сигнал с его задержанной во времени копией. 

Рассмотрим формулу. Я тут привёл формулу для непрерывных функций, но если мы берём дискретные величины, то операция интегрирования будет заменена на простое суммирование. Здесь есть две функции. Первая функция f (не обращайте пока что внимания на знак звёздочки, это комплексное сопряжение, но для действительных сигналов оно не важно), так вот, первая функция f умножается на вторую функцию g, при этом вторая функция сдвигается во времени на величину τ. От величины сдвига τ мы и строим зависимость коэффициента корреляции.

Рассмотрим графическое представление. Первую функцию f мы фиксируем на временной оси, а вторая g по этой оси будет перемещаться. Она перемещается из значений отрицательного сдвига между функциями в область положительных значений сдвига. Величина корреляции соответствует площади перекрытия двух графиков, и максимума она достигает, когда две фигуры максимально накладываются друг на друга. Стоит отметить, что если мы поменяем функции местами, то есть зафиксируем g и будем скользить функцией f, то вид корреляционной функции изменится на зеркальный. В случае автокорреляционной функции форма зависимости всегда симметрична, и имеет максимум в точке, равной нулевому сдвигу сигнала относительно самого себя.

Давайте посмотрим на несколько примеров подсчёта корреляционной функции для дискретных сигналов в MATLAB.

Автокорреляционная функция прямоугольного импульса имеет форму треугольника.

Взаимнокорреляционная функция пилообразного импульса и прямоугольного импульса несимметрична.

Автокорреляционная функция отрезка синусоиды симметрична, и имеет вид нарастающего и затухающего колебательного процесса с выраженным максимумом в моменте совпадения импульсов

А автокорреляционная функция бесконечной синусоиды – это такая же синусоида, с той же частотой.

Особо важно отметить автокорреляционную функцию случайного процесса, или шума. Она имеет один выраженный максимум, и при малейшем сдвиге значения её падают почти до нуля. Это говорит о том, что шум – слабо коррелированный процесс, и этим свойством мы будем пользоваться при обработке.

А обработка корреляционными методами – это важная часть ЦОС. При помощи вычисления взаимнокорреляционной функции  мы можем обнаруживать интересующие нас отрезки сигнала в эфире, в том числе на фоне шумов, находить сигналы, похожие на некий выбранный эталон, и оценивать степень схожести, или мы можем точно определять задержу распространения сигнала. К примеру, радиолокационная станция отправляет импульс известной формы в сторону цели и ждёт отражённый сигнал. Максимум корреляционной функции даст нам величину задержки между переданным и принятым импульсами, которую мы затем можем использовать для определения расстояния до цели.

Выполним корреляционную обработку сигнала в MATLAB. В данном случае мы будем пытаться найти фрагмент аудиосигнала в полном сигнале, в том числе на фоне шумов. Загружаемый аудиосигнал – эта запись звука кольца, крутящегося на столе. Давайте загрузим его и послушаем командой Sound. Так вот звучит фрагмент аудиосигнала, который мы попробуем найти. 

Область, которую мы выделили, обозначена на графике двумя пунктирными линиями. Давайте также построим график взаимной корреляционной функции исходного сигнала и выделенного фрагмента. Для этого воспользуемся функцией xcorr и передадим ей исходный сигнал и выделенный фрагмент.

В первую выходной переменной записываются отчёты функции, а во вторую – величины временного сдвига. На графике взаимной корреляционной функции мы видим явно выраженный максимум, в тот момент времени когда наш фрагмент совпадает с самим собой на исходном сигнале. Используем максимум вектора lags для того, чтобы отразить фрагмент на сигнале. 

Теперь давайте добавим шум к исходному сигналу и к фрагментам.

Причем, обратите внимание, что мы добавляем разный шум к полному сигналу и к нашему фрагменту. Послушаем как звучит фрагмент на фоне шума. Уровень шума достаточно велик, и мы совершенно не слышим звука кольца.

Но даже в этом случае корреляционная обработка позволяет нам точно определить момент начала фрагмента, и мы также сможем показать где наш искомый фрагмент на всём сигнале. Пока что закончим с корреляционной функцией и обработкой. Тема следующей публикации – моделирование сигнала, то есть приближение его аналитической функцией.