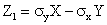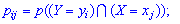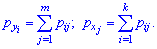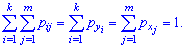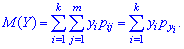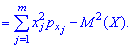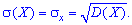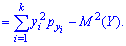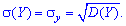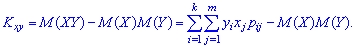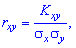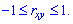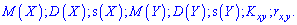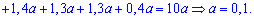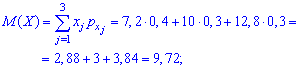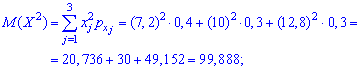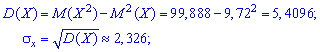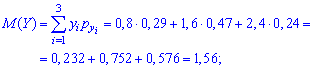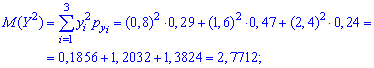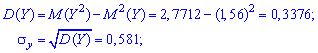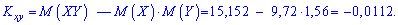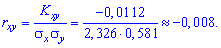Для описания системы двух случайных
величин, кроме математических ожиданий
и дисперсий составляющих пользуются и
другими характеристиками, к числу
которых относятся корреляционный
моментикоэффициент корреляции(кратко было упомянуто в конце Т.8.п.8.6).
Корреляционным моментом 
(иликовариацией, или моментом
связи) двух случайных величинX
иY называется
м. о. произведения отклонений этих
величин (см. равенство (5) п. 8.6):
(7)
.
Следствие 1. Для корреляционного
момента с.в. X иYтакже справедливы
равенства:
,
где
соответствующие централизованные с.в.X иY
(см. п.8.6.).
При
этом: если
—
двумерная д.с.в., то ковариация вычисляется
по формуле
(8)
;
если
—
двумерная н.с.в., то ковариация вычисляется
по формуле
(9)
Формулы (8) и (9) получены на основании
формул (6) п.12.1. Имеет место вычислительная
формула
(10)
которая
выводится из определения (9) и на основании
свойств м.о., действительно,
.
Следовательно, формул (36) и (37) можно
переписать в виде
(11)
;
Корреляционный момент служит для
характеристики связи между величинами
X иY.
Как
будет показано ниже, корреляционный
момент равен нулю, если XиY являются
независимыми;
Следовательно, если корреляционный
момент не равен нулю, то X
и Y – зависимые
случайные величины.
Теорема12.1. Корреляционный момент
двух независимых случайных величин X
иY равен нулю,
т.е. для независимых с.в. X
иY,
Доказательство.Так какX
иYнезависимые
случайные величины, то их отклонения
и 
также
независимы. Пользуясь свойствами
математического ожидания (математическое
ожидание произведения независимых с.
в. равно произведению математических
ожиданий сомножителей
,
,
поэтому
.
Замечание. Из этой теоремы следует,
что если
то с.в. X иY
зависимы и в таких случаях с.в. X
иYназываюткоррелированными. Однако из того,
что
не следует независимость с.в.X
иY.
В этом случае (
с.в.X иYназываютнекоррелированными, тем
самым из
независимости
вытекает некоррелированность;
обратное утверждение, вообще говоря,
неверно (см. далее пример 2.)
Рассмотрим основные свойства
корреляционного момента.
Cвойства ковариации:
1.Ковариация симметрична, т.е.
.
Непосредственно следует из формулы
(38).
2. Имеют место равенства:
т.е.
дисперсия с.в. является ковариацией её
с самой собой.
Эти равенства прямо следуют из определения
дисперсии и равенство (38) соотвеиственно
при
3. Справедливы равенства:
Эти
равенства выводятся из определения
дисперсии, ковариации с.в.
и
,
свойств 2.
По определению дисперсии (с учётом
централизованности с.в.
)
мы имеем
теперь,
на основании (33) и свойств 2 и 3, получим
первое (со знаком плюс) свойство 3.
Аналогично,
вторая часть свойства3, выводится из
равенство
.
4. Пусть
постоянные
числа,
тогда справедливы равенства:
Обычно
эти свойства называются свойствами
однородностью первого порядка и
периодичностью по аргументам.
Докажем
первое равенство, при этом будем
использовать свойства м.о.
.
.
Теорема 12.2. Абсолютное значение
корреляционного момента двух
произвольных случайных величин X
и Y не превышает
среднего геометрического их дисперсий:
т.е.
(12)
Доказательство. Заметим, что для
независимых с.в. неравенство выполняется
(с.м. теорему 12.1.). Итак, пусть с.в.X
и Y зависимые.
Рассмотрим стандартные с.в.
и
и вычислим дисперсию с.в.
с учётом свойства 3, имеем: с одной
стороны
С другой стороны
Следовательно,
с учётом того, что
и
—
нормированные (стандартизированные)
с.в., то для них м.о. равна нулю, а дисперсия
равна 1, поэтому, пользуясь свойством
м.о.
получим
а
следовательно, на основании того, что
получим
Отсюда
следует, что
т.е.
=
Утверждение доказано.
Из определения и свойства ковариации
следует, что она характеризует и степень
зависимости с.в., и их рассеяния вокруг
точки
Размерность ковариации равна произведению
размерностей случайных величинXиY. Другими словами,
величина корреляционного момента
зависит от единиц измерения случайных
величин. По этой причине для одних и тех
же двух величинXиY,
величина корреляционного момента
будет иметь различные значения в
зависимости от того, в каких единицах
были измерены величины.
Пусть, например, X
и Y
были измерены в
сантиметрах и
;
если измерить XиY в миллиметрах,
то
Эта особенность корреляционного момента
и есть недостатком этой числовой
характеристики, так как сравнение
корреляционных моментов различных
систем случайных величин становится
затруднительным.
Для того чтобы устранить этот недостаток,
вводят новую числовую характеристику-
— «коэффициент корреляции».
Коэффициентом корреляции
случайных величин
и
называют отношение корреляционного
момента к произведению средних
квадратических отклонений этих величин:
(13)
.
Так как размерность
равна произведению размерностей величин
и
,
имеет размерность величины
σyимеет размерность величины
,
то
есть просто число (т.е. «безразмерная
величина»). Таким образом, величина
коэффициента корреляции не зависит от
выбора единиц измерения с.в., в этом
состоитпреимуществокоэффициента
корреляции перед корреляционным
моментом.
В Т.8. п.8.3 нами было введено понятие
нормированной с.в.
,
формула (18), и доказана теорема о том,
что
и
(см.
там же теорема 8.2.). Здесь докажем следующее
утверждение.
Теорема 12.3. Длялюбых двух случайных
величин
и
справедливо
равенство
.Другими словами, коэффициент корреляции
любых двух с.в.X
иYравно
корреляционному моменту их соответствующих
нормированныхс.в.
и 
.
Доказательство. По определению
нормированных случайных величин
и
и
.
Учитывая свойство математического
ожидания:
и равенство (40) получим
Утверждение
доказано.
Рассмотрим некоторые часто встречающие
свойства коэффициента корреляции.
Свойства коэффициента корреляции:
1. Коэффициент
корреляции по абсолютной величине
непревосходит 1, т.е.
Это
свойство прямо следует из формулы (41)
— определения коффициента корреляции
и теоремы 13.5. ( см. равенство (40)).
2. Если случайные величины
и
независимы,
токоэффициент корреляции
равен нулю, т.е.
.
Это свойство является прямым
следствием равенства (40) и теоремы 13.4.
Следующее свойство
сформулируем в виде отдельной теоремы.
Теорема 12.4.
Если
с.в.
и
между
собой связаны линейной функциональной
зависимостью, т.е.
то
при этом
и
наоборот, если
,то
с.в.
и
между собой связаны линейной функциональной
зависимостью, т.е. существуют постоянные
и
такие, что имеет место равенство
Доказательство.
Пусть
тогда на основании
свойства 4 ковариации, имеем
и
поскольку,
,
поэтому
Следовательно,
.
Равенство в одну сторону получено. Пусть
далее,
,
тогда
следует
рассматривать два случая:1)
и
2)
Итак, рассмотрим первый случай. Тогда
по определению
и
следовательно из равенства
,
где
.
В нашем случае
,
поэтому из равенства (см. доказательство
теоремы 13.5.)
=
,
получаем,
что
,
значит
постоянна.
Так как
и поскольку
,
то
действительно,
.
Следовательно,
.
Аналогично,
показывается, что для
имеет место (проверьте самостоятельно!)
,
.
Некоторые выводы:
1. Если
и
независимыес.в., то 
2. Если с.в.
и
между
собой связаны линейно, то
.
3. В остальных случаях
:
В этом
случае говорят, что с.в.
и
связаны между собойположительной
корреляцией, если
в случаях же
отрицательной
корреляцией. Чем ближе
к единице, тем больше оснований считать,
чтос.в.
и
связаны линейной зависимостью.
Отметим, что корреляционные моменты и
дисперсии системы с.в. обычно задаются
корреляционной матрицей:
.
Очевидно, что определитель
корреляционной матрицы удовлетворяет:
.
Как уже было отмечено, если две случайные
величины зависимы, то они могут быть
как коррелированными, так инекоррелированными.Другими словами,
корреляционный момент двух зависимых
величин может бытьне равен нулю,
но может иравняться нулю.
Пример 1. Закон распределения
дискретной с.в.задан таблицей
|
|
-1 |
0 |
1 |
|
0 |
|
|
|
|
1 |
|
|
|
Найти
коэффициент корреляции
Решение. Находим законы распределения
составляющих
и
:
Теперь
вычислим м.о. составляющих:
.
Этих
величин можно было находить на основании
таблицы распределения с.в.
из
равенства (1) пункта 12.1. Например,
.
Аналогично,
находите
самостоятельно.
Вычислим
дисперсии составляющих при это будем
пользоваться вычислительной формулой:
Следовательно,
Далее, на основании первой формулы
(6) имеем:
Составим
закон распределения
,
а затем найдём
:
При
составлении таблицы закона распределения
следует выполнять действия:
1) оставить лишь различные значения
всевозможных произведений
.
2) для определения вероятности данного
значения
,
нужно
складывать все соответствующие
вероятности, находящиеся на пересечении
основной таблицы, благоприятствующие
наступлению данного значения.
В нашем примере с.в.
принимает
всего три различных значения
.
Здесь первое значение (
)
соответствует произведению
из второй строки и
из первого столбца, поэтому на их
пересечении находится вероятностное
число
аналогично
,
которое
получено из суммы вероятностей,
находящихся на пересечениях соответственно
первой строки и первого столбца (0,15 ;
0,40; 0,05) и одно значение
,
которое находится на пересечении второй
строки и второго столбца, и наконец,
,
которое находится на пересечении второй
строки и третьего столбца.
Из нашей таблицы находим:
Находим
корреляционный момент, используя формулу
(38):
Находим
коэффициент корреляции по формуле
(41)
Таким образом, отрицательная корреляция.
Упражнение.Закон
распределения дискретной с.в. задан
таблицей
|
|
-1 |
0,5 |
1 |
|
0,2 |
|
|
|
|
1 |
|
|
|
Найти коэффициент корреляции
Рассмотрим
пример, где окажется две зависимые
случайные величинымогут бытьнекоррелированными.
Пример 2. Двумерная случайная величина
)задана функцией плотностью
Докажем, что
и
зависимые,нонекоррелированные
случайные величины.
Решение.Воспользуемся ранее
вычисленными плотностями распределения
составляющих
и
:
Так
как
,то 
и
зависимые
величины. Для того, чтобы доказать
некоррелированность
и
,
достаточно убедиться в том, что
Найдем
корреляционный момент по формуле:
Поскольку дифференциальная функция
симметрична относительно
оси OY,
то
аналогично
,
в силу симметрии
относительно оси OX.
Поэтому,
вынося
постоянный множитель
Внутренний интеграл равен
нулю (подынтегральная функция нечетна,
пределы интегрирования симметричны
относительно начала координат),
следовательно,
,
т.е. зависимые случайные величины
и
между собой некоррелируют.
Итак, из коррелированности двух
случайных величин следует их зависимость,
но из некоррелированности ещё нельзя
заключить о независимости этих величин.
Однако, для нормально
распределённых с.в. такой вывод является
исключением,
т.е. из некоррелированности
нормально распределенных
с.в. вытекает их независимость.
Этому вопросу посвящается
следующий пункт.
Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используют и другие характеристики; к их числу относятся корреляционный момент и коэффициент корреляции.
Корреляционным моментом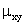 
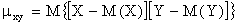
случайных величин X и Y называют математическое ожидание произведения отклонений этих величин: 
.
Для вычисления корреляционного момента дискретных величин используют формулу
,
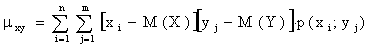
а для непрерывных величин – формулу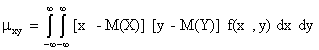 
.
Корреляционный момент служит для характеристики связи между величинами X и Y . Как будет показано ниже, корреляционный момент равен нулю, если X и Y независимы; следовательно, если корреляционный момент не равен нулю, то X и Y – зависимые случайные величины.
Корреляционный момент можно записать в виде
.
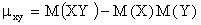
ТЕОРЕМА 13.1.18. Корреляционный момент двух независимых случайных величин X и Y равен нулю.
Доказательство. Так как X и Y – независимые случайные величины, то их отклонения X – M(X) и Y – M(Y) также независимы. Пользуясь свойствами математического ожидания (математическое ожидание произведения независимых случайных величин равно произведению математических ожиданий сомножителей) и отклонения (математическое ожидание отклонения равно нулю), получим
.
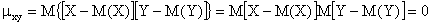
Из определения корреляционного момента следует, что он имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина корреляционного момента зависит от единиц измерения случайных величин. По этой причине для одних и тех же двух величин величина корреляционного момента имеет различные значения в зависимости от того, в каких единицах были измерены величины.
Пусть, например, X и Y были измерены в сантиметрах и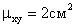 
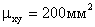
; если измерить X и Y в миллиметрах, то и 
. Такая особенность корреляционного момента является недостатком этой числовой характеристики, поскольку сравнение корреляционных моментов различных систем случайных величин становится затруднительным. Для того, чтобы устранить этот недостаток, вводят новую числовую характеристику – коэффициент корреляции.
Коэффициентом корреляции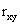 
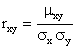
случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:
.
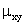
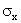
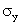
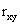
Так как размерность равна произведению размерностей величин X и Y,
имеет размерность величины X, 
имеет размерность величины Y, то — безразмерная величина. Таким образом, величина коэффициента корреляции не зависит от выбора единиц измерения случайных величин. В этом состоит преимущество коэффициента корреляции перед корреляционным моментом.
Очевидно, коэффициент корреляции независимых случайных величин равен нулю, так как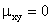 
.
ТЕОРЕМА 13.1.19. Абсолютная величина корреляционного момента двух случайных величин X и Y не превышает среднего геометрического их дисперсий:
.
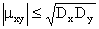
Доказательство. Введем в рассмотрение случайную величину 
и найдем ее дисперсию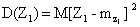 
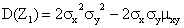
. Выполнив выкладки, получим
.
Любая дисперсия неотрицательна, поэтому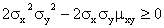 
.
Отсюда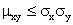 
(13.1.51)
Введя случайную величину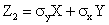 
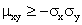
, аналогично найдем
.(13.1.52)
Объединим (1.51) и (1.52):
, (13.1.53)
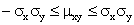
или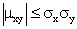 
.
Итак, 
.
ТЕОРЕМА 13.1.20. Абсолютная величина коэффициента корреляции не превышает единицы:
.
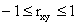
Доказательство. Разделим обе части двойного неравенства (13.1.53) на произведение положительных чисел :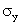
.
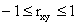
Итак, .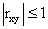
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Сохранить или поделиться с друзьями
Вы находитесь тут:
На нашем сайте Вы можете получить решение задач и онлайн помощь
Подробнее
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
—
определить одномерные законы распределения случайных величин X и Y;
— найти
условные плотности распределения вероятностей величин;
—
вычислить математические ожидания mx и my;
—
вычислить дисперсии σx и σy;
—
вычислить ковариацию μxy;
—
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |
Законом распределения двух дискретных случайных величин называют перечень возможных значений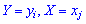 
и соответствующих им вероятностей совместного появления. В табличной форме этот закон имеет следующий вид
При подаче таблице использованы следующие обозначения
Условие нормировки для двух дискретных случайных величин имеет следующий вид:
Основные числовые характеристики для случайных величин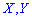 
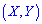
, образующих систему 
Математическое ожидание определяется по формуле
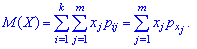
Дисперсия и среднее квадратическое отклонение для каждой дискретной величины определяют по правилам
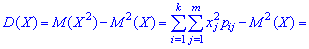
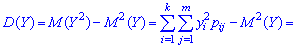
При изучении системы двух и более случайных величин приходится выяснять наличие связи между этими величинами и его характер. С соответствующей целью применяют корреляционный момент
В случае нулевого значения корреляционного момента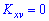 
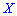
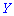
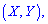
связь между величинами 
и
, и, принадлежащих системе 
отсутствует.
Когда момент отличен от нуля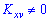 
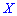
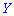
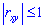
, то между дискретными величинами 
и 
существует корреляционная связь. Тесноту корреляционной связи характеризует коэффициент корреляции
, или 
Итак, если случайные величины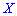 
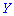
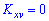
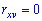
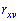
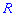
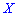
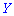
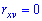
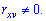
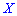
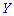
и 
независимы, то корреляционный момент равен нулю 
и 
. Равенство нулю 
является необходимым, но не достаточным условием независимости случайных величин. Может существовать система зависимых случайных величин, в которой коэффициент корреляции равен нулю. Примером такой системы является система двух случайных величин, которая равномерно распределена внутри круга радиусом 
с центром в начале координат. Две случайные величины 
и 
называют некоррелированными, если коэффициент корреляции равен нулю 
, и коррелированными в противном случае 
Следовательно, если 
и 
независимы, то они будут и некоррелированными. Но с некоррелированности случайных величин в общем случае не следует их независимость.
——————————————
Приведем решение распространенного на практике примера.
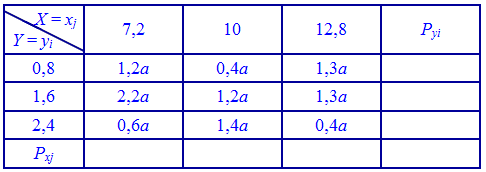
Пример 1. Задан закон распределения системы двух дискретных случайных величин (X,Y):
Найти неизвестную константу 
. Вычислить математическое ожидание, дисперсию и среднее матиматичне отклонения, корреляционный момент и коэффициент корреляции
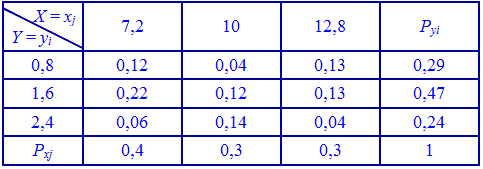
Решение. Применяя условие нормирования, находим каонстанту
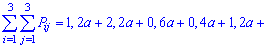
По найденным 
закон системы набирает такой вид:
Основные числовые характеристики вычисляем по приведенным выше формулам. Математическое ожидание величины X получит значение
Дисперсия и среднее квадратичное отклонение набудут вида
Аналогичные вычисления выполняем для нахождения числовых характеристик случайной величины Y
Находим математическое ожидание появления обоих событий
Значение корреляционного момента вычисляем по формуле
Поскольку корреляционный момент отличен от нуля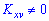 
, то между соответствующими величинами X и Y существует корреляционная связь.
Для измерения тесноты корреляционной связи вычислим коэффициент корреляции
——————————
Подобных примеров можно найти немало в интернете и решебниках по теории вероятностей. Принцип их решения остается неизменным, поэтому хорошо проанализируйте приведенный пример. Если возникают трудности в вычислениях — обращайтесь, мы Вам поможем.