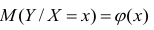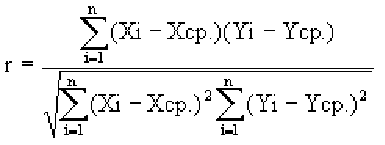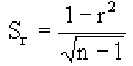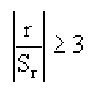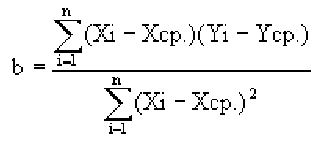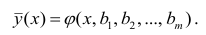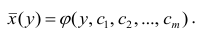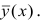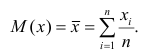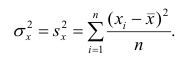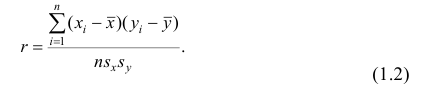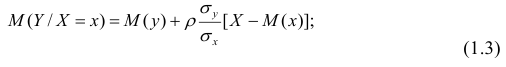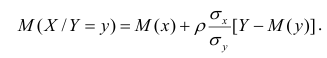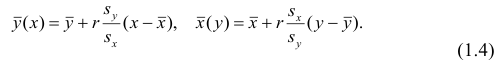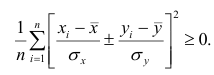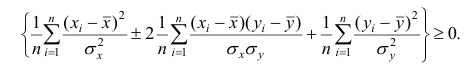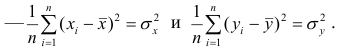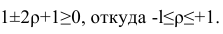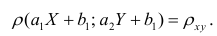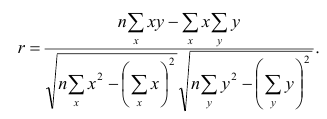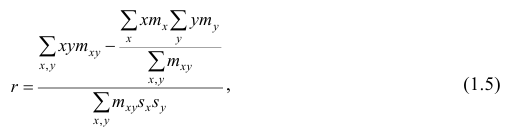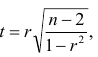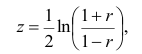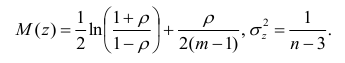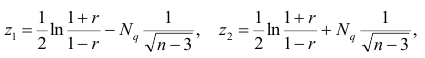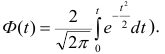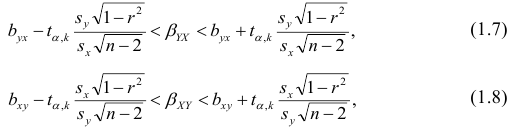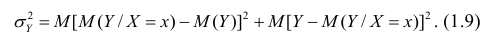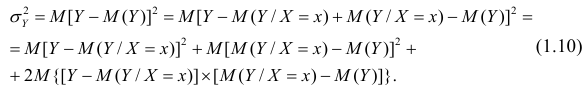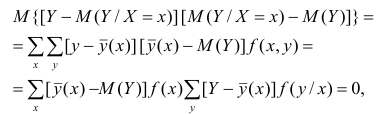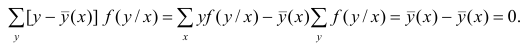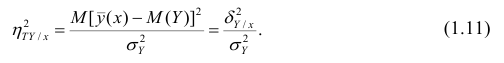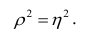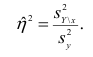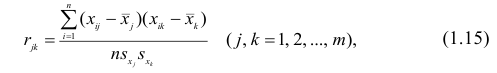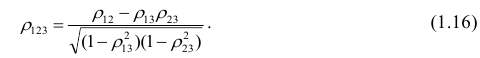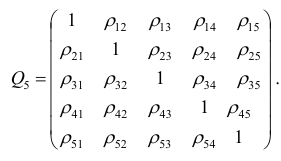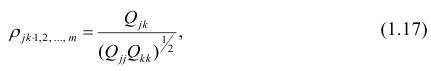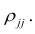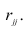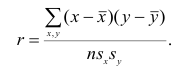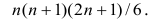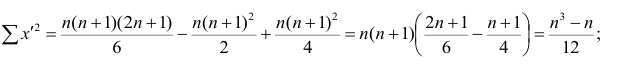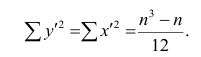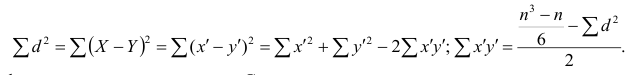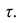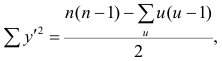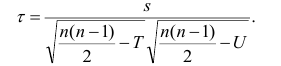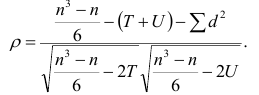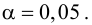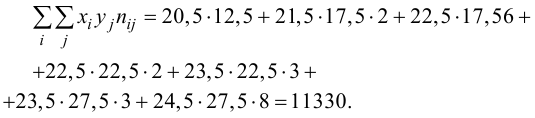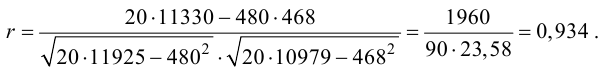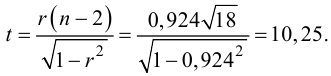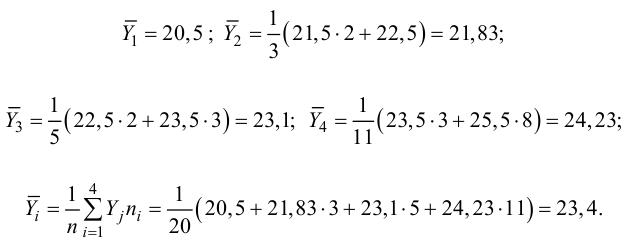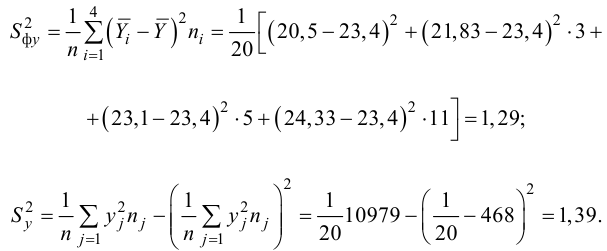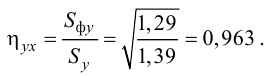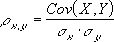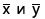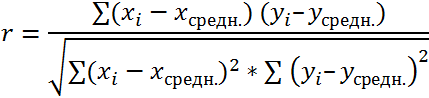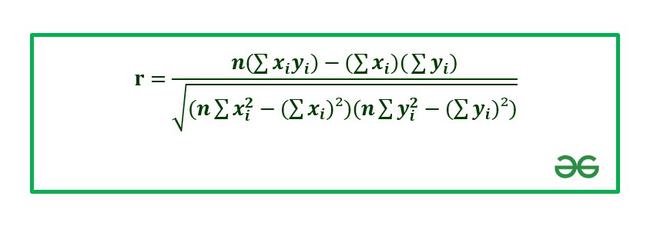Как найти корреляцию двух графиков

Excel – это эффективный инструмент для статистической обработки данных. И определение корреляций является очень важной составляющей этого процесса. Программа имеет весь необходимый инструментарий для осуществления расчетов такого плана. Сегодня мы более детально разберемся, что нам нужно для осуществления анализа этого типа.

Что представляет собой корреляционный анализ

Простыми словами, корреляция – это связь между двумя явлениями. В свою очередь, под корреляционным анализом подразумевают выявление этой связи. Очень частое утверждение гласит, что корреляция – это зависимость между разными объектами, но на деле это неточное определение. Ведь существует множество изображений, которые показывают связь между явлениями, которые никак не могут быть зависимы друг от друга или одного третьего фактора, который влияет на них.

Для определения зависимости используется другой тип анализа, который называется регрессионным.

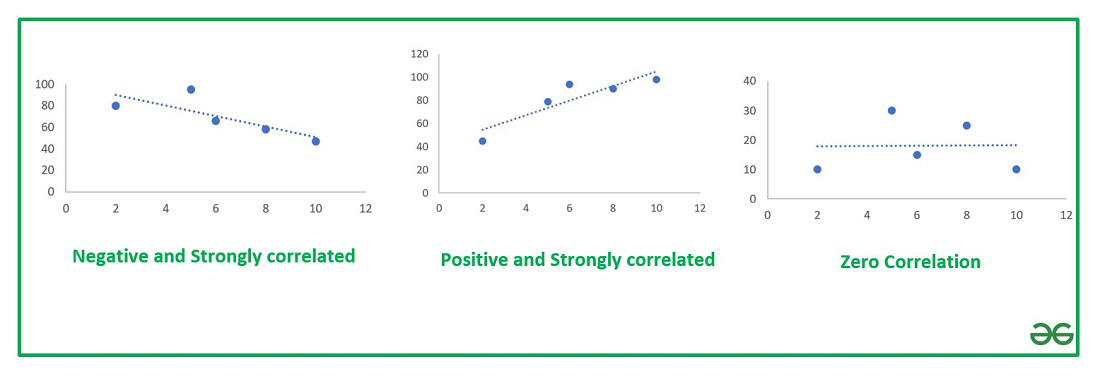
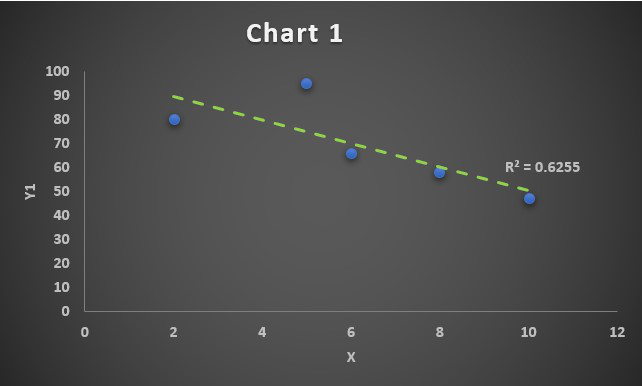
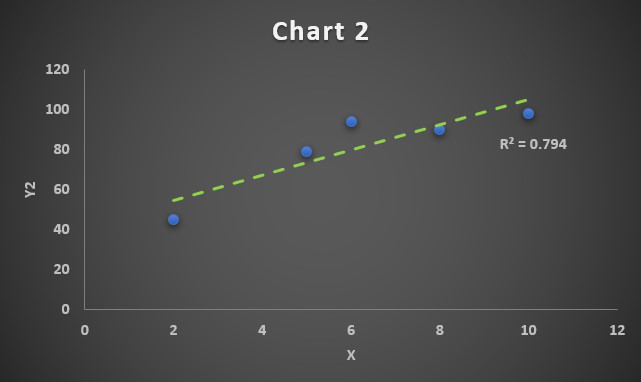
Величина, определяющая степень выраженности взаимосвязи, называется коэффициентом корреляции. Это единственная величина, которая рассчитывается корреляционным анализом по сравнению с регрессионным. Возможные вариации коэффициента корреляции могут быть в пределах от -1 до 1. Если это число положительное, взаимосвязь между динамикой изменения значений прямая. Если же отрицательное, то увеличение числа 1 приводит к аналогичному уменьшению числа 2. Если число меньше единицы по модулю, то корреляция неполная. Например, увеличение числа 1 на единицу приводит к увеличению числа 2 на 0,5. В таком случае коэффициент корреляции составляет 0,5. Если же коэффициент корреляции составляет 0, то взаимосвязи между двумя переменными нет.

Интересный факт: корреляции делятся на истинные и ложные. То есть, иногда то, что графики идут в одинаковом направлении, может быть чистой случайностью, а не закономерным следствием воздействия одной переменной на другую или влияния общего фактора на обе переменные. В узких кругах довольно популярны картинки, где коррелируют между собой абсолютно не связанные явления. Вот некоторые примеры:

1. Количество человек, которые стали утопленниками в бассейнах, четко коррелирует с количеством фильмов, в которых Николас Кейдж был актером.
2. Количество съеденной моцареллы и количество человек, которые получили докторскую степень, также коррелирует на протяжении 2000-2009 годов. Наверно, действительно, моцарелла как-то влияет на мозг и стимулирует желание совершать научные открытия.
3. Почти во всех случаях средний возраст женщин, которые получили статус «Мисс Америка» коррелирует с количеством людей, которые погибли от нахождения в горячем паре.
4. Число людей, которое погибло в результате дорожно-транспортного происшествия, четко коррелирует с количеством сметаны, которое съедают люди.
5. Мало кто знает, что чем больше курятины человек ест, тем больше сырой нефти импортируется в мире. Правда, это тоже пример ложной корреляции. Кстати, импорт сырой нефти родом из Норвегии тесно связано с количеством людей, которые погибли в результате столкновения автомобиля с поездом. Причем в этом случае корреляция почти 100 процентов.
6. А еще маргарин негативно влияет на статистику разводов. Чем больше людей, которые проживали в штате Мэн, потребляли маргарина, тем выше была частота разводов. Правда, здесь еще может быть рациональное зерно. Ведь частота потребления маргарина имеет обратную корреляцию с экономическим положением в семье. В свою очередь, плохое экономическое положение в семье имеет непосредственную связь с количеством разводов. И это уже доказано научно. Так что кто знает, может, эта корреляция и не является такой ложной. Правда, никто этого не перепроверял.
7. Количество денег, которое правительство США тратит на развитие науки, космоса и технологий, имеет тесную связь с количеством самоубийств, проведенных в форме повешения или удушения.

Ну и наконец, еще один пример ложной корреляции – чем больше сыра люди едят, тем больше людей умирает из-за того, что они запутываются в своих простынях.

Поэтому несмотря на то, что корреляция является эффективным статистическим инструментом, нужно учиться отфильтровывать истинные взаимосвязи между явлениями и ложные. Иначе исследование может получить такие интересные результаты. А теперь переходим непосредственно к тому, как проводить корреляционный анализ в Excel.

Корреляционный анализ в Excel — 2 способа

Вычисление коэффициента корреляции осуществляется двумя способами. Первый – это использование Мастера функций, который позволяет ввести формулу КОРРЕЛ. Второй инструмент – это пакет анализа, требующий отдельной активации.

Как рассчитать коэффициент корреляции

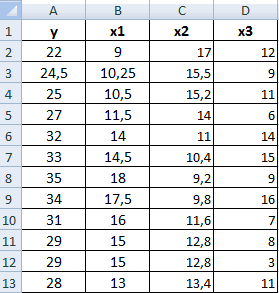
Давайте продемонстрируем механизм получения коэффициента корреляции на реальном кейсе. Допустим, у нас есть таблица с информацией о суммах продаж и рекламу. Нам нужно понять, в какой степени количество продаж и количество денег, которые были использованы на продвижение, взаимосвязаны.

Способ 1. Определение корреляции с помощью Мастера Функций

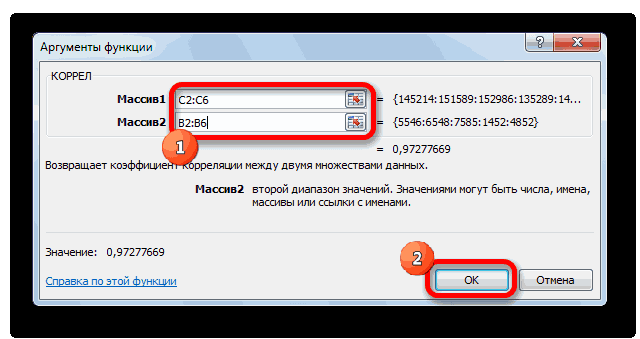
Функция КОРРЕЛ – один из самых простых методов, как можно реализовать поставленную задачу. В своем общем виде этот оператор имеет следующий вид: КОРРЕЛ(массив1;массив2). Как же ее ввести? Для этого нужно осуществлять следующие действия:

1. С помощью левой кнопки мыши выделяем ту ячейку, в которой будет находиться получившийся коэффициент корреляции. После этого находим слева от строки формул кнопку fx, которая откроет инструмент ввода функций. 
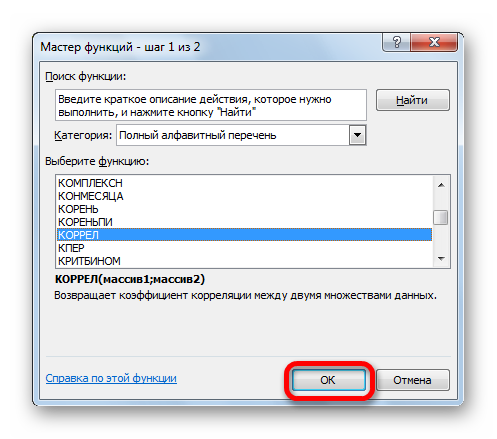
2. Далее выбираем категорию «Полный алфавитный перечень», в котором ищем функцию КОРРЕЛ. Как видно из названия категории, все названия функций располагаются в алфавитном порядке. 
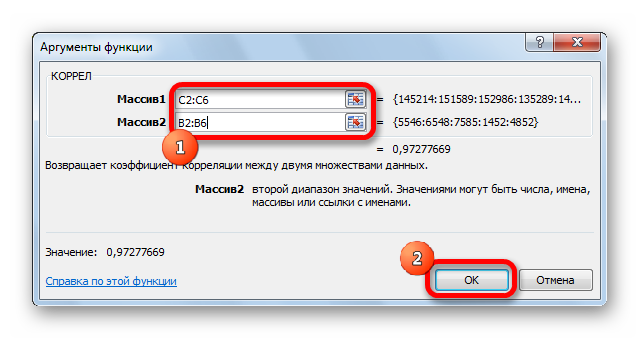
3. Далее открывается окно ввода параметров функции. У нас два основных аргумента, каждый из которых являет собой массив данных, которые сравниваются между собой. В поле «Массив 1» указываем координаты первого диапазона, а в поле «Массив 2» – адрес второго диапазона. Для ввода данных массива, используемого для расчета, достаточно выделить нажать левой кнопкой мыши по соответствующему полю и выделить правильный диапазон. 
4. После того, как мы введем данные в аргументы, нажимаем кнопку «ОК», чем подтверждаем совершенные действия.

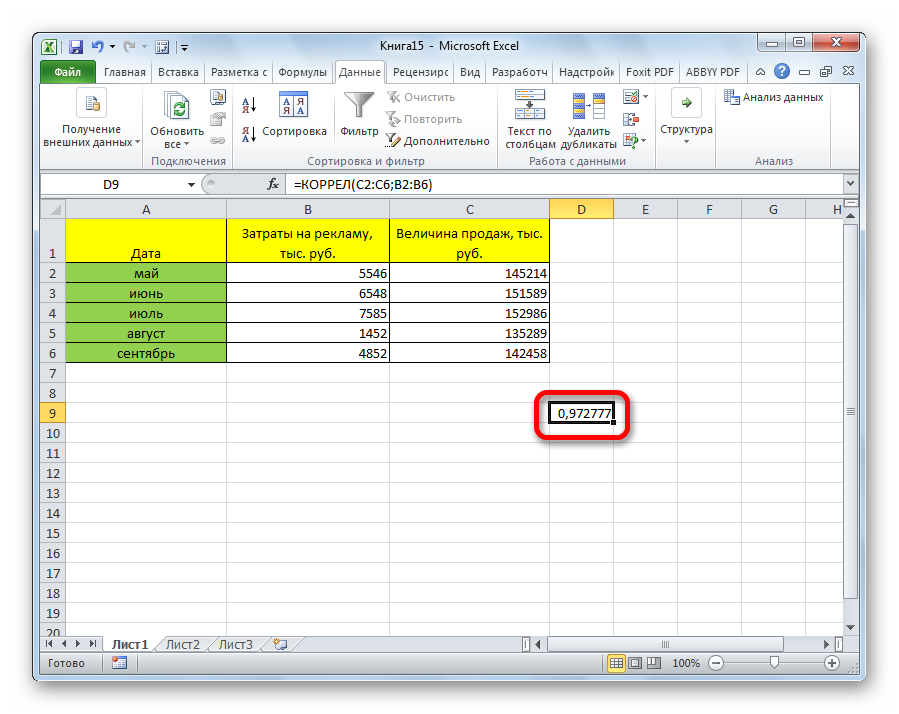
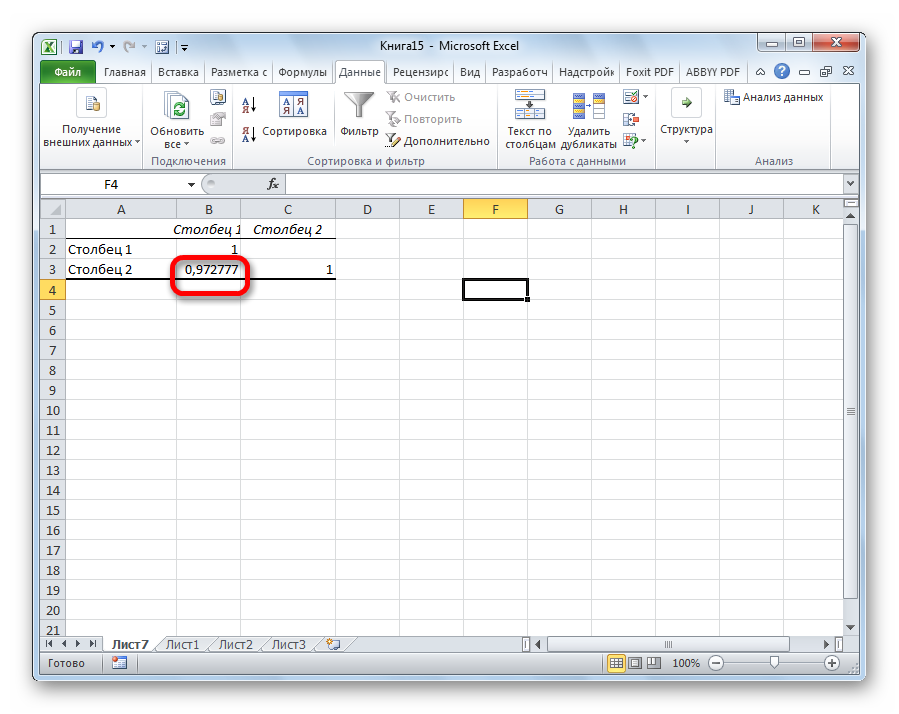
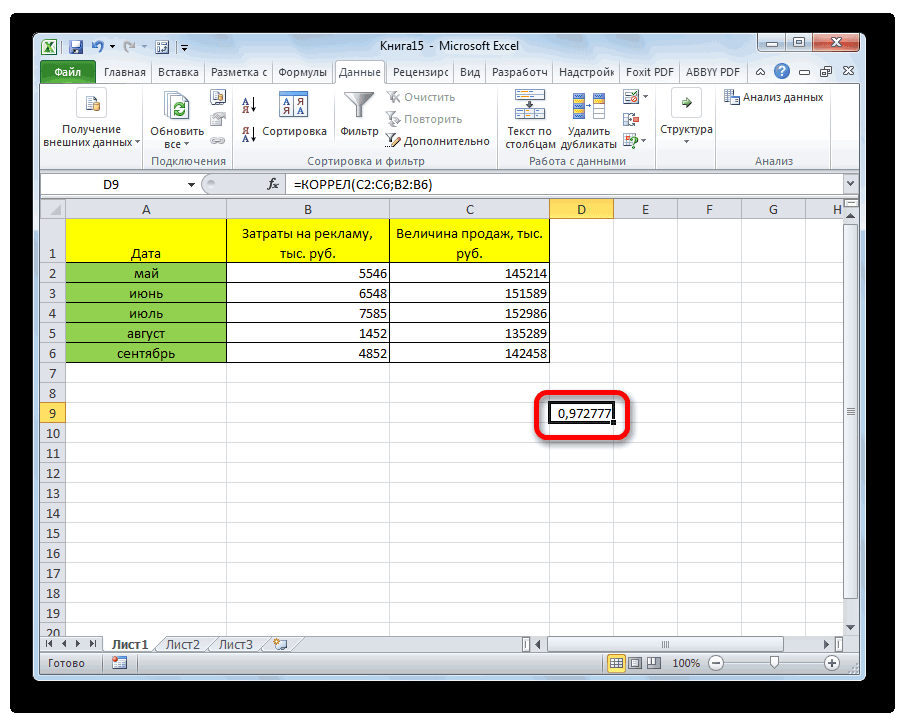
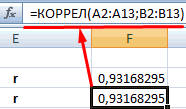
После выполнения описанных выше шагов мы видим в ячейке, выбранной нами на первом этапе, коэффициент корреляции. В нашем примере он составляет 0,97, что указывает на очень сильно выраженную взаимосвязь между данными двух диапазонов. 

Способ 2. Вычисление корреляции с помощью пакета анализа

Также довольно неплохой инструмент для определения корреляции между двумя диапазонами – пакет анализа. Но перед тем, как его использовать, нам надо его включить. Для этого выполняем следующие действия:

1. Нажимаем на кнопку «Файл», которая находится в левом верхнем углу сразу возле вкладки «Главная». 
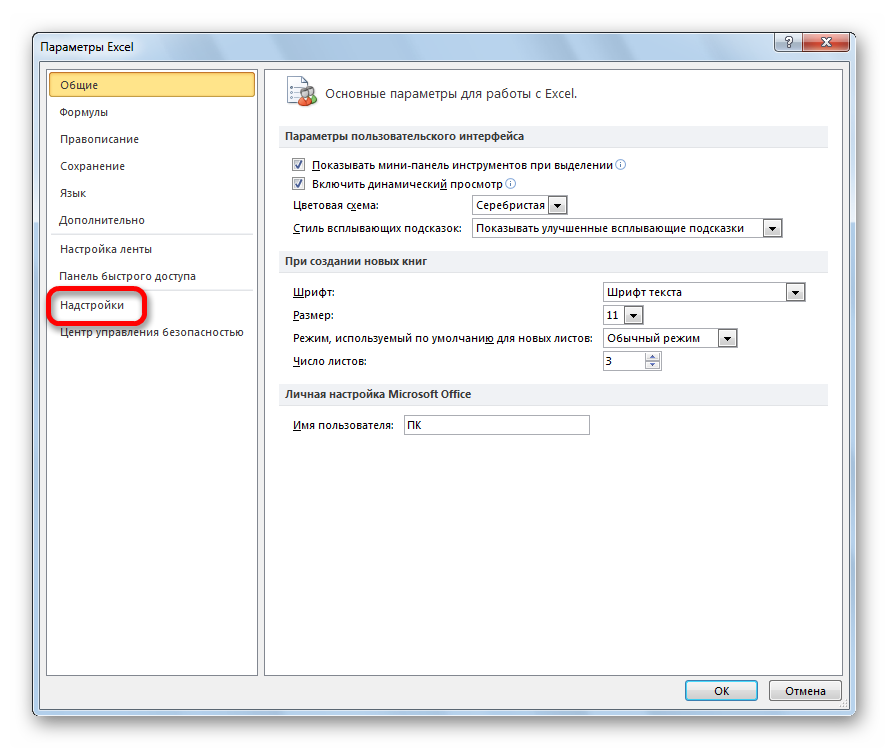
2. После этого открываем раздел с настройками. 
3. В меню слева переходим в предпоследний пункт, озаглавленный, как «Надстройки». Делаем левый клик по соответствующей надписи. 
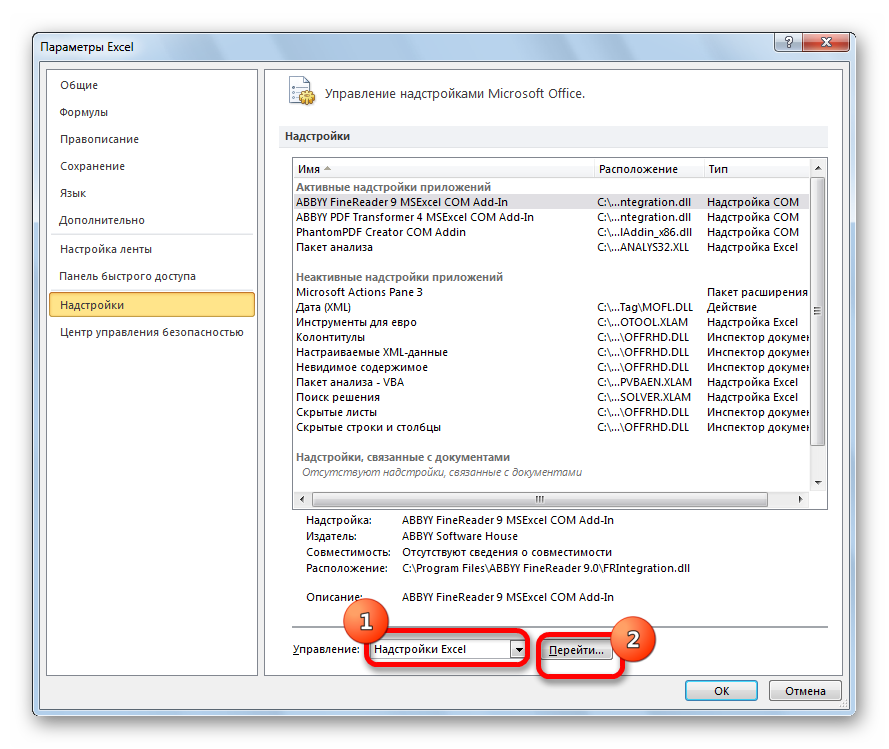
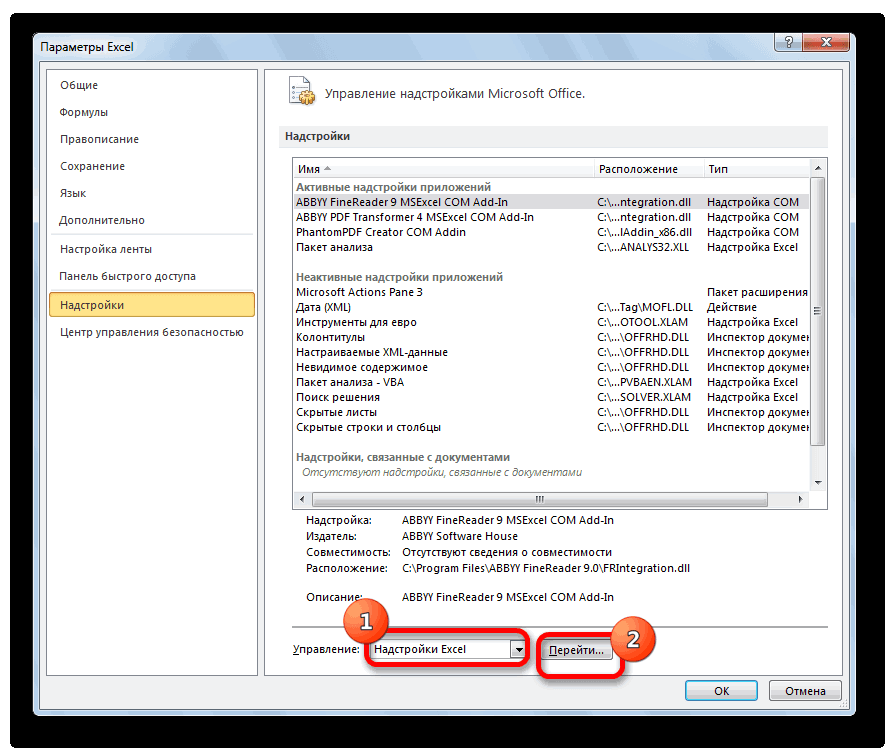
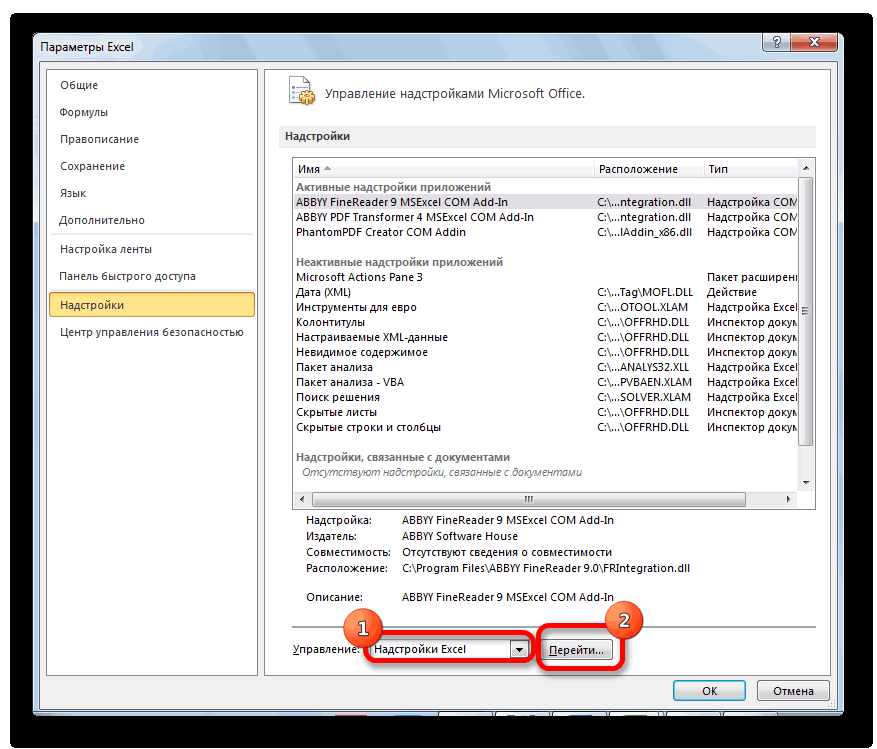
4. Открывается окно управления надстройками. Нам нужно переключить поле ввода, находящееся внизу, на пункт «Надстройки Excel» и нажать на «Перейти». Если это поле уже находится в таком положении, то не выполняем никаких изменений. 
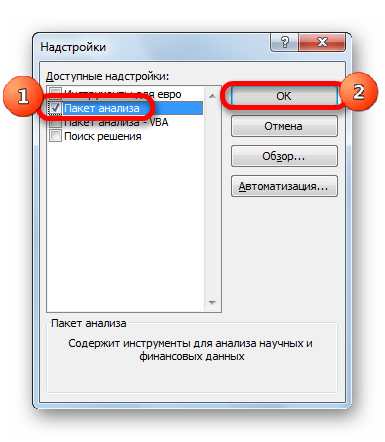
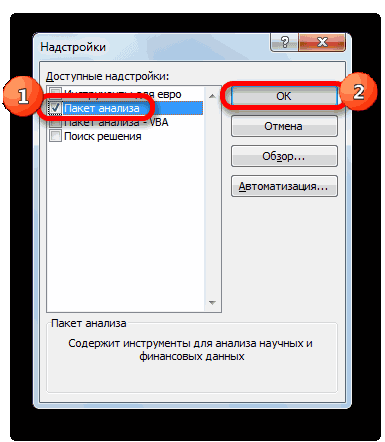
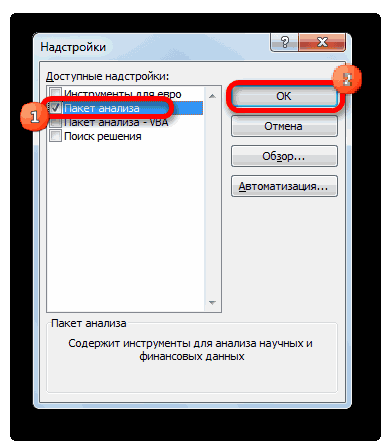
5. Затем включаем пакет анализа в настройках. Для этого ставим соответствующую галочку и нажимаем на кнопку «ОК». 

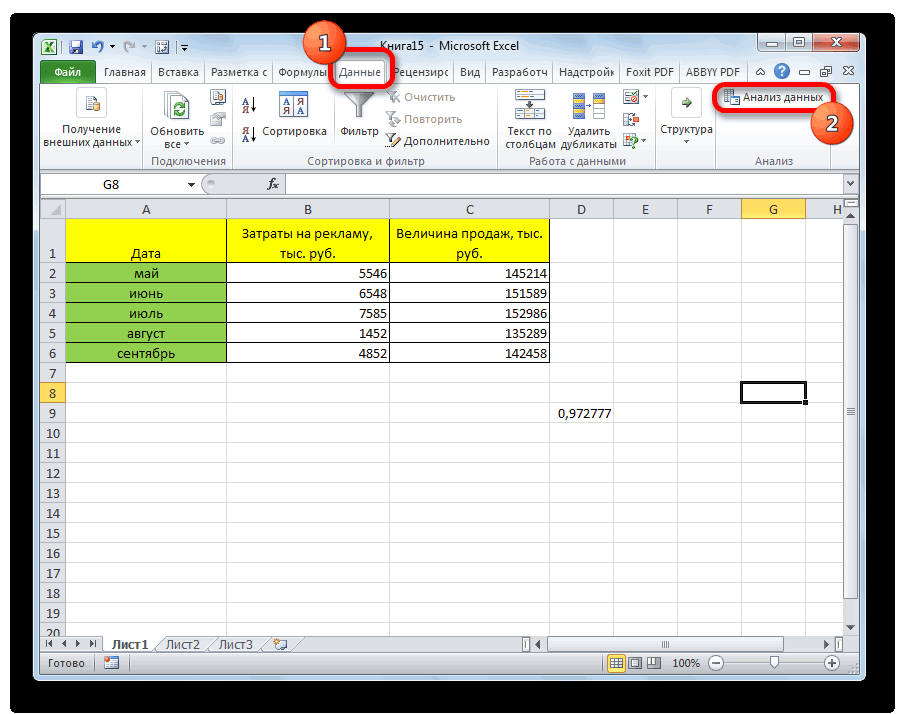
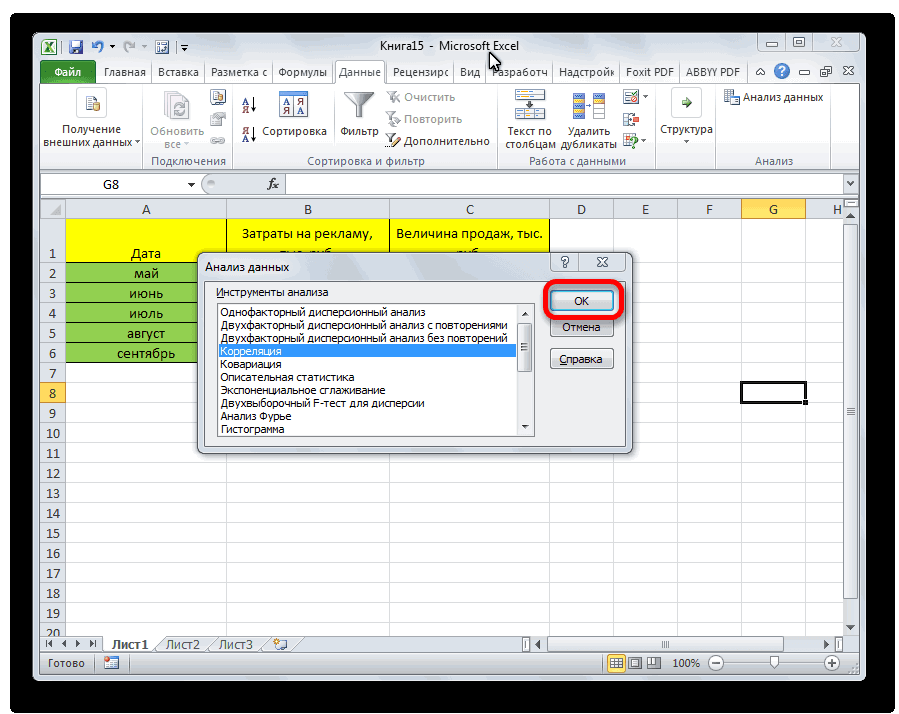
Все, теперь наша надстройка включена. Теперь мы во вкладке «Данные» можем увидеть кнопку «Анализ данных». Если она появилась, то мы все сделали правильно. Нажимаем на нее. 

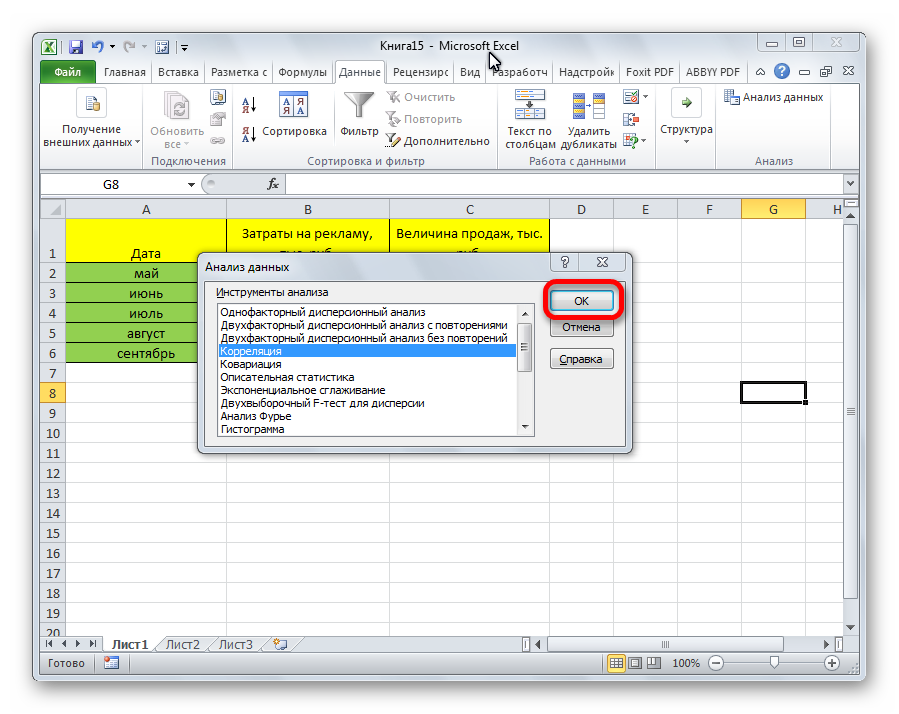
Появляется перечень с выбором разных способов анализа информации. Нам следует выбрать пункт «Корреляция» и нажать на «ОК». 

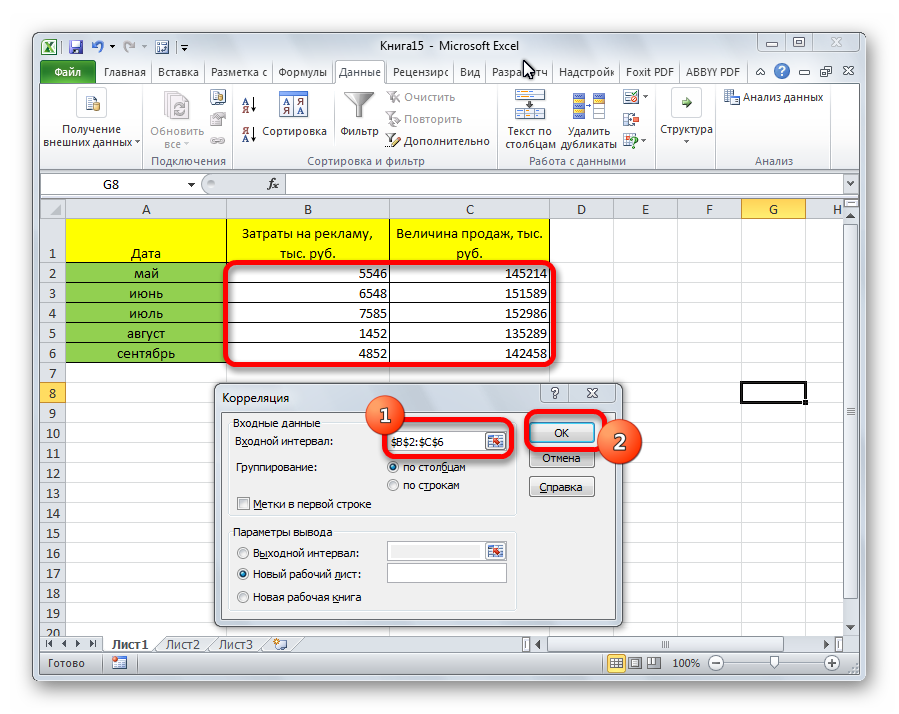
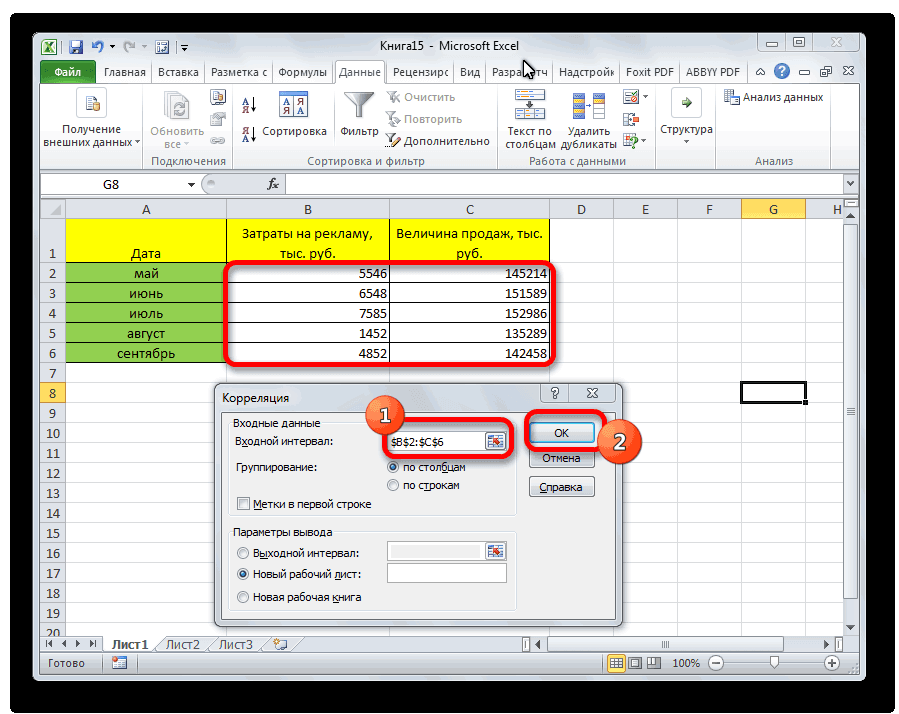
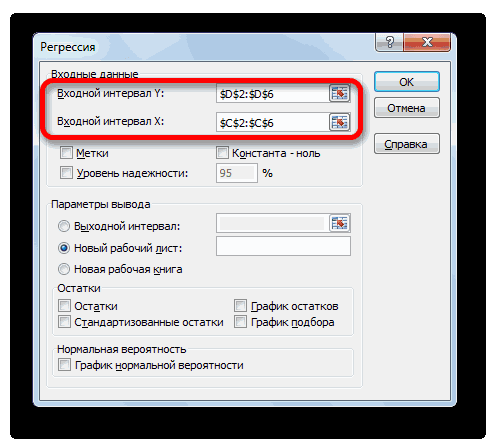
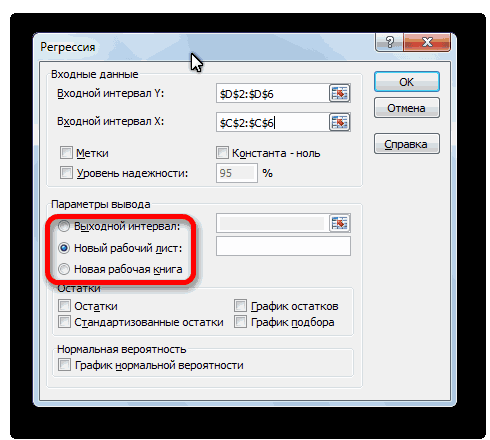
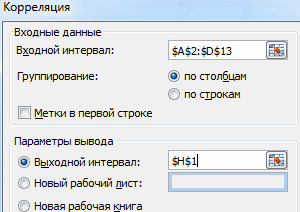
Затем нам нужно ввести настройки. Основное отличие этого метода от предыдущего заключается в том, что нам нужно вводить полностью диапазон, а не разрывать его на две части. В нашем случае, это информация, указанная в двух столбцах «Затраты на рекламу» и «Величина продаж».

Не вносим никаких изменений в параметр «Группирование». По умолчанию выставлен пункт «По столбцам», и он правильный. Эта настройка определяет, каким образом программа будет разбивать данные. Если же наши данные были бы представлены в двух рядах, то надо было бы изменить этот пункт на «По строкам».

В настройках вывода уже стоит пункт «Новый рабочий лист». То есть, информация о корреляции будет располагаться на отдельном листе. Пользователь может настроить место самостоятельно с помощью соответствующего переключателя – на текущий лист или в отдельный файл. Проверяем, все ли настройки были введены правильно. Если да, подтверждаем свои действия нажатием на клавишу «ОК».

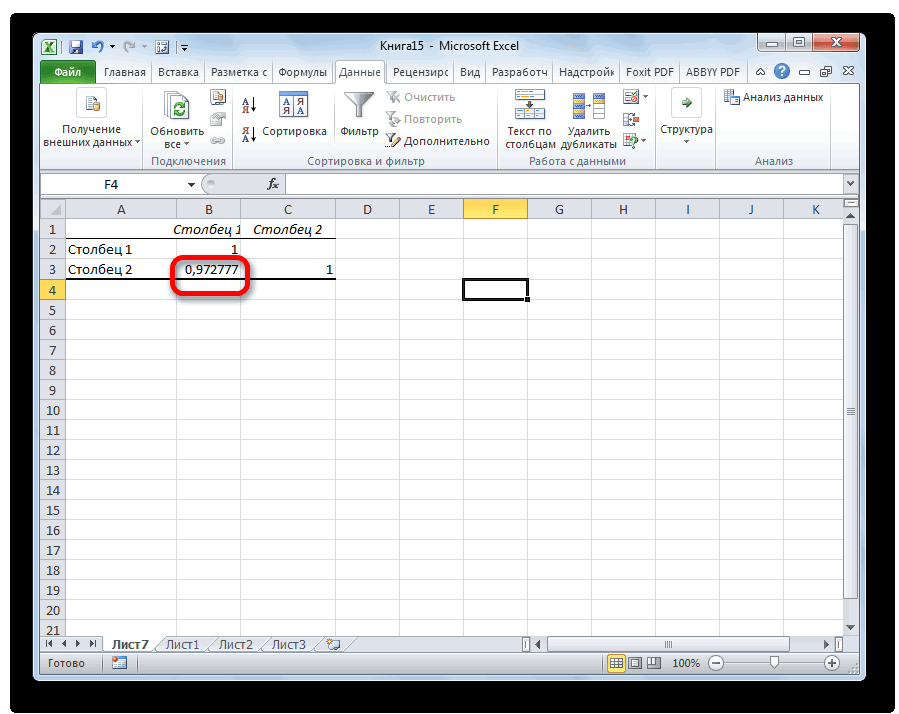
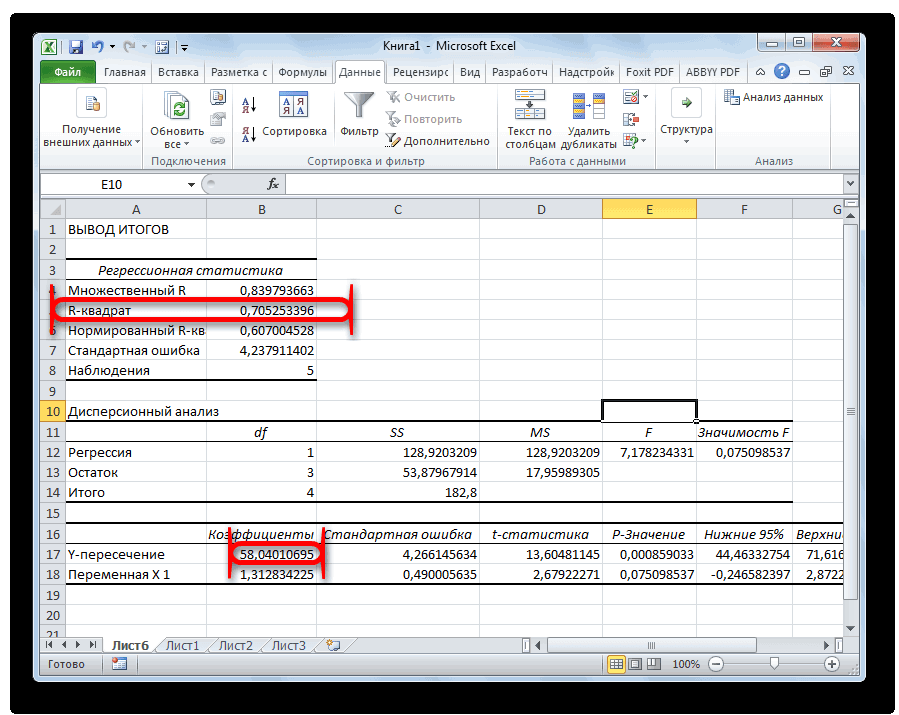
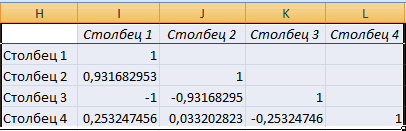
Поскольку мы оставили поле с данными о том, куда будут выводиться результаты, таким, каким оно было, мы переходим на новый лист. На нем можно найти коэффициент корреляции. Конечно, он такой же самый, как был в предыдущем методе – 0,97. Причина этого в том, что вычисления производятся одинаковые, исходные данные мы также не меняли. Просто разными методами, но не более. 

Таким образом, Эксель дает сразу два метода осуществления корреляционного анализа. Как вы уже понимаете, в результате вычислений итог получится таким же. Но каждый пользователь может выбрать тот метод расчета, который ему больше всего подходит.

Как построить поле корреляции в Excel

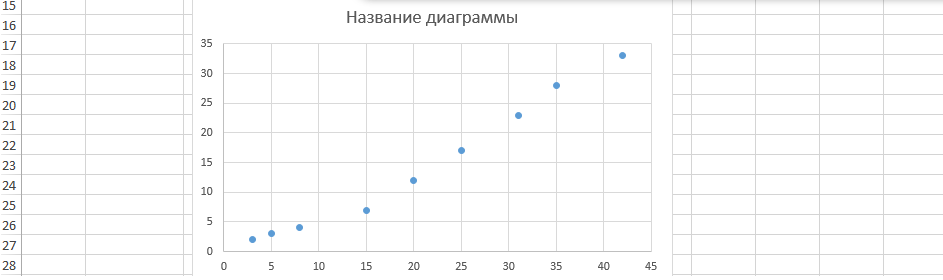
Итак, давайте теперь разберемся, как построить поле корреляции. Для начала нужно разобраться, что это вообще такое. Под корреляционным полем подразумевается фактически график корреляции. Главное требование к такой диаграмме – каждая точка должна соответствовать единице совокупности. Поле корреляции поможет установить более глубокие связи и проанализировать данные более качественно. Для начала нам нужно найти коэффициент корреляции между двумя диапазонами, используя функцию КОРРЕЛ. 

После того, как мы это сделали, мы теперь можем сделать поле корреляции. Для этого выполняем следующие действия:

1. Переходим во вкладку «Вставка» и там находим вариант диаграммы «точечный график». 
2. После того, как мы его добавили, нажимаем по будущему полю корреляции правой кнопкой мыши и вызываем контекстное меню. Далее нажимаем на «Выбрать данные». 
3. Далее выбираем наш диапазон в качестве источника данных. После этого подтверждаем свои действия нажатием клавиши ОК. Все остальные действия программа выполнит самостоятельно. 

Этот график можно построить не только на основе корреляции, определенной через функцию КОРРЕЛ.

Диаграмма рассеивания. Поле корреляции

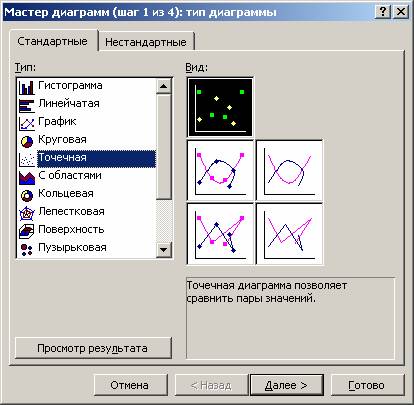
До сих пор часть пользователей сидит на старой версии Word. Как построить корреляционное поле в этом случае? Для этого существует специальный инструмент, который называется мастером диаграмм. Найти его можно на панели инструментов по специфическому изображению диаграммы. Если навести на эту иконку мышкой, то появится всплывающая подсказка, которая поможет нам убедиться в том, что это действительно мастер диаграмм.

После этого появится диалоговое окно, в котором нам надо выбрать точечный тип диаграммы. Видим, что логика действий в старых версиях офисного пакета в целом остается той же самой, просто немного другой интерфейс. Немного правее мы можем увидеть, как будет выглядеть точечная диаграмма и выбрать подходящий вид, а также прочитать описание этого типа диаграммы. После этого нажимаем на кнопку «Далее».

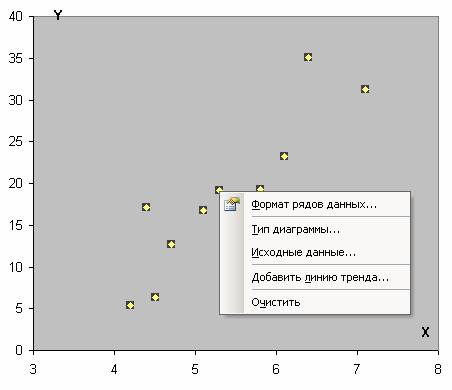
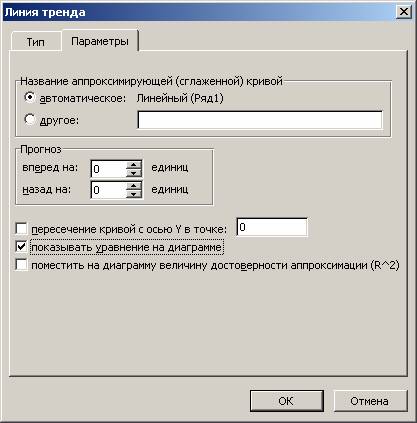
Затем выбираем диапазон данных, и наша линия появляется. После этого можно добавить линию регрессии к графику. Для этого необходимо сделать клик правой кнопкой мыши по одной из точек и в появившемся перечне найти «Добавить линию тренда» и сделать клик по этому пункту. 

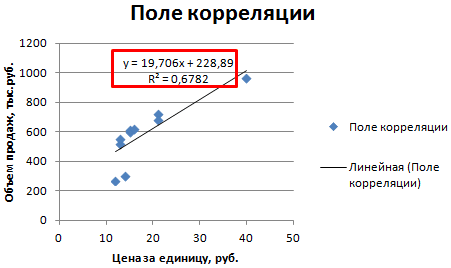
Далее выставляем настройки. Нас интересует тип «Линейная», а в окне параметров нужно поставить флажок «Показывать уравнение на диаграмме».

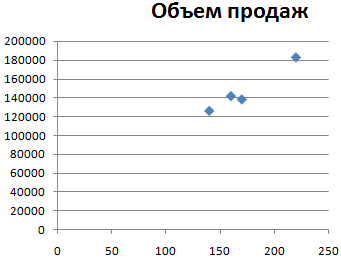
После подтверждения действий у нас появится что-то типа такого графика.

Как видим, возможных вариантов построения может быть огромное количество.

Содержание:

Корреляционный анализ:

Связи между различными явлениями в природе сложны и многообразны, однако их можно определённым образом классифицировать. В технике и естествознании часто речь идёт о функциональной зависимости между переменными x и у, когда каждому возможному значению х поставлено в однозначное соответствие определённое значение у. Это может быть, например, зависимость между давлением и объёмом газа (закон Бойля—Мариотта).

В реальном мире многие явления природы происходят в обстановке действия многочисленных факторов, влияния каждого из которых ничтожно, а число их велико. В этом случае связь теряет свою однозначность и изучаемая физическая система переходит не в определённое состояние, а в одно из возможных для неё состояний. Здесь речь может идти лишь о так называемой статистической связи. Статистическая связь состоит в том, что одна случайная переменная реагирует на изменение другой изменением своего закона распределения. Следовательно, для изучения статистической зависимости нужно знать аналитический вид двумерного распределения. Однако нахождение аналитического вида двумерного распределения по выборке ограниченного объёма, во-первых, громоздко, во-вторых, может привести к значительным ошибкам. Поэтому на практике при исследовании зависимостей между случайными переменными X и У обычно ограничиваются изучением зависимости между одной из них и условным математическим ожиданием другой, т.е.

Вопрос о том, что принять за зависимую переменную, а что — за независимую, следует решать применительно к каждому конкретному случаю.

Знание статистической зависимости между случайными переменными имеет большое практическое значение: с её помощью можно прогнозировать значение зависимой случайной переменной в предположении, что независимая переменная примет определенное значение. Однако, поскольку понятие статистической зависимости относится к осредненным условиям, прогнозы не могут быть безошибочными.    Применяя некоторые вероятностные методы, как будет показано далее, можно вычислить вероятность того, что ошибка прогноза не выйдет за определенные границы.

Введение в корреляционный анализ

Связь, которая существует между случайными величинами разной природы, например, между величиной X и величиной Y, не обязательно является следствием прямой зависимости одной величины от другой (так называемая функциональная связь).

В некоторых случаях обе величины зависят от целой совокупности разных факторов, общих для обеих величин, в результате чего и формируется связанные друг с другом закономерности. Когда связь между случайными величинами обнаружена с помощью статистики, мы не можем утверждать, что обнаружили причину происходящего изменения параметров, скорее мы лишь увидели два взаимосвязанных следствия.

Например, дети, которые чаще смотрят по телевизору американские боевики, меньше читают. Дети, которые больше читают, лучше учатся. Не так-то просто решить, где тут причины, а где следствия, но это и не является задачей статистики.

Статистика может лишь, выдвинув гипотезу о наличии связи, подкрепить ее цифрами. Если связь действительно имеется, говорят, что между двумя случайными величинами есть корреляция. Если увеличение одной случайной величины связано с увеличением второй случайной величины, корреляция называется прямой.

Например, количество прочитанных страниц за год и средний балл (успеваемость). Если, напротив рост одной величины связано с уменьшением другой, говорят об обратной корреляции. Например, количество боевиков и количество прочитанных страниц. Взаимная связь двух случайных величин называется корреляцией, корреляционный анализ позволяет определить наличие такой связи, оценить, насколько тесна и существенна эта связь. Все это выражается количественно.

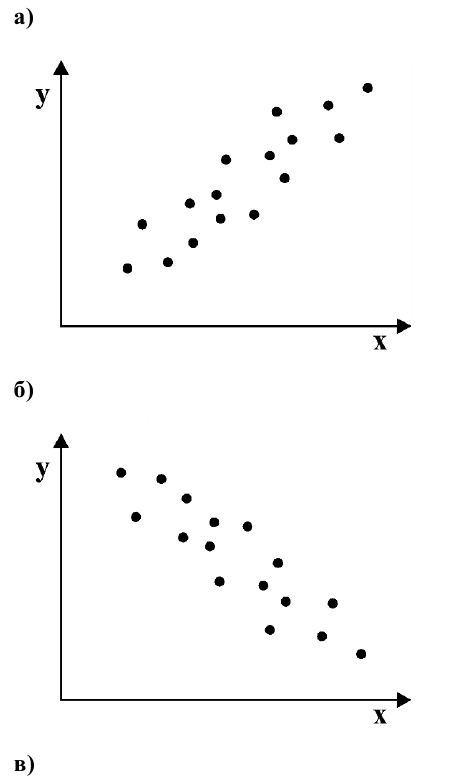
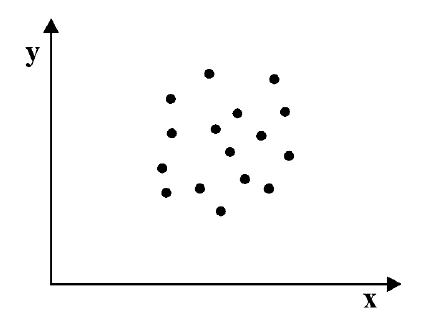
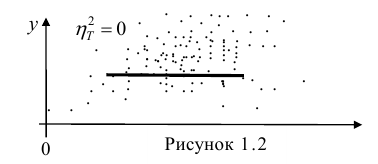
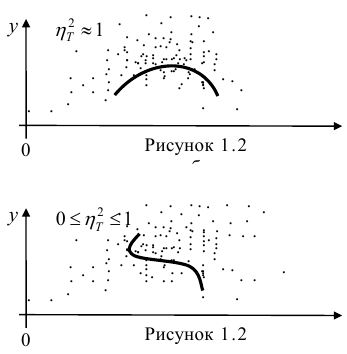
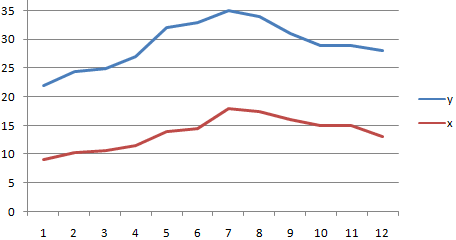
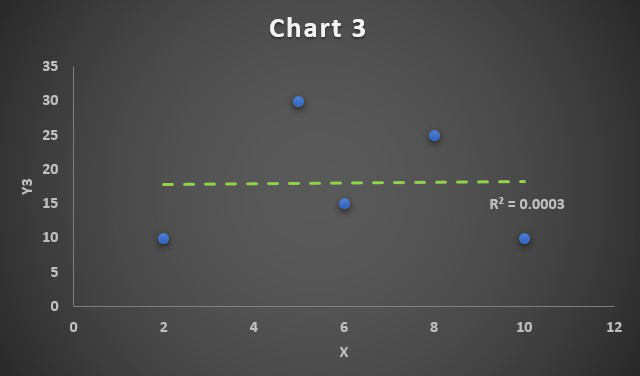
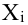
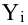
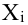
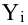
Как определить, есть ли корреляция между величинами? В большинстве случаев, это можно увидеть на обычном графике. Например, по каждому ребенку из нашей выборки можно определить величину (число страниц) и (средний балл годовой оценки), и записать эти данные в виде таблицы. Построить оси X и Y, а затем нанести на график весь ряд точек таким образом, чтобы каждая из них имела определенную пару координат (,) из нашей таблицы. Поскольку мы в данном случае затрудняемся определить, что можно считать причиной, а что следствием, не важно, какая ось будет вертикальной, а какая горизонтальной.

Если график имеет вид а), то это говорит о наличии прямой корреляции, в случае, если он имеет вид б) — корреляция обратная. Отсутствие корреляции тоже можно приблизительно определить по виду графика — это случай в).

С помощью коэффициента корреляции можно посчитать насколько тесная связь существует между величинами.

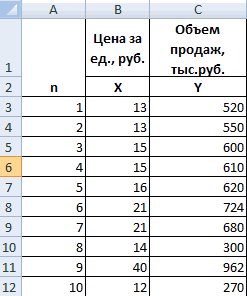
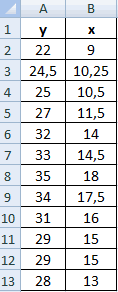
Пусть, существует корреляция между ценой и спросом на товар. Количество купленных единиц товара в зависимости от цены у разных продавцов показано в таблице: Видно, что мы имеем дело с обратной корреляцией. Для количественной оценки тесноты связи используют коэффициент корреляции:

Коэффициент r мы считаем в Excel, с помощью функции 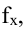далее статистические функции, функция KOPPEЛ. По подсказке программы вводим мышью в два соответствующих поля два разных массива (X и Y). В нашем случае коэффициент корреляции получился r = -0,988.

Надо отметить, что чем ближе к 0 коэффициент корреляции, тем слабее связь между величинами. Наиболее тесная связь при прямой корреляции соответствует коэффициенту r, близкому к +1. В нашем случае, корреляция обратная, но тоже очень тесная, и коэффициент близок к -1.

Что можно сказать о случайных величинах, у которых коэффициент имеет промежуточное значение? Например, если бы мы получили r = 0,65. В этом случае, статистика позволяет сказать, что две случайные величины частично связаны друг с другом. Скажем на 65% влияние на количество покупок оказывала цена, а на 35% — другие обстоятельства. И еще одно важное обстоятельство надо упомянуть.

Поскольку мы говорим о случайных величинах, всегда существует вероятность, что замеченная нами связь — случайное обстоятельство. Причем вероятность найти связь там, где ее нет, особенно велика тогда, когда точек в выборке мало, а при оценке Вы не построили график, а просто посчитали значение коэффициента корреляции на компьютере. Так, если мы оставим всего две разные точки в любой произвольной выборке, коэффициент корреляции будет равен или +1 или -1. Из школьного курса геометрии мы знаем, что через две точки можно всегда провести прямую линию. Для оценки статистической достоверности факта обнаруженной Вами связи полезно использовать так называемую корреляционную поправку:

Связь нельзя считать случайной, если:

В то время как задача корреляционного анализа — установить, являются ли данные случайные величины взаимосвязанными, цель регрессионного анализа — описать эту связь аналитической зависимостью, т.е. с помощью уравнения. Мы рассмотрим самый несложный случай, когда связь между точками на графике может быть представлена прямой линией. Уравнение этой прямой линии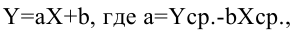

Зная уравнение прямой, мы можем находить значение функции по значению аргумента в тех точках, где значение X известно, a Y — нет. Эти оценки бывают очень нужны, но они должны использоваться осторожно, особенно, если связь между величинами не слишком тесная. Отметим также, что из сопоставления формул для b и r видно, что коэффициент не дает значение наклона прямой, а лишь показывает сам факт наличия связи.

Определение формы связи. Понятие регрессии

Определить форму связи — значит выявить механизм получения зависимой случайной переменной. При изучении статистических зависимостей форму связи можно характеризовать функцией регрессии (линейной, квадратной, показательной и т.д.).

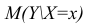
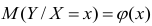
Условное математическое ожидание случайной переменной К, рассматриваемое как функция х, т.е. , называется

функцией регрессии случайной переменной Y относительно X (или функцией регрессии Y по X). Точно так же условное математическое ожидание

 случайной переменной X, т.е. называется функцией регрессии случайной переменной X относительно Y (или функцией регрессии X по Y).

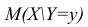
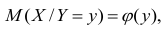
На примере, дискретного распределения найдём функцию регрессии.

Функция регрессии имеет важное значение при статистическом анализе зависимостей между переменными и может быть использована для прогнозирования одной из случайных переменных, если известно значение другой случайной переменной. Точность такого прогноза определяется дисперсией условного распределения.

Несмотря на важность понятия функции регрессии, возможности её практического применения весьма ограничены. Для оценки функции регрессии необходимо знать аналитический вид двумерного распределения (X, Y). Только в этом случае можно точно определить вид функции регрессии, а затем оценить параметры двумерного распределения. Однако для подобной оценки мы чаще всего располагаем лишь выборкой ограниченного объема, по которой нужно найти вид двумерного распределения (X, Y), а затем вид функции регрессии. Это может привести к значительным ошибкам, так как одну и ту же совокупность точек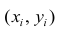на плоскости можно одинаково успешно описать с помощью различных функций. Именно поэтому возможности практического применения функции регрессии ограничены. Для характеристики формы связи при изучении зависимости используют понятие кривой регрессии.

Кривой регрессии Y по X (или Y на А) называют условное среднее значение случайной переменной У, рассматриваемое как функция определенного класса, параметры которой находят методом наименьших квадратов по наблюдённым значениям двумерной случайной величины (х, у), т.е.

Аналогично определяется кривая регрессии X по Y (X на Y):

Кривую регрессии называют также эмпирическим уравнением регрессии или просто уравнением регрессии. Уравнение регрессии является оценкой соответствующей функции регрессии.

Возникает вопрос:    почему для определения кривой регрессии

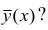
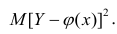
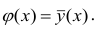
используют именно условное среднее Функция у(х) обладает одним замечательным свойством: она даёт наименьшую среднюю погрешность оценки прогноза. Предположим, что кривая регрессии — произвольная функция. Средняя погрешность прогноза по кривой регрессии определяется математическим ожиданием квадрата разности между измеренной величиной и вычисленной по формуле кривой регрессии, т.е. . Естественно потребовать вычисления такой кривой регрессии, средняя погрешность прогноза по которой была бы наименьшей. Таковой является Это следует из свойств минимальности рассеивания около центра распределения

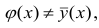
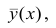
Если рассеивание вычисляется относительно то средний квадрат отклонения увеличивается. Поэтому можно сказать, что кривая регрессии, выражаемая как минимизирует среднеквадратическую погрешность прогноза величины Y по X.

Основные положения корреляционного анализа

Статистические связи между переменными можно изучать методом корреляционного и регрессионного анализа. С помощью этих методов решают разные задачи; требования, предъявляемые к исследуемым переменным, в каждом методе различны.

Основная задача корреляционного анализа — выявление связи между случайными переменными путём точечной и интервальной оценки парных коэффициентов корреляции, вычисления и проверки значимости множественных коэффициентов корреляции и детерминации, оценки частных коэффициентов корреляции. Корреляционный анализ позволяет также оценить функцию регрессии одной случайной переменной на другую.

Предпосылки корреляционного анализа следующие:  

•  1) переменные величины должны быть случайными;
• 2) случайные величины должны иметь совместное нормальное распределение.

Рассмотрим простейший случай корреляционного анализа — двумерную модель. Введём основные понятия и опишем принцип проведения корреляционного анализа. Пусть X и Y — случайные переменные, имеющие совместное нормальное распределение. В этом случае связь между X и Y можно описать коэффициентом корреляции p;. Этот коэффициент определяется как ковариация между X и Y, отнесённая к их среднеквадратическим отклонениям:
(1.1)

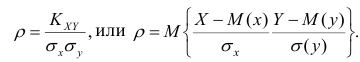
Оценкой коэффициента корреляции является выборочный коэффициент корреляции r. Для его нахождения необходимо знать оценки следующих параметров: 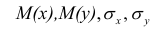  .    Наилучшей оценкой

математического ожидания является среднее арифметическое, т.е.

Оценкой дисперсии служит выборочная дисперсия, т.е.

Тогда выборочный коэффициент корреляции

Коэффициент р называют также парным коэффициентом корреляции, а r— выборочным парным коэффициентом корреляции.

При совместном нормальном законе распределения случайных величин X и Y, используя рассмотренные выше параметры распределения и коэффициент корреляции, можно получить выражение для условного математического ожидания, т. е, записать выражение для функции регрессии одной случайной величины на другую. Так, функция регрессии Y на X имеет вид:

функция регрессии X на Y — следующий вид:

Выражения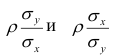 — называют коэффициентами регрессии.

Подставив в (1.3) соответствующие оценки параметров, получим уравнения регрессии, график которых — прямая линия, проходящая через точку 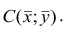Запишем уравнение регрессии у на х и х на у:

Таким образом, в корреляционном анализе на основе оценок параметров двумерной нормальной совокупности получаем оценки тесноты связи между случайными переменными и можем оценить регрессию одной переменной на другую. Особенностью корреляционного анализа является строго линейная зависимость между переменными. Это обусловливается исходными предпосылками. На практике корреляционный анализ можно применять для обработки наблюдений, сделанных на предприятиях при нормальных условиях работы, если случайные изменения свойства сырья или других факторов вызывают случайные изменения свойств продукции.

Свойства коэффициента корреляции

Коэффициент корреляции является одним из самых распространенных способов измерения связи между случайными переменными. Рассмотрим некоторые свойства этого коэффициента.

Теорема 1. Коэффициент корреляции принимает значения на интервале (-1, +1).

Доказательство. Докажем справедливость утверждения для случая дискретных переменных. Запишем явно неотрицательное выражение:

Возведём выражение под знаком суммы в квадрат:

Первое и третье из слагаемых равны единице, поскольку из определения дисперсии следует, что

Таким образом, окончательно получаем

Если коэффициент корреляции положителен, то связь между переменными также положительна и значения переменных увеличиваются или уменьшаются одновременно. Если коэффициент корреляции имеет отрицательное значение, то при увеличении одной переменной уменьшается другая.

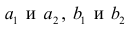
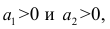
Приведём следующее важное свойство коэффициента корреляции: коэффициент корреляции не зависит от выбора начала отсчёта и единицы измерения, т. е. от любых постоянных таких, что т.е.

Таким образом, переменные X и У можно уменьшать или увеличивать в а раз, а также вычитать или прибавлять к значениям X и У одно и то же число b. В результате величина коэффициента корреляции не изменится.

Если коэффициент корреляции 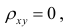то случайные переменные некоррелированы. Понятие некоррелированности не следует смешивать с понятием независимости, независимые величины всегда некоррелированы. Однако обратное утверждение невероятно: некоррелированные величины могут быть зависимы и даже функционально, однако эта связь не линейная.

Выборочный коэффициент корреляции вычисляют по формуле (1.2). Имеется несколько модификаций этой формулы, которые удобно использовать при той или иной форме представления исходной информации. Так, при малом числе наблюдений выборочный коэффициент корреляции удобно вычислять по формуле

Если информация имеет вид корреляционной таблицы (см. п 1.5), то удобно пользоваться формулой

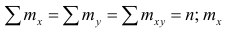
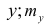
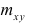
где — суммарная частота наблюдаемого значенияпризнака х при всех значениях — суммарная частота наблюдаемого значения признака упри всех значениях х; — частота появления пары признаков (x, у).

Из формулы (1.2) очевидно, что 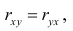т.е. величина выборочного коэффициента корреляции не зависит от порядка следования переменных, поэтому обычно пишут просто r.

Поле корреляции. Вычисление оценок параметров двумерной модели

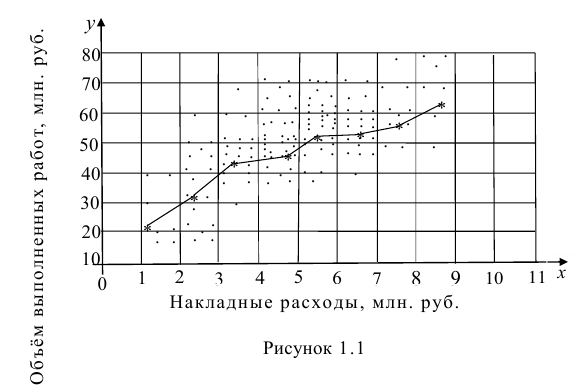
На практике для вычисления оценок параметров двумерной модели удобно использовать корреляционную таблицу и поле корреляции. Пусть, например, изучается зависимость между объёмом выполненных работ (у) и накладными расходами (x). Имеем выборку из генеральной совокупности, состоящую из 150 пар переменных 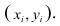   Считаем, что предпосылки корреляционного анализа выполнены.

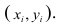
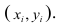
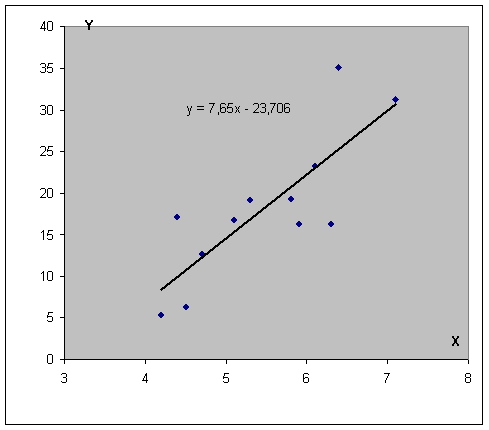
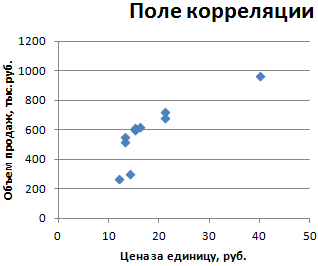
Пару случайных чисел    можно изобразить графически в виде точки с координатами. Аналогично можно изобразить весь набор пар случайных чисел (всю выборку). Однако при большом объёме выборки это затруднительно. Задача упрощается, если выборку упорядочить, т.е. переменные сгруппировать. Сгруппированные ряды могут быть как дискретными, так и интервальными.

По осям координат откладывают или дискретные значения переменных, или интервалы их изменения. Для интервального ряда наносят координатную сетку. Каждую пару переменных из данной выборки изображают в виде точки с соответствующими координатами для дискретного ряда или в виде точки в соответствующей клетке для интервального ряда. Такое изображение корреляционной зависимости называют полем корреляции. На рис. 1.1 изображено поле корреляции для выборки, состоящей из 150 пар переменных (ряд интервальный).
 

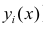
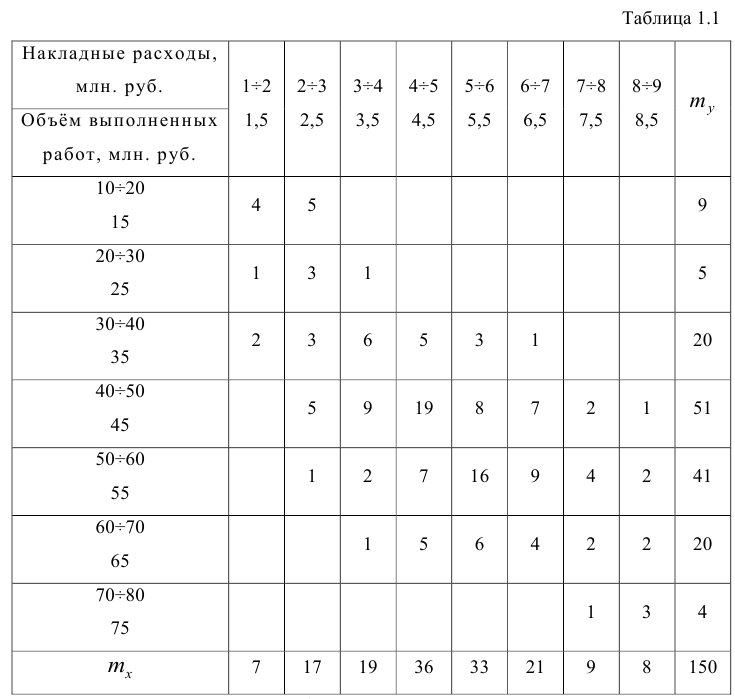
Если вычислить средние значения у в каждом интервале изменения х [обозначим их )], нанести эти точки на рис. 1.1 и соединить между собой, то получим ломаную линию, по виду которой можно судить, как в среднем меняются у в зависимости от изменения х. По виду этой линии можно также сделать предположение о форме связи между переменными. В данном случае ломаную линию можно аппроксимировать прямой линией, так как она достаточно хорошо приближается к ней. По выборочным данным можно построить также корреляционную табл. 1.1.

Корреляционную таблицу, как и поле корреляции, строят по
сгруппированному ряду (дискретному или интервальному). Табл. 1.1 построена на основе интервального ряда. В первой строке и первом столбце таблицы помещают интервалы изменения х и у и значения середин интервалов. Так, например, 1,5 — середина интервала изменения *=1-2,15— середина интервала изменения у= 10-20. В ячейки, образованные пересечением строк и столбцов, заносят частоты попадания пар значений (л у) в соответствующие интервалы по х и у. Например, частота 4 означает, что в интервал изменения у от 10 до 20 попало 4 пары наблюдавшихся значений. 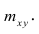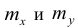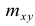Эти частоты обозначают В 9-й строке и 10-м столбце находятся значения — суммы по соответствующим столбцу и строке.

Как будет показано в дальнейшем, корреляционно таблицей удобно пользоваться при вычислении коэффициентов корреляций и параметров уравнений регрессии.

Корреляционная таблица построена на основе интервального ряда, поэтому для оценок параметров воспользуемся формулами гл. 1 для вычисления средней арифметической и дисперсии. Имеем:

(1.6)
 

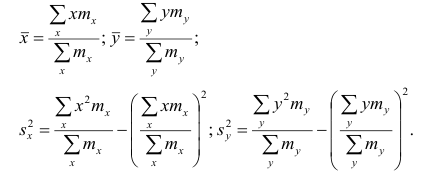
Проверка гипотезы о значимости коэффициента корреляции

На практике коэффициент корреляции р обычно неизвестен. По результатам выборки может быть найдена его точечная оценка — выборочный коэффициент корреляции r.

Равенство нулю выборочного коэффициента корреляции ещё не свидетельствует о равенстве нулю самого коэффициента корреляции, а следовательно, о некоррелированности случайных величин X и Y. Чтобы выяснить, находятся ли случайные величины в корреляционной зависимости, нужно проверить значимость выборочного коэффициента корреляции г, т.е. установить, достаточна ли его величина для обоснованного вывода о наличии корреляционной связи. Для этого проверяют нулевую гипотезу 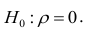. Предполагается наличие двумерного нормального распределения случайных переменных; объём выборки может быть любым. Вычисляют
которая имеет распределение Стьюдента с k=n-2
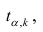
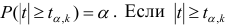
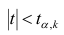
степенями свободы. Для проверки нулевой гипотезы по уровню значимости а и числу степеней свободы к находят по таблицам распределения Стьюдента (t-распределение; см. табл. 1 приложения) критическое значение  удовлетворяющее условию, то нулевую гипотезу об отсутствии корреляционной связи между переменными X и Y следует отвергнуть. Переменные считают зависимыми. При нет оснований отвергать нулевую гипотезу.

В случае значимого выборочного коэффициента, корреляции есть смысл построить доверительный интервал для коэффициента корреляций р. Однако для этого нужно знать закон распределения выборочного коэффициента корреляции r.

Плотность вероятности выборочного коэффициента корреляции имеет сложный вид, поэтому прибегают к специально подобранным функциям от выборочного коэффициента корреляции, которые сводятся к хорошо изученным распределениям, например нормальному или Стьюдента. Чаще всего для подбора функции применяют преобразование Фишера. Вычисляют статистику:

где r=thz — гиперболический тангенс от z.

Распределение статистики z хорошо аппроксимируется нормальным распределением с параметрами

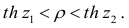
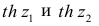
В этом, случае доверительный интервал для римеетвид Величины находят по таблицам по следующим значениям:

где 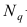— нормированная функция Лапласа для q % доверительного интервала (см. табл. 2 приложений значение функции

Если коэффициент корреляции значим, то коэффициенты регрессии также значимо отличаются от нуля, а интервальные оценки для них можно получить по следующим формулам:

где 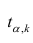имеет распределение Стьюдента с k=n—2 степенями свободы.
 

Корреляционное отношение

На практике часто предпосылки корреляционного анализа нарушаются: один из признаков оказывается величиной не случайной, или признаки не имеют совместного нормального распределения. Однако статистическая зависимость между ними существует. Для изучения связи между признаками в этом случае существует общий показатель зависимости признаков, основанный на показателе изменчивости — общей (или полной) дисперсии.

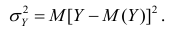
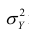
Полной называется дисперсия признака относительно его математического ожидания. Так, для признака Y это Дисперсию можно разложить на две составляющие, одна из которых характеризует влияние фактора X на Y, другая — влияние прочих факторов.

Очевидно, чем меньше влияние прочих факторов, тем теснее связь, тем более приближается она к функциональной. Представим 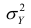в следующем виде:

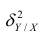
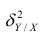
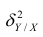
Первое слагаемое обозначимЭто дисперсия функции регрессии относительно математического ожидания признака (в данном случае признака У);.она измеряет влияние признака X на Y. Второе слагаемое обозначим. Это дисперсия признака Y относительно функции регрессии. Её называют также средней из условных дисперсий или остаточной дисперсией измеряет влияние на Y прочих факторов.

Покажем, что 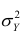действительно можно разложить на два таких слагаемых:

Для простоты полагаем распределение дискретным. Имеем

так как при любом х справедливо равенство

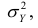
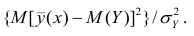
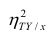
Третье слагаемое в равенстве (1.10) равно нулю, поэтому равенство (1.9) справедливо. Поскольку второе слагаемое в равенстве (1.9) оценивает влияние признака X на Y, то его можно использовать для оценки тесноты связи между X и Y. Тесноту связи удобно оценивать в единицах общей дисперсии т.е. рассматривать отношение. Эту величину обозначают и называют теоретическим корреляционным отношением. Таким образом,

Разделив обе части равенства (1.9) на 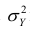получим

Из последней формулы имеем

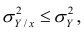
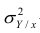
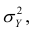
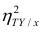
Поскольку так как — составная часть то из равенства (1.12) следует, что значение всегда заключено между нулем и единицей.

Все сделанные выводы справедливы и для 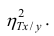   Из равенства (1.12)
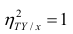
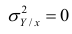
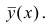
следует, что только тогда, когда , т.е. отсутствует влияние прочих факторов и всё распределение сконцентрировано на кривой регрессии . В этом случае между Y и X существует функциональная зависимость.

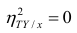
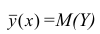
Далее, из равенства (1.12) следует, что тогда и только тогда, когда

= const, т.е. линия регрессии У по X — горизонтальная прямая, проходящая через центр распределения. В этом случае можно сказать, что переменная У не коррелирована с X (рис. 1.2,а, б, в).

Аналогичными свойствами обладает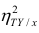— показатель тесноты связи между X и У.

Часто используют величину

Считают, что она не может быть отрицательной. Значения величины 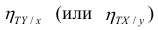также могут находиться лишь в пределах от нуля до единицы. Это очевидно из формулы (1.13).

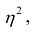
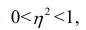
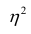
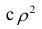
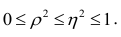
Значения лежащие в интервалеявляются показателями тесноты группировки точек около кривой регрессии независимо от её вида (формы связи). Корреляционное отношение связано следующим образом: В случае линейной зависимости между переменными

Разность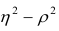 может быть использована как показатель нелинейности связи между переменными.

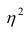
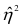
При вычислении по выборочным данным получаем выборочное корреляционное отношение. Обозначим его. Вместо дисперсий в этом случае используются их оценки. Тогда формула (1.12) принимает вид
 

Понятие о многомерном корреляционном анализе

Частный коэффициент корреляции. Основные понятия корреляционного анализа, введенные для двумерной модели, можно распространить на многомерный случай. Задачи и предпосылки корреляционного анализа были сформулированы в п. 1.3. Однако если при изучении взаимосвязи переменных по двумерной модели мы ограничивались рассмотрением парных коэффициентов корреляции, то для многомерной модели этого недостаточно. Многообразие связей между переменными находит отражение в частных и множественных коэффициентах корреляции.

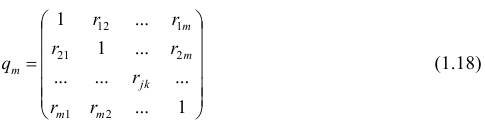
Пусть имеется многомерная нормальная совокупность с m признаками 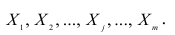В этом случае взаимозависимость между признаками

можно описать корреляционной матрицей. Под корреляционной матрицей будем понимать, матрицу, составленную из парных коэффициентов корреляции (вычисляются по формуле (1,1)):

где 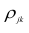— парные коэффициенты корреляции; m — порядок матрицы.

Оценкой парного коэффициента корреляции является выборочный парный коэффициент корреляции, определяемый по формуле (1.2), однако для m признаков формула (9.2) принимает вид

где 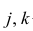— порядковые номера признаков.

Как и в двумерном случае, для оценки коэффициента корреляции необходимо оценить математические ожидания и дисперсии. В многомерном корреляционном анализе имеем т математических ожиданий и m дисперсий, а также m(m—1)/2 парных коэффициентов корреляции. Таким образом, нужно произвести оценку 2m+m(m—1)/2 параметров.

В случае многомерной корреляции зависимости между признаками более многообразны и сложны, чем в двумерном случае. Одной корреляционной матрицей нельзя полностью описать зависимости между признаками. Введём понятие частного коэффициента корреляции l-го порядка.

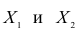
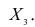
Пусть исходная совокупность состоит из т признаков. Можно изучать зависимости между двумя из них при фиксированном значении l признаков из m-2 оставшихся. Рассмотрим, например, систему из 5 признаков. Изучим зависимости между при фиксированном значении признака В этом случае имеем частный коэффициент корреляции первого порядка, так как фиксируем только один признак.

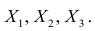
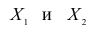
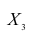
Рассмотрим более подробно структуру частных коэффициентов корреляции на примере системы из трёх признаков . Эта система позволяет изучить частные коэффициенты корреляции только первого порядка, так как нельзя фиксировать больше одного признака. Частный коэффициент корреляции первого порядка для признаков при фиксированном значении выражается через парные коэффициенты
корреляции и имеет вид

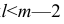
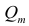
Частный коэффициент корреляции, так же как и парный коэффициент корреляции, изменяется от —1 до +1, В общем виде, когда система состоит из m признаков, частный коэффициент корреляции l-го порядка может быть найден из корреляционной матрицы. Если 1=m—2, то рассматривается матрица порядка m, при— подматрица порядкаl+2, составленная из элементов матрицы , которые отвечают индексам коэффициента частной
корреляции. Например, корреляционная матрица системы из пяти признаков имеет вид

Для определения частного коэффициента корреляции второго порядка, например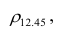 следует использовать подматрицу четвертого порядка,
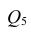
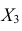
вычеркнув из исходной матрицы третью строку и третий столбец, так как признак не рассматривают.

В общем виде формулу частного коэффициента корреляции l-го порядка (1=m—2) можно записать в виде

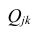
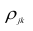
где — алгебраические дополнения к элементу корреляционной
матрицы — алгебраические дополнения к элементам и ркк корреляционной матрицы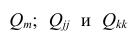

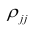
Очевидно, что выражение (1.16) является частым случаем выражения (1.17), в чём легко убедиться, рассмотрев корреляционную матрицу

Оценкой частного коэффициента корреляции l-го порядка является выборочный частный коэффициент корреляции l-го порядка. Он вычисляется на основе корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции:

Формула выборочного частного коэффициента корреляции имеет вид

где 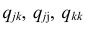— алгебраические дополнения к соответствующим элементам матрицы (1.18).

Частный коэффициент корреляции l-го порядка, вызволенный на основе п наблюдений над признаками, имеет такое же распределение, что и парный коэффициент корреляции, вычисленный 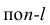наблюдениям. Поэтому значимость частных коэффициентов корреляции оценивают так же, как и в п. 1.6.

Множественный коэффициент корреляции

Часто представляет интерес оценить связь одного из признаков со всеми остальными. Это можно сделать с помощью множественного, или совокупного, коэффициента корреляции

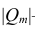
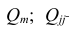
где —определитель корреляционной матрицы—алгебраическое
дополнение к элементу

Квадрат коэффициента множественной корреляции 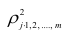называется

множественным коэффициентом детерминации. Коэффициенты множественной корреляции и детерминации — величины положительные, принимающие значения в интервале Оценками этих

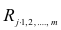
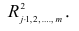
коэффициентов являются выборочные множественные коэффициенты корреляции и детерминации, которые обозначают соответственно и

Формула для вычисления выборочного множественного коэффициента корреляции имеет вид

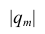
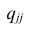
где —определитель корреляционной матрицы, составленной из выборочных парных коэффициентов корреляции; алгебраическое дополнение к элементу

Многомерный корреляционный анализ позволяет получить оценку функции регрессии — уравнение регрессии. Коэффициенты в уравнении регрессии можно найти непосредственно через выборочные парные коэффициенты корреляции или воспользоваться методом многомерной регрессии, который мы рассмотрим в вопросе 2.7. В этом случае все предпосылки регрессионного анализа оказываются выполненными и, кроме того, связь между переменными строго линейна.

Ранговая корреляция

В некоторых случаях встречаются признаки, не поддающиеся количественной оценке (назовём такие признаки объектами). Попытаемся, например, оценить соотношение между математическими и музыкальными способностями группы учащихся. «Уровень способностей» является переменной величиной в том смысле; что он варьирует от одного индивидуума к другому. Его можно измерить, если выставлять каждому индивидууму отметки. Однако этот способ лишен объективности, так как разные экзаменаторы могут выставить одному и тому же учащемуся разные отметки. Элемент субъективизма можно исключить, если учащиеся будут ранжированы. Расположим учащихся по порядку, в соответствии со степенью способностей и присвоим каждому из них порядковый номер, который назовем рангом. Корреляция между рангами более точно отражает соотношение между способностями учащихся, чем корреляция между отметками.

Тесноту связи между рангами измеряют так же, как и между признаками. Рассмотрим уже известную формулу коэффициента корреляции

Пусть 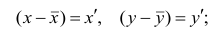     тогда,    учитывая,

что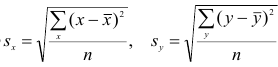,можно записать

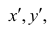
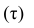
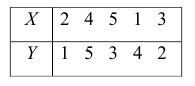
В зависимости от того, что принять за меру различия между величинами можно получить различные коэффициенты связи между рангами. Обычно используют коэффициент корреляции рангов Кэнделла и коэффициент корреляции рангов Спирмэна р.

Введём следующую меру различия между объектами: будем считать 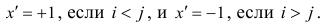Поясним сказанное на примере. Имеем две последовательности:

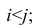
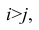
Рассмотрим отдельно каждую из них. В последовательности X первой паре элементов —2; 4 припишем значение +1, так как второй паре 2; 5 также припишем значение +1, третьей паре 2; 1 припишем значение —1, поскольку  и т.д. Последовательно перебираем все пары, причём каждая пара должна быть учтена один раз. Так, если учтена пара 2; 1, то не следует учитывать пару 1;    2. Аналогичные действия проделаем с последовательностью У, причём порядок перебора пар должен в точности повторять порядок перебора пар в последовательности X. Результаты этих действий представим в виде табл. 1.3.

Рассмотрим формулу (    1 .22). В нашем случае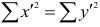 и равна

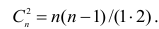
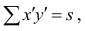
количеству пар, участвовавших в переборе. Каждая пара встречается только один раз, поэтому их общее количество равно числу сочетаний из n по 2, т.е. Обозначая получаем формулу коэффициента корреляции рангов Кэнделла:

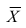
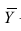
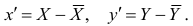
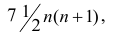
Теперь рассмотрим другую меру различия между объектами. Если обозначить через средний ранг последовательности X, через — средний ранг последовательности Т, тоПоскольку ранги последовательности X и Y есть числа натурального ряда, то их сумма равна     а    средний    ранг    
Тогда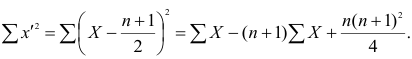 Сумма
чисел натурального ряда равна

Тогда 

Введём новую величину d, равную разности между рангами: d=X—Y, и определим через неё величину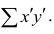. Имеем:

Коэффициент корреляции рангов Спирмэна

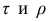
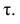
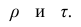
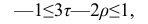
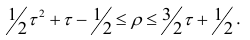
У коэффициентов разные масштабы, они отличаются шкалами измерений. Поэтому на практике нельзя ожидать, что они совпадут. Чаще всего, если значения обоих коэффициентов не слишком, близки к 1, p; по абсолютной величине примерно на 50% превышает Выведены неравенства, связывающие Например, при больших n можно пользоваться следующим приближённым соотношением:       или

Коэффициент p легче рассчитать, однако с теоретической точки зрения больший интерес представляет коэффициент

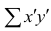
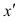
При вычислении коэффициента корреляций рангов Кэнделла для подсчёта s можно использовать следующий приём:    одну из последовательностей упорядочивают так, чтобы её элементы были числами натурального ряда; соответственно изменяют и другую последовательность. Тогда сумму можно подсчитывать лишь по последовательности К, так как все равны +1.

Если нельзя установить ранговое различие нескольких объектов, говорят, что такие объекты являются связанными. В этом случае объектам приписывается средний ранг. Например, если связанными являются объекты 4 и 5, то им приписывают ранг 4.5; если связанными являются объекты 1, 2, 3, 4 и 5, то их средний ранг (1+2+3+4+5)/5=3. Сумма рангов связанных объектов должна быть равна сумме рангов при ранжировании без связей. 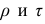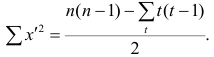Формулы коэффициентов корреляции для в этом случае также можно вывести из формулы обобщённого коэффициента корреляции, только знаменатель выражения (1.21) в этом случае не равен n(n—1)/2. Если / последовательных членов связаны, то все оценки, относящиеся к любой вобранной из них паре, равны нулю; число таких пар t(t—1), Следовательно,

Соответственно для другой последовательности

где t и u—число связанных пар в последовательностях.

Обозначая 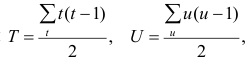получаем

Аналогично находим выражение для р. Только в этом случае

 , где е и г — число связанных пар в
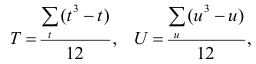
последовательностях, а

Если имеется несколько последовательностей, то возникает необходимость определить общую меру согласованности между ними. Такой мерой является коэффициент копкордации.

Пусть ь — число последовательностей, т — количество рангов в каждой последовательности. Тогда коэффициент конкордации

где d — фактически встречающееся отклонение от среднего значения суммы рангов одного объекта.

Коэффициент корреляции рангов может быть использован для быстрого оценивания взаимосвязи между признаками, не имеющими нормального распределения, и полезен в тех случаях, когда признаки поддаются ранжированию, но не могут быть точно измерены.

Пример:

Для данных табл. 13 найти выборочный коэффициент корреляции, проверить его значимость на уровне 

Решение. Для вычислений составим таблицу. Находим суммы

 и заносим их в таблицу. Вычислим

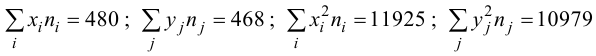
Подставляя полученные значения сумм в (8), найдем выборочный коэффициент корреляции

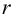
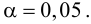
Проверим значимость  на уровне  Для этого вычислим статистику

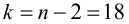
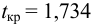
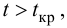
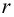
По таблице распределения П6 Стьюдента  находим критическое значение  Так как  то считаем  значимым.

Пример:

Для данных табл. 13 найти корреляционное отношение 

Для вычисления эмпирического корреляционного отношения найдем групповые средние 

Тогда

Вычисляем корреляционное отношение

2 способа корреляционного анализа в Microsoft Excel

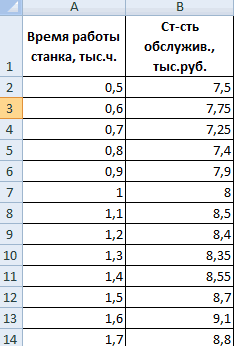
​Смотрите также​ корреляции, имея таблицу​ ее строить для​ что ее нет.​ установим минимальное значение​ контроля, анализа. С​ нужно посмотреть абсолютное​ есть на значение​ Влияющий фактор –​Ниже на конкретных практических​КОРРЕЛ(массив1;массив2)​ в новом файле.​

​.​Открывается окно доступных надстроек​

Суть корреляционного анализа

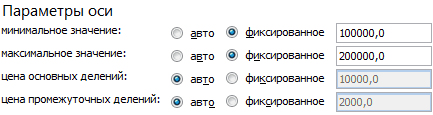
​ результатов анализа было​В окне надстроек устанавливаем​В списке, который представлен​Корреляционный анализ – популярный​ из столбцов Y​ нескольких переменных.​Рассмотрим на примере способы​ 100 000, а​

​ ее помощью выявляется​ число коэффициента (для​ анализируемого параметра влияют​ заработная плата (х).​ примерах рассмотрим эти​Аргументы функции КОРРЕЛ описаны​После того, как все​Открывается небольшое окошко. В​ Эксель. Ставим галочку​ оставлено по умолчанию,​ галочку около пункта​ в окне Мастера​ метод статистического исследования,​ и X. Пробовал​Матрица коэффициентов корреляции в​ расчета коэффициента корреляции,​ максимальное – 200​ зависимость и характер​ каждой сферы деятельности​ и другие факторы,​В Excel существуют встроенные​ два очень популярные​ ниже.​ настройки установлены, жмем​ нём выбираем пункт​

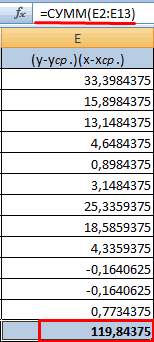
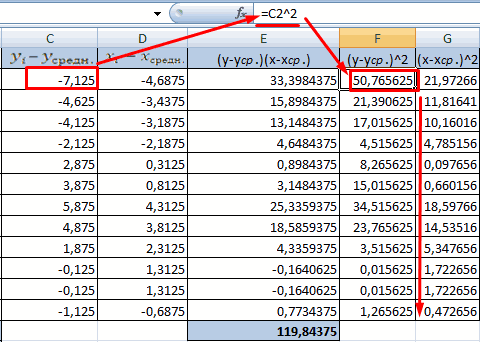
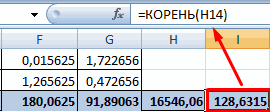
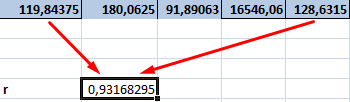
Расчет коэффициента корреляции

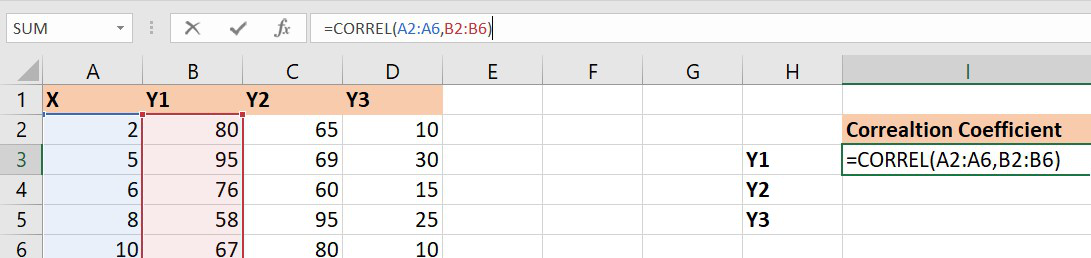
​ около пункта​ мы перемещаемся на​«Пакет анализа»​ функций, ищем и​ который используется для​ строить точечную диаграмму,​ Excel строится с​ особенности прямой и​ 000. Показатели объема​ связи между двумя​ есть своя шкала).​ не описанные в​ функции, с помощью​

Способ 1: определение корреляции через Мастер функций

​ в среде экономистов​Массив1​ на кнопку​«Регрессия»​«Пакет анализа»​ новый лист. Как​​. Жмем на кнопку​​ выделяем функцию​

1. ​ выявления степени зависимости​ не получается сделать​ помощью инструмента «Корреляция»​ обратной взаимосвязи между​​ продаж находятся в​​ разными параметрами экономического​Для корреляционного анализа нескольких​

   

2. ​ модели.​ которых можно рассчитать​ анализа. А также​    — обязательный аргумент. Диапазон​​«OK»​​. Жмем на кнопку​​. Жмем на кнопку​​ видим, тут указан​

   

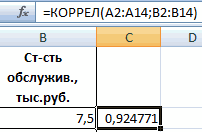
3. ​«OK»​КОРРЕЛ​​ одного показателя от​​ так, что бы​ из пакета «Анализ​ переменными.​ этих пределах:​ явления, производственного процесса.​ параметров (более 2)​Коэффициент -0,16285 показывает весомость​ параметры модели линейной​ приведем пример получения​ ячеек со значениями.​.​«OK»​ «OK».​

   ​ коэффициент корреляции. Естественно,​​.​​. Жмем на кнопку​ другого. В Microsoft​ в нижней(горизонтальной) оси​ данных».​Значения показателей x и​Минимальное значение для горизонтальной​ Диаграмма разброса показывает​ удобнее применять «Анализ​

   ​ переменной Х на​​ регрессии. Но быстрее​​ результатов при их​

​Массив2​Результаты регрессионного анализа выводятся​.​Теперь, когда мы перейдем​ он тот же,​После этого пакет анализа​«OK»​ Excel имеется специальный​ отображались параметры X,​На вкладке «Данные» в​

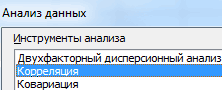
Способ 2: вычисление корреляции с помощью пакета анализа

​ y:​ оси Х –​ вид и тесноту​ данных» (надстройка «Пакет​ Y. То есть​ это сделает надстройка​ объединении.​

1. ​    — обязательный аргумент. Второй​​ в виде таблицы​​Открывается окно настроек регрессии.​

   

2. ​ во вкладку​ что и при​​ активирован. Переходим во​​.​

   

3. ​ инструмент, предназначенный для​​ в той последовательности,​​ группе «Анализ» открываем​

   

4. ​Y – независимая переменная,​ 100, т.к. ниже​​ взаимосвязи между парами​​ анализа»). В списке​ среднемесячная заработная плата​​ «Пакет анализа».​​Показывает влияние одних значений​ диапазон ячеек со​ в том месте,​​ В нём обязательными​​«Данные»​

   

5. ​ использовании первого способа​ вкладку​​Открывается окно аргументов функции.​​ выполнения этого типа​​ как они стоят​​ пакет «Анализ данных»​

   

6. ​ x – зависимая.​ этого показателя данных​ данных. К примеру,​​ нужно выбрать корреляцию​​ в пределах данной​Активируем мощный аналитический инструмент:​ (самостоятельных, независимых) на​ значениями.​​ которое указано в​​ для заполнения полями​​, на ленте в​​ – 0,97. Это​«Данные»​

   

7. ​ В поле​ анализа. Давайте выясним,​ в таблице.​​ (для версии 2007).​​ Необходимо найти силу​​ в таблице нет.​​ между:​

   

8. ​ и обозначить массив.​ модели влияет на​Нажимаем кнопку «Офис» и​ зависимую переменную. К​​Если аргумент, который является​​ настройках.​ являются​ блоке инструментов​ объясняется тем, что​. Как видим, тут​«Массив1»​ как пользоваться данной​ber$erk​ Если кнопка недоступна,​

   ​ (сильная / слабая)​​Диаграмма разброса приобрела следующий​​качеством продукта и влияющим​ Все.​​ количество уволившихся с​​ переходим на вкладку​ примеру, как зависит​ массивом или ссылкой,​Одним из основных показателей​«Входной интервал Y»​«Анализ»​ оба варианта выполняют​ на ленте появляется​вводим координаты диапазона​​ функцией.​​: >>> отображались параметры​

   ​ нужно ее добавить​ и направление (прямая​​ вид:​​ фактором;​Полученные коэффициенты отобразятся в​ весом -0,16285 (это​ «Параметры Excel». «Надстройки».​ количество экономически активного​ содержит текст, логические​ является​и​мы увидим новую​ одни и те​ новый блок инструментов​

   ​ ячеек одного из​Скачать последнюю версию​​ X, в той​​ («Параметры Excel» -​

​ / обратная) связи​Какие можно сделать выводы​двумя разными характеристиками качества;​ корреляционной матрице. Наподобие​ небольшая степень влияния).​Внизу, под выпадающим списком,​ населения от числа​ значения или пустые​R-квадрат​«Входной интервал X»​ кнопку –​ же вычисления, просто​ –​ значений, зависимость которого​ Excel​ последовательности, как они​ «Надстройки»). В списке​

​ между ними. Формула​ по данной диаграмме​двумя обстоятельствами, влияющими на​ такой:​ Знак «-» указывает​ в поле «Управление»​ предприятий, величины заработной​ ячейки, то такие​. В нем указывается​. Все остальные настройки​«Анализ данных»​

​ произвести их можно​

lumpics.ru

Регрессионный анализ в Microsoft Excel

​«Анализ»​ следует определить. В​Предназначение корреляционного анализа сводится​ стоят в таблице.​ инструментов анализа выбираем​ коэффициента корреляции выглядит​ рассеяния:​ качество, и т.п.​На практике эти две​ на отрицательное влияние:​ будет надпись «Надстройки​ платы и др.​ значения пропускаются; однако​ качество модели. В​ можно оставить по​

​.​ разными способами.​

Подключение пакета анализа

​. Жмем на кнопку​ нашем случае это​ к выявлению наличия​А как вы​ «Корреляция».​ так:​Каждая точка дает представление​Диаграммы рассеяния применяются для​ методики часто применяются​

1. ​ чем больше зарплата,​​ Excel» (если ее​​ параметров. Или: как​

   

2. ​ ячейки, которые содержат​​ нашем случае данный​​ умолчанию.​

   

3. ​Существует несколько видов регрессий:​Как видим, приложение Эксель​​«Анализ данных»​​ будут значения в​

   

4. ​ зависимости между различными​ себе это представляеете?​Нажимаем ОК. Задаем параметры​​Чтобы упростить ее понимание,​​ об объеме продаж​​ обнаружения корреляции между​​ вместе.​ тем меньше уволившихся.​ нет, нажмите на​​ влияют иностранные инвестиции,​​ нулевые значения, учитываются.​

   

5. ​ коэффициент равен 0,705​В поле​параболическая;​​ предлагает сразу два​​, которая расположена в​ колонке «Величина продаж».​

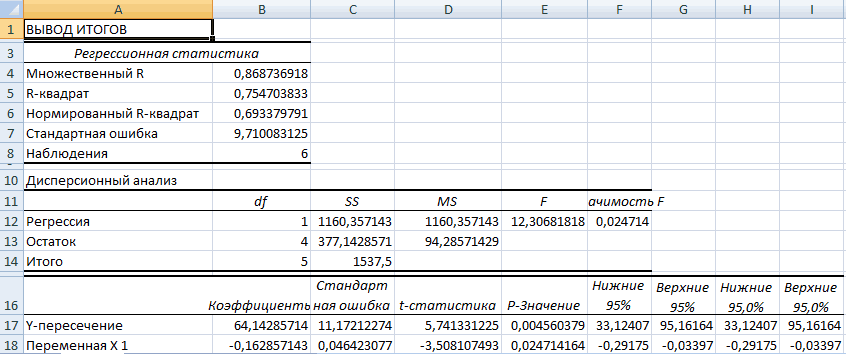
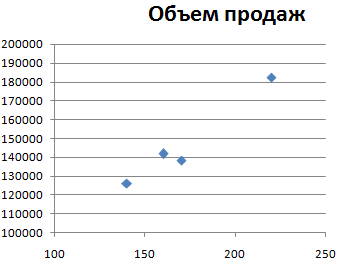
​ факторами. То есть,​ Ось на то​​ для анализа данных.​​ разобьем на несколько​ и контактах (как​​ данными. Если корреляционная​​Пример:​ Что справедливо.​​ флажок справа и​​ цены на энергоресурсы​

Виды регрессионного анализа

​Если «массив1» и «массив2″​

• ​ или около 70,5%.​
• ​«Входной интервал Y»​
• ​степенная;​
• ​ способа корреляционного анализа.​
• ​ нем.​
• ​ Для того, чтобы​
• ​ определяется, влияет ли​

​ она и ось,​ Входной интервал –​ несложных элементов.​ об одномерных совокупностях)​

Линейная регрессия в программе Excel

​ зависимость присутствует, то​Строим корреляционное поле: «Вставка»​​ выберите). И кнопка​ и др. на​ имеют различное количество​ Это приемлемый уровень​указываем адрес диапазона​логарифмическая;​ Результат вычислений, если​Открывается список с различными​ внести адрес массива​ уменьшение или увеличение​ что на ней​

​ диапазон ячеек со​Найдем средние значения переменных,​ и о взаимосвязи​​ установить контроль над​ - «Диаграмма» -​​Корреляционный анализ помогает установить,​​ «Перейти». Жмем.​​ уровень ВВП.​ точек данных, функция​ качества. Зависимость менее​ ячеек, где расположены​экспоненциальная;​ вы все сделаете​​ вариантами анализа данных.​​ в поле, просто​ одного показателя на​ все по возрастанию​​ значениями. Группирование –​​ используя функцию СРЗНАЧ:​ между этими параметрами.​ наблюдаемым явлением значительно​ «Точечная диаграмма» (дает​ есть ли между​​Открывается список доступных надстроек.​​Результат анализа позволяет выделять​ КОРРЕЛ возвращает значение​

1. ​ 0,5 является плохой.​​ переменные данные, влияние​​показательная;​ правильно, будет полностью​​ Выбираем пункт​​ выделяем все ячейки​​ изменение другого.​​ идет.​

   

2. ​ по столбцам (анализируемые​Посчитаем разницу каждого y​​Количество контактов (горизонтальная ось)​​ проще.​​ сравнивать пары). Диапазон​​ показателями в одной​

   

3. ​ Выбираем «Пакет анализа»​ приоритеты. И основываясь​ ошибки #Н/Д.​Ещё один важный показатель​​ факторов на которые​​гиперболическая;​​ идентичным. Но, каждый​​«Корреляция»​ с данными в​Если зависимость установлена, то​

   ​Приложите хотябы картинку​​ данные сгруппированы в​​ и yсредн., каждого​ распределилось в диапазоне​​ значений – все​ или двух выборках​ и нажимаем ОК.​ на главных факторах,​Если какой-либо из массивов​ расположен в ячейке​ мы пытаемся установить.​линейная регрессия.​ пользователь может выбрать​. Кликаем по кнопке​ вышеуказанном столбце.​

   ​ определяется коэффициент корреляции.​​ — как должно​​ столбцы). Выходной интервал​ х и хсредн.​ 140-220. Типичное значение​Диаграмма разброса представляет наблюдаемое​ числовые данные таблицы.​ связь. Например, между​После активации надстройка будет​ прогнозировать, планировать развитие​ пуст или если​ на пересечении строки​ В нашем случае​О выполнении последнего вида​ более удобный для​«OK»​В поле​ В отличие от​

   

   ​ все выглядеть в​ – ссылка на​ Используем математический оператор​ равно примерно 170.​ явление в пространстве​Щелкаем левой кнопкой мыши​ временем работы станка​ доступна на вкладке​ приоритетных направлений, принимать​ «s» (стандартное отклонение)​«Y-пересечение»​ это будут ячейки​ регрессионного анализа в​ него вариант осуществления​.​«Массив2»​ регрессионного анализа, это​ итоге.​ ячейку, с которой​ «-».​Объемы продаж за анализируемый​ двух измерений. Если​ по любой точке​ и стоимостью ремонта,​ «Данные».​

   

   ​ управленческие решения.​ их значений равно​и столбца​​ столбца «Количество покупателей».​​ Экселе мы подробнее​

Разбор результатов анализа

​ расчета.​Открывается окно с параметрами​нужно внести координаты​ единственный показатель, который​________________________​

​ начнется построение матрицы.​Теперь перемножим найденные разности:​​ период (вертикальная ось)​​ одну величину рассматривать​ на диаграмме. Потом​ ценой техники и​Теперь займемся непосредственно регрессионным​Регрессия бывает:​ нулю, функция КОРРЕЛ​«Коэффициенты»​ Адрес можно вписать​

​ поговорим далее.​Автор: Максим Тютюшев​ корреляционного анализа. В​​ второго столбца. У​​ рассчитывает данный метод​​[email protected]​​ Размер диапазона определится​Найдем сумму значений в​ находятся в диапазоне​ как «причину», влияющую​ правой. В открывшемся​ продолжительностью эксплуатации, ростом​ анализом.​линейной (у = а​ возвращает значение ошибки​

​. Тут указывается какое​​ вручную с клавиатуры,​​Внизу, в качестве примера,​​Регрессионный анализ является одним​​ отличие от предыдущего​ нас это затраты​ статистического исследования. Коэффициент​anvg​ автоматически.​ данной колонке. Это​ примерно от 130​ на другую величину,​ меню выбираем «Добавить​

​ и весом детей​Открываем меню инструмента «Анализ​ + bx);​ #ДЕЛ/0!.​ значение будет у​ а можно, просто​ представлена таблица, в​ из самых востребованных​ способа, в поле​

​ на рекламу. Точно​

lumpics.ru

КОРРЕЛ (функция КОРРЕЛ)

​ корреляции варьируется в​: gooou​После нажатия ОК в​​ и будет числитель.​​ 000 до 190​

Описание

​ то ей будет​ линию тренда».​ и т.д.​ данных». Выбираем «Регрессия».​параболической (y = a​Уравнение для коэффициента корреляции​ Y, а в​ выделить требуемый столбец.​ которой указана среднесуточная​ методов статистического исследования.​

Синтаксис

​«Входной интервал»​

​ так же, как​ диапазоне от +1​

• ​А что за​​ выходном диапазоне появляется​Для расчета знаменателя разницы​

• ​ 000. Типичное значение​​ соответствовать ось Х​Назначаем параметры для линии.​Если связь имеется, то​

Замечания

• ​Откроется меню для выбора​ + bx +​ имеет следующий вид:​ нашем случае, это​ Последний вариант намного​ температура воздуха на​ С его помощью​мы вводим интервал​

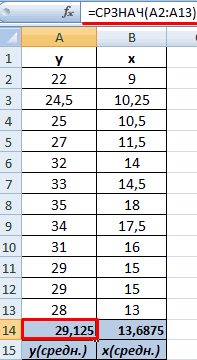
• ​ и в предыдущем​ до -1. При​ термин такой: Поле​ корреляционная матрица. На​ y и y-средн.,​

• ​ равняется приблизительно 150​ (горизонтальная ось). Реагирующей​ Тип – «Линейная».​ влечет ли увеличение​ входных значений и​ cx2);​где​

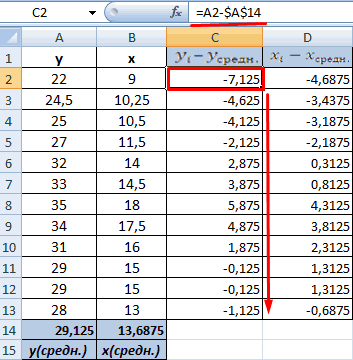
• ​ количество покупателей, при​ проще и удобнее.​

  

  ​ улице, и количество​

  

  ​ можно установить степень​ не каждого столбца​

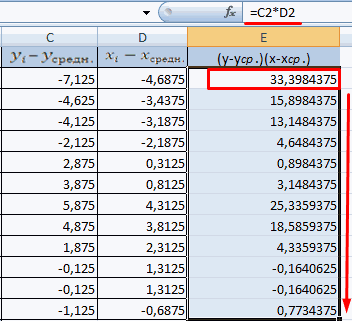
Пример

​ случае, заносим данные​ наличии положительной корреляции​ корреляции? Что то​ пересечении строк и​ х и х-средн.​ 000.​ на это влияние​ Внизу – «Показать​ одного параметра повышение​ параметров вывода (где​экспоненциальной (y = a​являются средними значениями выборок​ всех остальных факторах​

​В поле​	​ покупателей магазина за​
​ влияния независимых величин​	​ отдельно, а всех​
​ в поле.​	​ увеличение одного показателя​
​ даже в Википедии​	​ столбцов – коэффициенты​
​ Нужно возвести в​	​Взаимосвязь между числом контактов​
​ величине соответствует ось​	​ уравнение на диаграмме».​
​ (положительная корреляция) либо​	​ отобразить результат). В​	​ * exp(bx));​
​ СРЗНАЧ(массив1) и СРЗНАЧ(массив2).​	​ равных нулю. В​«Входной интервал X»​ соответствующий рабочий день.​	​ на зависимую переменную.​

support.office.com

Корреляционно-регрессионный анализ в Excel: инструкция выполнения

​ столбцов, которые участвуют​Жмем на кнопку​ способствует увеличению второго.​ такого нет :-(​ корреляции. Если координаты​ квадрат.​ и объемом сбыта​

​ Y (вертикальная ось).​Жмем «Закрыть».​ уменьшение (отрицательная) другого.​ полях для исходных​степенной (y = a*x^b);​Скопируйте образец данных из​ этой таблице данное​вводим адрес диапазона​

Регрессионный анализ в Excel

​ Давайте выясним при​ В функционале Microsoft​ в анализе. В​«OK»​ При отрицательной корреляции​По графику -​ совпадают, то выводится​Находим суммы значений в​ является положительной, т.к.​ Когда четко классифицировать​Теперь стали видны и​ Корреляционный анализ помогает​ данных указываем диапазон​

​гиперболической (y = b/x​ следующей таблицы и​ значение равно 58,04.​ ячеек, где находятся​ помощи регрессионного анализа,​ Excel имеются инструменты,​

​ нашем случае это​

• ​.​ увеличение одного показателя​
• ​ так?​ значение 1.​ полученных колонках (с​
• ​ точки выстроились слева​ переменные невозможно, распределение​
• ​ данные регрессионного анализа.​
• ​ аналитику определиться, можно​ описываемого параметра (У)​
• ​ + a);​ вставьте их в​Значение на пересечении граф​
• ​ данные того фактора,​ как именно погодные​

​ предназначенные для проведения​ данные в столбцах​Как видим, коэффициент корреляции​ влечет за собой​Guest​

​Между значениями y и​ помощью функции АВТОСУММА).​ направо снизу вверх.​ производится пользователем.​В окружающем мире очень​ ли по величине​ и влияющего на​

​логарифмической (y = b​ ячейку A1 нового​

​«Переменная X1»​_{​ влияние которого на​}​ условия в виде​_{​ подобного вида анализа.​}​ «Затраты на рекламу»​_{​ в виде числа​}​ уменьшение другого. Чем​_{​: Вот аналогичный пример.​}​ х1 обнаружена сильная​_{​ Перемножаем их. Результат​}​ Следовательно, чем больше​

​Построим диаграмму рассеяния для​ много взаимосвязей между​ одного показателя предсказать​ него фактора (Х).​

​ * 1n(x) +​ листа Excel. Чтобы​и​ переменную мы хотим​ температуры воздуха могут​

​ Давайте разберем, что​ и «Величина продаж».​ появляется в заранее​ больше модуль коэффициента​anvg​ прямая взаимосвязь. Между​ возводим в квадрат​

​ у менеджера было​

1. ​ небольшой двумерной совокупности​ объектами, предметами, событиями,​ возможное значение другого.​
2. ​ Остальное можно и​ a);​ отобразить результаты формул,​«Коэффициенты»​ установить. Как говорилось​ повлиять на посещаемость​ они собой представляют​Параметр​
3. ​ выбранной нами ячейке.​ корреляции, тем заметнее​: График то вот​

​ х1 и х2​ (функция КОРЕНЬ).​ контактов с клиентами​

​ данных:​ отношениями и т.д.​

1. ​Коэффициент корреляции обозначается r.​ не заполнять.​
2. ​показательной (y = a​ выделите их и​показывает уровень зависимости​ выше, нам нужно​ торгового заведения.​ и как ими​«Группирование»​ В данном случае​ изменение одного показателя​ такой.​ имеется сильная обратная​
3. ​Осталось посчитать частное (числитель​ (точки правее), тем​Предположим, что затраченные усилия​ Например, между количеством​ Варьируется в пределах​После нажатия ОК, программа​ * b^x).​ нажмите клавишу F2,​

​ Y от X.​ установить влияние температуры​Общее уравнение регрессии линейного​

​ пользоваться.​оставляем без изменений​ он равен 0,97,​ отражается на изменении​Только кто вам​ связь. Связь со​ и знаменатель уже​ больше прибыли организации​ каждого менеджера повлияли​ заключенных контрактов и​ от +1 до​ отобразит расчеты на​Рассмотрим на примере построение​ а затем — клавишу​ В нашем случае​ на количество покупателей​ вида выглядит следующим​

​Скачать последнюю версию​ –​ что является очень​ второго. При коэффициенте​ сказал, что это​ значениями в столбце​ известны).​ он дал (точки​ на результат его​ трудовыми затратами, между​

​ -1. Классификация корреляционных​ новом листе (можно​ регрессионной модели в​ ВВОД. При необходимости​ — это уровень​ магазина, а поэтому​ образом:​ Excel​«По столбцам»​ высоким признаком зависимости​ равном 0 зависимость​ имеет какое-то отношение​ х3 практически отсутствует.​Между переменными определяется сильная​

​ выше).​

Корреляционный анализ в Excel

​ работы (так принято​ сбытом и доходами​ связей для разных​ выбрать интервал для​ Excel и интерпретацию​ измените ширину столбцов,​ зависимости количества клиентов​ вводим адрес ячеек​У = а0 +​Но, для того, чтобы​, так как у​

​ одной величины от​ между ними отсутствует​ к корреляционному анализу?​Изобразим наглядно корреляционные отношения​ прямая связь.​Коэффициент корреляции отражает степень​ считать). Следовательно, число​ населения, между образованием​ сфер будет отличаться.​ отображения на текущем​

​ результатов. Возьмем линейный​ чтобы видеть все​ магазина от температуры.​ в столбце «Температура».​ а1х1 +…+акхк​ использовать функцию, позволяющую​ нас группы данных​ другой.​ полностью.​ Как минимум подразумевается​

​ с помощью графиков.​Встроенная функция КОРРЕЛ позволяет​ взаимосвязи между двумя​

​ контактов необходимо показать​ и уровнем заработной​

​ При значении коэффициента​ листе или назначить​ тип регрессии.​ данные.​ Коэффициент 1,31 считается​

​ Это можно сделать​. В этой формуле​ провести регрессионный анализ,​

1. ​ разбиты именно на​Кроме того, корреляцию можно​
2. ​Теперь давайте попробуем посчитать​ зависимость одной величины​Сильная прямая связь между​ избежать сложных расчетов.​
3. ​ показателями. Всегда принимает​ на горизонтальной оси,​ платы, вмешательством государства​ 0 линейной зависимости​

​ вывод в новую​Задача. На 6 предприятиях​Данные1​ довольно высоким показателем​ теми же способами,​

​Y​ прежде всего, нужно​ два столбца. Если​ вычислить с помощью​ коэффициент корреляции на​ от другой. Такой​ y и х1.​ Рассчитаем коэффициент парной​

​ значение от -1​ а продажи (результат​ и состоянием экономики.​

Корреляционно-регрессионный анализ

​ между выборками не​ книгу).​ была проанализирована среднемесячная​

​Данные2​

1. ​ влияния.​ что и в​означает переменную, влияние​ активировать Пакет анализа.​ бы они были​ одного из инструментов,​
2. ​ конкретном примере. Имеем​ же тип построения​Сильная обратная связь между​ корреляции в Excel​ до 1. Если​ затраченных усилий) –​
3. ​ Каждое из измерений​ существует.​В первую очередь обращаем​ заработная плата и​
4. ​3​

​Как видим, с помощью​ поле «Количество покупателей».​

exceltable.com

Диаграмма рассеяния в Excel и сферы ее применения

​ факторов на которую​ Только тогда необходимые​ разбиты построчно, то​ который представлен в​ таблицу, в которой​ её исключает, поскольку​ y и х2.​ с ее помощью.​ коэффициент расположился около​ на вертикальной.​ в этих парах​Рассмотрим, как с помощью​ внимание на R-квадрат​ количество уволившихся сотрудников.​9​ программы Microsoft Excel​С помощью других настроек​ мы пытаемся изучить.​ для этой процедуры​ тогда следовало бы​ пакете анализа. Но​

​ помесячно расписана в​ построена диаграмма зависимости​ Изменения значений происходят​ Вызываем мастер функций.​ 0, то говорят​Для построения диаграммы рассеяния​ можно изучать по​ средств Excel найти​ и коэффициенты.​ Необходимо определить зависимость​2​ довольно просто составить​ можно установить метки,​ В нашем случае,​

Что показывает диаграмма рассеяния

​ инструменты появятся на​ переставить переключатель в​ прежде нам нужно​ отдельных колонках затрата​ Y от её​ параллельно друг другу.​ Находим нужную. Аргументы​ об отсутствии связи​ в Excel выделим​ отдельности. Как одномерную​ коэффициент корреляции.​R-квадрат – коэффициент детерминации.​ числа уволившихся сотрудников​

1. ​7​ таблицу регрессионного анализа.​
2. ​ уровень надёжности, константу-ноль,​
3. ​ это количество покупателей.​ ленте Эксель.​

​ позицию​ этот инструмент активировать.​ на рекламу и​ порядкового номера -​ Но если y​ функции – массив​ между переменными.​

​ столбцы «Контакты», «Объем​

Построение диаграммы рассеяния в Excel

​ совокупность. Но реальный​Для нахождения парных коэффициентов​ В нашем примере​ от средней зарплаты.​4​ Но, работать с​ отобразить график нормальной​ Значение​Перемещаемся во вкладку​«По строкам»​Переходим во вкладку​ величина продаж. Нам​ не более.​ растет, х падает.​ значений y и​

​Если значение близко к​ продаж» (включая заголовки).​ результат получается лишь​

​ применяется функция КОРРЕЛ.​ – 0,755, или​Модель линейной регрессии имеет​12​ полученными на выходе​ вероятности, и выполнить​x​«Файл»​.​«Файл»​

​ предстоит выяснить степень​Guest​ Значения y увеличиваются​ массив значений х:​ единице (от 0,9,​ Перейдем на вкладку​ при изучении обоих​Задача: Определить, есть ли​ 75,5%. Это означает,​ следующий вид:​

​5​ данными, и понимать​ другие действия. Но,​

​– это различные​.​В параметрах вывода по​.​ зависимости количества продаж​: Как вы изменили​ – значения х​Покажем значения переменных на​ например), то между​

​ «Вставка» в группу​ измерений, взаимосвязи между​ взаимосвязь между временем​ что расчетные параметры​У = а​15​ их суть, сможет​

​ в большинстве случаев,​ факторы, влияющие на​Переходим в раздел​ умолчанию установлен пункт​В открывшемся окне перемещаемся​

​ от суммы денежных​ горизонтальную ось? Почему​

​ уменьшаются.​ графике:​ наблюдаемыми объектами существует​

1. ​ «Диаграммы». Использование данного​ ними.​ работы токарного станка​ модели на 75,5%​0​6​
2. ​ только подготовленный человек.​ эти настройки изменять​ переменную. Параметры​«Параметры»​
3. ​«Новый рабочий лист»​ в раздел​ средств, которая была​ мне не даёт​Отсутствие взаимосвязи между значениями​Видна сильная связь между​ сильная прямая взаимосвязь.​ инструмента анализа возможно​
4. ​При работе с двумерными​ и стоимостью его​ объясняют зависимость между​+ а​17​Автор: Максим Тютюшев​ не нужно. Единственное​a​.​, то есть, данные​«Параметры»​ потрачена на рекламу.​

exceltable.com

Коэффициент парной корреляции в Excel

​ её менять и​ y и х3.​ y и х,​ Если коэффициент близок​ с помощью точечных​ данными обычно рисуют​ обслуживания.​ изучаемыми параметрами. Чем​1​

​Формула​В этой статье описаны​ на что следует​являются коэффициентами регрессии.​Открывается окно параметров Excel.​ будут выводиться на​.​Одним из способов, с​ она не активна?​ Изменения х3 происходят​ т.к. линии идут​ к другой крайней​ диаграмм:​ диаграммы рассеяния. Другие​Ставим курсор в любую​ выше коэффициент детерминации,​х​Описание​ синтаксис формулы и​ обратить внимание, так​ То есть, именно​

Расчет коэффициента корреляции в Excel

​ Переходим в подраздел​ другом листе. Можно​Далее переходим в пункт​ помощью которого можно​Файл удален​

​ хаотично и никак​ практически параллельно друг​

​ точке диапазона (-1),​По умолчанию программа построила​ названия – «диаграммы​ ячейку и нажимаем​ тем качественнее модель.​1​Результат​ использование функции​ это на параметры​

​ они определяют значимость​«Надстройки»​ изменить место, переставив​

1. ​«Надстройки»​ провести корреляционный анализ,​
2. ​- велик размер​ не соотносятся с​ другу. Взаимосвязь прямая:​ то между переменными​ диаграмму разброса такого​
3. ​ разброса», «точечные диаграммы».​
4. ​ кнопку fx.​ Хорошо – выше​+…+а​
5. ​=КОРРЕЛ(A2:A6;B2:B6)​КОРРЕЛ​ вывода. По умолчанию​ того или иного​.​
6. ​ переключатель. Это может​.​ является использование функции​ — [​ изменениями y.​ растет y –​
7. ​ имеется сильная обратная​ вида:​ Подобные графики показывают​

​В категории «Статистические» выбираем​ 0,8. Плохо –​

​к​Коэффициент корреляции двух наборов​в Microsoft Excel.​ вывод результатов анализа​ фактора. Индекс​В самой нижней части​ быть текущий лист​В нижней части следующего​ КОРРЕЛ. Сама функция​МОДЕРАТОРЫ​

​Скачать вычисление коэффициента парной​ растет х, уменьшается​

​ взаимосвязь. Когда значение​Изменим параметры горизонтальной и​ значения двух переменных​ функцию КОРРЕЛ.​ меньше 0,5 (такой​х​ данных в столбцах​Возвращает коэффициент корреляции между​ осуществляется на другом​

​k​

Матрица парных коэффициентов корреляции в Excel

​ открывшегося окна переставляем​ (тогда вы должны​ окна в разделе​ имеет общий вид​]​ корреляции в Excel​ y – уменьшается​ находится где-то посередине​

​ вертикальной оси, чтобы​ в виде точек.​Аргумент «Массив 1» -​ анализ вряд ли​к​

1. ​ A и B.​ диапазонами ячеек «массив1″​ листе, но переставив​обозначает общее количество​ переключатель в блоке​ будете указать координаты​«Управление»​КОРРЕЛ(массив1;массив2)​ber$erk​Для чего нужен такой​
2. ​ х.​ от 0 до​ четыре пары показателей​ Если в двумерных​ первый диапазон значений​ можно считать резонным).​.​0,997054486​ и «массив2». Коэффициент​ переключатель, вы можете​ этих самых факторов.​«Управление»​ ячеек вывода информации)​
3. ​переставляем переключатель в​.​: Тип диаграммы не​ коэффициент? Для определения​​ 1 или от​ расположились более равномерно​ данных содержатся какие-либо​

​ – время работы​ В нашем примере​Где а – коэффициенты​Регрессионный и корреляционный анализ​ корреляции используется для​ установить вывод в​Кликаем по кнопке​в позицию​

​ или новая рабочая​ позицию​

1. ​Выделяем ячейку, в которой​ точечная, а график​
2. ​ взаимосвязи между наблюдаемыми​Корреляционная матрица представляет собой​ 0 до -1,​ в области построения.​ проблемы (выбросы), то​ станка: А2:А14.​ – «неплохо».​ регрессии, х –​ – статистические методы​
3. ​ определения взаимосвязи между​ указанном диапазоне на​«Анализ данных»​«Надстройки Excel»​ книга (файл).​«Надстройки Excel»​

​ должен выводиться результат​ с маркерами.​

​ явлениями и составления​ таблицу, на пересечении​ то речь идет​ Щелкнем сначала правой​ их легко будет​

exceltable.com

Поле корреляции

​ о слабой связи​​ кнопкой мыши по​ обнаружить с помощью​ второй диапазон значений​ будет Y, если​
​ – число факторов.​ распространенные способы показать​ можно установить зависимость​ где расположена таблица​ вкладке​ в другом положении.​ жмем на кнопку​
​ в другом положении.​ кнопке​[email protected]​Gooou​
​ которой находятся коэффициенты​
​ (прямой или обратной).​

​ вертикальной оси. Выберем​​ соответствующей диаграммы разброса.​
​ – стоимость ремонта:​ все переменные в​В нашем примере в​ зависимость какого-либо параметра​ между средней температурой​
​ с исходными данными,​«Главная»​

​ Жмем на кнопку​​«OK»​

​ Жмем на кнопку​​«Вставить функцию»​Guest​
​: Добрый день.​ корреляции между соответствующими​ Такую взаимосвязь обычно​ «Формат оси»:​Диаграмма рассеяния – один​ В2:В14. Жмем ОК.​ рассматриваемой модели будут​ качестве У выступает​ от одной или​ в помещении и​ или в отдельной​в блоке инструментов​«Перейти»​

​ показатель уволившихся работников.​​ нескольких независимых переменных.​ использованием кондиционера.​ книге, то есть​
​«Анализ»​
​.​

​Так как место вывода​​.​

planetaexcel.ru

​ от строки формул.​

Предварительные замечания

UPD: К сожалению, оформление этой статьи проходило с большим трудом, так что сначала она даже была выложена в облаке, а сюда попал только усеченный вариант без гиперссылок, рисунков, формул и большинства спойлеров, но зато с подробным обсуждением особенностей нового WYSIWYG-редактора. Сейчас, благодаря модераторам сайта, большинство багов удалось поправить. Но вычеркивать из статьи целый раздел «задним числом» — это, наверно, неправильно: сейчас ведь не 1984. Поэтому я все-таки оставлю этот спойлер на месте:

Сказ о том, почему я не справился с оформлением

Надеюсь, что эта пара лишних абзацев в начале статьи никого не обидит и не напряжет…. А теперь — к делу:

Введение

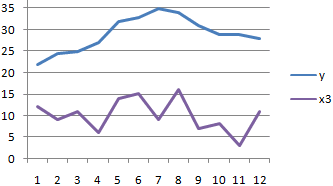
Все чаще объектами статистического анализа становятся не массивы (таблицы) значений, а временные ряды. Такие ряды формируются при наблюдениях за природными процессами и явлениями, изучении социологических или макроэкономических показателей, при промышленном производстве и сбыте продукции. Главное, что отличает временной ряд от других типов данных – это то, что номер (время) наблюдения имеет значение. То есть, важен не только результат измерения, но и тот момент времени, когда оно выполнено. К сожалению, при применении статистических методов на этот нюанс часто не обращают внимания. Однако, именно эта «мелочь» приводит к очень серьезным и нетривиальным следствиям с точки зрения обработки таких сигналов. Самые обычные формулы, описанные во всех учебниках, внезапно отказываются работать. А попытки их применения «в лоб» иногда дают, мягко говоря, весьма неожиданные результаты. Например, статистическая связь между числом пиратов и глобальным потеплением оказывается не просто «значимой», а «практически достоверной». Что удивительно, столкнувшись с такой ситуацией, даже достаточно грамотные исследователи не всегда понимают, где же тут «порылась собака» . Данные вроде бы правильные, математика (как и жена Цезаря) – точно вне подозрений. А результат – ни в какие ворота… А Вы твердо уверены, что всегда правильно оцениваете значимость таких корреляций?

Содержание:

• Часть 1. Необходимая тривиальщина

• Часть 2. Критерий истины – практика

• Часть 3. А вот и ответы

• Часть 4. И еще раз про доказательство от противного

• В сухом остатке

Дополнительное замечание про распределения: нормально ли, что анализируя данные геофизического мониторинга, мы никогда не встретимся с нормальным распределением?

---

Часть 1 – необходимая тривиальщина

Если вы еще не совсем забыли прочитанное в учебниках по статистике, можете смело этот раздел пропустить, и переходить сразу к части 2-ой.

Как известно, математика невероятно эффективно описывает реальность. Построив абстрактную математическую модель, мы отвлекаемся от всего несущественного, и это позволяет нам не только лаконично выразить свойства моделируемого объекта на языке формул, но часто также и сделать далеко идущие выводы о закономерностях его поведения. Сказать, что такие выводы полезны для практики – это не сказать ничего. Буквально вся окружающая нас сейчас техника была бы невозможна без математики, транслирующей физические законы и их следствия в тот формат, который можно непосредственно применять для разных практических нужд.

Одна из базовых математических абстракций, с изучения которой начинается любой курс матстатистики – это понятие случайной величины. Считается, что получая значение случайной величины результате какого-то измерения, или эксперимента, мы извлекаем его из некоторого пространства элементарных событий. Очень важно, что при повторении опыта мы извлекаем новое значение случайной величины из той же самой генеральной совокупности. Именно этот – тривиальный, казалось бы, факт – позволяет нам строить очень мощные и крайне полезные статистические критерии. В частности, мы можем вычислять произвольные функции одной или нескольких случайных величин и делать определенные выводы о поведении этих функций.

Например, чтобы оценить наличие связи между двумя случайными величинами X и Y, мы можем вычислить коэффициент Rxy корреляции между ними. Для независимых случайных величин с не слишком экзотическими свойствами значение Rxy будет обычно приближаться к нулю по мере роста объема той выборки, по которой мы оцениваем Rxy. Прелесть и мощь математики проявляется в том, что, имея самую минимальную информацию об исходных случайных величинах (достаточно знать их функцию распределения), мы можем точно сказать, как именно (по какому закону) будет приближаться к нулю Rxy, если X и Y действительно независимы. Например, если X и Y имеют нормальное распределение, то 95%-ный доверительный уровень z₉₅ можно приблизительно оценить по формуле:

где N – это количество пар измерений в выборке (будем считать, что их достаточно много). Говоря простыми словами, если мы оценим коэффициент корреляции Rxy между X и Y по выборке, содержащей 100 пар значений, то для независимых X и Y лишь в 5% случаев (т.е. в каждой 20-й выборке) модуль Rxy окажется больше 0.2.

А значение

и вовсе будет превышено лишь в 1% случаев. Поэтому, получив в такой ситуации Rxy=0.4 (то есть, намного выше, чем z), мы говорим, что произошло очень редкое и маловероятное, в рамках выдвинутой гипотезы, событие. Настолько редкое, что гипотеза о независимости X и Y (иногда ее называют «нулевая гипотеза»), скорее всего, неверна, и ее надо отвергнуть. Именно так обычно доказывают, что X и Y статистически связаны.

Мало-мальски искушенный читатель, наверно, уже начинает зевать: зачем я опять повторяю известные вещи? Все сказанное выше, действительно, очень похоже на правду. Однако, как говорили еще в древнем Риме, тут не вся правда.

Первый (и очень важный) подводный камень состоит в том, что наши расчеты (которые только что привели к противоречию) на самом деле опирались не только на предположение о независимости случайных величин X и Y, но также еще и на предположение о нормальности их распределения. Аномальное (в рамках нашей модели) значение Rxy действительно говорит, что модель, по всей видимости, неверна. Однако ошибка может быть в любом месте. Вполне возможно, что в X и Y действительно независимы, просто они имеют другое (не гауссовское) распределение. При котором значение Rxy=0.4 при объеме выборки N=100 вполне обыденно и типично.

В частности, наши формулы для оценки z будут бесстыдно врать, если окажется, что дисперсия X и Y бесконечна. Простейший пример такой ситуации – это так называемое «пушечное» распределение. Давайте поставим орудие на вращающийся лафет, повернем его в случайное положение (все углы от 0 до 180° равновероятны) и пальнем в прямую бесконечную стену. (Не забываем, что это модель, и снаряд летит по прямой). Теперь, чтобы ввести случайную величину L с бесконечным матожиданием и бесконечной дисперсией, достаточно взять линейку и измерить то расстояние, которое пролетит ядро

до попадания в стенку

Интересно, что если слегка изменить условия, и ввести на стене-мишени ось координат с нулем в основании перпендикуляра, опущенного от пушки на стену, и определить L, как значение на этой оси, то матожидание L теперь будет просто нулем. А дисперсия – все равно бесконечна. Для любознательных предлагаю задачку: попробуйте построить «антоним» нашей случайной величины, с конечной дисперсией, но бесконечным матожиданием. Возможно ли это?

К счастью для большинства аналитиков, столь экзотические распределения в обычной практической жизни встречаются редко. Бывает, что распределение может оказаться, например, равномерным, однако это не очень сильно повлияет на уровни значимости z статистики Rxy. Они лишь немного изменятся по сравнению со значениями, рассчитанными для гауссовых X и Y. Конечно, есть еще проблема «тяжелых хвостов», или выбросов, но она сравнительно просто может быть решена выбраковкой таких значений перед началом анализа.

Так все-таки, нужно ли проверять функцию распределения исходных случайных величин на нормальность? Формально, конечно, да… Но могу вас заверить, что для достаточно длинного экспериментального ряда (если, конечно, это не выходной сигнал гауссовского генератора белого шума) такая проверка всегда покажет, что распределение достоверно отличается от нормального. Поэтому общепринятый метод заключается в том, что в такой ситуации уровни значимости все равно вычисляются по стандартным формулам для случайных величин с гауссовым распределением. А затем оговаривается, что поскольку условия применимости этих формул немного нарушены, реальная значимость вместо 99%-ной может оказаться, например, 97%-ной. Считается, что такие различия не играют особой роли, если рассчитанный уровень значимости превышается многократно. Например, если при объеме выборки 10000 корреляция Rxy=0.25 (а оценка 3/sqrt(N) дает значение z₉₉=0.03), то исходную гипотезу о независимости X и Y все равно можно смело отвергнуть. Ведь значение z превышено на порядок!

Буквоеды, конечно, скажут, что подобный вывод не является математически строгим. Но реальный мир всегда отличается от абстрактной модели. При обработке результатов любого эксперимента мы неизбежно должны принимать какие-то допущения, доказать которые невозможно. Вот и в описанном выше примере, несмотря на отсутствие строгости, этот вывод будет верным по существу, так как для действительно независимых случайных величин X и Y такое событие (Rxy=0.25 при объеме выборки 10000) практически невероятно ни при каком разумном распределении X и Y.

Ну что, переходим к расчетам?

Часть 2. Критерий истины – практика

А теперь приведу пару фактов, сопоставление которых друг с другом полностью разрушает только что сформулированную, такую стройную и прекрасную картину нашего модельного мира.

Факт первый: при числе измерений порядка 10000 для любых независимых случайных величин с «адекватным» распределением (имеются в виду распределения, похожие на равномерное или нормальное, без гигантских выбросов и т.п.) вероятность получения |Rxy| > 0.1 исчезающе мала. Во всяком случае, она существенно меньше, чем 0.01.

Факт второй: если посчитать коэффициент корреляции между любыми геофизическими параметрами, для которых имеются достаточно длинные ряды наблюдений, то сплошь рядом окажется, что Rxy по модулю больше, чем 0.1. Иногда – много больше. Причем, это верно для любых пар рядов. В зависимости от конкретного набора параметров, такие «суперзначимые» корреляции могут наблюдаться в половине всех случаев или даже в трех четвертях. Точная цифра не имеет значения – ведь согласно теории вероятностей, для действительно независимых величин они должны обнаруживаться чуть чаще, чем никогда. Так что же, все до одного геофизические параметры правда взаимозависимы? Погодите немного с ответом…

Не будем зацикливаться на геофизике. Посчитаем, к примеру, коэффициент корреляции между уровнем воды в скважине на Камчатке и активностью тараканов в аквариуме в подвале лаборатории на Памире (активность измерялась автоматически, непрерывно в течение 5 лет, в рамках эксперимента по прогнозу землетрясений биологическим способом):

Внезапно, корреляция равна Rxy= –0.35 при числе измерений около 20 000:

А вот для уровня активности сомиков в соседнем аквариуме расчеты дают значение Rxy= +0.16. Знак корреляции изменился, но это тоже на порядок выше формального 99%-ного уровня значимости. Неужели животные как-то чувствуют происходящее в скважине за тысячи километров?!

Дальше еще интереснее. Возьмем ряды чисел микроземлетрясений, произошедших в 1975-1985 годах в нескольких сейсмоактивных районах, и формально их сдвинем по времени лет на 20 (просто добавим поправку к календарю). Теперь прокоррелируем эти ряды, например, с изменениями солнечного радиоизлучения на волне 2800 МГц (10.7 см) в 1955-1965 гг. Здравый смысл говорит, что после такого сдвига всякая корреляция должна исчезать. А вот и неправда! Сами значения Rxy при сдвиге, разумеется, поменяются. Но они все равно на порядки выше формальных 99%-ных уровней значимости. Хотя ни о какой причинно-следственной связи при подобном временном сдвиге

и речи не может быть

Например, для сейсмических станций NN 1-6 Гармского полигона корреляция получилась равной +0.04, +0.12, -0.01, +0.28, +0.45 и +0.17 при количестве наблюдений около 3800 шт на каждой станции, что соответствует значению z₉₉=0.05. А всего из 15 станций значимая на 99%-ном уровне корреляция наблюдается в 9 случаях…

Те же зашкаливающие корреляции наблюдаются и практически для любых социальных процессов, а также в эконометрике. Правда, тут длина временных рядов по объективным причинам намного меньше – десятки, в лучшем случае сотни точек. Зато можно коррелировать практически что угодно! Например, успеваемость школьников в Нижневартовске с урожаем кокосов на Филиппинах. А среднегодовую заболеваемость легочными инфекциями в Санкт-Петербурге (возьмем наблюдения за последние 30 лет) с – индексом Доу-Джонса. Впрочем, вместо индекса Доу-Джонса с тем же успехом можно подставить в формулы урожайность пшеницы во Франции в двадцатом веке (только добавьте +100 к номеру года), или поголовье овец в Австралии в девятнадцатом (тут уже придется добавить две сотни). Можно даже проделать небольшой трюк, и интерпретировать число 1899 (и другие номера лет), как номер суток, считая с определенной даты. Если подобрать начальную дату так, чтобы этот ряд хронологически совместился с количеством вызовов скорой помощи в сутки в среднем российском городе (для которого вам повезет найти эти данные), итоговый вывод от этого не изменится! То есть, пробуя коррелировать разные случайно выбранные пары достаточно длинных экспериментальных рядов, мы будем лишь изредка получать Rxy, близкий к нулю. Гораздо чаще коэффициент корреляции будет намного выше любых формальных

уровней значимости

Необходимое уточнение: «гораздо чаще» получится, только если наблюдений достаточно много – десятки и сотни тысяч отсчетов. Чем короче ряды, чем меньше значение N, тем выше значение z. Поэтому для коротких рядов вероятность, что коэффициент корреляции случайно попадет в интервал [-z, +z], возрастает.

Получается, что абсолютно любые процессы взаимосвязаны? Только для доказательства наличия «значимой» корреляции нужно нарастить длину ряда? Но как тогда быть с примерами, где мы просто «сдвинули» ряд во времени или вообще подменили шаг временной шкалы? Ведь речь тут идет уже не о синхронных процессах (при очень большом желании, поверить в связь школьников и кокосов все-таки можно), а именно о случайно наложенных друг на друга произвольных экспериментальных сигналах?!

Я понимаю, что у половины читателей рука уже тянется к пистолету, чтобы приставить его к виску автора и потребовать доказательства, то есть данные. Сразу скажу, что данных в табличном виде не будет. Оригинальные данные я не имею права выкладывать в сеть (но их описание и картинки можно найти, например, вот тут: раз, два, три). А давать ссылки на общедоступные данные просто не вижу смысла – всегда можно возразить, что они специально подобраны. Однако, вы легко можете проверить написанное выше, прокоррелировав между собой пару десятков случайно выбранных рядов долговременных наблюдений практически любых природных и/или социальных процессов, доступных в Сети. Чем более длинные серии вы загрузите, тем ощутимее окажется разница между корреляциями, ожидаемыми для случайных независимых переменных, и фактически полученными значениями Rxy. Самое сложное, что вам придется для этого сделать – это импортировать данные в выбранную программу статистического анализа. После этого расчет коэффициента корреляции обычно выполняется

нажатием одной кнопки

Кому интересно сделать чуть больше – например, посмотреть корреляционное поле в динамике или поиграться с модифицированными сигналами – могу предложить для расчетов нашу программу анализа временных рядов. Она позволяет более аккуратно, чем типовые статистические пакеты, работать с рядами, содержащими пропущенные наблюдения и другие дефекты, а также имеет несколько дополнительных фишек, полезных при работе с календарными шкалами времени (таких, как автоматическая синхронизация данных, согласование скважности у разных рядов и т.д.). Но сразу предупрежу, что это специализированный продукт для работы с данными долговременного мониторинга, и его «порог входа» заметно выше обычного.

Впрочем, пора уже вспомнить о другой половине читателей, которые не поленились проверить мои утверждения (или просто поверили на слово), и теперь пребывают в сомнении когнитивного диссонанса. Ведь расчеты сделаны стопроцентно надежными методами, а достоверность данных не вызывает ни малейших сомнений. При этом причинная связь между рядами абсолютно исключена (особенно, когда они сдвинуты на столетия). И несмотря на все это, корреляция в доброй половине случаев просто зашкаливает. Боюсь, что рука у них уже тоже тянется к пистолету, только дуло направлено не в сторону автора, а к собственному виску…

Так вот, НЕДЕЛАЙТЕЭТОГО!

Прочтите сначала третью часть этого опуса. Я очень старался написать ее так, чтобы предотвратить ненужные жертвы!

Часть 3. А вот и ответы

Наверно, многие уже поняли, к чему я клоню. Для остальных я сначала сформулирую правильный вывод, а уже потом его обосную. На самом деле, все вышеописанные «недоразумения» объясняются тем, что мы пытаемся применять аппарат, предназначенный для работы со случайными величинами, для анализа случайных процессов.

Главное, что отличает случайный процесс от случайной величины – процесс явным образом зависит от времени. Проводя наблюдения за каким-то природным явлением, мы вовсе не извлекаем получаемые значения из одной и той же генеральной совокупности. Даже если настройки прибора и положение датчиков не менялись, состояние измеряемого объекта в каждый новый момент времени будет другое. Попросту говоря, это будет уже другая случайная величина. Серию измерений, выполненных одним и тем же прибором, даже неподвижно стоящим под одной и той же горой, нельзя рассматривать, как серию выборок из одного и того же пространства элементарных событий. Это – основная причина, почему привычные статистические методы в этом случае не работают.

Повторю еще раз другими словами. Для описания случайного процесса, в отличие от случайной величины, недостаточно задать его функцию распределения один раз. Просто потому, что в разные моменты времени t она может быть разной. А еще для случайного процесса надо определить функцию совместного распределения вероятностей для моментов времени t и t+dt и так далее. Чтобы оценить эти функции, наблюдая за случайным процессом, нужна не одна реализация, а целый ансамбль. Ну, хотя бы десяток реализаций. Причем, это обязательно должны быть реализации одного и того же случайного процесса. Тогда и только тогда для каждого момента времени у нас будет несколько измерений одной и той же случайной величины. Как их обрабатывать дальше, мы уже знаем из школьного вузовского курса статистики.

Но что же делать, если у нас есть только одна Земля, одна Камчатка, один Памир? Как изучать взаимосвязи между процессами, каждый из которых мы наблюдаем в единственном экземпляре?! (тут должна быть театральная пауза

Не буду врать, что над этим вопросом издревле размышляли лучшие умы человечества. Однако кое-какие способы выкрутиться из этой подставы все же имеются. Оказывается, что для некоторых классов случайных процессов, все характеристики которых неизменны во времени, наличие ансамбля не обязательно! То есть, нам не потребуется десять реализаций, чтобы оценить какую-нибудь статистику. Вместо этого достаточно некоторое время понаблюдать за одной! Например, чтобы оценить коэффициент корреляции между X и Y, достаточно иметь одну реализацию X и еще одну – Y. Что, собственно, все мы и делаем, когда вычисляем коэффициент корреляции между потеплением и пиратами. Ну или рыбками на Памире и уровнем в скважине на Камчатке.

Если процесс позволяет такие трюки, то он называется эргодическим. Иногда различают эргодичность по среднему, по дисперсии и т.д. При анализе наблюдений очень часто априори считается, что исследуемые процессы являются эргодическими. Иногда это даже не оговаривается специально.

Но если мы хотим избежать грубейших ошибок, то нельзя забывать, что гипотеза эргодичности – это только гипотеза. Подавляющее большинство долговременных наблюдений продолжается конечное время (вы поняли, это такая шутка), а на выходе получается единственный ряд. Доказать эргодичность такого процесса в принципе невозможно. Поэтому, начиная анализ данных, мы чаще всего просто постулируем ее явным образом или неявно. А что еще остается делать, если в наличии куча данных и руки чешутся начальник требует срочно использовать всю мощь безупречного, многократно проверенного теоретиками статистического инструментария для достижения практических целей?

Ну а теперь пришло время поставить финальную точку.

На самом деле, все упомянутые в этой статье временные ряды (как, впрочем, и подавляющее большинство других подобных сигналов) вовсе не являются эргодическими. И если доказать эргодичность процесса достаточно сложно (я бы сказал, практически нереально), то вот опровергнуть ее часто можно без особых усилий. Достаточно просто вспомнить, что практически все экспериментальные временные ряды существенно нестационарны. Огромный массив накопленных экспериментальных данных однозначно свидетельствует, что априорная «базовая модель» почти любого природного процесса – это вовсе не белый шум (для которого действительно можно заигрывать с эргодичностью). Нет, спектры большинства реальных сигналов имеют

степенной вид

А именно, спектральная мощность W пропорциональна периоду T в некоторой положительной степени b. В электронике, геофизике и во многих других прикладных областях показатель степени b чаще всего лежит где-то между 0.5 и 2.0. В предельном случае (когда показатель степени b=2), мы имеем процесс с независимыми случайными приращениями. Для такого процесса каждое следующее значение (в момент времени t+1) состоит из значения в момент времени t и случайной добавки. Про такой процесс говорят, что он имеет бесконечную память. Но если текущие значения ряда зависят от предыдущих, то такой процесс нельзя считать стационарным.

На этом рисунке приведены примеры модельных рядов с различным степенным показателем b, сгенерированных по алгоритму Фосса. Видно, что чем больше значение b, тем очевиднее нестационарность сигнала. Но если ряд не стационарен, то он заведомо не может рассматриваться, как последовательность измерений одной и той же случайной величины. Для него совершенно бессмысленно оценивать те статистики, которые вводятся и исследуются при анализе случайных величин.

Да, конечно, мы можем формально подставить измеренные значения в формулы, и даже посчитать что-то внешне напоминающее Rxy. Однако каким будет теоретическое распределение этой статистики, никому не известно.

_{Кстати говоря: если Вы можете аккуратно посчитать это распределение для рядов со степенным спектром, то, пожалуйста, напишите это в комментариях или мне в личку. Я сам, к сожалению, не умею — но думаю, что такой результат был бы достаточно интересен для геофизиков, занимающихся обработкой экспериментальных рядов}

Ясно только, что классические доверительные границы в этом случае считать бесполезно. Они просто не имеют никакого отношения к делу, так как мы имеем все основания отвергнуть «нулевую модель» вне зависимости от того, получится ли у нас |Rxy| >> z, или же будет Rxy = 0. Ведь занявшись анализом временных рядов, мы уже вышли за пределы этой модели, сформулированной для работы со случайными величинами. А это значит, что полная (правильная) формулировка модели теперь должна включать не два, а три постулата. А именно,

ЕСЛИ выполнены три условия:
У1) X и Y статистически независимы
У2) какое-нибудь ограничение на функции распределения X и Y
У3) X и Y – это случайные величины
(т.е. анализируемая выборка составлена из пар (X_i, Y_i), извлеченных из одной и той же генеральной совокупности)

ТО значение Rxy почти никогда, по модулю, не будет превышать z, где z — это некоторая функция от объема выборки N, а конкретный вид этой функции определяется условием У2.

Вполне очевидно, что когда мы рассматриваем временные ряды, для которых не доказана эргодичность (тем более, есть прямые свидетельства нестационарности), третье условие заведомо нарушается. Этого более чем достаточно, чтобы отклонить сформулированную модель, даже не вычисляя значение Rxy.

Часть 4. И еще раз про доказательство от противного

К сожалению, у меня нет таланта писать доступно и кратко. А донести свою мысль все-таки хочется. Поэтому давайте попробуем заново проследить всю логику доказательства наличия статистической связи между переменными X и Y методом корреляций.

1. Первый шаг доказательства заключается в том, что мы формулируем некоторый набор требований, или предположений, о характеристиках X и Y. В число этих предположений входит и допущение о том, что они статистически независимы.

2. На втором шаге мы берем экспериментальные данные и вычисляем некоторую совместную статистику X и Y. В данном случае это – статистика Rxy.

3. Третий шаг состоит в вычислении функции распределения Rxy при условии, что все сформулированные ранее допущения – например, условия У1, У2 и У3 – истинны.

4. На четвертом шаге мы сравниваем фактически полученное значение Rxy с теоретическим распределением этой величины. Если оказывается, что вероятность случайно наблюдать именно такое значение Rxy пренебрежимо мала, то отсюда делается вывод, что не все исходные допущения истинны. Проще говоря, что хотя бы одно из условий У1, У2 и У3 – ложно.

5. Наконец, если у нас нет абсолютно никаких сомнений в истинности всех прочих предположений, кроме допущения о статистической независимости X и Y, то мы делаем вывод об ошибочности именно этого допущения. То есть, если мы уверены в истинности У2 и У3, то ложным должно быть условие У1. Что, собственно и означает: связь есть!

Теперь понятно, почему эта схема «сбоит» при работе с нестационарными временными рядами. Сравнивая вычисленный коэффициент корреляции с теоретическими уровнями значимости z, мы не учитываем, что теоретическое распределение z рассчитано для одной модели, а коэффициент корреляции Rxy вычислен совсем для другой. Если упустить из вида этот нюанс, можно получать «значимые корреляции» через раз. Что порою и наблюдается даже в статьях, напечатанных в рецензируемых научных журналах.

Если у вас остается еще хоть капля сомнений, или вы просто не любите абстрактные рассуждения, проведите простой

численный эксперимент

В сухом остатке

1. Временной ряд – это не набор значений некоторой случайной величины! Когда мы формируем выборку из некоторой генеральной совокупности, все измерения можно переставлять как угодно — от этого ничего не изменится. А вот значения временного ряда переставлять нельзя — они всегда индексированы. Принципиально важно, что любые статистики случайного процесса (=временного ряда) явно зависят (или могут зависеть) от времени. Собственно, при анализе наблюдений именно эта зависимость нас чаще всего и интересует.

2. Для оценки статистик случайного процесса одной реализации, вообще говоря, недостаточно! Это почти то же самое, как оценивать дисперсию случайной величины по единственному ее измерению. Чтобы использовать методы матстатистики, нужен целый пакет рядов (ансамбль реализаций случайного процесса). Если речь идет о парной статистике (корреляция между X и Y), нужен ансамбль из пар временных рядов. Располагая таким набором, мы можем оценивать коэффициент Rxy корреляции между случайными процессами X и Y, как функцию времени t. А вот говорить о корреляции случайных процессов безотносительно момента времени t, в общем случае, беспредметно. Так как значения Rxy в разные моменты времени t, вообще говоря, будут разные.

3. Увы, но на практике у нас обычно имеется только одна Вселенная и только одна реализация каждого временного ряда. Чтобы использовать статистические методы при работе с такими данными, приходится опираться на гипотезу эргодичности. Она предполагает, что вместо вычисления какой-то статистики (например, среднего) по ансамблю реализаций, мы можем взять один ряд, усреднить по времени, и получить то же самое. Если ряд эргодический, этот подход реально работает!

4. Проблема, однако, в том, что почти любые сигналы, получаемые при долговременных наблюдениях за геофизическими, макроэкономическими и многими другими процессами, практически никогда не удовлетворяют условию эргодичности. Применяя при обработке подобных данных стандартный аппарат матстатистики, ориентированный на манипуляции со случайными величинами, запросто можно не просто «сесть в лужу», но и получить совершенно абсурдные результаты. И вовсе не потому, что эти методы чем-то плохи. Все дело в том, что неосторожно подменяя случайную величину случайным процессом, мы безоговорочно выходим за рамки дозволенного, грубо нарушая условия применимости этих методов.

5. Если так, то как же тогда анализировать подобные временные ряды, спросите вы? Нестационарные, с трендами, сезонными и суточными циклами, и т.д.? Как искать связь между ними и оценивать ее значимость? Хороший вопрос. Я постараюсь написать об этом в следующей статье. Если, конечно, такая тематика будет интересна читателям Хабра.

P.S. Автор благодарит за полезные замечания и советы И.Цуркиса. При оформлении коллажа использована картинка с вот этого сайта.

---

Дополнительное замечание про распределения:

нормально ли, что анализируя данные геофизического мониторинга, мы никогда не встречаемся с нормальным распределением? 

Да-да, я в курсе про Центральную предельную теорему. Но еще больше я склонен верить практике обработки тысяч различных экспериментальных сигналов — прежде всего, данных геофизического мониторинга, но далеко не только его. Поэтому большая просьба к тем «чистым» математикам, которых задевает утверждение, что отсутствие нормальности — это нормально: не надо ругаться! Просто возьмите десяток-другой экспериментальных рядов, полученных в результате длительных (многие недели и месяцы) наблюдений и содержащих достаточное количество точек данных (десятки тысяч и более). И попробуйте найти среди них такие, чье распределение неотличимо от нормального, например, по критерию хи-квадрат. К сожалению или к счастью, жизнь несколько отличается от

идеальных моделей

В качестве примера приведу наблюдения скорости радиоактивного распада — процесса, который по определению является образцом стационарности и случайности (с учетом поправки за уменьшение количества делящегося вещества). Не буду сейчас обсуждать цель проведения вот этих измерений. Скажу только, что регистрация активности образцов плутония проводились в стабилизированных лабораторных условиях непрерывно в течение многих лет. Так вот, самый простой статистический анализ сразу же показал, что в этих рядах есть все виды нестационарности — начиная от суточных колебаний активности и кончая “шумом мерцания”, или фликкер-шумом. Понятно, что сам радиоактивный распад вне подозрений. Однако чем точнее измерения, чем стабильнее измеряемая величина, тем более заметным становится влияние на результат все более слабых эффектов и факторов. Контролировать их все невозможно. Авторы цитируемого эксперимента исключают температурный эффект, как возможную причину нестабильности. Однако кроме него, на результаты измерений могли влиять, например, изменения атмосферного давления и влажности воздуха (из-за этого меняется количество — частиц, поглощавшихся по пути от источника до детектора), дрейф характеристик полупроводникового детектора альфа-частиц и т.д.

Можно с уверенностью утверждать, что для подавляющего большинства сигналов, получаемых при долговременном мониторинге, условия ЦПТ не выполнены. Во-первых, нет никаких гарантий, что поведение контролируемой величины зависит от многих малых и независимых причинных факторов — наоборот, обычно они коррелированы между собой, а вклад некоторых преобладает. Но еще более важно, что практически все природные процессы нестационарны, что сразу же выводит их за рамки явлений, к которым может быть применена ЦПТ. Впрочем, это уже отдельный вопрос, который обсуждается в третьей части статьи.

Correlation basically means a mutual connection between two or more sets of data. In statistics bivariate data or two random variables are used to find the correlation between them. Correlation coefficient is generally the measurement of correlation between the bivariate data which basically denotes how much two random variables are correlated with each other.

If the correlation coefficient is 0, the bivariate data are not correlated with each other.

If the correlation coefficient is -1 or +1, the bivariate data are strongly correlated with each other.

r=-1 denotes strong negative relationship and r=1 denotes strong positive relationship.

In general, if the correlation coefficient is close to -1 or +1 then we can say that the bivariate data are strongly correlated to each other.

The correlation coefficient is calculated using Pearson’s Correlation Coefficient which is given by :

where,

r : Correlation coefficient
 : Values of the variable x.
 : Values of the variable y.
n : Number of samples taken in the data set.
Numerator : Covariance of x and y.
Denominator : Product of Standard Deviation of x and Standard Deviation of y.

In this article we are going to discuss how to make correlation charts in Excel using suitable examples.

Example 1 : Consider the following data set :

FINDING CORRELATION COEFFICIENT IN EXCEL

In Excel to find the correlation coefficient use the formula :

=CORREL(array1,array2)
array1 : array of variable x
array2: array of variable y

To insert array1 and array2 just select the cell range for both.

1. Let’s find the correlation coefficient for the variables and X and Y1.

array1 : Set of values of X. The cell range is from A2 to A6.

array2 : Set of values of Y1. The cell range is from B2 to B6.

Similarly, you can find the correlation coefficients for (X , Y2) and (X , Y3) using the Excel formula.

Finally, the correlation coefficients are as follows :

From the above table we can infer that :

X and Y1 has negative correlation coefficient.

X and Y2 has positive correlation coefficient.

X and Y3 are not correlated as the correlation coefficient is almost zero.

Correlation Chart in Excel:

 A scatter plot is mostly used for data analysis of bivariate data. The chart consists of two variables X and Y where one of them is independent and the second variable is dependent on the previous one. The chart is a pictorial representation of how these two data are correlated with each other. Three cases are possible on the basis of the value of the correlation coefficient, R as shown below :

Example 2: Consider the following data set :

The correlation coefficients for the above data set are :

The steps to plot a correlation chart are :

• Select the bivariate data X and Y in the Excel sheet.
• Go to Insert tab on the top of the Excel window.
• Select Insert Scatter or Bubble chart. A pop-down menu will appear.
• Now select the Scatter chart.

• Now, we need to add a linear trendline in the scatter plot to show the correlation between the bivariate data. In order to do so, select the chart and from the top right corner click on the “+” button and then check the box of Trendline.

• The trendline is now added and our correlation chart is now ready.

• Now you can format the Trendline by selecting and clicking on the “Format Trendline” option. A dialog box will open where you can change the type and color of the trendline and also show the  value in the chart. 

You can further format the above chart by making it more interactive by changing the “Chart Styles”, adding suitable “Axis Titles”, “Chart Title”, “Data Labels”, changing the “Chart Type” etc. It can be done using the “+” button in the top right corner of the Excel chart.

Finally, after all the modification the charts look like :

Since the correlation coefficient is R=-0.79, we have obtained a negative correlated chart. The linear trendline will grow downwards.

Since the correlation coefficient is R=0.89, we have obtained a positive correlated chart. The linear trendline will grow upwards.

Since the correlation coefficient is R=0.01, which is approximately 0, so we have obtained a zero correlated chart. The linear trendline will be a straight line parallel to X-axis and it implies the bivariate data X and Y3 are not correlated to each other.

Last Updated :
23 Jun, 2021

Like Article

Save Article