Учебник
Геометрия, 9 класс
Теорема косинусов
Теорема косинусов
Если в треугольнике даны две стороны и угол между ними, то такой треугольник один, единственный. Т.е. любой другой треугольник с такими данными будет в точности равен ему, по 2-му признаку равенства треугольников. Ну, раз единственный и неповторимый, то его третья сторона должна быть однозначно определяема.
_____________________________________________________________________________________
Теорема косинусов Квадрат стороны треугольника равен сумме квадратов двух
других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
$AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos ACB$
_____________________________________________________________________________________
Факты:
- Теорема косинусов позволяет найти косинус любого угла по трем известным сторонам, а значит, и сам угол.
- Если из трех сторон и одного угла известны три величины, то четвертое неизвестное можно всегда вычислить.
- Теорема косинусов дает возможность вычислять медианы треугольника, применяя теорему к малым треугольникам.
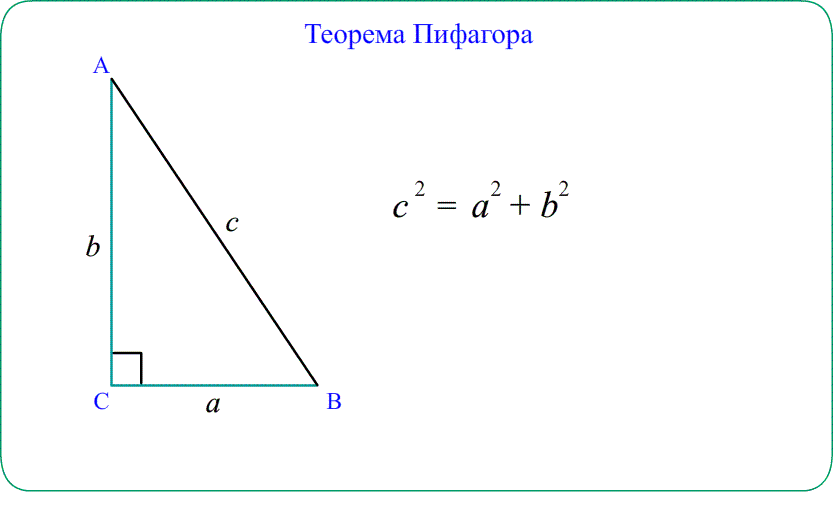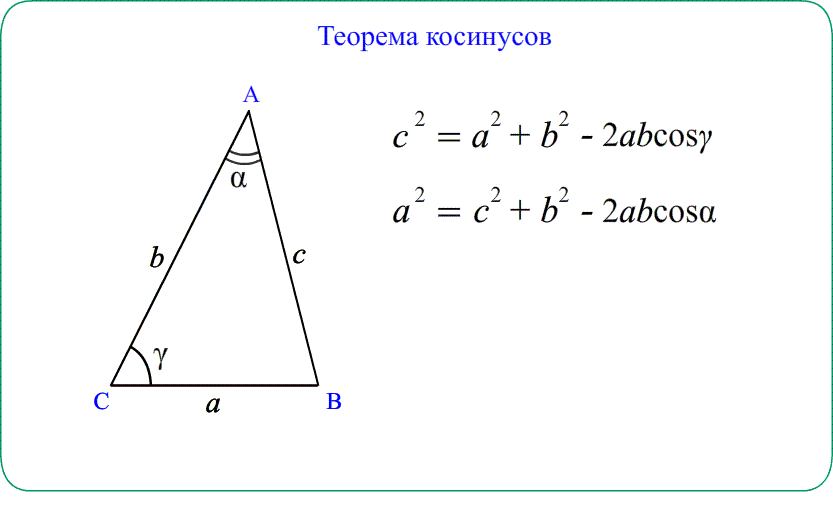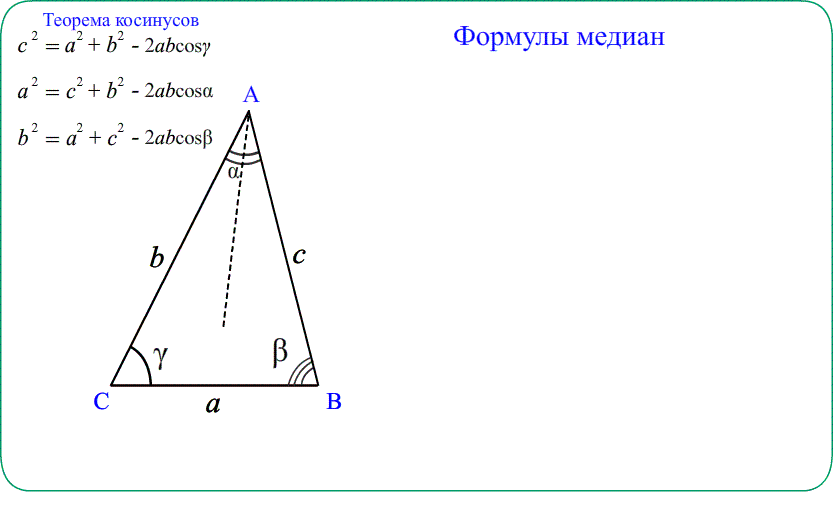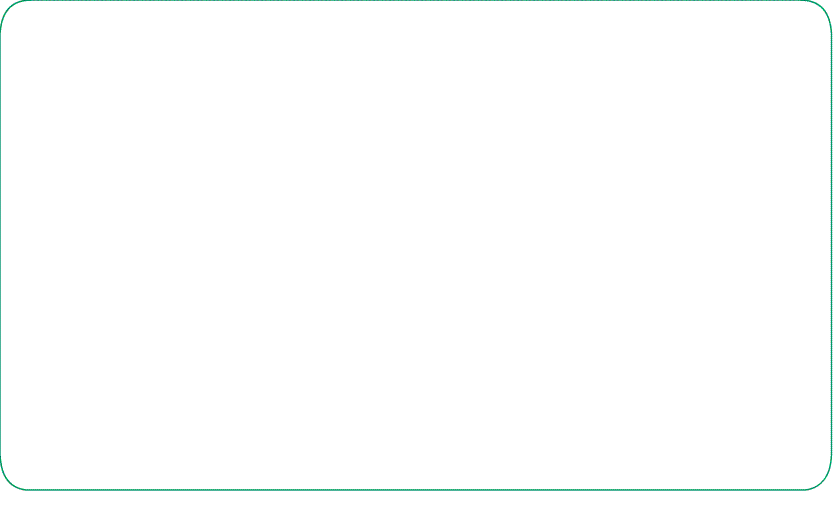
- Для прямоугольного треугольника теорема косинусов «упрощается» до теоремы Пифагора $AB^2=AC^2+BC^2$.
А если угол тупой? Что означает тригонометрия больших углов?
$cos130=-cos50$, $sin115=sin65$ , $tg135=-tg45$.
Связь тригонометрии тупых углов $90 < alpha < 180$ с тригонометрией острых выражается формулами:
$sinalpha=sinleft(180-alpharight)$ $cosalpha=-cosleft(180-alpharight)$ $tgalpha=-tgleft(180-alpharight)$ $ctgalpha=-ctgleft(180-alpharight)$
Если $b^2+c^2-a^2>0$, то $alpha$ — острый; если $b^2+c^2-a^2=0$, то $alpha$ — прямой; если $b^2+c^2-a^2<0$ , то угол $alpha$ — тупой.
Расчет треугольников по теореме косинусов
Задача 1: В треугольнике $ABC$ сторона $AC$ равна $7sqrt{3}$ см, сторона $BC$ равна $1$ см , угол $C$ = $150^o$ . Найти длину стороны $AB$.
- Решение: Применим теорему косинусов $AB^2=left(7sqrt{3}right)^2+1-14sqrt{3}cos150$ .
- Тупой угол в $150^o$ выразим через острый : $cos150=cosleft(180-30right)=-cos30=-frac{sqrt{3}}{2}$. $Rightarrow$
- $AB^2=147+1-28sqrt{3}left(-frac{sqrt{3}}{2}right)$ , $AB^2= 148 + 21 = 169$ $Rightarrow$ Ответ: $AB = 13$
Задача 2: В треугольнике $ABC$ сторона $AC$ равна $17$ см, сторона $BC$ равна $14$ см , угол $ACB$ = $60^o$ .
Найти длину третьей стороны .
- Решение: Из теоремы косинусов для угла $angle ACB$ : $Rightarrow$ $AB^2=17^2+14^2-2cdot17cdot14cdotcos60$ $Rightarrow$
- квадрат стороны $AB^2= 289+196-238 = 247$ $Rightarrow$ Ответ: $AB = sqrt{247}$
Задача 3: В $bigtriangleup ABC$ известны $AC=3$ , $BC=5$ см, $AB=6$ .
Найти косинус угла $C$ и медиану $BM$ .
- Решение: Из теоремы косинусов для стороны $AB$ выразим косинус требуемого угла $ACB$:
- $cos ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}=frac{9+25-36}{30}=-frac{1}{15}$ . Отрицательное значение косинуса говорит о том, что это тупой угол $>90^o$
- Для нахождения медианы $ВМ$ распишем еще раз теорему косинусов, но уже для треугольника $ВМС$ от угла $С$:
- $BM^2=BC^2+MC^2-2cdot BCcdot MCcdotcos C$ учтем, что медиана делит сторону пополам $MC=frac{AC}{2}=1,5$
- Подставим $BM^2=25+2,25-2cdot5cdot1.5cdotleft(-frac{1}{15}right)=27,25+1=28,25$, получим $BM=sqrt{28,25}=0,5sqrt{113}$
- Ответ: $cos ACB=-frac{1}{15}$ , $BM=0,5sqrt{113}$ .
Задача 4: В прямоугольном $bigtriangleup ABC$ известны $AB=9$ , $BC=3$ см ; $M$ делит $AB$ : $frac{AM}{MB}=frac{1}{2}$.
Найти $CM$ .
- Решение: По свойству аддитивности отрезка $AM + MB = 9$ , по условию $frac{AM}{MB}=frac{1}{2}$ $Rightarrow$ $AM = 3$ , $MB = 6$
- Из прямоугольного $bigtriangleup ABC$ по определению косинуса угла: $cos B=frac{BC}{AB}=frac{3}{9}=frac{1}{3}$ .
- Из $bigtriangleup CMB$ по теореме косинусов найдем $CM$ : $CM^2=CB^2+MB^2-2cdot CBcdot MBcdotcos B$ , подставим числа
- $CM^2=3^2+6^2-2cdot3cdot6cdotfrac{1}{3}=33$ $Rightarrow$ требуемый отрезок $CM=sqrt{33}$ . Ответ: $CM=sqrt{33}$
Задача 5: Одна из сторон треугольника больше другой на $8$ см, а угол между ними $120^o$ .
Найдите периметр треугольника, если длина третьей стороны $28$ см .
- Решение: Метод введения неизвестного: Обозначим одну из сторон треугольника как $x$ ,
- выразим нужные величины через х и составим уравнение: величина другой стороны будет равна $x+8$ см.
- По теореме косинусов: $28^2=x^2+left(x+8right)^2-2xcdotleft(x+8right)cdotcos120$ , где $cos120=cosleft(180-60right)=-cosleft(60right)=-0,5$,
- Итак, составили уравнение $784=x^2+x^2+16x+64-2xleft(x+8right)left(-0,5right)$ $Rightarrow$ $3x^2+24x+720=0$
- решим квадратное уравнение : один корень отрицательный — не нужен , другой $x=frac{-24+96}{6}=12$
- Периметр $P=12+left(12+8right)+28=60$. Ответ: $60$.
Задача 6: В $bigtriangleup ABC$ известны стороны $a=15$ , $b=18$, $c=25$ . Найти: углы $α$, $β$, $γ$ (приближённо) .
- Решение: Углы $α$ и $β$ найдём по теореме косинусов для соответствующих углов.
- $cosalpha=frac{b^2+c^2-a^2}{2bc}$ , вычисляем $cosalpha=frac{18^2+25^2-15^2}{2cdot18cdot25}approx0,8$ , привлекаем калькулятор: $alphaapprox36,4^o$ ;
- $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , вычисляем $cosbeta=frac{15^2+25^2-18^2}{2cdot15cdot25}approx0,7$ , …. калькулятор: $betaapprox45,3^o$ .
- Найдём $γ$ по теореме о 180 = сумма углов: $gamma=180-left(alpha+betaright)$ и $gammaapprox180-left(36,4+45,3right)approx98,3$ .
- Ответ: $alphaapprox36,4^o$ , $betaapprox45,3^o$ , $gammaapprox98,3$

Задача 7: В $bigtriangleup ABC$ $AB=c=3$ м, $AC = b = 6$ м. , $alpha=60$ . Найти: сторону $a = BC$ , углы $β$, $γ$ .
- Решение: Треугольник задан двумя сторонами и углом между ними, следовательно, он задан полностью.
- По теореме косинусов $a^2=b^2+c^2-2bccdotcosalpha$ найдём сторону $a$:
- $a^2=6^2+3^2-2cdot6cdot3cdotcos60=36+9-36cdotfrac{1}{2}=27$ $Rightarrow$ $a=3sqrt{3}$ .
- По теореме косинусов найдем и угол $β$ : $cosbeta=frac{a^2+c^2-b^2}{2ac}$ , $cosbeta=frac{27+9-36}{18sqrt{3}}=0$ $Rightarrow$ $β=90$ .
- Значит $bigtriangleup ABC$ — прямоугольный , тогда угол $γ=90-α$ . Ответ: $a=3sqrt{3}$ , $β = 90$ , $γ=30$ .
Задача 8: Стороны треугольника равны $11$ , $12$ и $13$ . Найти биссектрису, проведенную к стороне, равной 12.
- дано: $AB=11$ , $BC=12$ , $AC=13$ Найти биссектрису $AK=?$ .
- Решение: Найдем косинус угла из теоремы косинусов : $AB^2=AC^2+BC^2-2cdot ACcdot BCcdotcos angle ACB$
- Выразим косинус $cos angle ACB=frac{AC^2+BC^2-AB^2}{2cdot ACcdot BC}$ , $cos angle ACB=frac{13^2+12^2-11^2}{2cdot 13cdot 12}=frac{19}{39}$
- Найдем отрезки $BK$ , $KC$ на которые биссектриса делит сторону … по теореме биссектрис $frac{BK}{KC}=frac{AB}{AC}$
- Система уравнений: $frac{BK}{KC}=frac{11}{13}$ и аддитивность $BK+KC=BC=12$. Получаем $BK=5,5$ , $BK=6,5$
- Теперь, для нахождения биссектрисы $AK$ еще раз используем теорему косинусов для треугольника $bigtriangleup AKC$
- $AK^2=AC^2+KC^2-2cdot ACcdot KCcdotcos angle ACB$ подставим значения $AK^2=13^2+6,5^2-2cdot 13cdot 6,5cdot frac{11}{13}=frac{429}{4}$.
- Ответ: $AK=frac{sqrt429}{2}$.
Задача 9: Стороны треугольника равны $11$ , $12$ и $13$ . Найти медиану, проведенную к большей стороне.
- Решение: Воспользуемся формулой для длины медианы: $m_c=frac{1}{2}sqrt{2a^2+2b^2-c^2}$
- Подставим значения $m_c=frac{1}{2}sqrt{2cdot11^2+2cdot12^2-13^2}=frac{1}{2}sqrt{242+288-169}=frac{1}{2}sqrt{361}=frac{19}{2}=9,5$ Ответ: $m_c=9,5$
Задача 10: В треугольнике $ABC$ $AB=11$ , $AC=23$ , медиана $AK=10$ . Найти $BC$ .
- Решение: Воспользуемся формулой для длины медианы и подставим в неё данные из условия:
- $AK=frac{1}{2}sqrt{2cdot11^2+2cdot23^2-BC}$ $Rightarrow$ $100=frac{1}{4}left(242+1058-BC^2right)$ $Rightarrow$ $BC^2=900$ Ответ: $BC=30$ .
Упражнения:
Теорема косинусов отлично помогает в решении треугольников. Решение треугольника – это нахождение всех его сторон и углов. Но если нам даны только стороны треугольника, как определить углы в нем? Вот тогда и приходит на помощь теорема косинусов. Это общий случай теоремы Пифагора, подходящий для треугольника с любым углом, не только с углом 900.
Теорема и доказательство
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла между ними.
Доказательство теоремы косинусов
Докажем теорему. Для этого нарисуем треугольник ABC и докажем, что:
Если рассматривать стороны треугольника, как векторы, то будет справедливо равенство:
.
В теореме в квадрате, значит возведем векторное равенство в квадрат, получим:
Так как, ,
, а скалярное произведение векторов равно произведению их модулей на косинус угла между ними, то есть
.
Подставим все в формулу (2):
.
Что и требовалось доказать.
Следствие теоремы косинусов
Проведем высоты :
Обратим внимание, что . То есть
– это проекция стороны
на сторону
треугольника
. Если угол А острый, то
, если угол А тупой, то косинус угла А будет отрицательным и
. То есть из теоремы косинусов вытекает важное следствие:
квадрат стороны треугольника равен сумме квадратов двух других сторон “
” удвоенное произведение одной из них на проекцию другой на эту сторону. Знак
надо брать, если угол тупой, а знак
, если угол острый.
Задачи на теорему косинусов
Задача 1
Найдите , если дано:
,
,
.
Решение: Так как нам известен угол между сторонами и
и известна сторона
– мы сможем найти сторону
, если воспользуемся теоремой косинусов.
Из теоремы косинусов выразим сторону
.
Получим:
Обозначим
Тогда
Получаем квадратное уравнение. Подставим в него значения и решим:
Находим дискриминант:
.
Тогда .
– не может быть длиной стороны треугольника.
Ответ: 12.
Задача 2
В треугольника ABC ,
,
. Найдите
Решение: Нарисуем треугольник ABC. Это равнобедренный треугольник.
Запишем теорему косинусов для сторону так как нам дан угол между двумя другими сторонами:
.
Так как , то из формулы (1), получим:
Сделаем замену: :
,
перенесем в правую часть равенства и получим квадратное уравнение:
,
Подставим значения:
Так как , значит,
.
Ответ: 6
Задача 3
Решите треугольник ABC, если известно, что ,
,
.
Решение: Решить треугольник – это значит, найти все его стороны и все углы. Нам два угла даны, значит, зная, что сумма всех углов в треугольнике равна получим:
.
Обозначим неизвестные стороны треугольника: ,
.
Выразим сторону треугольник по теореме косинусов:
Выразим сторону треугольника по теореме косинусов:
или
Решим уравнения (1) и (2) совместно, записав их в систему уравнений:
Преобразуем второе уравнение системы:
Сложим первое и второе уравнения системы и запишем получившееся уравнение вместо второго уравнения, получим:
Из второго уравнения выразим :
Итак, мы выразили из второго уравнения системы, теперь возьмем и подставим его в первое уравнение и сделаем необходимые преобразования.
, раскрываем скобки и умножим левую и правую части уравнения на 2:
Разделим левую и правую части уравнения на 2:
.
Получили квадратное уравнение. Решим его.
Находим дискриминант:
Тогда корни уравнения:
.
Оба значения подходят – они положительны. Находим, :
– отрицательное значение нам не подходит.
.
Таким образом, получаем следующие значения ,
.
Вы можете самостоятельно сделать проверку и убедиться в том, что данные значения верны.
Ответ: ,
.
Теорема косинусов для треугольника очень помогает в решении геометрических задач, однако некоторые задачи усложняются, если не знать еще одну теорему – синусов. Например, третью задачу мы могли решить гораздо проще – используя теорему синусов, с помощью которой мы бы довольно быстро получили тот же результат для . Однако, с ней мы бы получили лишь приближенное значение
. Теорема косинусов дает нам точный результат. Однако, в дальнейшем, когда вы выучите две теоремы – рекомендуем решать задачи, используя их обе.
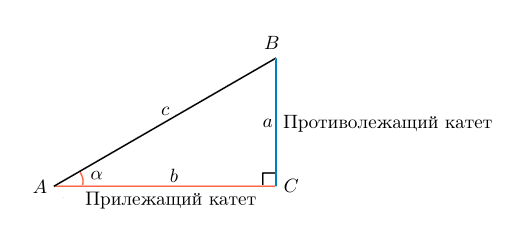
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
Теорема косинусов (ЕГЭ 2022)
Что же такое теорема косинусов?
Представь себе, это такая… теорема Пифагора для произвольного треугольника. Она однажды тебя спасёт!
Дальше смотри рисунки и ты все поймешь. Один рисунок лучше тысячи слов 🙂
Разберёшься в ней – будь уверен, что любая задача с треугольником окажется тебе под силу!
Поехали!
Теорема косинусов — коротко о главном
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2abcos gamma )
Почему теорема косинусов это… теорема Пифагора
И причем тут теорема Пифагора? Сейчас поясню.
Согласно теореме Пифагора в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}})
А что будет, если угол ( displaystyle angle C), скажем, острый?
Вроде ясно, что величина ( displaystyle {{c}^{2}}) должна быть меньше, чем ( displaystyle {{a}^{2}}+{{b}^{2}}). Но вот на сколько меньше?
А если угол ( displaystyle angle C) – тупой?
Ну, тогда величина ( displaystyle {{c}^{2}}) больше, чем ( displaystyle {{a}^{2}}+{{b}^{2}})?
Но, опять же, на сколько? И как это связано с величиной ( displaystyle angle C)?
Обрати внимание на вот эту добавку к теорему Пифагора: ( displaystyle «-2abcos gamma »).
Вот она и «адаптирует» теорему Пифагора под острые и тупые углы треугольника. Сейчас мы докажем теорему косинусов и ты увидишь в теореме косинусов теорему Пифагора своими глазами.
Доказательство теоремы косинусов
Итак, для всякого (и остроугольного, и тупоугольного и даже прямоугольного!) треугольника верна теорема косинусов.
Теорема косинусов гласит: квадрат любой стороны треугольника равен сумме квадратов двух других сторон треугольника минус удвоенное произведение этих сторон на косинус угла между ними.
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}-2abcos gamma )
Рассмотрим три случая:
- угол С острый,
- угол С тупой,
- угол С прямой.
И убедимся, что для всех трех случаев теорема косинусов работает!
Угол С острый
( displaystyle angle C<{{90}^{circ }})
Проведем высоту ( displaystyle AH) из точки ( displaystyle A) и рассмотрим треугольник ( displaystyle AHB).
Он прямоугольный, можно пользоваться теоремой Пифагора:
( displaystyle {{c}^{2}}=A{{H}^{2}}+H{{B}^{2}})
Что такое ( displaystyle AH) и ( displaystyle HB) ?
( displaystyle AH) можно выразить из треугольника (прямоугольного!) ( displaystyle AHC).
( displaystyle AH=bsin gamma )
А вот ( displaystyle BH=a-CH=a-bcos gamma ) (снова из ( displaystyle Delta AHC) ).
Подставляем:
Угол С тупой
( displaystyle angle C>{{90}^{circ }})
Начинаем точно также: опускаем высоту из точки ( displaystyle A).
И снова:
( displaystyle {{c}^{2}}=A{{H}^{2}}+H{{B}^{2}})
А теперь, внимание, отличие!
( displaystyle AH=bsin left( {{180}^{circ }}-gamma right)) — это из ( displaystyle Delta AHC) , который теперь оказался снаружи ( displaystyle Delta ABC), а
( displaystyle BH=a+bcos left( {{180}^{circ }}-gamma right)).
Вспоминаем, что:
Угол С прямой
( displaystyle angle C={{90}^{circ }}).
Но тогда ( displaystyle cos gamma =0) и теорема косинусов просто превращается в теорему Пифагора:
( displaystyle {{c}^{2}}={{a}^{2}}+{{b}^{2}}).
В каких же задачах бывает полезна теорема косинусов?
Ну, например, если у тебя даны две стороны треугольника и угол между ними, то ты прямо сразу можешь найти третью сторону.
Или, если тебе даны все три стороны, то ты тут же найдешь косинус любого угла по формуле:
( displaystyle {cos gamma =frac{{{a}^{2}}+{{b}^{2}-{c}^{2}}}{2{a}{b}}})
И даже, если тебе даны две стороны и угол НЕ между ними, то третью сторону тоже можно найти, решая квадратное уравнение. Правда, в этом случае получается иногда два ответа и нужно соображать, какой же из них выбрать, или оставить оба.
Попробуй применять и не бояться – теорема косинусов почти также легка в обращении, как и теорема Пифагора.
И приходи к нам на бесплатные вебинары и занятия ( о них ниже).
Бонус: Вебинар на решение задач по теореме косинусов и синусов
Теорема косинусов (и синусов) — универсальный инструмент при решении треугольников — это теоремы косинусов и синусов.
А как мы уже знаем, почти любая задача в планиметрии сводится именно к треугольникам.
Этот вебинар из нашего курса подготовки к ЕГЭ по математике (о нем ниже). Вы выучите сами теоремы и научитесь применять их при решении задач первой части.
Берите ручку и бумагу и решайте вместе с Алексеем Шевчуком.
Самые бюджетные курсы по подготовке к ЕГЭ на 90+
Алексей Шевчук — ведущий мини-групп
математика, информатика, физика
+7 (905) 541-39-06 — WhatsApp/Телеграм для записи
alexei.shevchuk@youclever.org — email для записи
- тысячи учеников, поступивших в лучшие ВУЗы страны
- автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
- закончил МФТИ, преподавал на малом физтехе;
- репетиторский стаж — c 2003 года;
- в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов — как обычно дурацкая ошибка:);
- отзыв на Профи.ру: «Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами».
Как находить косинус в треугольнике
Нередко в геометрических (тригонометрических) задачах требуется найти косинус угла в треугольнике, потому что косинус угла позволяет однозначно определить величину самого угла.

Инструкция
Чтобы найти косинус угла в треугольнике, длины сторон которого известны, можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат длины стороны произвольного треугольника равняется сумме квадратов двух его других сторон без удвоенного произведения длин этих сторон на косинус угла между ними:
а?=b?+c?-2*b*c*соs?, где:
а, b, с – стороны треугольника (точнее их длины),
? – угол, противоположный стороне а (его величина).
Из приведенного равенства легко находится соs?:
соs?=( b?+c?-а? )/(2*b*c)
Пример 1.
Имеется треугольник со сторонами а, b, с, равными 3, 4, 5 мм, соответственно.
Найти косинус угла, заключенного между большими сторонами.
Решение:
По условию задачи имеем:
а=3,
b=4,
с=5.
Обозначим противоположный стороне а угол через ?, тогда, согласно выведенной выше формуле, имеем:
соs?=(b?+c?-а? )/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40=32/40=0,8
Ответ: 0,8.
Если треугольник прямоугольный, то для нахождения косинуса угла достаточно знать длины всего двух любых сторон (косинус прямого угла равен 0).
Пусть имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.
Рассмотрим все варианты:
Пример 2.
Найти соs?, если известны длины сторон а и b (катеты треугольника)
Воспользуемся дополнительно теоремой Пифагора:
c?=b?+а?,
с=v(b?+а?)
соs?=(b?+c?-а? )/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)
Чтобы проверить правильность полученной формулы, подставим в нее значения из примера 1, т.е.
а=3,
b=4.
Проделав элементарные вычисления, получаем:
соs?=0,8.
Аналогично находится косинус в прямоугольном треугольнике в остальных случаях:
Пример 3.
Известны а и с (гипотенуза и противолежащий катет), найти соs?
b?=с?-а?,
b=v(c?-а?)
соs?=(b?+c?-а? )/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.
Подставляя значения а=3 и с=5 из первого примера, получаем:
соs?=0,8.
Пример 4.
Известны b и с (гипотенуза и прилежащий катет).
Найти соs?
Произведя аналогичные (показанные в примерах 2 и 3 преобразования), получим, что в этом случае косинус в треугольнике вычисляется по очень простой формуле:
соs?=b/с.
Простота выведенной формулы объясняется элементарно: фактически, прилежащий к углу ? катет является проекцией гипотенузы, поэтому его длина равна длине гипотенузы, умноженной на соs?.
Подставляя значения b=4 и с=5 из первого примера, получим:
соs?=0,8
Значит, все наши формулы верны.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.


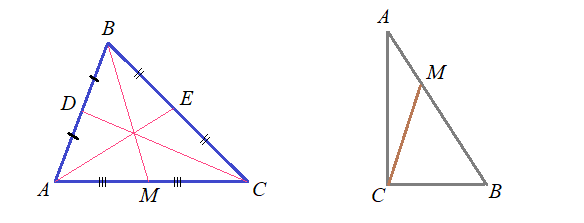






![Rendered by QuickLaTeX.com [left{ begin{aligned} AB^2={x}^2+y^2-2{xy} cdot cos {45^{circ}}\ y^2={x}^2+16-8{x}cdot cos {30^{circ}}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-30320ec6e39a25f00186bb323ebb0a4b_l3.png)
![Rendered by QuickLaTeX.com [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ y^2={x}^2+16-4{x}cdot sqrt{3}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-8678bdf8bad15043893e9bf2593a42ba_l3.png)
![Rendered by QuickLaTeX.com [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ -16={x}^2-y^2-4{x}cdot sqrt{3}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-76cf8b6954d16cd69742ca39f37aedfc_l3.png)
![Rendered by QuickLaTeX.com [left{ begin{aligned} 16={x}^2+y^2-{xy} cdot sqrt{2}\ 0=2{x}^2-xy sqrt{2}-4{x}cdot sqrt{3}.\ end{aligned} right.]](https://repetitor-mathematics.ru/wp-content/ql-cache/quicklatex.com-67d0d01169f7374358518053704d8414_l3.png)