|
|
Основы программирования Каждый профессионал когда-то был чайником. Наверняка вам знакомо состояние, когда “не знаешь как начать думать, чтобы до такого додуматься”. Наверняка вы сталкивались с ситуацией, когда вы просто не знаете, с чего начать. Эта книга ориентирована как раз на таких людей, кто хотел бы стать программистом, но совершенно не знает, как начать этот путь. Подробнее… |
Раздел: Стандартные функции Паскаля
Тригонометрические функции Cos и Sin в Паскале вычисляют соответственно косинус угла и синус угла. Можете сразу перейти к просмотру видео, где я рассказал об этих функциях. Но также рекомендую прочитать статью — не вся информация вошла в видеоролик.
На всякий случай (для тех, кто подзабыл математику) я расскажу, что такое косинус (Cos) и синус (Sin) угла. Но позже — в конце статьи. А сейчас синтаксис в Паскале и некоторые особенности работы с этими функциями.
Синтаксис функции Cos:
function Cos(Х : ValReal) : ValReal;
Синтаксис функции Sin:
function Sin(Х : ValReal) : ValReal;
О типе ValReal я рассказывал здесь.
Функция Cos возвращает косинус угла Х. Функция Sin возвращает синус угла Х. Значение угла передаётся через параметр Х и выражается в радианах.
ВНИМАНИЕ! Не в градусах, а в радианах!
Так как мы больше привыкли измерять углы в градусах, то, если мы не хотим попрощаться с этой привычкой, нам придётся переводить градусы в радианы.
Формула перевода градусов в радианы проста:
Радиан := Пи * Градус / 180
Как известно, число ПИ равно 3,14 (примерно). Можно использовать непосредственно число для преобразования градусов в радианы.
Однако удобнее использовать предопределённую константу Pi, как это сделано в примере ниже.
program cossin;
var x, y, z : single;
begin
Write('Введите угол в градусах: ');
ReadLn(z);
y := Pi * z / 180; //Перевести градусы в радианы
x := Cos(y);
WriteLn('Cos(', z:0:1, ') = ', x:0:4);
x := Sin(y);
WriteLn('Sin(', z:0:1, ') = ', x:0:4);
WriteLn('Пи = ', Pi:0:10);
ReadLn;
end.
Здесь мы объявляем три переменных. Затем просим пользователя ввести угол в градусах и читаем введённое значение в переменную z.
Затем преобразуем градусы в радианы и сохраняем полученный результат в переменную у.
Ну а затем уже используем функции Cos и Sin для получения нужных нам косинуса и синуса для угла, указанного пользователем.
А напоследок выводим значение числа ПИ, которое берём из предопределённой в Паскале константы Pi.
Ну а теперь пришло время выполнить своё обещание, то есть рассказать подробнее о косинусах и синусах.
Что такое косинус и синус угла
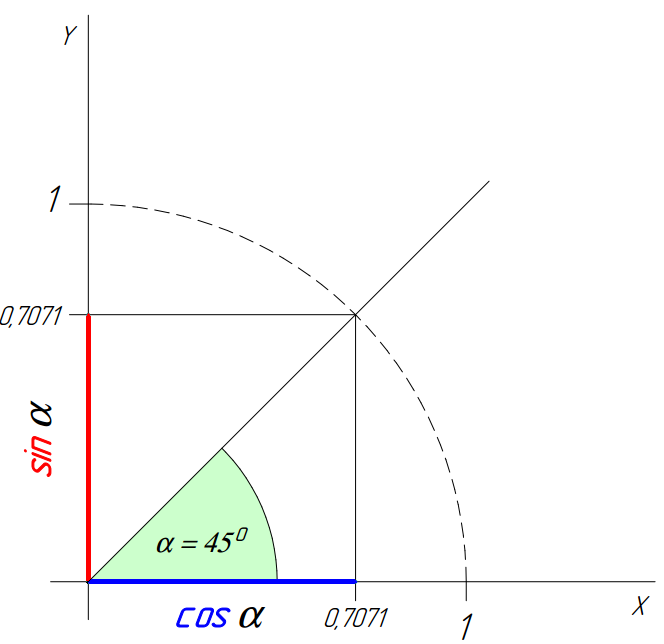
Для начала внимательно посмотрите на рисунок.
Как видно из рисунка, величина тригонометрических функций зависит от угла между осью Х и прямой, проведенной из центра координат.
На рисунке угол равен 45 градусам. При таком значении угла синус равен косинусу (0,7071).
Если угол равен 0 градусов (прямая совпадает с осью Х), то косинус равен 1, а синус равен 0. Если угол равен 90 градусов (прямая совпадает с осью Y), то косинус равен 0, а синус равен 1.
В любом случае значения этих функций лежат в пределах от –1 до +1 включительно. Например, синус 30 градусов равен 0,5. В этом случае значение 0,5 – это так называемая обратная функция. Если необходимо указать, что функция является обратной, то к названию функции добавляют приставку arc. Пример (в функции cos угол указан в градусах):
cos(60) = arccos(0,5)
Остальные тригонометрические функции – это выражения, содержащие синус и/или косинус:
tg(X) = sin(X) / cos(X) - тангенс угла Х ctg(X) = cos(X) / sin(X) - котангенс угла Х sec(X) = 1 / cos(X) - секанс угла Х cosec(X) = 1 / sin(X) - косеканс угла Х
И хотя в Паскале есть функции для вычисления других тригонометрических функций, вы можете вполне обойтись без них, используя приведённые выше формулы.
И теперь у вас достаточно знаний, чтобы написать какую-нибудь свою полезную программку для вычисления тригонометрических функций. Это требуется очень часто студентам, школьникам и инженерам.
|
|
Как стать программистом 2.0
Эта книга для тех, кто хочет стать программистом. На самом деле хочет, а не просто мечтает. И хочет именно стать программистом с большой буквы, а не просто научиться кулебякать какие-то примитивные программки… |
|
|
Помощь в технических вопросах
Помощь студентам. Курсовые, дипломы, чертежи (КОМПАС), задачи по программированию: Pascal/Delphi/Lazarus; С/С++; Ассемблер; языки программирования ПЛК; JavaScript; VBScript; Fortran; Python и др. Разработка (доработка) ПО ПЛК (предпочтение — ОВЕН, CoDeSys 2 и 3), а также программирование панелей оператора, программируемых реле и других приборов систем автоматизации. |
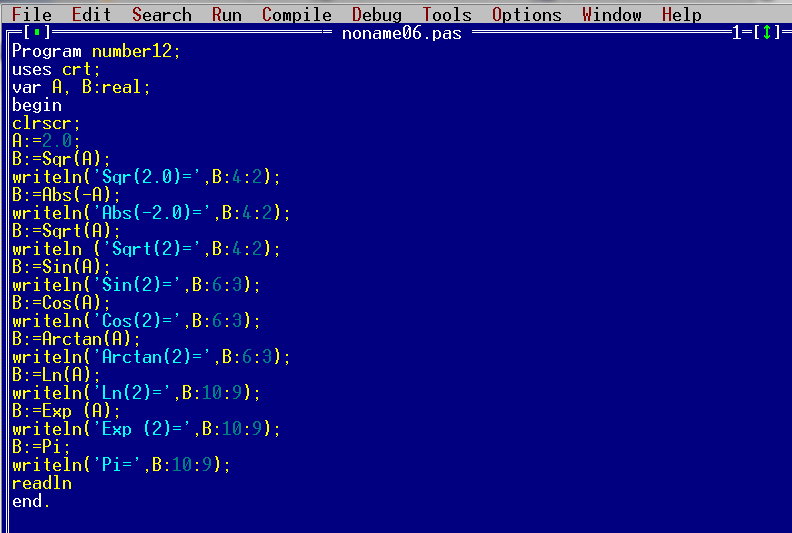
Мы уже знаем, какие существуют функции для целых переменных. Это – нахождение модуля числа (Функция Abc), а также возведение числа в квадрат (Функция Sqr). В этом уроке мы рассмотрим функции, применяемые к дробным числам. Это функции Sqr — квадрат числа, Abs — модуль числа, Sqrt — корень числа, а также известные всем математические функции Sin, Cos, Arctan, Ln, Exp, Pi.
Program number12;
uses crt;
var A, B:real;
begin
clrscr;
A:=2.0;
B:=Sqr(A);
writeln('Sqr(2.0)=',B:4:2);
B:=Abs(-A);
writeln('Abs(-2.0)=',B:4:2);
B:=Sqrt(A);
writeln ('Sqrt(2)=',B:4:2);
B:=Sin(A);
writeln('Sin(2)=',B:6:3);
B:=Cos(A);
writeln('Cos(2)=',B:6:3);
B:=Arctan(A);
writeln('Arctan(2)=',B:6:3);
B:=Ln(A);
writeln('Ln(2)=',B:10:9);
B:=Exp (A);
writeln('Exp (2)=',B:10:9);
B:=Pi;
writeln('Pi=',B:10:9);
readln
end.
В строке №7 записывается функция Sqr. Это функция возведения числа в квадрат.
В строке №9 записывается операция нахождения модуля числа.
Функции Sqr и Abs мы разбирали в уроке Abs, Sqr в Pascal.
В строке №11 записывается функция Sqrt. Данная функция подсчитывает корень числа, стоящего в скобках после слова Sqrt. В нашем случае функция Sqrt будет считать корень из числа «2».
В строке №13 записываем функцию Sin. Данная функция будет подсчитывать синус числа, стоящего в скобках после записи функции.
Строка №15. Функция Cos подсчитывает косинус числа, стоящего в скобках после функции.
Строка №17. Функция Arctan вычисляет арктангенс числа, стоящего в скобках после записи функции.
Строка №19. Функция Ln подсчитывает логарифм числа, стоящего в скобках после записи функции.
Строка №21. Функция Exp возводит число «e» (экспонента — 2.72…) в степень, значение которой указывается в скобках после слова Exp. Т.е. в нашем случае число «e» будет возведено в степень «2».
Строка №23. Переменной «B» будет присвоено значение числа «?».
Дополнение к материалу.
- Функции Sqrt, Sin, Cos, Arctan, Ln, Exp, Pi определены только для вещественных (дробных) чисел.
- В Паскале не существует операции возведения в степень. Есть только операция возведения числа в квадрат (Sqr). Чтобы возвести число в степень используют операцию умножения. Например, чтобы возвести число 3 в 5-ю степень необходимо записать 3*3*3*3*3
Навигация
Главная
Скачать Turbo Pascal
Скачать справочник
Turbo Pascal Онлайн
Форум |
Группа ВК |
Чат
Лекции
Алфавитный указатель
Содержание справки
Язык Turbo Pascal
Стандартные модули
Функции и процедуры
Директивы компилятора
Примеры программ
Меню Turbo Pascal
Ада-2020. Современный Паскаль
Адское программирование
Статьи по Ада-2020
Отзывы и идеи
Об этом сайте
Чат
Войти
Форум
Загрузка…
Язык:
Русский
English
Cos (функция)
Возвращается косинус параметра (X — угол в радианах).
Объявление
Function Cos(X : Real) : Real;
Режим
Windows, Real, Protected
Замечания
Параметр X — выражение вещественного типа. Результат — косинус числа X, где X — угол в радианах.
См. также
- Лекция №2.2: Типы данных и операции
- Pi
- Sin
- ArcCos
- ArcTan
- ArcTan2
- Тригонометрические функции в Wikipedia
Пример
Язык:
Русский
English
{Cos.PAS}
{ Пример программы для функции Cos }
var
R : Real;
begin
R := Cos(Pi);
end.
На занятии будет объяснен алгоритм работы с функциями на Паскале, рассмотрены стандартные функции. Будут разобраны примеры использования функций с параметрами и без параметров.
Содержание:
- Стандартные функции языка Pascal
- Арифметические функции (основные)
- Функции преобразования типов
- Пользовательские функции Pascal
- Самостоятельная работа
Арифметические функции (основные)
| Функция | Назначение | Тип результата |
|---|---|---|
| abs (x) | абсолютное значение аргумента | совпадает с типом аргумента |
| sqr (x) | квадрат аргумента | совпадает с типом аргумента |
| sqrt (x) | квадратный корень аргумента | вещественный |
| cos (x) | косинус аргумента | вещественный |
| sin (x) | синус аргумента | вещественный |
| arctan (x) | арктангенс аргумента | вещественный |
| exp (x) | ex | вещественный |
| ln (x) | натуральный логарифм | вещественный |
| int (x) | целая часть числа | вещественный |
| frac (x) | дробная часть числа | вещественный |
Функции преобразования типов
| round (x) | — округляет вещественное число до ближайшего целого. |
| trunc (x) | — выдает целую часть вещественного числа, отбрасывая дробную. |
Пользовательские функции Pascal
Функция в Паскале — это подпрограмма, которая в отличие от процедуры всегда возвращает какое-либо значение. Для этого в теле функции её имени присваивается вычисленное значение — результат, который она возвращает.
- Функция – это подпрограмма, результатом работы которой является определенное значение.
- Функции используются для:
- выполнения одинаковых расчетов в различных местах программы;
- для создания общедоступных библиотек функций.
- Синтаксис:
- заголовок начинается служебным словом
function - описание формальных параметров (тех, значения которых передаются из основной программы в функцию):
- параметры-переменные — параметры, значения которых становятся доступны и в основной программе (возвращаются в программу)
- тип возвращаемого функцией результата описывается в конце заголовка функции через двоеточие:
- Вызывается функция в теле основной программы, только если ее имя фигурирует в каком-либо выражении. В отличие от процедуры, которая вызывается отдельно.
- Внутри функции можно объявлять и использовать локальные переменные:
- значение, которое является результатом, записывается в переменную, имя которой совпадает с названием функции; объявлять ее НЕ НАДО:
Рассмотрим синтаксис:
var …;{объявление глобальных переменных} function название (параметры): тип результата; var…; {объявление локальных переменных} begin … {тело функции} название:=результат; {результат вычислений всегда присваивается функции} end; begin … {тело основной программы} end.
Пример: написать функцию, которая вычисляет наибольшее из заданных двух значений
Решение:
Вызов функции:
PascalABC.NET:
Правила описания функции:
1. Мы должны написать тип значения, которое возвращает функция.
2. Переменная Result хранит результат функции.
function f(x: real): real; begin Result := x * x + 1; end;
Вызов функции стоит в выражении:
// основная программа begin var x := 5; var r := Sqrt(x) + f(x); end.
Задача function 0. Написать функцию, которая вычисляет наибольшее из заданных трех значений. Функция с тремя параметрами.
✍ Пример результата:
Введите три числа: 4 1 6 наибольшее = 6
Пример: Написать функцию на Паскале, которая складывает два любых числа
✍ Пример результата:
первое число: 2 второе число: 5 сумма = 7

✍ Решение:
1 2 3 4 5 6 7 8 9 10 11 12 |
var x,y:integer; function f(a,b:integer):integer; begin f:= a+b; end; begin writeln('первое число:'); readln(x); writeln('второе число:'); readln(y); writeln('сумма= ',f(x,y)); end. |
В рассмотренном примере использования функции в Паскале: функция f имеет два целочисленных параметра — a и b. Через двоеточие в заголовке функции (строка 2) указано, что значение, вычисляемое функцией, будет тоже целочисленным. В теле функции вычисляемая сумма присваивается имени функции. А в основной программе вызов функции осуществляется в качестве параметра оператора writeln.
Таким образом, главное отличие функции от процедуры — это то, что функция производит какие-либо вычисления и выдает в программу результат в виде значения, в то время как процедура чаще всего выполняет какие-либо действия с результатом, например, выводит его на экран (функция этого делать не может).
Задача function 1. При помощи функции найти среднее арифметическое двух чисел (функция с двумя параметрами).
✍ Пример результата:
Введите два числа: 4 7 среднее арифметическое = 5,5
Пример: Составить программу с функцией для вычисления факториала числа.
Показать решение:
| Pascal | PascalABC.NET | ||||
|
|
В рассмотренном примере функция имеет один параметр — a. Вычисляемое функцией значение имеет целочисленный тип, это указывается в заголовке функции (строка 2). В теле функции в цикле for вычисляется факториал числа. Результат вычисления присваивается имени функции (строка 9). В теле программы для вывода результата функции она вызывается в операторе writeln (строка 14), который и выводит результат на экран.
PascalABC.NET:
Короткое определение функции:
function Sq(x: real) := x * x + 1; begin var x := 10; var r := Sq(x) + Sq(2) end.
Короткая запись
Если тело функции состоит только из одного оператора, PascalABC.NET позволяет использовать при описании сокращенный синтаксис, без ключевых слов begin и end:
1 2 3 4 5 6 |
## function SumXY(x,y: real) := x + y; // основная программа begin Print (SumXY(9,2)); //11 end; |
Задача function 2. Составить функцию, которая определяет сумму всех чисел от 1 до N и привести пример ее использования. N — параметр функции.
Пример:
Введите число: 100 сумма = 5050
Задача function 3. Составить функцию, которая определяет, сколько зерен попросил положить на N-ую клетку изобретатель шахмат (на 1-ую – 1 зерно, на 2-ую – 2 зерна (в два раза больше предыдущего результата), на 3-ю – 4 зерна, на 4-ю – 8 зерен…). N — параметр функции.
Пример:
Введите номер клетки: 28 На 28-ой клетке 134217728 зерен.
Задача function 4. Описать функцию IsDigit(A), которая возвращает истину, если целое число A представляет цифру (то есть A лежит в диапазоне 0–9). В основной программе вывести значение этой функции для N (N ≥ 0) данных чисел.
Пример:
Введите N: 3 Введите число: 2 >>> true Введите число: 34 >>> false Введите число: 4 >>> true
Задача function 5. Вычисление степени числа с помощью функции на языке Паскаль.
Пример:
Введите число: 3 Введите степень числа: 2 Результат 3^2 = 9
Задача function 6. Описать функцию Calc(A, B, Operation) вещественного типа, выполняющую над ненулевыми вещественными числами A и B одну из арифметических операций и возвращающую ее результат. Вид операции определяется целым параметром Operation: 1 — вычитание, 2 — умножение, 3 — деление, остальные значения — сложение. С помощью Calc выполнить для данных A и B операции, определяемые данными целыми N1, N2, N3.
Пример:
Введите два числа: 5 7 Введите номер операции (1 — вычитание, 2 — умножение, 3 — деление, остальные значения — сложение): 2 Результат 5*7 = 35
* Из задачника М. Э. Абрамян (Proc22)
Самостоятельная работа
1 вариант: Описать функцию CircleS(R) вещественного типа, находящую площадь круга радиуса R (R — вещественное). С помощью этой функции найти площади трех кругов с данными радиусами. Площадь круга радиуса R вычисляется по формуле S=π∗R2. В качестве значения Пи использовать 3.14.
* Из задачника М. Э. Абрамян (Proc18)
Пример:
Введите радиус: 5.2 Площадь круга = 16,328 ___ Введите радиус: 6.3 Площадь круга = 19,782 ___ Введите радиус: 7.1 Площадь круга = 22,294
2 вариант: Описать функцию TriangleP(a, h), находящую периметр равнобедренного треугольника по его основанию a и высоте h, проведенной к основанию (a и h — вещественные). С помощью этой функции найти периметры трех треугольников, для которых даны основания и высоты (периметр = сумме длин всех сторон). Для нахождения боковой стороны b треугольника использовать теорему Пифагора: b2=(a/2)2+h2.
* Из задачника М. Э. Абрамян (Proc20)
Пример:
Введите основание треугольника: 6 Введите высоту треугольника: 5 Периметр треугольника = 17,83095 ___ Введите основание треугольника: ... Введите высоту треугольника: ... Периметр треугольника = ... ___ Введите основание треугольника: ... Введите высоту треугольника: ... Периметр треугольника = ...
Потренируйтесь в решении задач по теме, щелкнув по пиктограмме: