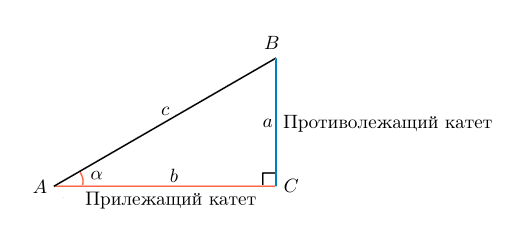
Как находить косинус в треугольнике
Нередко в геометрических (тригонометрических) задачах требуется найти косинус угла в треугольнике, потому что косинус угла позволяет однозначно определить величину самого угла.

Инструкция
Чтобы найти косинус угла в треугольнике, длины сторон которого известны, можно воспользоваться теоремой косинусов. Согласно этой теореме, квадрат длины стороны произвольного треугольника равняется сумме квадратов двух его других сторон без удвоенного произведения длин этих сторон на косинус угла между ними:
а?=b?+c?-2*b*c*соs?, где:
а, b, с – стороны треугольника (точнее их длины),
? – угол, противоположный стороне а (его величина).
Из приведенного равенства легко находится соs?:
соs?=( b?+c?-а? )/(2*b*c)
Пример 1.
Имеется треугольник со сторонами а, b, с, равными 3, 4, 5 мм, соответственно.
Найти косинус угла, заключенного между большими сторонами.
Решение:
По условию задачи имеем:
а=3,
b=4,
с=5.
Обозначим противоположный стороне а угол через ?, тогда, согласно выведенной выше формуле, имеем:
соs?=(b?+c?-а? )/(2*b*c)=(4?+5?-3?)/(2*4*5)=(16+25-9)/40=32/40=0,8
Ответ: 0,8.
Если треугольник прямоугольный, то для нахождения косинуса угла достаточно знать длины всего двух любых сторон (косинус прямого угла равен 0).
Пусть имеется прямоугольный треугольник со сторонами а, b, с, где с – гипотенуза.
Рассмотрим все варианты:
Пример 2.
Найти соs?, если известны длины сторон а и b (катеты треугольника)
Воспользуемся дополнительно теоремой Пифагора:
c?=b?+а?,
с=v(b?+а?)
соs?=(b?+c?-а? )/(2*b*c)=(b?+b?+а?-а?)/(2*b*v(b?+а?))=(2*b?)/(2*b*v(b?+а?))=b/v(b?+а?)
Чтобы проверить правильность полученной формулы, подставим в нее значения из примера 1, т.е.
а=3,
b=4.
Проделав элементарные вычисления, получаем:
соs?=0,8.
Аналогично находится косинус в прямоугольном треугольнике в остальных случаях:
Пример 3.
Известны а и с (гипотенуза и противолежащий катет), найти соs?
b?=с?-а?,
b=v(c?-а?)
соs?=(b?+c?-а? )/(2*b*c)=(с?-а?+с?-а?)/(2*с*v(с?-а?))=(2*с?-2*а?)/(2*с*v(с?-а?))=v(с?-а?)/с.
Подставляя значения а=3 и с=5 из первого примера, получаем:
соs?=0,8.
Пример 4.
Известны b и с (гипотенуза и прилежащий катет).
Найти соs?
Произведя аналогичные (показанные в примерах 2 и 3 преобразования), получим, что в этом случае косинус в треугольнике вычисляется по очень простой формуле:
соs?=b/с.
Простота выведенной формулы объясняется элементарно: фактически, прилежащий к углу ? катет является проекцией гипотенузы, поэтому его длина равна длине гипотенузы, умноженной на соs?.
Подставляя значения b=4 и с=5 из первого примера, получим:
соs?=0,8
Значит, все наши формулы верны.
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Теорема косинусов и синусов
О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Теорема косинусов
Страница содержит полную информацию о теореме косинусов, а также калькулятор, с помощью которого можно найти стороны и угол треугольника и формулу теоремы косинусов.
Теорема косинусов обобщает теорему Пифагора на произвольные плоские треугольники и устанавливает соотношение между сторонами треугольника и его углами.
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Нахождение углов треугольника по заданным сторонам
Нахождение углов треугольника по заданным сторонам с использованием теоремы косинусов.
От нашего пользователя поступил запрос на создание калькулятора, рассчитывающего углы треугольника по заданным сторонам — Расчет углов треугольника.
Для треугольника, в отличие от, скажем, четырехугольника, эта задача имеет решение, ибо треугольник можно однозначно определить по трем сторонам (а также по двум сторонам и углу между ними, и по стороне и двум прилежащим углам).
Стороны в треугольнике, кстати сказать, должны следовать неравенству треугольника, то есть, сумма любых двух сторон должна быть больше третьей стороны.
Математически (см. рисунок) это выражается системой
c» />
a» />
b» />
В случае невыполнения хотя бы одного из условий треугольник называют вырожденным. Собственно, это и не треугольник уже.
Идем дальше — при известных сторонах углы проще всего определить, пользуясь теоремой косинусов, частным случаем которой является теорема Пифагора (см. рисунок)
Калькулятор ниже рассчитывает углы по введенным длинам сторон. Если треугольник вырожденный, то в результате будут нули.
http://mnogoformul.ru/teorema-kosinusov
http://planetcalc.ru/534/
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.
Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.
В случае с рисунком, описанным выше: cosα=bccosalpha=frac{b}{c}
Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.
Решение
Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.
a2+b2=c2a^2+b^2=c^2
62+b2=1026^2+b^2=10^2
36+b2=10036+b^2=100
b2=64b^2=64
b=8b=8
Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:
cosα=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8
Ответ
0.8
Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.
Решение
Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:
P=a+b+cP=a+b+c
25=9+4+c25=9+4+c
c=12c=12
При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:
cosα=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82
Ответ
0.820.82
Решение задач по математике от экспертов сайта Студворк!
Тест по теме “Вычисление косинуса”
Теорема косинусов и теорема Пифагора. В этой статье мы рассмотрим теорему косинусов и как она используется для нахождения элементов треугольника. А так же разберём её взаимосвязь с теоремой Пифагора.
Знать эту теорему НЕОБХОДИМО. Что мы можем найти, используя её?
Если нам будут известны две стороны и угол между ними, мы без труда найдём третью сторону. Для этого нужно просто подставить в формулу известные величины. Для других сторон всё то же самое:
Можно ли использовать теорему косинусов для нахождения третьей стороны, если известны любые две стороны и угол, не лежащий между этими сторонами? Например, нам известны стороны a и b и угол альфа. Тогда из формулы
мы можем найти сторону «с». Приводим к виду:
То есть, мы получаем квадратное уравнение с переменной «с» (все остальные величины нам известны). Решив его, получим искомую сторону.
Мы можем найти любой угол, если нам известны все три стороны треугольника:
Разумеется, что учить все эти формулы не нужно, так как достаточно понимать сам смысл Теоремы косинусов. А косинус любого угла не трудно выразить используя простые алгебраические преобразования.
*Если вы вычисляете косинус тупого угла, то имейте ввиду, что должно получиться отрицательное значение, так как косинус угла от 90 до 180 градусов отрицателен. Если при решении в задачах получите положительное значение, то ищите ошибку.
Следующий вопрос: а если нам дана сторона и любые два угла, что делать? В этом случае теорема косинусов не используется, а на помощь приходит теорема синусов, её мы рассмотрим в одной из следующих статей, не пропустите!
Если вы будете в совершенстве владеть теоремами Пифагора, косинусов, синусов и свойствами подобия треугольников, то для вас не возникнет никаких сложностей с решением треугольников (в большинстве задач).
Следующий факт знают все, но всё же о взаимосвязи теоремы косинусов с теоремой Пифагора сказать стоит. Посмотрите на исходный рисунок, если угол альфа равен 90 градусов, то получим:
То есть, по сути, теорема Пифагора это как бы частный случай теоремы косинусов.
Рассмотрим прямоугольный треугольник. Покажем то же самое, но с другими обозначениями:
По теореме косинусов:
Так как угол С равен 90, то
Напомню, что зная любые две стороны в прямоугольном треугольнике, мы всегда можем найти третью. А далее без труда можем найти значение любой тригонометрической функции острого угла в нём. Можете изучить статью об этом.
Получить материал статьи в формате PDF
На этом всё. Успехов вам!!!
С уважением, Александр Крутицких.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Для нахождения элементов в произвольном треугольнике используется теорема синусов или теорема косинусов.
Теорема синусов
Стороны треугольника пропорциональны синусам противолежащих углов:
asinA=bsinB=csinC
(в решении задачи одновременно пишутся две части, они образуют пропорцию).
Теорема синусов используется для вычисления:
-
неизвестных сторон треугольника, если даны два угла и одна сторона;
-
неизвестных углов треугольника, если даны две стороны и один прилежащий угол.
Так как один из углов треугольника может быть тупым, значение синуса тупого угла находится по формуле приведения
sin180°−α=sinα
.
Наиболее часто используемые тупые углы:
sin120°=sin180°−60°=sin60°=32;sin150°=sin180°−30°=sin30°=12;sin135°=sin180°−45°=sin45°=22.
Радиус описанной окружности
, где (R) — радиус описанной окружности.
Выразив радиус, получаем
R=a2sinA
, или
R=b2sinB
, или
R=c2sinC
.
Для вычисления элементов прямоугольного треугольника достаточно (2) данных величин (две стороны или сторона и угол).
Для вычисления элементов произвольного треугольника необходимо хотя бы (3) данных величины.
Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:
Также теорема исполняется для любой стороны треугольника:
Теорема косинусов используется для вычисления:
-
неизвестной стороны треугольника, если даны две стороны и угол между ними;
-
вычисления косинуса неизвестного угла треугольника, если даны все стороны треугольника.
Значение косинуса тупого угла находится по формуле приведения
cos180°−α=−cosα
.
Наиболее часто используемые тупые углы:
cos120°=cos180°−60°=−cos60°=−12;cos150°=cos180°−30°=−cos30°=−32;cos135°=cos180°−45°=−cos45°=−22.
Если необходимо найти приблизительное значение синуса или косинуса другого угла или вычислить угол по найденному синусу или косинусу, то используется таблица или калькулятор.
Источники:
Рис. 1-3. Треугольник, окружность, © ЯКласс.