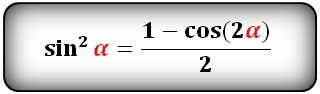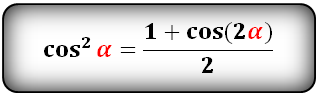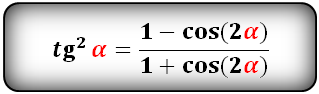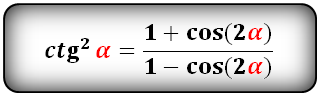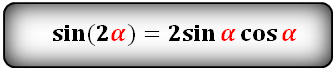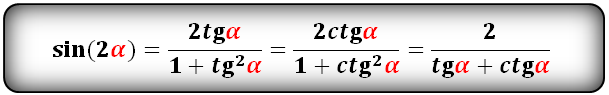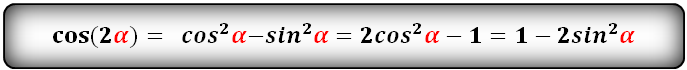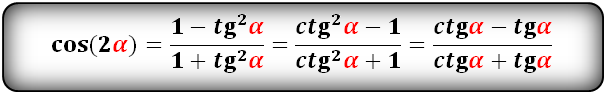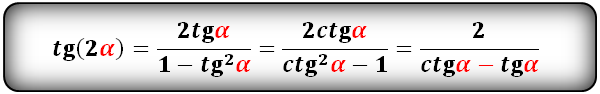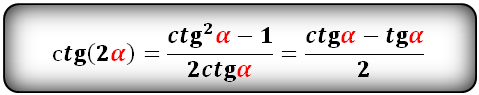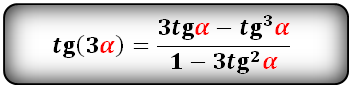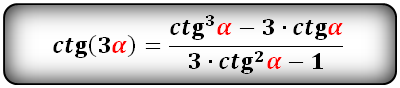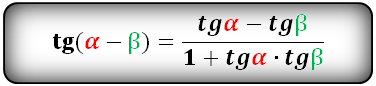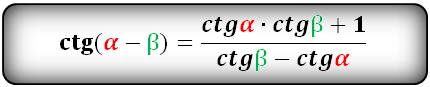Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.
Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)
sin(2α)- через sin и cos:
sin(2α)- через tg и ctg:
cos(2α)- через sin и cos:
cos(2α)- через tg и ctg:
tg(2α) и сtg(2α):
Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):
Тригонометрические формулы преобразования разности аргументов
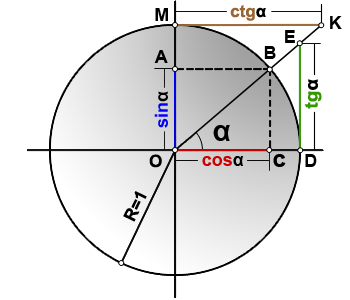
sin(α)=OA
cos(α)=OC
tg(α)=DE
ctg(α)=MK
R=OB=1
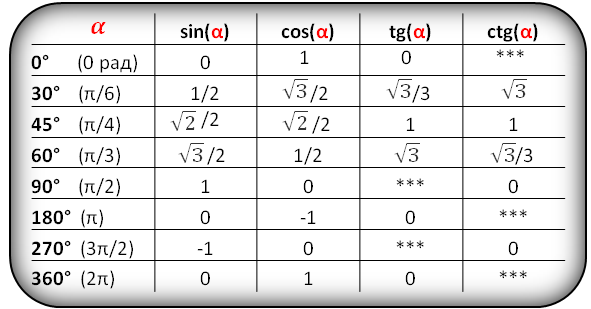
Значения функций для некоторых углов, α
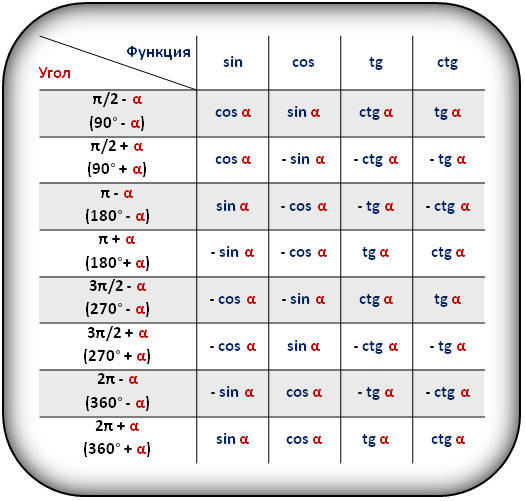
В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).
- Определение
- График косинуса
- Свойства косинуса
- Обратная к косинусу функция
- Таблица косинусов
Определение
Косинус острого угла α (cos α) – это отношение прилежащего катета (b) к гипотенузе (c) в прямоугольном треугольнике.
cos α = b / c
Например:
b = 4
c = 5
cos α = b / c = 4 / 5 = 0.8
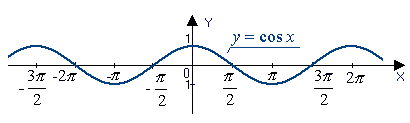
График косинуса
Функция косинуса пишется как y = cos (x). График называется косинусоидой и в общем виде выглядит следующим образом:
Косинусоида – периодическая функция с основным периодом T = 2π.
Свойства косинуса
Ниже в табличном виде представлены основные свойства косинуса с формулами:
Обратная к косинусу функция
Арккосинус x – это обратная к косинусу функция x, при -1≤x≤1.
Если косинус у равняется х (cos y = x), значит арккосинус x равен у:
arccos x = cos-1 x = y
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
Таблица косинусов
| x (°) | x (рад) | cos x |
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
microexcel.ru
| tg(2α) = | 2tg(α)
1 – tg2(α) |
| ctg(2α) = | ctg2(α) – 1
2ctg(α) |
© Школяр. Математика (при поддержке «Ветвистого древа») 2009—2021
Определения
Синусом острого угла прямоугольного треугольника называется отношение противолежащего к этому углу катета к гипотенузе.
Синус угла А обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего к этому углу катета к гипотенузе.
Косинус угла А обозначается cos A.
Наглядно это видно на следующем рисунке:
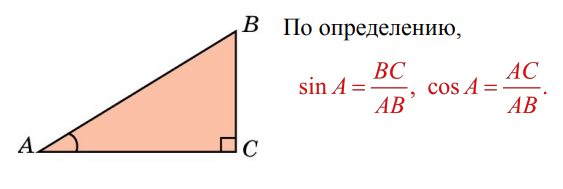
Функция косинуса: свойства и значения функции косинус
Определение
Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.
- Основные свойства функции косинус следующие:
- Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
- Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
- Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
- Функция чётная, т. е. cos(-x) = cos(x);
- Функция периодическая. Её период равен 2π;
- Наибольшего своего значения функция косинус x достигает в точках x=2πk;
- Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
- Область возрастания функции cos(x): -π+2πk<=x<=2πk;
- Область убывания функции cos(x): 2πk<= π+2πk;
- Функция не имеет разрывов, т. е. непрерывна.
График функции косинус
Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние [frac{pi}{2}] влево. Он выглядит следующим образом:
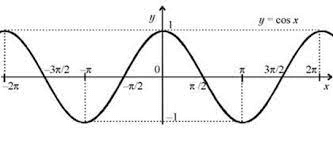
Как построить график функции косинус икс
График функции косинуса можно построить следующим образом:
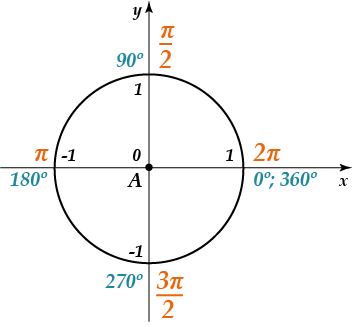
Используем данные единичной окружности, приведённой на рисунке выше.
Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.
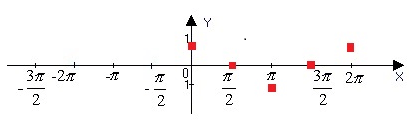
Соединим их плавной линией
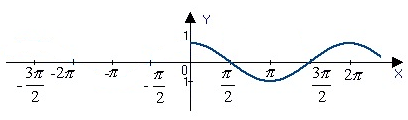
Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.
Нет времени решать самому?
Наши эксперты помогут!
Как найти значение функции косинуса при x равном 45 градусам
Построим прямоугольный треугольник с катетами, равняющимися единице. Сумма углов любого треугольника, как известно, равна 180 градусам. Если вычтем из них прямой угол, получим сумму двух оставшихся углов. Это углы при вершинах A и B. Так как катеты равны, то и выше названные углы равны и каждый из них составляет (180 – 90)/2 = 45 градусов.
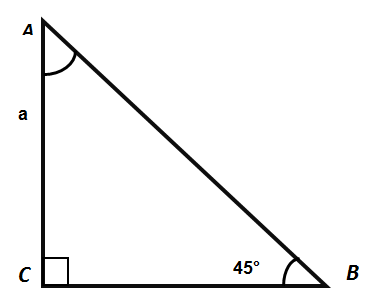
По теореме Пифагора гипотенуза его в этом случае будет равна [c=sqrt{a^{2}+a^{2}}=sqrt{1+1}=sqrt{2}]
Из определения косинуса находим [cos (a)=1 / sqrt{2}]
После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.