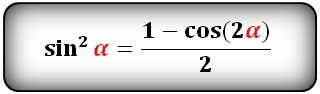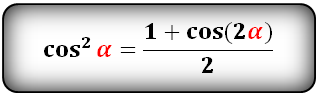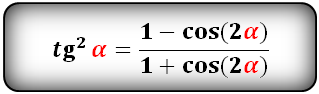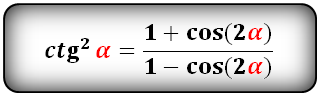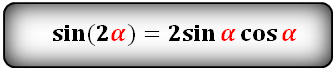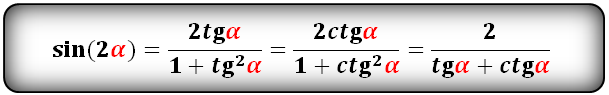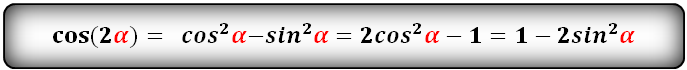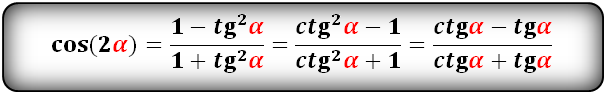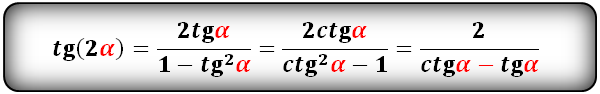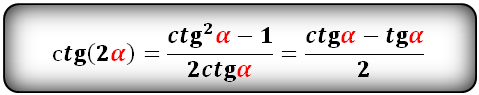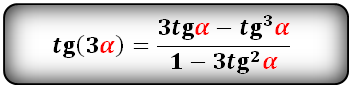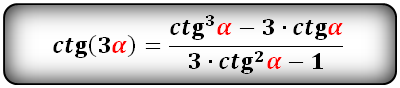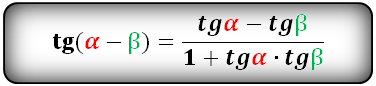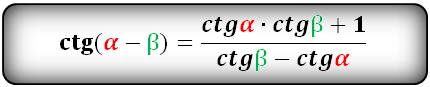Как найти косинус икс от числа - Исправление недочетов и поиск решений вместе с Examum.ru

Примеры:

(cos{⁡30^°}=)(frac{sqrt{3}}{2})
(cos⁡)(frac{π}{3})(=)(frac{1}{2})
(cos⁡2=-0,416…)

Содержание:

Аргумент и значение
Коcинус острого угла
Косинус числа
Косинус любого угла
Знаки по четвертям
Связь с другими функциями
Функция

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.

Пример:

1) Пусть дан угол и нужно определить косинус этого угла.

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить косинус.

Косинус острого угла больше (0) и меньше (1)

Если при решении задачи косинус острого угла получился больше 1 или отрицательным, то значит где-то в решении есть ошибка.

Косинус числа

Числовая окружность позволяет определить косинус любого числа, но обычно находят косинус чисел как-то связанных с Пи: (frac{π}{2}), (frac{3π}{4}), (-2π).

Например, для числа (frac{π}{6}) — косинус будет равен (frac{sqrt{3}}{2}). А для числа (-)(frac{3π}{4}) он будет равен (-)(frac{sqrt{2}}{2}) (приблизительно (-0,71)).

Косинус для других часто встречающихся в практике чисел смотри в тригонометрической таблице.

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Благодаря числовой окружности можно определять косинус не только острого угла, но и тупого, отрицательного, и даже большего, чем (360°) (полный оборот). Как это делать — проще один раз увидеть, чем (100) раз услышать, поэтому смотрите картинку.

Теперь пояснение: пусть нужно определить косинус угла КОА с градусной мерой в (150°). Совмещаем точку О с центром окружности, а сторону ОК – с осью (x). После этого откладываем (150°) против часовой стрелки. Тогда ордината точки А покажет нам косинус этого угла.

Если же нас интересует угол с градусной мерой, например, в (-60°) (угол КОВ), делаем также, но (60°) откладываем по часовой стрелке.

И, наконец, угол больше (360°) (угол КОС) — всё аналогично тупому, только пройдя по часовой стрелке полный оборот, отправляемся на второй круг и «добираем нехватку градусов». Конкретно в нашем случае угол (405°) отложен как (360° + 45°).

Несложно догадаться, что для откладывания угла, например, в (960°), надо сделать уже два оборота ((360°+360°+240°)), а для угла в (2640°) — целых семь.

Стоит запомнить, что:

Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.

Знаки косинуса по четвертям

С помощью оси косинусов (то есть, оси абсцисс, выделенной на рисунке красным цветом) легко определить знаки косинусов по четвертям числовой (тригонометрической) окружности:

— там, где значения на оси от (0) до (1), косинус будет иметь знак плюс (I и IV четверти – зеленая область),
— там, где значения на оси от (0) до (-1), косинус будет иметь знак минус (II и III четверти – фиолетовая область).

Пример. Определите знак (cos 1).
Решение: Найдем (1) на тригонометрическом круге. Будем отталкиваться от того, что (π=3,14). Значит единица, примерно, в три раза ближе к нулю (точке «старта»).

Если провести перпендикуляр к оси косинусов, то станет очевидно, что (cos⁡1) – положителен.
Ответ: плюс.

Связь с другими тригонометрическими функциями:

— синусом того же угла (или числа): основным тригонометрическим тождеством (sin^2⁡x+cos^2⁡x=1)
— тангенсом того же угла (или числа): формулой (1+tg^2⁡x=)(frac{1}{cos^2⁡x})
— котангенсом и синусом того же угла (или числа): формулой (ctgx=)(frac{cos{x}}{sin⁡x})
Другие наиболее часто применяемые формулы смотри здесь.

Функция (y=cos{x})

Если отложить по оси (x) углы в радианах, а по оси (y) — соответствующие этим углам значения косинуса, мы получим следующий график:

График данной функции называется косинусоида и обладает следующими свойствами:

— область определения – любое значение икса: (D(cos{⁡x} )=R)
— область значений – от (-1) до (1) включительно: (E(cos{x} )=[-1;1])
— четная: (cos⁡(-x)=cos{x})
— периодическая с периодом (2π): (cos⁡(x+2π)=cos{x})
— точки пересечения с осями координат:
ось абсцисс: (()(frac{π}{2})(+πn),(;0)), где (n ϵ Z)
ось ординат: ((0;1))
— промежутки знакопостоянства:
функция положительна на интервалах: ((-)(frac{π}{2})(+2πn;) (frac{π}{2})(+2πn)), где (n ϵ Z)
функция отрицательна на интервалах: (()(frac{π}{2})(+2πn;)(frac{3π}{2})(+2πn)), где (n ϵ Z)
— промежутки возрастания и убывания:
функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z)
функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z)
— максимумы и минимумы функции:
функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z)
функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).

Смотрите также:

Синус
Тангенс
Котангенс
Решение уравнения (cos⁡x=a)

Источник

Содержание материала

Определение косинуса угла
Видео
Определение угла с помощью косинуса
Косинус любого угла
Производные
Тригонометрическое определение
Угол поворота
Тригонометрические функции углового и числового аргумента
Функция (y=cos{x})

Определение косинуса угла

Определение

Косинус — это прилежащая сторона катет к гипотенузе, обозначается как (cos).

Угловые значения функции в градусах (cos):

[cos 0^{circ}=1 ; cos 30^{circ}=frac{sqrt{3}}{2} ; cos 45^{circ}=frac{sqrt{2}}{2} ; cos 60^{circ}=frac{1}{2} ;][cos 90^{circ}=0 ; cos 120^{circ}=-frac{1}{2} ; cos 135^{circ}=-frac{sqrt{2}}{2} ; cos 150^{circ}=-frac{sqrt{3}}{2} ;][cos 180=-1 ; cos 210^{circ}=-frac{sqrt{3}}{2} ; cdot cos 225^{circ}=-frac{sqrt{2}}{2} ;][cos 240^{circ}=-frac{1}{2} ; cos 270^{circ}=0 ; cos 300^{circ}=frac{1}{2} ; . cos 315^{circ}=frac{sqrt{2}}{2} ;][cos 330^{circ}=frac{sqrt{3}}{2} ; cos 360^{circ}=1]

Формулы кратности значения угла:

[cos 2 a=cos ^{2} a-sin ^{2} a][cos 2 a=1-sin ^{2} a][cos 2 a=2 cos ^{2} a-1][cos 3 a=cos ^{3} a-3 sin ^{2} a][cos 3 a=-3 cos a+4 cos ^{3} a]

Формулы угла, определяющие половину тригонометрического значения (половинного угла):

[cos ^{2} frac{a}{2}=frac{1+cos a}{2}]

Видео

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Косинус любого угла

Стоит запомнить, что:

Производные

( ( sin x )’ = cos x )( ( cos x )’ = — sin x ). Вывод формул > > >

Производные n-го порядка:( left( sin x right)^{(n)} = sinleft( x + ndfrac{pi}2 right) )( left( cos x right)^{(n)} = cosleft( x + ndfrac{pi}2 right) ).

Тригонометрическое определение

С помощью формул, указанных выше, можно найти синус и косинус острого угла. Но нужно научиться вычислять синус и косинус угла произвольной величины. Прямоугольный треугольник не даёт такой возможности (тупого угла, например, в нём быть не может); следовательно, нужно более общее определение синуса и косинуса, содержащее указанные формулы как частный случай.

На помощь приходит тригонометрическая окружность. Пусть дан некоторый угол; ему отвечает одноимённая точка на тригонометрической окружности.

Рис. 2. Тригонометрическое определение синуса и косинуса

Косинус угла — это абсцисса точки. Синус угла — это ордината точки.

На рис. 2 угол взят острым, и легко понять, что данное определение совпадает с общим геометрическим определением. В самом деле, мы видим прямоугольный треугольник с единичной гипотенузой O и острым углом. Прилежащий катет этого треугольника есть cos (сравните с рис. 1) и одновременно абсцисса точки ; противолежащий катет есть sin (как на рис. 1) и одновременно ордината точки.

Но теперь мы уже не стеснены первой четвертью и получаем возможность распространить данное определение на любой угол . На рис. 3 показано, что такое синус и косинус угла во второй, третьей и четвёртой четвертях.

Рис. 3. Синус и косинус во II, III и IV четвертях

Угол поворота

Определения, данные выше, относятся к острым углам. В тригонометрии вводится понятие угла поворота, величина которого, в отличие от острого угла, не ограничена рамками от 0 до 90 градусов.Угол поворота в градусах или радианах выражается любым действительным числом от —∞ до +∞.

Тригонометрические функции углового и числового аргумента

Каждому значению угла α соответствует определенное значение синуса и косинуса этого угла. Также, как всем углам α, отличным от α = 90 ° + 180 ° · k , k ∈ Z ( α = π 2 + π · k , k ∈ Z ) соответствует определенное значение тангенса. Котангенс, как сказано выше, определен для всех α, кроме α = 180 ° · k , k ∈ Z ( α = π · k , k ∈ Z ).

Можно сказать, что sin α, cos α, tg α, ctg α — это функции угла альфа, или функции углового аргумента.

Аналогично можно говорить о синусе, косинусе, тангенсе и котангенсе, как о функциях числового аргумента. Каждому действительному числу t соответствует определенное значение синуса или косинуса числа t. Всем числам, отличным от π 2 + π · k , k ∈ Z соответствует значение тангенса. Котангенс, аналогично, определен для всех чисел, кроме π · k , k ∈ Z.

Основные функции тригонометрии

Синус, косинус, тангенс и котангенс — основные тригонометрические функции.

Из контекста обычно понятно, с каким аргументом тригонометрической функции (угловой аргумент или числовой аргумент) мы имеем дело.

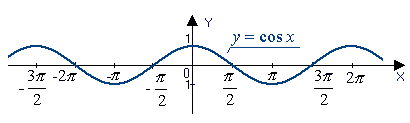
Функция (y=cos{x})

График данной функции называется косинусоида и обладает следующими свойствами:

— область определения – любое значение икса: (D(cos{⁡x} )=R) — область значений – от (-1) до (1) включительно: (E(cos{x} )=[-1;1]) — четная: (cos⁡(-x)=cos{x}) — периодическая с периодом (2π): (cos⁡(x+2π)=cos{x}) — точки пересечения с осями координат: ось абсцисс: (()(frac{π}{2})(+πn),(;0)), где (n ϵ Z) ось ординат: ((0;1)) — промежутки знакопостоянства: функция положительна на интервалах: ((-)(frac{π}{2})(+2πn;) (frac{π}{2})(+2πn)), где (n ϵ Z) функция отрицательна на интервалах: (()(frac{π}{2})(+2πn;)(frac{3π}{2})(+2πn)), где (n ϵ Z) — промежутки возрастания и убывания: функция возрастает на интервалах: ((π+2πn;2π+2πn)), где (n ϵ Z) функция убывает на интервалах: ((2πn;π+2πn)), где (n ϵ Z) — максимумы и минимумы функции: функция имеет максимальное значение (y=1) в точках (x=2πn), где (n ϵ Z) функция имеет минимальное значение (y=-1) в точках (x=π+2πn), где (n ϵ Z).

Смотрите также:

Синус Тангенс Котангенс Решение уравнения (cos⁡x=a)

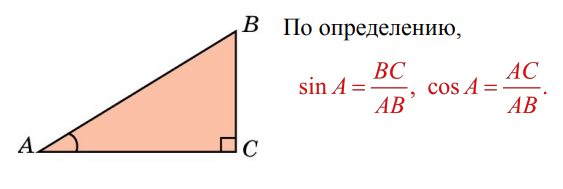
Функция косинуса: свойства и значения функции косинус

Определение

Функцией косинуса называют элементарную тригонометрическую функцию, выражающую зависимость угла при вершине треугольника от отношения прилежащей его стороны к гипотенузе.

Основные свойства функции косинус следующие:
1. Область определения функции косинуса (значений, которые может принимать аргумент x) – множество всех действительных чисел;
2. Значения функции косинус – это (+1) и (-1) и множество действительных чисел между ними.
3. Наименьшее значение функции косинус равно 1, а наибольшее – (-1);
4. Функция чётная, т. е. cos(-x) = cos(x);
5. Функция периодическая. Её период равен 2π;
6. Наибольшего своего значения функция косинус x достигает в точках x=2πk;
7. Наименьшее значение функции косинус x будет в точках x= π/2+2πk;
8. Область возрастания функции cos(x): -π+2πk<=x<=2πk;
9. Область убывания функции cos(x): 2πk<= π+2πk;
10. Функция не имеет разрывов, т. е. непрерывна.

График функции косинус

Графиком функции является косинусоида. Он получается из графика синуса с помощью параллельного переноса на расстояние [frac{pi}{2}] влево. Он выглядит следующим образом:

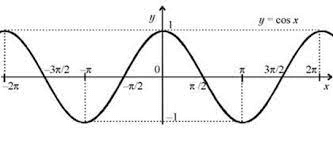
Как построить график функции косинус икс

График функции косинуса можно построить следующим образом:

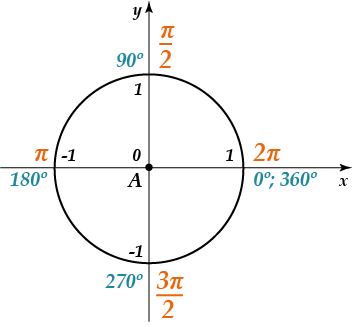
Используем данные единичной окружности, приведённой на рисунке выше.

Из рисунка единичной окружности видно, что в точке ноль ордината функции равна единице. В точке π/2 по оси X значение Y равно 0. В точке π по оси X ордината равна (-1). В точке 3π/2 значение функции снова равно 0, а в точке 2π значение по оси X равно 1. Отметим все названные точки.

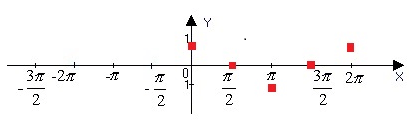
Соединим их плавной линией

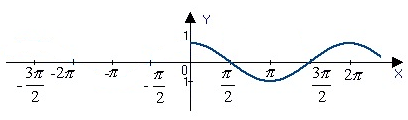
Т. к. наша функция чётная (свойство №4), её график симметричен оси Y. Зеркально отразим его. Помимо этого нам известно, что период функции равен 2π. Из данного свойства следует неограниченная повторяемость кусочка функции между 0 и 2π в обе стороны вдоль оси X. График функции косинус x построен.

Нет времени решать самому?

Наши эксперты помогут!

Как найти значение функции косинуса при x равном 45 градусам

Построим прямоугольный треугольник с катетами, равняющимися единице. Сумма углов любого треугольника, как известно, равна 180 градусам. Если вычтем из них прямой угол, получим сумму двух оставшихся углов. Это углы при вершинах A и B. Так как катеты равны, то и выше названные углы равны и каждый из них составляет (180 – 90)/2 = 45 градусов.

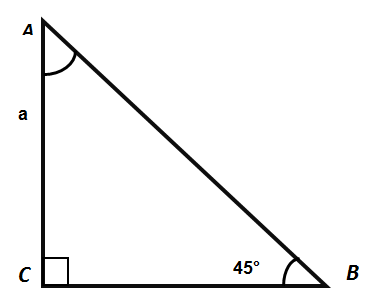
По теореме Пифагора гипотенуза его в этом случае будет равна [c=sqrt{a^{2}+a^{2}}=sqrt{1+1}=sqrt{2}]

Из определения косинуса находим [cos (a)=1 / sqrt{2}]

После вычисления и округления числа получим 0,7071. Это и есть косинус 45 градусов.

Источник

Уравнения разложения тригонометрических функций:квадрат синус альфа, косинус альфа, тангенс альфа, котангенс альфа.

Формулы преобразования функций двойного угла (2α) в выражение через одинарный угол (α)

sin(2α)- через sin и cos:

sin(2α)- через tg и ctg:

cos(2α)- через sin и cos:

cos(2α)- через tg и ctg:

tg(2α) и сtg(2α):

Формулы преобразования функций (синус, косинус, тангенс, котангенс), тройного угла (3α) в выражение через одинарный угол (α):

Тригонометрические формулы преобразования разности аргументов

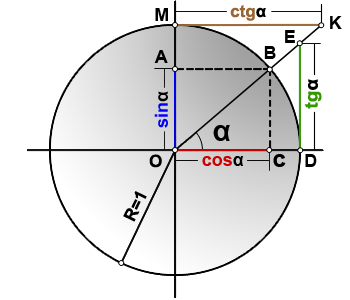
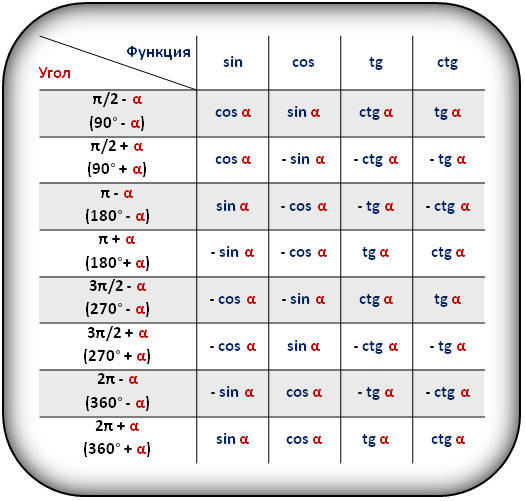
sin(α)=OA

cos(α)=OC

tg(α)=DE

ctg(α)=MK

R=OB=1

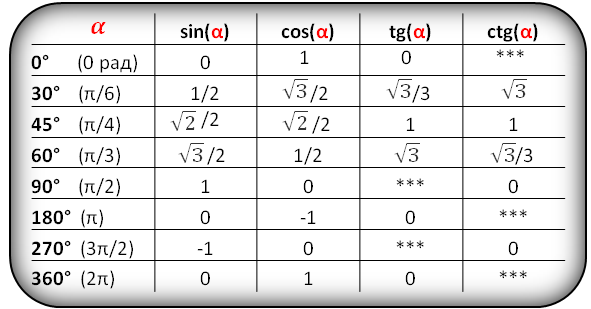
Значения функций для некоторых углов, α

В таблице показаны формулы приведения для тригонометрических функций (sin, cos, tg, ctg).

Источник

Онлайн-калькулятор cos бесплатного помогает вычислить значение косинуса заданного угла в градусах, радианах, миллирадианах и π радианах. Здесь у нас есть для вас гораздо больше, включая то, как найти кривую косинуса, некоторый элементарный закон косинуса и многое другое! Итак, давайте начнем с общего определения косинуса.

Что такое косинус в математике?

В математике тригонометрические функции – это действительные функции, относящиеся к прямоугольному треугольнику с двумя сторонами длины и одной гипотенузой. Предполагая прямоугольный треугольник, функция угла cos (x) определяется как длина смежной стороны, деленная на длину гипотенузы. Значение этой тригонометрической функции cos (x) для данного угла можно вычислить с помощью калькулятор cos. Кроме того, диапазон косинуса равен (- 1 ≤ cos ≤ 1 ), а период косинуса равен (2π ).

Формула косинуса:

Формула для функции косинуса:

$$ cos (θ) = frac { text {смежный} b} { text {hypotenuse} c} $$

Чтобы решить cos вручную, просто используйте значение смежной длины и разделите его на гипотенузу.

Кроме того, онлайн-калькулятор секущей используется для нахождения секущей заданного угла в градусах, радианах или π радианах.

Как найти косинус угла?

Поскольку косинус угла θ – это отношение между соседней длиной угла и гипотенузой, примените следующую формулу, чтобы найти косинус угла:

$$ cos (α) = frac {b} {c} $$

Пример 1:

Рассчитать значение cos θ?

Решение:

Если длина соседней стороны равна 12, а значение гипотенузы равно 6, то согласно формуле cos:

[cos θ = frac {12} {6} = 2 ]

Пример 2:

Найдите значения Cos 60 °.

Решение:

Используя таблицу косинусов или калькулятор,

[Cos 60 ° = frac {1} {2} = 0,5 ]

Вы также можете использовать cos калькулятор для безошибочного расчета.

График косинуса:

График косинуса представляет собой повторяющуюся кривую вверх / вниз. Эта кривая называется косинусоидальной волной. При построении графика всегда помните:

Кривая начнется с 0 углов.
Как только кривая начнется, она сначала уменьшится до значения -1.
После уменьшения кривая увеличится до значения 1, а затем весь процесс будет продолжаться без ограничений.

Таблица для косинуса:

Значение функции косинуса для всех общих углов можно быстро выбрать из следующей таблицы для быстрых вычислений:

Градусы (°)	Радианы	cos (x)
180°	π	-1
150°	5π/6	-√3/2
135°	3π/4	-√2/2
120°	2π/3	-1/2
90°	π/2	0
60°	π/3	1/2
45°	π/4	√2/2
30°	π/6	√3/2
0°	0	1

Как работает Cosine Calculator?

Этот калькулятор cos показывает, как быстро найти косинус всего за два шага.

Более того, онлайн-калькулятор синусов поможет вам определить тригонометрические значения синуса для заданного угла в градусах, радианах или π радианах.

Вход:

Введите значение заданного угла θ.
На втором этапе просто выберите градус, радиан, м радиан или пи (π) радиан из раскрывающегося меню.
Нажмите кнопку «Рассчитать».

Выход:

Этот cos калькулятор определит следующий результат, используя формулу косинуса и таблицу.

Отображается значение косинуса в радианах, градусах, м радианах или пи (π) радианах.
Он отображает ответы в простейшей форме.
Единица измерения угла будет предоставлена так же, как и ваш ввод.

FAQs:

Для чего используется косинус?

Если у вас есть треугольник и вы хотите связать все его три стороны с одним углом, вам нужно применить правило косинуса. Однако, чтобы найти длину стороны, вы должны знать две другие стороны, а также противоположный угол.

Для чего в реальной жизни используется косинус?

Косинус тригонометрической функции обычно используется для определения местоположения и расчета расстояний в системе GPS смартфонов и устройств IOS. Кроме того, он также может использоваться в космических полетах и баллистических траекториях.

Почему Cos положительный?

Cos помечен как положительный по той причине, что θ всегда будет измеряться от положительной оси x.

Зачем нужны тригонометрические функции?

Практически все тригонометрические навыки помогают студентам, которые работают со сложными углами и размерами за сравнительно короткое время. Они также могут быть реализованы во многих других областях. такие как:

Архитектура
Инженерное дело
Наук
Математика и др.

Заключение:

Что ж, благодаря калькулятор cos, который обеспечивает бесплатную поддержку для вычисления значения функции косинуса, когда мы захотим. Кроме того, это отличный выбор для всех тех студентов и профессионалов, которые с энтузиазмом знакомятся с новыми вещами и хотят получить больше знаний о тригонометрии. Так что просто возьмите в руки этот калькулятор, чтобы получать компенсацию за него.

Other Languages: Cosine Calculator, Cos Hesaplama, Cosinus Kalkulator, Kalkulator Cosinus, Cosinus Rechner, Cos 計算, Cosinus Kalkulačka, Calcul Cos, Calcular Coseno, Calcolo Coseno.

Источник

Аргумент и значение

Косинус острого угла

Косинус острого угла можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к гипотенузе.

Косинус острого угла больше (0) и меньше (1)

Косинус числа

Значение косинуса всегда лежит в пределах от (-1) до (1). При этом вычислен косинус может быть для абсолютно любого угла и числа.

Косинус любого угла

Косинус прямого угла равен нулю. Косинус тупого угла — отрицателен.

Знаки косинуса по четвертям

Связь с другими тригонометрическими функциями:

Функция (y=cos{x})

Определение косинуса угла

Видео

Определение угла с помощью косинуса

Косинус любого угла

Производные

Тригонометрическое определение

Угол поворота

Тригонометрические функции углового и числового аргумента

Функция (y=cos{x})

Теги

Функция косинуса: свойства и значения функции косинус

График функции косинус

Как построить график функции косинус икс

Как найти значение функции косинуса при x равном 45 градусам

Что такое косинус в математике?

Формула косинуса:

Как найти косинус угла?

Пример 1:

Пример 2:

График косинуса:

Таблица для косинуса:

Как работает Cosine Calculator?

Вход:

Выход:

FAQs:

Для чего используется косинус?

Для чего в реальной жизни используется косинус?

Почему Cos положительный?

Зачем нужны тригонометрические функции?

Заключение: