Как найти косинус угла авс в треугольнике

Определение косинуса угла

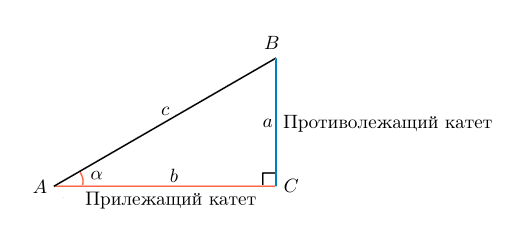
Косинусом угла в прямоугольном треугольнике называют отношение прилежащего катета к гипотенузе.

Для простоты запоминания можно дать такое определение: косинус угла — это отношение ближнего от рассматриваемого угла катета к гипотенузе.

В случае с рисунком, описанным выше: cos⁡α=bccosalpha=frac{b}{c}

Задача 1

Гипотенуза прямоугольного треугольника равна 10 см10text{ см}. Один из катетов равен 6 см6text{ см}. Найдите косинус угла, прилежащего к наибольшему катету.

Решение

Пользуясь теоремой Пифагора вычислим длину неизвестного нам катета.

a2+b2=c2a^2+b^2=c^2

62+b2=1026^2+b^2=10^2

36+b2=10036+b^2=100

b2=64b^2=64

b=8b=8

Катет bb длиннее катета aa. Нам нужно найти косинус угла, прилежащего к наибольшему катету, то есть, к катету bb:

cos⁡α=bc=810=0.8cosalpha=frac{b}{c}=frac{8}{10}=0.8

Ответ

0.8

Задача 2

Две стороны треугольника равны 4 см4text{ см} и 9 см9text{ см}. Периметр его равен 25 см25text{ см}.
Найдите косинус угла, прилежащего к неизвестной стороне и стороне с длиной 4 см4text{ см}.

Решение

Найдем третью сторону треугольника. Так как известен периметр, это будет легко сделать:

P=a+b+cP=a+b+c

25=9+4+c25=9+4+c

c=12c=12

При нахождении косинуса угла нам поможет следствие из теоремы косинусов, которое выглядит так:

cos⁡α=b2+c2−a22⋅b⋅c=42+122−922⋅4⋅12=16+144−8196=7996≈0.82cosalpha=frac{b^2+c^2-a^2}{2cdot bcdot c}=frac{4^2+12^2-9^2}{2cdot 4cdot 12}=frac{16+144-81}{96}=frac{79}{96}approx0.82

Ответ

0.820.82

Решение задач по математике от экспертов сайта Студворк!

Тест по теме “Вычисление косинуса”

Косинус в треугольнике

Что такое косинус в треугольнике? Как найти косинус острого угла в прямоугольном треугольнике?

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Например, для угла A треугольника ABC

Соответственно, косинус угла A в треугольнике ABC — это

Для угла B треугольника ABC

прилежащим является катет BC.

Соответственно, косинус угла B в треугольнике ABC

равен отношению BC к AB:

Таким образом, косинус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины прилежащего катета на длину гипотенузы.

Длины отрезков — положительные числа, поэтому косинус острого угла прямоугольного треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то косинус острого угла прямоугольного треугольника — число, меньшее единицы.

Косинус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

Косинус зависит от величины угла.

Если в треугольнике изменить длины сторон, но не изменять угол, значение косинуса этого угла не изменится.

в треугольниках ABC и FPK

Косинус угла в произвольном (не прямоугольном треугольнике) определяется через теорему косинусов. О том, как это делать, мы будем говорить позже.

Теорема косинусов и синусов

О чем эта статья:

Формулировка и доказательство теоремы косинусов

Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.

Формула Теоремы Пифагора:

a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.

Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Формула теоремы косинусов:

a 2 = b 2 + c 2 — 2bc cos α

В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:

В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).

BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2

cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.

Что и требовалось доказать.

Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.

С помощью теоремы косинусов можно найти косинус угла треугольника:

• Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
• Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
• Когда b 2 + c 2 — a 2

Сформулируем еще одно доказательство теоремы косинусов.

Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:

• AD = b × cos α,
• DB = c – b × cos α.

Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:

• h 2 = b 2 — (b × cos α) 2
• h 2 = a 2 — (c – b × cos α) 2

Приравниваем правые части уравнений:

• b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2

• a 2 = b 2 + c 2 — 2bc × cos α

Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.

Определим стороны b и c:

• b 2 = a 2 + c 2 — 2ac × cos β;
• c 2 = a 2 + b 2 — 2ab × cos γ.

Формулировка теоремы для каждой из сторон треугольника

Теорема косинусов справедлива для всех сторон треугольника, то есть:

a 2 = b 2 + c 2 — 2bc cos α

b 2 = c 2 + a 2 — 2ca cos β

c 2 = a 2 + b 2 — 2ab cos γ

Теорема косинусов может быть использована для любого вида треугольника.

Косинусы углов треугольника

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

Определение угла с помощью косинуса

А теперь обратим внимание на углы.

Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).

Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.

Рассмотрение пределов изменения cos α и sin α

Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.

Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α

Примеры решения задач

При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.

Пример 1. Дан треугольник АВС. Найти длину СМ.

∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.

Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:

Из треугольника СМВ по теореме косинусов найдём СМ:

Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.

• Если c 2 2 + b 2 , то ∠C — острый.

Что такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Синус, косинус и тангенс острого угла прямоугольного треугольника.

Приветствую Вас дорогие учащиеся.

Сейчас рассмотрим что же такое синус, косинус, тангенс и котангенс в прямоугольном треугольнике?

Это тема не сложная, главное это запомнить правила. И так начнем:

Вспомним, что такое прямоугольный треугольник?

Прямоугольным треугольником, называется треугольник у которого один из углов прямой (составляет 90 градусов). Две стороны которые прилежат к прямому углу, называются катетами, а сторона лежащая напротив прямого угла, называется гипотенузой.

Синус (sin(a)) — это отношение противолежащего катета к гипотенузе;

Косинус (cos(a)) — это отношение прилежащего катета к гипотенузе;

Тангенс (tg(a)) — это отношение противолежащего катета к прилежащему катету;
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу;

Котангенс (ctg(a)) — это отношение прилежащего катета к противолежащему.
Другое (равносильное) определение: котангенсом острого угла называется отношение косинуса угла к его синусу;

Пусть дан прямоугольный треугольник ABC с прямым углом C.

Найти sin(a); cos(a); tg(a); ctg(a) Отношение сторон в прямоугольном треугольнике

Аналогично рассуждаем относительно угла B.

Найти sin(b); cos(b); tg(b); ctg(b) Отношение сторон в прямоугольном треугольнике

Пример:

Найти тангенс угла С (tg(C)) треугольника ABC.

Хочешь готовиться к экзаменам бесплатно? Репетитор онлайн бесплатно. Без шуток. ЗДЕСЬ

источники:

http://skysmart.ru/articles/mathematic/teorema-kosinusov-i-sinusov

http://tutomath.ru/uroki/sinus-kosinus-tangens.html

Что такое косинус в треугольнике? Как найти косинус острого угла в прямоугольном треугольнике?

Определение

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

  Например, для угла A треугольника ABC

прилежащий катет — это AC.

Соответственно, косинус угла A в треугольнике ABC — это

   

  Для угла B треугольника ABC

прилежащим является катет BC.

Соответственно,  косинус угла B в треугольнике ABC

равен отношению BC к AB:

   

Таким образом, косинус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины прилежащего катета на длину гипотенузы.

Длины отрезков — положительные числа, поэтому косинус острого угла прямоугольного треугольника также является положительным числом.

Поскольку длина катета всегда меньше длины гипотенузы, то косинус острого угла прямоугольного треугольника — число, меньшее единицы.

Вывод:

Косинус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:

   

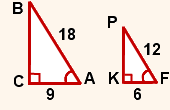
Косинус зависит от величины угла.

Если в треугольнике изменить длины сторон, но не изменять угол, значение косинуса этого угла не изменится.

Например,

в треугольниках ABC и FPK

∠A=60º, ∠F=60º.

   

   

Косинус угла в произвольном (не прямоугольном треугольнике) определяется через теорему косинусов. О том, как это делать, мы будем говорить позже.

Чтобы найти синус и косинус угла в прямоугольном треугольнике, нужно вспомнить определения. Синус угла равен отношению противоположного катета к гипотенузе.  Косинус угла равен отношению прилежащего катета к гипотенузе.

Если у нас есть треугольник (ABC), рисунок выше, для которого (С)— прямой угол, то сторонами (BC) и (AC) будут катеты, а сторона (AB) — гипотенуза. Следовательно, по определению, синус угла (ABC) равен отношению катета (АС) к гипотенузе: синус угла (ABC=frac{AC}{AB})  и синус угла (BAC=frac{BC}{AB}).

косинус угла (ABC=frac{BC}{AB}) и косинус угла (BAC=frac{AC}{AB}).

Чаще всего известно лишь часть данных, например катет и угол, нужно выразить неизвестную величину. Подумайте, как это сделать.

Берем тот же треугольник (ACB) с прямым углом (С) в котором мы знаем катеты: (BC = 3), (AC = 4). Для вычисления синуса угла с необходимо разделить катет на гипотенузу: (sin ∠BAC = frac{BC} { AB}).

Гипотенузу вычислим из теоремы Пифагора: (AC^2+BC^2=AB^2)  (9+16=25) (AB=5) откуда синус равен:

(sin ∠ BAC = frac{3}{5})

Самое главное помнить, что сумма всех углов в треугольнике равна 180 °.Найдем угол  (ABC):

(180)° (-30)° (-90)°(=60)°.

(sin) (60)° возьмем из табличного значения: (frac{ sqrt{3}} { 2})

Табличные значения (sin) и (cos):

Чтобы лучше понимать значения табличные значения синуса и косинуса представим их на координатной окружности: где ось ординат ((y)) линия синуса, ось абсцисс ((x)) – линия косинуса. Если вы забыли значения синуса и косинуса (90) и (180) можно нарисовать рисунок и посмотреть значения, не забывая, что на первом месте стоит (x), на втором (y)   ((x,y));

Теорема синусов:

Теорема косинусов:

Формулировка и доказательство теоремы косинусов

Вспомним теорему Пифагора (рис. 1).

Рис. 1. Иллюстрация к теореме

 

К данному выражению прибавим и отнимем квадрат второго катета:

 

 

Но так как

 ,

то

 

Эту формулу мы получили для катетов в прямоугольном треугольнике, но оказывается, что аналогичная связь между стороной а и косинусом противолежащего угла справедлива и для произвольного треугольника, это покажет нам теорема косинусов. Она звучит так:

Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.

Чтобы записать формулой данную теорему, принимаем стандартные значения.

Рис. 2. Иллюстрация к теореме

 (рис. 2)

В доказательстве теоремы используем формулу длины отрезка в координатах. Рассмотрим данную формулу.

Рис. 3. Иллюстрация к теореме

 

Рис. 4. Иллюстрация к теореме

В доказательстве теоремы косинусов BC – это сторона треугольника АВС, обозначенная а (рис. 4). Вводим удобную систему координат и находим координаты нужных нам точек. У точки В координаты (с;0). А координаты точки С – (b, при

 – основное тригонометрическое тождество.

 

Что и требовалось доказать.

Формулировка теоремы для каждой из сторон заданного треугольника

Эта теорема справедлива для всех сторон треугольника (рис. 5), то есть:

Рис. 5. Иллюстрация к теореме

 

 

 

Таким образом, теорема косинусов обобщает теорему Пифагора, то есть используется для произвольного треугольника.

Описание формулы косинуса угла из теоремы косинусов

Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:

 

 

 

Аналогично:

 

 

Определение угла с помощью косинуса

Теперь найдём углы.

Вспомним, что косинус угла из промежутка  однозначно определяет угол (в отличие от синуса).

    

Рис. 6. Иллюстрация к теореме

Поясним это. Дана единичная полуокружность (рис. 6). Если нам задан , то нам задана точка на верхней полуокружносте и задан угол α. Следовательно,  однозначно определяет точку М(), и однозначно определяется угол .

Рассмотрение пределов изменения

Рассмотрим пределы изменения синуса и косинуса α, если α – угол треугольника, то есть он лежит в пределах от 0.

Рис. 7. Иллюстрация к теореме

Предел изменения косинуса (рис. 7):

 

Предел изменения синуса (рис. 7):

 

Если , то

Если  

Если

Теорема косинусов активно используется при решении задач, вот одна из них.

Задача 1 с применением теоремы косинусов

Рис. 8. Иллюстрация к задаче

Дано: Треугольник АВС. , АВ = 9, ВС = 3, ,  где М- точка на гипотенузе  АВ (рис. 8).

Найти: СМ

Решение:

Так как АМ+МВ = 9, а  , то АМ = 3, МВ = 6.

Из треугольника АВС найдём :

 

Из треугольника СМВ по теореме косинусов найдём СМ:

 

 

 

Задача 2 с применением теоремы косинусов

Дано: треугольник АВС, со сторонами – 5, 8, 10 (рис. 9).

Найти: остроугольный ли треугольник.

Решение:

Рис. 9. Иллюстрация к задаче       

В треугольнике АВС наибольшая сторона ВС. Напротив наибольшей стороны находится наибольший угол, то есть следует сначала оценить его. .

По теореме косинусов:

 

 

Косинус угла α меньше 0, следовательно,  тупой, поэтому данный треугольник АВС не остроугольный.

Задача 3 на доказательство с помощью теоремы косинусов

Дано: треугольник АВС,  (рис. 10)

Доказать:тупой.

Доказательство:

Рис. 10. Иллюстрация к задаче

Для доказательства достаточно написать теорему косинусов для угла :

 

Так как , то , следовательно, тупой. Что и требовалось доказать.

Данная задача показывает, что с помощью теоремы косинусов можно определить тупой угол или острый. Рисунки 10,11 и 12 иллюстрируют это.

Рис. 11. Иллюстрация к задаче

Если  , то  (рис. 11)

 

Рис. 12. Иллюстрация к задаче

Если  , то  острый (рис. 12).

Подведение итогов урока

На данном уроке мы рассмотрели и доказали теорему косинусов и решили задачи с её применением.

Список литературы

1. Атанасян Л. С. и др. Геометрия 7–9 классы. Учебник для общеобразовательных учреждений. – М.: Просвещение, 2010.
2. Фарков А. В. Тесты по геометрии: 9 класс. К учебнику Л. С. Атанасяна и др. – М.: Экзамен, 2010.
3. Погорелов А. В. Геометрия, уч. для 7–11 кл. общеобр. учрежд. – М.: Просвещение, 1995.

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Profmeter.com.ua (Источник).
2. Webmath.ru (Источник).
3. Treugolniki.ru (Источник).

Домашнее задание

1. В треугольнике  ,  и . Найти угол, противолежащий стороне AB.
2. Задан треугольник , длины сторон которого , , . Найти длину третьей стороны рассматриваемого треугольника.
3. В произвольном треугольнике АВС биссектриса ВЕ перпендикулярна медиане АD, причем ВЕ = AD = 4. Найти стороны треугольника АВС.