Таблица косинусов
Таблица косинусов — это записанные в таблицу посчитанные значения косинусов углов от 0° до 360°. Используя таблицу косинусов Вы сможете провести расчеты даже если под руками не окажется инженерного калькулятора. Чтобы узнать значение косинуса от нужного Вам угла, достаточно найти его в таблице или вычислить с помощью калькулятора.
Калькулятор — косинус угла
cos(°) = 1
Калькулятор — арккосинус угла
arccos() = 0°
Таблица косинусов в радианах
| α | 0 | π6 | π4 | π3 | π2 | π | 3π2 | 2π |
| cos α | 1 | √32 | √22 | 12 | 0 | -1 | 0 | 1 |
Таблица косинусов углов от 0° до 180°
| cos(0°) = 1 cos(1°) = 0.999848 cos(2°) = 0.999391 cos(3°) = 0.99863 cos(4°) = 0.997564 cos(5°) = 0.996195 cos(6°) = 0.994522 cos(7°) = 0.992546 cos(8°) = 0.990268 cos(9°) = 0.987688 cos(10°) = 0.984808 cos(11°) = 0.981627 cos(12°) = 0.978148 cos(13°) = 0.97437 cos(14°) = 0.970296 cos(15°) = 0.965926 cos(16°) = 0.961262 cos(17°) = 0.956305 cos(18°) = 0.951057 cos(19°) = 0.945519 cos(20°) = 0.939693 cos(21°) = 0.93358 cos(22°) = 0.927184 cos(23°) = 0.920505 cos(24°) = 0.913545 cos(25°) = 0.906308 cos(26°) = 0.898794 cos(27°) = 0.891007 cos(28°) = 0.882948 cos(29°) = 0.87462 cos(30°) = 0.866025 cos(31°) = 0.857167 cos(32°) = 0.848048 cos(33°) = 0.838671 cos(34°) = 0.829038 cos(35°) = 0.819152 cos(36°) = 0.809017 cos(37°) = 0.798636 cos(38°) = 0.788011 cos(39°) = 0.777146 cos(40°) = 0.766044 cos(41°) = 0.75471 cos(42°) = 0.743145 cos(43°) = 0.731354 cos(44°) = 0.71934 cos(45°) = 0.707107 |
cos(46°) = 0.694658 cos(47°) = 0.681998 cos(48°) = 0.669131 cos(49°) = 0.656059 cos(50°) = 0.642788 cos(51°) = 0.62932 cos(52°) = 0.615661 cos(53°) = 0.601815 cos(54°) = 0.587785 cos(55°) = 0.573576 cos(56°) = 0.559193 cos(57°) = 0.544639 cos(58°) = 0.529919 cos(59°) = 0.515038 cos(60°) = 0.5 cos(61°) = 0.48481 cos(62°) = 0.469472 cos(63°) = 0.45399 cos(64°) = 0.438371 cos(65°) = 0.422618 cos(66°) = 0.406737 cos(67°) = 0.390731 cos(68°) = 0.374607 cos(69°) = 0.358368 cos(70°) = 0.34202 cos(71°) = 0.325568 cos(72°) = 0.309017 cos(73°) = 0.292372 cos(74°) = 0.275637 cos(75°) = 0.258819 cos(76°) = 0.241922 cos(77°) = 0.224951 cos(78°) = 0.207912 cos(79°) = 0.190809 cos(80°) = 0.173648 cos(81°) = 0.156434 cos(82°) = 0.139173 cos(83°) = 0.121869 cos(84°) = 0.104528 cos(85°) = 0.087156 cos(86°) = 0.069756 cos(87°) = 0.052336 cos(88°) = 0.034899 cos(89°) = 0.017452 cos(90°) = 0 |
cos(91°) = -0.017452 cos(92°) = -0.034899 cos(93°) = -0.052336 cos(94°) = -0.069756 cos(95°) = -0.087156 cos(96°) = -0.104528 cos(97°) = -0.121869 cos(98°) = -0.139173 cos(99°) = -0.156434 cos(100°) = -0.173648 cos(101°) = -0.190809 cos(102°) = -0.207912 cos(103°) = -0.224951 cos(104°) = -0.241922 cos(105°) = -0.258819 cos(106°) = -0.275637 cos(107°) = -0.292372 cos(108°) = -0.309017 cos(109°) = -0.325568 cos(110°) = -0.34202 cos(111°) = -0.358368 cos(112°) = -0.374607 cos(113°) = -0.390731 cos(114°) = -0.406737 cos(115°) = -0.422618 cos(116°) = -0.438371 cos(117°) = -0.45399 cos(118°) = -0.469472 cos(119°) = -0.48481 cos(120°) = -0.5 cos(121°) = -0.515038 cos(122°) = -0.529919 cos(123°) = -0.544639 cos(124°) = -0.559193 cos(125°) = -0.573576 cos(126°) = -0.587785 cos(127°) = -0.601815 cos(128°) = -0.615661 cos(129°) = -0.62932 cos(130°) = -0.642788 cos(131°) = -0.656059 cos(132°) = -0.669131 cos(133°) = -0.681998 cos(134°) = -0.694658 cos(135°) = -0.707107 |
cos(136°) = -0.71934 cos(137°) = -0.731354 cos(138°) = -0.743145 cos(139°) = -0.75471 cos(140°) = -0.766044 cos(141°) = -0.777146 cos(142°) = -0.788011 cos(143°) = -0.798636 cos(144°) = -0.809017 cos(145°) = -0.819152 cos(146°) = -0.829038 cos(147°) = -0.838671 cos(148°) = -0.848048 cos(149°) = -0.857167 cos(150°) = -0.866025 cos(151°) = -0.87462 cos(152°) = -0.882948 cos(153°) = -0.891007 cos(154°) = -0.898794 cos(155°) = -0.906308 cos(156°) = -0.913545 cos(157°) = -0.920505 cos(158°) = -0.927184 cos(159°) = -0.93358 cos(160°) = -0.939693 cos(161°) = -0.945519 cos(162°) = -0.951057 cos(163°) = -0.956305 cos(164°) = -0.961262 cos(165°) = -0.965926 cos(166°) = -0.970296 cos(167°) = -0.97437 cos(168°) = -0.978148 cos(169°) = -0.981627 cos(170°) = -0.984808 cos(171°) = -0.987688 cos(172°) = -0.990268 cos(173°) = -0.992546 cos(174°) = -0.994522 cos(175°) = -0.996195 cos(176°) = -0.997564 cos(177°) = -0.99863 cos(178°) = -0.999391 cos(179°) = -0.999848 cos(180°) = -1 |
Таблица косинусов углов от 181° до 360°
| cos(181°) = -0.999848 cos(182°) = -0.999391 cos(183°) = -0.99863 cos(184°) = -0.997564 cos(185°) = -0.996195 cos(186°) = -0.994522 cos(187°) = -0.992546 cos(188°) = -0.990268 cos(189°) = -0.987688 cos(190°) = -0.984808 cos(191°) = -0.981627 cos(192°) = -0.978148 cos(193°) = -0.97437 cos(194°) = -0.970296 cos(195°) = -0.965926 cos(196°) = -0.961262 cos(197°) = -0.956305 cos(198°) = -0.951057 cos(199°) = -0.945519 cos(200°) = -0.939693 cos(201°) = -0.93358 cos(202°) = -0.927184 cos(203°) = -0.920505 cos(204°) = -0.913545 cos(205°) = -0.906308 cos(206°) = -0.898794 cos(207°) = -0.891007 cos(208°) = -0.882948 cos(209°) = -0.87462 cos(210°) = -0.866025 cos(211°) = -0.857167 cos(212°) = -0.848048 cos(213°) = -0.838671 cos(214°) = -0.829038 cos(215°) = -0.819152 cos(216°) = -0.809017 cos(217°) = -0.798636 cos(218°) = -0.788011 cos(219°) = -0.777146 cos(220°) = -0.766044 cos(221°) = -0.75471 cos(222°) = -0.743145 cos(223°) = -0.731354 cos(224°) = -0.71934 cos(225°) = -0.707107 |
cos(226°) = -0.694658 cos(227°) = -0.681998 cos(228°) = -0.669131 cos(229°) = -0.656059 cos(230°) = -0.642788 cos(231°) = -0.62932 cos(232°) = -0.615661 cos(233°) = -0.601815 cos(234°) = -0.587785 cos(235°) = -0.573576 cos(236°) = -0.559193 cos(237°) = -0.544639 cos(238°) = -0.529919 cos(239°) = -0.515038 cos(240°) = -0.5 cos(241°) = -0.48481 cos(242°) = -0.469472 cos(243°) = -0.45399 cos(244°) = -0.438371 cos(245°) = -0.422618 cos(246°) = -0.406737 cos(247°) = -0.390731 cos(248°) = -0.374607 cos(249°) = -0.358368 cos(250°) = -0.34202 cos(251°) = -0.325568 cos(252°) = -0.309017 cos(253°) = -0.292372 cos(254°) = -0.275637 cos(255°) = -0.258819 cos(256°) = -0.241922 cos(257°) = -0.224951 cos(258°) = -0.207912 cos(259°) = -0.190809 cos(260°) = -0.173648 cos(261°) = -0.156434 cos(262°) = -0.139173 cos(263°) = -0.121869 cos(264°) = -0.104528 cos(265°) = -0.087156 cos(266°) = -0.069756 cos(267°) = -0.052336 cos(268°) = -0.034899 cos(269°) = -0.017452 cos(270°) = -0 |
cos(271°) = 0.017452 cos(272°) = 0.034899 cos(273°) = 0.052336 cos(274°) = 0.069756 cos(275°) = 0.087156 cos(276°) = 0.104528 cos(277°) = 0.121869 cos(278°) = 0.139173 cos(279°) = 0.156434 cos(280°) = 0.173648 cos(281°) = 0.190809 cos(282°) = 0.207912 cos(283°) = 0.224951 cos(284°) = 0.241922 cos(285°) = 0.258819 cos(286°) = 0.275637 cos(287°) = 0.292372 cos(288°) = 0.309017 cos(289°) = 0.325568 cos(290°) = 0.34202 cos(291°) = 0.358368 cos(292°) = 0.374607 cos(293°) = 0.390731 cos(294°) = 0.406737 cos(295°) = 0.422618 cos(296°) = 0.438371 cos(297°) = 0.45399 cos(298°) = 0.469472 cos(299°) = 0.48481 cos(300°) = 0.5 cos(301°) = 0.515038 cos(302°) = 0.529919 cos(303°) = 0.544639 cos(304°) = 0.559193 cos(305°) = 0.573576 cos(306°) = 0.587785 cos(307°) = 0.601815 cos(308°) = 0.615661 cos(309°) = 0.62932 cos(310°) = 0.642788 cos(311°) = 0.656059 cos(312°) = 0.669131 cos(313°) = 0.681998 cos(314°) = 0.694658 cos(315°) = 0.707107 |
cos(316°) = 0.71934 cos(317°) = 0.731354 cos(318°) = 0.743145 cos(319°) = 0.75471 cos(320°) = 0.766044 cos(321°) = 0.777146 cos(322°) = 0.788011 cos(323°) = 0.798636 cos(324°) = 0.809017 cos(325°) = 0.819152 cos(326°) = 0.829038 cos(327°) = 0.838671 cos(328°) = 0.848048 cos(329°) = 0.857167 cos(330°) = 0.866025 cos(331°) = 0.87462 cos(332°) = 0.882948 cos(333°) = 0.891007 cos(334°) = 0.898794 cos(335°) = 0.906308 cos(336°) = 0.913545 cos(337°) = 0.920505 cos(338°) = 0.927184 cos(339°) = 0.93358 cos(340°) = 0.939693 cos(341°) = 0.945519 cos(342°) = 0.951057 cos(343°) = 0.956305 cos(344°) = 0.961262 cos(345°) = 0.965926 cos(346°) = 0.970296 cos(347°) = 0.97437 cos(348°) = 0.978148 cos(349°) = 0.981627 cos(350°) = 0.984808 cos(351°) = 0.987688 cos(352°) = 0.990268 cos(353°) = 0.992546 cos(354°) = 0.994522 cos(355°) = 0.996195 cos(356°) = 0.997564 cos(357°) = 0.99863 cos(358°) = 0.999391 cos(359°) = 0.999848 cos(360°) = 1 |
Свойства тригонометрических функций
Отсюда вытекает много интересных свойств и тригонометрических формул.
Во-первых, надеюсь, все знают, что в прямоугольном треугольнике самая большая сторона – это гипотенуза.
Поэтому из определения синуса и косинуса ((sin(alpha)=frac{a}{c}; quad cos(alpha)=frac{b}{c})) следует, что они всегда меньше единицы, ведь мы катет (меньшую сторону) делим на гипотенузу (большую сторону треугольника). И как мы узнаем позже, синус и косинус всегда больше минус единицы. То есть синус и косинус могут принимать только значения из промежутка:
$$ sin(alpha) in [-1;1];$$
$$ cos(alpha) in [-1;1];$$
Для тангенса и котангенса никаких ограничений нет, они могут принимать абсолютно любые значения.
Теперь выведем несколько формул, без которых нам точно потом не обойтись. Например, можно обратить внимание, что тангенс выражается через деление синуса на косинус, просто расписав их по определению:
$$frac{sin(alpha)}{cos(alpha)}=frac{frac{a}{c}}{frac{b}{c}}=frac{a}{c}*frac{c}{b}=frac{a}{b};$$
А последняя формула есть ни что иное, как определение тангенса:
$$ tg(alpha)=frac{a}{b};$$
Значит
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}.$$
Аналогичные рассуждения можно провести для котангенса:
$$frac{cos(alpha)}{sin(alpha)}=frac{frac{b}{c}}{frac{a}{c}}=frac{b}{c}*frac{c}{a}=frac{b}{a};$$
А котангенс по определению:
$$ctg(alpha)=frac{b}{a};$$
Значит
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}.$$
Кроме этого, легко заметить, что функции тангенса и котангенса взаимно обратны:
$$tg(alpha)*ctg(alpha)=frac{a}{b}*frac{b}{a}=1.$$
А теперь мы подобрались к не самой очевидной тригонометрической формуле, но одной из самых главных во всей тригонометрии. Основное тригонометрическое тождество:
$$sin^2(alpha)+cos^2(alpha)=1. qquad (1)$$
Выводится оно тоже из определений синуса и косинуса с использованием теоремы Пифагора (гипотенуза в прямоугольном треугольнике равна сумме квадратов катетов (c^2=a^2+b^2;)):
$$sin^2(alpha)+cos^2(alpha)=left(frac{a}{c}right)^2+left(frac{b}{c}right)^2=left(frac{a^2}{c^2}right)+left(frac{b^2}{c^2}right)=frac{a^2+b^2}{c^2}=frac{c^2}{c^2}=1.$$
С основным тригонометрическим тождеством вы будете сталкиваться постоянно и в 9-м и в 10-м классах.
И разберем еще две важные формулы:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
Выводится она очень легко, опять же, используя определения тангенса и косинуса. Рекомендую потренироваться и сделать это самим.
$$1+left(frac{a}{b}right)^2=frac{1}{frac{b^2}{c^2}};$$
$$left(frac{b^2}{b^2}right)+left(frac{a^2}{b^2}right)=1*frac{c^2}{b^2};$$
$$frac{b^2+a^2}{b^2}=frac{c^2}{b^2};$$
Используем теорему Пифагора:
$$frac{c^2}{b^2}=frac{c^2}{b^2};$$
Получили верное равенство, значит формула верна.
И вторая аналогичная формула для котангенса:
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)};$$
Вывод один в один, сделайте сами.
Для удобства соберем все формулы вместе.
$$sin^2(alpha)+cos^2(alpha)=1. qquad(1)$$
$$ tg(alpha)=frac{sin(alpha)}{cos(alpha)}. qquad(2)$$
$$ctg(alpha)=frac{cos(alpha)}{sin(alpha)}. qquad(3)$$
$$tg(alpha)*ctg(alpha)=1.qquad(4)$$
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)}. qquad(5)$$
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}. qquad(6)$$
Это далеко не все тригонометрические формулы, их гораздо больше. Но для начала и для 9-го класса этого вполне достаточно.
Зачем же они нужны? Оказывается, эти формулы помогают связать тригонометрические функции между собой. Посмотрите внимательно на первую формулу (1): зная, например, чему равен косинус, можно легко найти синус, и наоборот.
Пример 1
Пусть (cos(alpha) =frac{1}{2}), найдите (sin(alpha)=?)
Берем основное тригонометрическое тождество (формула (1)) и подставляем в него известный по условию задачи (cos(alpha)=frac{1}{2}:)
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(frac{1}{2}right)^2=1;$$
А дальше просто решаем получившееся уравнение относительно синуса:
$$sin^2(alpha)=1-left(frac{1}{2}right)^2;$$
$$sin^2(alpha)=1-frac{1}{4};$$
Приводим к общему знаменателю:
$$sin^2(alpha)=frac{4}{4}-frac{1}{4};$$
$$sin^2(alpha)=frac{3}{4};$$
И здесь внимательно решаем квадратное уравнение:
$$sin(alpha)=pmfrac{sqrt{3}}{2};$$
Обратите внимание на (pm). Синус может быть как положительным, так и отрицательным, так как при подстановке и возведении в квадрат минус сгорает. Значит здесь получается два ответа.
Ответ:(sin(alpha)=pmfrac{sqrt{3}}{2}.)
Аналогично, зная хотя бы одну тригонометрическую функцию, можно найти все остальные, используя тригонометрические формулы. Рассмотрим еще пример:
Пример 2
Пусть (sin(alpha) =frac{1}{3}), найдите (ctg(alpha)=?)
Смотрим на наш список формул и находим такую, в которой есть и синус и котангенс — это формула (6):
$$1+сtg^2(alpha)=frac{1}{sin^2(alpha)}.$$
Подставляем известный из условия синус (sin(alpha) =frac{1}{3}):
$$1+сtg^2(alpha)=frac{1}{left(frac{1}{3}right)^2}.$$
Перевернем правую часть:
$$1+сtg^2(alpha)=left(frac{3}{1}right)^2.$$
$$1+сtg^2(alpha)=9.$$
Теперь решим уравнение и найдем котангенс:
$$сtg^2(alpha)=8.$$
$$сtg(alpha)=pmsqrt{8}=pmsqrt{4}*sqrt{2}=pm2sqrt{2}.$$
Ответ:(сtg(alpha)=pm2sqrt{2}).
Выглядит пугающе, но учить вам это НЕ НУЖНО! В некоторых школах есть изверги, которые заставляют учить такую таблицу, но в этом совершенно нет необходимости. В дальнейшем мы научимся сами выводить все значения тригонометрических функций только из маленькой таблицы.
Обратите внимание, что синус некоторого угла в треугольнике всегда положителен, неважно, тупой или острый угол. А вот косинус, тангенс и котангенс в треугольнике положительны только от острых углов и отрицательны от тупых.
Тут может возникнуть вопрос, как может существовать синус, косинус, тангенс или котангенс от тупого угла, большего чем (90^o), если мы давали определение всех тригонометрических функций через прямоугольный треугольник, в котором нет углов больших (90^o). Ну что ж, да тригонометрические функции существуют для любых углов и острых, и тупых, но для самого начала тригонометрии определения через прямоугольный треугольник нам более чем достаточно. Просто запомните выводы, которые мы сделали в предыдущем абзаце.
Рассмотрим пример на тригонометрию по типу схожий с заданиями ОГЭ. Обычно задачи сводятся просто к нахождению тригонометрической функции некоторого угла, нарисованного на рисунке:
Пример 2
По рисунку определить значение (sin(alpha)=?)
По определению синус в прямоугольном треугольнике – это отношение противолежащего катета к гипотенузе. Первым делом достроим наш синий угол (angle{ABC}) до прямоугольного треугольника, для этого опустим из точки (A) высоту (AH) к (BC). Получили прямоугольный треугольник (AHB). Теперь можем воспользоваться определением синуса:
$$sin(alpha)=frac{AH}{AB};$$
По клеточкам на рисунке найдем длину отрезка (AH=15). А гипотенузу (AB) найти по клеточкам не выйдет, так как она идет по диагонали. Но мы можем найти опять по клеточкам второй катет в прямоугольном треугольнике (BH=12) и применить теорему Пифагора:
$$AB^2=AH^2+BH^2;$$
$$AB^2=15^2+12^2=225+144=369;$$
$$AB=sqrt{369}=3sqrt{41};$$
Подставим в формулу для синуса и найдем его:
$$sin(alpha)=frac{AH}{AB}=frac{15}{3sqrt{41}};$$
Ответ: (sin(alpha)= frac{15}{3sqrt{41}}.)
Разберем еще примеры посложнее на нахождение тригонометрических функций друг через друга. Некоторые даже будут из реального ЕГЭ:
Пример 3
Пусть (tg(alpha)=sqrt{3}), найти (cos(alpha)=?), если известно, что (alpha<90^o).
Задание из ЕГЭ по профильной математике.
Условие аналогично условию в примерах №1 и 2, но появилось еще какое-то ограничение на угол (alpha), пока не будем обращать на него внимания, и решаем как обычно. Воспользуемся формулой (5), в ней есть и косинус, и тангенс, как раз одна из функций нам дана, а другую надо найти:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(sqrt{3})^2=frac{1}{cos^2(alpha)};$$
$$1+3=frac{1}{cos^2(alpha)};$$
$$4=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{4};$$
$$cos(alpha)=pmfrac{1}{2}.$$
У нас опять получилось два ответа из-за квадрата. В условии сказано, что задание из первой части ЕГЭ, а значит два ответа быть не может. Для этого нам и дано, что (alpha<90^o). Это означает, что угол (alpha) острый, а значит косинус у острого угла обязательно должен быть положительный.
Ответ: (cos(alpha)=frac{1}{2}.)
Пример 4
Пусть (tg(alpha) =-2), найти (sin(alpha)=?), при (90^o<alpha<180^o).
Опять обратимся к нашим формулам (1-6) и пытаемся найти такую, в которой есть и синус и тангенс. И тут оказывается, что такой формулы нет. Но нам никто не запрещает, зная тангенс и используя формулу (5), найти косинус:
$$1+tg^2(alpha)=frac{1}{cos^2(alpha)};$$
$$1+(-2)^2=frac{1}{cos^2(alpha)};$$
$$5=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{5};$$
$$cos^2(alpha)=pmsqrt{frac{1}{5}};$$
Так как согласно условию (alpha>90^o), то значение косинуса должно быть отрицательным:
$$cos(alpha)=-sqrt{frac{1}{5}};$$
А потом, уже зная косинус, по основному тригонометрическому тождеству (1) можно найти требуемый в задаче синус:
$$sin^2(alpha)+cos^2(alpha)=1;$$
$$sin^2(alpha)+left(-sqrt{frac{1}{5}}right)^2=1;$$
$$sin^2(alpha)+frac{1}{5}=1;$$
$$sin^2(alpha)=-frac{1}{5}+1;$$
$$sin^2(alpha)=frac{4}{5};$$
$$sin(alpha)=pmsqrt{frac{4}{5}};$$
Синус у нас положительный и при острых ((alpha<90^o)) и при тупых углах ( (90<alpha<180) ):
$$sin(alpha)=sqrt{frac{4}{5}};$$
Ответ: (sin(alpha)=sqrt{frac{4}{5}}.)
Итак, зная значение хотя бы одной из четырех тригонометрических функций, при помощи формул (1-6) можно найти три оставшихся, именно для этого формулы и нужны.
Зная угол (angle{A}=60^o), мы знаем все тригонометрические функции от этого угла. Смотрите в таблицу (1):
$$sin(60^o)=frac{sqrt{3}}{2};$$
$$cos(60^o)=frac{1}{2};$$
$$tg(60^o)=sqrt{3};$$
$$ctg(60^o)=frac{1}{sqrt{3}};$$
С другой стороны, можно расписать функции по определению через отношение сторон в прямоугольном треугольнике:
$$sin(angle{A})=frac{BC}{AB};$$
$$cos(angle{A})=frac{AC}{AB};$$
$$tg(angle{A})=frac{BC}{AC};$$
$$ctg(angle{A})=frac{AC}{BC};$$
Не пугайтесь, все нам не понадобится. Воспользуемся пока формулами:
$$cos(60^o)=frac{1}{2};$$
$$cos(angle{A}=60^o)=frac{AC}{AB};$$
Нам известны косинус (angle{A}) и сторона (AC), а значит, мы можем найти гипотенузу (AB):
$$frac{1}{2}=frac{5}{AB};$$
$$AB=frac{5}{frac{1}{2}}=5*frac{2}{1}=10;$$
Нашли гипотенузу, теперь найдем последнюю сторону (BC). Для этого нам нужна любая формула с (BC), например:
$$sin(angle{A})=frac{BC}{AB};$$
Синус знаем, (AB) только что нашли — выражаем (BC):
$$BC=AB*sin(60^o)=10*frac{sqrt{3}}{2}=5*sqrt{3}.$$
Ответ: (AB=10;) (BC=5*sqrt{3}.)
Подведем итоги. Зная любую сторону в прямоугольном треугольнике и хотя бы один из острых углов, можно найти все остальные стороны при помощи тригонометрии.
Рассмотрим задачу посложнее.
Пример 6
Дан прямоугольный треугольник (bigtriangleup{ABC}), в котором угол (angle{C}=90^o), угол (tg(angle{A})=frac{1}{5}), сторона (AB=13). В треугольнике из прямого угла (angle{C}) проведена высота (CH). Найти (AH).
Первым делом обратите внимание на один очень важный факт. Если провести высоту в прямоугольном треугольнике из прямого угла, то она поделит треугольник еще на два прямоугольных. В нашем случае (bigtriangleup{ACH}) и (bigtriangleup{CHB}) тоже будут прямоугольными. А значит в них выполняются все соотношения для тригонометрических функций.
Например, в (bigtriangleup{ACH}) для угла (angle{A}) противолежащим катетом будет (CH), а прилежащим — сторона (AH), гипотенуза будет соответственно (AC). А значит можно записать формулы, следующие из определения тригонометрических функций:
$$sin(angle{A})=frac{CH}{AC};$$
$$cos(angle{A})=frac{AH}{AC};$$
$$tg(angle{A})=frac{CH}{AH};$$
$$ctg(angle{A})=frac{AH}{CH};$$
Аналогичные соотношения можно записать и для (bigtriangleup{CHB}) и (bigtriangleup{ABC}). Не буду нагромождать, запишите эти соотношения сами в качестве тренировки.
Следующий важный момент, на который следует обратить внимание — это углы в получившихся треугольниках. Обозначим угол (angle{CAB}=alpha). Тогда, так как (angle{CHA}=90^o), можно выразить угол:
$$angle{ACH}=180-angle{CAB}-angle{CHA}=180-alpha-90=90-alpha;$$
Напомню, что треугольник (bigtriangleup{ABC}) прямоугольный с прямым углом (angle{ACB}=90^o).
Значит
$$angle{HCB}=angle{ACB}-angle{ACH}=90-(90-alpha)=alpha=angle{CAB};$$
Важный факт: (angle{HCB}=angle{CAB})! А равенство этих углов само собой означает и равенство всех тригонометрических функций. То есть, например, (sin(angle{HCB})=sin(angle{ACB})). Точно так же у них равны и косинусы, и тангенсы, и даже котангенсы!
Аналогичные рассуждения можно провести для углов (angle{ACH}=angle{CBA}).
Запомните это!
А теперь приступим непосредственно к решению задачи. Нам известна гипотенуза (AB) и (tg(alpha)). По определению тангенса в (bigtriangleup{ABC}):
$$tg(angle{A})=frac{CB}{AC};$$
Либо из (bigtriangleup{ACH}):
$$tg(angle{A})=frac{CH}{AH};$$
В этих формулах есть проблема: нет известной нам стороны, гипотенузы (AB). А значит, у нас две неизвестные, и решить мы не можем.
Но зная тангенс, мы легко можем найти косинус по формуле:
$$1+tg(alpha)^2=frac{1}{cos^2(alpha)};$$
$$1+left(frac{1}{5}right)^2=frac{1}{cos^2(alpha)};$$
$$1+frac{1}{25}=frac{1}{cos^2(alpha)};$$
$$frac{26}{25}=frac{1}{cos^2(alpha)};$$
$$cos^2(alpha)=frac{1}{frac{26}{25}}=1*frac{25}{26}=frac{25}{26};$$
$$cos(alpha)=pmsqrt{frac{25}{26}}=pmfrac{5}{sqrt{26}};$$
Так как (anglealpha) это острый угол из прямоугольного треугольника, то его косинус точно будет положительным:
$$cos(alpha)=frac{5}{sqrt{26}}.$$
Не самый приятный косинус, но что делать, будем решать так, как есть.
С другой стороны, из (bigtriangleup{ABC}):
$$cos(alpha)=frac{AC}{AB};$$
Подставим известное (AB):
$$frac{5}{sqrt{26}}=frac{AC}{13};$$
$$AC=13*frac{5}{sqrt{26}}=frac{13*5}{sqrt{26}};$$
Либо косинус еще можно расписать в (bigtriangleup{ACH}):
$$cos(alpha)=frac{AH}{AC}=frac{5}{sqrt{26}};$$
Подставим найденное (AC):
$$frac{AH}{frac{13*5}{sqrt{26}}}=frac{5}{sqrt{26}};$$
$$AH=frac{5}{sqrt{26}}*frac{13*5}{sqrt{26}}=frac{5*13*5}{26}=frac{25}{2}=12,5.$$
Ответ: (AH=12,5.)
Содержание статьи
- Что такое косинус угла и как его применять в решении задач
- Как рассчитать косинус угла без формул
- Калькулятор расчета косинуса онлайн
- Примеры решения задач по геометрии по нахождению неизвестных величин с применением таблицы косинусов Брадиса
Таблица косинусов –
это удобное решение для проведения быстрых расчетов, когда нужно получить числовое значение косинуса того или иного угла. В статье мы узнаем, что такое косинус, чем похожи и как связаны таблица синусов и косинусов, как использовать таблицу синусов Брадиса для получения конкретных числовых значений косинуса того или иного угла.
Что такое косинус угла и как его применять в решении задач
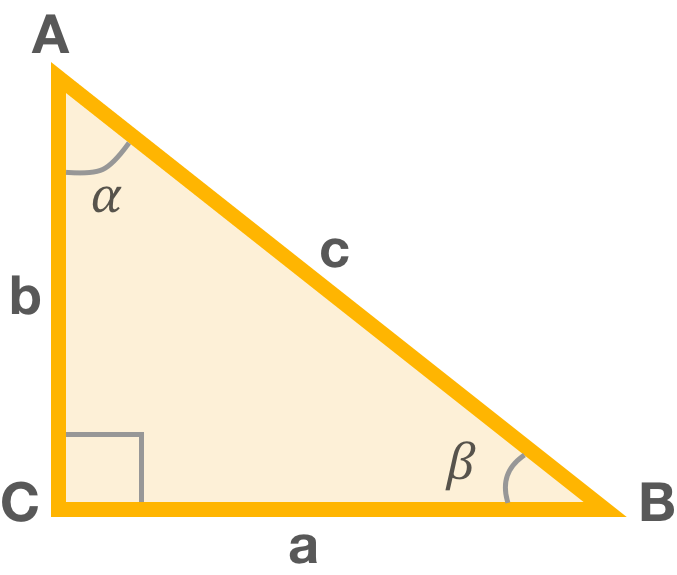
Начнем с того, что каждый знает, что такое прямоугольный треугольник. Им называется такой треугольник, у которого один из углов (C) прямой (равен 90°), остальные два угла (? и ?) острые. Он имеет стандартное обозначение углов и сторон. Тогда, что такое косинус угла, можно рассмотреть дальше.
Прямой угол всегда равен 90°, острый – всегда меньше, а тупой – больше 90°
Согласно теореме косинусов, что бы рассчитать угол α или β, нужно знать длину гипотенузы (АВ) и прилежащий к этому углу катет.
Косинус – это отношение прилежащей стороны к гипотенузе:
- cos α = b деленное на с;
- cos β = а(BC)/с(AB) .
То есть, если вам нужно узнать, например, какой высоты делать крышу над домом, если известна ширина дома и угол наклона крыши, что бы снег не задерживался, то высоту конька рассчитать не составит труда, применяя теорему косинусов. Нужно помнить, что такие функции, как косинусы и синусы в формулах зависят от угла. Синус работает с противолежащей стороной, косинус с работает прилежащей.
Это тригонометрические формулы для вычисления углов в треугольнике через тригонометрические функции синус, косинус, тангенс, котангенс
Косинус – отношение прилежащего катета к гипотенузе
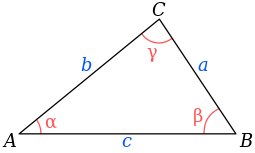
Если треугольник не прямоугольный, его параметры также можно рассчитать, используя теорему Евклида. Суть ее в том, что треугольник, лежащий на плоскости, и имеющий стороны а, b, с, а также углом α, который находится напротив стороны а, может быть рассчитан по следующей формуле:
а²= b²+с²-2²· b· cos α или:
Отсюда можем найти cos α, cos α =( b²+2²- а²) : 2bс.
Небольшое уточнение: если угол α менее 90°, тогда b²+2²- а² > 0, если α =90°, то b²+2²- а²=0, если α >90°,то есть угол тупой, то и b²+2²- а²< 0.
То же самые расчеты делаем для других углов треугольника:
- с² = а² + b² – 2аb cosγ,
- b² = а² + с² – 2ас cosβ.
Как рассчитать косинус угла без формул
Есть некоторые углы, рассчитать косинус которых можно без формул, применяя таблицу синусов и косинусов π. В ней расчет идет через число π, которое делится на целое число, в зависимости от размера угла, то есть sin 30° = π : 6 или 0,5, cos 30° = √3: 2. В такой таблице есть данные косинуса 30 градусов, косинуса 45 градусов, косинуса 60 градусов, косинуса 90 градусов, косинуса 120 градусов, косинус 180 градусов, косинус 270 градусов, косинус 360 градусов, косинус 0, а также аналогичные значения синусов.
Ниже приведена таблица косинусов, дополнительно указаны синусы в их числовом выражении.
| Значение угла α (градусов) | Значение угла α в радианах | COS (косинус) |
|---|---|---|
| Косинус 0 градусов | 0 | 1 |
| Косинус 15 градусов | π/12 | 0.9659 |
| Косинус 30 градусов | π/6 | 0.866 |
| Косинус 45 градусов | π/4 | 0.7071 |
| Косинус 50 градусов | 5π/18 | 0.6428 |
| Косинус 60 градусов | π/3 | 0.5 |
| Косинус 65 градусов | 13π/36 | 0.4226 |
| Косинус 70 градусов | 7π/18 | 0.342 |
| Косинус 75 градусов | 5π/12 | 0.2588 |
| Косинус 90 градусов | π/2 | 0 |
| Косинус 105 градусов | 5π/12 | -0.2588 |
| Косинус 120 градусов | 2π/3 | -0.5 |
| Косинус 135 градусов | 3π/4 | -0.7071 |
| Косинус 140 градусов | 7π/9 | -0.766 |
| Косинус 150 градусов | 5π/6 | -0.866 |
| Косинус 180 градусов | π | -1 |
| Косинус 270 градусов | 3π/2 | 0 |
| Косинус 360 градусов | 2π | 1 |
Калькулятор расчета косинуса онлайн
Примеры решения задач по геометрии по нахождению неизвестных величин с применением таблицы косинусов Брадиса
Пример 1: Для примера решим следующую задачу. Берем прямоугольный треугольник, у него нужно найти оба угла, но известны гипотенуза с = 12 см, сторона b = 9,2 см. По теореме косинусов
cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.
Но наше значение меньше табличного на 0,0006, что становит 3′. Тогда мы вычитаем эту поправку 3′, 39°54′ – 3′ = 39°51′. Второй угол находим, исходя из того, что сумма всех углов в треугольнике не должна превышать 180°. Поэтому 180° – (90° + 39°51′) = 50° 09′. Угол β = 50° 09′. Решаем задачу дальше. Ищем сторону а. Для этого мы можем использовать два способа.
- по формуле а²= b²+с²-2²· b· cos α находим сторону а;
- по формуле cos β=sinα = а: с, а = с · cos β.
Второй вариант немного проще в вычислении. Обращаемся к таблице Брадиса снова. У нас ближайшее значение 50° 06′ = 0,6414. Поправка на 3′ составляет 0, 0007. Тогда 0, 6414 + 0,0007 = 0,6421.
По условию с = 12 см, тогда а = 12 · 0,6421 = 7,7 см. Задача решена. Если значения углов простые, таблица косинусов и синусов может упростить вычисление. Можно использовать следующие тождества: sin (90°+15°) = cos 15°= cos (90°-75°) = sin 75° Функции повторяются, только нужно учитывать знак. Если нужно найти косинус 145 градусов, находим угол до 90 градусов. 180 °– 145° = 35°. Косинус 35 градусов будет 0,8192 по таблице, если это 145°, это будет значение с отрицательным значением -0,8192.
Пример 2: Рассмотрим треугольник с произвольными углами, ни один из которых не равен 90°. Мы имеем две стороны с =12 см, b = 8,2 см, а также угол α, который равен 31°12′. Найти третью сторону. Формула, которая применялась в предыдущей задаче, не подходит, так как у нас треугольник не прямоугольный (по крайней мере мы это ещё не рассчитали). Используем формулу из теоремы косинусов:
а² = b²+с²-2²· b· cos α. Косинус угла находим на пересечении угла 31° и 12′. Он равен числу 0,8554, которое мы и подставляем в формулу.
а² = 67, 24 + 144 -4 · 8,2 · 0,8554 = 211,24 – 28,07 = 183,17. Находим а = √183,17 = 13, 54 (см)
Если будет стоять задание найти ещё и углы треугольника, используем формулу:
с² = а² + b² – 2аb cos γ, отсюда cos γ = (b² + а² – с²): 2 bс. cos γ = (8,2² + 13,54² – 12²): 2· 8,2·12 = (64,24 + 183, 17 – 144): 196,8 = 0, 5255. Открываем таблицу Брадиса. Это число соответствует 58° 18′. Согласно теореме о правилах трёх углов в треугольнике находим третий угол:
180° – 58° 18′-31°12′ =89° 30′. Задача решена!
Можно не рассчитывать самому, а использовать сервис и высчитать косинус онлайн, когда регистрируешься на сайте, и любое вычисление приходит автоматически. Минус такого сервиса, его нельзя применять на экзамене по математике. В качестве справочного материала таблицы предоставляются. Естественно, надо хорошо уметь ими пользоваться, так как на экзамен отводится ограниченное количество времени.
| COS | 0′ | 6′ | 12′ | 18′ | 24′ | 30′ | 36′ | 42′ | 48′ | 54′ | 60′ | 1′ | 2′ | 3′ | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| COS | 60′ | 54′ | 48′ | 42′ | 36′ | 30′ | 24′ | 18′ | 12′ | 6′ | 0′ | 1′ | 2′ | 3′ | |
| 90° | 0.0000 | ||||||||||||||
| 89° | 0.0000 | 17 | 35 | 52 | 70 | 87 | 105 | 122 | 140 | 157 | 175 | 3 | 6 | 9 | |
| 88° | 175 | 192 | 209 | 227 | 244 | 262 | 279 | 297 | 314 | 332 | 349 | 3 | 6 | 9 | |
| 87° | 349 | 366 | 384 | 401 | 419 | 436 | 454 | 471 | 488 | 506 | 523 | 3 | 6 | 9 | |
| 86° | 523 | 541 | 558 | 576 | 593 | 610 | 628 | 645 | 663 | 680 | 698 | 3 | 6 | 9 | |
| 85° | 698 | 715 | 732 | 750 | 767 | 785 | 802 | 819 | 837 | 854 | 0.0872 | 3 | 6 | 9 | |
| 84° | 0.0872 | 889 | 906 | 924 | 941 | 958 | 976 | 993 | 1011 | 1028 | 1045 | 3 | 6 | 9 | |
| 83° | 1045 | 1063 | 1080 | 1097 | 1115 | 1132 | 1149 | 1167 | 1184 | 1201 | 1219 | 3 | 6 | 9 | |
| 82° | 1219 | 1236 | 1253 | 1271 | 1288 | 1305 | 1323 | 1340 | 1357 | 1374 | 1392 | 3 | 6 | 9 | |
| 81° | 1392 | 1409 | 1426 | 1444 | 1461 | 1478 | 1495 | 1513 | 1530 | 1547 | 1564 | 3 | 6 | 9 | |
| 80° | 1564 | 1582 | 1599 | 1616 | 1633 | 1650 | 1668 | 1685 | 1702 | 1719 | 0.1736 | 3 | 6 | 9 | |
| 79° | 0.1736 | 1754 | 1771 | 1788 | 1805 | 1822 | 1840 | 1857 | 1874 | 1891 | 1908 | 3 | 6 | 9 | |
| 78° | 1908 | 1925 | 1942 | 1959 | 1977 | 1994 | 2011 | 2028 | 2045 | 2062 | 2079 | 3 | 6 | 9 | |
| 77° | 2079 | 2096 | 2113 | 2130 | 2147 | 2164 | 2181 | 2198 | 2215 | 2233 | 2250 | 3 | 6 | 9 | |
| 76° | 2250 | 2267 | 2284 | 2300 | 2317 | 2334 | 2351 | 2368 | 2385 | 2402 | 2419 | 3 | 6 | 8 | |
| 75° | 2419 | 2436 | 2453 | 2470 | 2487 | 2504 | 2521 | 2538 | 2554 | 2571 | 0.2588 | 3 | 6 | 8 | |
| 74° | 0.2588 | 2605 | 2622 | 2639 | 2656 | 2672 | 2689 | 2706 | 2723 | 2740 | 2756 | 3 | 6 | 8 | |
| 73° | 2756 | 2773 | 2790 | 2807 | 2823 | 2840 | 2857 | 2874 | 2890 | 2907 | 2924 | 3 | 6 | 8 | |
| 72° | 2942 | 2940 | 2957 | 2974 | 2990 | 3007 | 3024 | 3040 | 3057 | 3074 | 3090 | 3 | 6 | 8 | |
| 71° | 3090 | 3107 | 3123 | 3140 | 3156 | 3173 | 3190 | 3206 | 3223 | 3239 | 3256 | 3 | 6 | 8 | |
| 70° | 3256 | 3272 | 3289 | 3305 | 3322 | 3338 | 3355 | 3371 | 3387 | 3404 | 0.3420 | 3 | 5 | 8 | |
| 69° | 0.3420 | 3437 | 3453 | 3469 | 3486 | 3502 | 3518 | 3535 | 3551 | 3567 | 3584 | 3 | 5 | 8 | |
| 68° | 3584 | 3600 | 3616 | 3633 | 3649 | 3665 | 3681 | 3697 | 3714 | 3730 | 3746 | 3 | 5 | 8 | |
| 67° | 3746 | 3762 | 3778 | 3795 | 3811 | 3827 | 3843 | 3859 | 3875 | 3891 | 3907 | 3 | 5 | 8 | |
| 66° | 3097 | 3923 | 3939 | 3955 | 3971 | 3987 | 4003 | 4019 | 4035 | 4051 | 4067 | 3 | 5 | 8 | |
| 65° | 4067 | 4083 | 4099 | 4115 | 4131 | 4147 | 4163 | 4179 | 4195 | 4210 | 0.4226 | 3 | 5 | 8 | |
| 64° | 0.4226 | 4242 | 4258 | 4274 | 4289 | 4305 | 4321 | 4337 | 4352 | 4368 | 4384 | 3 | 5 | 8 | |
| 63° | 4384 | 4399 | 4415 | 4431 | 4446 | 4462 | 4478 | 4493 | 4509 | 4524 | 4540 | 3 | 5 | 8 | |
| 62° | 4540 | 4555 | 4571 | 4586 | 4602 | 4617 | 4633 | 4648 | 4664 | 4679 | 4695 | 3 | 5 | 8 | |
| 61° | 4695 | 4710 | 4726 | 4741 | 4756 | 4772 | 4787 | 4802 | 4818 | 4833 | 4848 | 3 | 5 | 8 | |
| 60° | 4848 | 4863 | 4879 | 4894 | 4909 | 4924 | 4939 | 4955 | 4970 | 4985 | 0.5000 | 3 | 5 | 8 | |
| 59° | 0.5000 | 5015 | 5030 | 5045 | 5060 | 5075 | 5090 | 5105 | 5120 | 5135 | 5150 | 3 | 5 | 8 | |
| 58° | 5150 | 5165 | 5180 | 5195 | 5210 | 5225 | 5240 | 5255 | 5270 | 5284 | 5299 | 2 | 5 | 7 | |
| 57° | 5299 | 5314 | 5329 | 5344 | 5358 | 5373 | 5388 | 5402 | 5417 | 5432 | 5446 | 2 | 5 | 7 | |
| 56° | 5446 | 5461 | 5476 | 5490 | 5505 | 5519 | 5534 | 5548 | 5563 | 5577 | 5592 | 2 | 5 | 7 | |
| 55° | 5592 | 5606 | 5621 | 5635 | 5650 | 5664 | 5678 | 5693 | 5707 | 5721 | 0.5736 | 2 | 5 | 7 | |
| 54° | 0.5736 | 5750 | 5764 | 5779 | 5793 | 5807 | 5821 | 5835 | 5850 | 5864 | 0.5878 | 2 | 5 | 7 | |
| 53° | 5878 | 5892 | 5906 | 5920 | 5934 | 5948 | 5962 | 5976 | 5990 | 6004 | 6018 | 2 | 5 | 7 | |
| 52° | 6018 | 6032 | 6046 | 6060 | 6074 | 6088 | 6101 | 6115 | 6129 | 6143 | 6157 | 2 | 5 | 7 | |
| 51° | 6157 | 6170 | 6184 | 6198 | 6211 | 6225 | 6239 | 6252 | 6266 | 6280 | 6293 | 2 | 5 | 7 | |
| 50° | 6293 | 6307 | 6320 | 6334 | 6347 | 6361 | 6374 | 6388 | 6401 | 6414 | 0.6428 | 2 | 4 | 7 | |
| 49° | 0.6428 | 6441 | 6455 | 6468 | 6481 | 6494 | 6508 | 6521 | 6534 | 6547 | 6561 | 2 | 4 | 7 | |
| 48° | 6561 | 6574 | 6587 | 6600 | 6613 | 6626 | 6639 | 6652 | 6665 | 6678 | 6691 | 2 | 4 | 7 | |
| 47° | 6691 | 6704 | 6717 | 6730 | 6743 | 6756 | 6769 | 6782 | 6794 | 6807 | 6820 | 2 | 4 | 6 | |
| 46° | 6820 | 6833 | 6845 | 6858 | 6871 | 6884 | 6896 | 8909 | 6921 | 6934 | 6947 | 2 | 4 | 6 | |
| 45° | 6947 | 6959 | 6972 | 6984 | 6997 | 7009 | 7022 | 7034 | 7046 | 7059 | 0.7071 | 2 | 4 | 6 | |
| 44° | 0.7071 | 7083 | 7096 | 7108 | 7120 | 7133 | 7145 | 7157 | 7169 | 7181 | 7193 | 2 | 4 | 6 | |
| 43° | 7193 | 7206 | 7218 | 7230 | 7242 | 7254 | 7266 | 7278 | 7290 | 7302 | 7314 | 2 | 4 | 6 | |
| 42° | 7314 | 7325 | 7337 | 7349 | 7361 | 7373 | 7385 | 7396 | 7408 | 7420 | 7431 | 2 | 4 | 6 | |
| 41° | 7431 | 7443 | 7455 | 7466 | 7478 | 7490 | 7501 | 7513 | 7524 | 7536 | 7547 | 2 | 4 | 6 | |
| 40° | 7547 | 7559 | 7570 | 7581 | 7593 | 7604 | 7615 | 7627 | 7638 | 7649 | 0.7660 | 2 | 4 | 6 | |
| 39° | 0.7660 | 7672 | 7683 | 7694 | 7705 | 7716 | 7727 | 7738 | 7749 | 7760 | 7771 | 2 | 4 | 6 | |
| 38° | 7771 | 7782 | 7793 | 7804 | 7815 | 7826 | 7837 | 7848 | 7859 | 7869 | 7880 | 2 | 4 | 5 | |
| 37° | 7880 | 7891 | 7902 | 7912 | 7923 | 7934 | 7944 | 7955 | 7965 | 7976 | 7986 | 2 | 4 | 5 | |
| 36° | 7986 | 7997 | 8007 | 8018 | 8028 | 8039 | 8049 | 8059 | 8070 | 8080 | 8090 | 2 | 3 | 5 | |
| 35° | 8090 | 8100 | 8111 | 8121 | 8131 | 8141 | 8151 | 8161 | 8171 | 8181 | 0.8192 | 2 | 3 | 5 | |
| 34° | 0.8192 | 8202 | 8211 | 8221 | 8231 | 8241 | 8251 | 8261 | 8271 | 8281 | 8290 | 2 | 3 | 5 | |
| 33° | 8290 | 8300 | 8310 | 8320 | 8329 | 8339 | 8348 | 8358 | 8368 | 8377 | 8387 | 2 | 3 | 5 | |
| 32° | 8387 | 8396 | 8406 | 8415 | 8425 | 8434 | 8443 | 8453 | 8462 | 8471 | 8480 | 2 | 3 | 5 | |
| 31° | 8480 | 8490 | 8499 | 8508 | 8517 | 8526 | 8536 | 8545 | 8554 | 8563 | 8572 | 2 | 3 | 5 | |
| 30° | 8572 | 8581 | 8590 | 8599 | 8607 | 8616 | 8625 | 8634 | 8643 | 8652 | 0.8660 | 1 | 3 | 4 | |
| 29° | 0.8660 | 8669 | 8678 | 8686 | 8695 | 8704 | 8712 | 8721 | 8729 | 8738 | 8746 | 1 | 3 | 4 | |
| 28° | 8746 | 8755 | 8763 | 8771 | 8780 | 8788 | 8796 | 8805 | 8813 | 8821 | 8829 | 1 | 3 | 4 | |
| 27° | 8829 | 8838 | 8846 | 8854 | 8862 | 8870 | 8878 | 8886 | 8894 | 8902 | 8910 | 1 | 3 | 4 | |
| 26° | 8910 | 8918 | 8926 | 8934 | 8942 | 8949 | 8957 | 8965 | 8973 | 8980 | 8988 | 1 | 3 | 4 | |
| 25° | 8988 | 8996 | 9003 | 9011 | 9018 | 9026 | 9033 | 9041 | 9048 | 9056 | 0.9063 | 1 | 3 | 4 | |
| 24° | 0.9063 | 9070 | 9078 | 9085 | 9092 | 9100 | 9107 | 9114 | 9121 | 9128 | 9135 | 1 | 2 | 4 | |
| 23° | 9135 | 9143 | 9150 | 9157 | 9164 | 9171 | 9178 | 9184 | 9191 | 9198 | 9205 | 1 | 2 | 3 | |
| 22° | 9205 | 9212 | 9219 | 9225 | 9232 | 9239 | 9245 | 9252 | 9259 | 9256 | 9272 | 1 | 2 | 3 | |
| 21° | 9272 | 9278 | 9285 | 9291 | 9298 | 9304 | 9311 | 9317 | 9323 | 9330 | 9336 | 1 | 2 | 3 | |
| 20° | 9336 | 9342 | 9348 | 9354 | 9361 | 9367 | 9373 | 9379 | 9383 | 9391 | 0.9397 | 1 | 2 | 3 | |
| 19° | 9397 | 9403 | 9409 | 9415 | 9421 | 9426 | 9432 | 9438 | 9444 | 9449 | 0.9455 | 1 | 2 | 3 | |
| 18° | 9455 | 9461 | 9466 | 9472 | 9478 | 9483 | 9489 | 9494 | 9500 | 9505 | 9511 | 1 | 2 | 3 | |
| 17° | 9511 | 9516 | 9521 | 9527 | 9532 | 9537 | 9542 | 9548 | 9553 | 9558 | 9563 | 1 | 2 | 3 | |
| 16° | 9563 | 9568 | 9573 | 9578 | 9583 | 9588 | 9593 | 9598 | 9603 | 9608 | 9613 | 1 | 2 | 2 | |
| 15° | 9613 | 9617 | 9622 | 9627 | 9632 | 9636 | 9641 | 9646 | 9650 | 9655 | 0.9659 | 1 | 2 | 2 | |
| 14° | 9659 | 9664 | 9668 | 9673 | 9677 | 9681 | 9686 | 9690 | 9694 | 9699 | 9703 | 1 | 1 | 2 | |
| 13° | 9703 | 9707 | 9711 | 9715 | 9720 | 9724 | 9728 | 9732 | 9736 | 9740 | 9744 | 1 | 1 | 2 | |
| 12° | 9744 | 9748 | 9751 | 9755 | 9759 | 9763 | 9767 | 9770 | 9774 | 9778 | 9781 | 1 | 1 | 2 | |
| 11° | 9781 | 9785 | 9789 | 9792 | 9796 | 9799 | 9803 | 9806 | 9810 | 9813 | 9816 | 1 | 1 | 2 | |
| 10° | 9816 | 9820 | 9823 | 9826 | 9829 | 9833 | 9836 | 9839 | 9842 | 9845 | 0.9848 | 1 | 1 | 2 | |
| 9° | 0.9848 | 9851 | 9854 | 9857 | 9860 | 9863 | 9866 | 9869 | 9871 | 9874 | 9877 | 0 | 1 | 1 | |
| 8° | 9877 | 9880 | 9882 | 9885 | 9888 | 9890 | 9893 | 9895 | 9898 | 9900 | 9903 | 0 | 1 | 1 | |
| 7° | 9903 | 9905 | 9907 | 9910 | 9912 | 9914 | 9917 | 9919 | 9921 | 9923 | 9925 | 0 | 1 | 1 | |
| 6° | 9925 | 9928 | 9930 | 9932 | 9934 | 9936 | 9938 | 9940 | 9942 | 9943 | 9945 | 0 | 1 | 1 | |
| 5° | 9945 | 9947 | 9949 | 9951 | 9952 | 9954 | 9956 | 9957 | 9959 | 9960 | 9962 | 0 | 1 | 1 | |
| 4° | 9962 | 9963 | 9965 | 9966 | 9968 | 9969 | 9971 | 9972 | 9973 | 9974 | 9976 | 0 | 0 | 1 | |
| 3° | 9976 | 9977 | 9978 | 9979 | 9980 | 9981 | 9982 | 9983 | 9984 | 9985 | 9986 | 0 | 0 | 0 | |
| 2° | 9986 | 9987 | 9988 | 9989 | 9990 | 9990 | 9991 | 9992 | 9993 | 9993 | 9994 | 0 | 0 | 0 | |
| 1° | 9994 | 9995 | 9995 | 9996 | 9996 | 9997 | 9997 | 9997 | 9998 | 9998 | 0.9998 | 0 | 0 | 0 | |
| 0° | 9998 | 9999 | 9999 | 9999 | 9999 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 1.0000 | 0 | 0 | 0 | |
| 1.0000 |
Как найти наибольший косинус треугольника
Теорема косинусов для треугольника: формула и задачи
В данной публикации мы рассмотрим одну из главных теорем евклидовой геометрии, теорему косинусов, которая определяет соотношение сторон в треугольнике, а также, научимся применять ее на практике для решения задач.
Формулировка и формула теоремы
В плоском треугольнике квадрат стороны равняется сумме квадратов двух других сторон минус удвоенное произведение данных сторон, умноженное на косинус угла между ними.
a 2 = b 2 + c 2 – 2 ⋅ b ⋅ c ⋅ cos α
Следствие из теоремы
Формула теоремы может применяться для того, чтобы найти косинус угла в треугольнике:
При этом:
- если b 2 + c 2 – a 2 > 0, значит угол α – острый;
- если b 2 + c 2 – a 2 = 0, значит угол α равен 90 градусам (терема косинусов принимает вид Теоремы Пифагора);
- если b 2 + c 2 – a 2 Примеры задач
Задание 1
В треугольнике известны длины двух сторон – 5 и 9 см, а также, угол между ними – 60°. Найдите длину третьей стороны.
Решение:
Применим формулу теоремы, приняв известные стороны за b и c, а неизвестную за a:
a 2 = 5 2 + 9 2 – 2 ⋅ 5 ⋅ 9 ⋅ cos 60° = 25 + 81 – 45 = 61 см 2 . Следовательно, сторона
Задание 2
Самая большая сторона треугольника равна 26 см, а две другие – 16 и 18 см. Найдите угол между меньшими сторонами.
Решение:
Примем бОльшую сторону за a. Чтобы найти угол между сторонами b и c, воспользуемся следствием из теоремы:
Следовательно, угол α = arccos (-1/6) ≈ 99,59°.
Теорема косинусов и синусов
О чем эта статья:
Формулировка и доказательство теоремы косинусов
Для начала вспомним теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Формула Теоремы Пифагора:
a 2 > + b 2 > = c 2 >, где a, b — катеты, с — гипотенуза.
Теорема косинусов звучит так: квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Формула теоремы косинусов:
a 2 = b 2 + c 2 — 2bc cos α
В доказательстве теоремы косинусов используем формулу длины отрезка в координатах. Рассмотрим данную формулу:
В доказательстве теоремы косинусов BC — это сторона треугольника АВС, которая обозначена буквой а. Введем удобную систему координат и найдем координаты нужных нам точек. У точки В координаты (с; 0).
Координаты точки С — (b cos α; b sin α) при α ∈ (0° ; 180°).
BC 2 = a 2 = (b cos α — c) 2 + b 2 sin 2 α = b 2 cos 2 α + b 2 sin 2 α — 2bc cos α + c 2 = b 2 (cos 2 α + sin 2 α) — 2bc cos α + c 2
cos 2 α + sin 2 α = 1 — основное тригонометрическое тождество.
Что и требовалось доказать.
Совет: чтобы быстрее разобраться в сложной теме, запишитесь на онлайн-курсы по математике для детей и подростков.
С помощью теоремы косинусов можно найти косинус угла треугольника:
- Когда b 2 + c 2 — a 2 > 0, угол α будет острым.
- Когда b 2 + c 2 — a 2 = 0, угол α будет прямым.
- Когда b 2 + c 2 — a 2
Сформулируем еще одно доказательство теоремы косинусов.
Пусть нам дан треугольник ABC, в котором из вершины C на сторону AB опустили высоту CD. Это значит:
- AD = b × cos α,
- DB = c – b × cos α.
Запишем теорему Пифагора для двух прямоугольных треугольников ADC и BDC:
- h 2 = b 2 — (b × cos α) 2
- h 2 = a 2 — (c – b × cos α) 2
Приравниваем правые части уравнений:
- b 2 — (b × cos α) 2 = a 2 — (c — b × cos α) 2
- a 2 = b 2 + c 2 — 2bc × cos α
Если один из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определим стороны b и c:
- b 2 = a 2 + c 2 — 2ac × cos β;
- c 2 = a 2 + b 2 — 2ab × cos γ.
Формулировка теоремы для каждой из сторон треугольника
Теорема косинусов справедлива для всех сторон треугольника, то есть:
a 2 = b 2 + c 2 — 2bc cos α
b 2 = c 2 + a 2 — 2ca cos β
c 2 = a 2 + b 2 — 2ab cos γ
Теорема косинусов может быть использована для любого вида треугольника.
Косинусы углов треугольника
Теорема косинусов позволяет найти как косинус, так и угол треугольника. Найдём косинусы углов:
Определение угла с помощью косинуса
А теперь обратим внимание на углы.
Как мы уже знаем, косинус угла из промежутка (0°; 180°) определяет угол (в отличие от его синуса).
Пусть нам дана единичная полуокружность. Если нам задан cos α, то нам задана точка на верхней полуокружности и задан угол α. Следовательно, cos α однозначно определяет точку М(cos α; sin α), и однозначно определяется угол ∠AOM.
Рассмотрение пределов изменения cos α и sin α
Рассмотрим пределы изменения синуса и косинуса α. Вспомним, что если α — угол треугольника, то он лежит в пределах от 0° до 180°.
Предел изменения косинуса: -1 0, то α ∈ (0°;90°)
Если cos α
Примеры решения задач
При помощи теоремы косинусов можно решать задачки по геометрии. Рассмотрим интересные случаи.
Пример 1. Дан треугольник АВС. Найти длину СМ.
∠C = 90°, АВ = 9, ВС = 3, AM/MB = 1/2, где М — точка на гипотенузе АВ.
-
Так как АМ + МВ = 9, а AM/MB = 1/2, то АМ = 3, МВ = 6.
Из треугольника АВС найдем cos B:
Из треугольника СМВ по теореме косинусов найдём СМ:
Пример 2. Дан треугольник АВС, в котором a2+ b22 + b 2 2 , то cos C 2 = a 2 + b 2 , то ∠C = 90°.
- Если c 2 2 + b 2 , то ∠C — острый.
Косинус в треугольнике
Что такое косинус в треугольнике? Как найти косинус острого угла в прямоугольном треугольнике?
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
Например, для угла A треугольника ABC
Соответственно, косинус угла A в треугольнике ABC — это
Для угла B треугольника ABC
прилежащим является катет BC.
Соответственно, косинус угла B в треугольнике ABC
равен отношению BC к AB:
Таким образом, косинус острого угла в прямоугольном треугольнике — это некоторое число, получаемое в результате деления длины прилежащего катета на длину гипотенузы.
Длины отрезков — положительные числа, поэтому косинус острого угла прямоугольного треугольника также является положительным числом.
Поскольку длина катета всегда меньше длины гипотенузы, то косинус острого угла прямоугольного треугольника — число, меньшее единицы.
Косинус любого острого угла прямоугольного треугольника больше нуля, но меньше единицы:
Косинус зависит от величины угла.
Если в треугольнике изменить длины сторон, но не изменять угол, значение косинуса этого угла не изменится.
в треугольниках ABC и FPK
Косинус угла в произвольном (не прямоугольном треугольнике) определяется через теорему косинусов. О том, как это делать, мы будем говорить позже.
http://skysmart.ru/articles/mathematic/teorema-kosinusov-i-sinusov
12mistrx
+10
Решено
1 год назад
Алгебра
10 — 11 классы
Как высчитывать cos угла более 90*?
Смотреть ответ
Ответ
5
(1 оценка)
1
ant20202020
1 год назад
Светило науки — 4249 ответов — 10853 помощи
по формулам приведения приводите его к косинусу острого угла, находите, чему этот косинус равен , например, Вам надо посчитать cos120°=cos(180°-60°)=-cos60°= -0.5
(1 оценка)
Остались вопросы?
Задай вопрос
Найди нужный
Новые вопросы по предмету Математика
Запиши числа 1, 1, 3, 3, 5, 5, 7 и 7 в таком порядке, чтобы между единицами стояло одно число, между тройками — два числа, между пятёркам …
Запиши числа 1, 1, 3, 3, 5, 5, 7 и 7 в таком порядке, чтобы между единицами стояло одно число, между тройками — два числа, между пятёркам …
Iнвестор вклав 6000 грн пiд 10% річних при умові нарахування складних відсотків. Яку суму він отримає через 3 роки?
Помогите пожалуйста!Найдите корни уравнения если они существуют:Пункт a)
СРОЧНО!!! Встановіть відповідність між прямою на малюнку та рівнянням, яким вона задана
https://vashotvet.com/task/13337535

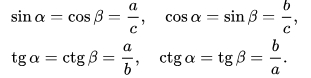
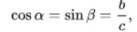 cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.
cos α = b : с, cos α = 9,2: 12 = 0, 7667. Далее открываем таблицу Брадиса и научимся, как ею пользоваться для нахождения косинуса угла. С левой стороны таблицы мы напротив косинусов находим ближайшее значение 0, 7672, которое соответствует 39°, поднимаем линию до значения минут и находим 54′.


