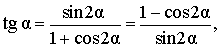Синус, косинус и тангенс острого угла прямоугольного треугольника
Изучение тригонометрии мы начнем с прямоугольного треугольника. Определим, что такое синус и косинус, а также тангенс и котангенс острого угла. Это основы тригонометрии.
Напомним, что прямой угол — это угол, равный 90 градусов. Другими словами, половина развернутого угла.
Острый угол — меньший 90 градусов.
Тупой угол — больший 90 градусов. Применительно к такому углу «тупой» — не оскорбление, а математический термин 
Нарисуем прямоугольный треугольник. Прямой угол обычно обозначается C. Обратим внимание, что сторона, лежащая напротив угла, обозначается той же буквой, только маленькой. Так, сторона, лежащая напротив угла A, обозначается .
Угол A обозначается соответствующей греческой буквой .
Гипотенуза прямоугольного треугольника — это сторона, лежащая напротив прямого угла.
Катеты — стороны, лежащие напротив острых углов.
Катет , лежащий напротив угла
, называется противолежащим (по отношению к углу
). Другой катет
, который лежит на одной из сторон угла
, называется прилежащим.
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
sin A
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
cos A
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
tg A
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
tg A
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что то же самое, отношение косинуса к синусу):
ctg A
Обратите внимание на основные формулы для синуса, косинуса, тангенса и котангенса, которые приведены ниже. Они пригодятся нам при решении задач.
| sin |
sin |
|
| cos |
1+tg |
cos |
| tg |
1+ctg |
sin |
| ctg |
tg |
Давайте докажем некоторые из них.
- Сумма углов любого треугольника равна
. Значит, сумма двух острых углов прямоугольного треугольника равнa
.
- С одной стороны,
как отношение противолежащего катета к гипотенузе. С другой стороны,
, поскольку для угла
катет а будет прилежащим. Получаем, что
. Иными словами,
.
- Возьмем теорему Пифагора:
. Поделим обе части на
получаем
то есть
Мы получили основное тригонометрическое тождество. - Поделив обе части основного тригонометрического тождества на
, получим:
Это значит, что если нам дан тангенс острого угла
, то мы сразу можем найти его косинус. Аналогично,
Хорошо, мы дали определения и записали формулы. А для чего все-таки нужны синус, косинус, тангенс и котангенс?
Мы знаем, что сумма углов любого треугольника равна .
Знаем соотношение между сторонами прямоугольного треугольника. Это теорема Пифагора: .
Получается, что зная два угла в треугольнике, можно найти третий. Зная две стороны в прямоугольном треугольнике, можно найти третью. Значит, для углов — свое соотношение, для сторон — свое. А что делать, если в прямоугольном треугольнике известен один угол (кроме прямого) и одна сторона, а найти надо другие стороны?
С этим и столкнулись люди в прошлом, составляя карты местности и звездного неба. Ведь не всегда можно непосредственно измерить все стороны треугольника.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Мы тоже нарисуем таблицу значений синуса, косинуса, тангенса и котангенса для «хороших» углов от до
.
| 0 | |||||
| sin |
0 | ||||
| cos |
0 | ||||
| tg |
0 | − | |||
| ctg |
− | 0 |
Обратите внимание на два прочерка в таблице. При соответствующих значениях углов тангенс и котангенс не существуют.
Докажем теорему:
Если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы этих углов равны, косинусы этих углов равны и тангенсы этих углов равны.
В самом деле, пусть АВС и — два прямоугольных треугольника с прямыми углами С и
и равными острыми углами А и
Треугольники АВС и подобны по первому признаку подобия треугольников, поэтому
Из этих равенств следует, что т. е. sin А = sin
Аналогично, т. е. cos А = cos
и
т. е. tg A = tg
Это значит, что синус, косинус и тангенс зависят только от величины угла.
Разберем несколько задач по тригонометрии из Банка заданий ФИПИ.
Задача 1. В треугольнике ABC угол C равен , sin A = 0,1. Найдите cos B.
Задача решается за четыре секунды.
Поскольку , sin A = cos B = 0,1.
Задача 2. В треугольнике угол
равен
,
,
.
Найдите .
Решение:
Отсюда
Найдем AC по теореме Пифагора.
Ответ: 4,8.
Задача 3. В треугольнике АВС угол С равен AВ = 13, ВС = 5. Найдите косинус и тангенс острого угла А. Ответ округлите до сотых.
Решение:
Для угла А противолежащий катет – это ВС,
АВ является гипотенузой треугольника, лежит против Значит, sin A
Катет, прилежащий к – это катет АС, следовательно, cos А
Длину катета АС найдем по теореме Пифагора:
Тогда
cos А
tg A
Ответ: 0,92; 0,42.
Заметим, что если катеты прямоугольного треугольника равны 5 и 12, то гипотенуза равна 13. Это одна из так называемых Пифагоровых троек. О них мы расскажем в других статьях сайта.
Задача 4. В треугольнике АВС угол С равен AC = 2, sin A=
Найдите BC.
Решение:
AC = b = 2, BC = a, AB = c.
Так как sin A
По теореме Пифагора получим
Ответ: 0,5.
Задача 5. В треугольнике АВС угол С равен
tg A =
Найдите AB.
Решение:
AC = b = 4, tg A
Ответ: 7.
Задача 6.
В треугольнике АВС угол С равен CH – высота, AB = 13, tg A =
Найдите AH.
Решение:
AВ = с = 13, tg A = тогда b = 5a.
По теореме Пифагора ABC:
тогда
(по двум углам), следовательно
откуда
Ответ: 12,5.
Задача 7. В треугольнике АВС угол С равен
CH – высота, BC = 3, sin A =
Найдите AH.
Решение:
Так как sin A = тогда
c = АВ = 18.
sin A = = cos B =
Рассмотрим BHC:
=
получим
тогда BH = = 0,5,
AH = AB — BH = 18 — 0,5 = 17,5.
Ответ: 17,5.
Задача 8. В треугольнике АВС угол С равен 90 CH — высота, BC = 3, cos A =
Найдите АH.
Решение:
Так как для АВС:
A =
sin В =
а для ВНС: sin В =
=
, откуда СН =
По теореме Пифагора найдем ВН:
Высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой. Поэтому для АВС получим:
тогда
Ответ: 17,5.
Задача 9. В треугольнике АВС угол С равен 90 CH — высота, СН = 24 и BН = 7. Найдите sin A.
Решение:
По определению sin A= =
=
Рассмотрим BHC :
ВС найдем по теореме Пифагора:
ВС=
тогда а значит и sin A =
= 0,28.
Ответ: 0,28.
Задача 10. В треугольнике АВС угол С равен 90 CH — высота, СН = 8 и BН = 4. Найдите tg A.
Решение:
По определению sin A = =
=
cos A =
=
=
тогда tg A = который найдем из
BHC:
Ответ: 0,5.
Задача 11. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, tg A =
Найдите АН.
Решение:
По определению tg A=
Для BHC:
, значит
СН =
Для АHC: tg A=
то
AH =
Ответ: 27.
Задача 12. В треугольнике АВС угол С равен 90 CH — высота, BН = 12, sin A =
Найдите АВ.
Решение:
Так как cos В = = sin A =
Из СВН имеем cos В =
=
тогда ВС =
В АВС имеем sinA =
=
тогда AВ =
Ответ: 27.
Задача 13. В треугольнике АВС угол С равен 90 из вершины прямого угла к гипотенузе проведена высота СН. Найдите cos A, AC и AB, если СН = 12, ВС = 20.
Решение:
Найдем НВ по теореме Пифагора из ВСН:
sin В = =
Для АВС: cos A =
получили cos A = 0,6.
Найдем АС и АВ несколькими способами.
1-й способ.
Так как cos A = то пусть АС = 3х, АВ = 5х,
тогда по теореме Пифагора получим
х = 5 ( так как х0). Значит,
2-й способ.
(по двум углам), значит
или
k = тогда
АС =
;
АВ =
3-й способ.
(высота прямоугольного треугольника, проведенная из вершины прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой) , тогда
АН = 144:16 = 9.
АВ = АН + НВ = 9 + 16 = 25.
По теореме Пифагора найдем АС:
=
Ответ: cos A = 0,6; АС = 15, АВ = 25.
Задача 14.
Высота ВН прямоугольного треугольника АВС, проведенная из вершины прямого угла В, равна 24 и отсекает от гипотенузы АС отрезок НС, равный 18.
Найдите АВ и cos А.
Решение:
Из прямоугольного ВНС по теореме Пифагора найдем гипотенузу ВС и cos C:
ВС = =
cos C =
Для АВС: sin А =
= cos C =
Для АНВ: sin А =
=
то
=
АВ =
Из основного тригонометрического тождества найдем
cos A =
Ответ: АВ = 40, cos A = 0,8.
Задача 15.
Гипотенуза АС прямоугольного треугольника АСЕ равна 50, sin А =
Найдите площадь треугольника.
Решение:
В прямоугольном АСЕ sin А =
значит
= 14.
Второй катет найдем, используя теорему Пифагора:
Площадь прямоугольного треугольника равна S =
поэтому
Ответ: 336.
Задача 16.
В треугольнике АВС угол С — прямой, катеты АВ = 13 и ВС = 12, СК — высота.
Найдите sin Результат округлите до сотых.
Решение:
A-общий,
),
значит sin
Найдем АС по теореме Пифагора из САВ:
Тогда sin
Ответ: 0,38.
Задача 17. В треугольнике АВС АС = ВС, АВ = 72, cos A = Найдите высоту СН.
Решение:
Так как АС = ВС, то АВС — равнобедренный с основанием АВ, тогда
высота СН является медианой, то есть АН = НВ =
Поскольку АСН — прямоугольный,
cos A =
то есть
АС =
По теореме Пифагора тогда
Ответ: 15.
Задача 18. В треугольнике АВС угол С равен 90 sin A =
AC = 10
Найдите АВ.
Решение:
1-й способ.
Поскольку sin A =
то можно обозначить
ВС = 11х, АВ = 14х.
По теореме Пифагора
(14х- 11х)(14х + 11х) = 3 100;
учитывая, что длина стороны положительна, х = 2,
следовательно, АВ = 14 2 = 28.
2-й способ.
Воспользуемся основным тригонометрическим тождеством
cos A =
По определению cos A = значит
Так как АС=10 то
откуда АВ =
= 28.
Ответ: 28.
Задача 19. Найдите углы ромба АВСD, если его диагонали АС и ВD равны 4 и 4.
Решение:
Пусть ВАО =
Диагонали ромба делят его углы пополам, значит, =
Диагонали ромба взаимно перпендикулярны и точкой пересечения делятся пополам, следовательно, в прямоугольном треугольнике АВО катет АО = а катет ВО =
Поэтому tg откуда
Ответ:
Часто в задачах встречаются треугольники с углами и
или с углами
и
. Основные соотношения для них запоминайте наизусть!
Для треугольника с углами и
катет, лежащий напротив угла в
, равен половине гипотенузы.
Треугольник с углами и
— равнобедренный. В нем гипотенуза в
раз больше катета.
Задача 20.
В треугольнике АВС угол С равен 90 угол А равен 30
АВ = 2
Найдите высоту CH.
Решение:
Рассмотрим АВС:
По свойству катета, лежащего против угла имеем ВС =
АВ =
В BHC:
то
следовательно, ВН =
BC =
По теореме Пифагора найдем НС:
Ответ: 1,5.
Задача 21.
В треугольнике АВС угол С равен 90 CH — высота, АВ = 2,
Найдите АH.
Решение:
Из АВС найдем ВС =
АВ = 1 (по свойству катета, лежащего против угла 30
),
то
Из ВСН:
то
следовательно,
ВН = ВС =
АН = АВ — НВ = 2 — = 1,5.
Ответ: 1,5.
Еще раз повторим, что такое синус, косинус и тангенс угла в прямоугольном треугольнике.
Как запомнить эти соотношения? Лучший способ – решать много задач, и на уроках геометрии, и готовясь к ЕГЭ. Тогда все формулы, равенства, соотношения запомнятся сами собой.
Мы рассмотрели задачи на решение прямоугольных треугольников — то есть на нахождение неизвестных сторон или углов. Но это не всё! В вариантах ЕГЭ по математике множество задач, где фигурирует синус, косинус, тангенс или котангенс внешнего угла треугольника. Об этом — в следующей статье.
Если вам понравился разбор данной темы — записывайтесь на курсы подготовки к ЕГЭ по математике онлайн
Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Синус, косинус и тангенс острого угла прямоугольного треугольника» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
Содержание
- Определения синуса, косинуса, тангенса и котангенса угла
- Основное тригонометрическое тождество
- Зависимость между синусом, косинусом, тангенсом и котангенсом
- Чётность, нечётность и периодичность тригонометрических функций
- Формулы сложения
- Формулы двойного и тройного аргумента
- Формулы понижения степени
- Формулы приведения
- Формулы суммы и разности синусов
- Формулы суммы и разности косинусов
- Формулы суммы и разности тангенсов
- Преобразование произведения синусов и косинусов в сумму (разность)
- Выражение синуса и косинуса через тангенс половинного аргумента
Косинус – чётная функция, а синус, тангенс и котангенс – нечётные функции аргумента :
Синус и косинус – периодические с периодом функции, а тангенс и котангенс – периодические с периодом
функции:
Число является наименьшим положительным периодом синуса и косинуса, а число
– наименьшим
положительным периодом тангенса и котангенса.
Для любого целого справедливы равенства
Наиболее часто встречающиеся тригонометрические формулы:
(blacktriangleright) Основные тождества: [begin{array}{|l|l|}
hline sin^2 alpha+cos^2 alpha =1& mathrm{tg}, alpha cdot
mathrm{ctg}, alpha =1 \
&(sinalphane 0, cosalphane 0)\[0.5ex]
hline &\
mathrm{tg}, alpha=dfrac{sin alpha}{cos alpha}
&mathrm{ctg}, alpha
=dfrac{cos alpha}{sin alpha} \&\
1+mathrm{tg}^2, alpha =dfrac1{cos^2 alpha} & 1+mathrm{ctg}^2, alpha=dfrac1{sin^2 alpha}\&\
(cosalphane 0)& (sinalphane 0) \
hline
end{array}]
(blacktriangleright) Формулы сложения углов: [begin{array}{|l|r|}
hline &\
sin{(alphapm beta)}=sinalphacdot cosbetapm sinbetacdot
cosalpha & cos{(alphapm beta)}=cosalphacdot cosbeta mp
sinalphacdot sinbeta\ &\
hline &\
mathrm{tg}, (alphapm beta)=dfrac{mathrm{tg}, alphapm
mathrm{tg}, beta}{1 mp mathrm{tg}, alphacdot
mathrm{tg}, beta} & mathrm{ctg}, (alphapmbeta)=-dfrac{1mp mathrm{ctg}, alphacdot mathrm{ctg}, beta}{mathrm{ctg}, alphapm mathrm{ctg}, beta}\&\
cosalphacosbetane 0&sinalphasinbetane 0\
hline
end{array}]
(blacktriangleright) Формулы двойного и тройного углов: [begin{array}{|lc|cr|}
hline sin {2alpha}=2sin alphacos alpha & qquad &qquad & cos{2alpha}=cos^2alpha -sin^2alpha\
sin alphacos alpha =dfrac12sin {2alpha} && & cos{2alpha}=2cos^2alpha -1\
& & & cos{2alpha}=1-2sin^2 alpha\
hline &&&\
mathrm{tg}, 2alpha = dfrac{2mathrm{tg},
alpha}{1-mathrm{tg}^2, alpha} && & mathrm{ctg}, 2alpha
= dfrac{mathrm{ctg}^2, alpha-1}{2mathrm{ctg}, alpha}\&&&\
cosalphane 0, cos2alphane 0 &&& sinalphane 0,
sin2alphane 0\
hline &&&\
sin {3alpha}=3sin alpha -4sin^3alpha && &
cos{3alpha}=4cos^3alpha -3cos alpha\&&&\
hline
end{array}]
(blacktriangleright) Формулы понижения степени: [begin{array}{|lc|cr|}
hline &&&\
sin^2alpha=dfrac{1-cos{2alpha}}2 &&&
cos^2alpha=dfrac{1+cos{2alpha}}2\&&&\
hline
end{array}]
(blacktriangleright) Формулы произведения функций: [begin{array}{|c|}
hline \
sinalphasinbeta=dfrac12bigg(cos{(alpha-beta)}-cos{(alpha+beta)}bigg)\\
cosalphacosbeta=dfrac12bigg(cos{(alpha-beta)}+cos{(alpha+beta)}bigg)\\
sinalphacosbeta=dfrac12bigg(sin{(alpha-beta)}+sin{(alpha+beta)}bigg)\\
hline
end{array}]
(blacktriangleright) Формулы суммы/разности функций: [begin{array}{|lc|cr|}
hline &&&\
sinalpha+sinbeta=2sin{dfrac{alpha+beta}2}cos{dfrac{alpha-beta}2}
&&&
sinalpha-sinbeta=2sin{dfrac{alpha-beta}2}cos{dfrac{alpha+beta}2}\&&&\
cosalpha+cosbeta=2cos{dfrac{alpha+beta}2}cos{dfrac{alpha-beta}2}
&&& cosalpha
-cosbeta=-2sin{dfrac{alpha-beta}2}sin{dfrac{alpha+beta}2}\&&&\
mathrm{tg}, alpha pm mathrm{tg},
beta=dfrac{sin{(alphapmbeta)}}{cosalphacosbeta} &&&
mathrm{ctg}, alphapm mathrm{ctg}, beta= — dfrac{sin{(alphapm beta)}}{sinalphasinbeta}\&&&\
hline
end{array}]
(blacktriangleright) Выражение синуса и косинуса через тангенс половинного угла: [begin{array}{|l|r|}
hline &\
sin{2alpha}=dfrac{2mathrm{tg}, alpha}{1+mathrm{tg}^2, alpha} & cos{2alpha}=dfrac{1-mathrm{tg}^2, alpha}{1+mathrm{tg}^2, alpha}\&\
cosalphane 0 & sinalphane 0\
hline
end{array}]
(blacktriangleright) Формула вспомогательного аргумента: [begin{array}{|c|}
hline text{Частный случай}\
hline \
sinalphapm cosalpha=sqrt2cdot
sin{left(alphapm dfrac{pi}4right)}\\
sqrt3sinalphapm cosalpha=2sin{left(alphapm dfrac{pi}6right)}\\
sinalphapm sqrt3cosalpha=2sin{left(xpm dfrac{pi}3right)}\\
hline text{Общий случай}\
hline\
asinalphapm bcosalpha=sqrt{a^2+b^2}cdot sin{(alphapm
phi)}, cosphi=dfrac a{sqrt{a^2+b^2}}, sinphi=dfrac
b{sqrt{a^2+b^2}}\\
hline
end{array}]
Зная идею вывода формул, вы можете запомнить лишь несколько из них. Тогда остальные формулы вы всегда сможете быстро вывести.
Вывод всех основных тождеств был рассказан в предыдущем разделе “Введение в тригонометрию”.
(blacktriangleright) Вывод формулы косинуса разности углов (cos{(alpha
-beta)}=cosalphacosbeta+sinalphasinbeta)
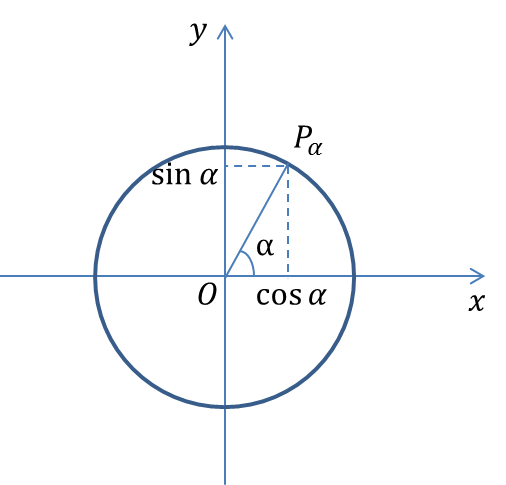
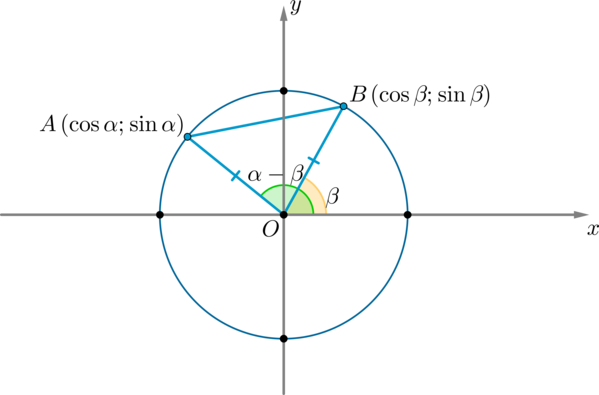
Рассмотрим тригонометрическую окружность и на ней углы (alpha) и (beta). Пусть этим углам соответствуют точки (A) и (B) соответственно. Тогда координаты этих точек: (A(cosalpha;sinalpha), B(cosbeta;sinbeta)).
Рассмотрим (triangle AOB: angle AOB=alpha-beta). По теореме косинусов:
(AB^2=AO^2+BO^2-2AOcdot BOcdot
cos(alpha-beta)=1+1-2cos(alpha-beta) (1)) (т.к. (AO=BO=R) – радиус окружности)
По формуле расстояния между двумя точками на плоскости:
(AB^2=(cosalpha-cosbeta)^2+(sinalpha-sinbeta)^2=cos^2alpha-2cosalphacosbeta+cos^2beta+)
(+sin^2alpha-2sinalphasinbeta+sin^2beta=big(cos^2alpha+sin^2alphabig)+big(cos^2beta+sin^2betabig)-2big(cosalphacosbeta+sinalphasinbetabig)=)
(=1+1-2big(cosalphacosbeta+sinalphasinbetabig) (2))
Таким образом, сравнивая равенства ((1)) и ((2)):
(1+1-2big(cosalphacosbeta+sinalphasinbetabig)=1+1-2cos(alpha-beta))
Отсюда и получается наша формула.
(blacktriangleright) Вывод остальных формул суммы/разности углов:
Остальные формулы с легкостью выводятся с помощью предыдущей формулы, свойств четности/нечетности косинуса/синуса и формул приведения (sin x=cos(90^circ-x)) и (cos x=sin (90^circ-x)):
1) (cos(alpha+beta)=cos(alpha-(-beta))=cosalphacos(-beta)+sinalphasin(-beta)=cosalphacosbeta-sinalphasinbeta)
2) (sin(alpha+beta)=cos(90^circ-(alpha+beta))=cos((90^circ-alpha)-beta)=)
(+cos(90^circ-alpha)cosbeta+sin(90^circ-alpha)sinbeta=sinalphacosbeta+cosalphasinbeta)
3) (sin(alpha-beta)=sin(alpha+(-beta))=sinalphacos(-beta)+sin(-beta)cosalpha=sinalphacosbeta-sinbetacosalpha)
4) (mathrm{tg},(alphapmbeta)=dfrac{sin (alphapmbeta)}{cos
(alphapmbeta)}=dfrac{sinalphacosbetapmsinbetacosalpha}{cosalphacosbetampsinalphasinbeta}=)
разделим числитель и знаменатель дроби на (cosalphacosbetane
0)
(при (cosalpha=0 Rightarrow
mathrm{tg},(alphapmbeta)=mp mathrm{ctg},beta), при (cosbeta=0 Rightarrow
mathrm{tg},(alphapmbeta)=pm mathrm{ctg},alpha)):
(=dfrac{mathrm{tg},alphapmmathrm{tg},beta}{1mpmathrm{tg},alphacdot
mathrm{tg},beta})
Таким образом, данная формула верна только при (cosalphacosbetane 0).
5) Аналогично, только делением на (sinalphasinbetane 0), выводится формула котангенса суммы/разности двух углов.
(blacktriangleright) Вывод формул двойного и тройного углов:
Данные формулы выводятся с помощью предыдущих формул:
1) (sin
2alpha=sin(alpha+alpha)=sinalphacosalpha+sinalphacosalpha=2sinalphacosalpha)
2) (cos2alpha=cos(alpha+alpha)=cosalphacosalpha-sinalphasinalpha=cos^2alpha-sin^2alpha)
Используя основное тригонометрическое тождество (sin^2alpha+cos^2alpha=1), получим еще две формулы для косинуса двойного угла:
2.1) (cos2alpha=cos^2alpha-sin^2alpha=cos^2alpha-(1-cos^2alpha)=2cos^2alpha-1)
2.2) (cos2alpha=cos^2alpha-sin^2alpha=(1-sin^2alpha)-sin^2alpha=1-2sin^2alpha)
3) (mathrm{tg},2alpha=dfrac{sin2alpha}{cos2alpha}=dfrac{2sinalphacosalpha}{cos^2alpha-sin^2alpha}=)
разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0 Rightarrow mathrm{tg},2alpha=0)):
(=mathrm{tg},2alpha=dfrac{2mathrm{tg},alpha}{1-mathrm{tg}^2,alpha})
Таким образом, эта формула верна только при (cosalphane 0), а также при (cos2alphane 0) (чтобы существовал сам (mathrm{tg},2alpha)).
4) (mathrm{ctg},2alpha=dfrac{cos^2alpha-sin^2alpha}{2sinalphacosalpha}=dfrac{mathrm{ctg}^2,alpha-1}{2mathrm{ctg},alpha})
По тем же причинам при (sinalphane 0, sin2alphane 0).
5) (sin3alpha=sin(alpha+2alpha)=sinalphacos2alpha+cosalphasin2alpha=sinalpha(1-2sin^2alpha)+cosalphacdot
2sinalphacosalpha=)
(=sinalpha-2sin^3alpha+2sinalpha(1-sin^2alpha)=3sinalpha-4sin^3alpha)
6) Аналогично выводится, что (cos3alpha=cos(alpha+2alpha)=4cos^3alpha-3cosalpha)
(blacktriangleright) Вывод формул понижения степени:
Данные формулы — просто по-другому записанные формулы двойного угла для косинуса:
1) (cos2alpha=2cos^2alpha-1 Rightarrow
cos^2alpha=dfrac{1+cos2alpha}2)
2) (cos2alpha=1-2sin^2alpha Rightarrow
sin^2alpha=dfrac{1-cos2alpha}2)
Заметим, что в данных формулах степень синуса/косинуса равна (2) в левой части, а в правой части степень косинуса равна (1).
(blacktriangleright) Вывод формул произведения функций:
1) Сложим формулы косинуса суммы и косинуса разности двух углов:
(cos(alpha-beta)=cosalphacosbeta+sinalphasinbeta)
(cos(alpha+beta)=cosalphacosbeta-sinalphasinbeta)
Получим: (cos(alpha+beta)+cos(alpha-beta)=2cosalphacosbeta
Rightarrow
cosalphacosbeta=dfrac12Big(cos(alpha-beta)+cos(alpha+beta)Big))
2) Если вычесть из формулы косинуса суммы косинус разности, то получим:
(sinalphasinbeta=dfrac12Big(cos(alpha-beta)-cos(alpha+beta)Big))
3) Сложим формулы синуса суммы и синуса разности двух углов:
(sin(alpha+beta)=sinalphacosbeta+sinbetacosalpha)
(sin(alpha-beta)=sinalphacosbeta-sinbetacosalpha)
Получим: (sinalphacosbeta=dfrac12Big(sin(alpha-beta)+sin(alpha+beta)Big))
(blacktriangleright) Вывод формул суммы/разности функций:
Обозначим (alpha+beta=x, alpha-beta=y). Тогда: (alpha=dfrac{x+y}2, beta=dfrac{x-y}2). Подставим эти значения в предыдущие три формулы:
1) (2cos{dfrac{x+y}2}cos{dfrac{x-y}2}=cos x+cos y)
Получили формулу суммы косинусов.
2) (2sin {dfrac{x+y}2}sin {dfrac{x-y}2}=cos y-cos x)
Получили формулу разности косинусов.
3) (2sin {dfrac{x+y}2}cos {dfrac{x-y}2}=sin y+sin x)
Получили формулу суммы синусов.
4) Формулу разности синусов можно вывести из формулы суммы синусов:
(sin x-sin y=sin x+sin(-y)=2sin {dfrac{x-y}2}cos
{dfrac{x+y}2})
5) (mathrm{tg},alphapmmathrm{tg},beta=dfrac{sinalpha}{cosalpha}pmdfrac{sinbeta}{cosbeta}=dfrac{sinalphacosbetapmsinbetacosalpha}{cosalphacosbeta}=dfrac{sin(alphapmbeta)}{cosalphacosbeta})
Аналогично выводится формула суммы котангенсов.
(blacktriangleright) Вывод формул выражения синуса и косинуса через тангенс половинного угла:
1) (sin2alpha=dfrac{sin2alpha}1=dfrac{2sinalphacosalpha}{sin^2alpha+cos^2alpha}=)
(разделим числитель и знаменатель дроби на (cos^2alphane 0) (при (cosalpha=0) и (sin2alpha=0)):)
(=dfrac{2mathrm{tg},alpha}{1+mathrm{tg}^2,alpha})
2) Так же, только делением на (sin^2alpha), выводится формула для косинуса.
(blacktriangleright) Вывод формул вспомогательного угла:
Данные формулы выводятся с помощью формул синуса/косинуса суммы/разности углов.
Рассмотрим выражение (asin x+bcos x). Домножим и разделим это выражение на (sqrt{a^2+b^2},):
(asin x+bcos x=sqrt{a^2+b^2}left(dfrac a{sqrt{a^2+b^2}}sin x+
dfrac b{sqrt{a^2+b^2}}cos x right)=sqrt{a^2+b^2}big(a_1sin x+b_1cos xbig))
Заметим, что таким образом мы добились того, что (a_1^2+b_1^2=1),
т.к. (left(dfrac a{sqrt{a^2+b^2}}right)^2+left(dfrac
b{sqrt{a^2+b^2}}right)^2=dfrac{a^2+b^2}{a^2+b^2}=1)
Таким образом, можно утверждать, что существует такой угол (phi), для которого, например, (cos phi=a_1, sin phi=b_1). Тогда наше выражение примет вид:
(sqrt{a^2+b^2},big(cos phi sin x+sin phicos
xbig)=sqrt{a^2+b^2},sin (x+phi)) (по формуле синуса суммы двух углов)
Значит, формула выглядит следующим образом: [{large{asin x+bcos x=sqrt{a^2+b^2},sin (x+phi),}} quad text{где } cos phi=dfrac
a{sqrt{a^2+b^2}}] Заметим, что мы могли бы, например, принять за (cos phi=b_1, sin phi=a_1) и тогда формула выглядела бы как [asin x+bcos x=sqrt{a^2+b^2},cos (x-phi)]
(blacktriangleright) Рассмотрим некоторые частные случаи формул вспомогательного угла:
(a) sin xpmcos x=sqrt2,left(dfrac1{sqrt2}sin
xpmdfrac1{sqrt2}cos xright)=sqrt2, sin
left(xpmdfrac{pi}4right))
(b) sqrt3sin xpmcos x=2left(dfrac{sqrt3}2sin xpm
dfrac12cos xright)=2, sin left(xpmdfrac{pi}6right))
(c) sin xpmsqrt3cos x=2left(dfrac12sin
xpmdfrac{sqrt3}2cos
xright)=2,sinleft(xpmdfrac{pi}3right))
Основные тригонометрические формулы
Содержание
 Связи между тригонометрическими функциями одного угла Связи между тригонометрическими функциями одного угла |
 Тригонометрические функции суммы и разности двух углов Тригонометрические функции суммы и разности двух углов |
 Тригонометрические функции двойного угла Тригонометрические функции двойного угла |
 Формулы понижения степени для квадратов тригонометрических функций Формулы понижения степени для квадратов тригонометрических функций |
 Формулы понижения степени для кубов синуса и косинуса Формулы понижения степени для кубов синуса и косинуса |
 Выражение тангенса угла через синус и косинус двойного угла Выражение тангенса угла через синус и косинус двойного угла |
 Преобразование суммы тригонометрических функций в произведение Преобразование суммы тригонометрических функций в произведение |
 Преобразование произведения тригонометрических функций в сумму Преобразование произведения тригонометрических функций в сумму |
 Выражение тригонометрических функций через тангенс половинного угла Выражение тригонометрических функций через тангенс половинного угла |
 Тригонометрические функции тройного угла Тригонометрические функции тройного угла |
Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
Косинус двойного угла |
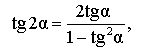 |
Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
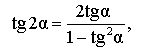 |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
|
Выражение квадрата синуса через косинус двойного угла |
|
|
Выражение квадрата косинуса через косинус двойного угла |
|
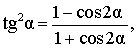 |
Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
| Сумма синусов |
|
|
| Разность синусов |
|
|
| Сумма косинусов |
|
|
| Разность косинусов |
|
|
| Сумма тангенсов |
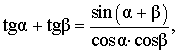 |
| Разность тангенсов |
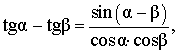 |
Преобразование произведения тригонометрических функций в сумму
| Произведение синусов |
|
|
| Произведение косинусов |
|
|
| Произведение синуса и косинуса |
|
|
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
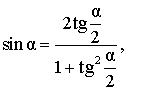 |
Выражение синуса угла через тангенс половинного угла |
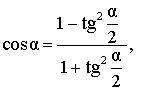 |
Выражение косинуса угла через тангенс половинного угла |
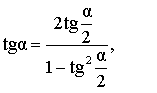 |
Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
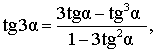 |
Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
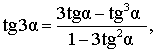 |
- Определение
- График косинуса
- Свойства косинуса
- Обратная к косинусу функция
- Таблица косинусов
Определение
Косинус острого угла α (cos α) – это отношение прилежащего катета (b) к гипотенузе (c) в прямоугольном треугольнике.
cos α = b / c
Например:
b = 4
c = 5
cos α = b / c = 4 / 5 = 0.8
График косинуса
Функция косинуса пишется как y = cos (x). График называется косинусоидой и в общем виде выглядит следующим образом:
Косинусоида – периодическая функция с основным периодом T = 2π.
Свойства косинуса
Ниже в табличном виде представлены основные свойства косинуса с формулами:
Обратная к косинусу функция
Арккосинус x – это обратная к косинусу функция x, при -1≤x≤1.
Если косинус у равняется х (cos y = x), значит арккосинус x равен у:
arccos x = cos-1 x = y
Например:
arccos 1 = cos-1 1 = 0° (0 рад)
Таблица косинусов
| x (°) | x (рад) | cos x |
| 180° | π | -1 |
| 150° | 5π/6 | -√3/2 |
| 135° | 3π/4 | -√2/2 |
| 120° | 2π/3 | -1/2 |
| 90° | π/2 | 0 |
| 60° | π/3 | 1/2 |
| 45° | π/4 | √2/2 |
| 30° | π/6 | √3/2 |
| 0° | 0 | 1 |
microexcel.ru