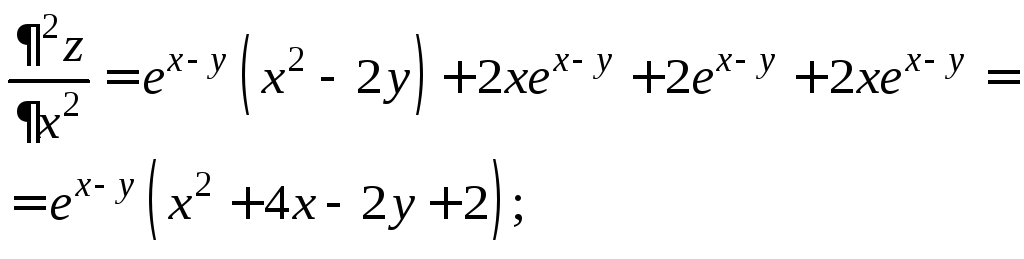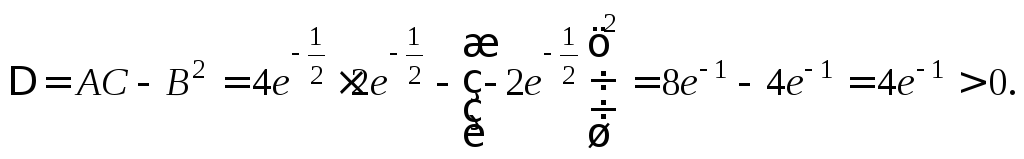Как найти косинус угла между градиентами - Исправление недочетов и поиск решений вместе с Examum.ru

Найдём градиент скалярного поля [math]U[/math] в точке [math]M[/math] и модуль:

[math]mathbf{grad}U=frac{partial{U}}{partial{x}},mathbf{i}+frac{partial{U}}{partial{y}},mathbf{j}+frac{partial{U}}{partial{y}},mathbf{k}=frac{3}{2}x^2,mathbf{i}+18y^2,mathbf{j}+9sqrt{6},z^2,mathbf{k}[/math]

[math]left.{mathbf{grad}U}right|_M=frac{3}{2}{!left(sqrt2right)!}^2,mathbf{i}+18{!left(frac{1}{sqrt2}right)!}^2,mathbf{j}+9sqrt6{left(frac{1}{sqrt3}right)!}^2,mathbf{k}=3,mathbf{i}+9,mathbf{j}+3sqrt6,mathbf{k}[/math]

[math]left|left.{mathbf{grad}U}right|_Mright|=sqrt{3^2+9^2+{!left({3sqrt6}right)!}^2}=sqrt{9+81+54}=sqrt{144}=12[/math]

Найдём градиент скалярного поля [math]V[/math] в точке [math]M[/math] и модуль:

[math]mathbf{grad}V=frac{partial{V}}{partial{x}},mathbf{i}+frac{partial{V}}{partial{y}},mathbf{j}+frac{partial{V}}{partial{y}},mathbf{k}=frac{2x}{yz^2},mathbf{i}-frac{x^2}{y^2z^2},mathbf{j}-frac{2x^2}{yz^3},mathbf{k}[/math]

[math]left.{mathbf{grad}V}right|_M=frac{2sqrt2}{frac{1}{sqrt2}left(frac{1}{sqrt3}right)^2},mathbf{i}-frac{left(sqrt2right)^2}{left(frac{1}{sqrt2}right)^2left(frac{1}{sqrt3}right)^2},mathbf{j}-frac{2left(sqrt2right)^2}{frac{1}{sqrt2}left(frac{1}{sqrt3}right)^3},mathbf{k}=12,mathbf{i}-12,mathbf{j}-12sqrt6,mathbf{k}[/math]

[math]left|left.{mathbf{grad}V}right|_Mright|=sqrt{12^2+{!left(-12right)!}^2+{!left(-12sqrt6right)!}^2}=sqrt{12^2cdot8}=24sqrt2[/math]

Вычислим скалярное произведение градиентов полей [math]U[/math] и [math]V[/math] в точке [math]M[/math]

[math]leftlangle{left.{mathbf{grad}U}right|_M,,left.{mathbf{grad}V}right|_M}rightrangle=3cdot12+9cdot(-12)+3sqrt6cdotleft(-12sqrt6right)=36-108-216=-288[/math]

Вычислим значение косинуса угла между градиентами

[math]cosalpha=frac{leftlangle{left.{mathbf{grad}U}right|_M,,left.{mathbf{grad}V}right|_M}rightrangle}{left|left.{mathbf{grad}U}right|_Mright|cdotleft|left.{mathbf{grad}V}right|_Mright|}=frac{-288}{12cdot24sqrt2}=-frac{1}{sqrt2}[/math]

Следовательно, искомый угол [math]alpha[/math] есть

[math]alpha=arccos!left(-frac{1}{sqrt2}right)=pi-arccosfrac{1}{sqrt2}=pi-frac{pi}{4}=frac{3pi}{4}=135^circ[/math]

Также смотрите ещё примеры

viewtopic.php?f=35&t=313

viewtopic.php?f=35&t=3289

Источник

Производной
функции
в точке
по направлению
называется предел

где

если предел
существует.

Если функция
дифференцируема, то производная по
направлению вычисляется по формуле

(18.31)

где
– направляющие косинусы вектора

В частности, если
– функция двух переменных, то формула
(18.31) производной по направлению примет
вид:

(18.32)

где
– угол между вектороми осьюОх.

Градиентомфункциив точкеназывается вектор

(18.33)

или, то же самое,

Связь между
градиентом функции и производной по
направлению устанавливает формула

где
– угол между векторамии

Градиент функции
указывает направление наибыстрейшего
возрастания функции. Наибольшее значение
производной
достигаемое в направление градиента,
равно

В
частности, если
– функция двух переменных, то

Пример
1. Найти
производную функции
в точкепо направлению вектораобразующего с положительным направлением
осиОх
угол

Решение.
Используя
формулу (18.32),
вычислим
частные производные функции z
в точке A:

Так
как
то

Пример
2. Найти
производную функции
в точкепо направлению к точке

Решение.
Найдем вектор

Его направляющие
косинусы равны:

Найдем
значения частных производных функции
u
в точке

Тогда
по формуле (18.31) получим:

Пример
3. Найти
длину и направление (указать направляющие
косинусы) градиента функции
в точке

Решение.
Вычислим
частные производные функции u
в точке М.

Используем
формулу (18.33) при условии, что частные
производные вычисляем в заданной точке

Тогда

Вычисляем
длину полученного вектора:

Используем
тот факт, что направляющие косинуса
равны координатам единичного вектора
направления, определяемого вектором
дроби. Поэтому

Задания

I уровень

1.1.Найдите
производную функциив точкепо направлению вектора

1.2.Найдите
производную функциив точкепо направлению вектора

1.3.Найдите
величину и направление градиента функциив точке

II уровень

2.1.Найдите
производную указанной функции в точкепо направлению к точке

2.2.Найдите
величину и направление градиента функциизаданной неявно, в точке

2.3.Найдите
угол между градиентами функциив точкахи

2.4.Найдите
производную функциив точкев направленииперпендикулярном к линии уровня,
проходящей через эту точку.

III уровень

3.1. Найдите
градиент функциив точкахи

3.2.Определите,
в каких точках градиент функцииудовлетворяет условию:

1) параллелен оси
Оу;

2) перпендикулярен
оси Оу;

3) равен нулю.

3.3.Выясните,
в каких точках градиент функцииудовлетворяет условию:

1) перпендикулярен
прямой
2)
равен нулю.

3.4.Определите,
в каких точках выполнено равенствоесли

3.5.Найдите
градиент функциизаданной неявно уравнением:

1)
2)3)

3.6.Определите
направление наибыстрейшего возрастания
функции:

1)
2)

3)
4)

18.8. Экстремумы функций двух переменных

Функция
имеет в точкелокальный максимум (минимум),
если существует такая-окрестность
точкиМ₀, что для всех точекиз этой окрестности (отличных отМ₀)
выполняется неравенство

Максимум и минимум
функции называются ее экстремумами(локальными), а точкаМ₀, в
которой достигается экстремум, называетсяточкой экстремума.

Необходимое
условие экстремума: если
в точке
дифференцируемая функцияимеет экстремум, то ее частные производные
в этой точке равны нулю:

(18.34)

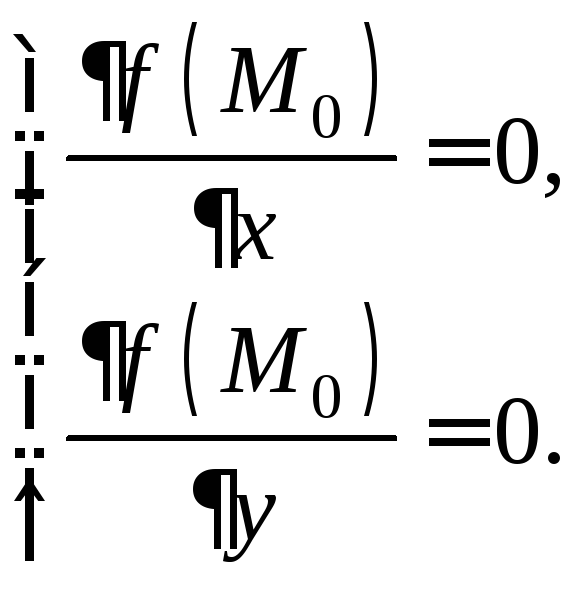
Точки, в которых
частные производные существуют и равны
нулю, называются стационарными.

Точки из области
определения функции, в которых частные
производные равны нулю или не существуют,
называются критическими точками.

Не всякая критическая
точка является точкой экстремума.

Достаточное
условие экстремума. Пусть– стационарная точка дважды непрерывно
дифференцируемой функцииОбозначим:

Тогда:

1) если
то функция имеет в точкеМ₀локальный экстремум (максимум прии минимум при);

2) если
то в точкеМ₀функция не имеет
экстремума;

3) если
то в точкеМ₀функция может
иметь локальный экстремум, а может и не
иметь его (нужны дополнительные
исследования).

Допустим, что
функция f(x;y) определена на
некотором множестве

Число Сназываютнаибольшим значением функции(глобальный максимум) на множестве
D, если

записывают так:

Число сназываютнаименьшим значением функции(глобальным минимумом) на множествеD, если

записывают так:

Теорема
Вейерштрасса. Непрерывная на
замкнутом ограниченном множествефункциядостигает на этом множестве своего
наибольшего и наименьшего значений.

Для нахождения
наибольшего и наименьшего значений
функции в области
нужно:

1) найти критические
точки функции, принадлежащие D, и
вычислить значение функции в них;

2) найти наибольшее
и наименьшее значения функции на границах
области

3) сравнить все
полученные значения функции и выбрать
из них наибольшее и наименьшее.

Если область
определения функции не является
замкнутой, то для нахождения наибольшего
и наименьшего значений функции необходимо:

1) найти критические
точки функции, принадлежащие D;

2) исследовать
найденные критические точки на экстремум
(локальный);

3) вычислить значения
функции в точках локального максимума
(минимума) и отобрать среди них наибольшее
(наименьшее).

Пример
1. Исследовать
на экстремум функцию

Решение.
Находим частные производные первого
порядка:

Приравниваем их
к нулю, чтобы найти стационарные точки:

Решая
систему уравнений, получим:
т. е.

Вычисляем
значения частных производных второго
порядка в точке М₀:

Тогда
Следовательно, в точкеэкстремума нет.

Пример
2. Найти
экстремум функции

Решение.
Частные
производные первого порядка:

Стационарные
точки:

Частные производные
второго порядка:

Тогда

Получаем:

Поскольку
то в точкефункция имеет минимум:

Пример
3. Найти
наибольшее и наименьшее значения функции
в областиограниченной прямыми

Решение.
1) Вычислим частные производные и найдем
критические точки:

Получим:
– критическая точка, принадлежащая
области

Вычислим в ней
значение функции:

2)
Исследуем функцию z
на границе области
(рис. 18.4).

Рис. 18.4

Уравнение
границы AB:
Подставляем число –3 вместох
в аналитическое задание функции:
где

Исследуем
полученную функцию, как функцию одной
переменной, на наибольшее значение.

Найдем критические
точки:

Получаем
– критическая точка, при этом

Вычисляем
значение функции в точке
и на концах отрезка:

Уравнение
границы BC:
На этом участке уравнение функции имеет
вид:где

Поскольку
то дляполучаем критическую точкуТогда

Уравнение
границы AC:
ТогдагдеКритическая точкапринадлежащая

Вычисляем
значение функции для

3)
Из всех полученных значений z
выбираем наименьшее и наибольшее:

Задания

Соседние файлы в папке Часть 3

Источник

Как найти угол между градиентами функции в точках

&nbsp &nbsp &nbsp &nbsp Вариант 1 &nbsp &nbsp Вариант 2 &nbsp &nbsp Вариант 3 &nbsp &nbsp Вариант 4 &nbsp &nbsp Вариант 5 &nbsp &nbsp Вариант 6

&nbsp &nbsp &nbsp &nbsp Вариант 7 &nbsp &nbsp Вариант 8 &nbsp &nbsp Вариант 9 &nbsp &nbsp Вариант 10 &nbsp &nbsp Вариант 11 &nbsp &nbsp Вариант 12

&nbsp &nbsp Вариант 13 &nbsp &nbsp Вариант 14 &nbsp &nbsp Вариант 15 &nbsp &nbsp Вариант 16 &nbsp &nbsp Вариант 17 &nbsp &nbsp Вариант 18

&nbsp &nbsp Вариант 19 &nbsp &nbsp Вариант 20 &nbsp &nbsp Вариант 21 &nbsp &nbsp Вариант 22 &nbsp &nbsp Вариант 23 &nbsp &nbsp Вариант 24

&nbsp &nbsp Вариант 25 &nbsp &nbsp Вариант 26 &nbsp &nbsp Вариант 27 &nbsp &nbsp Вариант 28 &nbsp &nbsp Вариант 29 &nbsp &nbsp Вариант 30

&nbsp &nbsp &nbsp &nbsp 2.29 Найти угол между градиентами скалярных полей U(x,y,z) и V(x,y,z) в точке M.

Задачка по математике

Найти угол между градиентами в двух точках.
функция z=arcsin(x/(x+y))
Точки: (1,1) и (3,4).
Проверьте пожалуйста решение. В нем явно есть ошибка. Или предложите другой ход решения.
Частные производные и градиенты получились такие:

Повторно перерешал и нашел частные производные. Сам ошибок не нашел — примелькались уже. Вот подробный ход решения:

Высшая математика и экономика

Задача 1.
Найти производную скалярного поля в точке по направлению проходящей через эту точку нормали к поверхности , образующей острый угол с положительным направлением оси .

Задача 2.
Найти угол между градиентами скалярных полей и в точке М.

— искомый угол.

Источник

ОТВЕТ: $dfrac{2pi}{3}$ , или .

Объяснение: Найдем частные производные 1-го порядка функции :

$v'_x=dfrac{3x^2}{sqrt2}-0+0= dfrac{3x^2}{sqrt2};\\v'_y=0-dfrac{3y^2}{sqrt2}+0=- dfrac{3y^2}{sqrt2};\\v'_z=0-0+dfrac{24z^2}{sqrt3}=dfrac{24z^2}{sqrt3}.$

Градиент функции :

$nabla v=(v'_x; v'_y; v'_z)=(dfrac{3x^2}{sqrt2}; -dfrac{3y^2}{sqrt2}; dfrac{24z^2}{sqrt3});\\nabla v|_{M_0}=(dfrac{3cdot2}{sqrt2}; -dfrac{3cdot2}{sqrt2}; dfrac{24cdot3}{4sqrt3}) =(3sqrt2; -3sqrt2; 6sqrt3).$

Аналогичным образом находим градиент функции в точке M_o :

$u'_x=dfrac{2x}{y^2z^3};\\u'_y=dfrac{-2x^2}{y^3z^3};\\u'_z= dfrac{-3x^2}{y^2z^4};\\nabla u=(u'_x; u'_y; u'_z)=(dfrac{2x}{y^2z^3}; dfrac{-2x^2}{y^3z^3};dfrac{-3x^2}{y^2z^4});\\nabla u|_{M_0}=(dfrac{2sqrt2cdot2^3}{2cdot3sqrt3}; dfrac{-2cdot2cdot2^3}{2sqrt2cdot3sqrt3};dfrac{-3cdot2cdot2^4}{2cdot3^2})=(dfrac{8sqrt6}{9}; -dfrac{8sqrt6}{9}; -dfrac{16}{3}).$

По определению скалярного произведения:

$nabla vcdotnabla u=|nabla v|cdot|nabla u|cdot cosvarphiRightarrow\\Rightarrow cosvarphi=dfrac{nabla vcdotnabla u}{|nabla v|cdot|nabla u|}.$

Модули градиентов:

$|nabla v|=sqrt{(3sqrt2)^2+(-3sqrt2)^2+(6sqrt3)^2}=sqrt{18+18+108}=sqrt{144}=12;\\|nabla u|=sqrt{(dfrac{8sqrt6}{9})^2+(-dfrac{8sqrt6}{9})^2+(-dfrac{16}{3})^2}=sqrt{dfrac{8^2cdot6}{81} +dfrac{8^2cdot6}{81} +dfrac{16^2}{9} }=\\=sqrt{dfrac{2^2cdot3cdot8^2+3^2cdot16^2}{81}}=dfrac{sqrt{2^8cdot3+2^8cdot3^2}}{9}=dfrac{2^4sqrt{12}}{9}=dfrac{16sqrt{4cdot3}}{9}=dfrac{32sqrt{3}}{9}.$

Скалярное произведение градиентов:

$nabla vcdot nabla u=3sqrt2cdotdfrac{8sqrt6}{9}+(-3sqrt2)cdot(-dfrac{8sqrt6}{9})-6sqrt3cdotdfrac{16}{3}=2cdotdfrac{8cdotsqrt{12}}{3}-32sqrt3=dfrac{32sqrt3}{3}-32sqrt3=-dfrac{64sqrt3}{3}.$

Косинус искомого угла:

$cosvarphi=dfrac{-dfrac{64sqrt3}{3}}{12cdotdfrac{32sqrt3}{9}} =-dfrac{64sqrt3}{3}:dfrac{4cdot32sqrt3}{3}=-dfrac{64sqrt3}{3} cdotdfrac{3}{2cdot64sqrt3}=-dfrac{1}{2}.$

Отсюда искомый угол:

$varphi =arccos(-dfrac{1}{2})=dfrac{2pi}{3}=120textdegree.$

Источник