Угол между плоскостями.
Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:
cos α = |2·4 + 4·3 + (-4)·0| √ 2 2 + 4 2 + (-4) 2 √ 4 2 + 3 2 + 0 2 = |8 + 12| √ 36 √ 25 = 20 30 = 2 3
Ответ: косинус угла между плоскостями равен cos α = 2 3 .
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
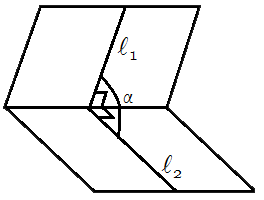
Угол между плоскостями
Углом между плоскостями именуется такой угол, который образовался между перпендикулярными прямыми, опущенными в пределах этих плоскостей к линии их пересечения.
Рассмотрим данное понятие наглядно с помощью картинки:
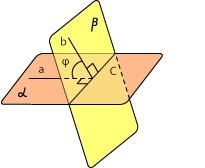
Допустим, α и β — пересекающиеся плоскости. Проведем к линии с перпендикуляр a, который принадлежит α. Далее проведем прямую b, лежащую в β и образующую с прямой c угол в 90°. Угол между α и β равен углу, который образовался между а и b, обозначенному на картинке как φ. В записи это выглядит следующим образом:
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
На схеме видно, что при пересечении α и β возникают четыре угла, но углом между плоскостями считается острый угол. В случае, когда плоскости при пересечении создают прямые углы, они считаются перпендикулярными друг другу.
Расположение плоскостей и формула вычисления угла между ними
Существует несколько вариаций взаимного расположения двух плоскостей.
Параллельность
Две плоскости считаются параллельными в том случае, если у них отсутствуют общие точки.
Возьмем за условие, что плоскости α, расположенной в некоторой прямоугольной системе координат, соответствует общее уравнение: А1х+В1у+С1z+D1=0. А плоскость β определяется общим уравнением вида: А2х+В2у+С2z+D2=0.
Согласно теореме о параллельности плоскостей, чтобы α и β являлись параллельными, достаточно отсутствия решений системы линейных уравнений вида:
То есть приведенная выше система должна быть несовместной.
Доказательство
Допустим, указанные плоскости, соответствующие уравнениям А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 параллельны друг другу, следовательно, у них отсутствуют общие точки. Это значит, что нет ни одной точки в прямоугольной системе координат, находящейся в трехмерном пространстве, чьи координаты отвечали бы условиям обоих уравнений одновременно или:
не имеет решения.
В случае, если данная система уравнений не имеет решений, то в прямоугольной системе координат трехмерного пространства отсутствуют точки с координатами, одновременно отвечающими условиям обоих уравнений, входящих в рассматриваемую систему. Отсюда можно сделать вывод, что плоскости α и β с соответствующими им уравнениями А1х+В1у+С1z+D1=0 и А2х+В2у+С2z+D2=0 не обладают ни одной общей точкой, а значит, являются параллельными. Теорема доказана.
Перпендикулярность
Две плоскости перпендикулярны друг другу, в ситуации, когда они при взаимном пересечении образуют прямой угол, то есть угол в 90°.
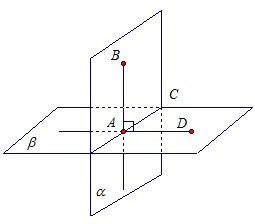
Если одна из двух плоскостей проходит через прямую, которая перпендикулярна другой плоскости, то такие плоскости являются перпендикулярными.
Доказательство
- α∩β=AC, причем AB⊥AC по условию.
- Проведем прямую AD, принадлежащую плоскости β и перпендикулярную AC.
- ∠BAD=90°, поскольку AB⊥β. Следовательно, заданные плоскости перпендикулярны, что и требовалось доказать.
Плоскость, перпендикулярная к прямой, по которой пересекаются две заданные плоскости, перпендикулярна к каждой из этих плоскостей.
Явность перпендикулярных пересекающихся плоскостей достигается при необходимом и достаточном условии, что нормальные векторы данных плоскостей при пересечении образовали прямой угол.
Доказательство
Допустим, в трехмерном пространстве существует некоторая прямоугольная система координат. При наличии нормальных векторов заданных плоскостей α и β с координатами:
то необходимо и достаточно, чтобы эти векторы приняли вид:
(left(overrightarrow,overrightarrowright)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Отсюда следует, что:
— нормальные векторы плоскостей α и β. Чтобы заданные плоскости были перпендикулярными, достаточно, чтобы скалярное произведение данных векторов ровнялось нулю, то есть принимало вид:
(left(overrightarrow,overrightarrowright)=0Leftrightarrow A_1times A_2+B_1times B_2+C_1times C_2=0)
Угол между плоскостями
Для вычисления угла между двумя пересекающимися плоскостями используют метод координат. Суть данного способа заключается в нахождении косинуса угла, образованного при пересечении плоскостей.
Предположим, что плоскости P1 и P2 заданы следующими уравнениями:
Найдем косинус угла между P1 и P2 по формуле:
Запишем в ответе модуль косинуса угла, поскольку за величину угла между плоскостями принимают острый угол.
Примеры решения задач
Задача №1
Плоскости заданы уравнениями:
Определить пересекаются ли α и β. В случае пересечения заданных плоскостей найти угол между ними.
Найдем угол между заданными плоскостями:
Далее вычислим косинус угла между α и β:
В ответе запишем модуль найденной величины.
Ответ: плоскости α и β пересекаются, а косинус угла между ними равен ½.
Задача №2
Плоскость α проходит через точку A(1,1,−1) и перпендикулярна к плоскостям, заданным уравнениями:
Составьте уравнение плоскости α.
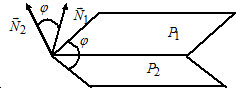
Необходимым и достаточным условием перпендикулярности α к плоскостям β и φ является параллельность α к нормалям β и φ — N1 и N2, иными словами, α должна быть перпендикулярна к произведению векторов [N1,N2].
Следующим шагом выпишем уравнение плоскости α, проходящей через точку A(1,1,−1) и перпендикулярную вектору [N1,N2]=(−14,7,7):
Угол между плоскостями. Метод координат. Задание 14
Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.
Величина двугранного угла измеряется величиной соответствующего линейного угла.
Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:
Пусть наши плоскости и
заданы уравнениями:
:
:
Косинус угла между плоскостями находится по такой формуле:
В ответе мы записываем , так как величиной угла между плоскостями называется величина меньшего двугранного угла.
Решим задачу, которая была предложена на пробнике для подготовке к ЕГЭ 17 марта 2012 года.
В правильной четырехугольной призме со стороной основания 12 и высотой 21 на ребре
взята точка М так, что
. На ребре
взята точка K так, что
. Найдите угол между плоскостью
и плоскостью
.
Сделаем чертеж. Так как мы будем использовать метод координат, сразу введем систему координат:
Теперь перед нами стоит задача написать уравнения плоскости и плоскости
Подробный алгоритм нахождения уравнения плоскости по трем точкам я описывала здесь.
После того, как мы найдем коэффициенты в уравнениях плоскости и плоскости
, подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол.
19
Мар 2012
13 Задание (2022) (C2)ВИДЕОУРОКИ
Угол между плоскостями. Метод координат. Задание 14
Угол между плоскостями. Метод координант.
В этой статье я расскажу, как решать задачи на нахождение угла между плоскостями с помощью метода координат.
Сначала немного теории.
Две пересекающиеся плоскости образуют две пары равных между собой двугранных углов.
Величина двугранного угла измеряется величиной соответствующего линейного угла.
Чтобы построить линейный угол двугранного угла, нужно взять на линии пересечения плоскостей произвольную точку, и в каждой плоскости провести к этой точке луч перпендикулярно линии пересечения плоскостей. Угол, образованный этими лучами и есть линейный угол двугранного угла:
Пусть наши плоскости и
заданы уравнениями:
:
:
Косинус угла между плоскостями находится по такой формуле:
В ответе мы записываем , так как величиной угла между плоскостями называется величина меньшего двугранного угла.
Решим задачу, которая была предложена на пробнике для подготовке к ЕГЭ 17 марта 2012 года.
В правильной четырехугольной призме со стороной основания 12 и высотой 21 на ребре
взята точка М так, что
. На ребре
взята точка K так, что
. Найдите угол между плоскостью
и плоскостью
.
Сделаем чертеж. Так как мы будем использовать метод координат, сразу введем систему координат:
Теперь перед нами стоит задача написать уравнения плоскости и плоскости
Подробный алгоритм нахождения уравнения плоскости по трем точкам я описывала здесь.
После того, как мы найдем коэффициенты в уравнениях плоскости и плоскости
, подставим их в формулу для нахождения косинуса угла между плоскостями, и найдем угол.
Предлагаю вам посмотреть подробное видеорешение этой задачи:
КУПИТЬ видеокурс «Векторы и координаты. Часть В и Задание 14»
И.В. Фельдман, репетитор по математике.
Для вас другие записи этой рубрики:
- Решение задачи с параметром с помощью параметрической плоскости. Задание С5
- Видеотека. Решение текстовых задач на проценты.
- Наибольшее и наименьшее значение функции. Задание В15 (2014)
- Видеолекция «Метод координат. Задание 14. Углы в пространстве»
- Задание 14 из ЕГЭ по математике 2.06.2017
- Видеорешение диагностической работы от 1 марта 2012 года

|
Отзывов (50)
| Метки: решение задания С2
Угол между плоскостями.
Определение.
Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.
Определение.
Двугранный угол между плоскостями равен углу образованному прямыми l1 и l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.
Формула для вычисления угла между плоскостями
Если заданы уравнения плоскостей A1x + B1y + C1z + D1 = 0 и A2x + B2y + C2z + D2 = 0, то угол между плоскостями можно найти, используя следующую формулу
| cos α = | |A1·A2 + B1·B2 + C1·C2| |
| √A12 + B12 + C12√A22 + B22 + C22 |
Примеры задач на вычисление угла между плоскостями
Пример 1.
Найти угол между плоскостями 2x + 4y — 4z — 6 = 0 и 4x + 3y + 9 = 0.
Решение. Подставим в формулу вычисления угла между плоскостями соответствующие коэффициенты:
cos α =
|2·4 + 4·3 + (-4)·0|√22 + 42 + (-4)2√42 + 32 + 02
=
|8 + 12|√36√25
=
2030
=
23
Ответ: косинус угла между плоскостями равен cos α = 23.
Задачу можно очень сильно упростить. Точка К — центр грани А1B1C1D1 — принадлежит прямым B1D1 и A1C1, то есть — обеим плоскостям. Точно так же центр грани ABB1A1 — точка М принадлежит A1B и B1A, то есть опять таки обеим плоскостям. Таким образом КМ — линия пересечения плоскостей.
Треугольники А1КМ и В1КМ — равносторонние. Если считать, что их сторона равна 1, то ребро куба равно √2, а высота треугольника А1КМ (и В1КМ — тоже) равна √3/2;
То есть если обозначить косинус угла между перпендикулярами к КМ из точек A1 и В1 как х, то по теореме косинусов
(√2)^2 = (√3/2)^2 + (√3/2)^2 — 2*(√3/2)*(√3/2)*x; x = -1/3; Конечно, знак тут никакой роли не играет, просто выбранный для вычисления треугольник — тупоугольный. Дополнительный к нему угол имеет косинус 1/3; это просто вопрос выбора.
На самом деле, самое простое решение этой задачи получается, если применить координатный метод. Пусть Р — середина А1В1. Пусть начало координат лежит в ней, ось Z проходит через точку М, Х — через точку К, Y — через точки А1 и В1.
Здесь я принимаю ребро куба равным 2, то есть РА1 = РВ1 = РК = РМ = 1;
Плоскость ВА1С1 — то есть плоскость А1КМ проходит через точки К = (1,0,0); А1 = (0,-1,0); М = (0,0,-1);
уравнение такой плоскости x — y — z = 1; (можете проверить, что все три точки удовлетворяют этому уравнению)
Отсюда нормальный вектор к этой плоскости q = (1,-1,-1);
модуль этого вектора равен √3
Плоскость АВ1С1 — то есть плоскость В1КМ проходит через точки К = (1,0,0); В1 = (0,1,0); М = (0,0,-1);
уравнение такой плоскости x + y — z = 1;
Отсюда нормальный вектор к этой плоскости l = (1, 1,-1);
модуль этого вектора тоже равен √3;
осталось вычислить угол между нормальными векторами (равный, очевидно, углу между плоскостями), для чего надо их скалярно перемножить и разделить на модули. Скалярное произведение равно ql = 1 — 1 + 1 = 1; а произведение модулей равно 3, откуда косинус угла равен 1/3.
Видно, что тут ответ получается сам собой. Но большое преимущество такого метода в том, что им легко получать углы между плоскостями и в более сложных случаях, когда применение простых геометрических методов затруднительно.
2023-02-20
В кубе $ABCDA_{1}B_{1}C_{1}D_{1}$ найдите косинус угла между плоскостями $BA_{1}C_{1}$ и $AB_{1}D_{1}$.
Решение:
Диагональ $DB_{1}$ куба $ABCDA_{1}B_{1}C_{1}D_{1}$ перпендикулярна плоскости $BA_{1}C_{1}$, т.к. она перпендикулярна двум пересекающимся прямым $A_{1}C_{1}$ и $BC_{1}$ этой плоскости (по теореме о трёх перпендикулярах). Аналогично диагональ $CA_{1}$ перпендикулярна плоскости $AB_{1}D_{1}$. Следовательно, угол $alpha$ между плоскостями $BA_{1}C_{1}$ и $AB_{1}D_{1}$ равен углу между прямыми $DB_{1}$ и $CA_{1}$, соответственно перпендикулярными этим плоскостям.
Рассмотрим сечение $CDD_{1}C_{1}$. Диагонали прямоугольника $CDD_{1}C_{1}$ равны и делятся точкой $O$ пересечения пополам. Пусть ребро куба равно $a$. Тогда
$OC=OD=frac{1}{2}DB_{1}=frac{1}{2}cdot asqrt{3}=frac{asqrt{3}}{2}.$
По теореме косинусов
$cosalpha=cosangle COD=frac{OC^{2}+OD^{2}-CD^{2}}{2OCcdot OD}=frac{frac{3}{4}a^{2}+frac{3}{4}a^{2}-a^{2}}{2cdotfrac{asqrt{3}}{2}cdotfrac{asqrt{3}}{2}}=frac{1}{3}.$