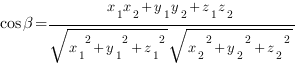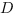Как найти косинус угла между скрещивающимися прямыми - Исправление недочетов и поиск решений вместе с Examum.ru

25
Апр 2012

13 Задание (2022) (C2)

В этой статье я расскажу, как находить угол между скрещивающимися прямыми с помощью метода координат.

Если мы решили использовать этот метод, то будем придерживаться такого алгоритма:

1. Вводим систему координат.

2. Находим координаты направляющих векторов данных прямых.

3. По формуле косинуса угла между векторами находим косинус угла между направляющими векторами.

Косинус угла между векторами 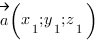$vec{a}(x_1;y_1;z_1)$ и $vec{b}(x_2;y_2;z_2)$ вычисляется по формуле:

$cos{beta}={{x_1}{x_2}+{y_1}{y_2}+{z_1}{z_2}}/{sqrt{{x_1}^2+{y_1}^2+{z_1}^2}{sqrt{{x_2}^2+{y_2}^2+{z_2}^2}} }$

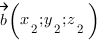
Вот, собствено, и все.

Важное уточнение: за угол между прямыми принимают меньший из двух углов, образованный этими прямыми, поэтому косинус угла между прямыми должен быть больше нуля, и он равен модулю косинуса угла между направляющими векторами.

Решим задачу.

В правильной шестиугольной призме , все ребра которой равны 1, найти косинус угла между прямыми и :1. Введем систему координат:

2. а) Найдем координаты направляющего вектора прямой A_1B , для этого найдем координаты точек A_1 и .

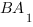
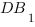
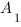
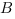
Длину отрезка найдем по тереме косинусов из треугольника AOE :

$AE =sqrt{1^2+1^2-2*1*1cos{120^{circ}}}=sqrt{3}$

$A_1(0;sqrt{3};1)$ ;

Чтобы найти координаты вектора $vec{A_1B }$ , из координат конца вычтем координаты начала. Получим: $vec{A_1B }(1;0;-1)$

б) Найдем координаты направляющего вектора прямой B_1D , для этого найдем координаты точек B_1 и

$B_1 (1;sqrt{3};1)$

$vec{B_1D }(0;-sqrt{3};-1)$

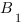
3. Найдем косинус угла 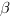beta между векторами $vec{A_1B }$ и $vec{B_1D }$ .

$cos{beta}=delim{|}{{{1}*{0}+{0}*({-sqrt{3}})+({-1})({-1})}/{sqrt{({-1})^2+{0}^2+({-1})^2}{sqrt{{0}^2+({-sqrt{3}})^2+({-1})^2}} }}{|}=$

Ответ:

И.В. Фельдман, репетитор по математике.

|
Отзывов (9)
| Метки: решение задания С2

Источник

Учебник

Геометрия, 10 класс

Угол между скрещивающимися прямыми в пространстве

Скрещивающиеся прямые — не параллельны, не имеют общих точек, не пересекаются.

Признаки Скрещивающихся прямых

1-ая прямая лежит в плоскости, а 2-ая пересекает плоскость в точке не из 1-ой, то прямые скрещивающиеся.
Через каждую из скрещивающихся прямых проходит плоскость, параллельная другой прямой. Единственная.
Скрещивающиеся $a$ и $b$ : есть пара пареллельных плоскостей $alpha$ и $beta$, таких что $ain alpha$, $bin beta$

Задача 1: В прямоугольном параллелепипеде $ABCDMNKL$ найти угол между

скрещивающимися прямыми $AN$ и $BK$, если известны ребра $BA=36$, $BN=15$, $BC=20$

Как находить угол между двумя стереометрическими объектами? по алгоритму параллельных переносов, совмещений.
Свойство инвариантности углов при параллельном переносе стереометрических объектов — прямых, плоскостей:
Если объекты $A$ и $B$ параллельны соответственно $A’$ и $B’$, то углы между парами равные: $angle left(A;Bright)=angle left(A’;B’right)$
В нашем случае, $BKparallel AL$, поэтому равны углы $angle left(AN;BKright)=angle left(AN;ALright)=angle NAL$
Перетащим $BK$ по плоскости $BKLA$ вдоль $BA$ до совмещения с точкой $A$. Тогда $BK$ совметится с отрезком $AL$.
Итак, мы ищем угол $angle NAL$. Найдем его через теорему косинусов в треугольнике $ANL$ для угла $angle NAL$ :
*** $NL^2=AN^2+AL^2-2cdot ANcdot NLcdot cos angle NAL$
Стороны $AN$, $NL$ и $AL$ можем признать диагоналями граней — прямоугольников, значит, найти их по теоремам Пифагора.
Решение: $AN=sqrt{36^2+15^2}=39$ $AL=sqrt{20^2+15^2}=25$ $NL=sqrt{36^2+20^2}=4cdot sqrt{106}$
Из теоремы косинусов $cos angle NAL=frac{AN^2+AL^2-NL^2}{2cdot ANcdot AL}=frac{39^2+25^2-16cdot 106}{2cdot 39cdot 25}=frac{450}{1950}=frac{3}{13}$ Ответ: $angle NAL=arccos frac{3}{13}$
Признак: $NAL$ — плоскость угла: $ANin NAL$ и $BKparallel NAL$

case I 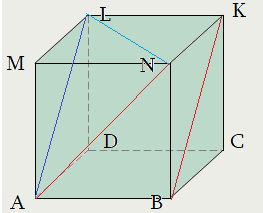case II

Алгоритм: нахождение угла между прямыми путем параллельного переноса (демонстрация по II, прямые $AN$, $BK$ ):

1-ый шаг: Выбираем точку, в которой хотим совместить прямые. Например, точку $Z$ — середину отрезка $BK$.

2-ой шаг: Для прямой $AN$ определим плоскость «скольжения» — плоскость, содержащая эту прямую и точку $Z$. Это $ANC$

3-ий шаг: Двинем прямую $AN$ по плоскости $ANC$ оставаясь параллельно «как стержень». Она совместится с отрезком $ZX$.

4-ый шаг: Что за точка $X$ ? угол $angle XZB$ — именно то, что нам нужно: $angle XZB=angle left(XZ;BKright)=angle left(AN;BKright)$.

Признак: — увидеть ту главную плоскость угла , которая параллельна обеим скрещивающимся прямым. Здесь это $XZB$.

Задача 2: В правильной треугольной призме все ребра 1. Найти косинус угла $angle left(AB;CMright)$

$ABCMNK$ правильная призма: в основании правильный $bigtriangleup ABC$ , ребро $BN$ перпендикулярно основанию.
Нужен угол между $AB$ и $CM$. Выберем Точкой совмещения $M$. Прямая $CM$ уже проходит через нее.
Прямая $AB$ и точка $M$ лежат в плоскости $ABNM$. Значит, $ABNM$ — плоскость сколжения. $AB$ перейдет в $MN$.
Путем параллельного совмещения $AB$ с $MN$ мы устоновили, что искомый угол — это $angle CMN$.
Косинус угла $angle CMN$ можно найти по теореме косинусов треугольника $CMN$: $cos angle CMN=frac{CM^2+MN^2-CN^2}{2cdot CMcdot MN}$
Признак: $CMN$ — плоскость угла: $ABparallel CMN$ и $MCin CMN$

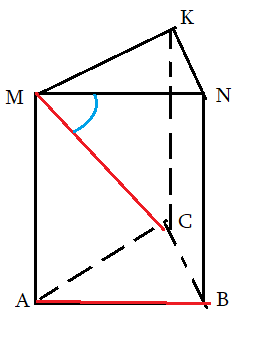
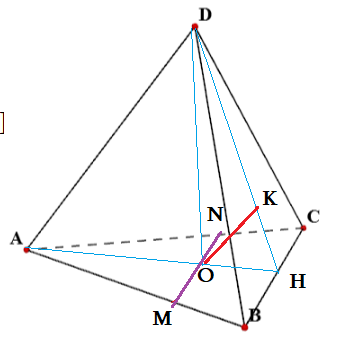
k задачe 2 к задаче 3

Задача 3: В правильном тетраэдре $DABC$ все ребра 1 см. Найти угол между $AD$ и $BC$.

Для нахождения угла, совместим «движениями» наши прямые в точку $O$ — основание высоты $DO$ .
В правильном тетраэдре в основании равносторонный треугольник $DABC$, высота пирамиды попадает в центр окружностей.
Точка $O$ — пересечение высот, медиан, биссектрис. $O$ лежит на высоте $AH$ , $DH$ — высота грани $BDC$.
В точке $O$ проведем прямую параллельную прямой $BC$. Им будет линия $MN$
В точке $O$ проведем прямую $OK$, параллельную $AD$. Она будет лежат в плоскости $ADH$ Значит, $Kin DH$.
Итак, «взамен» наших $AD$ и $BC$ мы получили прямые $OK$ и $MN$ : $OKparallel AD$, $MNparallel BC$
по свойству углов при параллельном переносе $angle left(AD;BCright)=angle left(OK;MNright)=angle MOK$
Найти $angle MOK$ ? Легко! учтите, что у нас правильный тетраэдр и находите.
Признак: $MONK$ — плоскость угла: $ADparallel MONK$ и $BCparallel MONK$

Алгоритм: вычисление угла в пространстве или плоскости

В каком треугольнике этот угол? узнать стороны треугольника и найти угол по теореме косинусов.
Если треугольник окажется равнобедренным, то провести высоту и найти угол прямоугольного треугольника.
А если треугольник прямоугольный, то написать cos или sin или tg этого угла и найти как arc !

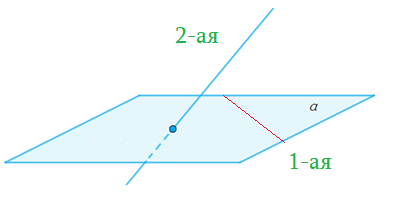
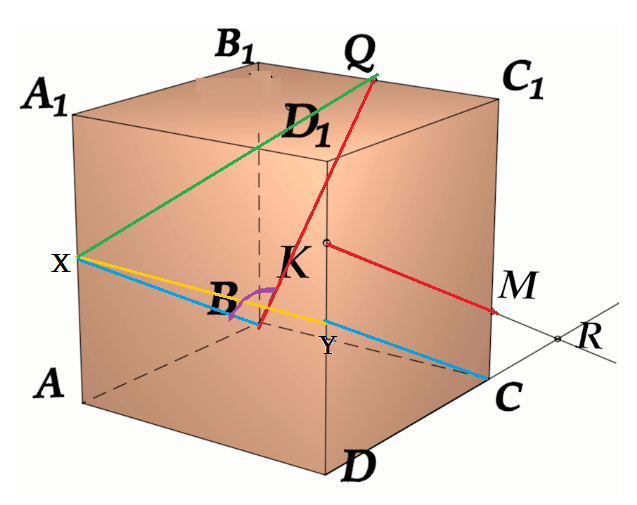
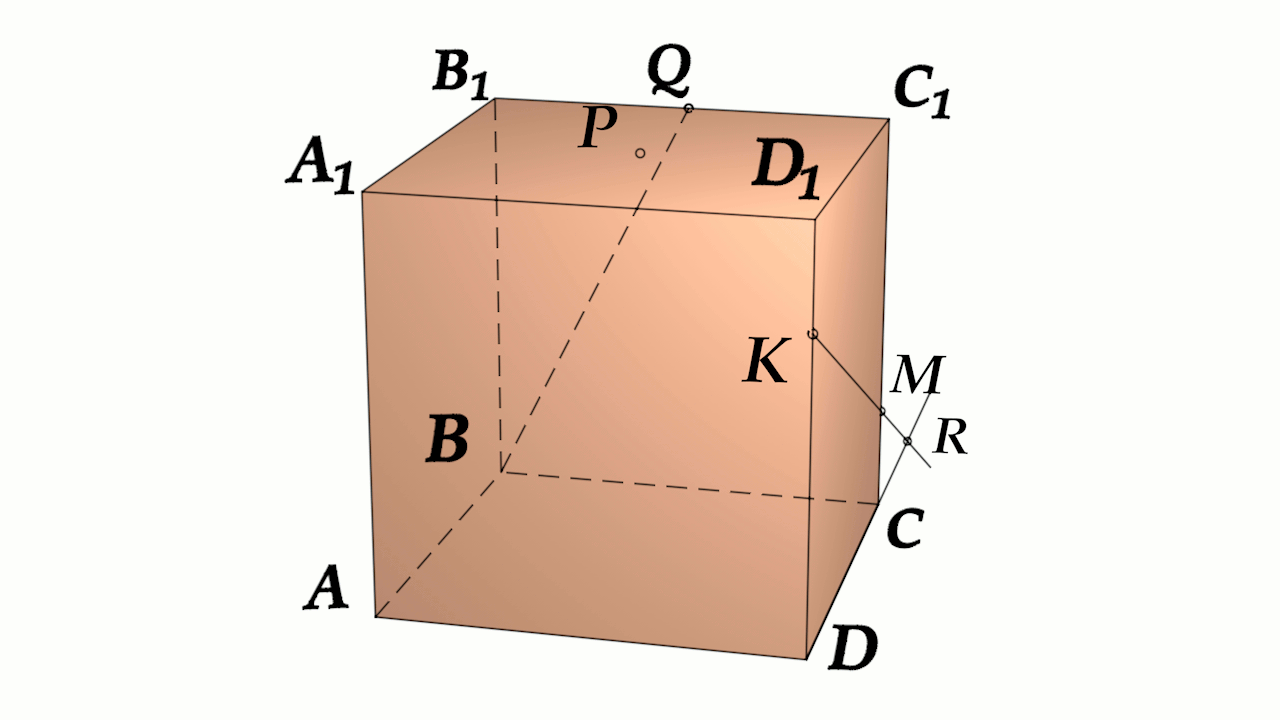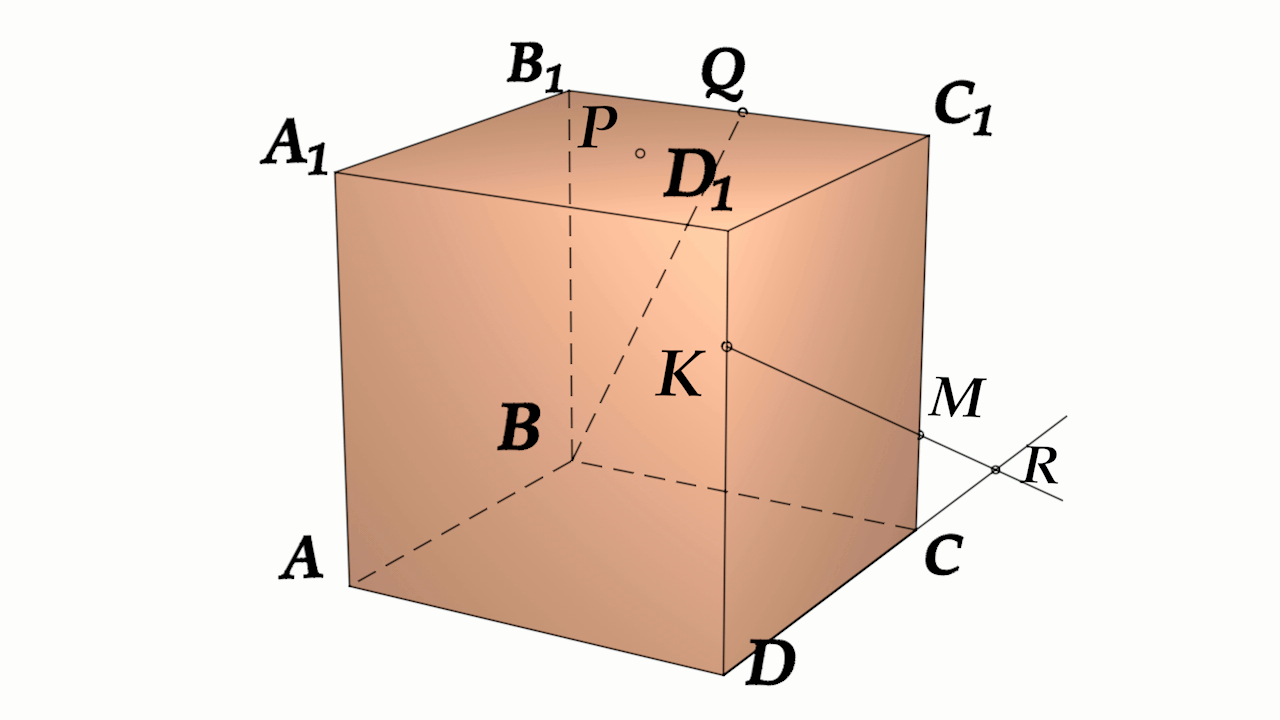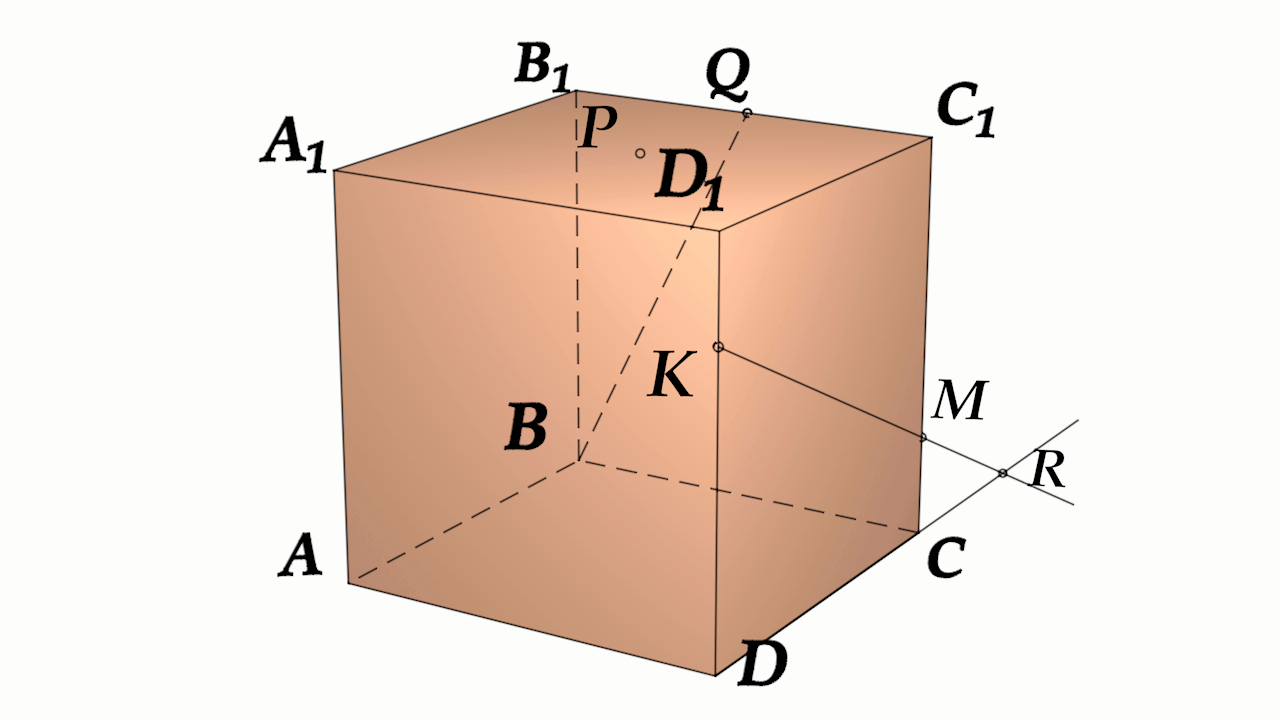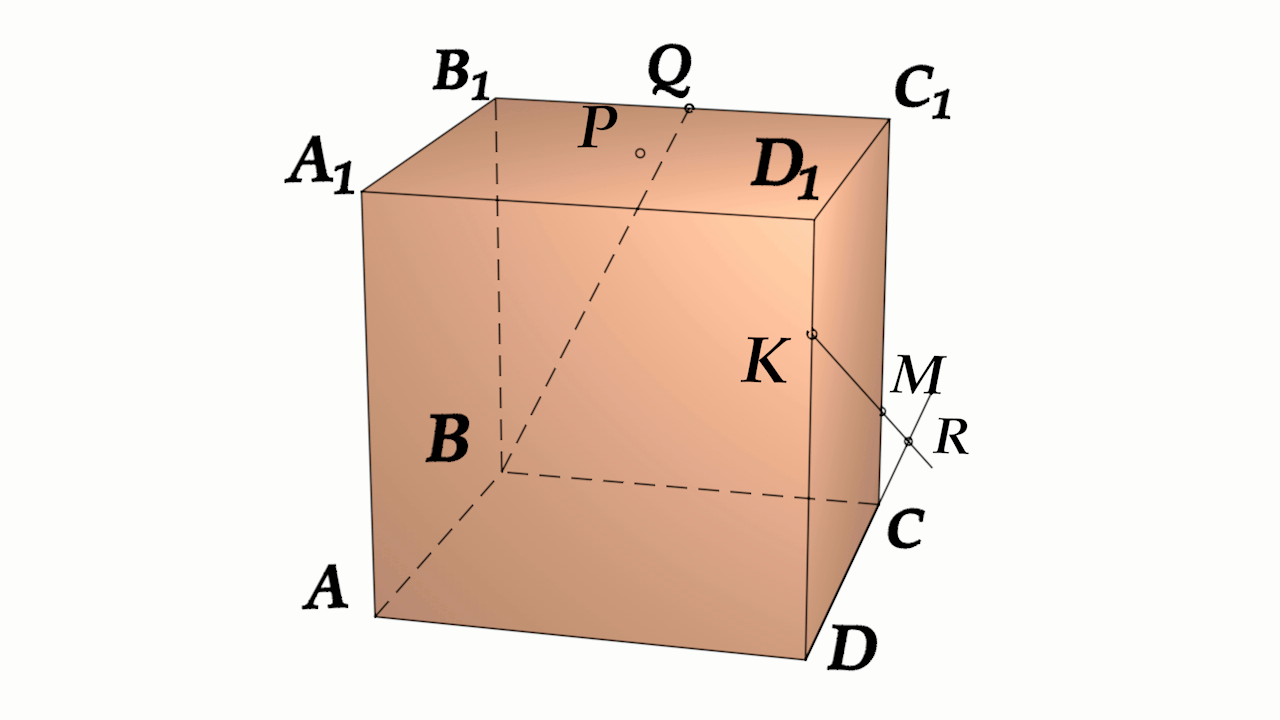
Задача 4: В кубе $ABCD{A_1}{B_1}{C_1}{D_1}$ все ребра равны 1. Точка $Q$ — середина ребра . Точка $K$

делит ребро $D_1D$ в соотношении 1 : 3 считая от вершины $D_1$, а точка $M$ делит $C_1C$ в соотношении

5 : 2 считая от вершины $C_1$. Найти угол между скрещивающимися прямыми $BQ$ и $KM$ .

Параллельными переносами добъемся совмещения в точке $B$. Для этого, перенесем $KM$ в два этапа.
Сперва соскользим $KM$ по грани $DD_1C_1C$ вдоль $C_1C$ до вершины $C$. Получим отрезок $CYparallel MK$
Затем, $CY$ протащим параллельно себе вдоль пути $CB$ и перейдем к отрезку $BXparallel CY$.
В итоге получили то, что надо: $KM$ параллельна $BX$, потому как $MKparallel CYparallel BX$.
Требуемый угол $angle left(MK;BQright)=angle left(BX;BQright)=angle XBQ$. Найдем его через треугольник $bigtriangleup XBQ$
В теореме косинусов нам нужны стороны этого треугольника. Вычислим постепенно, шаг за шагом, зная ребро куба 1:
Из отношения $frac{D_1K}{DK}=frac{1}{3}Rightarrow D_1K=frac{1}{4} DK=frac{3}{4}$. Из отношения $frac{C_1K}{CM}=frac{5}{2}Rightarrow C_1M=frac{5}{7} CM=frac{2}{7}$
$MKparallel CYRightarrow KY=MC$ отрезок $DY=D_1D-D_1K-KY=1-frac{1}{4}-frac{2}{7}=frac{13}{28}$
$BXparallel CYRightarrow BX=DY=frac{13}{28}$. По условию задачи $B_1Q=frac{1}{2}$.
Нужные нам стороны треугольника $bigtriangleup XBQ$ являются гипотенузами прямоугольных треугольников.
Зная все катеты, как части ребер, по теореме Пифагора найдем стороны $XB$, $BQ$, $XQ$.
Нужный угол $angle XBQ$ вычислим из теоремы косинусов $XQ^2=XB^2+BQ^2-2cdot XBcdot BQcdot cos angle XBQ$
наконец: $cos angle XBQ=frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$ $angle XBQ=arccos frac{XB^2+BQ^2-XQ^2}{2cdot XBcdot BQ}$
Признак: $XBQ$ — плоскость угла: $KMparallel XBQ$ и $BQin XBQ$

Задача 5: В правильной треугольной призме $ABCMNK$ все ребра равны 2. Точка $D$ делит

ребро $MN$ в отношении 3 : 2 считая от вершины $M$. Найдите угол между прямыми $AD$ и $BK$.

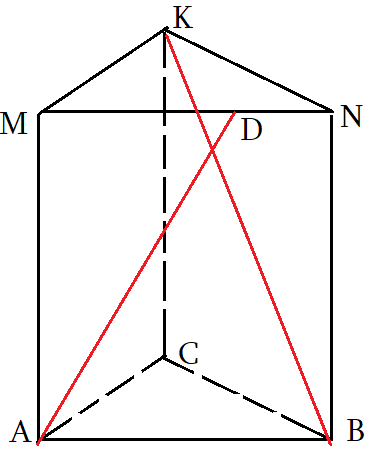
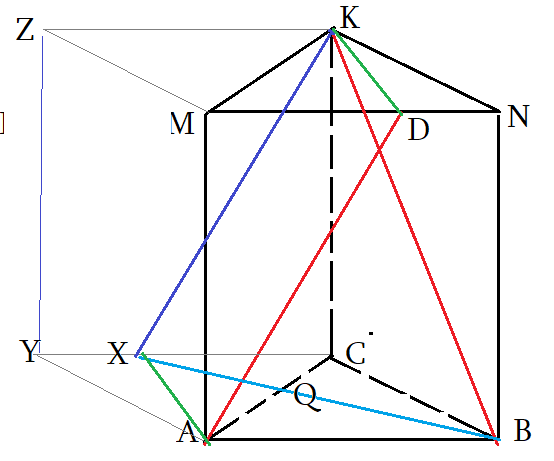
Чтоб найти угол между скрещивающимися прямыми, нужно «подвигать параллельно» $AD$ и $BK$ до совмещения.
Если двинуть $AD$ так, чтоб точка $D$ совпала с $K$ — т.е. скользить по плоскости $ADK$, но тогда другой конец $D$ вне рисунка.
Достроим призму до параллелепипеда $ABCYMNKZ$ и все нужные отрезки, «движения», плоскости будут внутри!
$AD$ скользит по плоскости $ADK$ и совпадет с $XK$. Точка $X$, конечно, окажется на ребре $YC$
по построению: $Xin CDK$ плоскости; $ADparallel XK$ , $XCparallel AB$ . Значит, $XK$ параллельна $AD$
Угол между прямыми $angle left(AD;BKright)=angle left(XK;BKright)=angle XKB$. Надо найти угол $angle XKB$.
Угол $XKB$ ищем , как обычно, через треугольник $bigtriangleup XKB$, с помощью теоремы косинусов.
Для этого надо найти стороны этого треугольника. Сторону $BK$ найдем по Пифагору для треугольника $bigtriangleup BKC$.
$XC=MD$, найдем $MD$ из отношения 3 : 2 для $MN$ . Затем, по Пифагору $bigtriangleup XKC$ найдем $XK$.
С вычислением $XB$ придется повозится через теорему косинусов треугольника $bigtriangleup XBC$, две его стороны известны.
А что с углом $angle XCB$? по условию $bigtriangleup ABC$ равносторонный, значит в параллелограмме $angle YCB=120$ градусов.
Ну и финально: как только найдем все стороны $bigtriangleup XKB$, мы найдем и его угол $angle XKB$ — то что надо!
Признак: $XKB$ — плоскость угла: $ADparallel XKB$ и $BKin XKB$

Упражнения:

Источник

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) :
$$ т.А(x_A,y_A,z_A); $$
$$ т.B(x_B,y_B,z_B); $$
Тогда координаты вектора (vec{AB}) можно определить по формуле:
$$ vec{AB}={x_B-x_A,y_B-y_A,z_B-z_A}. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора:
$$ a={x_a,y_a,z_a};$$
$$ b={x_b,y_b,z_b}; $$
тогда угол (alpha) между ними находится по формуле:
$$ cos{alpha}=frac{x_a*x_b+y_a*y_b+z_a*z_b}{sqrt{{x_a}^2+{y_a}^2+{z_a}^2}*sqrt{{x_b}^2+{y_b}^2+{z_b}^2}}. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой:
$$ A*x+B*y+C*z+D=0,$$
где (A,B,C,D) – какие-то числа.

Если найти (A,B,C,D), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

$$ K(x_K,y_K,z_K);,L(x_L,y_L,z_L);,P(x_P,y_P,z_P). $$

Подставим координаты точек в общее уравнение плоскости:

$$begin{cases} A*x_K+B*y_K+C*z_K+D=0,\ A*x_L+B*y_L+C*z_L+D=0, \ A*x_P+B*y_P+C*z_P+D=0.end{cases}$$

Получилась система из трех уравнений, но неизвестных 4: (A,B,C,D). Если наша плоскость не проходит через начало координат, то мы можем (D) приравнять (1), если же проходит, то (D=0). Объяснение этому простое: вы можете поделить каждое ваше уравнения на (D), от этого уравнение не изменится, но вместо (D) будет стоять (1), а остальные коэффициенты будут в (D) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Пример 3

Найти уравнение плоскости, проходящей через точки
$$ K(1;2;3);,P(0;1;0);,L(1;1;1). $$
Подставим координаты точек в уравнение плоскости (D=1):
$$begin{cases} A*1+B*2+C*3+1=0,\ A*0+B*1+C*0+1=0, \ A*1+B*1+C*1+1=0.end{cases}$$
$$begin{cases} A+2*B+3*C+1=0,\ B+1=0, \ A+B+C+1=0.end{cases}$$
$$begin{cases} A-2+3*C+1=0,\ B=-1, \ A=-C.end{cases}$$
$$begin{cases} A=-0.5,\ B=-1, \ C=0.5.end{cases}$$
Получаем искомое уравнение плоскости:
$$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

Зная координаты некоторой точки (M(x_M;y_M;z_M)), легко найти расстояние до плоскости (Ax+By+Cz+D=0:)
$$ rho=frac{|A*x_M+B*y_M+C*z_M+D|}{sqrt{A^2+B^2+C^2}}. $$

Пример 4

Найдите расстояние от т. (H (1;2;0)) до плоскости, заданной уравнением
$$ 2*x+3*y-sqrt{2}*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты:
$$ A=2,,B=3,,C=-sqrt{2},,D=4.$$
Подставим их в формулу для нахождения расстояния от точки до плоскости.
$$ rho=frac{|2*1+3*2-sqrt{2}*0+4|}{sqrt{2^2+3^2+{-sqrt{2}}^2}}. $$
$$ rho=frac{12}{sqrt{16}}=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Пример 5

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма (ABCFDE), ребра которой равны 2. Точка (G) — середина ребра (CE).

Докажите, что прямые (AD) и (BG) перпендикулярны.

Найдите расстояние между прямыми (AD) и (BG).

Решение:

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).

Источник