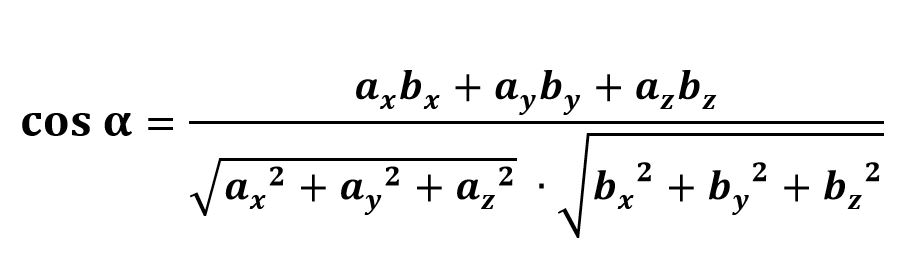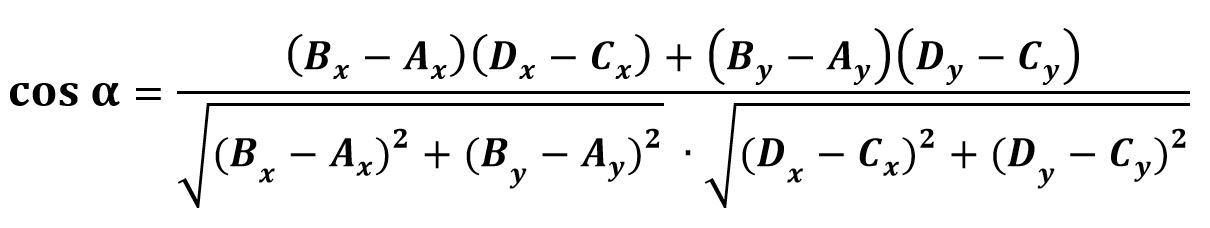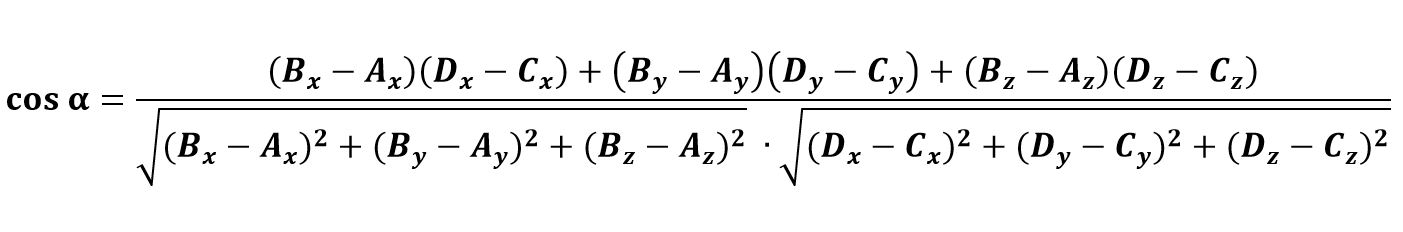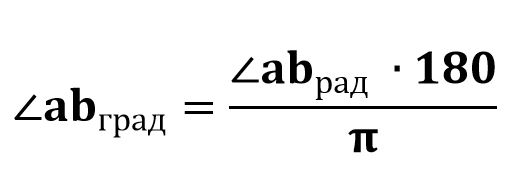© 2011-2023 Довжик Михаил
Копирование материалов запрещено.
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Если Вы хотите связаться со мной, имеете вопросы, предложения или хотите помочь развивать сайт OnlineMSchool пишите мне support@onlinemschool.com
Калькулятор онлайн.
Вычисление угла между векторами.
Этот калькулятор онлайн вычисляет угол между векторами в двух- или трехмерном пространстве.
Онлайн калькулятор для вычисления угла между векторами не просто даёт ответ задачи, он приводит подробное решение с
пояснениями, т.е. отображает процесс решения для того чтобы проконтролировать знания по математике и/или алгебре.
Этот калькулятор онлайн может быть полезен учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода чисел, рекомендуем с ними ознакомиться.
Правила ввода чисел
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5 или так 1,3
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Ввод: -2/3
Результат: ( -frac{2}{3} )
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: -1&5/7
Результат: ( -1frac{5}{7} )
Наши игры, головоломки, эмуляторы:
Немного теории.
Определение и основные свойства скалярного произведения векторов
Определение
Скалярным произведением двух ненулевых векторов ( vec{a} ) и ( vec{b} ) называется число (скаляр), равное произведению длин
этих векторов на косинус угла между ними. Если хотя бы один из векторов ненулевой, то угол не определен и скалярное произведение векторов
по определению полагают равным нулю.
Скалярное произведение векторов ( vec{a} ) и ( vec{b} ) обозначают ( vec{a} cdot vec{b} ). Итак,
( vec{a} cdot vec{b} = |vec{a}||vec{b}|cos varphi )
где ( varphi ) — угол между векторами ( vec{a} ) и ( vec{b} )
Типичным примером скалярного произведения векторов в физике является формула работы:
( A = |vec{a}||vec{b}|cos varphi )
где вектор ( vec{a} ) — сила, точка приложения которой перемещается из начала в конец вектора ( vec{b} )
Рассмотрим некоторые свойства скалярного произведения векторов.
1. ( vec{a} cdot vec{b} = vec{b} cdot vec{a} ) (свойство перестановочности сомножителей)
2. ( (alpha vec{a} ) cdot vec{b} = alpha ( vec{b} cdot vec{a} ) ) (свойство сочетательности относительно умножения на число)
3. ( vec{a} cdot ( vec{b} + vec{c} ) = vec{a} cdot vec{b} + vec{a} cdot vec{c} ) (свойство распределительности суммы векторов)
4. ( vec{a} cdot vec{a} = |vec{a}|^2 )
5. ( vec{a} cdot vec{b} = 0 ), если ( vec{a} bot vec{b} ) , и обратно, ( vec{a} bot vec{b} ) ,
если ( vec{a} cdot vec{b} = 0 ) и ( vec{a} neq vec{0}, ; vec{b} neq vec{0} ).
Выражение скалярного произведения через координаты векторов
Теорема
Если векторы ( vec{a} ) и ( vec{b} ) заданы своими координатами:
( vec{a} left( a_x; a_y; a_z right), ;; vec{b} left( b_x; b_y; b_z right) ), то их скалярное произведение можно
вычислить по формуле
( vec{a} cdot vec{b} = a_x cdot b_x + a_y cdot b_y + a_z cdot b_z )
Следствие
Необходимым и достаточным условием перпендикулярности векторов ( vec{a} left( a_x; a_y; a_z right) ) и
( vec{b} left( b_x; b_y; b_z right) ) является равенство
( a_x cdot b_x + a_y cdot b_y + a_z cdot b_z = 0 )
Следствие
Косинус угла между векторами ( vec{a} left( a_x; a_y; a_z right) ) , и ( vec{b} left( b_x; b_y; b_z right) ) определяется
равенством
$$ cos varphi = frac{ vec{a} cdot vec{b}}{ |vec{a}| |vec{b}| } =
frac{a_x cdot b_x + a_y cdot b_y + a_z cdot b_z}{sqrt{a_x^2 + a_y^2 + a_z^2} ; sqrt{b_x^2 + b_y^2 + b_z^2} } $$
Векторы – одна из тем школьной программы. При вычислении угла между векторами можно использовать специальный калькулятор. Это онлайн-сервис, которым могут воспользоваться клиенты фриланс-биржи «Напишем». Он поможет ускорить процесс решения задач или проверить правильность выполнения заданий.
Особенности сервиса
Известно, то между векторами всегда образуется угол. Чтобы его вычислить, нужно знать длины векторов и использовать формулу для определения их скалярного произведения. Процедура состоит из двух действий. Определяется:
- косинус угла между векторами;
- сам угол.
Схематически угол между векторами изображают так:
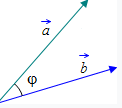
Формула определения скалярного произведения выглядит так:
[ vec{a} cdot vec{b}=|vec{a}| cdot|vec{b}| cdot cos (varphi) ]
Косинус определяется по формуле:
[ cos (varphi)=frac{vec{a} cdot vec{b}}{|vec{a}| cdot|vec{b}|} ]
Используя координатные соотношения, для вычисления косинуса угла между векторами используют следующую формулу:
[ cos (varphi)=frac{a_{x} cdot b_{x}+a_{y} cdot b_{y}+a_{z} cdot b_{z}}{sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}} cdot sqrt{b_{x}^{2}+b_{y}^{2}+b_{z}^{2}}} ]
Где [vec{a}=left{a_{x}, a_{y}, a_{z}right}] и [vec{b}=left{b_{x}, b_{y}, b_{z}right}].
Чтобы получить нужно е значение, данные подставляют в соответствующие окошки и нажимают клавишу «Решение».
Укажите размерность пространства
Укажите форму представления первого вектора
Укажите форму представления второго вектора
Задайте координаты первого вектора
a̅ =
{
;
}
Задайте координаты вектора b
b̅ =
{
;
}
Как найти угол между векторами
Чтобы вычислить угол между векторами a и b, где a = {ax; ay} и b = {bx; by} необходимо:
1.Вычислить скалярное произведение векторов a и b.
2. Вычислить длину вектора a.
3. Вычислить длину вектора b.
4. Вычислить произведение длин векторов a и b.
5. Вычислить косинус α. Разделить скалярное произведение векторов на произведение длин векторов.
6. Вычислить арккосинус α.

Формулы вычисления угла между векторами
Если векторы a и b заданы координатами, где a = {ax; ay} и b = {bx; by}, то косинус угла α вычисляется по формуле:
a = {ax; ay}
b = {bx; by}
Если векторы a и b заданы координатами, где a = {ax; ay} и b = {bx; by}, то угол в радианах вычисляется по формуле:
a = {ax; ay}
b = {bx; by}
Если векторы a и b заданы координатами, где a = {ax; ay; az} и b = {bx; by; bz}, то косинус угла α вычисляется по формуле:
a = {ax; ay; az}
b = {bx; by; bz}
Если векторы a и b заданы координатами, где a = {ax; ay; az} и b = {bx; by; bz}, то угол в радианах вычисляется по формуле:
a = {ax; ay; az}
b = {bx; by; bz}
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y) и B(x, y), вектор b задан точками C(x, y) и D(x, y), то косинус угла α вычисляется по формуле:
A = (Ax; Ay)
B = (Bx; By)
C = (Cx; Cy)
D = (Dx; Dy)
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y) и B(x, y), вектор b задан точками C(x, y) и D(x, y), то угол α в радианах вычисляется по формуле:
A = (Ax; Ay)
B = (Bx; By)
C = (Cx; Cy)
D = (Dx; Dy)
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то косинус угла α вычисляется по формуле:
A = (Ax; Ay; Az)
B = (Bx; By; Bz)
C = (Cx; Cy; Cz)
D = (Dx; Dy; Dz)
Если координаты обоих векторов заданы точками – вектора a задан точками A(x, y, z) и B(x, y, z), вектор b задан точками C(x, y, z) и D(x, y, z), то угол α в радианах вычисляется по формуле:
A = (Ax; Ay; Az)
B = (Bx; By; Bz)
C = (Cx; Cy; Cz)
D = (Dx; Dy; Dz)
Если необходимо вычислить значение угла в градусах, то необходимо значение угла между векторами умножить на 180 и получившееся значение разделить на π
Примеры вычисления угла между векторами
Пример 1. Найдем угол между векторами плоскости. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (5 ; 9)
Координаты точки B вектора AB: (-2 ; 11)
Координаты точки C вектора CD: (0 ; 12)
Координаты точки D вектора CD: (-3 ; 1)
| cos α = | AB ⋅ CD | |
| |AB| ⋅ |CD| |
Решение:
1) Вычислим модуль (длину) первого и второго векторов:
|AB| =
(Bx — Ax)2 + (By — Ay)2
=
(-2 — 5)2 + (11 — 9)2
=
(-7)2 + 22
=
49 + 4
=
53
= 7.28010988928052
|CD| =
(Dx — Cx)2 + (Dy — Cy)2
=
(-3 — 0)2 + (1 — 12)2
=
(-3)2 + (-11)2
=
9 + 121
=
130
= 11.4017542509914
2) Вычислим произведение модулей векторов:
|AB| ⋅ |CD| =
53
⋅
130
=
6890
3) Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay} = {-2 — 5 ; 11 — 9} = {-7 ; 2}
4) Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy} = {-3 — 0 ; 1 — 12} = {-3 ; -11}
5) Найдем скалярное произведение векторов: AB и CD
AB ⋅ CD = ABxCDx + AByCDy = -7 ⋅ (-3) + 2 ⋅ (-11) = 21 + (-22) = -1
6) Вычислим косинус угла между векторами:
| cos α = | AB ⋅ CD | = |
| |AB| ⋅ |CD| |
| -1 /
6890 = -0.0120473184147734 |
||
7) Вычислим значение угла ∠α между векторами:
∠α = 1.58284393664908 Radians
∠α = 90.6902771978651° Degrees
Пример 2. Найдем угол между векторами плоскости.
Координаты вектора a: (5 ; 9)
Координаты вектора b: (-1 ; 7)
Решение:
1) Вычислим модуль (длину) первого и второго векторов:
|a| =
ax2 + ay2
=
52 + 92
=
25 + 81
=
106
= 10.295630140987
|b| =
bx2 + by2
=
(-1)2 + 72
=
1 + 49
=
50
= 5
2
= 7.07106781186548
2) Вычислим произведение модулей векторов:
|a| ⋅ |b| =
106
⋅
50
=
5300
3) Найдем скалярное произведение векторов: a и b
a ⋅ b = axbx + ayby = 5 ⋅ (-1) + 9 ⋅ 7 = -5 + 63 = 58
4) Вычислим косинус угла между векторами:
| cos α = | a ⋅ b | = |
| |a| ⋅ |b| |
| 58 /
5300 = 0.796691270902396 |
||
5) Вычислим значение угла ∠α между векторами:
∠α = 0.648995558996501 Radians
∠α = 37.1847064532332° Degrees
Пример 3. Найдем угол между векторами пространства. Координаты обоих векторов заданны точками.
Координаты точки А вектора AB: (7; 0.2 ; 69)
Координаты точки B вектора AB: (-1 ; 0 ; 2/8)
Координаты точки C вектора CD: (-4 ; -6 ; 2)
Координаты точки D вектора CD: (3 ; 0 ; 9)
| cos α = | AB ⋅ CD | |
| |AB| ⋅ |CD| |
Решение:
1) Вычислим модуль (длину) первого и второго векторов:
|AB| =
(Bx — Ax)2 + (By — Ay)2 + (Bz — Az)2
=
(-1 — 7)2 + (0 — 0.2)2 + (2/8 — 69)2
=
(-8)2 + (-0.2)2 + (-275/4)2
=
64 + 0.04 + (75625/16)
=
|CD| =
(Dx — Cx)2 + (Dy — Cy)2 + (Dz — Cz)2
=
(3 — (-4))2 + (0 — (-6))2 + (9 — 2)2
=
72 + 62 + 72
=
49 + 36 + 49
=
134
= 11.5758369027902
2) Вычислим произведение модулей векторов:
|AB| ⋅ |CD| =
1916241/400
⋅
134
=
641940.735
3) Вычислим координаты первого вектора по двум точкам A и B:
AB = {Bx — Ax ; By — Ay; Bz — Az} = {-1 — 7 ; 0 — 0.2 ; 2/8 — 69} = {-8 ; -1/5 ; -275/4}
4) Вычислим координаты второго вектора по двум точкам C и D:
CD = {Dx — Cx ; Dy — Cy; Dz — Cz} = {3 — (-4) ; 0 — (-6) ; 9 — 2} = {7 ; 6 ; 7}
5) Найдем скалярное произведение векторов: AB и CD
AB ⋅ CD = ABxCDx + AByCDy + ABzCDz = -8 ⋅ 7 + (-1/5) ⋅ 6 + (-275/4) ⋅ 7 = -56 + (-6/5) + (-1925/4) = -10769/20 = -538.45
6) Вычислим косинус угла между векторами:
| cos α = | AB ⋅ CD | = |
| |AB| ⋅ |CD| |
| -538.45 /
641940.735 = -0.672044318228661 |
||
7) Вычислим значение угла ∠α между векторами:
∠α = 2.30776235411475 Radians
∠α = 132.225043009951° Degrees
Пример 4. Найдем угол между векторами пространства.
Координаты вектора a: (5 ; 1 ; 7)
Координаты вектора b: (2 ; 4 ; 6)
Решение:
1) Вычислим модуль (длину) первого и второго векторов:
|a| =
ax2 + ay2 + az2
=
52 + 12 + 72
=
25 + 1 + 49
=
75
= 5
3
= 8.66025403784439
|b| =
bx2 + by2 + bz2
=
22 + 42 + 62
=
4 + 16 + 36
=
56
= 2
14
= 7.48331477354788
2) Вычислим произведение модулей векторов:
|a| ⋅ |b| =
75
⋅
56
=
4200
3) Найдем скалярное произведение векторов: a и b
a ⋅ b = axbx + ayby + azbz = 5 ⋅ 2 + 1 ⋅ 4 + 7 ⋅ 6 = 10 + 4 + 42 = 56
4) Вычислим косинус угла между векторами:
| cos α = | a ⋅ b | = |
| |a| ⋅ |b| |
| 56 /
4200 = 0.864098759787715 |
||
5) Вычислим значение угла ∠α между векторами:
∠α = 0.527439299499548 Radians
∠α = 30.2200458106607° Degrees
Решение. Для нахождения косинуса угла между заданными векторами, воспользуемся формулой
Ответ. $begin cos phi=frac<14> <15>end$
Нахождение угла между векторами
Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.
Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →
Углом между векторами a → и b → называется угол между лучами О А и О В .
Полученный угол будем обозначать следующим образом: a → , b → ^
Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.
a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.
Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.
Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.
Нахождение угла между векторами
Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.
Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .
Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:
cos a → , b → ^ = a → , b → a → · b →
Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.
Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.
Решение
Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,
Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4
Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4
Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.
Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:
cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2
А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2
Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.
Решение
- Для решения задачи можем сразу применить формулу:
cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70
- Также можно определить угол по формуле:
cos a → , b → ^ = ( a → , b → ) a → · b → ,
но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70
Ответ: a → , b → ^ = — a r c cos 1 70
Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.
Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .
Решение
Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )
Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13
Ответ: cos A C → , B C → ^ = 3 13
Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:
A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,
b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^
и отсюда выведем формулу косинуса угла:
cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →
Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.
Хотя указанный способ имеет место быть, все же чаще применяют формулу:
http://www.webmath.ru/poleznoe/formules_13_9.php
http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/