Как найти косинус угла образованного высотами - Исправление недочетов и поиск решений вместе с Examum.ru

Мы уже находили косинусы углов треугольника по его сторонам в произвольном треугольнике и косинус острого угла прямоугольного треугольника.

Рассмотрим, как найти косинусы углов треугольника по его вершинам.

Задача

Дано: ΔABC,

A(-2;0), B(6;1), C(-3;-5).

1) Найти косинусы углов треугольника ABC;

2) Определить вид треугольника.

Решение:

1) Угол A образован векторами

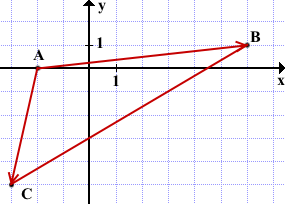
(Чертёж не обязательно делать на координатной плоскости. Достаточно выполнить его схематически, для упрощения понимания, какой угол какими векторами образован).

Следовательно,

$[cos A = frac{{overrightarrow {AB} cdot overrightarrow {AC} }}{{left| {overrightarrow {AB} } right| cdot left| {overrightarrow {AC} } right|}}.]$

Найдём координаты векторов:

$[overrightarrow {AB} (x_B - x_A ;y_B - y_A ),]$

$[overrightarrow {AC} (x_C - x_A ;y_C - y_A ),]$

Находим скалярное произведение векторов:

Поскольку скалярное произведение меньше нуля, угол, образованный данными векторами, тупой. Значит треугольник ABC — тупоугольный.

Длины (или модули) векторов:

$[left| {overrightarrow {AB} } right| = sqrt {8^2 + 1^2 } = sqrt {65} ,]$

$[left| {overrightarrow {AC} } right| = sqrt {( - 1)^2 + ( - 5)^2 } = sqrt {26} .]$

Отсюда

$[cos A = frac{{ - 13}}{{sqrt {65} cdot sqrt {26} }} = frac{{ - 13}}{{sqrt {5 cdot 13 cdot 2 cdot 13} }} = ]$

$[= frac{{ - 13}}{{13sqrt {10} }} = - frac{1}{{sqrt {10} }} = - frac{{sqrt {10} }}{{10}}.]$

2) Угол B образован векторами

Таким образом,

$[cos B = frac{{overrightarrow {BA} cdot overrightarrow {BC} }}{{left| {overrightarrow {BA} } right| cdot left| {overrightarrow {BC} } right|}}.]$

Так как

— противоположные векторы, то их координаты отличаются только знаками и векторы имеют одинаковую длину:

$[overrightarrow {BC} (x_C - x_B ;y_C - y_B ),]$

$[left| {overrightarrow {BC} } right| = sqrt {( - 9)^2 + ( - 6)^2 } = sqrt {117} .]$

$[cos B = frac{{78}}{{sqrt {65} cdot sqrt {117} }} = frac{{13 cdot 6}}{{sqrt {5 cdot 13 cdot 9 cdot 13} }} =]$

$[= frac{{13 cdot 6}}{{13 cdot 3sqrt 5 }} = frac{2}{{sqrt 5 }} = frac{{2sqrt 5 }}{5}.]$

3) Угол C образован векторами

$[cos C = frac{{overrightarrow {CA} cdot overrightarrow {CB} }}{{left| {overrightarrow {CA} } right| cdot left| {overrightarrow {CB} } right|}}.]$

$[cos C = frac{{39}}{{sqrt {26} cdot sqrt {117} }} = frac{{13 cdot 3}}{{sqrt {2 cdot 13 cdot 9 cdot 13} }} = ]$

$[= frac{{13 cdot 3}}{{13 cdot 3sqrt 2 }} = frac{1}{{sqrt 2 }} = frac{{sqrt 2 }}{2}.]$

Ответ:

$[cos A = - frac{{sqrt {10} }}{{10}},cos B = frac{{2sqrt 5 }}{5},cos C = frac{{sqrt 2 }}{2};]$

ΔABC — тупоугольный.

Источник

Вариант № 10

Задача 1 Разложить вектор По векторам и .

Пусть , т. е. ;

След., вектор .

Задача 2 Дано: Найти

Вычислим

Задача 3 Вычислить проекцию вектора на ось вектора , Если

Вект. ; рассм. ;

Вычислим ; ; .

Задача 4 Вычислить косинус угла, образованного векторами и .

Косинус угла между векторами Определим из равенства: ;

Вычислим ; ; .

Задача 5 Найти момент силы, приложенной в точке относительно точки, а также модуль и направляющие косинусы вектора силы

1) , где ; ;

;

2) ;

Направл. косинусы вектора : ; ;

Задача 6 Вычислить , если

Рассм.

; по условию задачи угол — острый, след. ;

Вычислим искомое скал. произв-е .

Задача 7 Лежат ли точки в одной плоскости?

Рассмотрим векторы и рассмотрим смешанное

Произведение , след. векторы Компланарны

И, след., точки лежат в одной плоскости.

Задача 8 Найти точку , симметричную точке Относительно прямой .

Рассмотрим один из нормальных векторов прямой ; его можно взять в качестве направляющего вектора прямой и записать уравнение прямой в виде:

или определим координаты точки пересечения прямых

И: ;

Определим теперь координаты искомой точки из условия, что т. есть середина отрезка :

Задача 9 Найти координаты вершин и уравнения диагоналей квадрата , если известны уравнение одной стороны

и координаты точки пересечения диагоналей .

1) составим ур-я диагоналей квадрата как ур-я прямых на пл-ти , проходящих через т. и

Составляющих угол со стороной ( ),

Т. е. прямых, для которых вып-ся след. соотношения:

А) рассм. случай

Б) рассм. случай

2) определим координаты вершин квадрата:

Т.- точка пересечения прямых : ;

Координаты точки определим из условия, что т.Есть середина отрезка :

;

Координаты точки определим из условия, что т.Есть середина отрезка :

Задача 10 Составить уравнение плоскости, проходящей через точку

параллельно векторам

Пусть — искомая плоскость;

Рассм. норм. вектор ;

Рассм. произв. т и рассм. вектор ; ;

, т. е. ; .

Задача 11 Составить канонические и параметрические уравнения прямой , заданной как пересечение двух плоскостей: .

Рассм. норм. векторы ; рассм. направл. вектор прямой : ; рассм. ;

Определим какую-либо точку ; рассм.

Положим , тогда ;

Запишем канонические ур-я прямой Как ур-я прямой, проходящей через т. параллельно вектору : ; параметрические ур-я прямой :

Задача 12 Найти основание перпендикуляра, опущенного из точки на плоскость .

Пусть т. — искомое основание перпендикуляра и — искомый перпендикуляр к плоскости ;

В качестве направл. вектора прямой возьмём нормальный вектор плоскости : и запишем канонические ур-я прямой

Как ур-я прямой, проходящей через т. А параллельно вектору : ; параметрические ур-я прямой :

Определим координаты т. как точки пересечения прямой с плоскостью :

;

Задача 13 Вычислить определитель третьего порядка, пользуясь определением; результат проверить разложением

Определителя по первой строке.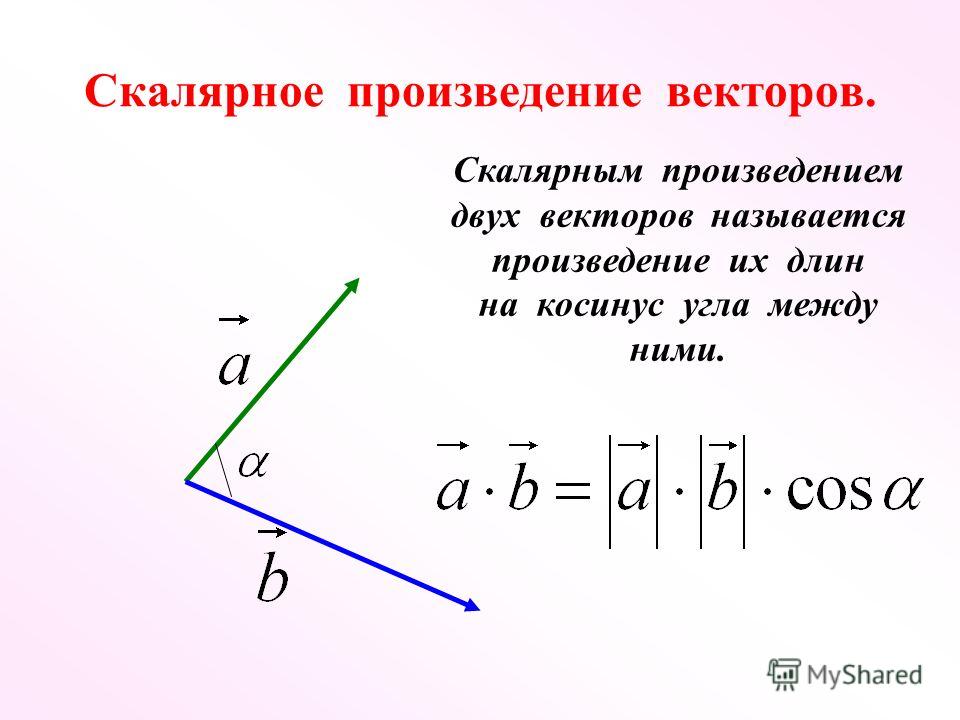

1) Непосредственное вычисление:

2) Разложение по 1-й строке:

Задача 14 Решить систему линейных уравнений по правилу Крамера и с помощью обратной матрицы.

Запишем данную систему уравнений в матричной форме: , (1) , где

Рассм. опред-ль матрицы : ,

след., матр. — невырожденная и можно примен. формулы Крамера и вычислять обратную матр.

;

1) решим с – му ур – й (1) по правилу Крамера, т. е. с помощью формул: , , , где ;

реш–е с–мы ур–й (1) в коорд. форме: вектор–решение с-мы (1): ;

2) получим реш–е с–мы ур–й (1) с помощью обратной матр. :

, след., матр.- невырожденная и существует обратная матр. ;

Умножим рав-во (1) слева на матрицу : Вычислим обратную матр. :

Находим алгебр. дополнения для всех эл-тов матрицы и составим из них м-цу :

;

Транспонируем м-цу и получим «присоединённую» м-цу ;

Разделим все эл-ты присоедин. м-цы на опр-ль и получим обратную матр. :

Находим теперь вектор-решение

Задача 15

Установить, являются ли векторы линейно зависимыми.

Вычислим ранг системы векторов методом Гаусса, т. е. выпишем матрицу их координат и приведём её к ступенчатому виду:

Ранг матрицы , след. данная система векторов линейно зависима.

Задача 16 Исследовать систему линейных уравнений на совместность и в случае совместности найти её решение методом Гаусса:

Выпишем расширенную матрицу данной системы ур-й и приведём её к ступенчатому виду:

Имеем ; так как , то по теореме Кронекера — Капелли данная система уравнений совместна, а так как , то система имеет бесконечное множество решений;

Объявим свободной переменной и выпишем общее решение системы в координатной форме:

;

общее решение данной системы ур-й:

Задача 17 Найти матрицу преобразования, выражающего Через , если

Запишем данные преобразования в матричной форме: , где матрицы и

Вектор — столбцы имеют вид: ;

Рассм. ;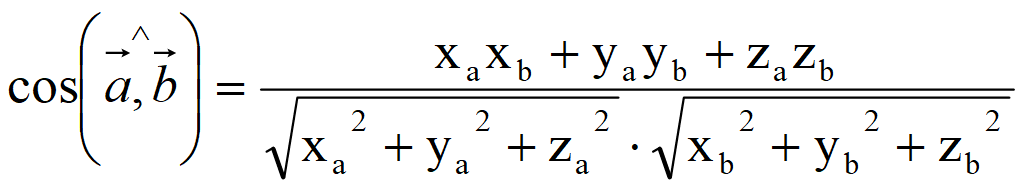

Вычислим матрицу .

Задача 18 Найти собственные числа и собственные векторы линейного преобразования, заданного матрицей

1) Находим собств. значения линейного преобразования , т. е. корни характеристического уравнения :

Рассм.

; — собств. значения (действ. и различные ) лин. преобр-я ;

2) находим собств. векторы линейного преобразования , соотв. собств. значениям :

А) рассм. ;

Рассм. Пусть , тогда вектор ;

Б) рассм. ;

пусть , тогда вектор ;

В) рассм. ;

рассм.

Пусть , тогда , вектор ;

След. собств. векторы линейного преобразования суть:

< Предыдущая		Следующая >

Контрольная работа.

Если известны координаты точек и , то координаты вектора — Студопедия

«Векторная алгебра»

Если известны координаты точек и , то координаты вектора

Разложение этого вектора по ортам :

Длина вектора находится по формуле а направляющие косинусы равны Орт вектора

Пример 8.Даны точки

Разложить вектор по ортам и найти его длину, направляющие косинусы, орт вектора . Найдем координаты векторов:

Вектор

Контрольные варианты к задаче 8.Даны точки А, В и С. Разложить вектор по ортам Найти длину, направляющие косинусы и орт вектора .

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

Задача 9.Если даны векторы то .

Тогда ; проекция вектора на направление вектора , условие перпендикулярности ненулевых векторов выглядит следующим образом:

Условие коллинеарности векторов: .

Пример 9. Даны вершины треугольника Найти угол при вершине А и проекцию вектора на сторону АС. С

Внутренний угол при вершине А образован векторами ,

А В

Тогда

Проекция на направление вектора :

Контрольные варианты к задаче 9

1. Даны векторы и Найти

2. Найти косинус угла, образованного вектором и осью OZ.

3. Даны векторы и . Найти косинус угла между диагоналями параллелограмма, построенного на векторах .

4. Даны векторы и . Вычислить

5. Найти косинус угла, образованного вектором и осью ОУ.

6. Даны векторы и . Найти косинус угла, образованного вектором и осью ОХ.

7. Даны векторы и . Найти

8. Вычислить проекцию вектора на ось вектора .

9. Определить угол между диагоналями параллелограмма, построенного на векторах и .

10. Определить, при каком значении m векторы и перпендикулярны.

11. Определить, при каком значении векторы и взаимно перпендикулярны.

12. Даны вершины треугольника: . Определить внутренний угол при вершине В.

13. Даны вершины треугольника: . Определить внутренний угол при вершине А.

14. Найти вектор , коллинеарный вектору и удовлетворяющий условию

15. Даны две точки и Вычислить проекцию вектора на ось вектора

16. Даны векторы: и . Вычислить

17. Найти острый угол между диагоналями параллелограмма, построенного на векторах , .

18. Даны три вектора: , , . Найти

19. Даны три вектора: , , . Найти

20. Найти острый угол между диагоналями параллелограмма, построенного на векторах и

21. Даны три вектора: , , . Вычислить

22. Найти вектор , зная, что он перпендикулярен векторам и

и удовлетворяет условию

23. Найти вектор , коллинеарный вектору и удовлетворяющий условию

24. Даны вершины треугольника: Определить внешний угол при вершине А.

25. Даны вершины треугольника: Определить внешний угол при вершине А.

26. Дан вектор и точки и Найти

27. В треугольнике с вершинами Определить внутренний угол при вершине А.

28. Даны векторы и Найти проекцию вектора на направление вектора

29. Даны вершины треугольника: Найти проекцию вектора на сторону

30. Даны векторы Найти проекцию вектора на вектор

Задача 10.Площадь параллелограмма, построенного на векторах

можно найти по формуле а площадь треугольника, построенного

на этих векторах:

Пример 10. Даны вершины треугольника Найти его площадь и длину высоты, опущенной из вершины С.

. Находим векторы

Векторное произведение

Так как где длина высоты, опущенной из вершины С на сторону АВ, .

Контрольные варианты к задаче 10

1. В параллелограмме ABCD даны векторы и Найти площадь параллелограмма, построенного на диагоналях параллелограмма

ABCD.

2. Даны три вершины параллелограмма , , . Найти длину высоты, опущенной из вершины С (через площадь

параллелограмма).

3. Найти площадь треугольника с вершинами , ,

(средствами векторной алгебры).

4. Найти площадь треугольника с вершинами , , (средствами векторной алгебры).

5. Даны три вершины треугольника: , , . Найти его высоту, приняв ВС за основание (через площадь треугольника).

6. На векторах и построен параллелограмм. Найти

площадь параллелограмма, сторонами которого являются диагонали данного параллелограмма.

7. Даны векторы и . Найти вектор перпендикулярный к векторам если модуль вектора численно равен площади треугольника, построенного на векторах и тройка векторов левая.

8. Даны точки , , Найти площадь параллелограмма, построенного на векторах и ( ).

9. На векторах и построен параллелограмм. Найти высоту, опущенную на основание (через площадь).

10. В треугольнике ABC, где , найти длину высоты, опущенной на сторону AB (через площадь треугольника; средствами векторной алгебры).

11. На векторах и построен параллелограмм. Найти площадь параллелограмма, построенного на диагоналях данного параллелограмма.

12. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

13. Найти площадь параллелограмма со сторонами если

14. Найти площадь треугольника со сторонами если ,

15. Дан треугольник с вершинами , и . Вычислить площадь треугольника и высоту, опущенную из вершины А (средствами векторной алгебры).

16. Даны векторы и Найти вектор , который пер-

пендикулярен векторам , если длина его численно равна площади треуго-

льника, построенного на векторах , и тройка векторов правая.

17. Даны точки , и . Вычислить площадь треугольника и высоту, опущенную из вершины С (средствами векторной алгебры).

18. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника ВСЕ (средствами векторной алгебры).

19. Даны точки , и . Найти площадь параллелограмма, построенного на векторах и

20. Даны три вершины треугольника: , , . Вычислить его высоту, опущенную из вершины В (через площадь, средствами векторной алгебры).

21. Дан треугольник с вершинами , и . Найти его высоту, опущенную из вершины А (через площадь, средствами векторной алгебры).

22. Даны векторы и Вычислить площадь треугольника, построенного на векторах

23. Даны векторы и Вычислить площадь треугольника, построенного на векторах

24. Найти площадь параллелограмма, построенного на векторах где

25. В треугольнике с вершинами , и точка E делит сторону АВ пополам. Найти площадь треугольника АСЕ (средствами векторной алгебры).

26. Даны векторы и Найти вектор , который перпендикулярен векторам если модуль вектора численно равен площади треугольника, построенного на векторах , и тройка векторов левая.

27. Даны точки , и . Найти длину высоты треугольника АВС, опущенной из вершины С (через площадь, средствами векторной алгебры).

28. Даны три вершины параллелограмма , и . Найти длину высоты, опущенной из вершины С (через площадь, средствами векторной алгебры).

29. На векторах и построен параллелограмм. Найти площадь параллелограмма, построенного на его диагоналях.

30. Даны векторы , и Вычислить площадь треугольника, построенного на векторах

Задача 11.Если даны координаты , то смешанное произведение векторов вычисляют по формуле

Объемы параллелепипеда и тетраэдра (треугольной пирамиды), построенных на векторах находятся с помощью смешанного произведения векторов:

Если > 0, то тройка векторов — правая.

Если < 0, то тройка левая.

Если = 0, то векторы компланарны.

Пример 11.Дан параллелепипед построенный на векторах и Найти высоту, проведенную из вершины на грань ABCD.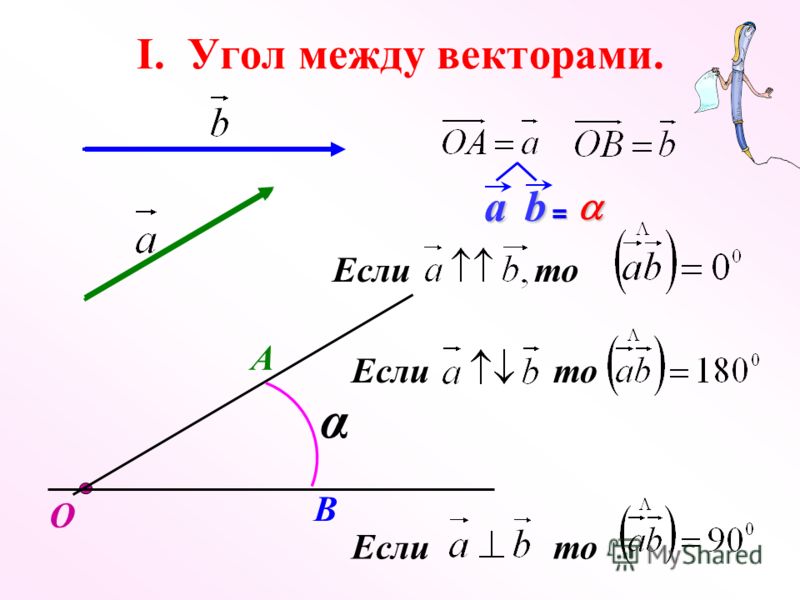

Объем равен произведению площади основания на высоту:

находится также по формуле , поэтому

Вычислим векторное произведение =

Тогда

Контрольные варианты к задаче 11

1. Найти объем треугольной пирамиды, построенной на векторах ,

и .

2. Найти объем треугольной пирамиды с вершинами ,

3. Найти значение , при котором векторы и образуют левую тройку, а объем параллелепипеда, построенного на них, равен 33.

4. Даны векторы Найти значение t, при котором выполняется равенство

5. Точки лежат в одной плоскости. Найти t .

6. Найти объем параллелепипеда, зная четыре его вершины:

7. Найти значение t, при котором векторы компланарны.

8. Точки служат вершинами параллелепипеда, объем которого равен 16. Найти t.

9. Даны векторы Найти значение t, при котором имеет место равенство

10. Векторы компланарны.

Найти t.

11. Даны векторы , Найти значение t, при котором имеет место равенство

12. Даны векторы Найти значение t, при котором имеет место равенство

13. Векторы образуют правую тройку, причем объем параллелепипеда, построенного на этих векторах, равен девяти. Найти t.

14. Векторы образуют левую тройку и служат ребрами параллелепипеда, объем которого равен 45. Вектор перпендикулярен плоскости ХОУ. Найти отличную от нуля координату вектора

15. Векторы образуют левую тройку. Объем построенного на них параллелепипеда равен 51. Найти t.

16. Найти объем треугольной пирамиды с вершинами в точках

17. Объем треугольной пирамиды равен пяти. Три его вершины находятся в точках Найти отличную от нуля координату четвертой вершины D, если она лежит на оси ОУ.

18. Точки и лежат в одной плоскости. Найти t.

19. Найти значение t, при котором векторы и компланарны.

20. Проверить, лежат ли точки и в одной плоскости.

21. Найти объем треугольной пирамиды, вершины которой находятся в точках

22. Даны векторы и Найти t, при котором имеет место равенство

23. Векторы образуют правую тройку. Объем построенной на них треугольной пирамиды равен . Найти t.

24. Вершины треугольной пирамиды находятся в точках и Найти значение t, если объем пирамиды равен 45.

25. Даны векторы Найти значение t, если имеет место равенство

26. Даны векторы Найти значение t, если имеет место равенство

27. Определить, при каком значении t векторы компланарны.

28. Даны векторы . Найти значение t, при котором имеет место равенство

29. Векторы образуют правую тройку, а объем построенного на них параллелепипеда равен 12. Найти значение t.

30. Даны векторы Найти значение t, если имеет место равенство

Задача № 12.Пусть вектор , причем векторы не образуют декартовый базис. Пусть известны тогда

Если векторы и , то

= +

Пример 12.При каком ненулевом значении t вектор будет еди-

ничным, если Вектор будет единичным, если его длина будет равна единице, т. е. .

Контрольные варианты к задаче 12

1. Даны векторы где Найти косинус угла между векторами

2. Найти если

3. Даны векторы найти если

4. Даны векторы Найти косинус угла между векторами если

5. При каком отличном от нуля значении параметра вектор будет единичным, если

6. Даны векторы найти если

7. Векторы служат сторонами параллелограмма. Найти косинус угла между диагональю и стороной если

8. Даны векторы . При каком значении параметра вектор , если

9. В параллелограмме АВСD найти длину диагонали , если

, .

10. В треугольнике АВС найти косинус внутреннего угла В, если

11. Даны векторы . Вычислить , если

12. При каком положительном значении параметра векторы имеют одинаковую длину, если

13. Даны векторы . Найти , если , .

14. В треугольнике АВС найти длину , если

15. Даны векторы . Найти , если

16. Дан вектор . Найти косинус угла между векторами , если .

17. Даны векторы . Найти , если , .

18. Даны векторы . Найти .

19. Даны векторы При каком значении параметра вектор , если

20. Дано: , . При каком значении параметра векторы и взаимно перпендикулярны?

21. Дан вектор — единичные векторы, образующие угол . Найти косинус угла между векторами .

22. Даны векторы . Найти , если ,

23. Дан вектор Найти , если .

24. Даны векторы . Найти длину вектора , если , .

25. Даны векторы . Найти , если , .

26. Векторы образуют угол . Зная, что найти длину вектора .

27. При каком значении параметра вектор будет единичным, если

28. При каком значении векторы имеют одинаковую длину, если ?

29. В треугольнике АВС найти косинус внутреннего угла при вершине В, если , где , .

30. Даны векторы . При каком значении параметра вектор , если , .

Задача 13. При решении этой задачи будем использовать свойства векторного произведения двух векторов. Модуль векторного произведения двух векторов

поэтому По свойствам векторного произведения

Площадь параллелограмма, постро-

енного на векторах , равна Площадь треугольника, построенного на векторах :

Пример 13.В параллелограмме ABCD даны векторы и Найти если Это условие в параллелограмме ABCD вектор Тогда Вектор

Использование закона косинусов и формулы скалярного произведения векторов для нахождения угла между тремя точками – Muthukrishnan

19 октября 2019 г.

Для любых 3 точек A, B и C на декартовой плоскости. Если нам нужно найти угол между этими точками, есть много способов сделать это. В этой статье я расскажу о двух часто используемых методах:

Формула закона косинусов
Формула продукта Vector Dot

Закон косинусов

Для любого заданного треугольника ABC со сторонами AB, BC и AC угол, образованный прямыми AB и BC, определяется по формуле:

Вот как мы можем вывести эту формулу:

То же самое можно расширить и для других углов.

Теперь, если нам даны 3 точки на декартовой плоскости, мы можем найти расстояние между любыми двумя точками, используя формулу Евклидова расстояния:

Итак, чтобы найти угол между тремя точками A (x1,y1), B (x2,y2) и C (x3,y3), наша формула становится:

В Python мы можем представить приведенную выше формулу, используя код:

 импортировать numpy как np
импортировать математику
def angle_between_three_points (точка A, точка B, точка C):
    
    x1x2s = math.pow((точкаA[0] - точкаB[0]),2)
    x1x3s = math.pow((точкаA[0] - точкаC[0]),2)
    x2x3s = math.pow((точкаB[0] - точкаC[0]),2)
    
    y1y2s = math.pow((точкаA[1] - точкаB[1]),2)
    y1y3s = math.pow((точкаA[1] - точкаC[1]),2)
    y2y3s = math.pow((точкаB[1] - точкаC[1]),2)
    cosine_angle = np.arccos((x1x2s + y1y2s + x2x3s + y2y3s - x1x3s - y1y3s)/(2*math.sqrt(x1x2s + y1y2s)*math.sqrt(x2x3s + y2y3s)))
    вернуть np.степеней (косинус_угол)
A = np.массив ([2,4])
B = np. массив ([8,7])
C = np.массив ([9,1])
print("Угол между точками:", angle_between_three_points(A,B,C))
# дает 72,89
А = np.массив ([0,0])
B = np.массив ([0,4])
C = np.массив ([4,0])
print("Угол между точками:", angle_between_three_points(A,B,C))
# дает 45.0

Векторное скалярное произведение

Три точки также могут быть представлены в виде вектора, как показано ниже.

где,

Скалярное произведение или скалярное произведение двух векторов представлено формулой:

, где || * || — величина вектора, а θ — угол между двумя векторами.

Из приведенной выше формулы мы можем представить угол, используя формулу:

В Python мы можем представить приведенную выше формулу, используя код:

 def angle_between_three_points (точка A, точка B, точка C):
    ВА = точка А - точка Б
    ВС = точка C - точка B
    пытаться:
        cosine_angle = np.dot (BA, BC) / (np.linalg.norm (BA) * np.linalg.norm (BC))
        угол = np.arccos(cosine_angle)
    кроме:
        распечатать("отл")
        поднять исключение («неверный косинус»)
    вернуть np. степени (угол)

Выше приведен код из моего поста, где я говорил о нахождении коллинеарности трех точек на плоскости с помощью угла, образованного точками.

Каталожные номера:

http://mathworld.wolfram.com/DotProduct.html
https://en.wikipedia.org/wiki/Euclidean_distance
https://en.wikipedia.org/wiki/Law_of_cosines

Теги: Математика

Проверено 23 июня 2021 г., 1:35 (время сайта).

Доступно по адресу: 192.168.31.181/муту/?p=1106

Как вычислить подобие косинуса в R

[Эта статья была впервые опубликована на сайте Methods – finnstats и любезно предоставлена R-блогерами]. (Вы можете сообщить о проблеме с содержанием на этой странице здесь)

Хотите поделиться своим контентом с R-блогерами? нажмите здесь, если у вас есть блог, или здесь, если у вас его нет.

Как вычислить косинусное сходство в R. Мерой сходства между двумя векторами в пространстве внутреннего произведения является косинусное сходство.

Формула для двух векторов, таких как A и B, и косинусного подобия может быть рассчитана следующим образом:

Косинусное сходство = ΣA _i B _i / (√ΣA _i √Σ8 ^{2 ^{² )}}

В основном косинусное сходство используется для измерения степени сходства документов независимо от их размера.

Другими словами, он вычисляет косинус угла, образованного двумя векторами, спроецированными в трех измерениях.

В этом руководстве описывается, как вычислить косинусное сходство между векторами в R при использовании функции косинуса().

Функцию cosine() можно загрузить из библиотеки lsa .

Сеть LSTM в R » Рекуррентная нейронная сеть »

Давайте создадим два вектора x и y и присвоим им некоторые значения.

#создать векторы

 x <- c(33, 33, 43, 55, 48, 37, 43, 24)
y <- c(37, 38, 42, 46, 46, 59, 41, 50)

#определить подобие косинуса

 библиотека (LSA)
косинус (х, у)
[1,] 0,9624844

На основании приведенного выше результата косинусное сходство между x и y составляет 0,9624844.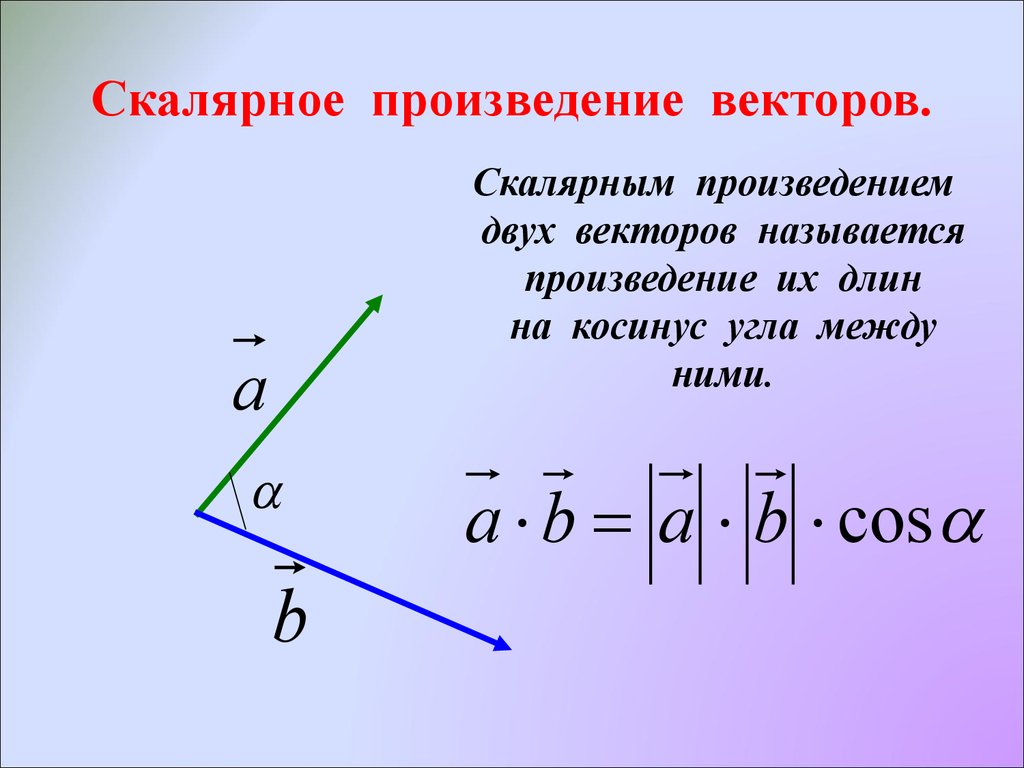

Повторные измерения ANOVA в R Полное руководство »

Мы можем вычислить косинусное сходство матрицы в R

Давайте создадим векторы x, y и z и создадим матрицу.

#define matrix

 x <- c(23, 24, 34, 35, 22, 25, 33, 24)
у <- с(10, 10, 22, 26, 16, 22, 11, 20)
z <- c(14, 15, 35, 16, 11, 23, 10, 41)
матрица <- cbind(x, y, z)

#рассчитать сходство косинуса

Корреляционный анализ в R? » Коэффициент корреляции Карла Пирсона »

 библиотека (LSA)
косинус (матрица)
x        y         z
х 1,0000000 0,9561517 0,8761308
у 0,9561517 1,0000000 0,9163248
z 0,8761308 0,9163248 1,0000000

Теперь вы можете увидеть косинусное сходство между x, y и z.

Косинусное сходство между векторами x и y составляет 0,9561517.

Косинусное сходство между векторами x и z составляет 0,8761308.

Косинусное сходство между векторами y и z составляет 0,9163248.

Для функции cosine() в качестве входных данных требовалась либо одна матрица, либо два вектора.

Источник

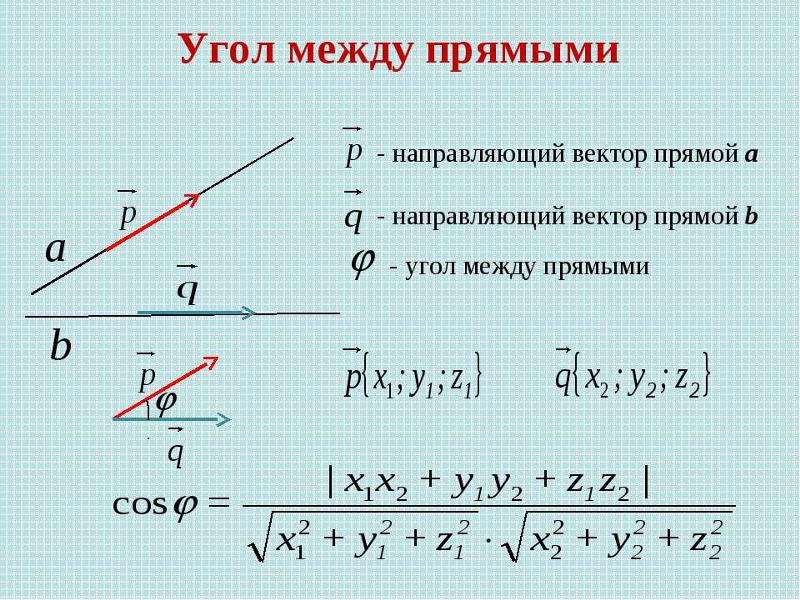
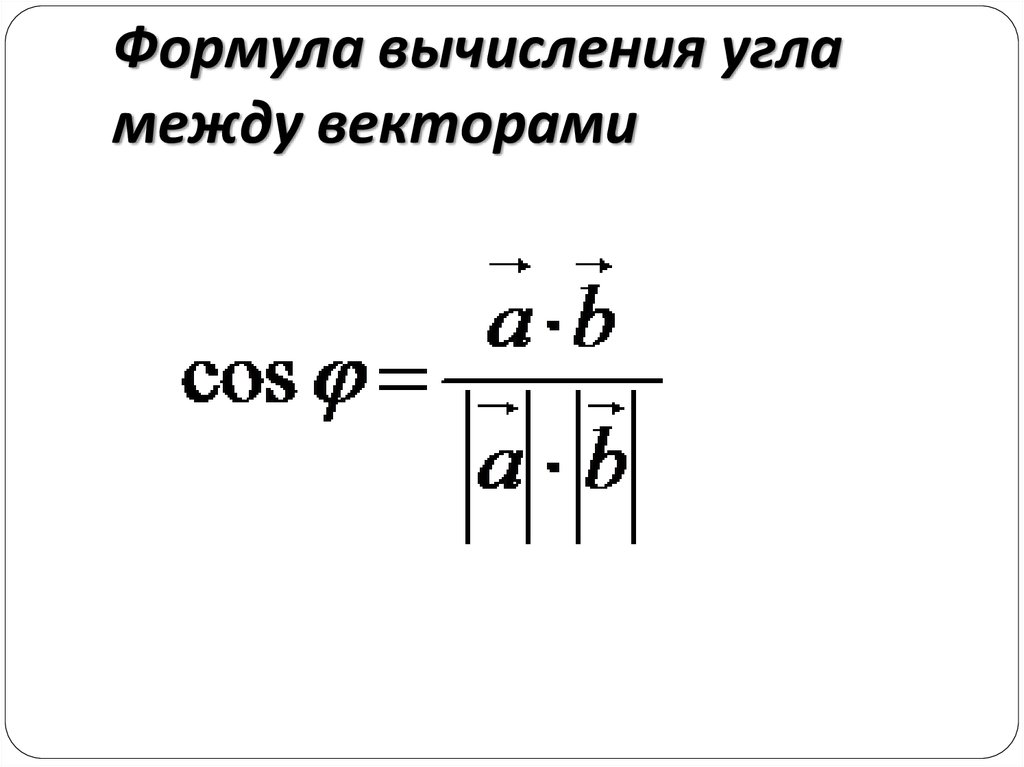
Угол между векторами.

Формула вычисления угла между векторами

cos α =	a · b
\| a \|·\| b \|

Примеры задач на вычисление угла между векторами

Примеры вычисления угла между векторами для плоских задачи

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 3 = 12 + 12 = 24.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 3 2 = √ 16 + 9 = √ 25 = 5

Найдем угол между векторами:

cos α =	a · b	=	24	=	24	= 0.96
\| a \| · \| b \|	5 · 5	25

Решение: Найдем скалярное произведение векторов:

a · b = 5 · 7 + 1 · 5 = 35 + 5 = 40.

Найдем модули векторов:

| a | = √ 7 2 + 1 2 = √ 49 + 1 = √ 50 = 5√ 2
| b | = √ 5 2 + 5 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α =	a · b	=	40	=	40	=	4	= 0.8
\| a \| · \| b \|	5√ 2 · 5√ 2	50	5

Примеры вычисления угла между векторами для пространственных задач

Решение: Найдем скалярное произведение векторов:

a · b = 3 · 4 + 4 · 4 + 0 · 2 = 12 + 16 + 0 = 28.

Найдем модули векторов:

| a | = √ 3 2 + 4 2 + 0 2 = √ 9 + 16 = √ 25 = 5
| b | = √ 4 2 + 4 2 + 2 2 = √ 16 + 16 + 4 = √ 36 = 6

Найдем угол между векторами:

cos α =	a · b	=	28	=	14
\| a \| · \| b \|	5 · 6	15

Решение: Найдем скалярное произведение векторов:

a · b = 1 · 5 + 0 · 5 + 3 · 0 = 5.

Найдем модули векторов:

| a | = √ 1 2 + 0 2 + 3 2 = √ 1 + 9 = √ 10
| b | = √ 5 2 + 5 2 + 0 2 = √ 25 + 25 = √ 50 = 5√ 2

Найдем угол между векторами:

cos α = a · b | a | · | b | = 5 √ 10 · 5√ 2 = 1 2√ 5 = √ 5 10 = 0.1√ 5

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Нахождение угла между векторами

Длина вектора, угол между векторами – эти понятия являются естественно-применимыми и интуитивно понятными при определении вектора как отрезка определенного направления. Ниже научимся определять угол между векторами в трехмерном пространстве, его косинус и рассмотрим теорию на примерах.

Для рассмотрения понятия угла между векторами обратимся к графической иллюстрации: зададим на плоскости или в трехмерном пространстве два вектора a → и b → , являющиеся ненулевыми. Зададим также произвольную точку O и отложим от нее векторы O A → = b → и O B → = b →

Углом между векторами a → и b → называется угол между лучами О А и О В .

Полученный угол будем обозначать следующим образом: a → , b → ^

Очевидно, что угол имеет возможность принимать значения от 0 до π или от 0 до 180 градусов.

a → , b → ^ = 0 , когда векторы являются сонаправленными и a → , b → ^ = π , когда векторы противоположнонаправлены.

Векторы называются перпендикулярными, если угол между ними равен 90 градусов или π 2 радиан.

Если хотя бы один из векторов является нулевым, то угол a → , b → ^ не определен.

Нахождение угла между векторами

Косинус угла между двумя векторами, а значит и собственно угол, обычно может быть определен или при помощи скалярного произведения векторов, или посредством теоремы косинусов для треугольника, построенного на основе двух данных векторов.

Согласно определению скалярное произведение есть a → , b → = a → · b → · cos a → , b → ^ .

Если заданные векторы a → и b → ненулевые, то можем разделить правую и левую части равенства на произведение длин этих векторов, получая, таким образом, формулу для нахождения косинуса угла между ненулевыми векторами:

cos a → , b → ^ = a → , b → a → · b →

Данная формула используется, когда в числе исходных данных есть длины векторов и их скалярное произведение.

Исходные данные: векторы a → и b → . Длины их равны 3 и 6 соответственно, а их скалярное произведение равно — 9 . Необходимо вычислить косинус угла между векторами и найти сам угол.

Решение

Исходных данных достаточно, чтобы применить полученную выше формулу, тогда cos a → , b → ^ = — 9 3 · 6 = — 1 2 ,

Теперь определим угол между векторами: a → , b → ^ = a r c cos ( — 1 2 ) = 3 π 4

Ответ: cos a → , b → ^ = — 1 2 , a → , b → ^ = 3 π 4

Чаще встречаются задачи, где векторы задаются координатами в прямоугольной системе координат. Для таких случаев необходимо вывести ту же формулу, но в координатной форме.

Длина вектора определяется как корень квадратный из суммы квадратов его координат, а скалярное произведение векторов равно сумме произведений соответствующих координат. Тогда формула для нахождения косинуса угла между векторами на плоскости a → = ( a x , a y ) , b → = ( b x , b y ) выглядит так:

cos a → , b → ^ = a x · b x + a y · b y a x 2 + a y 2 · b x 2 + b y 2

А формула для нахождения косинуса угла между векторами в трехмерном пространстве a → = ( a x , a y , a z ) , b → = ( b x , b y , b z ) будет иметь вид: cos a → , b → ^ = a x · b x + a y · b y + a z · b z a x 2 + a y 2 + a z 2 · b x 2 + b y 2 + b z 2

Исходные данные: векторы a → = ( 2 , 0 , — 1 ) , b → = ( 1 , 2 , 3 ) в прямоугольной системе координат. Необходимо определить угол между ними.

Решение

Для решения задачи можем сразу применить формулу:

cos a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 2 2 + 0 2 + ( — 1 ) 2 · 1 2 + 2 2 + 3 2 = — 1 70 ⇒ a → , b → ^ = a r c cos ( — 1 70 ) = — a r c cos 1 70

Также можно определить угол по формуле:

cos a → , b → ^ = ( a → , b → ) a → · b → ,

но предварительно рассчитать длины векторов и скалярное произведение по координатам: a → = 2 2 + 0 2 + ( — 1 ) 2 = 5 b → = 1 2 + 2 2 + 3 2 = 14 a → , b → ^ = 2 · 1 + 0 · 2 + ( — 1 ) · 3 = — 1 cos a → , b → ^ = a → , b → ^ a → · b → = — 1 5 · 14 = — 1 70 ⇒ a → , b → ^ = — a r c cos 1 70

Ответ: a → , b → ^ = — a r c cos 1 70

Также распространены задачи, когда заданы координаты трех точек в прямоугольной системе координат и необходимо определить какой-нибудь угол. И тогда, для того, чтобы определить угол между векторами с заданными координатами точек, необходимо вычислить координаты векторов в виде разности соответствующих точек начала и конца вектора.

Исходные данные: на плоскости в прямоугольной системе координат заданы точки A ( 2 , — 1 ) , B ( 3 , 2 ) , C ( 7 , — 2 ) . Необходимо определить косинус угла между векторами A C → и B C → .

Решение

Найдем координаты векторов по координатам заданных точек A C → = ( 7 — 2 , — 2 — ( — 1 ) ) = ( 5 , — 1 ) B C → = ( 7 — 3 , — 2 — 2 ) = ( 4 , — 4 )

Теперь используем формулу для определения косинуса угла между векторами на плоскости в координатах: cos A C → , B C → ^ = ( A C → , B C → ) A C → · B C → = 5 · 4 + ( — 1 ) · ( — 4 ) 5 2 + ( — 1 ) 2 · 4 2 + ( — 4 ) 2 = 24 26 · 32 = 3 13

Ответ: cos A C → , B C → ^ = 3 13

Угол между векторами можно определить по теореме косинусов. Отложим от точки O векторы O A → = a → и O B → = b → , тогда, согласно теореме косинусов в треугольнике О А В , будет верным равенство:

A B 2 = O A 2 + O B 2 — 2 · O A · O B · cos ( ∠ A O B ) ,

b → — a → 2 = a → + b → — 2 · a → · b → · cos ( a → , b → ) ^

и отсюда выведем формулу косинуса угла:

cos ( a → , b → ) ^ = 1 2 · a → 2 + b → 2 — b → — a → 2 a → · b →

Для применения полученной формулы нам нужны длины векторов, которые несложно определяются по их координатам.

Хотя указанный способ имеет место быть, все же чаще применяют формулу:

Угол между векторами. Ортогональные проекции векторов

Угол между векторами

Углом между двумя ненулевыми векторами называется угол между равными им векторами, имеющими общее начало, не превосходящий по величине числа .

Пусть в пространстве даны два ненулевых вектора и (рис.1.22). Построим равные им векторы и . На плоскости, содержащей лучи и , получим два угла . Меньший из них, величина которого не превосходит , принимается за угол между векторами и .

Поскольку направление нулевого вектора не определено, то не определен и угол между двумя векторами, если хотя бы один из них нулевой. Из определения следует, например, что угол между ненулевыми коллинеарными векторами либо равен нулю (если векторы одинаково направлены), либо равен (если векторы противоположно направлены).

Ортогональные проекции векторов

Движение по любой прямой может быть в двух направлениях. Ориентированной прямой называется прямая, на которой выбрано направление, т.е. одно из направлений считается положительным, а противоположное — отрицательным. Для измерения длин отрезков на прямой задается масштабный отрезок, который принимается за единицу.

Ориентированная прямая с заданным масштабным отрезком называется осью.

Любой ненулевой вектор , принадлежащий прямой, называется направляющим вектором для данной прямой, поскольку задает на ней ориентацию. Направление вектора принимается за положительное, а направление противоположного вектора — за отрицательное. Кроме того, длину вектора — можно принять за величину масштабного отрезка на этой прямой. Поэтому можно сказать, что любой ненулевой вектор определяет ось — прямую, содержащую этот вектор, задавая на ней направление и масштабный отрезок.

Ортогональной проекцией вектора на ось, задаваемую вектором , называется его проекция на ось вдоль прямой (или вдоль плоскости), перпендикулярной данной оси. Ортогональную проекцию вектора на ось, задаваемую вектором , будем обозначать .

Ортогональную проекцию вектора на прямую (см. разд. 1.2.2 и рис. 1.13) будем обозначать .

Ортогональную проекцию вектора а на плоскость (см. разд. 1.2.2 и рис. 1.14) будем обозначать .

Разность между вектором и его ортогональной проекцией называют ортогональной составляющей:

— — ортогональная составляющая вектора относительно вектора ;

— — ортогональная составляющая вектора относительно прямой ;

— — ортогональная составляющая вектора относительно плоскости .

На рис. 1.23 изображены ортогональные проекции вектора :

— на прямую (или на ось , задаваемую вектором ) вдоль прямой (рис.1.23,а);

— на прямую (или на ось , задаваемую вектором ) вдоль плоскости (рис.1.23,б);

— на плоскость вдоль прямой (рис.1.23,в).

На рис. 1.23 изображены ортогональные составляющие вектора :

— относительно оси (вектора ): (рис.1.23,а);

— относительно плоскости (рис.1.23,в).

Для ортогональных проекций справедлива следующая теорема (см. теорему 1.1 в разд. 1.5).

Теорема 1.2 (об ортогональных проекциях вектора).

1. Если на плоскости заданы две взаимно перпендикулярные прямые и , то любой вектор на плоскости можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,а).

2. Если в пространстве заданы три попарно перпендикулярные прямые и , пересекающиеся в одной точке, то любой вектор в пространстве можно однозначно представить в виде суммы своих ортогональных проекций на эти прямые, т.е. (рис. 1.24,6).

3. Квадрат длины вектора на плоскости или в пространстве равен сумме квадратов длин своих ортогональных проекций, т.е.

Первые два утверждения представляют собой частные случаи теоремы 1.1. Третье утверждение следует из теоремы Пифагора (для треугольника (рис. 1.24,а) или треугольников и (рис. 1.24,6)).

В формулировке теоремы 1.2 прямые можно заменить осями, задаваемыми попарно ортогональными векторами.

На рис.1.24,а проекции вектора на оси одновременно являются ортогональными составляющими: и . На рис. 1.24,6 вектор является проекцией вектора на плоскость , содержащую прямые и : , а вектор является ортогональной составляющей вектора относительно плоскости .

Алгебраическое значение длины проекции

Пусть – угол между ненулевым вектором и осью, задаваемой вектором , т.е. угол между ненулевыми векторами и .

Алгебраическим значением длины ортогональной проекции вектора на ось, задаваемую вектором , называется длина его ортогональной проекции , взятая с положительным знаком, если угол не превышает , и с отрицательным знаком, если угол больше , т.е.:

Например, для проекций, изображенных на рис. 1.25, 0″ png;base64,iVBORw0KGgoAAAANSUhEUgAAAE8AAAAVBAMAAAD1D64kAAAAMFBMVEVHcEwAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAlTPQ5AAAAEHRSTlMA/cBBpYEhURAxkWFx4MHQtTUEJQAAAVlJREFUKM9jYKAAsBGrkKsATaB5AhZVRUpK+mKoQty3/LCpZDCu3YAqYDiB9QZWq4tBBHsEnO/PwCaNx6X7l8FYcgwMIgwMJlomWhOYnZarNECFmZ3KDMAMOzeogBQDgzwDQ46gZ4s420GRwANQhRsNHB9AWHbOEIWiDAyCDGDFFxuYJKZCTWSWZjAMgOoxUUZWKMTAsLCA6QNIqBWIeQWAZsJcl/IYVWFgAJMCA0No6FpQWDgwOMI9lHId6kYUhQwMJ4D44AGGe3B1YKvZ5MAeBylUnABRCAIHDdhEmZCdyMBwiYFNBkgJTuAWYeAHupEtBBTHiQX94qVgeSNPWDgk8IAiVd7LMYBVUFCBYVMCyFieW55fNEDS+9zgieTOQgOw1ZAY5xC3WQBJZJygkGJfhoikORUMEDeCAbvoTvypVB4a0twK+FPppkcvoTpucDoQl7CnRuOTBQA/mUGNQvQK+QAAAABJRU5ErkJggg==» style=»vertical-align: middle;» />, поскольку угол между векторами и острый, a , так как угол между векторами и тупой.

Некоторые свойства проекций векторов переносятся на алгебраические значения их длин, в частности:

1. — алгебраическое значение длины ортогональной проекции суммы векторов равно сумме алгебраических значений длин ортогональных проекций слагаемых;

2. — алгебраическое значение длины ортогональной проекции произведения вектора на число равно произведению этого числа на алгебраическое значение длины ортогональной проекции вектора

1. Из определения алгебраического значения длины ортогональной проекции следует (см. также рис.1.25), что , т.е. алгебраическое значение длины ортогональной проекции ненулевого вектора на ось равна произведению длины этого вектора на косинус угла между вектором и осью.

Ортогональную проекцию вектора на ось, задаваемую вектором , можно представить в виде

Если — единичный вектор, то .

2. Равенство можно использовать как определение косинуса угла между ненулевыми векторами и (или, что то же самое, косинуса угла между осями, заданными ненулевыми векторами и (рис. 1.26)).

3. Углом между ненулевым вектором и прямой называется угол между вектором и его ортогональной проекцией на прямую . Величина угла может быть найдена по формуле

4. Углом между ненулевым вектором и плоскостью называется угол между вектором и его ортогональной проекцией на плоскость . Величина угла может быть найдена по формуле

Пример 1.7. Основания и равнобокой трапеции равны и соответственно; точка — середина стороны (рис. 1.27). Найти алгебраические значения длин ортогональных проекций векторов и на ось, задаваемую вектором .

Решение. Пусть — высота трапеции, — точка пересечения прямых и . По свойству равнобокой трапеции ; из равенства треугольников и .

Обозначим через искомые алгебраические значения длин ортогональных проекций.Тогда из равенств

и свойства 1 алгебраических значений длин проекций следует:

источники:

http://zaochnik.com/spravochnik/matematika/vektory/nahozhdenie-ugla-mezhdu-vektorami-primery-i-reshen/

http://mathhelpplanet.com/static.php?p=ugol-mezhdu-vektorami-i-ortogonalnye-proektsii-vektorov

Источник

Как найти косинус, если известна сторона и высота

2 ответа:

0

0

Совмести их в месте сторону и высоту

0

0

Косинус- отношения прилежащего катета к гепотенузе.если труг.не прямоугольный,то нужно провести высоту и из полученного прямог.треугольника искать косинус.

Как найти косинус, если известна сторона и высота

Косинус — отношения прилежащего катета к гепотенузе. если труг. не прямоугольный, то нужно провести высоту и из полученного прямог. треугольника искать косинус.
- Комментировать
- Жалоба
- Ссылка

Найди верный ответ на вопрос ✅ «Как найти косинус, если известна сторона и высота …» по предмету 📙 Геометрия, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.

Искать другие ответы

Новые вопросы по геометрии

Главная » Геометрия » Как найти косинус, если известна сторона и высота

Источник

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.

1.		2.
3.	.	4.
5.		6.
7.		8.
9.		10.
11.		12.
13.		14.
15.		16.
17.		18.
19.		20.
21.		22.
23.		24.
25.		26.
27.		28.
29.		30.