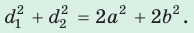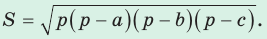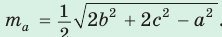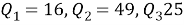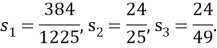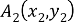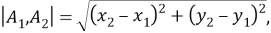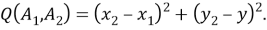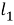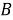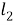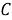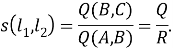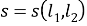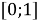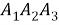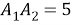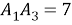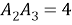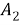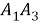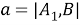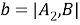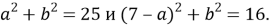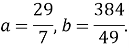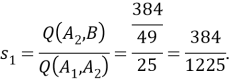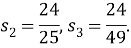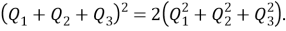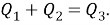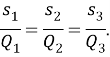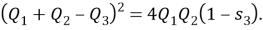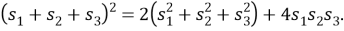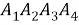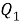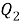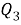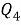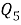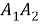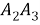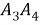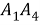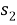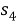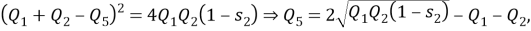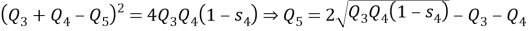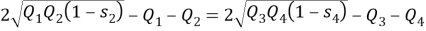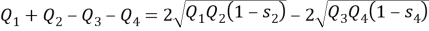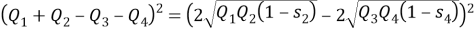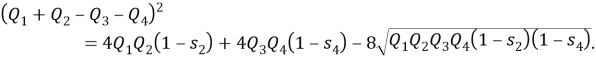Творческая работа учащегося «Теорема косинусов для четырёхугольника»
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Муниципальное автономное общеобразовательное учреждение
«Гимназия №1 Октябрьского района г. Саратова»
Научно-практическая конференция школьников.
Теорема косинусов для четырехугольника
Творческая работа ученицы 10 «А» класса
Всем известна теорема косинусов для треугольника
Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними .
Но не все знают, что существуют аналогичные теоремы и для других фигур.
Целью данной работы явилось:
Установить, существует ли теорема косинусов для фигур, отличных от треугольника
Доказать утверждение теоремы косинусов для четырехугольника
Применить теорему при решении задач
Получить полезные следствия из теоремы косинусов для четырехугольника
Теоретическая часть
Первая теорема косинусов
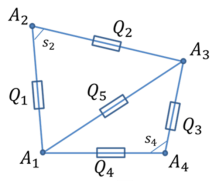
Рассмотрим четырехугольник (рис.1).
Возведем обе части равенства в квадрат
Так как скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними, то для вычисления скалярного произведения векторов будем откладывать векторы от одной точки.
Учитывая также, что скалярный квадрат вектора равен квадрату его длины, получаем:
Заметим, что , где угол, образованный продолжениями сторон .
Введем обозначения сторон четырехугольника (рис.2).
Полученное соотношение между сторонами четырехугольника называют первой теоремой косинусов для четырехугольника. Ее формулируют так:
Квадрат стороны четырехугольника равен сумме квадратов трех других его сторон без удвоенных произведений этих сторон, взятых попарно, и косинусов углов между ними.
Рассмотрим еще раз рис.2. Понятно, что
Тогда равенство теоремы косинусов может быть записано в виде
Теорему косинусов, так как она доказывалась с использованием векторов, можно считать верной и для невыпуклого четырехугольника, и для четырехугольника с самопересечением сторон.
Вторая теорема косинусов
Можно получить еще один аналог теоремы косинусов, который назовем второй теоремой косинусов для четырехугольника.
Рассмотрим четырехугольник с проведенными в нем диагоналями, длины которых обозначим e и f (рис.3А).
Построим вне этого четырехугольника
Ясно, что по двум углам
Составим отношения сходственных сторон
Построим вне этого четырехугольника
Тогда по двум углам.
Составим отношения сходственных сторон:
откуда
Заметим, что имеют равные длины.
Совместим рисунки 3Б и 3В на одном рисунке 4.
Рассмотрим четырехугольник и треугольник .
В четырехугольнике BDEF сумма равна сумме углов треугольника.
В треугольнике сумма всех углов равна 180, поэтому сумма четырехугольника равна 180.
– это односторонние углы при прямых и секущей , а значит, . Кроме того, . Значит, четырехугольник – параллелограмм. И , т.е. равен диагонали f .
Рассмотрим треугольник . Заметим, что равен сумме углов и четырехугольника .
Применим традиционную теорему косинусов к этому треугольнику:
Используя введенные обозначения, получим:
Так как сумма углов выпуклого четырехугольника равна 360,
Значит, в равенстве в качестве множителя + может участвовать и . Тогда вывод из равенства можно сформулировать так:
Квадрат произведения диагоналей четырехугольника равен сумме квадратов произведений противоположных сторон минус удвоенное произведение всех сторон четырехугольника на косинус суммы противоположных углов.
Это соотношение назовем второй теоремой косинусов для четырехугольников. Автором этого соотношения считают немецкого математика 19 века Карла Антона Бретшнайдера .
Получить из второй теоремы косинусов для четырехугольника теорему Птолемея.
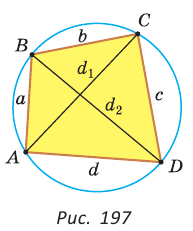
Рассмотрим четырехугольник (рис.5), который может быть вписан в окружность. В таком четырехугольнике суммы противоположных углов равны 180. Тогда в равенстве
. И соотношения для диагоналей и сторон четырехугольника принимает вид
Это равенство известно под названием теорема Птолемея :
Для четырехугольника, вписанного в окружность, произведение диагоналей равно сумме произведений противоположных сторон.
Доказать, что в параллелограмме с углом в 45 градусов квадрат произведения диагоналей равен сумме четвертых степеней двух его смежных сторон (рис.6).
c = a , d = b
Задача №3.
Получить из второй теоремы косинусов для четырехугольника теорему Стюарта.
Рассмотрим четырехугольник со сторонами и диагоналями (рис.7).
По теореме косинусов для этого четырехугольника справедливо равенство
Представим себе, что четырехугольник будет таким, что сумма сторон равна диагонали , то есть четырехугольник вырождается в треугольник (рис.8), то есть
Вычисляем по теореме косинусов для треугольника, получаем,
Тогда для этого вырожденного четырехугольника имеем
Полученное соотношение называется теоремой М. Стюарта.
Получить из теоремы Стюарта формулу длины медианы треугольника.
Решение.
Квадрат медианы равен четверти суммы удвоенных квадратов сторон треугольника, заключающих медиану, минус квадрат третьей стороны треугольника.
Получить из теоремы Стюарта формулу длины биссектрисы треугольника.
Если – биссектриса, то по свойству биссектрис в треугольнике
Квадрат биссектрисы треугольника равен разности произведений сторон треугольника, заключающих биссектрису, и отрезков противоположной стороны, на которые она разделена биссектрисой.
В данной работе получены следующие результаты:
сформулированы и доказаны две теоремы косинусов для четырехугольника;
с использованием доказанной теоремы доказана теорема Птолемея;
доказана теорема Стюарта;
получены два следствия из теоремы Стюарта: формула длины медианы и формула длины биссектрисы;
приведен пример использования теоремы косинусов для четырехугольника при решении задач.
Атанасян Л.С. ГЕОМЕТРИЯ. 7-9 кл. Москва, Издательство «Просвещение», 2006г.
Атанасян Л.С. ГЕОМЕТРИЯ. 10-11 кл. Москва, Издательство «Просвещение», 2006г.
Понарин Я.П. Элементарная геометрия в 3-х томах. Том 1. Планиметрия, преобразования плоскости. Москва, Издательство МЦНМО, 2004г.
Единая коллекция цифровых образовательных ресурсов https://school-collection.edu.ru
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
- Сейчас обучается 958 человек из 79 регионов
Курс повышения квалификации
Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО
- Сейчас обучается 338 человек из 71 региона
Курс профессиональной переподготовки
Математика: теория и методика преподавания в образовательной организации
- Сейчас обучается 685 человек из 74 регионов
Ищем педагогов в команду «Инфоурок»
- Гришина Ирина ВладимировнаНаписать 1664 15.07.2017
Номер материала: ДБ-603154
-
15.07.2017 2165
-
15.07.2017 648
-
15.07.2017 386
-
15.07.2017 827
-
15.07.2017 571
-
15.07.2017 177
-
15.07.2017 770
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В Госдуме предложили продлить каникулы для школьников до 16 января
Время чтения: 1 минута
ОНФ планирует решить проблему с низкими зарплатами водителей школьных автобусов в России
Время чтения: 1 минута
В Липецкой области начинающие педагоги получат 120 тысяч рублей
Время чтения: 0 минут
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Глава СПЧ предложил ввести подготовительные курсы перед обучением в школе для детей мигрантов
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.
Теорема косинусов. Доказательство теоремы косинусов.
Теорема косинусов — теорема евклидовой геометрии, которая обобщающает теорему Пифагора.
Теорема косинусов:

Квадрат стороны треугольника равняется сумме квадратов 2-х других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Следствие из теоремы косинусов.
- Теорема косинусов используется для определения cos угла треугольника:
h 2 = a 2 — (c – b cos α) 2 (2)
Приравниваем правые части уравнений (1) и (2):
b 2 — (b cos α) 2 = a 2 — (c — b cos α) 2
a 2 = b 2 + c 2 — 2bc cos α.
Если 1-н из углов при основании тупой (высота упирается в продолжение основания), полностью аналогичен рассмотренному выше.
Определить стороны b и c:
Теорема косинусов
Формула теоремы косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
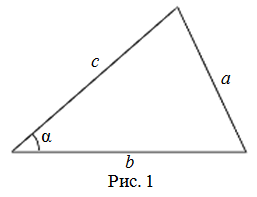
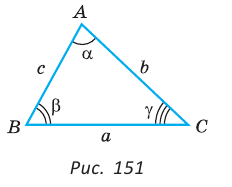
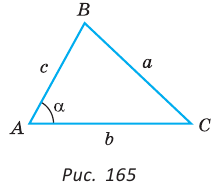
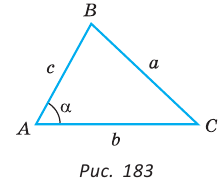
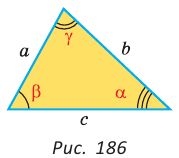
То есть для плоского треугольника (рис. 1) со сторонами $a$, $b$ и $c$ и углом $alpha$, противолежащим стороне $a$, справедливо соотношение:
Теорема косинусов является обобщением теоремы Пифагора. Утверждения, обобщающие теорему Пифагора и эквивалентные теореме косинусов, были сформулированы отдельно для случаев острого и тупого угла в 12 и 13 предложениях II книги «Начал» древнегреческого математика Евклида (ок. 300 г. до н. э.). Утверждения, эквивалентные теореме косинусов для сферического треугольника, применялись в сочинениях математиков стран Средней Азии. Теорему косинусов для сферического треугольника в привычном нам виде сформулировал выдающийся немецкий астролог, астроном и математик Региомонтан (1436 — 1476), назвав её «теоремой Альбатегния» (по имени выдающегося средневекового астронома и математика Абу Абдаллах Мухаммад ибн Джабир ибн Синан ал-Баттани (858 — 929).
В Европе теорему косинусов популяризовал французский математик Франсуа Виет (1540 — 1603) в 16 столетии. В начале 19 века её стали записывать в принятых по сей день алгебраических обозначениях.
Следствие из теоремы косинусов
Теорема косинусов может быть использована для нахождения косинуса угла треугольника (рис. 1):
Если $b^<2>+c^<2>-a^<2>>0$, то угол $alpha$ — острый;
Если $b^<2>+c^<2>-a^<2>=0$, то угол $alpha$ — прямой;
Если $b^<2>+c^<2>-a^ <2>lt 0$, то угол $alpha$ — тупой.
Примеры решения задач
Задание. В треугольнике $ABC AC=3, BC=5$ и $AB = 6 .$ Найти угол, противолежащий стороне $AB$
Решение. Согласно следствию из теоремы косинусов, имеем:
$$angle A C B=arccos left(-frac<1><15>right)$$
Ответ. $angle A C B=arccos left(-frac<1><15>right)$
Теорема косинусов не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Задан треугольник $ABC$, длины сторон которого $AC=17, BC=14, angle ACB=60^<circ>$. Найти длину третьей стороны рассматриваемого треугольника.
Решение. Согласно теореме косинусов
$$A B^<2>=A C^<2>+B C^<2>-2 cdot A C cdot B C cdot cos angle A C B=$$
$$=17^<2>+14^<2>-2 cdot 17 cdot 14 cdot cos 60^<circ>=289+196-238=24$$
http://www.calc.ru/Teorema-Kosinusov-Dokazatelstvo-Teoremy-Kosinusov.html
http://www.webmath.ru/poleznoe/formules_19_7.php
Содержание:
Теорема синусов, теорема косинусов:
Теорема синусов
Вы уже знаете, что в треугольнике против большей стороны лежит больший угол, а против большего угла — большая сторона. Пусть
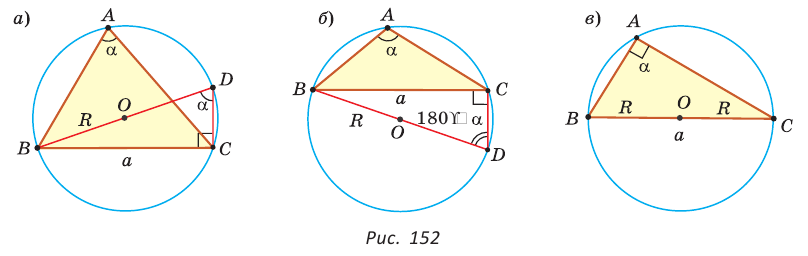
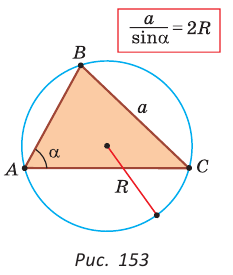
Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу окружности, описанной около треугольника, т. е.
Доказательство:
Пусть дан треугольник АВС, ВС = 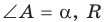
1) Угол 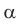
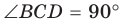
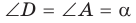
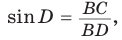
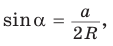
2) Угол 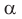
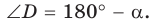
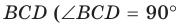
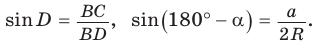
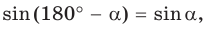
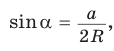
3) Для 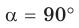
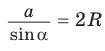
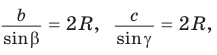
Теорема доказана.
Теорема синусов дает возможность решать широкий круг задач.
Так, пропорция 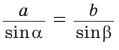
- зная две стороны треугольника и угол, противолежащий одной из них, найти синус угла, противолежащего другой стороне;
- зная два угла треугольника и сторону, противолежащую одному из этих углов, найти сторону, противолежащую другому углу.
С помощью формулы 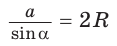
- зная сторону треугольника и противолежащий ей угол, найти радиус окружности, описанной около треугольника;
- зная угол треугольника и радиус описанной окружности, найти сторону треугольника, противолежащую данному углу;
- зная сторону треугольника и радиус его описанной окружности, найти синус угла, противолежащего данной стороне.
Повторение
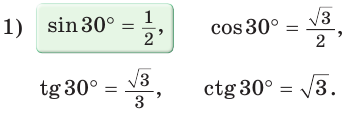
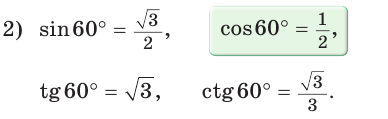
Пример:
В остроугольном треугольнике известны стороны 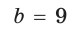
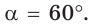
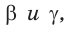
Решение:
По теореме синусов 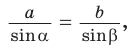
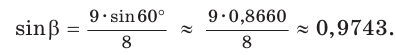
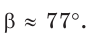
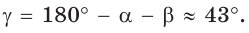
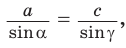
Ответ:
Замечание. Если бы по условию треугольник был тупоугольным с тупым углом 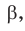
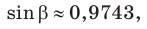
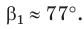
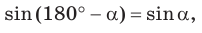
Пример:
Доказать справедливость формулы площади треугольника 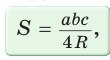
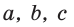
Доказательство:
Воспользуемся известной формулой площади треугольника: 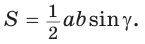
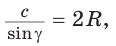
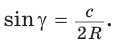
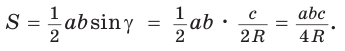
Замечание. Выведенная формула позволяет найти радиус описанной окружности треугольника
Пример:
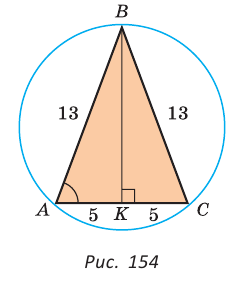
Найти радиус R окружности, описанной около равнобедренного треугольника АВС с основанием АС = 10 и боковой стороной ВС =13 (рис. 154).
Решение:
Способ 1. Из формулы 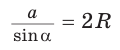
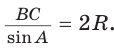
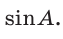
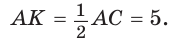
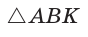
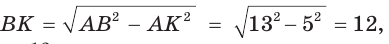
Тогда
Способ 2. Используем формулу 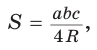
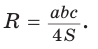
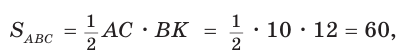
Ответ:
Замечание*. Напомним, что в главе II мы находили радиус R описанной окружности равнобедренного треугольника, проводя серединные перпендикуляры к его сторонам и используя подобие полученных прямоугольных треугольников. Также мы могли использовать формулу 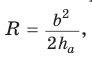
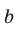
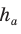
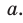
Заменив 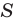
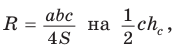
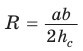

Теорема косинусов
Теорема косинусов позволяет выразить длину любой стороны треугольника через длины двух других его сторон и косинус угла между ними (например, длину стороны 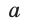
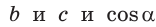
Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, т. е.
Доказательство:
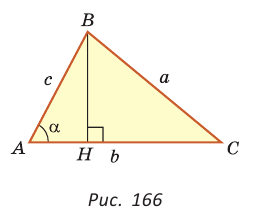
Докажем теорему для случая, когда в треугольнике АВС угол А и угол С острые (рис. 166).
Проведем высоту ВН к стороне АС. Из 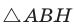
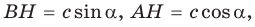
Из 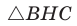
По основному тригонометрическому тождеству
Тогда
Справедливость теоремы для случаев, когда 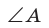
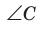
Для сторон 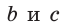
Замечание. Если 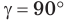
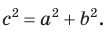
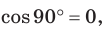
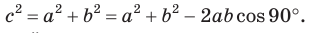
С помощью теоремы косинусов можно решить следующие задачи:
• зная две стороны и угол между ними, найти третью сторону треугольника;
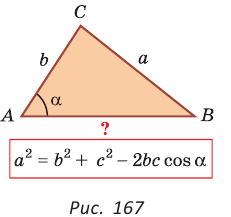
• зная две стороны и угол, противолежащий одной из этих сторон, найти третью сторону (рис. 167) (в этом случае возможны два решения).
Рассмотрим следствия из теоремы косинусов, которые дают возможность решить еще целый ряд задач.
Следствие:
Теорема косинусов позволяет, зная три стороны треугольника, найти его углы (косинусы углов). Из равенства 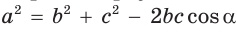
Для углов 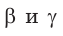
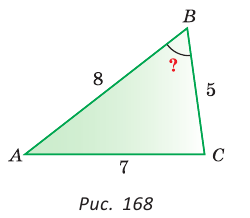
Пример:
В треугольнике АВС стороны АВ = 8, ВС = 5, АС = 7. Найдем ZB (рис. 168).
По теореме косинусов
Используя записанную выше формулу, можно сразу получить:
Следствие:
С помощью теоремы косинусов можно по трем сторонам определить вид треугольника: остроугольный, прямоугольный или тупоугольный.
Так, из формулы 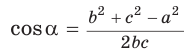
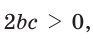
- если
то
и угол
острый;
- если
то
и угол
тупой;
- если
то
и угол
прямой.
При определении вида треугольника достаточно найти знак косинуса угла, лежащего против большей стороны, поскольку только больший угол треугольника может быть прямым или тупым.
Пример:
Выясним, каким является треугольник со сторонами a = 2, 6 = 3 и с = 4. Для этого найдем знак косинуса угла у, лежащего против большей стороны с. Так как 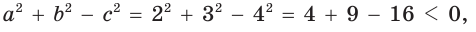
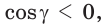
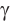
Сформулируем правило определения вида треугольника (относительно углов). Треугольник является:
- остроугольным, если квадрат его большей стороны меньше суммы квадратов двух других его сторон:
- тупоугольным, если квадрат его большей стороны больше суммы квадратов двух других его сторон:
- прямоугольным, если квадрат его большей стороны равен сумме квадратов двух других его сторон:
Следствие:
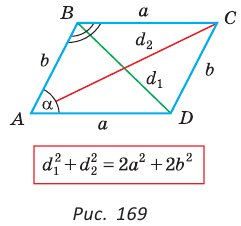
Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
Доказательство:
Пусть в параллелограмме ABCD 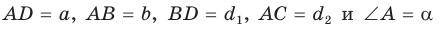
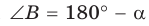
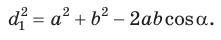
Из 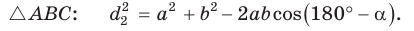
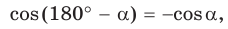
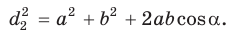
Сложив почленно равенство (1) и равенство (2), получим 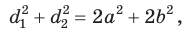
Данная формула дает возможность:
- • зная две соседние стороны и одну из диагоналей параллелограмма, найти другую диагональ;
- • зная две диагонали и одну из сторон параллелограмма, найти соседнюю с ней сторону.
Следствие:
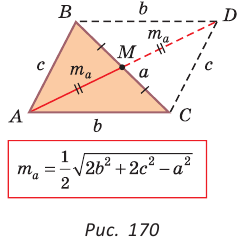
Медиану 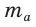
Доказательство:
Рассмотрим 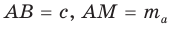
Проведем отрезки BD и DC. Так как у четырехугольника ABDC диагонали AD и ВС точкой пересечения делятся пополам, то он — параллелограмм. По свойству диагоналей параллелограмма 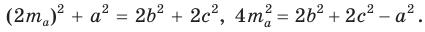
Утверждение доказано.
Аналогично:
Формула медианы позволяет:
- зная три стороны треугольника, найти любую из его медиан;
- зная две стороны и медиану, проведенную к третьей стороне, найти третью сторону;
- зная три медианы, найти любую из сторон треугольника.
Пример:
а) Дан треугольник АВС, а = 5, 5 = 3, 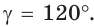
Решение:
а) По теореме косинусов
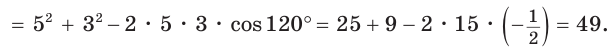
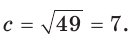
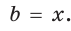
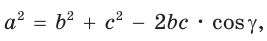
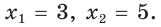
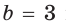
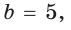
Ответ: а) 7; б) 3 или 5.
Пример:
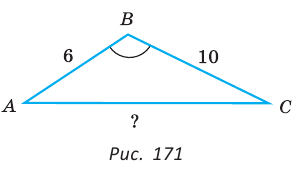
Две стороны треугольника равны 6 и 10, его площадь —
Найти третью сторону треугольника при условии, что противолежащий ей угол — тупой.
Решение:
Пусть в 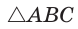
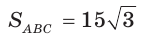
Поскольку 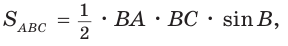
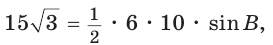
Так как 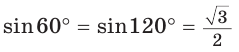
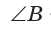

Ответ: 14.
Пример:
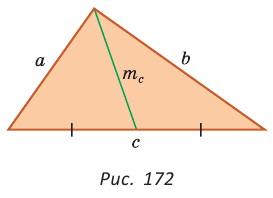
Найти площадь треугольника, две стороны которого равны 6 и 8, а медиана, проведенная к третьей стороне, равна 5.
Решение:
Обозначим стороны треугольника 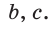
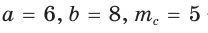
По формуле медианы 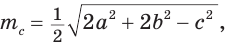
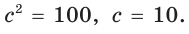
Ответ: 24.
Формула Герона
Мы знаем, как найти площадь треугольника по основанию и высоте, проведенной к этому основанию: 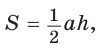
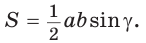
Теорема (формула Герона).
Площадь треугольника со сторонами 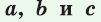
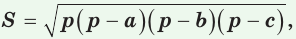
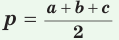
Доказательство:
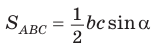
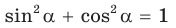
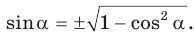
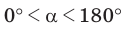
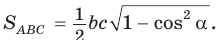
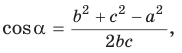
Тогда
Так как
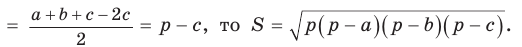
Решение треугольников
Решением треугольника называется нахождение его неизвестных сторон и углов (иногда других элементов) по данным, определяющим треугольник.
Такая задача часто встречается на практике, например в геодезии, астрономии, строительстве, навигации.
Рассмотрим алгоритмы решения трех задач.
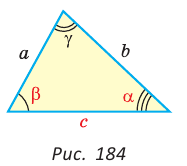
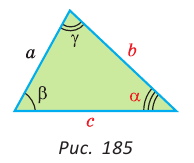
Пример №1 (решение треугольника по двум сторонам и углу между ними).
Дано: 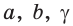
Найти :
Решение:
Рис. 184
1) По теореме косинусов
2) По следствию из теоремы косинусов
3) Угол 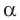
4) Угол
Замечание. Нахождение угла 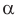
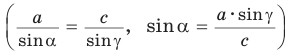
Пример №2 (решение треугольника по стороне и двум прилежащим к ней углам).
Дано: 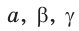
Найти:
Решение:
1) Угол
2) По теореме синусов 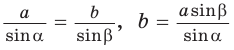
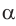
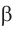
3) Сторону с можно найти с помощью теоремы косинусов или теоремы синусов: 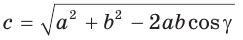
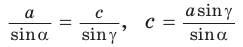
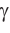
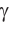
Пример №3 (решение треугольника по трем сторонам).
Дано: 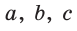
Найти: 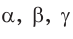
Решение:
1) По следствию из теоремы косинусов
2) Зная 
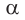
3) Аналогично находим угол
4) Угол
5) Радиус R описанной окружности треугольника можно найти по формуле 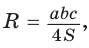
Замечание*. Вторым способом нахождения R будет нахождение косинуса любого угла при помощи теоремы косинусов 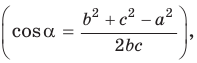
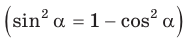
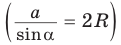
Пример №4
Найти площадь S и радиус R описанной окружности треугольника со сторонами 9, 12 и 15.
Решение:
Способ 1. Воспользуемся формулой Герона. Обозначим а = 9, b = 12, с = 15. Получим:
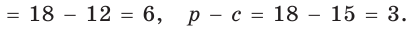
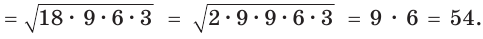
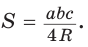
Ответ:
Способ 2. Так как 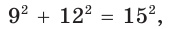
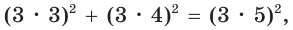
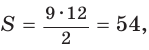
Пример №5
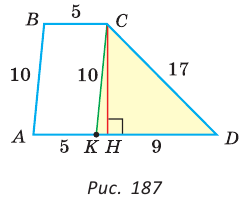
Найти площадь трапеции с основаниями, равными 5 и 14, и боковыми сторонами, равными 10 и 17.
Решение:
Пусть в трапеции ABCD основания AD = 14 и ВС = 5, боковые стороны АВ = 10 и 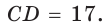
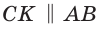
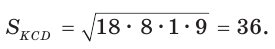
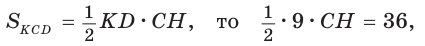
Ответ: 76.
Примеры решения задач с использованием теоремы синусов и теоремы косинусов
Пример:
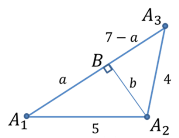
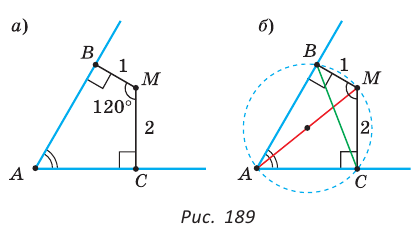
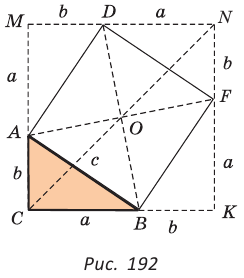
Внутри угла А, равного 60°, взята точка М, которая находится на расстоянии 1 от одной стороны угла и на расстоянии 2 от другой стороны. Найти расстояние от точки М до вершины угла А (рис. 189, а).
Решение:
Пусть 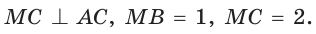
длину отрезка AM. Сумма углов четырехугольника АВМС равна 360°.
Поэтому
Так как в четырехугольнике АВМС 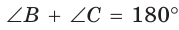
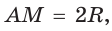
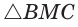
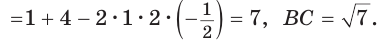
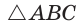
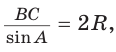
Ответ:
Замечание. Вторым способом решения будет продление отрезка ВМ до пересечения с лучом АС и использование свойств полученных прямоугольных треугольников. Рассмотрите этот способ самостоятельно.
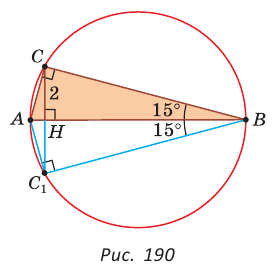
Пример №6
В прямоугольном треугольнике АВС известно: 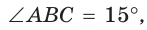
Решение:
Построим 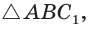
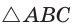
Поскольку 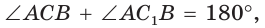
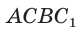
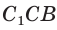
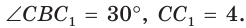
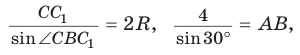
Ответ: 8.
Пример №7
Дан прямоугольный треугольник АВС с катетами ВС = а и АС = 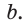
Решение:
Способ 1. Так как 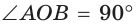
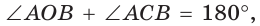
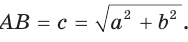
Пусть СО = х. По теореме косинусов из 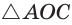
из 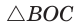
По свойству вписанного четырехугольника 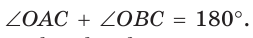
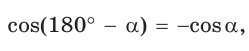
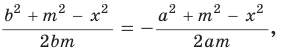
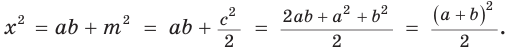
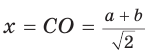
Способ 2. Используем теорему Птолемея, которая гласит: «Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон». Для нашей задачи получаем (см. рис. 191):
Способ 3. Достроим 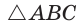
Ответ:
Пример №8
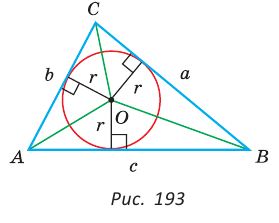
Точка О — центр окружности, вписанной в треугольник АВС, 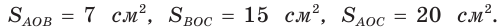
Решение:
Пусть 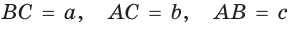
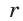
Тогда
Отсюда 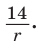
С другой стороны, 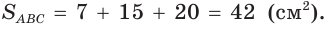
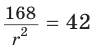
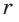
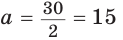
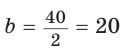
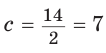
Ответ: 15 см; 20 см; 7 см.
Теорема Стюарта
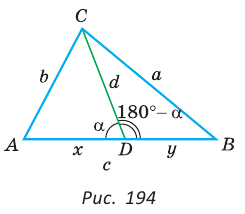
Следующая теорема позволяет найти длину отрезка, соединяющего вершину треугольника с точкой на противоположной стороне.
Теорема Стюарта. «Если а, b и с — стороны треугольника и отрезок d делит сторону с на отрезки, равные х и у (рис. 194), то справедлива формула
Доказательство:
По теореме косинусов из 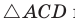
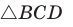
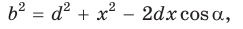
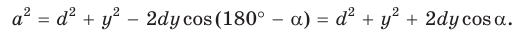
Умножим обе части равенства (1) на у, равенства (2) — на
Сложим почленно полученные равенства:
Из последнего равенства выразим
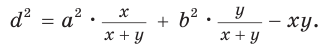
Следствие:
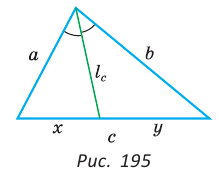
Биссектрису треугольника можно найти по формуле (рис. 195)
Доказательство:
По свойству биссектрисы треугольника 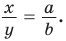
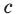
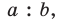
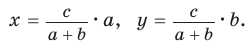
Пример №9
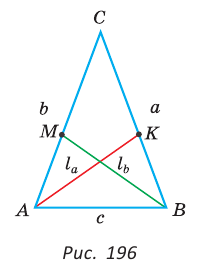
Доказать, что если в треугольнике две биссектрисы равны, то треугольник — равнобедренный (теорема Штейнера—Лемуса).
Доказательство:
Пусть дан треугольник АВС, 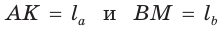
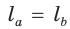
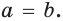
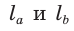
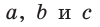
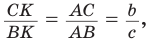
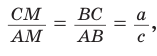
По формуле биссектрисы треугольника
Из условия 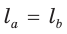
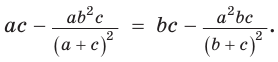
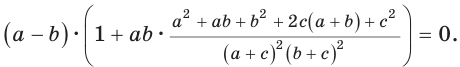
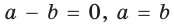
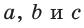
Теорема Птолемея о вписанном четырехугольнике
Произведение диагоналей вписанного четырехугольника равно сумме произведений его противоположных сторон, т. е.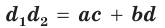
Доказательство:
Из 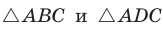
Так как 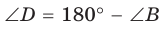
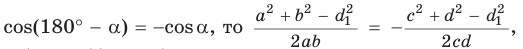
Аналогично из 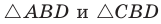
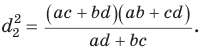
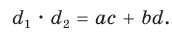
Запомните:
- Теорема синусов. Стороны треугольника пропорциональны синусам противолежащих углов. Отношение стороны треугольника к синусу противолежащего угла равно удвоенному радиусу его описанной окружности:
- Радиус описанной окружности треугольника можно найти, используя формулы:
- Теорема косинусов. Квадрат любой стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними:
- Пусть
— стороны треугольника и с — большая сторона. Если
, то треугольник тупоугольный, если
то треугольник остроугольный, если
, то треугольник прямоугольный.
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон:
- Формула Герона:
- Формула медианы:
- Параллельность прямых и плоскостей
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Углы и расстояния в пространстве
- Подобие треугольников
- Решение прямоугольных треугольников
- Параллелограмм
Муниципальное автономное общеобразовательное учреждение
«Гимназия №1 Октябрьского района г. Саратова»
Научно-практическая конференция школьников.
Теорема косинусов для четырехугольника
Творческая работа ученицы 10 «А» класса
Куприяновой Дарьи
Руководитель –
учитель математики
Гришина И. В.
Саратов
2016
Содержание
-
Задача №1……………………………………………………………
8
-
Задача №2…………………………………………………………….
8
-
Задача №3…………………………………………………………….
-
Задача №4…………………………………………………………….
-
Задача №5…………………………………………………………….
9
10
10
Заключение…………………………………………………………..
11
Литература…………………………………………….………..……
12
Введение
Всем известна теорема косинусов для треугольника
Квадрат стороны треугольника равен сумме квадратов двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними.
Но не все знают, что существуют аналогичные теоремы и для других фигур.
Целью данной работы явилось:
-
Установить, существует ли теорема косинусов для фигур, отличных от треугольника
-
Доказать утверждение теоремы косинусов для четырехугольника
-
Применить теорему при решении задач
-
Получить полезные следствия из теоремы косинусов для четырехугольника
Теоретическая часть
-
Первая теорема косинусов
Рассмотрим четырехугольник (рис.1).
Очевидно, что
Возведем обе части равенства в квадрат
Так как скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними, то для вычисления скалярного произведения векторов будем откладывать векторы от одной точки.
Учитывая также, что скалярный квадрат вектора равен квадрату его длины, получаем:
Заметим, что , где угол, образованный продолжениями сторон .
Введем обозначения сторон четырехугольника (рис.2).
Тогда
Значит,
Полученное соотношение между сторонами четырехугольника называют первой теоремой косинусов для четырехугольника. Ее формулируют так:
Квадрат стороны четырехугольника равен сумме квадратов трех других его сторон без удвоенных произведений этих сторон, взятых попарно, и косинусов углов между ними.
Рассмотрим еще раз рис.2. Понятно, что
Тогда,
Тогда равенство теоремы косинусов может быть записано в виде
Теорему косинусов, так как она доказывалась с использованием векторов, можно считать верной и для невыпуклого четырехугольника, и для четырехугольника с самопересечением сторон.
-
Вторая теорема косинусов
Можно получить еще один аналог теоремы косинусов, который назовем второй теоремой косинусов для четырехугольника.
Рассмотрим четырехугольник с проведенными в нем диагоналями, длины которых обозначим e и f (рис.3А).
Построим вне этого четырехугольника
Ясно, что по двум углам
Составим отношения сходственных сторон
; откуда
Построим вне этого четырехугольника
Тогда по двум углам.
Составим отношения сходственных сторон:
откуда
Заметим, что имеют равные длины.
Совместим рисунки 3Б и 3В на одном рисунке 4.
Рассмотрим четырехугольник и треугольник .
В четырехугольнике BDEF сумма равна сумме углов треугольника.
В треугольнике сумма всех углов равна 180, поэтому сумма четырехугольника равна 180.
– это односторонние углы при прямых и секущей , а значит, . Кроме того, . Значит, четырехугольник – параллелограмм. И , т.е. равен диагонали f.
Рассмотрим треугольник . Заметим, что равен сумме углов и четырехугольника .
Применим традиционную теорему косинусов к этому треугольнику:
Используя введенные обозначения, получим:
Так как сумма углов выпуклого четырехугольника равна 360,
то
Тогда .
Значит, в равенстве в качестве множителя + может участвовать и . Тогда вывод из равенства можно сформулировать так:
Квадрат произведения диагоналей четырехугольника равен сумме квадратов произведений противоположных сторон минус удвоенное произведение всех сторон четырехугольника на косинус суммы противоположных углов.
Это соотношение назовем второй теоремой косинусов для четырехугольников. Автором этого соотношения считают немецкого математика 19 века Карла Антона Бретшнайдера.
Практическая часть
Задача №1.
Получить из второй теоремы косинусов для четырехугольника теорему Птолемея.
Решение.
Рассмотрим четырехугольник (рис.5), который может быть вписан в окружность. В таком четырехугольнике суммы противоположных углов равны 180. Тогда в равенстве
. И соотношения для диагоналей и сторон четырехугольника принимает вид
, то есть
Это равенство известно под названием теорема Птолемея:
Для четырехугольника, вписанного в окружность, произведение диагоналей равно сумме произведений противоположных сторон.
Задача №2.
Доказать, что в параллелограмме с углом в 45 градусов квадрат произведения диагоналей равен сумме четвертых степеней двух его смежных сторон (рис.6).
Решение.
c=a, d=b
, следовательно
Задача №3.
Получить из второй теоремы косинусов для четырехугольника теорему Стюарта.
Решение.
Рассмотрим четырехугольник со сторонами и диагоналями (рис.7).
По теореме косинусов для этого четырехугольника справедливо равенство
Представим себе, что четырехугольник будет таким, что сумма сторон равна диагонали , то есть четырехугольник вырождается в треугольник (рис.8), то есть
Тогда
Вычисляем по теореме косинусов для треугольника, получаем,
что
Тогда для этого вырожденного четырехугольника имеем
Полученное соотношение называется теоремой М. Стюарта.
Задача №4.
Получить из теоремы Стюарта формулу длины медианы треугольника.
Решение.
Если , тогда
Квадрат медианы равен четверти суммы удвоенных квадратов сторон треугольника, заключающих медиану, минус квадрат третьей стороны треугольника.
Задача №5.
Получить из теоремы Стюарта формулу длины биссектрисы треугольника.
Решение.
Если – биссектриса, то по свойству биссектрис в треугольнике
и так как , то
Квадрат биссектрисы треугольника равен разности произведений сторон треугольника, заключающих биссектрису, и отрезков противоположной стороны, на которые она разделена биссектрисой.
Заключение
В данной работе получены следующие результаты:
-
сформулированы и доказаны две теоремы косинусов для четырехугольника;
-
с использованием доказанной теоремы доказана теорема Птолемея;
-
доказана теорема Стюарта;
-
получены два следствия из теоремы Стюарта: формула длины медианы и формула длины биссектрисы;
-
приведен пример использования теоремы косинусов для четырехугольника при решении задач.
Литература
-
Атанасян Л.С. ГЕОМЕТРИЯ. 7-9 кл. Москва, Издательство «Просвещение», 2006г.
-
Атанасян Л.С. ГЕОМЕТРИЯ. 10-11 кл. Москва, Издательство «Просвещение», 2006г.
-
Понарин Я.П. Элементарная геометрия в 3-х томах. Том 1. Планиметрия, преобразования плоскости. Москва, Издательство МЦНМО, 2004г.
-
Интернет-источник «Википедия» https://ru.wikipedia.org/wiki/
-
Единая коллекция цифровых образовательных ресурсов https://school-collection.edu.ru
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Библиографическое описание:
Гульманов, Н. К. Теорема косинусов для четырехугольника в терминах рациональной тригонометрии / Н. К. Гульманов, С. С. Айкеев, Н. А. Марчук. — Текст : непосредственный // Молодой ученый. — 2021. — № 11 (353). — С. 1-4. — URL: https://moluch.ru/archive/353/79187/ (дата обращения: 29.05.2023).
В статье авторы доказывают теорему косинусов для четырехугольников в терминах рациональной тригонометрии.
Ключевые слова:
рациональная тригонометрия, квадрация, апертура, теорема косинусов.
Новая форма тригонометрии, рассматриваемая в данной работе, называется рациональной тригонометрией. Основные понятия и законы рациональной тригонометрии для евклидовой геометрии впервые сформулированы в 2005 г. Н.Дж. Уайлдбергером [1].
Суть новой тригонометрии заключается в переопределении тригонометрических соотношений без использования тригонометрических функций с помощью введения вместо традиционных расстояний и углов таких понятий, как квадрация (quadrance) и апертура (spread). Данный подход позволяет отказаться от использования тригонометрических таблиц и, как следствие, приближенных вычислений, т. е. он зачастую оказывается более точным.
Законы рациональной тригонометрии заменяют теоремы косинусов, синусов и десятки других тригонометрических формул. Наиболее важными новыми законами являются тройная формула для квадрации, закон апертур, закон пересечений и тройная формула для апертур. Теорема Пифагора, переформулированная в терминах рациональной тригонометрии, также играет ключевую роль. Вывод этих законов прост, для освоения требуется знание базовой алгебры школьного уровня.
Несмотря на то, что идеи рациональной тригонометрии вызвали неоднозначное впечатление у математического сообщества, ее методы нашли применение в решении теоретических и практических задач геометрии, комбинаторики, робототехники.
Рациональная тригонометрия решает многие практические проблемы проще и элегантнее, чем классическая тригонометрия, и часто заканчивается ответами, которые наглядно более точны. На самом деле рациональная тригонометрия настолько элементарна, что почти все вычисления могут быть выполнены вручную. Таблицы или калькуляторы не нужны, хотя последние, безусловно, ускоряют вычисления.
Рассмотрим основные понятия рациональной тригонометрии –
квадрации
сторон треугольника:
.
и
апертуры
внутренних углов:
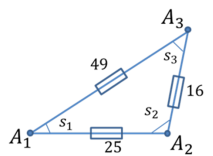
Рис. 1.
Объясним значение этих терминов и покажем, как эти числа были получены.
Квадрация — это квадрат расстояния между двумя точками. Если расстояние
между точками с заданными координатами
и
вычисляется по формуле:
то квадрация между точками
и
вычисляется по формуле:
С этой точки зрения квадрация является более фундаментальной величиной, поскольку он не включает функцию квадратного корня. На рисунке 1 маленькие прямоугольники вдоль сторон треугольника указывают на то, что измеряется квадрация, а не расстояние.
Апертура измеряет «разделение» двух пересекающихся прямых, т. е. насколько «далеко разбросаны» прямые друг от друга. Исторически существует ряд решений этой проблемы.
Рис. 2.
Наиболее знакомым является нахождение угла между прямыми (или нахождение разделения двух линий). Есть разные подходы к вопросу о том, как измерить разделение двух линий. Один из них является определение апертуры угла между прямыми. Возьмем любую точку
прямой
, затем опустим перпендикуляр из точки
на прямую
(см. Рис. 2). Пусть точка
будет основанием перпендикуляра. Апертура угла между прямыми
и
определяется как отношение квадраций
Число
не зависит от выбора первой прямой или выбора точки
на ней. Это уникальное число, принадлежащее интервалу
, однозначно измеряет разделение двух строк.
Вычислим апертуры внутренних углов треугольника
(см. Рис. 3), длины сторон которого равны
,
и
. Пусть точка B будет основанием высоты, опущенной из вершины
до прямой
, и пусть
и
.
Рис. 3.
Применяя теорему Пифагора для прямоугольных треугольников
и
, получим следующие равенства:
Решая систему, состоящую из этих двух уравнений, получаем, что:
Далее получаем:
Аналогично находим, что:
Справедливы следующие законы рациональной тригонометрии.
1.
Тройная формула для квадрации.
Три точки коллинеарны тогда и только тогда, когда
2.
Теорема Пифагора.
Треугольник
— прямоугольный тогда и только тогда, когда
3.
Закон апертуры.
Для любого треугольника
выполняется равенство
4.
Закон пересечений.
Для любого треугольника
справедливо
5.
Тройная формула апертур.
Для любого треугольника
выполняется равенство
Эти формулы связаны интересным образом, и их вывод достаточно прост. Существует также множество альтернативных формулировок этих законов, а также обобщений для четырех квадраций и апертур, которые становятся важными при изучении четырехугольников.
Сформулируем и докажем теорему косинусов для четырехугольника [2–4] в терминах рациональной тригонометрии.
Рассмотрим четырехугольник
(см. Рис. 4).
Рис. 4.
Пусть
,
,
,
и
будут квадрациями сторон
,
,
,
и диагонали
соответственно и пусть
и
будут апертурами углов
и
соответственно. Применяя закон пересечений для треугольников
и
получаем:
Полученное соотношение между квадрациями сторон четырехугольника назовем теоремой косинусов для четырехугольника в терминах рациональной тригонометрии.
Литература:
1. Wildberger N. J. Divine Proportions: Rational Trigonometry to Universal Geometry. — Sydney, 2005
2. Коксетер Г. С. М., Грейтцер С. П. Новые встречи с геометрией. М., 1978. (Серия Библиотека математического кружка)
3. Ceргeeв И. Н. Примeни мaтeмaтику. / Ceргeeв И. Н., Oлexник C. Н., Гaшкoв C. Б. — Мocквa: Нaукa, 1989 — C. 240
4. Шыныбeкoв A. Н. Гeoмeтрия: учeбник для 9 клacca oбщeoбрaзoвaтeльныx шкoл. / Шыныбeкoв A. Н. — Aлмaты: Aтaмурa, 2005. — C. 224
Основные термины (генерируются автоматически): рациональная тригонометрия, теорема косинусов, апертура, прямая, тройная формула, апертура угла, сторона треугольника, термин, треугольник.














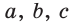
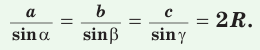
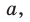
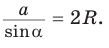
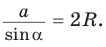
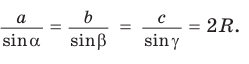
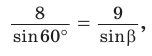
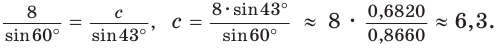
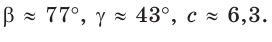


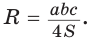
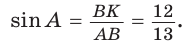
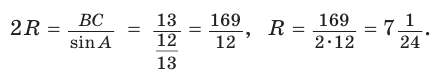
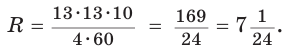
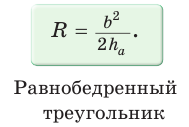
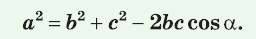
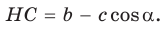
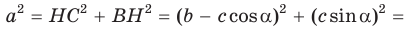
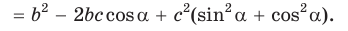
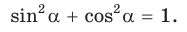
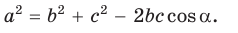
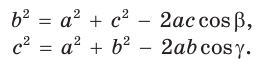
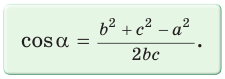
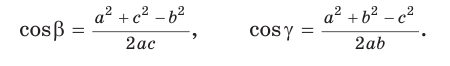

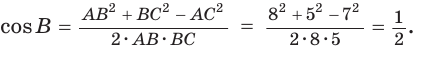
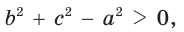 то
то 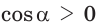 и угол
и угол 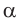 острый;
острый;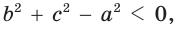 то
то 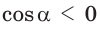 и угол
и угол 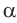 тупой;
тупой; то
то 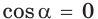 и угол
и угол 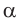 прямой.
прямой.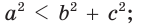
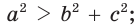
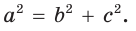
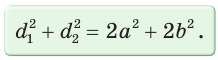
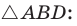
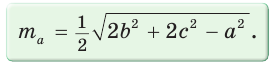
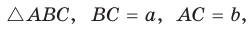
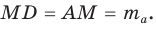
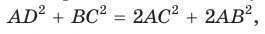
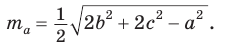
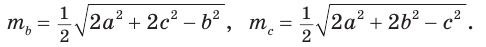
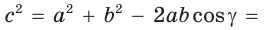
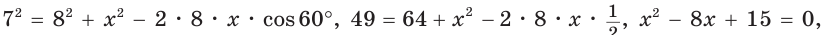
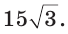
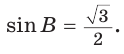
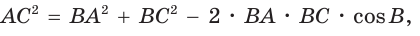
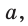
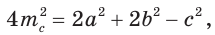
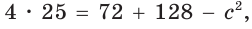
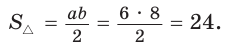
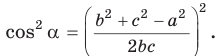
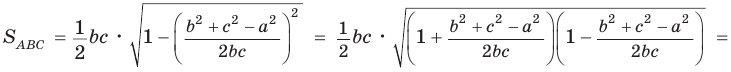
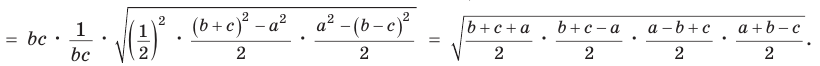
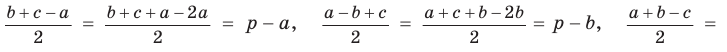
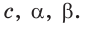
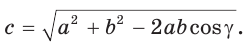
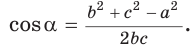
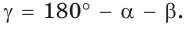
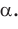
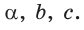
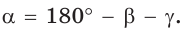
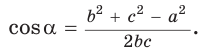
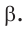
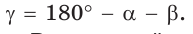
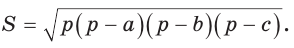
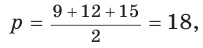
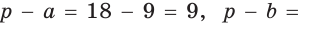
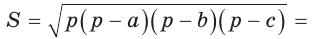
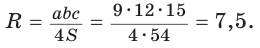
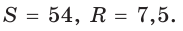
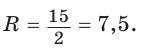
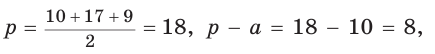
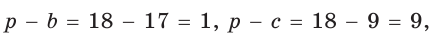
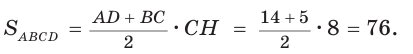
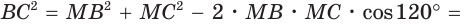
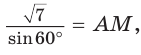
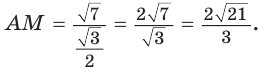
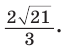
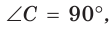
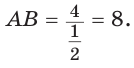
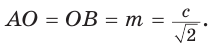
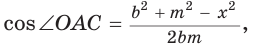
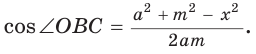
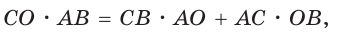
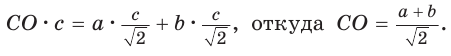
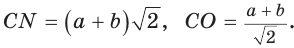
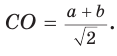
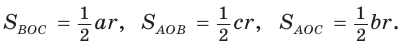
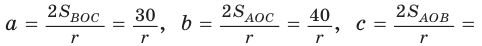
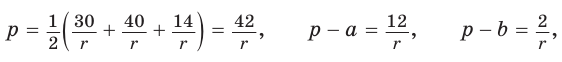
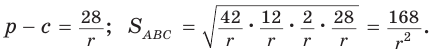
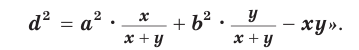
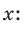
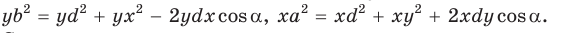
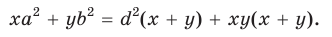
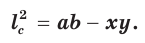
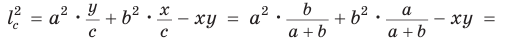
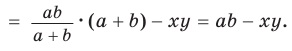
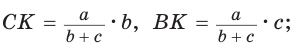
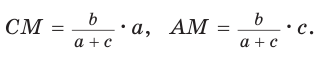
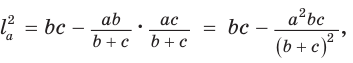
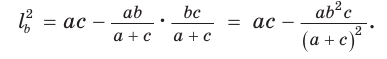
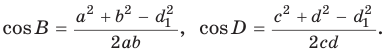
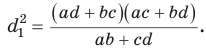
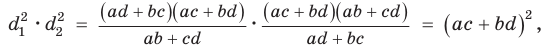
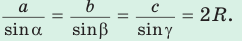
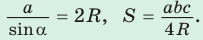
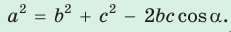
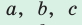 — стороны треугольника и с — большая сторона. Если
— стороны треугольника и с — большая сторона. Если 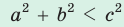 , то треугольник тупоугольный, если
, то треугольник тупоугольный, если 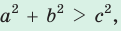 то треугольник остроугольный, если
то треугольник остроугольный, если 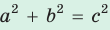 , то треугольник прямоугольный.
, то треугольник прямоугольный.