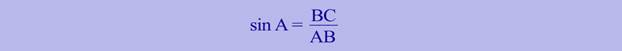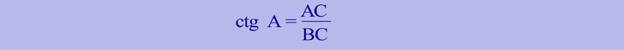Вспомним,
что синусом угла называется ордината точки , полученной поворотом точки вокруг начала координат на угол .
Косинусом угла называется абсцисса точки , полученной поворотом точки вокруг начала координат на угол .
Тангенсом угла называется отношение синуса угла к его косинусу.
Котангенсом угла называется отношение косинуса угла к его синусу.
Теперь приступим к рассмотрению новой темы. Итак,
пусть на координатной плоскости изображена единичная окружность с центром в
начале координат. Точка совершает поворот против часовой стрелки на угол
и оказывается в точке . По определению синуса и косинуса можем сказать,
что абсцисса точки равна , а ордината – . Затем точка совершает поворот на угол , противоположный углу , и оказывается в точке .
Тогда абсцисса точки равна , а ордината равна ? Верно.
Посмотрите на угол . Ось делит
его пополам, а значит, точки и симметричны относительно оси . Тогда абсциссы этих точек совпадают, а ординаты
имеют противоположные значения, то есть можем записать, что , а . Сразу отметим, что формулы
и справедливы при любых значениях .
А что можно сказать про тангенс противоположных углов? По
определению тангенса угла можем записать, что . По формуле числитель запишем как , по формуле знаменатель запишем как : . Таким образом, мы получили, что . Отметим, что здесь , , так как ранее мы с вами говорили, что тангенс этих углов не
определён.
Как быть с котангенсом противоположных углов? По определению
котангенса угла запишем: . По формуле числитель запишем как , а знаменатель по формуле запишем как : . Таким образом, получили, что . Здесь , , так как котангенс этих углов не определён.
Полученные формулы позволяют перейти от вычисления синуса,
косинуса, тангенса и котангенса отрицательных углов к вычислению их значений
для положительных углов.
Давайте найдём , , , .
Итак, вычислим . Воспользуемся формулой и запишем .
По формуле : .
По формуле : .
И вычислим . Воспользуемся формулой и запишем .
А теперь выполним несколько заданий.
Задание первое. Вычислите:
а) ; б) ; в) ; г) .
Решение.
Второе задание. Упростите
выражения: а) ; б) ; .
Решение.
Видеоурок косинус угла
ТРИГОНОМЕТРИЯ | Синус, Косинус, Тангенс, Котангенс
Геометрия 8. Урок 11- Синус, Косинус, Тангенс и Котангенс угла в прямоугольном треугольнике.
Геометрия 8 класс. Синус, косинус, тангенс и котангенс острого угла прям-ка.
Главная > Алгебра 10 класс > Косинус угла
Косинус угла — видеоурок
Видеоурок предназначен для учеников 10 классов. На этом видео уроке по алгебре подробно объясняется понятие косинуса угла. Также определяем знак косинуса на единичной окружности.
Содержание:
- § 1 Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника
- § 2 Решение задачи по теме урока
§ 1 Синус, косинус, тангенс и котангенс острого угла прямоугольного треугольника
В этом уроке мы познакомимся с такими понятиями, как синус, косинус, тангенс и котангенс острого угла в прямоугольном треугольнике, выведем несколько тригонометрических формул, а также рассмотрим решение задачи.
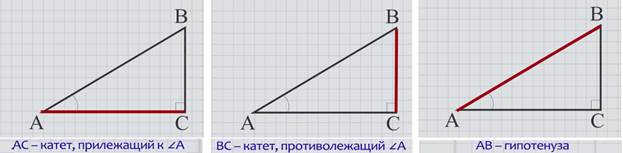
Начертим прямоугольный треугольник АВС с прямым углом С.
Сторона треугольника АС является катетом, прилежащим к углу А, сторона ВС – катетом, противолежащим углу А, АВ – гипотенуза.
Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе. Обозначается sin A.
Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе. Обозначается: cos A.
Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему катету. Обозначается tg А.
Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему катету. Обозначается сtg А.
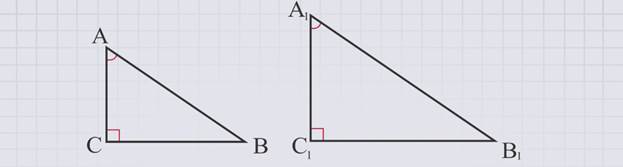
Докажем, что если острый угол одного прямоугольного треугольника равен острому углу другого прямоугольного треугольника, то синусы, косинусы и тангенсы этих углов равны.
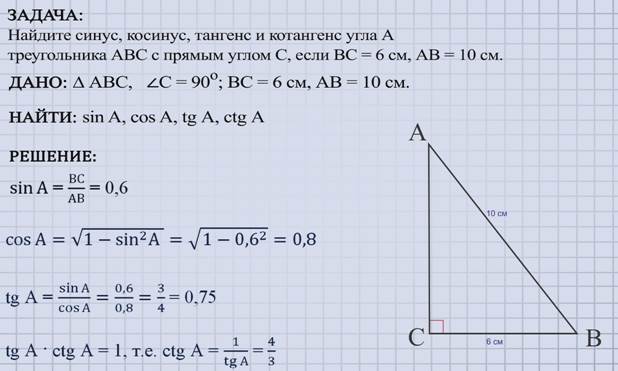
§ 2 Решение задачи по теме урока
В этом уроке мы познакомились с синусом, косинусом, тангенсом и котангенсом острого угла в прямоугольном треугольнике, вывели тригонометрические формулы и решили задачу, используя полученные знания.
Список использованной литературы:
- Л.С. Атанасян. Учебник. 8 класс.
- Н.Ф. Гаврилова. Поурочные разработки по геометрии. 8 класс. – Москва: «Вако», 2005.
- Л.С. Атанасян и др. Методические рекомендации к учебнику. – Москва: «Просвещение», 2001.
- Д.А. Мальцева. Математика. 9 класс. ГИА 2014. – Москва: Народное образование, 2013.
- О.В. Белицкая. Геометрия. 8 класс. Тесты. – Саратов: «Лицей», 2009.
- С.П. Бабенко, И.С. Маркова. Геометрия 8. Комплексная тетрадь для контроля знаний. – Москва: «Аркти», 2014.
Использованные изображения: