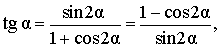Косинус двойного угла, формула
Данная формула позволяет найти Косинус двойного угла зная синус и косинус этого угла по отдельности:
[
cos(2α) = cos^2(α) — sin^2(α)
]
или
[
cos(2α) = 1 — 2sin^2(α)
]
или
[
cos(2α) = 2cos^2(α) — 1
]
Вычислить, найти косинус двойного угла, по формуле (1)
| α° (градусов) | α´ (минут) | α˝ (секунд) |
Вычислить
нажмите кнопку для расчета
Косинус двойного угла |
стр. 221 |
|---|
См. также:
Косинус двойного угла
В процессе решения задач с преобразованием тригонометрических функций бывает необходимо преобразовать значение двойного угла в выражение, в котором все члены имеют аргумент с одинарным его значением. Например, косинус два альфа необходимо преобразовать в выражение, в котором аргументом тригонометрической функции является альфа (одинарный угол). Ниже приведены тригонометрические преобразования косинуса с двойным аргументом функции.
Формулы косинуса двойного угла
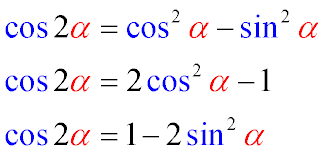
Далее приведены формулы (тождества) для преобразования косинуса двойного угла.
Косинус двойного угла равен разности квадрата косинуса одинарного угла и квадрата синуса этого угла
Косинус двойного угла равен удвоенному квадрату косинуса одинарного угла минус единица
Косинус двойного угла равен единице минус двойной синус квадрат одинарного угла
Зачем это нужно.
Если представить выражение cos 120 как косинус двойного угла
cos 120º = cos (2 * 60º)
оказывается, можно получить и точное значение для этого угла, применяя указанные выше формулы.
cos 120º = cos (2 * 60º)
cos 120º = 2 cos2 60º — 1
Мы привели косинус угла, значение которого мы «не знаем», к значению, которое нам известно.
Поскольку значение cos 60 = 1/2 , то вычислим полученное выражение:
2 cos2 60º — 1 = 2 (1/2)2 — 1 = 2 х 1/4 — 1 = -1/2
таким образом
cos 120º = -1/2
По аналогии, применяя формулы косинуса двойного угла, мы можем как решать тригонометрические уравнения, так и находить значения двойных углов тригонометрических функций на основании уже известных нам значений.
См. также:
0
Тригонометрические формулы понижения степени sin cos tg |
Описание курса
| Многоугольники
Автор: Виктория Андрианова, менеджер кафедры математики АПО.
Одна из моих учениц обучается в классе «Математическая вертикаль». Рассказала недавно, что начали изучать тригонометрию. Начало 9 класса и сразу тригонометрия. Так еще и на уроке геометрии. Сначала не поняла, начала разбираться в программе. И… мне захотелось этим поделиться.
Как показал опрос подписчиков нашей группы «Олимпиады по математике», большинству тригонометрические функции либо выводили через окружность единичного радиуса, либо вообще не выводили.
Я хочу показать достаточно простой и красивый способ их вывода через геометрию.
Классическое доказательство
Не берусь судить за все школы, но мне в 9 классе, как и большинству, все показывали через окружность с радиусом 1. Давайте сначала разберем это доказательство.
Косинус разности и косинус суммы
Чтобы вывести формулу косинуса суммы, отметим углы a и b так, как показано на рисунке ниже.
Из определений синуса и косинуса узнаем координаты точек А и В. Тогда вектор ОА равен (cos a, sin a), а ОВ равен (cos b, sin b). Также известно, что длины этих векторов равны 1. Давайте запишем скалярное произведение этих вектором двумя различными способами. Напомню необходимые формулы.
Тогда |OA|*|OB|*cos(a-b) = cos a * cos b + sin a * sin b. Но |ОА| = 1 и |ОВ| = 1.
Следовательно, cos(a-b) = cos a * cos b + sin a * sin b.
Формула для косинуса суммы доказывается аналогичным образом.
cos(a+b) = cos a * cos b — sin a * sin b.
Синус разности и синус суммы
Формулы синусов доказываются, когда мы уже вывели формулы для косинусов. Нужно только воспользоваться формулой приведения.
Формула синуса суммы доказывается подобным образом.
Доказательство через геометрию
Для начала давайте разберемся, что если у прямоугольного треугольника гипотенуза равна 1, то его катеты будут равны косинусу и синусу соответствующего угла.
Отсюда легко вывести основное тригонометрическое тождество. Достаточно записать теорему Пифагора для данного треугольника.
Косинус суммы
Когда мы разобрались со сторонами прямоугольного треугольника с единичной гипотенузой, выведем формулу косинуса суммы. Будем пользоваться следующей картинкой
Рассмотрим прямоугольный треугольник АНВ. В нем гипотенуза равна 1. Тогда длина отрезка АН является искомым cos (a+b). АН найдем путем вычитания из длины отрезка AD отрезок HD.
АС = cos (a) из треугольника АВС. Теперь мы можем найти АD из прямоугольного треугольника ACD. АD катет, прилежащий к углу b. Поэтому AD = AC * cos (b) = cos (a) * cos (b).
Заметим далее, что HD = BE (т.к. HDEB прямоугольник). ВС = sin (a) (из треугольника АВС). Тогда ВЕ = ВС * sin (b) = sin (a) * sin (b). НD = sin (a) * sin (b).
Отсюда искомый АН = cos (a+b) = cos (a) * cos (b) — sin (a) * sin (b).
Чтобы вывести формулу для косинуса разности, достаточно вместо угла b подставить угол -b.
cos (a-b) = cos (a) * cos (b) — sin (a) * sin (-b) = cos (a) * cos (b) +sin (a) * sin (b).
Синус суммы
Теперь выведем формулу синуса суммы при помощи той же картинки.
Синусом угла a+b будет отрезок ВН. Найдем его как сумму ЕС и CD.
ЕС = ВС * cos b. ВС = sin a. Тогда ЕС = sin (a) * cos (b).
CD = AC * sin b. AC = cos a. Отсюда CD = sin (b) * cos (a).
Наконец выразим ВН. ВН = sin (a+b) = sin (a) * cos (b) + sin (b) * cos (a).
Ну, а чтобы вывести синус разности, опять подставим в уже имеющуюся формулу угол -b.
sin (a-b) = sin (a) * cos (-b) + sin (-b) * cos (a) = sin (a) * cos (b) -sin (b) * cos (a).
Синус и косинус двойного угла
Конечно, зная формулы косинуса и синуса суммы, можно выразить формулы и для двойных углов. Но я предлагаю вам воспользоваться следующими картинками и вывести их самостоятельно.
Хочу заметить, что треугольники АВС в обоих случаях равны.
Сегодня будет максимально информативный блок на запоминание формул!
Представляю тебе формулы, которые чаще всего помогают выполнить числовые преобразования.
Синус двойного угла:
sin2α = 2sinα⋅cosα
Косинус двойного угла:
cos2α = cos2α − sin2α = 2cos2α − 1 = 1 − 2sin2α
Тангенс двойного угла:
tg2α = 2tgα/(1 − tg2α)
Аналогично для тройного угла!
👉🏻 Распознать, что требуются именно эти, а не какие-нибудь другие формулы очень просто: если ты видишь выражения сильно похожие на косинус, синус, тангенс двойных углов, то смело можно свернуть выражение в одну из этих формул в первую очередь ✨
Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter. Мы обязательно поправим!
Основные тригонометрические формулы
Содержание
 Связи между тригонометрическими функциями одного угла Связи между тригонометрическими функциями одного угла |
 Тригонометрические функции суммы и разности двух углов Тригонометрические функции суммы и разности двух углов |
 Тригонометрические функции двойного угла Тригонометрические функции двойного угла |
 Формулы понижения степени для квадратов тригонометрических функций Формулы понижения степени для квадратов тригонометрических функций |
 Формулы понижения степени для кубов синуса и косинуса Формулы понижения степени для кубов синуса и косинуса |
 Выражение тангенса угла через синус и косинус двойного угла Выражение тангенса угла через синус и косинус двойного угла |
 Преобразование суммы тригонометрических функций в произведение Преобразование суммы тригонометрических функций в произведение |
 Преобразование произведения тригонометрических функций в сумму Преобразование произведения тригонометрических функций в сумму |
 Выражение тригонометрических функций через тангенс половинного угла Выражение тригонометрических функций через тангенс половинного угла |
 Тригонометрические функции тройного угла Тригонометрические функции тройного угла |
Связи между тригонометрическими функциями одного угла
Тригонометрические функции суммы и разности двух углов
Тригонометрические функции двойного угла
| Формула | Название формулы |
| sin 2α = 2 sin α cos α | Синус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
Косинус двойного угла |
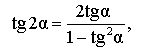 |
Тангенс двойного угла |
| Синус двойного угла |
| sin 2α = 2 sin α cos α |
| Косинус двойного угла |
|
cos 2α = cos 2α – sin2α cos 2α = 2cos 2α – 1 cos 2α = 1 – 2sin 2α |
| Тангенс двойного угла |
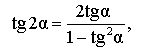 |
Формулы понижения степени для квадратов тригонометрических функций
| Формула | Название формулы |
|
Выражение квадрата синуса через косинус двойного угла |
|
|
Выражение квадрата косинуса через косинус двойного угла |
|
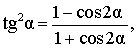 |
Выражение квадрата тангенса через косинус двойного угла |
Формулы понижения степени для кубов синуса и косинуса
| Формула | Название формулы |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
|
Выражение куба синуса через синус угла и синус тройного угла |
|
Выражение куба косинуса через косинус угла и косинус тройного угла |
Выражение тангенса через синус и косинус двойного угла
Преобразование суммы тригонометрических функций в произведение
| Сумма синусов |
|
|
| Разность синусов |
|
|
| Сумма косинусов |
|
|
| Разность косинусов |
|
|
| Сумма тангенсов |
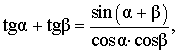 |
| Разность тангенсов |
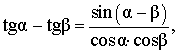 |
Преобразование произведения тригонометрических функций в сумму
| Произведение синусов |
|
|
| Произведение косинусов |
|
|
| Произведение синуса и косинуса |
|
|
Выражение тригонометрических функций через тангенс половинного угла
| Формула | Название формулы |
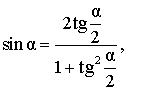 |
Выражение синуса угла через тангенс половинного угла |
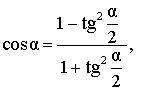 |
Выражение косинуса угла через тангенс половинного угла |
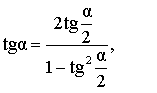 |
Выражение тангенса угла через тангенс половинного угла |
Тригонометрические функции тройного угла
| Формула | Название формулы |
| sin 3α = 3sin α – 4sin3α | Синус тройного угла |
| cos 3α = 4cos3α –3cos α | Косинус тройного угла |
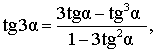 |
Тангенс тройного угла |
| Синус тройного угла |
| sin 3α = 3sin α – 4sin3α |
| Косинус тройного угла |
| cos 3α = 4cos3α –3cos α |
| Тангенс тройного угла |
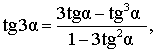 |