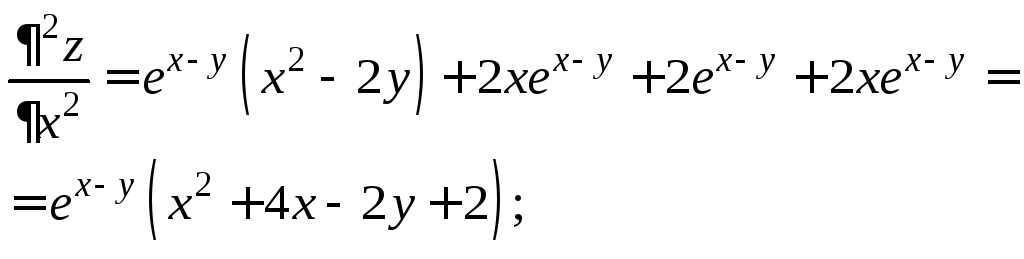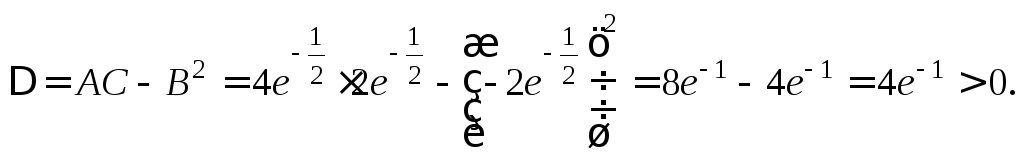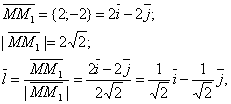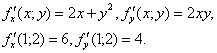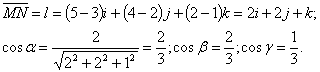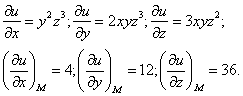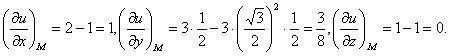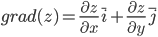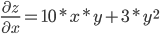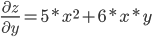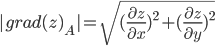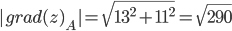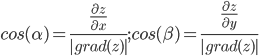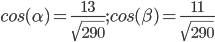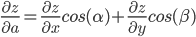Как найти косинусы градиента

Производной
функции
в точке
по направлению
называется предел

где

если предел
существует.

Если функция
дифференцируема, то производная по
направлению вычисляется по формуле

(18.31)

где
– направляющие косинусы вектора

В частности, если
– функция двух переменных, то формула
(18.31) производной по направлению примет
вид:

(18.32)

где
– угол между вектороми осьюОх.

Градиентомфункциив точкеназывается вектор

(18.33)

или, то же самое,

Связь между
градиентом функции и производной по
направлению устанавливает формула

где
– угол между векторамии

Градиент функции
указывает направление наибыстрейшего
возрастания функции. Наибольшее значение
производной
достигаемое в направление градиента,
равно

В
частности, если
– функция двух переменных, то

Пример
1. Найти
производную функции
в точкепо направлению вектораобразующего с положительным направлением
осиОх
угол

Решение.
Используя
формулу (18.32),
вычислим
частные производные функции z
в точке A:

Так
как
то

Пример
2. Найти
производную функции
в точкепо направлению к точке

Решение.
Найдем вектор

Его направляющие
косинусы равны:

Найдем
значения частных производных функции
u
в точке

Тогда
по формуле (18.31) получим:

Пример
3. Найти
длину и направление (указать направляющие
косинусы) градиента функции
в точке

Решение.
Вычислим
частные производные функции u
в точке М.

Используем
формулу (18.33) при условии, что частные
производные вычисляем в заданной точке

Тогда

Вычисляем
длину полученного вектора:

Используем
тот факт, что направляющие косинуса
равны координатам единичного вектора
направления, определяемого вектором
дроби. Поэтому

Задания

I уровень

1.1.Найдите
производную функциив точкепо направлению вектора

1)

2)

3)

4)

1.2.Найдите
производную функциив точкепо направлению вектора

1.3.Найдите
величину и направление градиента функциив точке

1)

2)

3)

4)

5)

II уровень

2.1.Найдите
производную указанной функции в точкепо направлению к точке

1)

2)

3)

4)

2.2.Найдите
величину и направление градиента функциизаданной неявно, в точке

1)

2)

3)

4)

2.3.Найдите
угол между градиентами функциив точкахи

2.4.Найдите
производную функциив точкев направленииперпендикулярном к линии уровня,
проходящей через эту точку.

III уровень

3.1. Найдите
градиент функциив точкахи

3.2.Определите,
в каких точках градиент функцииудовлетворяет условию:

1) параллелен оси
Оу;

2) перпендикулярен
оси Оу;

3) равен нулю.

3.3.Выясните,
в каких точках градиент функцииудовлетворяет условию:

1) перпендикулярен
прямой
2)
равен нулю.

3.4.Определите,
в каких точках выполнено равенствоесли

3.5.Найдите
градиент функциизаданной неявно уравнением:

1)
2)3)

3.6.Определите
направление наибыстрейшего возрастания
функции:

1)
2)

3)
4)

18.8. Экстремумы функций двух переменных

Функция
имеет в точкелокальный максимум (минимум),
если существует такая-окрестность
точкиМ₀, что для всех точекиз этой окрестности (отличных отМ₀)
выполняется неравенство

Максимум и минимум
функции называются ее экстремумами(локальными), а точкаМ₀, в
которой достигается экстремум, называетсяточкой экстремума.

Необходимое
условие экстремума: если
в точке
дифференцируемая функцияимеет экстремум, то ее частные производные
в этой точке равны нулю:

(18.34)

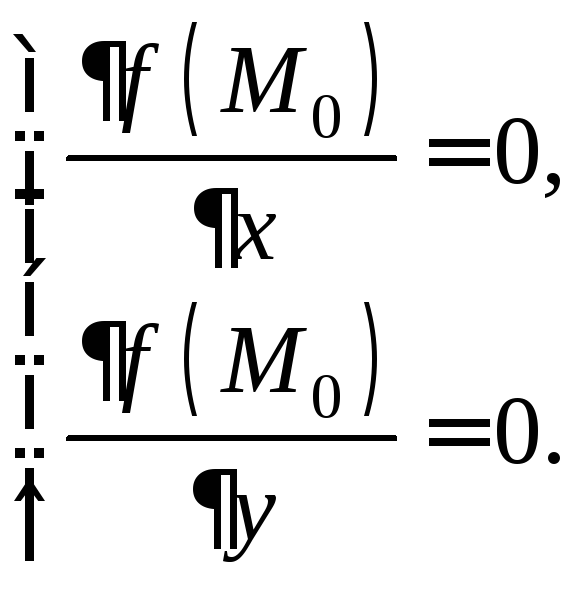
Точки, в которых
частные производные существуют и равны
нулю, называются стационарными.

Точки из области
определения функции, в которых частные
производные равны нулю или не существуют,
называются критическими точками.

Не всякая критическая
точка является точкой экстремума.

Достаточное
условие экстремума. Пусть– стационарная точка дважды непрерывно
дифференцируемой функцииОбозначим:

Тогда:

1) если
то функция имеет в точкеМ₀локальный экстремум (максимум прии минимум при);

2) если
то в точкеМ₀функция не имеет
экстремума;

3) если
то в точкеМ₀функция может
иметь локальный экстремум, а может и не
иметь его (нужны дополнительные
исследования).

Допустим, что
функция f(x;y) определена на
некотором множестве

Число Сназываютнаибольшим значением функции(глобальный максимум) на множестве
D, если

записывают так:

Число сназываютнаименьшим значением функции(глобальным минимумом) на множествеD, если

записывают так:

Теорема
Вейерштрасса. Непрерывная на
замкнутом ограниченном множествефункциядостигает на этом множестве своего
наибольшего и наименьшего значений.

Для нахождения
наибольшего и наименьшего значений
функции в области
нужно:

1) найти критические
точки функции, принадлежащие D, и
вычислить значение функции в них;

2) найти наибольшее
и наименьшее значения функции на границах
области

3) сравнить все
полученные значения функции и выбрать
из них наибольшее и наименьшее.

Если область
определения функции не является
замкнутой, то для нахождения наибольшего
и наименьшего значений функции необходимо:

1) найти критические
точки функции, принадлежащие D;

2) исследовать
найденные критические точки на экстремум
(локальный);

3) вычислить значения
функции в точках локального максимума
(минимума) и отобрать среди них наибольшее
(наименьшее).

Пример
1. Исследовать
на экстремум функцию

Решение.
Находим частные производные первого
порядка:

Приравниваем их
к нулю, чтобы найти стационарные точки:

Решая
систему уравнений, получим:
т. е.

Вычисляем
значения частных производных второго
порядка в точке М₀:

Тогда
Следовательно, в точкеэкстремума нет.

Пример
2. Найти
экстремум функции

Решение.
Частные
производные первого порядка:

Стационарные
точки:

Частные производные
второго порядка:

Тогда

Получаем:

Поскольку
то в точкефункция имеет минимум:

Пример
3. Найти
наибольшее и наименьшее значения функции
в областиограниченной прямыми

Решение.
1) Вычислим частные производные и найдем
критические точки:

Получим:
– критическая точка, принадлежащая
области

Вычислим в ней
значение функции:

2)
Исследуем функцию z
на границе области
(рис. 18.4).

Рис. 18.4

Уравнение
границы AB:
Подставляем число –3 вместох
в аналитическое задание функции:
где

Исследуем
полученную функцию, как функцию одной
переменной, на наибольшее значение.

Найдем критические
точки:

Получаем
– критическая точка, при этом

Вычисляем
значение функции в точке
и на концах отрезка:

Уравнение
границы BC:
На этом участке уравнение функции имеет
вид:где

Поскольку
то дляполучаем критическую точкуТогда

Уравнение
границы AC:
ТогдагдеКритическая точкапринадлежащая

Вычисляем
значение функции для

3)
Из всех полученных значений z
выбираем наименьшее и наибольшее:

Задания

Соседние файлы в папке Часть 3

• #
• #
• #
• #
• #
• #
• #
• #

Задача 2. Найти косинус угла a между градиентами поля в точках А(1, 2, 2) и В(-3, 1, 0). Решение.

Задача 3. Для функции найти производную по направлению внутренней нормали к цилиндрической поверхности x 2 + z 2 = a 2 + c 2 в точке M 0(a, b, c). Решение. Пусть f(x, y, z) = x 2 + z 2. Данная в условии поверхность – это поверхность уровня для f, проходящая через точку M 0. Имеем Функция f в точке M 0 растет быстрее всего по направлению grad f, значит, по направлению нормали к заданной поверхности.

Исходя из вида функции f, заключаем, что это – направление внешней нормали. Следовательно, единичный вектор внутренней нормали в точке M 0 будет равен

Задача 5. Вычислить поток векторного поля a = (z 2 – x, 1, y 5) через внутреннюю поверхность S: y 2 = 2 x, отсеченную плоскостями: x = 2, z = 0, z = 3. Решение.

Решение. I способ Контур L — окружность радиуса R, лежащая в плоскости z = 3. Выберем ориентацию как показано на рисунке, т. е. против часовой стрелки. Параметрические уравнения окружности имеют вид

II способ. Для вычисления циркуляции по теореме Стокса выберем какую-нибудь поверхность S, натянутую на контур. Естественно в качестве S взять круг, имеющий контур L своей границей. Уравнение поверхности S имеет вид: Согласно выбранной ориентации контура нормаль к поверхности необходимо взять равной

Задача 7. С помощью теоремы Стокса найти циркуляцию векторного поля По сечению x 2 + y 2 + z 2 = R 2 плоскостью z = 0. Решение. По формуле Стокса

Задача 8. Найти поток вектора через часть сферы x 2 + y 2 + z 2 = R 2 , при x ≥ 0, y ≥ 0, z ≥ 0, в направлении внешней нормали. Решение. По определению потока вектора через поверхность, находим

1 0
Градиент направлен по нормали к поверхности уровня (или к линии уровня, если поле плоское).

2 0
Градиент направлен в сторону возрастания функции поля.

3 0
Модуль градиента равен наибольшей производной по направлениювданной точке поля:

Эти свойства дают инвариантную характеристику градиента. Они говорят о том, что вектор gradU указывает направление и величину наибольшего изменения скалярного поля в данной точке.

Замечание 2.1.
Если функция U(x,y) есть функция двух переменных, то вектор

(2.3)

лежит в плоскости oxy.

Пусть U=U(x,y,z) и V=V(x,y,z) дифференцируемых в точке М 0 (x,y,z) функции. Тогда имеет место следующие равенства:

а) grad()= ; б) grad(UV)=VgradU+UgradV;

в) grad(U V)=gradU gradV; г) г) grad = , V ;

д) gradU( = gradU, где , U=U() имеет производную по .

Пример 2.1.
Дана функция U=x 2 +y 2 +z 2 . Определить градиент функции в точке М(-2;3;4).

Решение.
Согласно формуле (2.2) имеем

.

Поверхностями уровня данного скалярного поля являются семейство сфер x 2 +y 2 +z 2 , вектор gradU=(-4;6;8) есть нормальный вектор плоскостей.

Пример 2.2.
Найти градиент скалярного поля U=x-2y+3z.

Решение.
Согласно формуле (2.2) имеем

Поверхностями уровня данного скалярного поля являются плоскости

x-2y+3z=С; вектор gradU=(1;-2;3) есть нормальный вектор плоскостей этого семейства.

Пример 2.3.
Найти наибольшую крутизну подъема поверхности U=x y в точке М(2;2;4).

Решение.
Имеем:

Пример 2.4.
Найти единичный вектор нормали к поверхности уровня скалярного поля U=x 2 +y 2 +z 2 .

Решение.
Поверхности уровня данного скалярного Поля-сфера x 2 +y 2 +z 2 =С (С>0).

Градиент направлен по нормали к поверхности уровня, так что

Определяет вектор нормали к поверхности уровня в точке М(x,y,z). Для единичного вектора нормали получаем выражение

, где

.

Пример 2.5.
Найти градиент поля U= , где и постоянные векторы, r –радиус вектор точки.

Решение.
Пусть

Тогда:
. По правилу дифференцирования определителя получаем

Следовательно,

Пример 2.6.
Найти градиент расстояния , где P(x,y,z) — изучаемая точка поля, P 0 (x 0 ,y 0 ,z 0) — некоторая фиксированная точка.

Решение.
Имеем — единичный вектор направления .

Пример 2.7.
Найти угол между градиентами функций в точке М 0 (1,1).

Решение.
Находим градиенты данных функций в точке М 0 (1,1), имеем

; Угол между gradU и gradV в точке М 0 определяется из равенства

Отсюда =0.

Пример 2.8.
Найти производную по направлению, радиус- вектор равен

(2.4)

Решение.
Находим градиент этой функции:

Подставляя (2.5) в (2.4), получим

Пример 2.9.
Найти в точке М 0 (1;1;1) направление наибольшего изменения скалярного поля U=xy+yz+xz и величину этого наибольшего изменения в этой точке.

Решение.
Направление наибольшего изменения поля указывается вектором grad U(M). Находим его:

И, значит, . Это вектор определяет направление наибольшего возрастания данного поля в точке М 0 (1;1;1). Величина наибольшего изменения поля в этой точке равна

.

Пример 3.1.
Найти векторные линии векторного поля где -постоянный вектор.

Решение.
Имеем так что

(3.3)

Умножим числитель и знаменатель первой дроби на х, второй-на у, третий- на z и сложим почленно. Используя свойство пропорций, получим

Отсюда xdx+ydy+zdz=0, а значит

x 2 +y 2 +z 2 =A 1 , A 1 -const>0. Умножив теперь числитель и знаменатель первой дроби (3.3) на с 1 , второй –на с 2 , третий на с 3 и сложив почленно, получим

Откуда с 1 dx+c 2 dy+c 3 dz=0

И, следовательно, с 1 x+c 2 y+c 3 z=A 2 . A 2 -const.

Искомые уравнения векторных линий

Эти уравнения показывают, что векторные линии получаются в результате пересечения сфер, имеющих общий центр в начале координат, с плоскостями, перпендикулярными вектору . Отсюда следует, что векторные линии являются окружностями, центры которых находятся на прямой, проходящей через начало координат в направлении вектора с. Плоскости окружностей перпендикулярны указанной прямой.

Пример 3.2.
Найти векторную линию поля проходящую через точку (1,0,0).

Решение.
Дифференциальные уравнения векторных линий

отсюда имеем . Решая первое уравнение . Или если ввести параметр t, то будем иметь В этом случае уравнение принимает вид или dz=bdt, откуда z=bt+c 2 .

Если в каждой точке пространства или части пространства определено значение некоторой величины, то говорят, что задано поле данной величины. Поле называется скалярным, если рассматриваемая величина скалярна, т.е. вполне характеризуется своим числовым значением. Например, поле температур.
Скалярное поле задается скалярной функцией точки и = /(М). Если в пространстве введена декартова система координат, то и есть функция трех переменных х, yt z — координат точки М:
Определение. Поверхностью уровня скалярного поля называется множество точек, в которых функция f(M) принимает одно и то же значение. Уравнение поверхности уровня
Пример 1. Найти поверхности уровня скалярного поля
ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению Производная Градиент скалярного поля
Основные свойства градиента
Инвариантное определение градиента
Правила вычисления градиента
-4 Согласно определению уравнением поверхности уровня будет.
Это уравнение сферы (с Ф 0) с центром в начале координат.
Скалярное поле называется плоским, если во всех плоскостях, параллельных некоторой плоскости, поле одно и то же. Если указанную плоскость принять за плоскость хОу, то функция поля не будет зависеть от координаты z, т. е. будет функцией только аргументов х и у,
Плоское поле можно характеризовать помощьюлиний уровня — множестваточек плоскости, в которых функция /(ж, у) имеетодно и тоже значение. Уравнение линии уровня —
Пример 2. Найти линии уровня скалярного поля
Линии уровня задаются уравнениями
При с = 0 получаем пару прямых получаем семейство гипербол (рис. 1).
1.1. Производная по направлению
Пусть имеется скалярное поле, определяемое скалярной функцией и = /(Af). Возьмем точку Afo и выберем направление, определяемое вектором I. Возьмем другую точку М так, чтобы вектор М0М был параллелен вектору 1 (рис. 2). Обозначим длину вектора МоМ через А/, а приращение функции /(Af) — /(Afo), соответствующее перемещению Д1, через Ди. Отношение
определяет среднюю скорость изменения скалярного поля на единицу длины поданному направлению
Пусть теперь стремится к нулю так, чтобы вектор М0М все время оставался параллельным вектору I.
Определение. Если при Д/ О существует конечный предел отношения (5), то его называют производной функции в данной точке Afo поданному направлению I и обозначают символом зг!^ .
Так что, по определению,
Это определение не связано с выбором системы координат, т. е. носит**вариантный характер.
Найдем выражение для производной по направлению в декартовой системе координат. Пусть функция / дифференцируема в точке. Рассмотрим значение /(Af) в точке. Тогда полное приращение функции можно записать в следующем виде:
где а символы означают, что частные производные вычислены в точке Afo. Отсюда
Здесь величины jfi, ^ суть направляющие косинусы вектора. Так как векторы МоМ и I сонаправлены, то их направляющие косинусы одинаковы:
Так как M Afo, осгавая сь все время на прямой, параллельной вектору 1, то углы постоянные потому
Окончательно из равенств (7) и (8) получаем
Эамуан ис 1. Частные производные, являются производными функции и по направлениям координатныхосей ссчлвешне нно-
Пример 3. Найти производную функции
по направлению к точке
Вектор имеет длину. Его направляющие косинусы: По формуле (9) будем иметь
Тот факт, что, означает, что скалярное поле в точке в данном направлении возраста-
Для плоского поля производная по направлению I в точке вычисляется по формуле
где а — угол, образованный вектором I с осью Ох.
Зммчмм 2. Формула (9) для вычисления производной по направлению I в данной точке Afo остается в силе и тогда, когда точка М стремится к точке Мо по кривой, для которой вектор I является касательным в точке
ПрИШр 4. Вычислить производную скалярного поля
в точке Afo(l, 1). принадлежащей параболе по направлению этой кривой (в направлении возрастания абсциссы).
Направлением ] параболы в точке считается направление касательной к параболе в этой точке (рис.3).
Пусть касательная к параболе в точке Afo образует с осью Ох угол о. Тогда откуда направляющие косинусы касательной
Вычислим значения и в точке. Имеем
Теперь по формуле (10) получаем. Найти производную скалярного поля в точке по направлению окружности
Векторное уравнение окружности имеет вид. Находим единичный вектор т касательной к окружности
Точке соответствует значение параметра Значение г в точке Afo будет равно
Отсюда получаем направляющие косинусы касательной к окружности в точке
Вычислим значения частных производных данного скалярного поля в точке
Значит, искомая производная. Градиент скалярного поля
Пусть скалярное поле определяется скалярной функцией которая предполагается дифференцируемой.
Определение. Градиентом скалярного поля » в данной точке М называется вектор, обозначаемый символом grad и и определяемый равенством
Ясно, что этот вектор зависиткак от функции /, так и отточки М, в которой вычисляется ее производная.
Пусгь 1 — единичный вектор в направлении
Тогда формулу дл я производной по направлению можно записать в следующем виде:
.
тем самым производная от функ ии и по направлению 1 равна скалярному произведению градиента функ ии и(М) на орт 1° направления I.
2.1. Основные свойства градиента
Теорема 1. Градиент скалярного поля перпендикулярен к поверхности уровня (или к линии уровня, если поле плоское).
(2)
Проведем через произвольную точку М поверхность уровня и = const и выберем на этой поверхности гладкую кривую L, проходящую через точку М (рис. 4). Пусть I — векгор, касательный к кривой L в точке М.
Так как на поверхности уровня и(М) = и(М|) для любой точки Мj е L, то
С другой стороны, = (gradu, 1°). Поэтому. Это означает, что векторы grad и и 1° ортогональны,
Итак, векгор grad и ортогонален к любой касательной к поверхности уровня в точке М. Тем самым он ортогонален к самой поверхности уровня в точке М.
Теорема 2. Градиент направлен в сторону возрастания функции поля.
Ранее мы доказали, что градиент скалярного поля направлен по нормали к поверхности уровня, которая может быть ориентирована либо в сторону возрастания функции и(М), либо в сторону ее убывания.
Обозначим через п нормальк поверхности уровня, ориентированную в сторону возрастания функции ti(M), и найдем производную функции и в направлении этой нормали (рис. 5). Имеем
Так как по условию рис.5
и поэтому
ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению Производная Градиент скалярного поля
Основные свойства градиента
Инвариантное определение градиента
Правила вычисления градиента
Отсюда следует, что grad и направлен в ту же сторону, что и выбранная нами нормаль п, т. е. в сторону возрастания функции и(М).
Теорема 3. Длина градиента равна наибольшей производной по направлению в данной точке поля,
(здесь шах $ берется по всевозможным направлениям в данной точке М паю).
Имеем
где — угол между векторами 1 и grad п. Так как наибольшее значени
Пример 1. Найти направление наибольшего иэмонония скалярного поля
в точке а также величину этого наибольшего изменения в указанной точке.
Направление наибольшего изменения скалярного поля указывается вектором. Имеем
так что
Этот вектор определяет направление наибольшего возрастания поля в точко. Величина наибольшого изменения поля в этой точке равна
2.2. Инвариантное определение градиента
Величины, характеризующие свойства изучаемого объекта и не зависящие от выбора системы координат, называются инвариантами данного объекта. Например, длина кривой — инвариант этой кривой, а угол касательной к кривой с осью Ох — не инвариант.
Основываясь на доказанных выше трех свойствах градиента скалярного поля, можно дать следующее инвариантное определение градиента.
Определение. Градиент скалярного поля есть вектор, направленный по нормали к поверхности уровня в сторону возрастания функции поля и имеющий длину, равную наибольшей производной по направлению (в данной точке).
Пусть — единичный вектор нормали, направленный в сторону возрастания поля. Тогда
Пример 2. Найти градиент расстояния
— некоторая фиксированная точка, a M(x,y,z) — текущая.
4 Имеем
где — единичный вектор направления. Правила вычисления градиента
где с — постоянное число.
Приведенные формулы получаются непосредственно из определения градиента и свойств производных.
По правилу дифференцирования произведения
Доказательство аналогично доказательству свойства
Пусть F(и) — дифференцируемая скалярная функция. Тогда
4 По определению фадиента имеем
Применим ко всем слагаемым правой части правило дифференцирования сложной функции. Получим
В частности,
Формула (6) следует из формулы
Пример 3. Майти производную по направлению радиус-воктора г от функции
По формуле (3)
а по формуле В результате получим, что
Пример 4. Пусть дано плоское скалярное поле
— расстояния от некоторой точки плоскости до двух фиксированных точек этой плоскости.
Рассмотрим произвольный эллипс с фокусами Fj и F] и докажем, что всякий луч свота, вышедший из одного фокуса эллипса, после отражения от эллипса попадает в другой его фокус.
Линии уровня функции (7) суть
ВЕКТОРНЫЙ АНАЛИЗ Скалярное поле Поверхности и линии уровня Производная по направлению Производная Градиент скалярного поля
Основные свойства градиента
Инвариантное определение градиента
Правила вычисления градиента
Уравнения (8) описывают семейство эллипсов с фокусами в точках F) и Fj.
Согласно результату примера 2 имеем
Тем самым градиент заданного поля равен вектору PQ диагонали ромба, построенного на ортах г? и радиус-векторов. проведенных к точке Р(х, у) из фокусов F| и Fj, и значит, лежит на биссектрисе угла можду этими радиус-векторами (рис. 6). По тооромо 1 градиент PQ
перпендикулярен к эллипсу (8) в точке. Следова- Рис.6
тельно. нормаль к эллипсу (8) в любой ого точке делит
пополам угол между радиус-векторами, проведенными в эту точку. Отсюда и из того, что угол падения равон углу отражения, получаем: луч света, вышедший из одного фокуса эллипса, отразившись от него, непременно попадает в другой фокус этого эллипса.

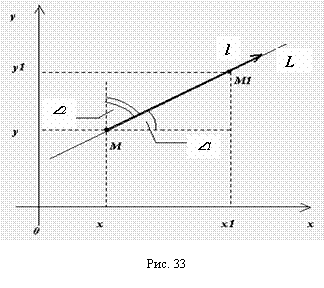
 Пусть Z=F(M) – функция, определенная в некоторой окрестности точки М(у; х); L={Cos; Cos} – единичный вектор (на рис. 33 1=, 2=); L – направленная прямая, проходящая через точку М; М1(х1; у1), где х1=х+х и у1=у+у – точка на прямой L; L – величина отрезка ММ1; Z=F(х+х, у+у)-F(X, Y) – приращение функции F(M) в точке М(х; у).

Определение. Предел отношения , если он существует, называется Производной функции Z=F(M) в точке M(X; Y) по направлению вектора L .

Обозначение.

Если функция F(M) дифференцируема в точке М(х; у), то в точке М(х; у) существует производная по любому направлению L, исходящему из М; вычисляется она по следующей формуле:

  (8)

Где Cos И Cos — направляющие косинусы вектора L.

Пример 46. Вычислить производную функции Z=X2+Y2X в точке М(1; 2) по направлению вектора ММ1, где М1 – точка с координатами (3; 0).

Решение. Найдем единичный вектор L, имеющий данное направление:

Откуда Cos=; Cos=-.

Вычислим частные производные функции в точке М(1; 2):

По формуле (8) получим

Пример 47. Найти производную функции U = Xy2Z3 в точке М(3; 2; 1) В направлении вектора MN, где N(5; 4; 2).

Решение. Найдем вектор  и его направляющие косинусы:

Вычислим значения частных производных в точке М:

Следовательно,

Определение. Градиентом Функции Z=F(M)  в точке М(х; у) называется вектор, координаты которого равны соответствующим частным производным  и, взятым в точке М(х; у).

Обозначение.

Пример 48. Найти градиент функции Z=X2+2Y2-5 в точке М(2; -1).

Решение. Находим частные производные:  и их значения в точке М(2; -1):

Пример 49. Найти величину и направление градиента функции  в точке

Решение. Найдем частные производные и вычислим их значения в точке М:

Следовательно,

Аналогично определяется производная по направлению для функции трех переменных U=F(X, Y, Z), выводятся формулы

Вводится понятие градиента

Подчеркнем, что Основные свойства градиента функции важнее для анализа экономических оптимизационных задач: в направлении градиента функция возрастает. В экономических задачах находят применение следующие свойства градиента:

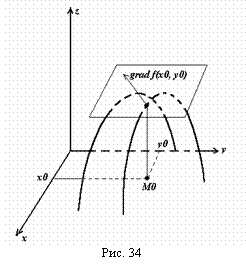
1) Пусть задана функция Z=F(X, Y), имеющая частные производные в области определения. Рассмотрим некоторую точку М0(х0, у0) из области определения. Значение функции в этой точке пусть равно F(X0, Y0). Рассмотрим график функции. Через точку (X0, Y0, F(X0, Y0)) трехмерного пространства проведем плоскость, касательную к поверхности графика функции. Тогда градиент функции, вычисленный в точке (х0, у0), рассматриваемый геометрически как вектор, приложенный в точке (X0, Y0, F(X0, Y0)), будет перпендикулярен касательной плоскости. Геометрическая иллюстрация приведена на рис. 34.

2)  Градиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого возрастания функции в точке М0. Кроме того, любое направление, составляющее с градиентом острый угол, является направлением роста функции в точке М0. Другими словами, малое движение из точки (х0, у0) по направлению градиента функции в этой точке ведет к росту функции, причем в наибольшей степени.

Рассмотрим вектор, противоположный градиенту. Он называется Антиградиентом. Координаты этого вектора равны:

Антиградиент функции F(X, Y) в точке М0(х0, у0) указывает направление наиболее быстрого убывания функции в точке М0. Любое направление, образующее острый угол с антиградиентом, является направлением убывания функции в этой точке.

3)  При исследовании функции часто возникает необходимость нахождения таких пар (х, у) из области определения функции, при которых функция принимает одинаковые значения. Рассмотрим множество точек (X, Y) из области определения функции F(X, Y), таких, что F(X, Y)=Const, где запись “Const” означает, что значение функции зафиксировано и равно некоторому числу из области значений функции.

Определение. Линией уровня функции U=F(X, Y) называется линия F(X, Y)=С на плоскости XOy, в точках которой функция сохраняет постоянное значение U=C.

Линии уровня геометрически изображаются на плоскости изменения независимых переменных в виде кривых линий. Получение линий уровня можно представить себе следующим образом. Рассмотрим множество С, которое состоит из точек трехмерного пространства с координатами (X, Y, F(X, Y)=Const), которые, с одной стороны, принадлежат графику функции Z=F(X, Y), с другой  — лежат в плоскости, параллельной координатной плоскости ХОУ, и отстоящей от неё на величину, равную заданной константе. Тогда для построения линии уровня достаточно поверхность графика функции пересечь плоскостью Z=Const и линию пересечения спроектировать на плоскость ХОУ. Проведенное рассуждение является обоснованием возможности непосредственно строить линии уровня на плоскости ХОУ.

Определение. Множество линий уровня называют Картой линий уровня.

Хорошо известны примеры линий уровня – уровни одинаковых высот на топографической карте и линии одинакового барометрического давления на карте погоды.

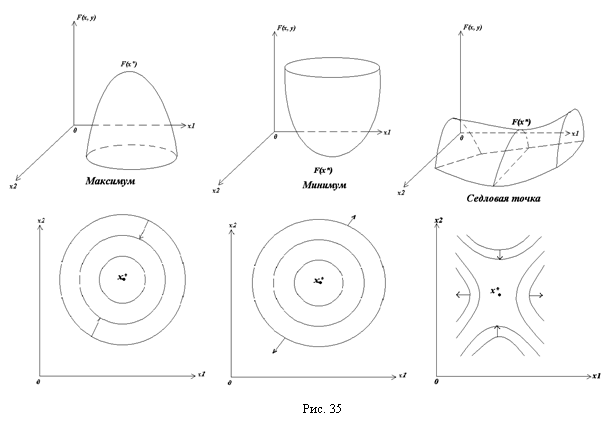
Определение. Направление, вдоль которого скорость увеличения функции максимальна, называется «предпочтительным» направлением, или Направлением наискорейшего роста.

«Предпочтительное» направление задается вектором-градиентом функции. На рис. 35 изображены максимум, минимум и седловая точка в задаче оптимизации функции двух переменных при отсутствии ограничений. В нижней части рисунка изображены линии уровня и направления наискорейшего роста.

Пример 50. Найти линии уровня функции U=X2+Y2.

Решение. Уравнение семейства линий уровня имеет вид X2+Y2=C (C>0). Придавая С различные действительные значения, получим концентрические окружности с центром в начале координат.

Построение линий уровня. Их анализ находит широкое применение в экономических задачах микро — и макроуровня, теории равновесия и эффективных решений. Изокосты, изокванты, кривые безразличия – это все линии уровня, построенные для разных экономических функций.

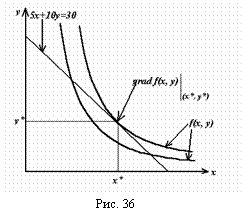
Пример 51. Рассмотрим следующую экономическую ситуацию. Пусть производство продукции описывается Функцией Кобба-Дугласа F(X, Y)=10х1/3у2/3, где Х – количество труда, У – количество капитала. На приобретение ресурсов выделено 30 у. ед., цена труда составляет 5 у. ед., капитала – 10 у. ед. Зададимся вопросом: какой наибольший выпуск можно получить в данных условиях? Здесь под «данными условиями» имеются в виду заданные технологии, цены на ресурсы, вид производственной функции. Как уже отмечалось, функция Кобба-Дугласа является монотонно возрастающей по каждой переменной, т. е. увеличение каждого вида ресурса ведет к росту выпуска. В данных условиях ясно, что увеличивать приобретение ресурсов можно до тех пор, пока хватает денег. Наборы ресурсов, стоимость которых составляет 30 у. ед., удовлетворяют условию:

5х + 10у = 30,

Т. е. определяют линию уровня функции:

G(X, Y) = 5х + 10у.

С другой стороны, с помощью линий уровня Функции Кобба-Дугласа (рис. 36) можно показать возрастание функции: в любой точке линии уровня направление градиента – это направление наибольшего возрастания, а для построения градиента в точке достаточно провести касательную к линии уровня в этой точке, построить перпендикуляр к касательной и указать направление градиента. Из рис. 36 видно, что движение линии уровня функции Кобба-Дугласа вдоль градиента следует производить до тех пор, пока она не станет касательной к линии уровня  5х + 10у = 30. Таким образом, с помощью понятий линии уровня, градиента, свойств градиента можно выработать подходы к наилучшему использованию ресурсов с точки зрения увеличения объемов выпускаемой продукции.

Определение. Поверхностью уровня функции U=F(X, Y, Z) называется поверхность F(X, Y, Z)=С, в точках которой функция сохраняет постоянное значение U=C.

Пример 52. Найти поверхности уровня функции U=X2+Z2—Y2.

Решение. Уравнение семейства поверхностей уровня имеет вид X2+Z2—Y2=С. Если С=0, то получаем X2+Z2—Y2=0 – конус; если  C<0, то X2+Z2—Y2=С – Семейство двуполостных гиперболоидов.

< Предыдущая		Следующая >

Градиент функции онлайн

Градиент функции — это вектор координатами которого являются частные производные этой функции по всем её переменным.

Градиент обозначается символом набла . Выражение градиента некоторой функции записывается следующим образом:

где , , — частные производные функции по переменным , , соответственно.

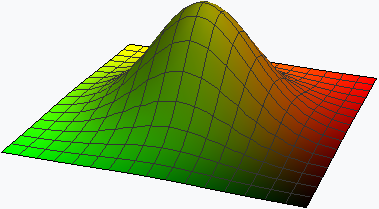
Вектор градиента указывает направление наискорейшего роста функции. Рассмотрим график функции .

Эта функция достигает своего единственного максимума в точке . График градиентного поля данной функции имеет вид:

Из данного градика видно, что в каждой точке вектор градиента направлен в сторону наискорейшего роста функции, т.е. в точку . При этом модуль вектора отражает скорость роста (крутизну подъёма) функции в этом направлении.

Задача вычисления градиента функции очень часто возникает при поиске эстремумов функции с использованием различных численных методов.

Наш онлайн калькулятор позволяет вычислить градиент практически любой функции как общем виде, так и в конкретной точке с описанием подробного хода решения на русском языке.

Нахождение градиента вектор-функции

Дата публикации Oct 20, 2018

ВЧасть 1Нам поставили задачу: вычислить градиент этой функции потерь:

Чтобы найти градиент, мы должны найти производную функцию. ВЧасть 2мы научились вычислять частную производную функции по каждой переменной. Однако большинство переменных в этой функции потерь являются векторами. Возможность найти частную производную векторных переменных особенно важна, поскольку нейронная сеть работает с большими объемами данных. Векторные и матричные операции — это простой способ представления операций с таким большим количеством данных. Как именно вы можете найти градиент вектор-функции?

Градиент скалярной функции

Скажи, что у нас есть функция,f (x, y) = 3x²y, Наши частные производные:

Если мы организуем эти части в горизонтальный вектор, мы получимградиентизР (х, у), или∇ f (x, y):

6yxэто изменение вР (х, у)в отношении изменения вИкс, в то время как3x²это изменение вР (х, у)в отношении изменения вY,

Что происходит, когда у нас есть две функции? Давайте добавим еще одну функцию,g (x, y) = 2x + y⁸, Частные производные:

Таким образом, градиент g (x, y):

Представляющие функции

Когда у нас есть несколько функций с несколькими параметрами, часто полезно представлять их более простым способом. Мы можем объединить несколько параметров функций в один векторный аргумент,Иксэто выглядит следующим образом:

Следовательно,Р (х, у, г)станетF (x₁, x₂, x₃)который становитсяе (Икс).

Мы также можем объединить несколько функций в вектор, например так:

В настоящее время,у = F (X)гдеF (X)является вектором из [f₁ (Икс), f₂ (Икс), f₃ (Икс) . п (Икс)]

Для нашего предыдущего примера с двумя функциями,f (x, y) ⇒ f (Икс)а такжеg (x, y) ⇒ g (Икс).Здесь векторИкс= [x₁, x₂], гдеx₁ = х, а такжеx₂ = у, Чтобы упростить его еще больше, мы можем объединить наши функции: [f (Икс),г(Икс)] = [f₁ (Икс), f₂ (Иксзнак равноf (x) = y.

Зачастую количество функций и количество переменных будет одинаковым, поэтому для каждой переменной существует решение.

Градиент вектор-функции

Теперь, когда у нас есть две функции, как мы можем найти градиент обеих функций? Если мы организуем оба их градиента в одну матрицу, мы переместимся из векторного исчисления в матричное исчисление. Эта матрица и организация градиентов нескольких функций с несколькими переменными, известна какМатрица Якобиана,

Есть несколько способов представления якобиана. Этот макет, где мы укладываем градиенты по вертикали, известен какмакет числителя, но другие документы будут использоватьрасположение знаменателя, который просто переворачивает его по диагонали:

Градиент функции идентичности

Давайте возьмем функцию идентичности,у = ф (х) = х, гдеFi (Икс) = xiи найдите его градиент:

Так же, как мы создали наш предыдущий якобиан, мы можем найти градиенты каждой скалярной функции и сложить их вертикально, чтобы создать якобиан тождественной функции:

Поскольку это функция идентичности, f₁ (Икс) = x₁, f₂ (Икс) = х₂ и тд. Следовательно,

Частичная производная функции по переменной, которой нет в функции, равна нулю. Например, частная производная 2x² по y равна 0. Другими словами,

Поэтому все, что не на диагонали якобиана, становится равным нулю. Между тем, частная производная любой переменной по отношению к себе равна 1. Например, частная производнаяИксв отношенииИксравен 1. Следовательно, якобиан становится:

Градиент комбинаций вектор-векторных функций

Элементарные бинарные операторыявляются операциями (такими как сложениевес+Иксиливес>Икскоторый возвращает вектор единиц и нулей), который применяет оператор последовательно, начиная с первого элемента обоих векторов, чтобы получить первый элемент вывода, затем второго элемента обоих векторов, чтобы получить второй элемент вывода… и так далее.

Эта статья представляет поэлементные бинарные операции с такими обозначениями:

Здесь ◯ означает любой поэлементный оператор (например, +), а не композицию функций.

Итак, как вы находите градиент поэлементной операции двух векторов?

Поскольку у нас есть два набора функций, нам нужны два якобиана, один из которых представляет градиент относительноИкси один по отношению квес:

Большинство арифметических операций нам понадобятся простые, поэтомуе (ш)часто просто векторвес, Другими словами,Fi (Wi) = Wi, Например, операцияW + хподходит к этой категории, так как она может быть представлена ​​каке (ж) + д (х)гдеfi (wi) + gi (xi) = wi + xi.

При этом условии каждый элемент в двух якобианах упрощается до:

На диагонали i = j, поэтому существует значение для частной производной. Вне диагонали, однако, i ≠ j, поэтому частные производные становятся равными нулю:

Мы можем представить это более кратко как:

Попробуем найти градиент функцииW + х, Мы знаем, что все вне диагонали равно 0. Значения частичных по диагонали относительновеса такжеИксявляются:

Итак, оба якобиана имеют диагональ 1. Это выглядит знакомо . это матрица тождеств!

Давайте попробуем это с умножением:ш * х, Значения частностей по диагонали относительновеса такжеИксявляются:

Следовательно, градиент по отношению квесизш * хявляетсяDiag (Икс)в то время как градиент по отношению кИксизш * хявляетсяDiag (вес).

Применяя те же шаги для вычитания и деления, мы можем суммировать все это:

Градиент векторных сумм

Одной из наиболее распространенных операций в глубоком обучении является операция суммирования. Как мы можем найти градиент функцииу = сумма (Икс)?

у = сумма (Икс)также может быть представлен как:

Следовательно, градиент может быть представлен как:

А так как частная производная функции по переменной, которой нет в функции, равна нулю, ее можно дополнительно упростить следующим образом:

Обратите внимание, что результатом является горизонтальный вектор.

Как насчет градиентау = сумма (Иксг)? Единственное отличие состоит в том, что мы умножаем каждый частный с константой, z:

Хотя это является производной по отношению кИкс, производная по скаляруZэто просто число:

Градиент комбинаций векторных функций правила цепочки

ВЧасть 2мы узнали о правилах цепей с несколькими переменными. Однако это работает только для скаляров. Давайте посмотрим, как мы можем интегрировать это в векторные вычисления!

Давайте возьмем векторную функцию,Yзнак равное(Икс)и найти градиент. Давайте определим функцию как:

И то и другоеf₁ (х)а такжеf₂ (х)являются составными функциями. Введем промежуточные переменные дляf₁ (х)а такжеf₂ (х)и переписать нашу функцию:

Теперь мы можем использовать наше правило цепочки переменных, чтобы вычислить производную вектораY, Просто вычислите производнуюf₁ (х)а такжеf₂ (х)и поместите их один над другим:

Вуаля! У нас есть наш градиент. Однако мы пришли к нашему решению со скалярными правилами, просто сгруппировав числа в вектор. Есть ли способ представить правило цепи с несколькими переменными для векторов?

Прямо сейчас наш градиент вычисляется с помощью:

Обратите внимание, что первый член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₁надИкси второй член градиентов обоихf₁ (х)а такжеf₂ (х)включает частичноеg₂надИкс Это как умножение матриц! Поэтому мы можем представить это как:

Давайте проверим наше новое представление правила цепочки векторов:

Мы получаем тот же ответ, что и скалярный подход! Если вместо одного параметраИксу нас есть векторный параметрИкснам просто нужно немного изменить наше правило, чтобы получить полное правило цепочки векторов:

В нашем примере выше,еэто чисто функцияг; то есть,фиявляется функциейсолдатно нетGJ(каждая функцияесоответствует ровно 1 функцииг),В этом случае все вне диагонали становится равным нулю, и:

Теперь у нас есть все части, которые мы находим в градиенте нейронной сети, с которой мы начали нашу серию:

Проверять, выписыватьсяЧасть 4чтобы узнать, как вычислить его производную!

Если вы еще этого не сделали, прочитайте части 1 и 2:

ЧитатьЧасть 4для грандиозного финала!

Скачать оригинал статьиВот,

Если вам понравилась эта статья, не забудьте оставить несколько хлопков! Оставьте комментарий ниже, если у вас есть какие-либо вопросы или предложения

Производная по направлению, градиент функции: объяснение, примеры

Понятие производной по направлению

Понятие производной по направлению рассматривается для функций двух и трёх переменных. Чтобы понять смысл производной по направлению, нужно сравнить производные по определению

Рассматривая функцию одной переменной, мы выяснили, что на оси Oy отображается приращение функции f(x) , соответствующее приращению аргумента x . Если мы имеем дело с функцией трёх переменных, то приращения аргументов x , y , z отображаются на осях Оx , Оy , Оz . Сам собой напрашивается вопрос: а где можно отобразить приращение уже не аргументов, а функции трёх переменных?

И вот ответ на этот вопрос: приращение функции трёх переменных отображается на некоторой прямой, направление которой определяется вектором, произвольно заданным в задаче.

Если рассматривается функция двух или трёх переменных, то два или три измерения задают аргументы, а упомянутая прямая, на которой отображается приращение функции, — это ещё одно измерение и для его акцентирования назовём это измерение не третьим или четвёртым, а нулевым, следуя программистской традиции (в программировании отсчёт чаще начинается не с единицы, а с нуля).

Для того, чтобы перейти к строгому математическому определению производной по направлению, нужно рассмотреть:

1) функцию u = f(M) , определённую в окрестности точки M с координатами x , y , z ;

Через точку M проводим прямую, одно из двух возможных направлений которых совпадает с направлением вектора l . На получившейся прямой отметим точку M 1 , координаты которой образуют суммы координат точки M и приращений соответствующих аргументов функции трёх переменных:

Величину отрезка MM 1 можно обозначить .

Функция u = f(M) при этом получит приращение

.

Определение производной по направлению. Предел отношения при , если он существует, называется производной функции u = f(M) по направлению вектора l и обозначается , то есть

.

Формула, которой нужно пользоваться для нахождения производной по направлению, следующая:

.

Смысл этой формулы: производная по направлению является линейной комбинацией частных производных, причём направляющие косинусы показывают вклад в производную по направлению соответствующей частной производной.

Примеры нахождения производной по направлению

Пример 1. Найти производную функции в точке M 0 (1; 2; 3) по направлению вектора .

Найдём направляющие косинусы, пользуясь определением скалярного произведения векторов:

Теперь можем найти производную по направлению данной функции по её формуле:

А сейчас — домашнее задание. В нём дана функция не трёх, а лишь двух переменных, но несколько иначе задан направляющий вектор. Так что придётся вновь повторить векторную алгебру.

Пример 2. Найти производную функции в точке M 0 (1; 2) по направлению вектора , где M 1 — точка с координатами (3; 0) .

Вектор, задающий направление производной, может быть дан и в такой форме, как в следующем примере — в виде разложения по ортам координатных осей, но эта хорошо знакомая тема из самого начала векторной алгебры.

Пример 3. Найти производную функции в точке M 0 (1; 1; 1) по направлению вектора .

Решение. Найдём направляющие косинусы вектора

Найдём частные производные функции в точке M 0 :

Следовательно, можем найти производную по направлению данной функции по её формуле:

.

Градиент функции

Градиент функции нескольких переменных в точке M 0 характеризует направление максимального роста этой функции в точке M 0 и величину этого максимального роста.

Как найти градиент?

Нужно определить вектор, проекциями которого на оси координат являются значения частных производных , , этой функции в соответствующей точке:

.

То есть, должно получиться представление вектора по ортам координатных осей, в котором на каждый орт умножается соответствующая его оси частная производная.

Для градиента функции двух переменных формула короче:

.

Пример 4. Найти градиент функции в точке M 0 (2; 4;) .

Решение. Найдём частные производные функции в точке M 0 :

Следовательно, можем записать искомый градиент данной функции:

.