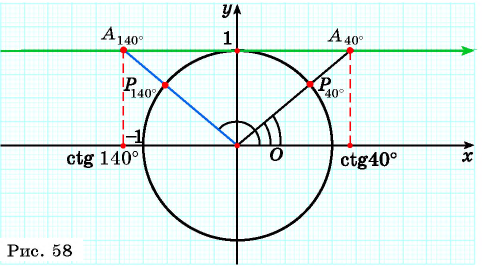
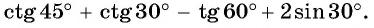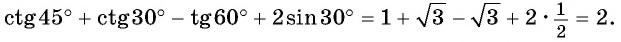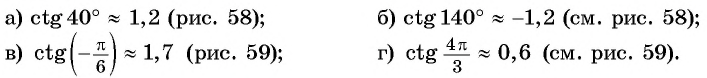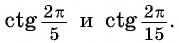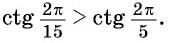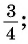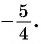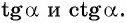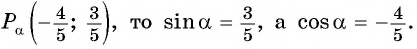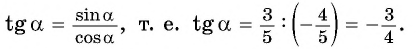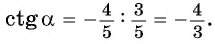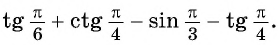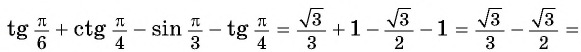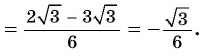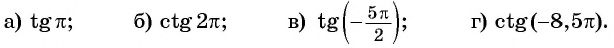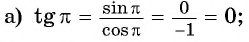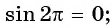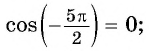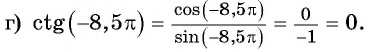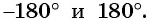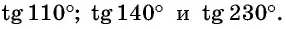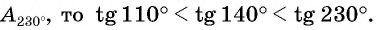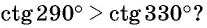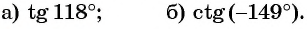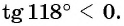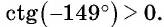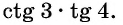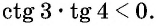Как найти синус угла в треугольнике? Не в прямоугольном, в любом
Если рассматриваемый треугольник является прямоугольным, то можно использовать базовое определение тригонометрической функции синуса для острых углов. По определению синусом угла называют соотношение длины катета, лежащего напротив этого угла, к длине гипотенузы этого треугольника. То есть, если катеты имеют длину А и В, а длина гипотенузы равна С, то синус угла α, лежащего напротив катета А, определяйте по формуле α=А/С, а синус угла β, лежащего напротив катета В — по формуле β=В/С. Синус третьего угла в прямоугольном треугольнике находить нет необходимости, так как угол, лежащий напротив гипотенузы всегда равен 90°, а его синус всегда равен единице.
2
Для нахождения синусов углов в произвольном треугольнике, как это ни странно, проще использовать не теорему синусов, а теорему косинусов. Она гласит, что возведенная в квадрат длина любой стороны равна сумме квадратов длин двух других сторон без удвоенного произведения этих длин на косинус угла между ними: А²=В²+С2-2*В*С*cos(α). Из этой теоремы можно вывести формулу для нахождения косинуса: cos(α)=(В²+С²-А²)/(2*В*С) . А поскольку сумма квадратов синуса и косинуса одного и того же угла всегда равна единице, то можно вывести и формулу для нахождения синуса угла α: sin(α)=√(1-(cos(α))²)= √(1-(В²+С²-А²)²/(2*В*С) ²).
3
Воспользуйтесь для нахождения синуса угла двумя разными формулами расчета площади треугольника, в одной из которых задействованы только длины его сторон, а в другой — длины двух сторон и синус угла между ними. Так как результаты их будут равны, то из тождества можно выразить синус угла. Формула нахождения площади через длины сторон (формула Герона) выглядит так: S=¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С)) . А вторую формулу можно написать так: S=А*В*sin(γ). Подставьте первую формулу во вторую и составьте формулу для синуса угла, лежащего напротив стороны С: sin(γ)= ¼*√((А+В+С) *(В+С-А) *(А+С-В) *(А+В-С) /(А*В)) . Синусы двух других углов можно найти по аналогичным формулам.
Синус, косинус, тангенс в прямоугольном треугольнике
Гипотенузой называется та сторона треугольника, что лежит против угла в 90 градусов, две оставшиеся стороны называются катетами прямоугольного треугольника.
Подробнее про прямоугольный треугольник здесь.
Синусом угла в прямоугольном треугольнике называется отношение противолежащего катета к гипотенузе.
Косинусом угла в прямоугольном треугольнике называется отношение прилежащего катета к гипотенузе.
Тангенсом угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему.
Котангенсом угла в прямоугольном треугольнике называется отношение прилежащего катета к противолежащему.
Бывает (и на ЕГЭ, ГИА), что приходится иметь дело с косинусами, синусами и тангенсами внешних углов треугольника. Формулы приведения позволяют увидеть, что есть еще и вот такая связь между смежными углами (помимо того, что их сумма равна 180):
Смотрите подборку задач на применение указанных соотношений в статье «Прямоугольный треугольник. Вычисление длин и углов» часть I, часть II.
Чтобы не потерять страничку, вы можете сохранить ее у себя:
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
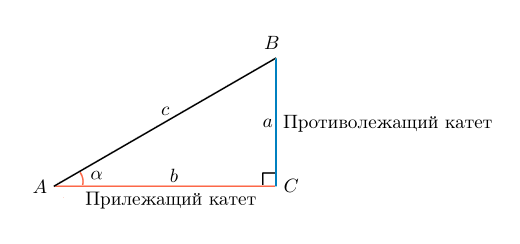
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
Рассмотрим прямоугольный треугольник A B C , угол C равен 90 °:
sin ∠ A = C B A B
cos ∠ A = A C A B
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
sin ∠ B = A C A B
cos ∠ B = B C A B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Такая окружность пересекает ось х в точках ( − 1 ; 0 ) и ( 1 ; 0 ) , ось y в точках ( 0 ; − 1 ) и ( 0 ; 1 )
На данной окружности будет три шкалы отсчета – ось x , ось y и сама окружность, на которой мы будем откладывать углы.
Углы на тригонометрической окружности откладываются от точки с координатами ( 1 ; 0 ) , – то есть от положительного направления оси x , против часовой стрелки. Пусть эта точка будет называться S (от слова start). Отметим на окружности точку A . Рассмотрим ∠ S O A , обозначим его за α . Это центральный угол, его градусная мера равна дуге, на которую он опирается, то есть ∠ S O A = α = ∪ S A .
Давайте найдем синус и косинус этого угла. До этого синус и косинус мы искали в прямоугольном треугольнике, сейчас будем делать то же самое. Для этого опустим перпендикуляры из точки A на ось x (точка B ) и на ось игрек (точка C ) .
Отрезок O B является проекцией отрезка O A на ось x , отрезок O C является проекцией отрезка O A на ось y .
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Поскольку O C A B – прямоугольник, A B = C O .
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Опускаем из точки A перпендикуляры к осям x и y . Точка B в этом случае будет иметь отрицательную координату по оси x . Косинус тупого угла отрицательный .
Можно дальше крутить точку A по окружности, расположить ее в III или даже в IV четверти, но мы пока не будем этим заниматься, поскольку в курсе 9 класса рассматриваются углы от 0 ° до 180 ° . Поэтому мы будем использовать только ту часть окружности, которая лежит над осью x . (Если вас интересует тригонометрия на полной окружности, смотрите видео на канале). Отметим на этой окружности углы 0 ° , 30 ° , 45 ° , 60 ° , 90 ° , 120 ° , 135 ° , 150 ° , 180 ° . Из каждой точки на окружности, соответствующей углу, опустим перпендикуляры на ось x и на ось y .
Координата по оси x – косинус угла , координата по оси y – синус угла .
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Тангенс – это отношение синуса к косинусу. При делении положительной величины на отрицательную результат отрицательный. Тангенс тупого угла отрицательный .
Котангенс – отношение косинуса к синусу. При делении отрицательной величины на положительную результат отрицательный. Котангенс тупого угла отрицательный .
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
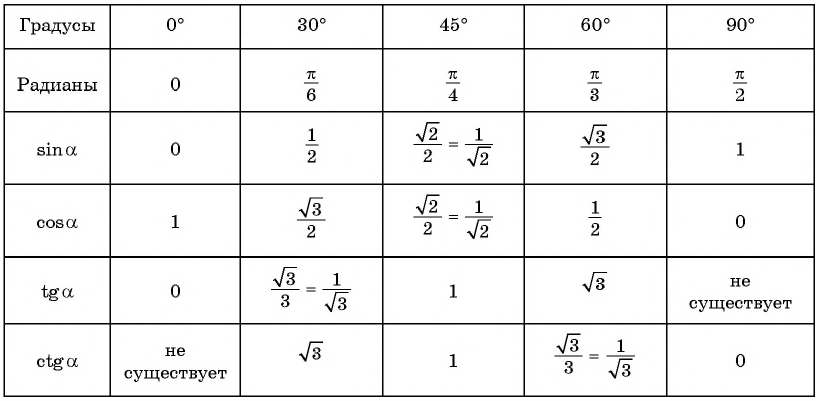
Тригонометрия: Таблица значений тригонометрических функций
0 °
30 °
45 °
60 °
90 °
sin α
0
1 2
2 2
3 2
1
cos α
1
3 2
2 2
1 2
0
tg α
0
3 3
1
3
нет
ctg α
нет
3
1
3 3
0
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Котангенс является обратно пропорциональной величиной к тангенсу. То есть, это отношение прилежащего катета к противолежащему.
Для простоты запоминания можно дать такое определение: котангенс угла — это отношение ближнего от рассматриваемого угла катета к дальнему катету.
В случае с рисунком, описанным выше: ctgα=bactgalpha=frac{b}{a}
ctgα=cosαsinαctgalpha=frac{cosalpha}{sinalpha}
Пусть в прямоугольном треугольнике синус угла равен 0.200.20, а косинус этого угла равен 0.980.98. Найдите котангенс данного по условию угла.
Решение
sinα=0.20sinalpha=0.20
cosα=0.98cosalpha=0.98
ctgα=cosαsinα=0.980.20=4.9ctgalpha=frac{cosalpha}{sinalpha}=frac{0.98}{0.20}=4.9
Ответ
4.94.9
После того, как мы изучили и тангенс, и котангенс, можно рассмотреть еще одно тождество:
tgα⋅ctgα=1tgalphacdotctgalpha=1
Вывод его прост:
tgα⋅ctgα=sinαcosα⋅cosαsinα=1tgalphacdotctgalpha=frac{sinalpha}{cosalpha}cdotfrac{cosalpha}{sinalpha}=1
Благодаря ему можно быстро и без каких-либо трудностей вычислять одну из этих величин.
Каков тангенс угла, если его котангенс равен 4.54.5?
Решение
ctgα=4.5ctgalpha=4.5
tgα⋅ctgα=1tgalphacdotctgalpha=1
tgα⋅4.5=1tgalphacdot4.5=1
tgα=14.5tgalpha=frac{1}{4.5}
tgα≈0.22tgalphaapprox0.22
Ответ
0.220.22
Еще одно тождество помогает решить задачи, связанные с котангенсом:
1+ctg2α=1sin2α1+ctg^2alpha=frac{1}{sin^2alpha}
Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат синуса.
Найдите котангенс угла, если квадрат его синуса равен 0.490.49.
Решение
sin2α=0.49sin^2alpha=0.49
1+ctg2α=1sin2α1+ctg^2alpha=frac{1}{sin^2alpha}
1+ctg2α=10.491+ctg^2alpha=frac{1}{0.49}
1+ctg2α≈2.041+ctg^2alphaapprox2.04
ctg2α≈1.04ctg^2alphaapprox1.04
ctgα≈1.02ctgalphaapprox1.02
Ответ
1.021.02
Решение задач по математике недорого от экспертов биржи!
Тест по теме «Вычисление котангенса»
Примеры:
(ctg:30^° =sqrt{3})
(ctg:(frac{π}{3})=frac{1}{sqrt{3}})
(ctg:2=-0,487…)
Содержание:
- Аргумент и значение
Котангенс острого угла
Котангенс числа или любого угла
Знаки по четвертям
Связь с другими функциями
Аргумент и значение

Аргументом может быть:
— как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев значение котангенса вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Значение котангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)
Котангенс острого угла
Котангенс можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к противолежащему.
Пример:
1) Пусть дан угол и нужно определить (ctgA).

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (ctg;A).

Вычисление котангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) котангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
(ctg: t=)(frac{cos:t}{sin:t})
Пример. Вычислите (ctg: frac{5π}{6}).
Решение: Найдем сначала (frac{5π}{6}) на круге. Затем найдем (cos:frac{5π}{6}) и (sin:frac{5π}{6}), а потом поделим одно на другое.

(ctg:frac{5π}{6}=)(frac{cos:frac{5π}{6}}{sin:frac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3})
Ответ: (-sqrt{3}).
Пример. Вычислите (ctg:frac{π}{2}).
Решение: Чтобы найти котангенс пи на (2) нужно найти сначала косинус и синус (frac{π}{2}). И то, и другое найдем с помощью тригонометрического круга:

Точка (frac{π}{2}) на числовой окружности совпадает с (1) на оси синусов, значит (sin:frac{π}{2}=1). Если из точки (frac{π}{2}) на числовой окружности провести перпендикуляр к оси косинусов, то мы попадем в точку (0), значит (cos:frac{π}{2}=0). Получается: (ctg:frac{π}{2}=)(frac{cos:frac{π}{2}}{sin:frac{π}{2}})(=)(frac{0}{1})(=0).
Ответ: (0).
Пример. Вычислите (ctg:(-765^circ)).
Решение: (ctg: (-765^circ)=)(frac{cos:(-765^circ)}{sin:(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin(-765^°)=-frac{sqrt{2}}{2});
(cos(-765^°)=frac{sqrt{2}}{2}) ;
получается (ctg(-765^°)= frac{sqrt{2}}{2} ∶ -frac{sqrt{2}}{2}=-1).
Ответ: (-1).
Пример. Найдите (ctg:frac{π}{3}).
Решение: (ctg: frac{π}{3}=)(frac{cos:frac{π}{3}}{sin:frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin(frac{π}{3})=frac{sqrt{3}}{2});
(cos(frac{π}{3})=frac{1}{2}) ;
получается (ctg(frac{π}{3})=frac{1}{2} ∶ frac{sqrt{3}}{2}= frac{1}{2} cdot frac{2}{sqrt{3}}=frac{1}{sqrt{3}}).
Ответ: (frac{1}{sqrt{3}}).
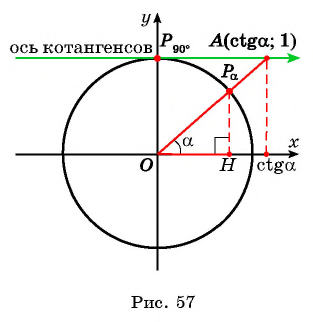
Однако можно определять значение котангенса и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:
Прямая проходящая через (frac{π}{2}) на числовой окружности и параллельная оси абсцисс (косинусов) называется осью котангенсов. Направление оси котангенсов и оси косинусов совпадает.

Ось котангенсов – это фактически копия оси косинусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси косинусов.
Чтобы определить значение котангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу котангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси котангенсов.
3) Найти координату пересечения этой прямой и оси.
Пример. Вычислите (ctg:frac{π}{4}).
Решение:
1) Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).
Ответ: (1).
Пример. Найдите значение (ctg: 30°) и (ctg: (-60°)).
Решение:
Для угла (30°) ((∠COA)) котангенс будет равен (sqrt{3}) (приблизительно (1,73)), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось котангесов.
(ctg;(-60°)=frac{sqrt{3}}{{3}}) (примерно (-0,58)).

Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение котангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом котангенс не определен для:
1) всех точек (C) (значение в Пи: …(0), (2π), (4π), (-2π), (-4π) …; и значение в градусах: …(0°),(360°), (720°),(-360°),(-720°)…)
2) всех точек (D) (значение в Пи: …(π), (3π), (5π), (-π), (-3π), (-5π) …; и значение в градусах: …(180°),(540°),(900°),(-180°),(-540°),(-900°)…) .
Так происходит потому, что в этих точках синус равен нулю. А значит, вычисляя значение котангенса мы придем к делению на ноль, что запрещено. И прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось котангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках котангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений он может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с котангенсом необходимо учитывать ограничения на ОДЗ.
Знаки по четвертям
С помощью оси котангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак котангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение котангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:
— синусом того же угла: формулой (1+ctg^2x=)(frac{1}{sin^2x})
— косинусом и синусом того же угла: (ctg:x=)(frac{cos:x}{sin:x})
— тангенсом того же угла: формулой (tg:x=)(frac{1}{ctg:x})
Другие наиболее часто применяемые формулы смотри здесь.
Смотрите также:
Формулы приведения
Решение уравнений (tgx=a) и (ctgx=a)
Ответ:
Синус (sin) – это одна из прямых тригонометрических функций. Находить синус угла в произвольном треугольнике проще всего с использованием теоремы косинусов (cos): квадрат длины любой стороны равен сумме квадратов длин двух других сторон за минусом их удвоенного произведения на косинус угла между ними.
Синус, косинус и тангенс — их еще называют тригонометрическими функциями угла — дают соотношения между сторонами и углами треугольника. Зная угол, можно найти все его тригонометрические функции по специальным таблицам. А зная синусы, косинусы и тангенсы углов треугольника и одну из его сторон, можно найти остальные.
Содержание:
Построим точку
По определению тангенса острого угла получим:
Определение тангенса угла
Определение:
Тангенсом угла 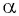
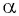
Например,
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов
Поскольку 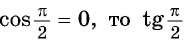
Через точку 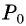
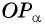
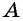
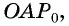
Из подобия треугольников 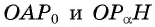
Поскольку 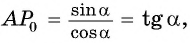
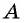
Прямая, перпендикулярная оси абсцисс, проходящая через точку 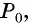
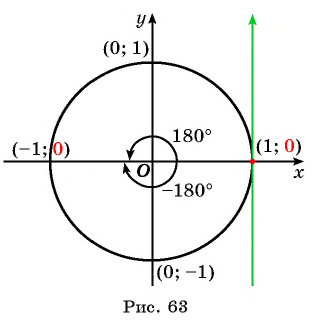
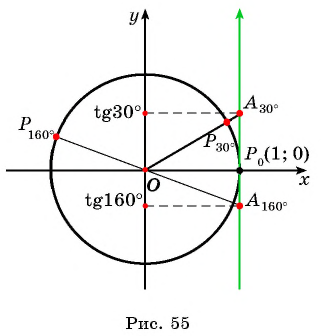
Нахождение тангенса произвольного угла
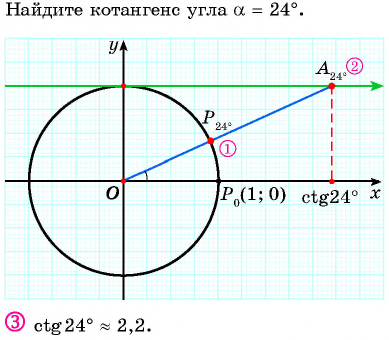
Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью тангенсов.
- Найти ординату точки пересечения прямой
с осью тангенсов.
Найдите тангенс угла
Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.
Пример №1
Определите с помощью оси тангенсов:
Решение:
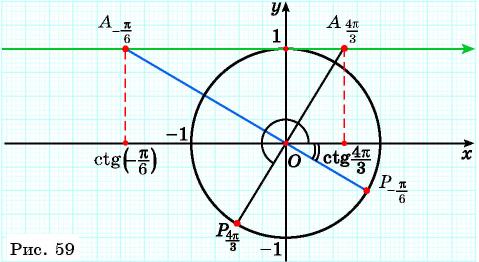
Пример №2
С помощью оси тангенсов сравните значения выражений
Решение:
Отметим на оси тангенсов точки, соответствующие углам 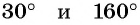
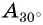
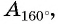
Для углов 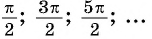
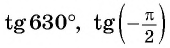
Построим точку 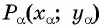
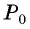
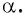
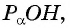
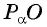
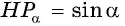
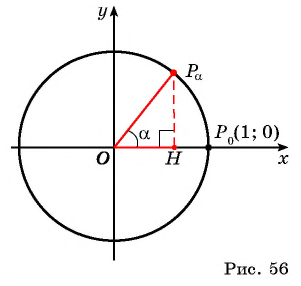
По определению котангенса острого угла получим:
Определение котангенса угла
Определение:
Котангенсом угла 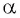
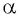
Например,
Поскольку
Воспользуемся полученным равенством и найдем значения котангенсов углов
Поскольку 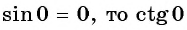
Найденные значения синуса, косинуса, тангенса и котангенса углов 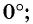
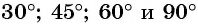
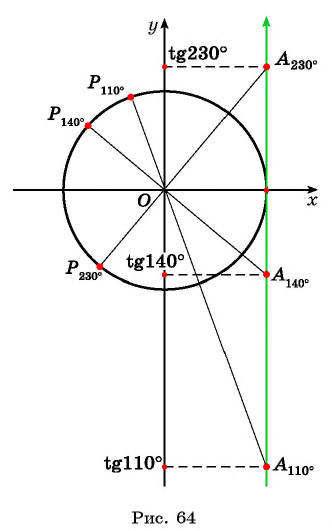
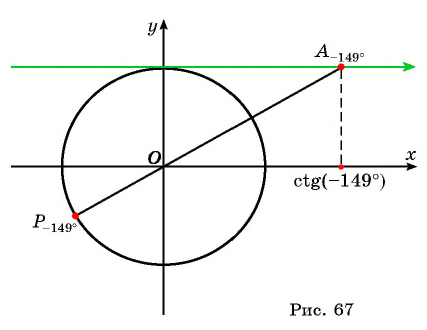
Нахождение котангенса произвольного угла
Для того чтобы найти котангенс произвольного угла 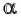
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью котангенсов.
- Найти абсциссу точки пересечения прямой
с осью котангенсов.
Значения котангенса произвольного угла с помощью оси котангенсов можно указать только приближенно.
- Заказать решение задач по высшей математике
Пример №3
Найдите значение выражения
Решение:
Через точку 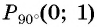
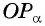
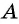
Получим треугольник 
Из подобия треугольников 
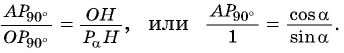
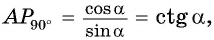
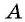
Прямая, перпендикулярная оси ординат, проходящая через точку 
Пример №4
Определите с помощью оси котангенсов:
Решение:
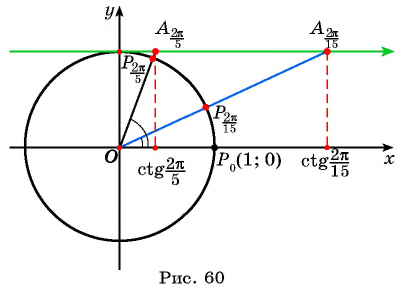
Пример №5
С помощью оси котангенсов сравните значения выражений
Решение:
Отметим на оси котангенсов точки, соответствующие углам 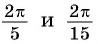
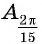
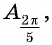
Для углов 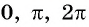
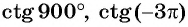
Пример №6
С помощью оси:
а) тангенсов найдите один из углов, тангенс которого равен
б) котангенсов найдите один из углов, котангенс которого равен
Решение:
а) 1 Отметим на оси тангенсов точку 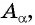
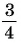
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 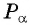
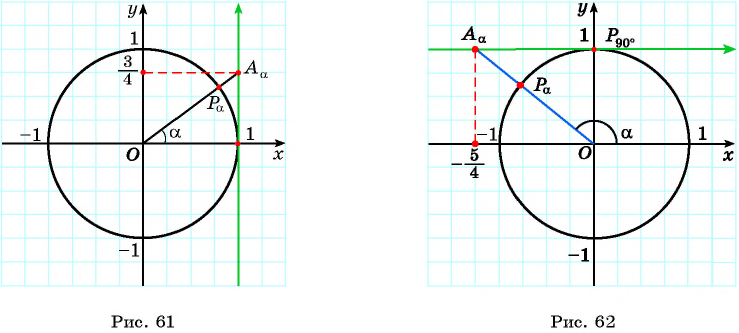
4 Отметим один из углов, соответствующий этой точке (см. рис. 61).
б) 1 Отметим на оси котангенсов точку 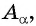
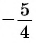
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 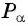
4 Отметим один из углов, соответствующий этой точке (см. рис. 62).
Пример №7
Точка 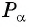
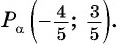
Решение:
Так как точка 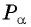
По определению тангенса:
По определению котангенса: 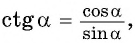
Пример №8
Найдите значение выражения
Решение:
Пример №9
Найдите, если это возможно, значение выражения:
Решение:
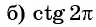
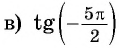
Пример №10
Если 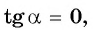
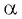
Выберите правильные ответы.
Решение:
Так как тангенсом угла 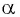
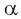
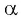
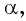
Можно также использовать ось тангенсов: найти точку на оси тангенсов, у которой ордината равна нулю (рис. 63), и определить соответствующие углы. Правильные ответы а) и г).
Пример №11
Расположите в порядке возрастания:
Решение:
Отметим на оси тангенсов точки, соответствующие углам 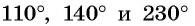
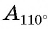
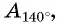
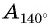
Пример №12
Верно ли, что
Решение:
Отметим на оси котангенсов точки, соответствующие углам 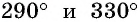
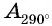
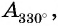
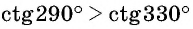
Пример №13
Определите знак выражения:
Решение:
а) Первый способ. По определению тангенса: 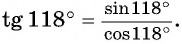
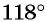
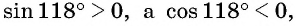
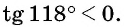
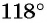
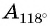
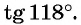
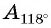
б) Первый способ. По определению котангенса 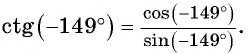
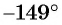
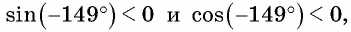
Второй способ. Отметим на оси котангенсов точку, соответствующую углу 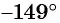
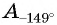
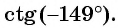
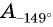
Пример №14
Определите знак произведения
Решение:
Так как угол 3 радиана находится во второй четверти, а угол 4 радиана — в третьей, то 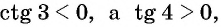
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла

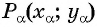
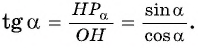
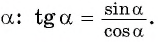
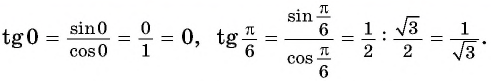
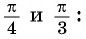
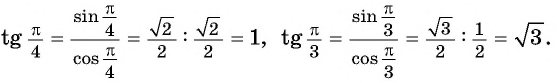
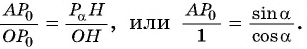
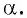
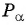 на единичной окружности.
на единичной окружности.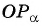 до пересечения с осью тангенсов.
до пересечения с осью тангенсов.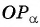 с осью тангенсов.
с осью тангенсов.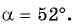
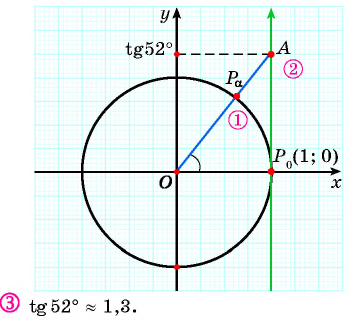

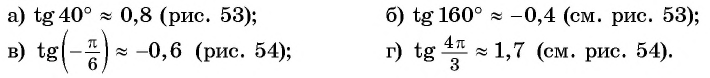
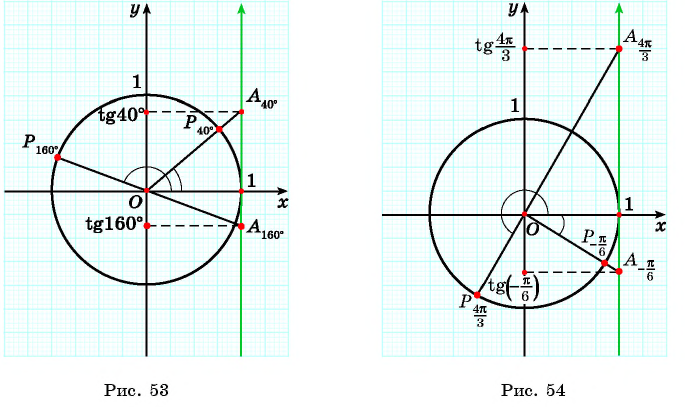
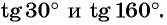
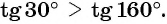
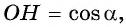
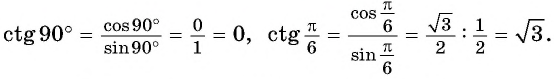
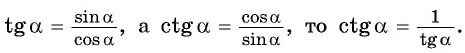
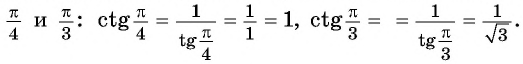
 на единичной окружности.
на единичной окружности.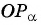 до пересечения с осью котангенсов.
до пересечения с осью котангенсов.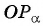 с осью котангенсов.
с осью котангенсов.