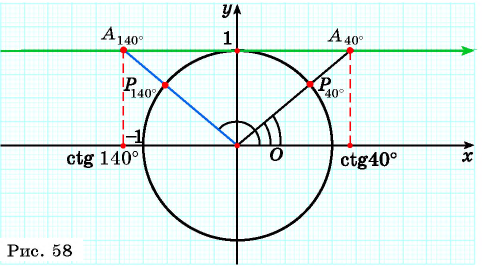
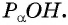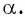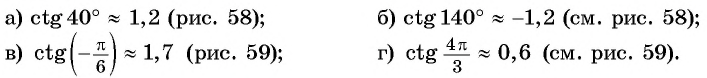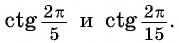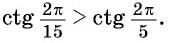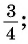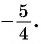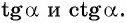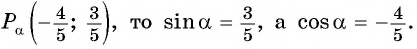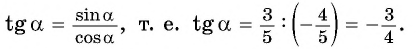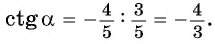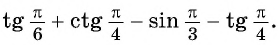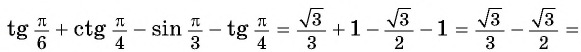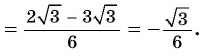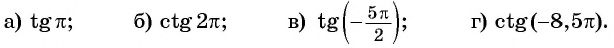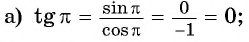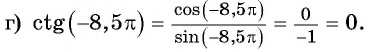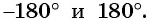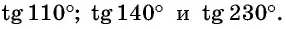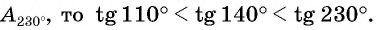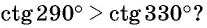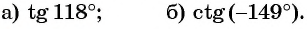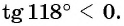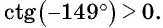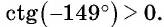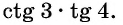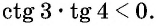Котангенс является обратно пропорциональной величиной к тангенсу. То есть, это отношение прилежащего катета к противолежащему.
Для простоты запоминания можно дать такое определение: котангенс угла — это отношение ближнего от рассматриваемого угла катета к дальнему катету.
В случае с рисунком, описанным выше: ctgα=bactgalpha=frac{b}{a}
ctgα=cosαsinαctgalpha=frac{cosalpha}{sinalpha}
Пусть в прямоугольном треугольнике синус угла равен 0.200.20, а косинус этого угла равен 0.980.98. Найдите котангенс данного по условию угла.
Решение
sinα=0.20sinalpha=0.20
cosα=0.98cosalpha=0.98
ctgα=cosαsinα=0.980.20=4.9ctgalpha=frac{cosalpha}{sinalpha}=frac{0.98}{0.20}=4.9
Ответ
4.94.9
После того, как мы изучили и тангенс, и котангенс, можно рассмотреть еще одно тождество:
tgα⋅ctgα=1tgalphacdotctgalpha=1
Вывод его прост:
tgα⋅ctgα=sinαcosα⋅cosαsinα=1tgalphacdotctgalpha=frac{sinalpha}{cosalpha}cdotfrac{cosalpha}{sinalpha}=1
Благодаря ему можно быстро и без каких-либо трудностей вычислять одну из этих величин.
Каков тангенс угла, если его котангенс равен 4.54.5?
Решение
ctgα=4.5ctgalpha=4.5
tgα⋅ctgα=1tgalphacdotctgalpha=1
tgα⋅4.5=1tgalphacdot4.5=1
tgα=14.5tgalpha=frac{1}{4.5}
tgα≈0.22tgalphaapprox0.22
Ответ
0.220.22
Еще одно тождество помогает решить задачи, связанные с котангенсом:
1+ctg2α=1sin2α1+ctg^2alpha=frac{1}{sin^2alpha}
Оно появляется путем деление каждого слагаемого основного тождества тригонометрии на квадрат синуса.
Найдите котангенс угла, если квадрат его синуса равен 0.490.49.
Решение
sin2α=0.49sin^2alpha=0.49
1+ctg2α=1sin2α1+ctg^2alpha=frac{1}{sin^2alpha}
1+ctg2α=10.491+ctg^2alpha=frac{1}{0.49}
1+ctg2α≈2.041+ctg^2alphaapprox2.04
ctg2α≈1.04ctg^2alphaapprox1.04
ctgα≈1.02ctgalphaapprox1.02
Ответ
1.021.02
Решение задач по математике недорого от экспертов биржи!
Тест по теме «Вычисление котангенса»
Примеры:
(ctg:30^° =sqrt{3})
(ctg:(frac{π}{3})=frac{1}{sqrt{3}})
(ctg:2=-0,487…)
Содержание:
- Аргумент и значение
Котангенс острого угла
Котангенс числа или любого угла
Знаки по четвертям
Связь с другими функциями
Аргумент и значение

Аргументом может быть:
— как число или выражение с Пи: (1,3), (frac{π}{4}), (π), (-frac{π}{3}) и т.п.
— так и угол в градусах: (45^°), (360^°),(-800^°), (1^° ) и т.п.
Для обоих случаев значение котангенса вычисляется одинаковым способом – либо через значения синуса и косинуса, либо через тригонометрический круг (см. ниже).
Значение котангенса – всегда действительное число (возможно, иррациональное): (1), (sqrt{3}), (-frac{1}{sqrt{3}}), (-0,1543…)
Котангенс острого угла
Котангенс можно определить с помощью прямоугольного треугольника — он равен отношению прилежащего катета к противолежащему.
Пример:
1) Пусть дан угол и нужно определить (ctgA).

2) Достроим на этом угле любой прямоугольный треугольник.

3) Измерив, нужные стороны, можем вычислить (ctg;A).

Вычисление котангенса числа или любого угла
Для чисел, а также для тупых, развернутых углов и углов больших (360°) котангенс чаще всего определяют с помощью синуса и косинуса, через их отношение:
(ctg: t=)(frac{cos:t}{sin:t})
Пример. Вычислите (ctg: frac{5π}{6}).
Решение: Найдем сначала (frac{5π}{6}) на круге. Затем найдем (cos:frac{5π}{6}) и (sin:frac{5π}{6}), а потом поделим одно на другое.

(ctg:frac{5π}{6}=)(frac{cos:frac{5π}{6}}{sin:frac{5π}{6}})(=-frac{sqrt{3}}{2}:frac{1}{2}=-frac{sqrt{3}}{2} cdot frac{2}{1}=-sqrt{3})
Ответ: (-sqrt{3}).
Пример. Вычислите (ctg:frac{π}{2}).
Решение: Чтобы найти котангенс пи на (2) нужно найти сначала косинус и синус (frac{π}{2}). И то, и другое найдем с помощью тригонометрического круга:

Точка (frac{π}{2}) на числовой окружности совпадает с (1) на оси синусов, значит (sin:frac{π}{2}=1). Если из точки (frac{π}{2}) на числовой окружности провести перпендикуляр к оси косинусов, то мы попадем в точку (0), значит (cos:frac{π}{2}=0). Получается: (ctg:frac{π}{2}=)(frac{cos:frac{π}{2}}{sin:frac{π}{2}})(=)(frac{0}{1})(=0).
Ответ: (0).
Пример. Вычислите (ctg:(-765^circ)).
Решение: (ctg: (-765^circ)=)(frac{cos:(-765^circ)}{sin:(-765^circ)})
Что бы вычислить синус и косинус (-765^°). Отложим (-765^°) на тригонометрическом круге. Для этого надо повернуть в отрицательную сторону на (720^°) , а потом еще на (45^°).

(sin(-765^°)=-frac{sqrt{2}}{2});
(cos(-765^°)=frac{sqrt{2}}{2}) ;
получается (ctg(-765^°)= frac{sqrt{2}}{2} ∶ -frac{sqrt{2}}{2}=-1).
Ответ: (-1).
Пример. Найдите (ctg:frac{π}{3}).
Решение: (ctg: frac{π}{3}=)(frac{cos:frac{π}{3}}{sin:frac{π}{3}}). Опять находим синус пи на 3 и косинус пи на 3 (хоть с помощью тригонометрического круга, хоть по таблице):
(sin(frac{π}{3})=frac{sqrt{3}}{2});
(cos(frac{π}{3})=frac{1}{2}) ;
получается (ctg(frac{π}{3})=frac{1}{2} ∶ frac{sqrt{3}}{2}= frac{1}{2} cdot frac{2}{sqrt{3}}=frac{1}{sqrt{3}}).
Ответ: (frac{1}{sqrt{3}}).
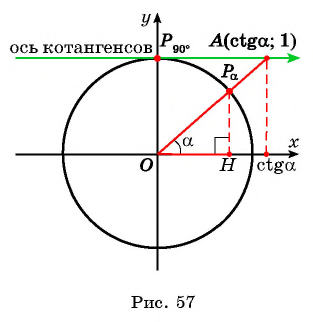
Однако можно определять значение котангенса и напрямую через тригонометрический круг — для этого надо на нем построить дополнительную ось:
Прямая проходящая через (frac{π}{2}) на числовой окружности и параллельная оси абсцисс (косинусов) называется осью котангенсов. Направление оси котангенсов и оси косинусов совпадает.

Ось котангенсов – это фактически копия оси косинусов, только сдвинутая. Поэтому все числа на ней расставляются так же как на оси косинусов.
Чтобы определить значение котангенс с помощью числовой окружности, нужно:
1) Отметить соответствующую аргументу котангенса точку на числовой окружности.
2) Провести прямую через эту точку и начало координат и продлить её до оси котангенсов.
3) Найти координату пересечения этой прямой и оси.
Пример. Вычислите (ctg:frac{π}{4}).
Решение:
1) Отмечаем (frac{π}{4}) на окружности.

2) Проводим через данную точку и начало координат прямую.

3) В данном случае координату долго искать не придется – она равняется (1).
Ответ: (1).
Пример. Найдите значение (ctg: 30°) и (ctg: (-60°)).
Решение:
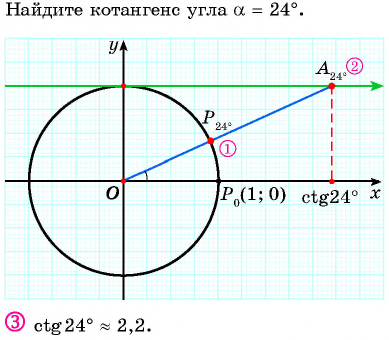
Для угла (30°) ((∠COA)) котангенс будет равен (sqrt{3}) (приблизительно (1,73)), потому что именно в таком значении сторона угла, проходящая через начало координат и точку (A), пересекает ось котангесов.
(ctg;(-60°)=frac{sqrt{3}}{{3}}) (примерно (-0,58)).

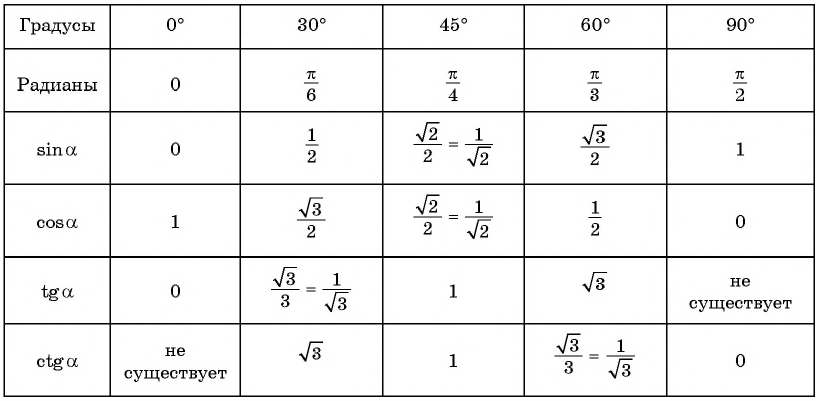
Значения для других часто встречающихся в практике углов смотри в тригонометрической таблице.
В отличие от синуса и косинуса значение котангенса не ограничено и лежит в пределах от (-∞) до (+∞), то есть может быть любым.

При этом котангенс не определен для:
1) всех точек (C) (значение в Пи: …(0), (2π), (4π), (-2π), (-4π) …; и значение в градусах: …(0°),(360°), (720°),(-360°),(-720°)…)
2) всех точек (D) (значение в Пи: …(π), (3π), (5π), (-π), (-3π), (-5π) …; и значение в градусах: …(180°),(540°),(900°),(-180°),(-540°),(-900°)…) .
Так происходит потому, что в этих точках синус равен нулю. А значит, вычисляя значение котангенса мы придем к делению на ноль, что запрещено. И прямая проходящая через начало координат и любую из этих точек никогда не пересечет ось котангенсов, т.к. будет идти параллельно ей. Поэтому в этих точках котангенс – НЕ СУЩЕСТВУЕТ (для всех остальных значений он может быть найден).
Из-за этого при решении тригонометрических уравнений и неравенств с котангенсом необходимо учитывать ограничения на ОДЗ.
Знаки по четвертям
С помощью оси котангенсов легко определить знаки по четвертям тригонометрической окружности. Для этого надо взять любую точку на четверти и определить знак котангенса для нее описанным выше способом. У всей четверти знак будет такой же.
Для примера на рисунке нанесены две зеленые точки в I и III четвертях. Для них значение котангенса положительно (зеленые пунктирные прямые приходят в положительную часть оси), значит и для любой точки из I и III четверти значение будет положительно (знак плюс).
С двумя фиолетовыми точками в II и IV четвертях – аналогично, но с минусом.

Связь с другими тригонометрическими функциями:
— синусом того же угла: формулой (1+ctg^2x=)(frac{1}{sin^2x})
— косинусом и синусом того же угла: (ctg:x=)(frac{cos:x}{sin:x})
— тангенсом того же угла: формулой (tg:x=)(frac{1}{ctg:x})
Другие наиболее часто применяемые формулы смотри здесь.
Смотрите также:
Формулы приведения
Решение уравнений (tgx=a) и (ctgx=a)
Что такое синус, косинус, тангенс, котангенс
18 мая 2022
Сегодня мы узнаем, что такое синус, косинус, тангенс и котангенс. Это первый и самый важный урок по тригонометрии на всём сайте.
Содержание:
- Ключевые определения: синус, косинус, тангенс, котангенс.
- Почему эти значения зависят только от углов?
- Стандартные углы: 30°, 45°, 60°.
- Простейшие свойства синуса, косинуса, тангенса, котангенса.
- Тригонометрия на координатной сетке.
Никаких сложных формул и длинных решений. Всё расписано максимально подробно. Изучите этот урок — и никаких проблем с тригонометрией не будет. Погнали!
1. Ключевые определения
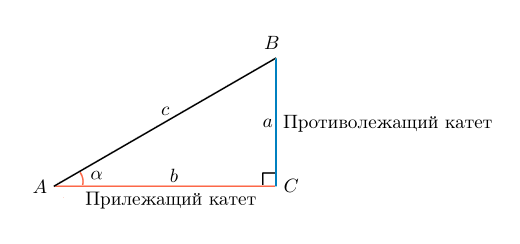
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Мы видим, что острый угол $alpha $ образован гипотенузой $c$ и катетом $b$. Такой катет будем называть прилежащим. А катет $a$, который не участвует в формировании угла $alpha $, назовём противолежащим:
Это общепринятые названия: как только в прямоугольном треугольнике отмечен острый угол, для него немедленно можно указать прилежащий катет и противолежащий. И тут мы переходим к ключевым определениям.
1.1. Синус, косинус, тангенс, котангенс
Итак, пусть дан прямоугольный треугольник с острым углом $alpha $.
Тогда:
Определение 1. Синус угла $alpha $ — это отношение противолежащего катета к гипотенузе:
[sin alpha =frac{text{противолежащий катет}}{text{гипотенуза}}=frac{a}{c}]
Определение 2. Косинус угла $alpha $ — это отношение прилежащего катета к гипотенузе:
[cos alpha =frac{text{прилежащий катет}}{text{гипотенуза}}=frac{b}{c}]
Определение 3. Тангенс угла $alpha $ — это отношение противолежащего катета к прилежащему:
[operatorname{tg}alpha =frac{text{противолежащий катет}}{text{прилежащий катет}}=frac{a}{b}]
Определение 3. Котангенс угла $alpha $ — это отношение прилежащего катета к противолежащему:
[operatorname{ctg}alpha =frac{text{прилежащий катет}}{text{противолежащий катет}}=frac{b}{a}]
Вот так всё просто! Берём один катет, делим его на гипотенузы (или на другой катет) — и получаем выражение для синуса, косинуса, тангенса и котангенса. Все эти выражения называются тригонометрическими («тригонометрия» = «треугольники измеряю»).
Рассмотрим пару примеров.
Задача 1. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Решение. Это классический прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5. Угол $alpha $ (он же — угол $A$ или угол $BAC$) образован прилежащим катетом $AB=3$гипотенузой $AC=5$. Следовательно катет $BC=4$ — противолежащий.
Имеем:
[begin{align}sin alpha& =frac{BC}{AC}=frac{5}{4} \ cos alpha& =frac{AB}{AC}=frac{3}{5} \ operatorname{tg}alpha& =frac{BC}{AB}=frac{4}{3} end{align}]
Далеко не всегда будут получаться такие красивые ответы. Чаще они будут содержать корни — это следствие теоремы Пифагора. Но важно понимать: как только мы находим длины катетов и гипотенузу, мы сразу можем найти и синусы, косинусы, тангенсы.
Далее в примерах мы не будем считать котангенсы, потому что из формулы котангенса очевидно, что они легко выражаются через тангенсы:
[operatorname{ctg}alpha =frac{1}{operatorname{tg}alpha }]
Но об этом чуть позже.
Задача 2. Дан треугольник $ABC$. Найдите синус, косинус и тангенс угла $alpha $.
Это равнобедренный прямоугольный треугольник с катетами $AB=BC=1$. Найдём гипотенузу по теореме Пифагора:
[begin{align}{{ AC}^{2}} & ={{AB}^{2}}+{{BC}^{2}}=1+1=2 \ AC & =sqrt{2} \ end{align}]
Теперь найдём синус, косинус и тангенс:
[begin{align}sin alpha &=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos alpha &=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}alpha&=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Простое правило, чтобы не запутаться, где прилежащий катет, а где противолежащий. Просто помните: приставка «ко» означает «вместе», «сообща». Поэтому «косинус» — это «катет, лежащий рядом, к гипотенузе», «котангенс» — это «катет, лежащий рядом, к противолежащему». И никак иначе.:)
1.2. Задачи для тренировки
Перед тем как переходить к следующей части урока, предлагаю 4 примера для тренировки.
Задача 3. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{5}{13} \ cos alpha &=frac{12}{13} \ operatorname{tg}alpha &=frac{5}{12} \ end{align}]
Задача 4. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Решение.
[begin{align}sin alpha &=frac{8}{17} \ cos alpha &=frac{15}{17} \ operatorname{tg}alpha &=frac{8}{15} \ end{align}]
Задача 5. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}}&={{3}^{2}}-{{1}^{2}}=9-1=8 \ l&=sqrt{8}=2sqrt{2} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{3} \ cos alpha&=frac{2sqrt{2}}{3} \ operatorname{tg}alpha&=frac{1}{2sqrt{2}}=frac{sqrt{2}}{4} \ end{align}]
Задача 6. ►
Дан прямоугольный треугольник с острым углом $alpha $. Найдите $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
Прилежащий катет по теореме Пифагора:
[begin{align}{{l}^{2}} &={{2}^{2}}-{{1}^{2}}=4-1=3 \ l &=sqrt{3} \ end{align}]
Синус, косинус и тангенс:
[begin{align}sin alpha&=frac{1}{2} \ cos alpha&=frac{sqrt{3}}{2} \ operatorname{tg}alpha&=frac{1}{sqrt{3}}=frac{sqrt{3}}{3} \ end{align}]
Как видим, считать синусы, косинусы и тангенсы совсем несложно. Перейдём теперь к принципиально важному вопросу: а зачем вообще всё это нужно?
2. Теорема о единственности
Ключевая идея: синус, косинус, тангенс и котангенс зависят только от величины угла $alpha $ и никак не зависят от прямоугольного треугольника, в котором идут вычисления.
Такого не произойдёт. Потому что есть теорема о единственности.
2.1. Формулировка теоремы
Теорема. Значение синуса, косинуса, тангенса и котангенса острого угла в прямоугольном треугольнике определяются только величиной этого угла и никак не зависят от самого треугольника.
2.2. Доказательство
Рассмотрим произвольный острый угол $alpha $. Для удобства обозначим его вершину буквой $A$:
А затем впишем в него два произвольных прямоугольных треугольника — $ABC$ и $AMN$. Любым удобным способом. Например, можно вписать эти треугольники вот так:
А можно и вот так — это не имеет никакого значения:
Рассмотрим треугольники $ABC$ и $AMN$. Угол $A$ у них общий; углы [angle ABC=angle AMN=90{}^circ ] по условию. Следовательно, треугольники $ABC$ и $AMN$ подобны по двум углам:
[Delta ABCsim Delta AMN]
Из подобия треугольников следует двойное равенство
[frac{AB}{AM}=frac{BC}{MN}=frac{AC}{AN}]
Выпишем второе равенство — получим пропорцию
[frac{BC}{MN}=frac{AC}{AN}]
Попробуем выразить $sin alpha $. Вспомним основное свойство пропорции: произведение крайних членов равно произведению средних. Поэтому
[BCcdot AN=MNcdot AC]
Разделим обе части равенства на длину каждой гипотенузы — $AN$ и $AC$:
[begin{align}frac{BCcdot AN}{ANcdot AC} &=frac{MNcdot AC}{ANcdot AC} \ frac{BC}{AC} &=frac{MN}{AN} end{align}]
Однако по определению синуса имеем:
[begin{align}sin BAC &=frac{BC}{AC} \ sin MAN &=frac{MN}{AN} \ end{align}]
Получается, что $sin BAC=sin MAN$. Другими словами, вне зависимости от выбора треугольника для данного угла $alpha $ мы всегда будем получать одно и то же значение $sin alpha $.
То же самое касается и $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ — они зависят лишь от градусной меры угла $alpha $ и никак не зависят от конкретного прямоугольного треугольника, в котором они находятся. Теорема доказана.
3. Стандартные углы
Итак, значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $ и $operatorname{ctg}alpha $ однозначно определяются величиной угла $alpha $. Нам не важен треугольник — важна только градусная мера угла. Можно один раз посчитать синусы, косинусы и т.д. для нужных углов, а затем просто подставлять их.
Но тут мы сталкиваемся с проблемой, из-за которой многие как раз и не понимают тригонометрию. Проблема состоит из двух пунктов:
- Для большинства углов $alpha $ нельзя найти точные значения $sin alpha $, $cos alpha $, $operatorname{tg}alpha $.
- Верно и обратное: для большинства «красивых» $sin alpha $, $cos alpha $ и т.д. нельзя подобрать подходящий угол $alpha $.
Звучит немного непонятно, поэтому разберём каждый пункт на конкретных примерах.
3.1. Три стандартных угла
Существует лишь три острых угла, для которых легко считаются синусы, косинусы и т.д. Это 30°, 45°, 60°. Вот их синусы, косинусы и тангенсы:
[begin{array}{c|ccc} alpha& 30{}^circ& 45{}^circ & 60{}^circ \ hlinesin alpha & frac{1}{2} & frac{sqrt{2}}{2} & frac{sqrt{3}}{2} \ cos alpha & frac{sqrt{3}}{2} & frac{sqrt{2}}{2} & frac{1}{2} \ operatorname{tg}alpha& frac{sqrt{3}}{3} & 1 & sqrt{3} \ end{array}]
Чтобы понять, чем эти углы такие особенные, просто посчитаем все эти синусы, косинусы и тангенсы. Начнём с $alpha =45{}^circ $. Для этого рассмотрим равнобедренный прямоугольный треугольник. Мы уже встречались с ним:
Поскольку в равнобедренном треугольнике $angle A=angle B=45{}^circ $, получим:
[begin{align}sin 45{}^circ &=sin A=frac{BC}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ cos 45{}^circ &=sin A=frac{AB}{AC}=frac{1}{sqrt{2}}=frac{sqrt{2}}{2} \ operatorname{tg}45{}^circ&=sin A=frac{BC}{AB}=frac{1}{1}=1 end{align}]
Это именно те значения, которые указаны в таблице!
Теперь разберёмся с углами $alpha =30{}^circ $ и $alpha =60{}^circ $. Здесь рассуждения будут чуть сложнее. Сначала рассмотрим равносторонний треугольник $ABC$ со стороной $AB=2$ (просто так удобнее) и проведём высоту $BH$:
Мы знаем, что высота $BH$ — ещё и медиана, и биссектриса. Поэтому $AH=CH=1$, $angle ABH=angle CBH=30{}^circ $.
Следовательно, треугольник $ABH$ — прямоугольный, да ещё и с острыми углами 30° и 60°. По теореме Пифагора легко найти $BH=sqrt{3}$. Нанесём все данные на чертёж:
Разберёмся с углом 60°:
[begin{align} sin{60}^circ &=sin A=frac{BH}{AB}=frac{sqrt{3}}{2} \ cos{60}^circ&=cos A=frac{AH}{AB}=frac{1}{2} \ operatorname{tg}{60}^circ&=operatorname{tg}A=frac{BH}{AH}=sqrt{3} \ end{align}]
И с углом 30°:
[begin{align} sin{30}^circ &=sin ABH=frac{AH}{AB} =frac{1}{2} \ cos{30}^circ &=cos ABH=frac{BH}{AB} =frac{sqrt{3}}{2} \ operatorname{tg}{30}^circ &=operatorname{tg} ABH=frac{AH}{BH} =frac{1}{sqrt{3}} =frac{sqrt{3}}{3} \ end{align}]
Попробуйте повторить все эти рассуждения самостоятельно. Это очень полезное упражнение!
Возникает вопрос: как быть с другими углами? Например, можно ли найти $sin {50}^circ $? Или, быть может, $cos {10}^circ $? Спойлер: можно, но это будут очень громоздкие выражения. И у нас пока не хватает технологий, чтобы их найти.
Поэтому идём дальше и посмотрим на ситуацию с другой стороны: как подобрать угол к заданному синусу, косинусу, тангенсу?
3.2. Что с другими углами?
Взгляните ещё раз на «классический» прямоугольный треугольник, с которого мы начинали наши рассуждения:
Катеты 4 и 3, гипотенуза 5 — вполне обычный треугольник. Для него можно посчитать, например, синус острого угла $alpha $:
[sin alpha =sin A=frac{BC}{AB}=frac{3}{5}=0,6]
Итак, мы знаем синус. Внимание, вопрос: каким должен быть угол $alpha $, чтобы $sin alpha =0,6$? Сколько градусов должно быть в угле $alpha $? Ответ: неизвестно.:)
Точнее, правильнее сказать, что у нас пока нет технологий, позволяющих найти такой угол $alpha $, чтобы $sin alpha =0,6$. Хотя такой угол точно есть, ведь мы предъявили треугольник, в котором он присутствует.
Из всех этих рассуждений сделаем важный вывод. В тригонометрии мы:
- Либо берём угол и считаем для него синусы, косинусы и т.д. Но лишь для трёх острых углов — 30°, 45°, 60° — всё будет считаться быстро и красиво. Такие углы называются табличными.
- Либо берём синус, косинус или тангенс и для него пытаемся подобрать острый угол. Но лишь для табличных значений мы сможем подобрать такие углы. И да: это будут углы 30°, 45°, 60°.
Ещё раз:
Мы можем посчитать лишь синус, косинус и тангенс для трёх табличных углов.
Например, $sin 30{}^circ $, $cos 45{}^circ $, $operatorname{tg}60{}^circ $ и т.д. А всякие $sin 15{}^circ $, $cos 25{}^circ $ или $operatorname{tg}89,5{}^circ $ — не сможем. По крайней мере пока.:)
И наоборот:
Зная $sin alpha $, $cos alpha $ или $operatorname{tg}alpha $, мы сможем назвать точный угол $alpha $ только в том случае, если все эти синусы, косинусы и тангенсы — среди табличных значений.
Например, мы точно знаем, что если $sin alpha =frac{sqrt{2}}{2}$, то $alpha =45{}^circ $. Но когда $sin alpha =0,6$, мы уже не можем назвать угол $alpha $ (хотя всегда можем построить такой угол).
С этой мыслью мы и переходим к следующему пункту — свойства тригонометрических выражений.
4. Свойства синуса, косинуса, тангенса
Мы разберём три ключевых свойства:
- Связь между синусом, косинусом и тангенсом.
- Связь между острыми углами прямоугольного треугольника.
- Основное тригонометрическое тождество.
Свойствам 2 и 3 далее в курсе будут посвящены отдельные уроки. Но основные идеи полезно взять на вооружение уже сейчас.
4.1. Связь между синусом, косинусом и тангенсом
Рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Выразим синус, косинус:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
А теперь выразим тангенс и заметим, что
[operatorname{tg}alpha =frac{a}{b}=frac{a}{c}cdot frac{c}{b}=frac{sin alpha }{cos alpha }]
Точно так же можно выразить и котангенс:
[operatorname{ctg}alpha =frac{b}{a}=frac{b}{c}cdot frac{c}{a}=frac{cos alpha }{sin alpha }]
Более того, сам тангенс и котангенс тоже связаны:
[operatorname{tg}alpha cdot operatorname{ctg}alpha =frac{a}{b}cdot frac{b}{a}=1]
Мы получили три важнейших тригонометрических формулы:
Основные формулы тригонометрии:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha };quad operatorname{ctg}alpha =frac{cos alpha }{sin alpha };quad operatorname{tg}alpha cdot operatorname{ctg}alpha =1]
Эти формулы нужно знать наизусть. И понимать, откуда они берутся.
4.2. Связь между острыми углами
Рассмотрим прямоугольный треугольник $ABC$, где $angle C=90{}^circ $. Пусть градусная мера $angle A=alpha $ градусов:
Мы помним, что сумма острых углов прямоугольного треугольника равна 90°. Поэтому если $angle A=alpha $, то угол $angle B=90{}^circ -alpha $. Но тогда:
[sin alpha =sin A=frac{BC}{AB}=cos B=cos left( 90{}^circ -alpha right)]
То же самое и с косинусами:
[cos alpha =cos A=frac{AC}{AB}=sin B=sin left( 90{}^circ -alpha right)]
И даже с тангенсами и котангенсами:
[begin{align} operatorname{tg}alpha&=operatorname{tg}A=frac{BC}{AC} =operatorname{ctg}B=operatorname{ctg}left( {90}^circ -alpharight) \ operatorname{ctg}alpha&=operatorname{ctg}A=frac{AC}{BC} = operatorname{tg}B=tgleft( {90}^circ -alpha right) \ end{align}]
Другими словами, если вместо $alpha $ поставить ${90}^circ -alpha $, то исходная тригонометрическая функция поменяется на ко-функцию:
[begin{align}sin left( {90}^circ-alpharight) &=cos alpha \ cos left( {90}^circ-alpharight) &=sin alpha \ operatorname{tg}left( {90}^circ-alpharight) &=operatorname{ctg}alpha\ operatorname{ctg}left( {90}^circ-alpharight) &=operatorname{tg}alphaend{align}]
Но это ещё не всё. Есть гораздо более интересная формула.
4.3. Основное тригонометрическое тождество
Вновь рассмотрим прямоугольный треугольник с катетами $a$ и $b$, гипотенузой $c$ и острым углом $alpha $:
Запишем выражения для $sin alpha $ и $cos alpha $:
[sin alpha =frac{a}{c};quad cos alpha =frac{b}{c}]
Далее заметим, что
[begin{align} {{sin }^{2}}alpha +{{cos }^{2}}alpha&={{left( frac{a}{c} right)}^{2}}+{{left( frac{b}{c} right)}^{2}}= \ & =frac{{{a}^{2}}}{{{c}^{2}}} +frac{{{b}^{2}}}{{{c}^{2}}}= \ & =frac{{{a}^{2}}+{{b}^{2}}}{{{c}^{2}}} end{align}]
В числителе можем применить теорему Пифагора: ${{a}^{2}}+{{b}^{2}}={{c}^{2}}$, поэтому
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =frac{{{c}^{2}}}{{{c}^{2}}}=1]
Правая часть этой формулы вообще не зависит от угла $alpha $.
Основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Это равенство связывает синус и косинус одного и того же угла и верно для всех $alpha $.
С помощью основного тригонометрического тождества можно вычислять косинус, зная синус, и наоборот.
Задача 7. Найдите $18cos alpha $ для острого угла $alpha $, если $sin alpha =frac{sqrt{65}}{9}$.
Решение. Запишем основное тригонометрическое тождество:
[{{sin }^{2}}alpha +{{cos }^{2}}alpha =1]
Подставим указанное значение $sin alpha $ и выразим $cos alpha $:
[begin{align}{{left( frac{sqrt{65}}{9} right)}^{2}}+{{cos }^{2}}alpha &=1 \ frac{65}{81}+{{cos }^{2}}alpha &=1 \ {{cos }^{2}}alpha &=frac{16}{81} \ cos alpha&=pm frac{4}{9} end{align}]
Поскольку косинус угла в прямоугольном треугольнике не может быть отрицательным, выбираем вариант $cos alpha ={4}/{9};$. Остаётся сделать финальный шаг:
[18cos alpha =18cdot frac{4}{9}=2cdot 4=8]
Вот и всё! Ответ: 8.
В следующем примере мы уже не будем подробно расписывать каждый шаг. Оформим всё так, как надо оформлять на контрольных и экзаменах.
Задача 8. Найдите $48operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{8}{sqrt{113}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-{{left( frac{8}{sqrt{113}} right)}^{2}}= \ & =1-frac{64}{113}=frac{49}{113} \ sin alpha&=pm frac{7}{sqrt{113}} end{align}]
Но ${0}^circ lt alpha lt {90}^circ $, поэтому $sin alpha gt 0$. Следовательно
[sin alpha =frac{7}{sqrt{113}}]
Найдём $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{7}{sqrt{113}}cdot frac{sqrt{113}}{8}=frac{7}{8}]
Окончательный ответ:
[48operatorname{tg}alpha =48cdot frac{7}{8}=6cdot 7=42]
Ответ: 42.
Заметка на будущее: замечание о том, что угол $alpha $ острый, весьма существенно. То, как мы сейчас определяем синусы, косинусы и тангенсы (через прямоугольный треугольник), называется геометрической тригонометрией. Её проходят в 8—9 классе.
Но в 10—11 классах появится алгебраическая тригонометрия, где синусы, косинусы и т.д. вполне могут быть отрицательными. И уже не получится просто так избавиться от минуса.
Но всё это будет чуть позже. А сейчас потренируемся.
Задача 9. ►
Найдите $52cos alpha $ для острого угла $alpha $, если $sin alpha =frac{5}{13}$.
Решение. Найдём $cos alpha $:
[begin{align}{{cos }^{2}}alpha &=1-{{sin }^{2}}alpha = \ &=1-frac{25}{169}=frac{144}{169} \ cos alpha&=pm frac{12}{13} end{align}]
Поскольку $cos alpha gt 0$ для острых $alpha $, выбираем $cos alpha ={12}/{13};$. Итого
[52cos alpha =52cdot frac{12}{13}=48]
Ответ: 48.
Задача 10. ►
Найдите $1+2operatorname{tg}alpha $ для острого угла $alpha $, если $cos alpha =frac{1}{sqrt{26}}$.
Решение. Найдём $sin alpha $:
[begin{align}{{sin }^{2}}alpha &=1-{{cos }^{2}}alpha = \ & =1-frac{1}{26}=frac{25}{26} \ sin alpha&=pm frac{5}{sqrt{26}} end{align}]
Поскольку $sin alpha gt 0$ для острых $alpha $, выбираем
[sin alpha =frac{5}{sqrt{26}}]
Считаем $operatorname{tg}alpha $:
[operatorname{tg}alpha =frac{sin alpha }{cos alpha }=frac{5}{sqrt{26}}cdot frac{sqrt{26}}{1}=5]
Откуда
[1+2operatorname{tg}alpha =1+2cdot 5=11]
Ответ: 11.
5. Тригонометрия на координатной сетке
Задачи, которые мы сейчас разберём, вполне могут встретиться в ОГЭ и даже ЕГЭ. Часто в них нет прямоугольного треугольника — есть лишь угол, в который этот треугольник предлагается вписать.
Для решения задач на координатной сетке достаточно посмотреть, через какие узлы сетки проходят интересующие нас лучи. И понять, какие из этих узлов имеет смысл соединить дополнительными построениями.
Звучит страшно, но на практике всё легко.:)
Задача 11. Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение. Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ на луч $BC$.
Треугольник $BAH$ — прямоугольный, причём угол $ABC$ — один из его острых углов. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{3}{4}=0,75]
Это и есть искомый тангенс.
Ответ: 0,75.
Ещё раз: важно, чтобы основание перпендикуляра попадало в узел сетки. Иначе нахождение длины катетов резко усложняется. Попробуйте сами:
Задача 12. ►
Найдите тангенс угла $ABC$, изображённого на координатной сетке:
Решение.
Дополнительное построение: $AHbot BC$ — перпендикуляр из точки $A$ к лучу $BC$.
Треугольник $BAH$ — прямоугольный с острым углом $ABC$. Поэтому
[operatorname{tg}ABC=frac{AH}{BH}=frac{2}{4}=frac{1}{2}]
Ответ: 0,5.
Разумеется, это были совсем простые задачи. Потому что один из лучей был параллелен линиям сетки.
Куда интереснее (и полезнее) рассмотреть ситуации, где лучи направлены под углом к сетке. Суть та же: ищем и соединяем узлы на лучах. Но тут уже нужна наблюдательность.
Задача 13. Найдите тангенс угла $MNK$, изображённого на координатной сетке:
Решение. Луч $KN$ содержит лишь две точки в узлах координатной сетки — собственно, $K$ и $N$. Понятно, что если продолжить луч за точку $K$, мы найдём ещё много таких точек, но будем решать задачу с тем, что есть.
Заметим, что прямая $MN$ наклонена к линиям сетки под углом 45° и образует диагонали квадратов. Это значит, что перпендикуляр к ней тоже будет наклонён под углом 45°.
Дополнительное построение: отрезок $KH$ — диагональ одного из квадратов сетки.
Очевидно, что угол $NHK$ прямой, поэтому треугольник $KHN$ прямоугольный и содержит искомый острый угол $MNK$. Находим тангенс:
[operatorname{tg}MNK=frac{HK}{HN}=frac{sqrt{2}}{2sqrt{2}}=frac{1}{2}=0,5]
Здесь мы предположили, что сторона квадрата сетки равна 1. Но с тем же успехом можно считать, что сторона квадрата $a$:
[operatorname{tg}MNK=frac{HK}{HN}=frac{asqrt{2}}{2asqrt{2}}=frac{1}{2}=0,5]
Ответ: 0,5.
Подобные задачи считаются довольно сложными. По статистике большинство выпускников 9 классов не способны их решать. Но вы-то теперь точно справитесь. Попробуйте:
Задача 14. ►
Найдите тангенс угла $DEF$, изображённого на координатной сетке:
Решение.
Дополнительное построение: отрезок $DH$.
Очевидно, $EH=DH$, угол $EHD$ прямой. Следовательно, треугольник $EDH$ — прямоугольный и равнобедренный. Поэтому $operatorname{tg}DEF=1$.
Либо можно посчитать «напролом», полагая, что сторона квадрата сетки равна $a$:
[operatorname{tg}DEF=frac{asqrt{10}}{asqrt{10}}=1]
Ответ: 1.
Вообще, поиск «правильных» узлов на координатной сетке — это своего рода искусство. И если углубляться в эту тему, то можно быстро выйти на «полуолимпиадные» задачи.
К тому же не существует «самого правильного» дополнительного построения. Задачу на координатной сетке всегда можно решить множеством различных способов. Так, в последнем примере можно было провести перпендикуляр вот так:
И даже так (хотя вряд ли этот способ можно назвать рациональным):
Во всех случаях ответ будет один и тот же. Поэтому не бойтесь экспериментировать. И переходите к следующему уроку — к действительно важным и полезным свойствам синусов, косинусов, тангенсов и котангенсов.:)
Смотрите также:
- Радианная и градусная мера угла
- Как быстро запомнить таблицу синусов и косинусов
- Сложные логарифмические неравенства
- Сложные выражения с дробями. Порядок действий
- Задача B5: площадь фигур с вершиной в начале координат
- Обход точек в стереометрии — 2

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Формулы котангенсов
Котангенс связан с тангенсом следующим соотношением:
Котангенса половинного угла
Также котангенс половинного угла выражается в виде
Котангенса двойного угла
Котангенс тройного угла
Сумма котангенсов
Разность котангенсов
Котангенс суммы двух углов
Котангенс разности двух углов
Примеры решения задач
| Понравился сайт? Расскажи друзьям! | |
Содержание:
Построим точку
По определению тангенса острого угла получим:
Определение тангенса угла
Определение:
Тангенсом угла 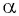
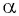
Например,
Используя определение тангенса угла и значения синуса и косинуса этого угла, найдем также значения тангенсов углов
Поскольку 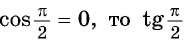
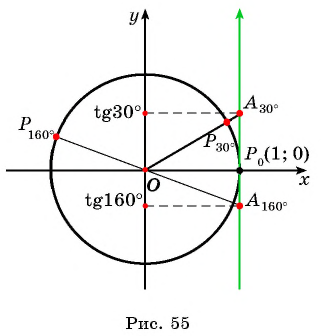
Через точку 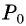
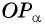
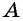
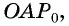
Из подобия треугольников 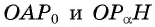
Поскольку 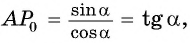
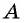
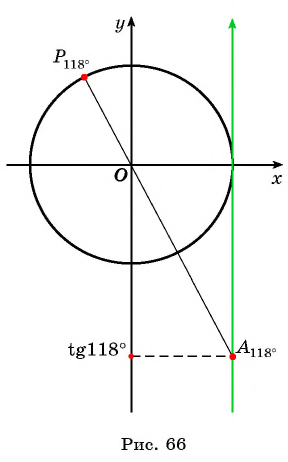
Прямая, перпендикулярная оси абсцисс, проходящая через точку 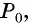
Нахождение тангенса произвольного угла
Для того чтобы найти тангенс произвольного угла а с помощью оси тангенсов, нужно:
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью тангенсов.
- Найти ординату точки пересечения прямой
с осью тангенсов.
Найдите тангенс угла
Значения тангенса произвольного угла с помощью оси тангенсов можно указать только приближенно. Для нахождения значения тангенса произвольного угла используют четырехзначные таблицы значений тангенса (синуса, косинуса)* или калькулятор. Методы высшей математики позволяют вычислять значения тангенса (синуса, косинуса) с любой заданной степенью точности.
Пример №1
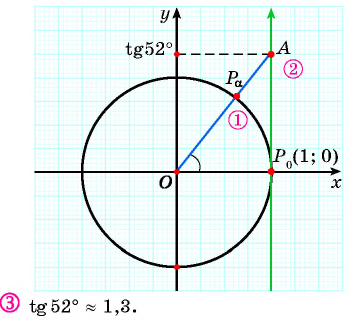
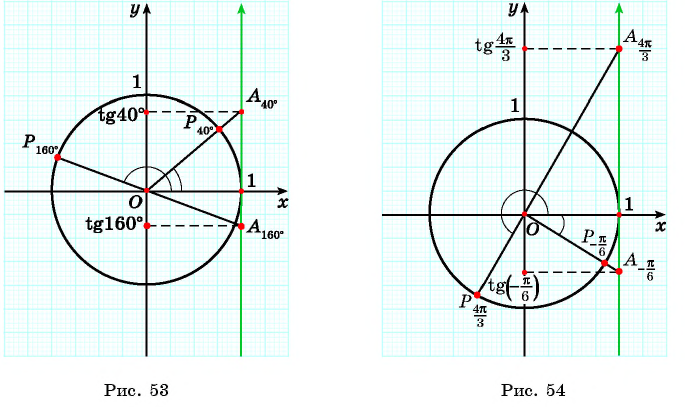
Определите с помощью оси тангенсов:
Решение:
Пример №2
С помощью оси тангенсов сравните значения выражений
Решение:
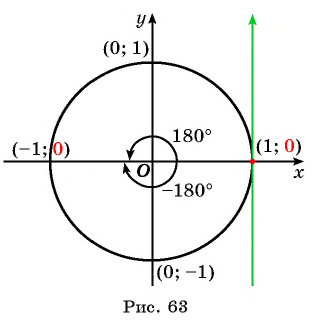
Отметим на оси тангенсов точки, соответствующие углам 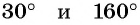
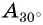
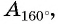
Для углов 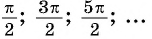
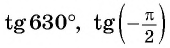
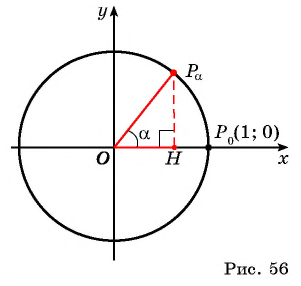
Построим точку 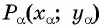
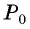
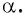
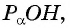
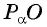
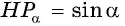
По определению котангенса острого угла получим:
Определение котангенса угла
Определение:
Котангенсом угла 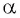
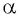
Например,
Поскольку
Воспользуемся полученным равенством и найдем значения котангенсов углов
Поскольку 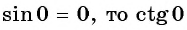
Найденные значения синуса, косинуса, тангенса и котангенса углов 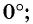
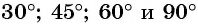
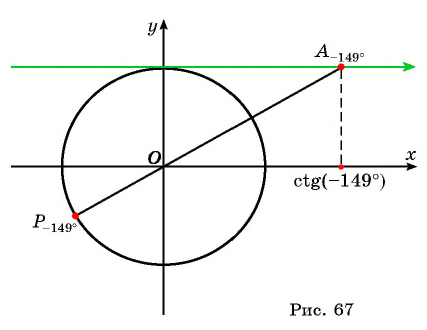
Нахождение котангенса произвольного угла
Для того чтобы найти котангенс произвольного угла 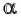
- Построить точку
на единичной окружности.
- Продолжить прямую
до пересечения с осью котангенсов.
- Найти абсциссу точки пересечения прямой
с осью котангенсов.
Значения котангенса произвольного угла с помощью оси котангенсов можно указать только приближенно.
- Заказать решение задач по высшей математике
Пример №3
Найдите значение выражения
Решение:
Через точку 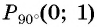
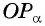
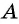
Получим треугольник 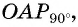
Из подобия треугольников 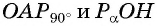
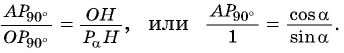
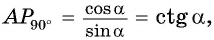
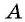
Прямая, перпендикулярная оси ординат, проходящая через точку 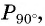
Пример №4
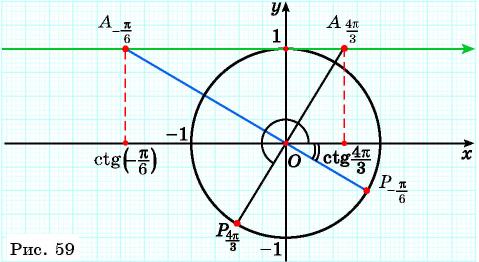
Определите с помощью оси котангенсов:
Решение:
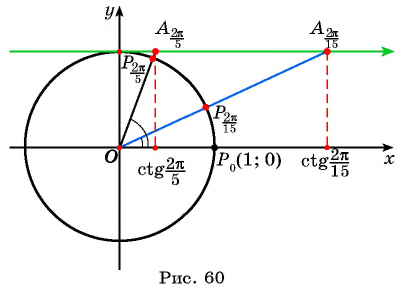
Пример №5
С помощью оси котангенсов сравните значения выражений
Решение:
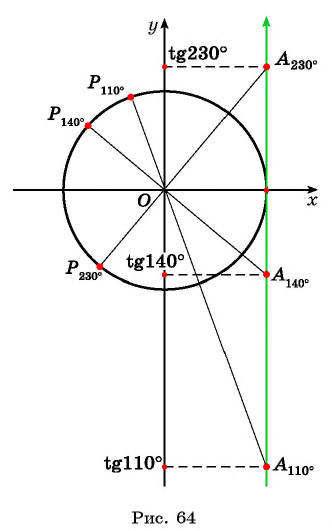
Отметим на оси котангенсов точки, соответствующие углам 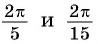
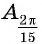
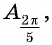
Для углов 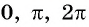
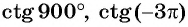
Пример №6
С помощью оси:
а) тангенсов найдите один из углов, тангенс которого равен
б) котангенсов найдите один из углов, котангенс которого равен
Решение:
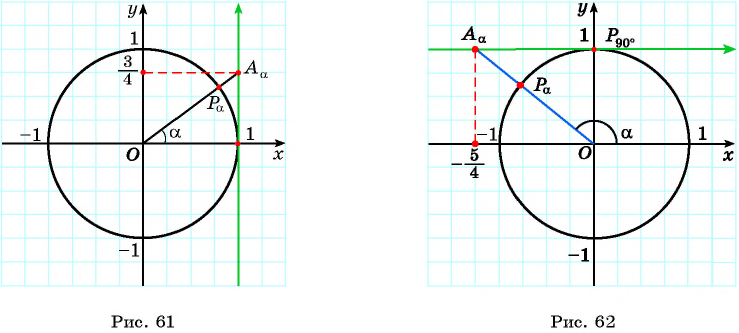
а) 1 Отметим на оси тангенсов точку 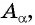
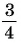
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 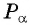
4 Отметим один из углов, соответствующий этой точке (см. рис. 61).
б) 1 Отметим на оси котангенсов точку 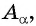
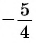
2 Соединим эту точку с началом координат.
3 Найдем соответствующую точку 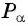
4 Отметим один из углов, соответствующий этой точке (см. рис. 62).
Пример №7
Точка 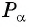
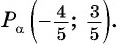
Решение:
Так как точка 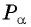
По определению тангенса:
По определению котангенса: 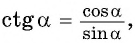
Пример №8
Найдите значение выражения
Решение:
Пример №9
Найдите, если это возможно, значение выражения:
Решение:
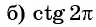
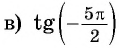
Пример №10
Если 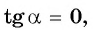
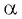
Выберите правильные ответы.
Решение:
Так как тангенсом угла 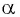
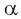
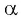
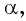
Можно также использовать ось тангенсов: найти точку на оси тангенсов, у которой ордината равна нулю (рис. 63), и определить соответствующие углы. Правильные ответы а) и г).
Пример №11
Расположите в порядке возрастания:
Решение:
Отметим на оси тангенсов точки, соответствующие углам 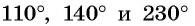
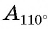
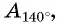
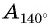
Пример №12
Верно ли, что
Решение:
Отметим на оси котангенсов точки, соответствующие углам 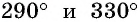
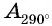
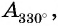
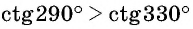
Пример №13
Определите знак выражения:
Решение:
а) Первый способ. По определению тангенса: 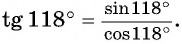
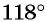
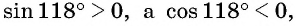
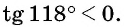
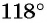
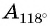
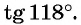
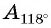
б) Первый способ. По определению котангенса 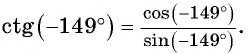
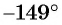
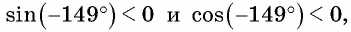
Второй способ. Отметим на оси котангенсов точку, соответствующую углу 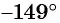
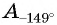
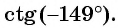
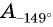
Пример №14
Определите знак произведения
Решение:
Так как угол 3 радиана находится во второй четверти, а угол 4 радиана — в третьей, то 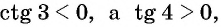
- Соотношения между синусом, косинусом, тангенсом и котангенсом одного и того же угла (тригонометрические тождества)
- Функция y=sin x и её свойства и график
- Функция y=cos x и её свойства и график
- Функции y=tg x и y=ctg x — их свойства, графики
- Дробно-рациональные неравенства
- Прогрессии в математике — арифметическая, геометрическая
- Единичная окружность — в тригонометрии
- Определение синуса и косинуса произвольного угла



























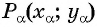
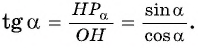
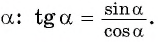
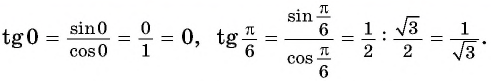
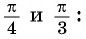
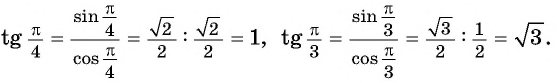
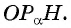
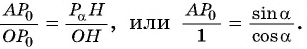
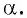
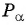 на единичной окружности.
на единичной окружности.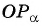 до пересечения с осью тангенсов.
до пересечения с осью тангенсов.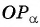 с осью тангенсов.
с осью тангенсов.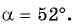

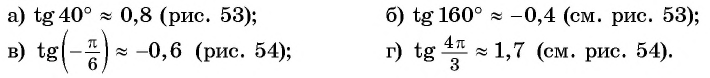
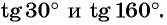
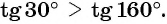
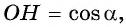
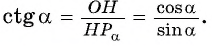
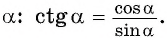
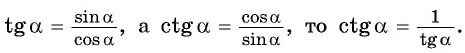
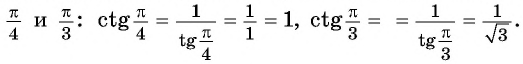
 на единичной окружности.
на единичной окружности.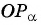 до пересечения с осью котангенсов.
до пересечения с осью котангенсов.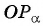 с осью котангенсов.
с осью котангенсов.