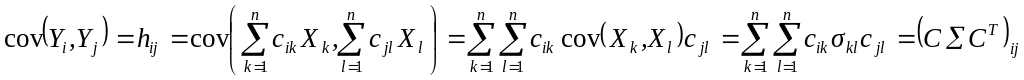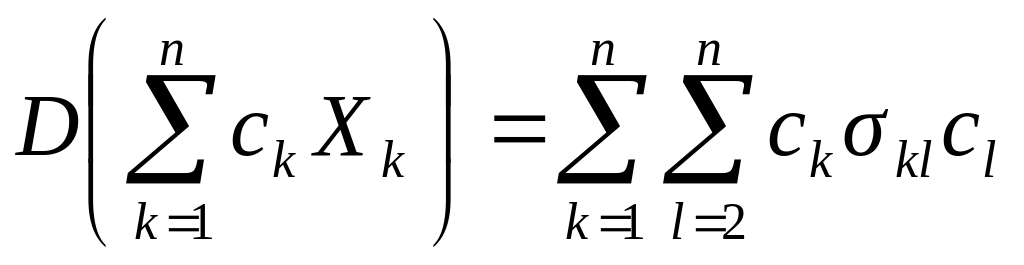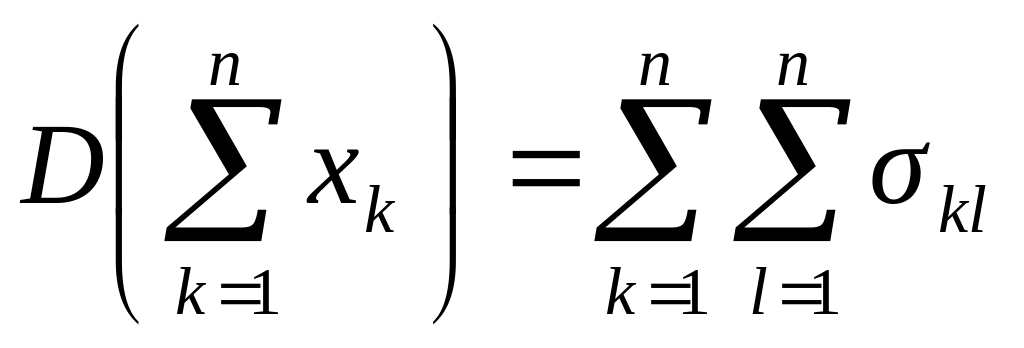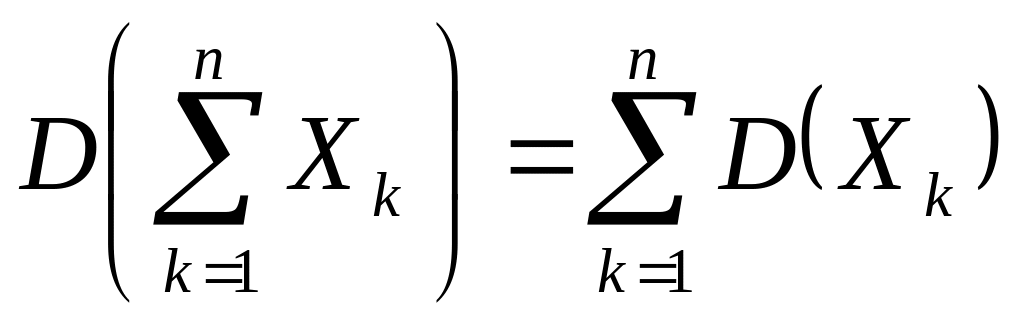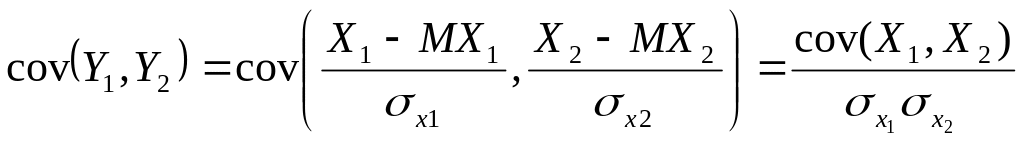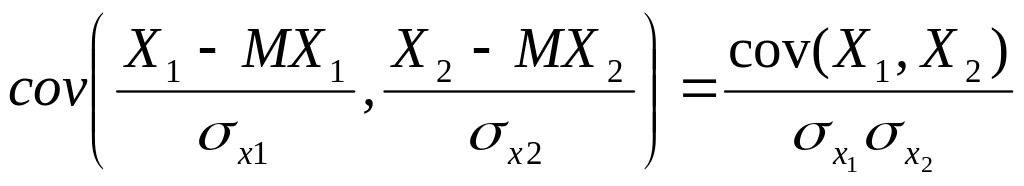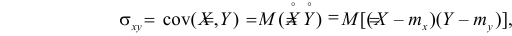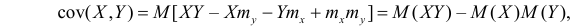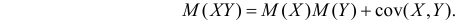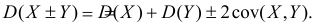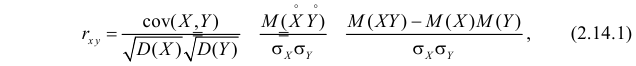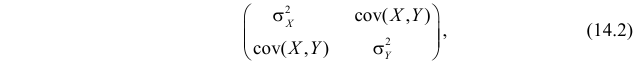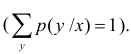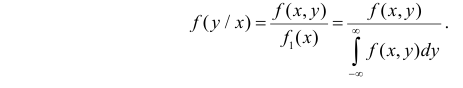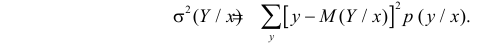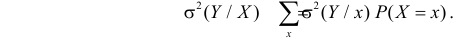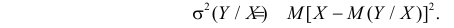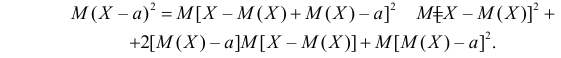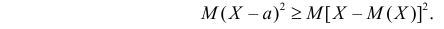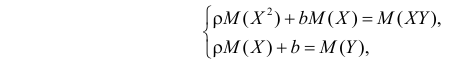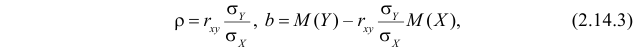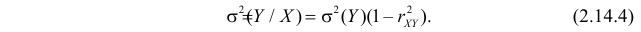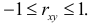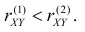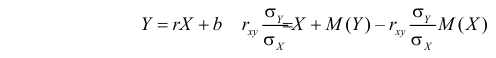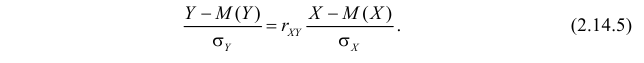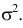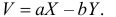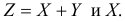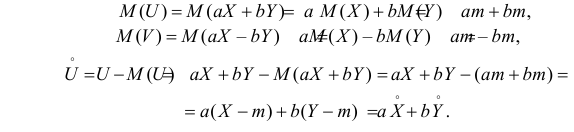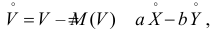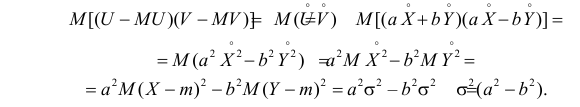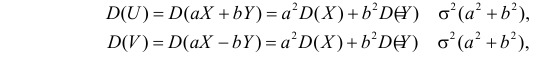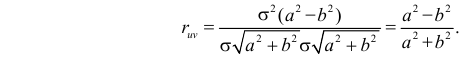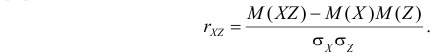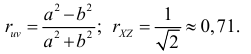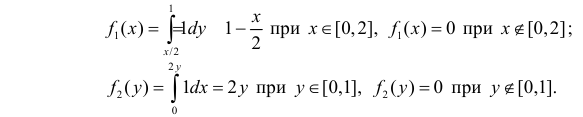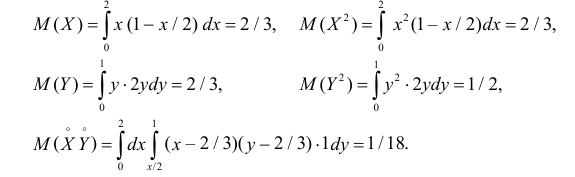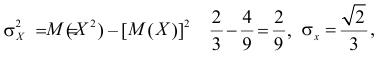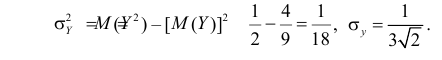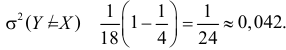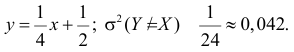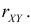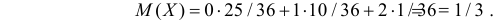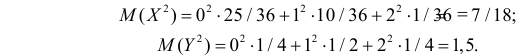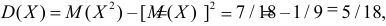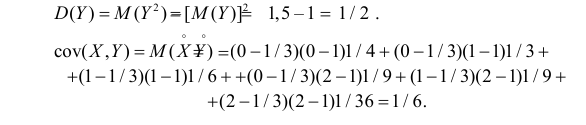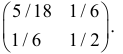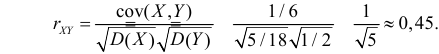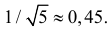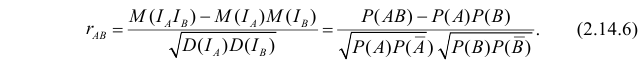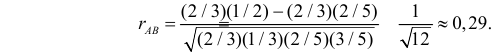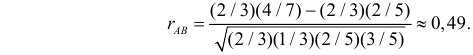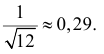Между
случайными величинами может существовать
функциональная взаимосвязь. Однако
связь может быть и такого рода, что закон
распределения одной случайной величины
изменяется в зависимости от значений,
принимаемых другой случайной величиной.
Такую зависимость называют стохастической
или вероятностной. Одной из характеристик
стохастической взаимосвязи двух
случайных величин является ковариация
случайных величин.
Определение
1.
Ковариацией
случайных величин Хi
и Хj
называется число, равное математическому
ожиданию произведения отклонений
случайных величин Хi
и Xj
от своих математических ожиданий
.
(1)
При
вычислении используется формула
.
(2)
Покажем
справедливость этого утверждения:
ij=M((Xi
– MXj)
(Xj
– MXj))
= M(Хi
Хj
– Xi
MXj
– MXj
Xj
+
MXj
MXj)
=M(Хi
Хj)
– MXj
MXj
– MXj
MXj
+ MXj
MXj
= M(Хi
Хj)
– MXj
MXj.
Если
Хi
и Хj
независимы, то ковариация равна нулю,
так как М(Хi
, Xj)
= МХiМXj.
Обратное утверждение неверно. Если
ковариация не равна нулю, то случайные
величины зависимы.
Рассмотрим
некоторые свойства ковариации:
1)
cov(X,
Y)
= cov(Y,
X);
2)
cov(X,
X)
= DX;
3)
cov(X
+
c,
Y
+
c)
= cov(X,
Y);
4)
cov(Xc1
+ Yc2,
Z)
= с1cov(X,
Z)
+ с2cov(Y,
Z),
с1,
c2
– const.
Пусть
задан случайный вектор X
=
(X1,
X2,…,
Xn).
Определение
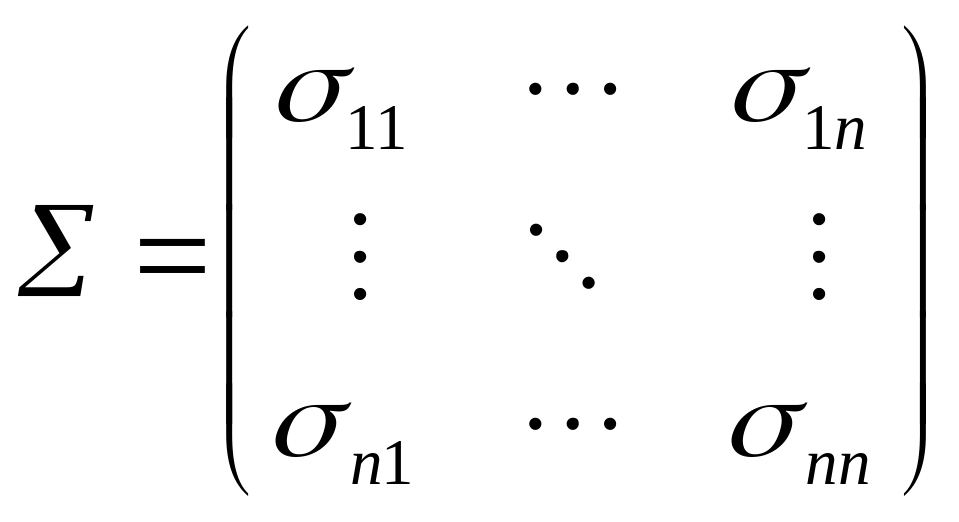
2. Ковариационной
матрицей случайного вектора X
= (X1,
X2,…,
Xn)
назвается матрица ,
элементами которой являются ковариации
:
(3)
Очевидно,
что матрица симметричная, а диагональные
элементы равны дисперсиям случайных
величин Хi,
ii
= DXi,
i
= 1,2,…
Определение
3. Определитель
ковариационной матрицы
называется обобщенной
дисперсией
случайного вектора, который характеризует
меру рассеивания случайного n-мерного
вектора.
В
теории вероятностей и её приложениях
часто появляется необходимость перейти
с помощью линейного преобразования к
новым случайным величинам, X
=
(X1,
X2,
…, Xn)→
Y
= (Y1,
Y2,
…,Ym),
при
этом
.
Обозначим
через С
=
{cij}
матрицу коэффициентов линейного
преобразования, через Х
и
Y
– векторы столбцы
,
тогда линейное преобразование можно
записать как Y
= CX.
Теорема
1.
Если для случайного вектора Х
существует
ковариационная матрица Σ, то при любых
значениях элементов матрицы С
существует
ковариационная матрица Н
для случайного вектора Y
=
CX,
причём
.
Доказательство.
Пусть
;
;
Следствие
1.
.
(4)
Доказательство.
Пусть
.
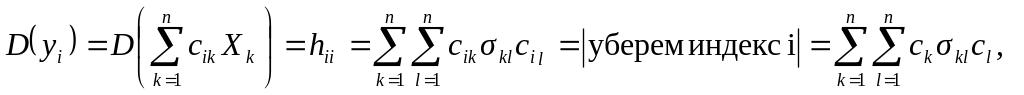
например,
если n
= 2, то
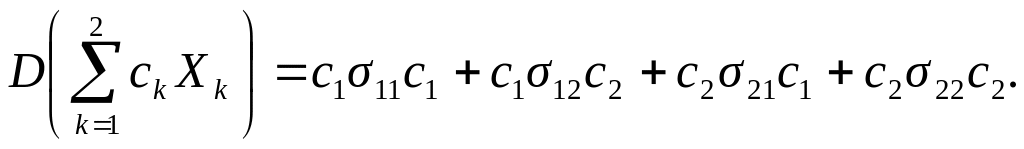
Следствие
2.
Если в формуле из следствия 1 предположить,
что
,
то
.
(5)
Следствие
3.
Если в формуле из следствия 1 предположить,
что n
=
1, то
.
Следствие
4.
Если в формуле из следствия 2 предположить,
что n
=
2, то
(6)
Следствие
5.
Если Хk
независимы, то в матрице
все недиагональные элементы равны нулю,
а диагональные элементы равны дисперсиям
соответствующих элементов Хк,
поэтому, учитывая следствие 2, имеем
.
Пример
1.
Вычислим ковариационную матрицу
случайного вектора Z
= (X,Y),
дисперсии случайных величин U1
= X+Y,
U2
= 2X–3Y
и ковариационную матрицу Н
вектора U
= (U1,
U2).
Распределение случайного вектора Z
задано в таблице.
-
J
1
2
3
4
pi
I
Yj
Xi
0
0,1
0,2
0,3
1
5
0,2
0,1
0,05
0,05
0,4
2
6
0
0,15
0,15
0,15
0,1
3
7
0
0
0,1
0,1
0,2
pj
0,2
0,25
0,3
0,25
МХ
= 5·0,4+6·0,4+7·0,2 = 5,8; М
Y
= 0·0,2+0,1·0,25+0,2·0,3+0,3·0,25 = 0,16;
М(Х,Y)=
5·0·0,2+5·0,1·0,1+5·0,05·0,2+5·0,05·0,3+6·0·0+6·0,1·0,1+6·0,15·0,2+6·0,1·0,3+7·0·0+7·0·0,1+7·0,1·0,2+7·0,1·0,3
= 0,975.
Матрица
имеет
вид
=
,
где
11
= cov(X,X),
12
= cov(X,Y),
21
= cov(Y,X),
22
= cov(Y,Y);
12
= 21
=
M(XY)-MXMY
= 0,975-5,8·0,16 = 0,047;
11
= cov(X,X)
= DX=MX2
–
(MX)2
= (52·0,4+62·0,4+72·0,2)
– 5,82
= 0,56;
22
= cov(Y,Y)
= DY
= MY2
–
(MY)2
= (0·0,2+0,12·0,25+0,22·0,3+0,32·0,25)
– 0,162
= 0,0114.
Следовательно,
=
.
Найдем
DU1
= D(X
+ Y)=
0,56
+ 0,047 + 0,047 + 0,0114 = 0,6654;
DU2
= D(2X
– 3Y)
=
c111c1
+ c112c2
+ c221c1+
c222c2
= 2·2·0,56 – 2·3·0,047 – 3·2·0,047 + 3·3·0,0114 = 1,778.
Ковариационную
матрицу вектора U
= (U1,
U2)
можно определить по формуле
,
где С
=
,
тогда Н
=
.
Из
свойств ковариации следует, что значение
ковариации линейно зависит от масштаба
измерения случайных величин. Если
изменить масштаб, то изменится и значение
ковариации, например, если от случайной
величины Х2
перейти к новой случайной величине Y2
=
с2
Х2,
то cov(X1,
Y2)
= c2cov(X1,X2).
Это свойство ковариации ограничивает
возможности его применения. Для получения
характеристики взаимосвязи случайных
величин, которая бы не зависела от
преобразования случайных величин вида
Y
= аX
+ в,
перейдем к рассмотрению нормированных
случайных величин.
Пусть
Х1,
Х2
– случайные величины. Тогда им
соответствуют нормированные величины:
,
.
Найдем
ковариацию Y1,Y2
– коэффициент
корреляции случайных величин.
Определение
4. Коэффициентом
корреляции случайных величин Х1,
Х2
называется число х1,
х2
равное ковариации нормированных
случайных величин Х1,
Х2,
т.е.
х1,
х2
=
.
Для
независимых случайных величин х1,х2
= 0, так как cov(X1,X2)
= 0. Обратное утверждение не верно (оно
справедливо только для нормально
распределенных случайных величин), но
если х1,х2
0, то случайные величины Х1,
Х2
– зависимы.
Определение
5.
Случайные
величины называются некоррелированными,
если
х1,
х2
= 0.
При
изменении масштаба случайной величины
значение корреляции не изменяется.
Рассмотрим
пример, который показывает, что из
равенства нулю коэффициента корреляции
не следует независимость случайных
величин.
Пусть
,
тогда
.
Теорема
2.
Абсолютное значение коэффициента
корреляции меньше либо равно 1:
.
Доказательство.
Пусть заданы случайные величины Х1,
Х2.
Рассмотрим нормированные случайные
величины
,
.
Тогда в соответствии с формулой (6)
следовательно,
.
Теорема
3.
,
тогда и только тогда, когда X1,
X2
связаны
линейной зависимостью, т.е. Х2
= Х1
+ ,
причем если
> 0, то
;
если <
0, то
Доказательство.
-
Пусть
.
Покажем, что Х1
и Х2
линейно
зависимы.
,
т.е.
Покажем,
что с = 0.
,
т.е.
,
следовательно
.
Запишем последнее равенство в виде
,
выразим
из него Х2:
,
обозначив
множитель при первом слагаемом ,
а два других через ,
получим, что
Х2
= Х1
+ .
Аналогичный
результат можно получить в предположении,
что
II.
Пусть Х2
= Х1
+ ,
покажем, что
.
,
,
следовательно
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
A covariance matrix is a type of matrix used to describe the covariance values between two items in a random vector. It is also known as the variance-covariance matrix because the variance of each element is represented along the matrix’s major diagonal and the covariance is represented among the non-diagonal elements. A covariance matrix is usually a square matrix. It is also positive semi-definite and symmetric. This matrix comes in handy when it comes to stochastic modeling and Principal component analysis.
What is Covariance Matrix?
The variance-covariance matrix is a square matrix with diagonal elements which represent the variance and the non-diagonal components that express covariance. The covariance of a variable can take any real value- positive, negative, or zero. A positive covariance suggests that the two variables have a positive relationship, whereas a negative covariance indicates that they do not. If two elements do not vary together, they have a zero covariance.
Covariance Matrix Example
Say there are 2 data sets X = [10, 5] and Y = [3, 9]. The variance of Set X = 12.5 and the variance of set Y = 18. The covariance between both variables is -15. The covariance matrix is as follows:
Covariance Matrix Formula
The general form of a covariance matrix is given as follows:
where,
How to find the Covariance Matrix?
The dimensions of a covariance matrix are determined by the number of variables in a given data set. If there are only two variables in a set, then the covariance matrix would have two rows and two columns. Similarly, if a data set has three variables, then its covariance matrix would have three rows and three columns.
The data pertains to marks scored by Anna, Caroline, and Laura in Psychology and History. Make a covariance matrix.
| Student | Psychology(X) | History(Y) |
|---|---|---|
| Anna | 80 | 70 |
| Caroline | 63 | 20 |
| Laura | 100 | 50 |
The following steps have to be followed:
Step 1: Find the mean of variable X. Sum up all the observations in variable X and divide the sum obtained with the number of terms. Thus, (80 + 63 + 100)/3 = 81.
Step 2: Subtract the mean from all observations. (80 – 81), (63 – 81), (100 – 81).
Step 3: Take the squares of the differences obtained above and then add them up. Thus, (80 – 81)2 + (63 – 81)2 + (100 – 81)2.
Step 4: Find the variance of X by dividing the value obtained in Step 3 by 1 less than the total number of observations. var(X) = [(80 – 81)2 + (63 – 81)2 + (100 – 81)2] / (3 – 1) = 343.
Step 5: Similarly, repeat steps 1 to 4 to calculate the variance of Y. Var(Y) = 633.
Step 6: Choose a pair of variables.
Step 7: Subtract the mean of the first variable (X) from all observations; (80 – 81), (63 – 81), (100 – 81).
Step 8: Repeat the same for variable Y; (70 – 47), (20 – 47), (50 – 47).
Step 9: Multiply the corresponding terms: (80 – 81)(70 – 47), (63 – 81)(20 – 47), (100 – 81)(50 – 47).
Step 10: Find the covariance by adding these values and dividing them by (n – 1). Cov(X, Y) = (80 – 81)(70 – 47) + (63 – 81)(20 – 47) + (100 – 81)(50 – 47)/3-1 = 481.
Step 11: Use the general formula for the covariance matrix to arrange the terms. The matrix becomes:
Properties of Covariance Matrix
- A covariance matrix is always square, implying that the number of rows in a covariance matrix is always equal to the number of columns in it.
- A covariance matrix is always symmetric, implying that the transpose of a covariance matrix is always equal to the original matrix.
- A covariance matrix is always positive and semi-definite.
- The eigenvalues of a covariance matrix are always real and non-negative.
Solved Examples on Covariance Matrix
Example 1: The marks scored by 3 students in Physics and Biology are given below:
| Student | Physics(X) | Biology(Y) |
|---|---|---|
| A | 92 | 80 |
| B | 60 | 30 |
| C | 100 | 70 |
Prepare the sample covariance matrix from the above data.
Solution:
Sample covariance matrix is given by
.
Here, μx = 84, n = 3
var(x) = [(92 – 84)2 + (60 – 84)2 + (100 – 84)2] / (3 – 1) = 448
Also, μy = 60, n = 3
var(y) = [(80 – 60)2 + (30 – 60)2 + (70 – 60)2] / (3 – 1) = 700
Now, cov(x, y) = cov(y, x) = [(92 – 84)(80 – 60) + (60 – 84)(30 – 60) + (100 – 84)(70 – 60)] / (3 – 1) = 520.
The population covariance matrix is given as:
Example 2. Prepare the population covariance matrix from the following table:
| Age | Number of People |
|---|---|
| 29 | 68 |
| 26 | 60 |
| 30 | 58 |
| 35 | 40 |
Solution:
Population variance is given by
.
Here, μx = 56.5, n = 4
var(x) = [(68 – 56.5)2 + (60 – 56.5)2 + (58 – 56.5)2 + (40 – 56.5)2 ] / 4 = 104.75
Also, μy = 30, n = 4
var(y) = [(29 – 30)2 + (26 – 30)2 + (30 – 30)2 + (35 – 30)2] / 4 = 10. 5
Now, cov(x, y) =
cov(x, y) = -27
The population covariance matrix is given as:
Example 3. Interpret the following covariance matrix:
Solution:
- The diagonal elements 60, 30, and 80 indicate the variance in data sets X, Y, and Z respectively. Y shows the lowest variance whereas Z displays the highest variance.
- The covariance for X and Y is 32. As this is a positive number it means that when X increases (or decreases) Y also increases (or decreases)
- The covariance for X and Z is -4. As it is a negative number it implies that when X increases Z decreases and vice-versa.
- The covariance for Y and Z is 0. This means that there is no predictable relationship between the two data sets.
Example 4. Find the sample covariance matrix for the following data:
| X | Y | Z |
|---|---|---|
| 75 | 10.5 | 45 |
| 65 | 12.8 | 65 |
| 22 | 7.3 | 74 |
| 15 | 2.1 | 76 |
| 18 | 9.2 | 56 |
Solution:
Sample covariance matrix is given by
.
n = 5, μx = 22.4, var(X) = 321.2 / (5 – 1) = 80.3
μy = 12.58, var(Y) = 132.148 / 4 = 33.037
μz = 64, var(Z) = 570 / 4 = 142.5
cov(X, Y) =
cov(X, Z) =
cov(Y, Z) =
The covariance matrix is given as:
FAQs on Covariance Matrix
Question 1: What is a covariance matrix?
Answer:
A covariance matrix is a type of matrix used to describe the covariance values between two items in a random vector.
Question 2: What is the general form of a 2 x 2 covariance matrix?
Answer:
The general form of a covariance matrix is given as follows:
Question 3: Is the Variance Covariance Matrix Symmetric?
Answer:
Yes, the variance-covariance matrix is symmetric. It means that the transposition of a covariance matrix will result in the original matrix. In other words, MT = M, where M is the covariance matrix.
Question 4: What are the Applications of the Covariance Matrix?
Answer:
The covariance matrix is commonly used in economics, financial engineering, and machine learning. The Cholesky decomposition performs a Monte Carlo simulation using the covariance matrix. This simulation is used to develop a variety of mathematical models.
Related Resources
- Chance and Probability
- Pie Chart
- Graphical Representation of Data
Last Updated :
09 Jan, 2023
Like Article
Save Article
| Определение: |
Пусть — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда ковариацией случайных величин (англ. covariance) и называется выражение следующего вида:
|
Содержание
- 1 Вычисление
- 2 Свойства ковариации
- 3 Неравенство Коши — Буняковского
- 4 Матрица ковариаций
- 5 Расстояние Махаланобиса
- 6 См. также
- 7 Источники информации
Вычисление
В силу линейности математического ожидания, ковариация может быть записана как:
Итого,
Свойства ковариации
- Ковариация симметрична:
- .
- Пусть случайные величины, а их две произвольные линейные комбинации. Тогда
- .
- Ковариация случайной величины с собой равна её дисперсии:
- .
| Утверждение: |
|
Если , то и не обязательно являются независимыми |
Неравенство Коши — Буняковского
| Утверждение: |
|
Докажем три аксиомы скалярного произведения:
удовлетвотряет трем аксиомам, а значит можно использовать в качестве скалярного произведения. |
| Теорема (неравенство Коши — Буняковского): |
|
Если принять в качестве скалярного произведения двух случайных величин ковариацию , то квадрат нормы случайной величины будет равен дисперсии и неравенство Коши-Буняковского запишется в виде:
|
| Доказательство: |
|
Для этого предположим, что — некоторое вещественное число, и рассмотрим очевидное неравенство , где и . Используя линейность математического ожидания, мы получаем такое неравенство: Обратим внимание, что левая часть является квадратным трехчленом, зависимым от . Мы имеем: , и Итак, наш квадратный трехчлен выглядит следующим образом: Для того, чтобы неравенство выполнялось для всех значений , дискриминант должен быть неположительным, то есть: |
Матрица ковариаций
Матрица ковариаций (англ. covariance matrix) — это матрица, элементы которой являются попарными ковариациями элементов одного или двух случайных векторов.
Ковариационная матрица случайного вектора — квадратная симметрическая неотрицательно определенная матрица, на диагонали которой располагаются дисперсии компонент вектора, а внедиагональные элементы — ковариации между компонентами.
| Определение: |
| Пусть — случайные вектора размерности и соответственно. — случайные величины. Тогда матрицей ковариаций векторов называется
|
Например, ковариационная матрица для случайного вектора выглядит следующим образом:
Замечание
- Если , то называется матрицей ковариации вектора и обозначается как — вариация (дисперсия) случайного вектора.
Свойства
- Матрица ковариации случайного вектора неотрицательно определена:
- Перестановка аргументов:
- Матрица ковариации аддитивна по каждому аргументу:
- Если , то
Расстояние Махаланобиса
Расстояние Махаланобиса (англ. Mahalanobis distance) — мера расстояния между векторами случайных величин, обобщающая понятие евклидова расстояния.
| Определение: |
| Пусть — многомерный вектор, — матрица ковариации, тогда расстояние Махаланобиса от до множества со средним значением определяется как |
Расстояние Махаланобиса двух случайных векторов с матрицей ковариации — это мера различия между ними.
Замечание
- Если матрица ковариации равняется единичной матрице, то расстояние Махалонобиса равняется расстоянию Евклида.
См. также
- Корреляция случайных величин
- Дисперсия случайной величины
Источники информации
- НГУ — Ковариация двух случайных величин
- Википедия — Ковариация
- Википедия — Матрица ковариации
- Википедия — Расстояние Махалонобиса
- Википедия — неравенство Коши — Буняковского (доказательство)
Содержание:
Ковариация:
Важную информацию о системе случайных величин
которая называется ковариацией или ковариационным моментом. Заметим, что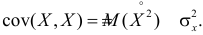
откуда
Кроме того,
Если случайные величины X и Y независимы, то их ковариация равна нулю и тогда
Ковариация содержит информацию о зависимости между величинами. Но значение 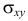
которая называется коэффициентом корреляции величин X и Y.
Величины 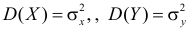
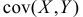
которую называют ковариационной матрицей системы случайных величин (X,Y).
Корреляционная зависимость
Наиболее простой и известной формой зависимости между величинами является функциональная зависимость, при которой каждому значению аргумента соответствует строго определенное значение функции. Функциональная зависимость может быть и между случайными величинами. Существует иной, широко распространенный в природе, тип зависимости между случайными величинами. Эта зависимость проявляется в том, что закон распределения одной случайной величины изменяется при изменении другой. Такая зависимость называется статистической.
Следует заметить, что функциональная зависимость бывает лишь в теоретических построениях или в условиях специально подготовленных опытов. Физический опыт в том и состоит, что исследователь старается по возможности исключить влияние всех посторонних факторов и наблюдать зависимость в чистом виде.
Явления окружающего нас мира взаимосвязаны и воздействие одной переменной на другую происходит при одновременном воздействии множества других переменных, поэтому даже функциональные зависимости проявляются как зависимости статистические.
Итак, при статистической зависимости изменение одной величины приводит к изменению закона распределения другой. Если Y – дискретная случайная величина, то это означает, что при каждом фиксированном значении 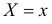
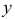
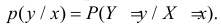
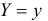
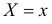
Набор возможных значений 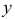
Для непрерывной случайной величины можно ввести понятие условной функции распределения или условной плотности вероятности. Если рассмотреть вероятности событий 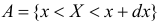
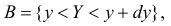
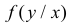
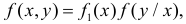
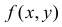
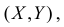
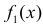
На протяжении этого раздела будем проводить выкладки только для дискретных случайных величин. Для непрерывных случайных величин все рассуждения и выводы останутся в силе, если заменить суммы на интегралы, а вероятности на плотности вероятности.
Статистическая зависимость сложна для изучения. Трудно проследить за изменением всего закона распределения сразу. Проще сосредоточиться на изучении изменения числовых характеристик, в первую очередь математического ожидания. Условный закон распределения имеет числовые характеристики такие же, как и обычные законы распределения. В частности, 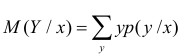
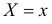
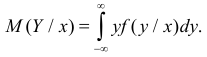
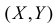
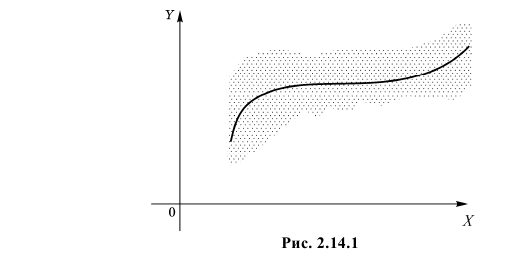
Корреляционной зависимостью Y от X называется функциональная зависимость условного среднего значения Y от X. Графиком корреляционной зависимости служит линия регрессии. Например, рост человека X и его вес Y связаны статистической зависимостью. Для каждого значения роста существует целое распределение возможных значений веса. Между этими величинами существует и корреляционная зависимость, которая для людей зрелого возраста выражается известной формулой:
Вместе с изменением условного среднего значения может изменяться и разброс Y относительно условного среднего значения. При каждом 142 значении 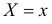
Всякую зависимость изучают для того, чтобы уметь по известному значению одной величины предсказывать значение другой. При статистической зависимости между величинами можно использовать для прогноза линию регрессии. Если стало известно, что 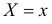
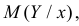
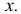
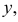
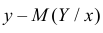
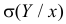
Представление о среднем квадрате ошибки прогноза Y по линии регрессии дает средняя из условных дисперсий
Здесь значения 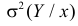
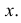
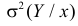
Заметим, что при прогнозе Y по любой другой линии средний квадрат ошибки прогноза будет больше. В самом деле, для любой постоянной
Второе слагаемое в правой части равно нулю, так как 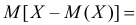
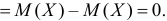
Равенство возможно лишь при 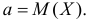
Линейная корреляция
Корреляция называется линейной, если линия регрессии одной величины на другую является прямой. В противном случае говорят о нелинейной корреляции.
Пусть линия регрессии имеет вид 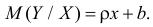
причем ее минимальное значение равно
Параметры 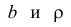
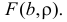
решения которой имеют вид
где 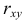
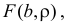
Из соотношений (2.14.3) и (2.14.4) можно извлечь информацию о свойствах коэффициента корреляции.
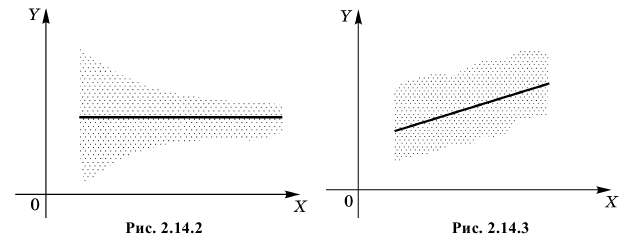
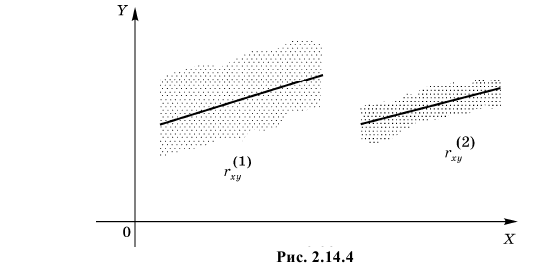
1. Так как 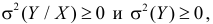
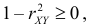
2. Если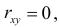
3. Из (2.14.3) следует, что угловой коэффициент линии регрессии 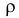
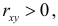
Если 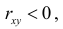
4. Если 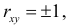
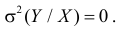
5. Из (2.14.4) следует, что 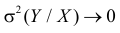
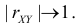
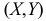
Коэффициент корреляции служит мерой линейной зависимости между величинами. Он показывает насколько статистическая зависимость близка к функциональной.
Отметим, что в силу (2.14.3) уравнение линии регрессии можно записать в виде
или
Пример №1
Случайные величины X и Y независимы и имеют одинаковое распределение с математическим ожиданием 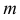
1) Найти коэффициент корреляции случайных величин 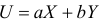
2) Найти коэффициент корреляции между случайными величинами
Решение. 1) По определению 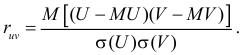
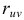
Аналогично,
Так как X и Y независимы, то
В результате имеем
2) Вычислим величины, которые необходимы для использования формулы
Так как X и Y независимы, то
Поэтому
Ответ.
Пример №2
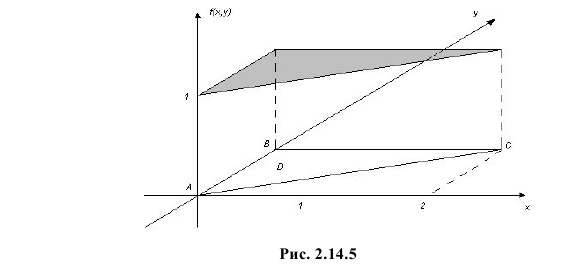
Равновозможны все положения случайной точки 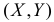
Решение. Равновозможность всех положений случайной точки 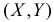
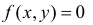
Площадь треугольника АВС равна 1. В точках треугольника положим 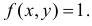
Маргинальные функции плотности вероятности величин X и Y равны соответственно:
Вычислим величины, необходимые для использования формул (2.14.3) и (2.14.5):
Тогда
По формулам (2.14.3), (2.14.5) находим коэффициент корреляции 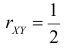
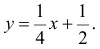
Ответ.
Пример №3
Подбрасывают два игральных кубика. Пусть X – число выпавших «пятерок», а Y – число нечетных очков. Найдите закон 149 распределения случайного вектора 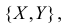
Решение. Если кубики однородны и симметричны, то вероятность выпадения каждой грани равна 1/6. Запишем сначала закон распределения случайного вектора 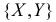
В клетках таблицы записаны вероятности 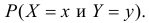
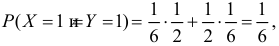
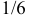
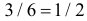
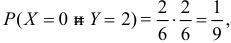
Заметим, что X имеет биномиальное распределение. Поэтому математическое ожидание можно было подсчитать проще: 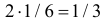
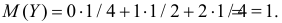
Тогда
Дисперсионная матрица случайного вектора имеет вид
Коэффициент корреляции равен
Ответ.
Замечание. Рассмотрим индикатор события A:
Известно, что 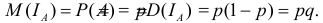
Коэффициент 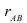
Если 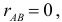
Чем ближе к плюс единице значение 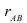
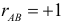
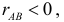
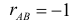
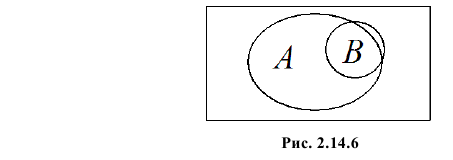
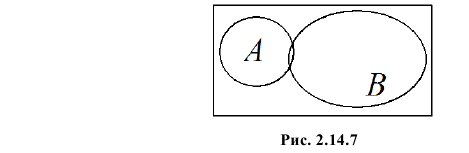
Пример №4
В одной урне четыре белых и два черных шара, а во второй два белых и три черных. Обозначим через A и B выбор белого шара соответственно из первой и второй урны. Ясно, что 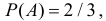
Решение. Для вычисления коэффициента корреляции воспользуемся формулой (2.14.6):
Заметим, что в случае добавлении не одного, а двух белых шаров во вторую урну этот коэффициент равен
Ответ.
- Функциональные преобразования двухмерных случайных величин
- Правило «трех сигм» в теории вероятности
- Производящие функции
- Теоремы теории вероятностей
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
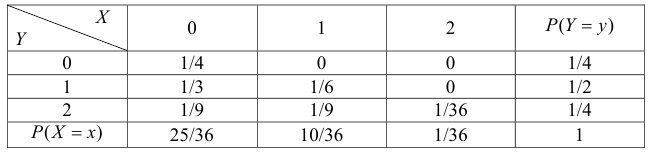
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
—
определить одномерные законы распределения случайных величин X и Y;
— найти
условные плотности распределения вероятностей величин;
—
вычислить математические ожидания mx и my;
—
вычислить дисперсии σx и σy;
—
вычислить ковариацию μxy;
—
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |