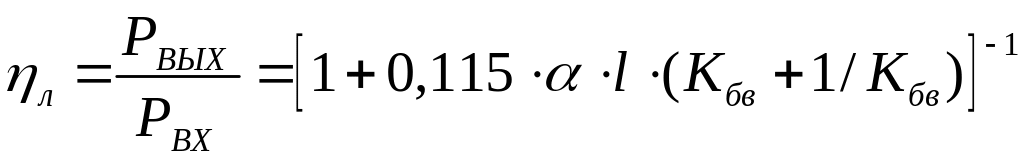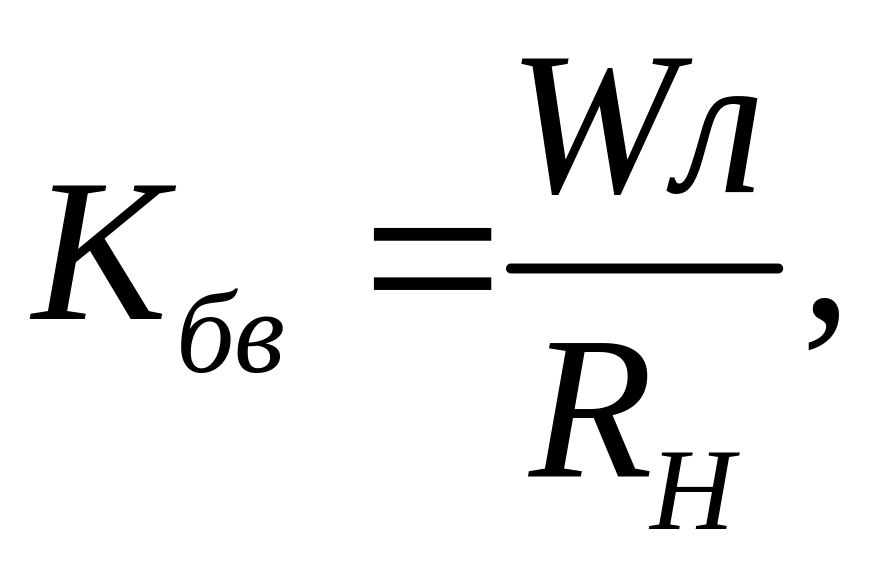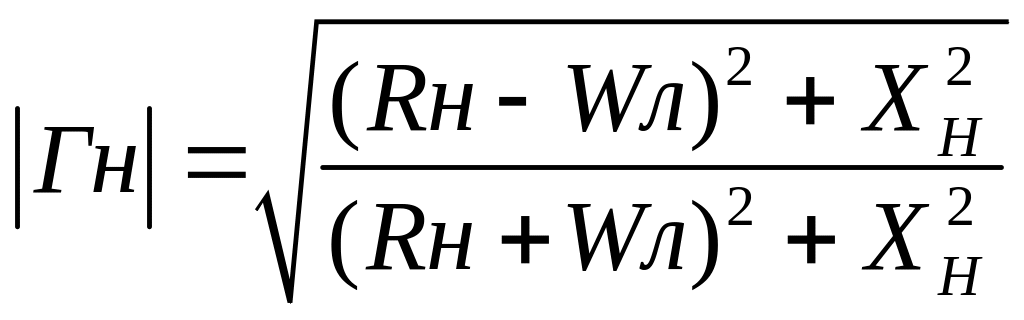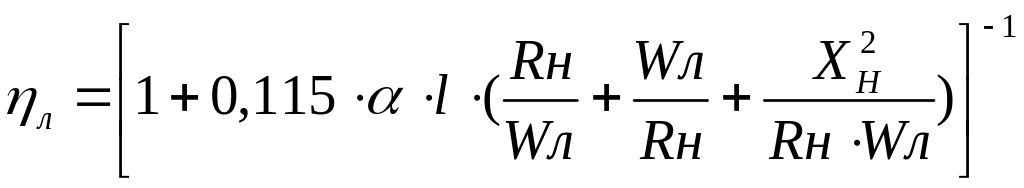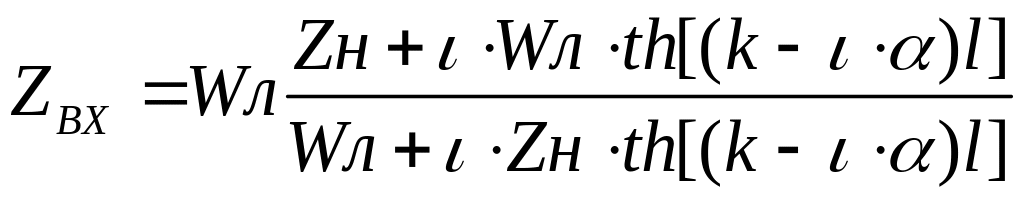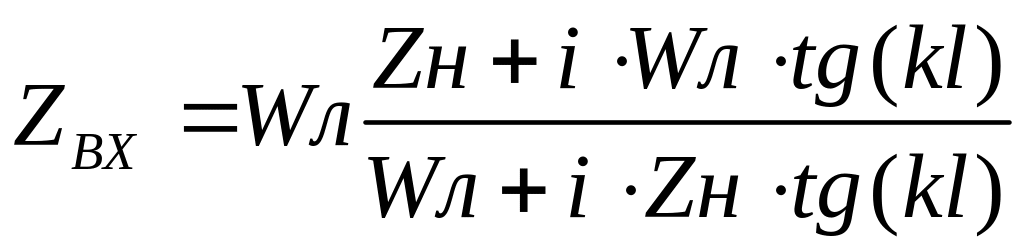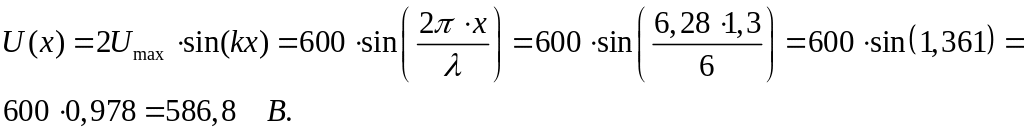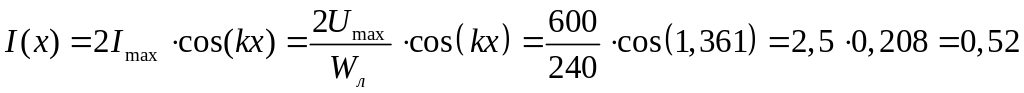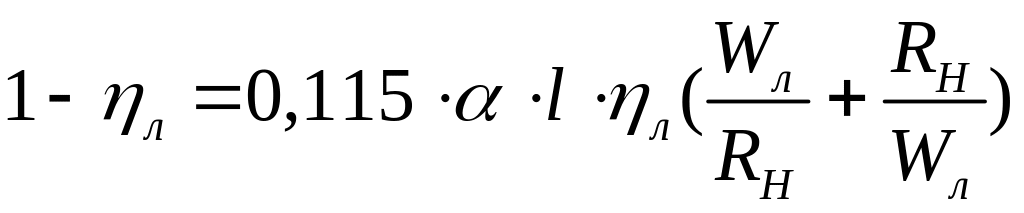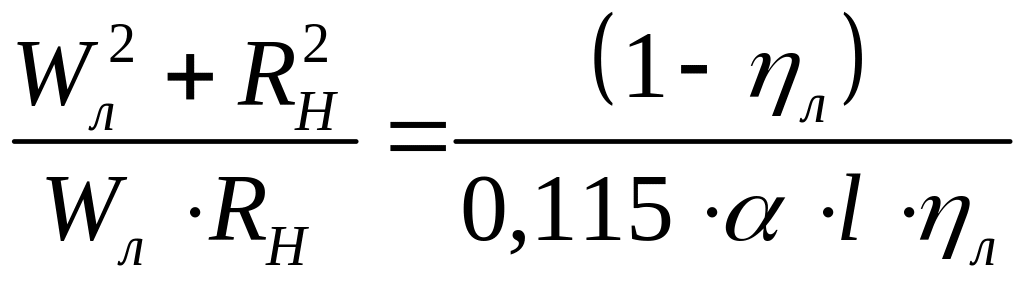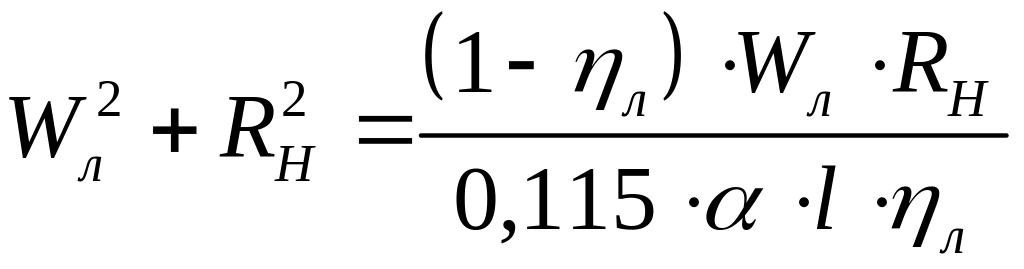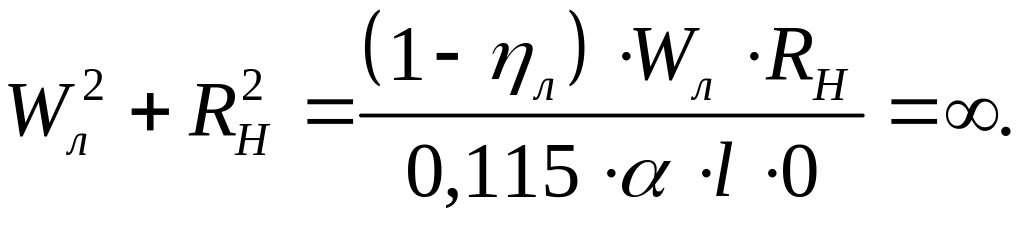Как найти кпд линии передач

3.1Основные формулы
для расчёта энергетических соотношений
в линиях передач

Коэффициент
полезного действия (КПД) линий передач,
согласованный с генератором и не
согласованной с нагрузкой определяется
по формуле

,
(3.1)

где
Р_ВЫХ
и Р_ВХ
 мощности на входе и на выходе линии
передачи, 
 коэффициент затухания дБ/м, а

—
длинна линии в метрах.

Коэффициент
бегущей волны К_бв—
определяется через максимальные (Uмакс,
Iмакс)
и минимальные (Uмин,
Iмин)
значения токов и напряжений

,
(3.2)

где│‌‌Гн│
 модуль
коэффициента отражения от нагрузки.

При
активной нагрузке и



а при


.
При комплексной нагрузке

.
(3.3)

В этом случае КПД

.
(3.4)

КПД линии
согласованной с нагрузкой

,
(3.5)

где
Pн-мощность,
отдаваемая в нагрузку,

Рвх—
мощность на входе линии.

Мощность потерь
в линии

. (3.6)

Распределение
напряжения U(x)
и I(x)
вдаль линии без потерь

,
(3.7)

,
(3.8)

где

,

Uн
и Iн
– амплитуда
тока и напряжения на нагрузке,

х
– расстояние от конца линии.

В
последних выражениях, в случае короткого
замыкания (КЗ), принимают Uн
= 0, а в случае
холостого хода (ХХ) Iн
= 0. При КЗ
получим

,
(3.9)

,
(3.10)

а при ХХ

,
(3.11)

,
(3.12)

где
2Umax—
напряжение в точках пучности,

2Imax=2Umax/Wл—
ток в этих же точках.

При
согласованной нагрузке (Zн=Wл)
в линии распространяются чисто бегущие
волны

U(x)=Uн,

(3.13)

I(x)=Uн/Wл,
(3.14)

Входное сопротивление
линии с потерями

,
(3.15)

где

—
сопротивление нагрузки,

Wл—
волновое сопротивление линии,

  коэффициент
затухания [м^-1],

—
длина линии,

—
волновое число.

Для линии без
потерь

,
(3.16)

При коротком замыкании

,
при холостом ходе

,
а при согласовании
.

Входное
сопротивление четверть волновой линии
с небольшими потерями определяется из
выражений:

для режима холостого
хода

,
(3.17)

и для короткого
замыкания

,
(3.18)

где
R₁—
погонное активное сопротивление ЛП.

Добротность
в контуре, образованного четверть
волновой линией, находится по формуле

.
(3.19)

3.2 Примеры решения
типовых задач расчёта энергетических
соотношений в линиях передач

3.2.1. Двухпроводная
воздушная (ε=1) линия передачи,
короткозамкнутая на конце имеет размеры:
диаметр проводов 2r =
4 мм, расстояние между проводами
d = 10 см, длина l
= 8 м. Определить амплитуду напряжения
на входе линии, если амплитуда тока на
конце линии 2I_max=
1,5 А, а частота питающего генератора f
= 15 МГц.

r
=
2
мм,
d
= 10
см,
l
= 8,
2I_max=
1,5 А, f
= 15 Мгц.
U_вх(l
= 8
)?

Решение.

1.Вычислим волновое
сопротивление W_л
двухпроводной
воздушной (ε=1)
линии передачи

W_л
=(276/( ε )^0,5)
∙
lg
(
d/
r
)
=(276/(
1
)^0,5)
∙
lg
(
10/
0,2
)
= 468,9 Ом.

2.Вычислим
амплитуду напряжения 2∙
U_max

2∙
U_max
= 2∙
I_max∙
W_л=
1,5∙
468,9
= 703,35 B.

3.Вычислим
ко­эффициент
фазы β

β
= 2∙π / λ
=2∙π ∙ f
/ c =
6,28 ∙15
∙10⁶/3∙10³
=0,314 рад./м.

4.Вычислим
амплитуду
напряжения
на входе линии

U_вх(l
= 8 )
= 2∙
U_max
∙sin
(β
∙
l)
= 703,35
∙sin
(0,314
∙
= 414,14
В.

Ответ
U_вх(l
= 8 )
= 414,14 В.

3.2.2.
Во сколько раз
возрастет максимальная амплитуда
напряжения на линии, если при неизменной
мощности в нагрузке КБВ упадет с 1 до
0,25? Как при этом изменится максимальная
амплитуда тока в линии?

Решение:

Ответ:
.

3.2.3.
От
генератора
на
вход линии
передачи, коротко- замкнутой
на конце, подается напряжение
U_BX
= 600
В
частотой
f
= 50
МГц.
Определить амплитуды
тока и напря­жения
на расстоянии
х
= 1,3
м от
конца линии, если ее вол­новое
сопротивление Wл
= 240
Ом.

Решение:

1. λ=с/
f=3∙10⁸
/5∙10⁷=6м.

При
х
= 1,3
м и КЗ
получим

А.

Ответ:

А.

3.2.4.

Напряжение
на зажимах генератора, питающего
разомкнутую линию передачи длиной l
= 12
м,
составля­ет U_BX
= 50 В.
Найти напряжение на конце линии, если
час­тота генератора
f = 10
Мгц.

Решение:

.

kx
=2π∙x/
λ=2π∙x
f /
c=6,28∙12∙
10⁷/
3∙10⁸=2,512.

B.

Ответ:

B.

3.2.5.

Линия
передачи нагружена на активное
сопро­тивление, больше волнового.
Определить величину напря­жения на
нагрузке, если минимальный ток в линии
I_мин
= 0,4
А,
максимальный ток I_мax
= 0,64
А,
а напряжение на расстоянии x
= λ
/4 от нагрузки
U
(х)
=
500
В.

Решение:

0,4/0,64=
0,625.

=
U_Н
соs(2π∙
λ
/4
λ)+

+i
I_НW_лsin(2π∙
λ
/4
λ)=0+i
I_НW_л
=500
В.

I_НW_л
=
I_НR_HK_бв=500
В.

При активной
нагрузке и



R_H=500/
(I_НK_бв).

U_H=I_Н
R_H=
I_Н500/
(I_НK_бв)=
500/K_бв=500/0,625=
800
В.

Ответ:

3.2.6.

Двухпроводная
воздушная (ε
= 1) линия переда­чи, разомкнутая на
конце, имеет размеры: диаметр прово­дов
2
r
= 4
мм,
расстояние между проводами
d
= 16
мм, длина
l
= 8
м.
Генератор, питающий линию, работает на
частоте
f
= 15
МГц.
Определить напряжение и ток на входе
линии, если на расстоянии
х
= 1,7
м
от ее конца амплитуда напряжения
U
(х)
=
42
В.
Решение:

Для
х=1,7м

kx
=2π∙x/
λ=2π∙x
f /
c=6,28∙1,7∙1,5∙
10⁷/
3∙10⁸=0,5338.

В.

W_Л,
Ом =
=

Ом.

A.

Для х=
l=

8 м

k
l
=0,314∙8=2,512.

В.

Ответ:

A.

В.

3.2.7.

Линия
передачи без потерь нагружена на активное
сопротивление
R_H
= 400
Ом,
равное волновому, и питается от генератора
синусоидальных колебании. Внутреннее
со­противление генератора R_Г=
600 Ом, ЭДС имеет амплитуду Э_Г
=
100
В.
Определить напряжение на зажимах
генератора
и
мощность,
выделяемую на нагрузке.

Решение:

R
=R_H
+R_Г=
400+600=1000
Ом.

I
=
Э_Г
/R=100/1000=0,1
A.

U
_Г
=
Э_Г
—I
R_Г=100-0,1∙600=40
B.

P=
U²/(2∙
R_H)
= 40²/(2∙
400)
= 2 Bт.

Ответ:
U
_Г
= 40 B. P=2
Bт.

3.2.8.

Линия
передачи нагружена на активное
сопротив­ление
R_H
= 90
Ом.
Каким должно быть волновое сопротив­ление
линии, чтобы КБВ в линии был равен 0,75?

Решение:

При активной
нагрузке и



а при


.

При активной
нагрузке и

имеем:

=
90∙0,75=67,5 Ом.

При активной
нагрузке и

имеем:

=90/0,75=120
Ом.

Ответ:
при

67,5
Ом, а при

120
Ом.

3.2.9.

При
каком активном
нагрузочном сопротивлении КПД ли­нии
длиной l
= 300
м,
с коэффициентом
затухания
α
= 2,61
дБ/км
и
с
волновым
сопротивлением
W_л
= 650
Ом,
будет равен: а) 0,8; б) 0?

Решение:

1.
Коэффициент полезного действия (КПД)
линий передач, согласованной с генератором
и не согласованной с нагрузкой определяется
по формуле

,

где
Р_ВЫХ
и Р_ВХ
 мощности на входе и на выходе линии
передачи, 
 коэффициент затухания дБ/м, а

—
длинна линии в метрах.

Коэффициент
бегущей волны К_бв.
Учтём, что при активной нагрузке и



а при


.

При

=0,8
получим:

и

.

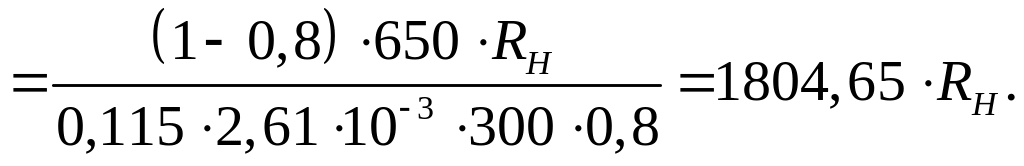
R_H1=280
Ом,
R_H2=1500
Ом.

Тогда
при

=0
получим:

Ответ: при

=0,8
R_H1=
280
Ом,
R_H2=1500
Ом,
а при

=0

3.3 Задачи для
самостоятельной работы

3.3.1. Двухпроводная
воздушная (ε=1) линия передачи,
короткозамкнутая на конце имеет размеры:
диаметр проводов 2r
мм, расстояние между проводами d
см, длина l м.
Определить амплитуду напряжения
на входе линии, если амплитуда тока на
конце линии 2I_max=
2,5 А, а частота питающего генератора f
= 12 МГц. Вариант задания для этой задачи
назначается преподавателем, и состоит
из трёх цифр. Ниже приведена таблица
2.17 с исходными данными согласно варианту
задания.

Таблица 2.17

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
2r, мм	4.4	3.7	3.6	3.9	4.8	4.1	3.6	3.4	3.7	4.2
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
d, см	10,1	11,2	10,3	9,7	9,8	11,1	9,2	9,3	11,3	9,8
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
l, м	11	12	13	9	9,85	9,5	11,5	11,2	10,3	8,9

3.3.2. От
генератора
на вход линии
передачи, короткозамкнутой
на конце, подается напряжение
U_BX
= 500
В частотой f МГц.
Определить амплитуды
тока и напря­жения на
расстоянии
х
м
от конца линии, если ее вол­новое
сопротивление Wл
Ом.
Вариант задания для этой задачи
назначается преподавателем, и состоит
из трёх цифр. Ниже приведена таблица
2.18 с исходными данными согласно варианту
задания.

Таблица 2.18

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
f МГц	60	55	50	65	70	66	68	54	75	48
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
х, м	1,25	1,15	1,28	1,3	1,35	1,32	1,38	1,25	1,17	1,25
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
Wл Ом	210	220	230	300	280	310	225	235	270	280

3.3.3.
Напряжение на зажимах генератора,
питающего разомкнутую линию передачи
длиной l
м,
составля­ет U_BX

В.
Найти напряжение на конце линии, если
час­тота генератора
f
Мгц.
Вариант
задания для этой задачи назначается
преподавателем, и состоит из трёх цифр.
Ниже приведена таблица 2.19 с исходными
данными согласно варианту задания.

Таблица 2.19

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
f , МГц	13,0	13,5	13,2	12,5	11,5	12,8	11,7	12,5	12,8	13,0
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
l, м	12,5	11,5	12,8	13,0	13,5	13,2	13,8	12,5	11,7	12,5
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
UBX, В	60	55	50	65	70	66	68	54	75	48

3.3.4.
Линия передачи нагружена на активное
сопро­тивление, больше волнового.
Определить величину напря­жения на
нагрузке, если минимальный ток в линии
I_мин
А,
максимальный ток I_мax
А,
а напряжение на расстоянии x
= λ
/4 от нагрузки
U
(х)
В.
Вариант
задания для этой задачи назначается
преподавателем, и состоит из трёх цифр.
Ниже приведена таблица 2.20
с исходными данными согласно варианту
задания.

Таблица 2.20

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
Iмин А	0,42	0,44	0,46	0,43	0,38	0,37	0,36	,0,43	0,44	0,39
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
Iмax А	0,64	0,68	0,65	0,62	0,63	0,46	0,58	0,6	0,57	0,55
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
U (х) В	600	550	500	650	700	660	680	540	750	480

3.3.5.
Двухпроводная воздушная (ε
= 1) линия переда­чи, разомкнутая на
конце, имеет размеры: диаметр прово­дов
2
r
,
мм,
расстояние между проводами
d
мм,
длина
l
= 8
м.
Генератор, питающий линию, работает на
частоте
f
= 12
МГц.
Определить напряжение и ток на входе
линии, если на расстоянии
х
м
от ее конца амплитуда напряжения
U
(х)
=
50
В.
Вариант
задания для этой задачи назначается
преподавателем, и состоит из трёх цифр.
Ниже приведена таблица 2.21
с исходными данными согласно варианту
задания.

Таблица 2.21

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
2 r , мм	4,2	4,4	4,6	4,3	3,8	3,7	3,6	, 4,3	4,4	3,9
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
х , м	1,25	1,35	1,28	1,4	1,55	1,62	1,58	1,65	1,47	1,55
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
d, мм	15,0	13,5	16,2	15,5	14,5	15,8	16,7	15,5	16,8	16,0

3.3.6.
Линия передачи без потерь нагружена на
активное
сопротивление
R_H
Ом,
равное волновому, и питается от генератора
синусоидальных колебании. Внутреннее
со­противление генератора R_Г
Ом, ЭДС
имеет амплитуду Э_Г
В.
Определить напряжение на зажимах
генератора
и
мощность,
выделяемую на нагрузке.
Вариант
задания для этой задачи назначается
преподавателем, и состоит из трёх цифр.
Ниже приведена таблица 2.22
с исходными
данными согласно варианту задания.

Таблица 2.22

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
RH, Ом	420	440	460	430	380	370	360	, 430	440	390
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
RГ, Ом	600	550	500	650	700	660	680	540	750	480
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
ЭГ, В	150	135	162	155	145	158	167	155	168	160

3.3.7.

При
каком активном
нагрузочном сопротивлении КПД ли­нии
длиной l
= 200
м,
с коэффициентом
затухания
α
дБ/км
и
с
волновым
сопротивлением
W_л
Ом,
будет равен: К.
Вариант
задания для этой задачи назначается
преподавателем, и состоит из трёх цифр.
Ниже приведена таблица 2.23
с исходными
данными согласно варианту задания.

Таблица 2.23

Первая цифра номера варианта	1	2	3	4	5	6	7	8	9	0
α, дБ/км	2,25	2,35	2,68	2,43	2,55	2,42	2,58	2,65	2,57	2,75
Вторая цифра номера варианта	1	2	3	4	5	6	7	8	9	10
Wл, Ом	600	550	500	650	700	660	680	540	750	480
Третья цифра номера варианта	1	2	3	4	5	6	7	8	9	10
К	0,82	0,64	0,76	0,53	0,68	0,77	0,86	,0,73	0,64	0,59

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

   Если линия электропередачи имеет небольшую длину, при которой можно пренебречь утечкой тока через изоляцию, то ее электрическую схему можно представить в виде последовательного соединения сопротивления линии R_Л, равного суммарному сопротивлению прямого и обратного проводов, и сопротивления нагрузки R_Н (рис. 1.23).

   При анализе работы линии нас интересуют, главным образом, три вопроса: напряжение на нагрузке, величина передаваемой мощности и коэффициент полезного действия передачи. Режимы работы линии удобно рассматривать в виде зависимостей различных величин от тока в линии, равного:

    Падение напряжения в линии ΔU и напряжение на нагрузке U₂ определяются следующими выражениями:

    Если U₁ и R_Л постоянны, то оба выражения представляют собой линейные функции тока (рис. 1.24). В режиме холостого хода (при I = 0) Δ U = 0, а U₂ = U₁. С ростом тока падение напряжения в линии возрастает, а напряжение на нагрузке уменьшается, и в режиме короткого замыкания (при R_Н = 0)

I=I_k=U₁/R₀ ,  ΔU=U ,  U₂=0; 

где, все входное напряжение гасится на сопротивлении линии.

    Мощность на входе линии линейно зависит от тока: P₁ = U₁I. При холостом ходе она равна нулю, а при коротком замыкании вычисляется по формуле:

    Потери мощности в линии представляют собой квадратичную функцию тока. Ее график – парабола, проходящая через начало координат. При I = 0: Δ P = 0; при I = I_K:

 т.е. в режиме короткого замыкания мощность, поступающая в цепь, полностью теряется в линии.

    Мощность, поступающая в нагрузку, равна разности мощности в начале линии и мощности, теряемой в проводах:

P₂ = P₁ — ΔP = U₁I — I²R_л .        (1.14)

    Последнее выражение представляет собой уравнение параболы со смещенной вершиной и с обращенными вниз ветвями, проходящими через точки I = 0 и I = I_K.

    Мощность нагрузки представляет собой довольно сложную зависимость от сопротивления R_Н:

(1.15)

При RН = 0:  Р2 = 0; при возрастании RН мощность Р2 сначала возрастает, достигает максимального значения и начинает убывать, стремясь к нулю при

R_Н →^∞           (рис. 1.25).

       Выясним, при каком сопротивлении нагрузки передаваемая ей мощность максимальна. Для этого продифференцируем функцию (1.15) по R_Н и приравняем ее к нулю:

Приравняв к нулю числитель производной, получим:

R_H + R_Л – 2R_H = 0,     или R_H = R_Л.

    То есть мощность, получаемая нагрузкой, максимальна, когда сопротивление нагрузки равно сопротивлению линии.

    Ток, протекающий при этом по линии, равен: т.е. составляет половину тока короткого замыкания, а мощность в конце линии равна:

Эти же результаты можно получить, исследуя на экстремум зависимость мощности P₂ от тока I (1.14).

    Коэффициент полезного действия равен отношению мощностей в начале и конце линии:

Он представляет собой линейную функцию тока. При холостом ходе, когда I = 0, он равен единице (нет передачи энергии – нет потерь). При коротком замыкании вся передаваемая мощность теряется в линии, и КПД равен нулю.

    Возможны и другие формулы для определения КПД:

    Из данной формулы следует, что коэффициент полезного действия передачи определяется отношением сопротивлений линии и нагрузки.

    При их равенстве, когда нагрузке передается максимальная мощность, h = 0,5 = 50 %. Этот режим, при котором теряется половина передаваемой энергии, на практике, естественно, не пригоден. В реальных линиях при передаче больших мощностей КПД составляет примерно 0,94–0,97. При этом сопротивление нагрузки значительно больше сопротивления линии.

    Для анализа режимов электропередачи полезной оказывается еще одна формула. Так как  I = P2/U2, а

,  то     

    То есть при одной и той же мощности нагрузки Р₂, потери Δ Р пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения. Для увеличения коэффициента полезного действия передачи необходимо повышение напряжения и снижение электрического сопротивления проводов линии путем увеличения их сечения и применения материалов с меньшим удельным сопротивлением.

    Пример 1.6. Линия электропередачи с проводами марки А-120 длиной l = 1000 км питает нагрузку мощностью Р₂ = 50 МВт. Каким должно быть напряжение в начале линии, чтобы КПД передачи был не ниже 90 %?

    Р е ш е н и е. Сопротивление одного километра провода марки А-120 R₀ = 0,27 Ом/км. Суммарное сопротивление прямого и обратного проводов линии составляет R_Л = 2lR₀ = 540 Ом.

    Принимая h = 0,9, из формулы (1.17) получаем:

Для выполнения условий задачи напряжение в начале линии должно быть не ниже 548 кВ.

Определение потерь напряжения и мощности в проводах линии и электропередачи

Определение потерь напряжения и мощности в проводах линии и
электропередачи

Лабораторная работа

Цель

1. Выяснить какое влияние оказывает нагрузка линии и сопротивление
её проводов на напряжение приемника.

2. Определить мощность потерь в проводах и КПД линии
электропередачи.

Теоретическое обоснование

Каждый приёмник электрической энергии рассчитан на определённое
номинальное напряжение. Так как приёмники могут находиться на значительных
расстояниях от питающих их электростанций, то потери напряжения в проводах
имеют важное значение. Допустимые потери напряжения в проводах для различных
установок не одинаковы, но не превышают 4-6% номинального напряжения.

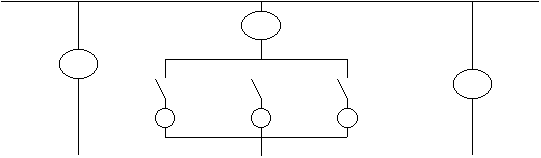
На рис. приведена схема электрической цепи, состоящая из источника
электрической энергии, приёмника и длинных соединительных проводов. При
прохождении по цепи электрического тока I показания вольтметра U₁,
включённого в начале линий, больше показаний вольтметра U₂,
включённого в конце линий.

Уменьшение напряжения в линии по мере удаления от источника
вызвано потерями напряжения в проводах линии Uⁱ=U₁-U₂ и численно равно
падению напряжения. Согласно закону Ома, падение напряжения в проводах линии
равно произведению тока в ней на сопротивление проводов: Uⁱⁱ=I*R тогда Uⁱ=U₁-U₂=Uⁱⁱ= — сопротивление проводов линии.

Мощность потерь в линии можно определить двумя способами:

Pⁱ=Uⁱ*I=(U₁-U₂)*I или Pⁱⁱ=I*R

Уменьшить потери напряжения и потери мощности в линии
электропередачи можно уменьшая силу тока в 
проводах либо увеличивая сечение 
проводов с целью уменьшения их сопротивления. Силу тока в проводах можно
уменьшить увеличивая напряжение в начале линии.

КПД линии электропередачи определяется отношением мощности,
отдаваемой электроприёмнику, к мощности, поступающей в линию, или отношением
напряжения в конце линии к напряжению в её начале:

Схема передачи электрической энергии:

Приборы и оборудование

Два вольтметра и амперметр электромагнитной системы, ламповый
реостат, двухполюсный автоматический выключатель, соединительного провода.

Порядок выполнения работы

Ознакомиться с приборами и оборудованием, предназначенными для
выполнения лабораторной работы, записать их технические характеристики.

Подать в цепь напряжение. Изменяя нагрузку с помощью лампового
реостата, при трёх её значениях записать показания приборов в таблице.

Вычислить потери двумя способами:

1. Как разность напряжений в конце и начале линий.

2. Как произведение силы тока на сопротивление проводов.

Определить мощность потерь в линии и КПД. Результаты вычислений
занести в таблицу.

Таблица изменения числа потребителей:

Изменяем напряжение в начале и конце линий.

Данные наблюдений	Результаты вычислений
Лампы, Вт	U1	U2	I	U	Pвх	Рвых	Р	%
40	150	149	0,13	1	19,5	19,4	0,1	99,3
60	148	146	0,2	2	29,6	29,2	0,4	98,6
100	150	148	0,3	2	45	44,4	0,6	98,7

; ;  ;  ;  ;

; ;  ;  ;  ;

; ;  ;  ;  ;

Вывод

На основе проведённого опыта выяснили, что факторами, влияющими на
потери в линиях являются: протяжённость линий; сечение проводника; состав
материала и количество потребителей. Чем больше потребителей, тем меньше КПД. .
Уменьшить потери напряжения и потери мощности в линии электропередачи можно
уменьшая силу тока в проводах либо увеличивая сечение проводов с целью
уменьшения их сопротивления.

Ответы на контрольные вопросы

Разность напряжений в начале и конце линий равна падению напряжения
в проводах и называется потерей напряжения.

U=IR

Сопротивление проводов зависит от материала из которого они
изготовлены, площади поперечного сечения и длины этих проводов.

КПД линии определяется отношением мощности, отдаваемой
электроприемнику, к мощности, поступающей в линию, или отношением напряжения в
конце линии к напряжению в ее начале.

Чем выше рабочее напряжение, тем ниже сила тока, а следовательно
меньше потерь.

Дата добавления: 31.10.2004

База рефератов на портале KM.RU существует с 1999 года. Она пополнялась не только готовыми рефератами, докладами, курсовыми, но и авторскими публикациями, чтобы учащиеся могли использовать их и цитировать при самостоятельном написании работ.

Это популяризирует авторские исследования и научные изыскания, что и является целью работы истинного ученого или публициста. Таким образом, наша база — электронная библиотека, созданная в помощь студентам и школьникам.

Уважаемые авторы! Если Вы все же возражаете против размещения Вашей публикации или хотите внести коррективы, напишите нам на почту info@corp.km.ru, мы незамедлительно выполним Вашу просьбу или требование.

Ознакомиться с приборами и оборудованием, предназначенными для выполнения лабораторной работы, записать их технические характеристики.

Подать в цепь напряжение. Изменяя нагрузку с помощью лампового реостата, при трёх её значениях записать показания приборов в таблице.

Вычислить потери двумя способами:

1. Как разность напряжений в конце и начале линий.

2. Как произведение силы тока на сопротивление проводов.

Определить мощность потерь в линии и КПД. Результаты вычислений занести в таблицу.

Таблица изменения числа потребителей:

Изменяем напряжение в начале и конце линий.

Источник

КПД источника тока

В процессе перемещения зарядов внутри замкнутой цепи, источником тока совершается определенная работа. Она может быть полезной и полной. В первом случае источник тока перемещает заряды во внешней цепи, совершая при этом работу, а во втором случае – заряды перемещаются во всей цепи. В этом процессе большое значение имеет КПД источника тока, определяемого, как соотношение внешнего и полного сопротивления цепи. При равенстве внутреннего сопротивления источника и внешнего сопротивления нагрузки, половина всей мощности будет потеряна в самом источнике, а другая половина выделится на нагрузке. В этом случае коэффициент полезного действия составит 0,5 или 50%.

КПД электрической цепи

Рассматриваемый коэффициент полезного действия в первую очередь связан с физическими величинами, характеризующими скорость преобразования или передачи электроэнергии. Среди них на первом месте находится мощность, измеряемая в ваттах. Для ее определения существует несколько формул: P = U x I = U2/R = I2 x R.

В электрических цепях может быть различное значение напряжения и величина заряда, соответственно и выполняемая работа тоже отличается в каждом случае. Очень часто возникает необходимость оценить, с какой скоростью передается или преобразуется электроэнергия. Эта скорость представляет собой электрическую мощность, соответствующую выполненной работе за определенную единицу времени. В виде формулы данный параметр будет выглядеть следующим образом: P=A/∆t. Следовательно, работа отображается как произведение мощности и времени: A=P∙∆t. В качестве единицы измерения работы используется джоуль (Дж).

Для того чтобы определить, насколько эффективно какое-либо устройство, машина электрическая цепь или другая аналогичная система, в отношении мощности и работы используется КПД – коэффициент полезного действия. Данная величина определяется как отношение полезно израсходованной энергии, к общему количеству энергии, поступившей в систему. Обозначается КПД символом η, а математически определяется в виде формулы: η = A/Q x 100% = [Дж]/[Дж] х 100% = [%], в которой А – работа выполненная потребителем, Q – энергия, отданная источником. В соответствии с законом сохранения энергии, значение КПД всегда равно или ниже единицы. Это означает, что полезная работа не может превышать количество энергии, затраченной на ее совершение.

Таким образом, определяются потери мощности в какой-либо системе или устройстве, а также степень их полезности. Например, в проводниках потери мощности образуются, когда электрический ток частично превращается в тепловую энергию. Количество этих потерь зависит от сопротивления проводника, они не являются составной частью полезной работы.

Существует разница, выраженная формулой ∆Q=A-Q, наглядно отображающей потери мощности. Здесь очень хорошо просматривается зависимость между ростом потерь мощности и сопротивлением проводника. Наиболее ярким примером служит лампа накаливания, КПД у которой не превышает 15%. Остальные 85% мощности превращаются в тепловое, то есть в инфракрасное излучение.

Что такое КПД источника тока

Рассмотренный коэффициент полезного действия всей электрической цепи, позволяет лучше понять физическую суть КПД источника тока, формула которого также состоит из различных величин.

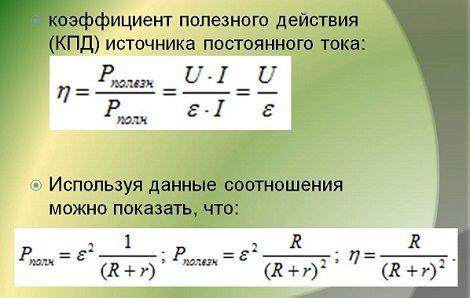
В процессе перемещения электрических зарядов по замкнутой электрической цепи, источником тока выполняется определенная работа, которая различается как полезная и полная. Во время совершения полезной работы, источника тока перемещает заряды во внешней цепи. При полной работе, заряды, под действием источника тока, перемещаются уже по всей цепи.

В виде формул они отображаются следующим образом:

• Полезная работа – Аполез = qU = IUt = I2Rt.
• Полная работа – Аполн = qε = Iεt = I2(R +r)t.

На основании этого, можно вывести формулы полезной и полной мощности источника тока:

• Полезная мощность – Рполез = Аполез /t = IU = I2R.
• Полная мощность – Рполн = Аполн/t = Iε = I2(R + r).

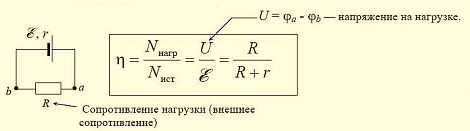
В результате, формула КПД источника тока приобретает следующий вид:

• η = Аполез/ Аполн = Рполез/ Рполн = U/ε = R/(R + r).

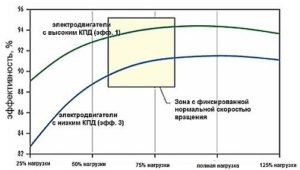
Максимальная полезная мощность достигается при определенном значении сопротивления внешней цепи, в зависимости от характеристик источника тока и нагрузки. Однако, следует обратить внимание на несовместимость максимальной полезной мощности и максимального коэффициента полезного действия.

Исследование мощности и КПД источника тока

Коэффициент полезного действия источника тока зависит от многих факторов, которые следует рассматривать в определенной последовательности.

Для определения величины тока в электрической цепи, в соответствии с законом Ома, существует следующее уравнение: i = E/(R + r), в котором Е является электродвижущей силой источника тока, а r – его внутренним сопротивлением. Это постоянные величины, которые не зависят от переменного сопротивления R. С их помощью можно определить полезную мощность, потребляемую электрической цепью:

• W1 = i x U = i2 x R. Здесь R является сопротивлением потребителя электроэнергии, i – ток в цепи, определяемый предыдущим уравнением.

Таким образом, значение мощности с использованием конечных переменных будет отображаться в следующем виде: W1 = (E2 x R)/(R + r).

Поскольку сила тока представляет собой промежуточную переменную, то в этом случае функция W1(R) может быть проанализирована на экстремум. С этой целью нужно определить значение R, при котором величина первой производной полезной мощности, связанная с переменным сопротивлением (R) будет равной нулю: dW1/dR = E2 x [(R + r)2 – 2 x R x (R + r)] = E2 x (Ri + r) x (R + r – 2 x R) = E2(r – R) = 0 (R + r)4 (R + r)4 (R + r)3

Из данной формулы можно сделать вывод, что значение производной может быть нулевым лишь при одном условии: сопротивление приемника электроэнергии (R) от источника тока должно достичь величины внутреннего сопротивления самого источника (R => r). В этих условиях значение коэффициента полезного действия η будет определяться как соотношение полезной и полной мощности источника тока – W1/W2. Поскольку в максимальной точке полезной мощности сопротивление потребителя энергии источника тока будет таким же, как и внутреннее сопротивление самого источника тока, в этом случае КПД составит 0,5 или 50%.

Задачи на мощность тока и КПД

Формула КПД электродвигателя

Что такое источник бесперебойного питания (ИБП)

Источник