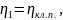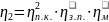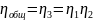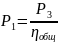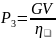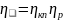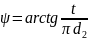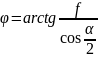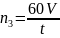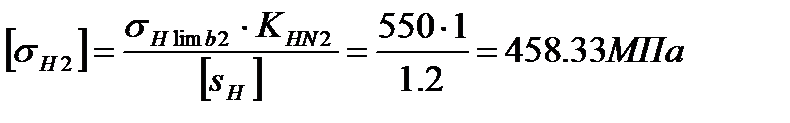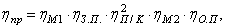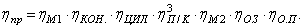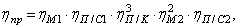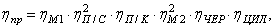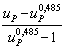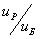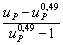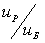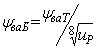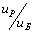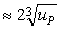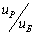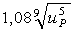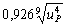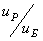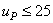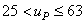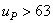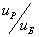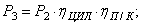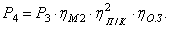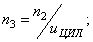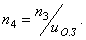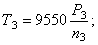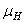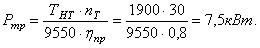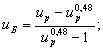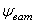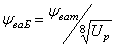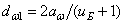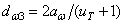Добавил:
Вуз:
Предмет:
Файл:
0713 / MU_k_KP_po_DMiOK_1.docx
Скачиваний:
2
Добавлен:
14.02.2023
Размер:
271.06 Кб
Скачать
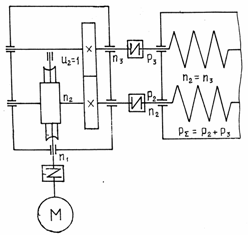
Чтобы найти значение
P1
и P2
необходимо установить значение
коэффициентов полезного действия каждой
ступени η1,
η2
и привода в цепи ηобщ.
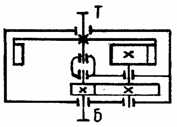
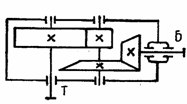
Для этого, исходя из схемы заданного
привода на рисунке 1, составляются
уравнения для определения кпд первой
и второй ступени. В уравнения вписываются
значения кпд элементов, входящих в
кинематическую цепочку передачи
мощности. В нашем примере на первой
ступени от вала электродвигателя до
быстроходного (входного) вала редуктора
имеется только клиноременная передача.
Поэтому значение кпд первой ступени
определяется по формуле:
. (13)
где
– коэффициент полезного действия
клиноременной передачи.
Для второй ступени
от быстроходного конца вала редуктора
до рабочего органа машины располагаются
две пары подшипников на валах
,
зубчатая передача
и соединительная муфта
.
При последовательном расположении
элементов привода
вычисляется по формуле:
. (14)
Общий кпд привода
равен:
. (15)
Справочные значения
кпд и передаточных отношений для
различных передач и механизмов приведены
в таблице 2.
Таблица 2. Средние
значения кпд η
и передаточных отношений u
механических передач
|
Тип передачи |
η |
u |
||
|
закрытая |
открытая |
|||
|
Зубчатая |
цилиндрическая |
0,96…0,98 |
0,92…0,94 |
3,15…6,3 |
|
коническая |
0,95…0,97 |
0,91…0,93 |
1,5…3,15 |
|
|
Червячная |
с однозаходным |
0,70…0,80 |
0,60…0,70 |
30…60 |
|
с двухзаходным |
0,75…0,85 |
15…30 |
||
|
с четырехзаходным |
0,80…0,90 |
8…15 |
||
|
Цепная |
0,95…0,97 |
0,90…0,93 |
1,5…3(4) |
|
|
Плоскоременная |
0,95…0,97 |
1,5…3 |
||
|
Клиноременная |
0,94…0,96 |
1,5…3(4) |
||
|
Плоскоременная |
0,93…0,95 |
2…4 |
||
|
Кпд одной пары Кпд |
Используя значение
кпд из таблицы 2 находим значение η1,
η2
и ηобщ
и заполняем соответствующие ячейки
матрицы 1. По значению η2
находим мощность на второй
ступени:
. (16)
Потребную мощность
на валу электродвигателя находим по
формуле:
(17)
или
. (18)
Найденные значения
P1,
P2
вносим в матрицу 1.
В заданиях по
конструированию приводов к домкратам
мощность P3
, подводимая к домкрату на
выходном валу привода необходимая для
подъема груза, определяется по формуле:
(кВт), (18)
где G–
вес поднимаемого груза, кН;
где V–
скорость поднимаемого груза, м/с;
где η–
коэффициент полезного действия домкрата.
Для реечного
домкрата η
задается в задании, а для винтового
определяется следующим образом:
. (20)
где ηкп–кпд
конической передачи домкрата вместе с
подшипниками, может быть принят равным
0,95;
ηр
– кпд передачи винт-гайка, определяемый
по зависимости:
; (21)
и
, (22)
где ψ,
t,
d2
, α
–соответственно угол подъема винтовой
линии, шаг, средний диаметр и угол профиля
резьбы, определяемый из стандарта;
f
– коэффициент трения в резьбе (может
быть принят равным 0,15).
Частота вращения
выходного вала редуктора при передаточном
числе конической передачи uк.п.=1
равна:
. (23)
Вычислением кпд
каждой ступени и привода в целом, а также
параметра мощность завершается этап
энергетического расчета.
Соседние файлы в папке 0713
- #
14.02.2023251.73 Кб02_Chervyachnoe_koleso.cdw
- #
14.02.2023267.69 Кб03_Stakan.cdw
- #
14.02.2023259.88 Кб04_kryshka.cdw
- #
14.02.2023233.85 Кб05_koleso_zubchatoe.cdw
- #
14.02.2023602.12 Кб0Detali_raschetka_Iotchenko1.xmcd
- #
- #
- #
14.02.2023607.86 Кб0Obschiy_vid.cdw
- #
- #
14.02.2023294.72 Кб0Rama.cdw
- #
14.02.2023552.8 Кб0Reduktor_Sborochny_chertezh.cdw
Определение общего КПД привода
КПД привода определяется по формуле [1, с.4]:

где ηМ – КПД муфты, принимаем ηМ=0.98;
ηЗП – КПД закрытой передачи, принимаем ηЗП=0,97;
ηОП – КПД открытой передачи, принимаем ηОП=0.95;
ηП – КПД, учитывающий потери на трение в подшипниках, ηП=0.99 [1,табл.1.1,с.5]. Тогда:
Определение угловых скоростей валов. Расчет мощностей и крутящих моментов на валах I, II и III.
Определим угловые скорости w1, w2 и w3:


Найдем значения мощностей на валах. Мощность на валу III:

где TIII – крутящий момент на валу III. TIII=2480 Нм (по условию).

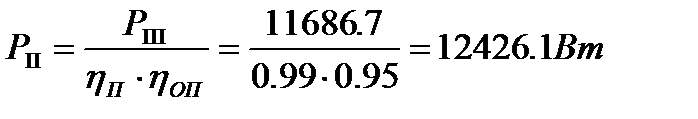

Определим требуемую мощность электродвигателя:
Далее вычислим моменты на валах привода:



Результаты энергокинематического расчета сведем в таблицу 1.1.
Таблица 1.1.Результаты энергокинематического расчета
| № вала | u | n, об/мин. | w, с -1 | Т, Нм | Р, Вт |
| 4.6 | 94.2 | 137.4 | 12939.8 | ||
| 195.6 | 20.5 | 606.2 | 12426.1 | ||
| 4.4 | |||||
| 4.7 | 11686.7 |
Расчет цилиндрической косозубой передачи.
Проектировочный расчет передачи по контактной выносливости.
По условию твердость шестерен НВ1=290. Выберем сталь 40ХН, термическая обработка – улучшение [1,стр. 34,табл.3.3].
Так как в задании нет особых требований к твердости зубчатых колес, выберем материал со средним механическими характеристиками – сталь 40Х; термическая обработка – улучшение, твердость HB=290 МПа.
Допускаемые контактные напряжения:

где 

КHL – коэффициент долговечности. При числе циклов нагружения больше базового, принимаем КHL = 1 для шестерни и колеса [с. 33].
[SH] — коэффициент безопасности, [SH] = 1.2 [1, с. 33].
Для косозубых колес расчетное допускаемое напряжение равно:

Тогда расчетное допускаемое контактное напряжение

Требуемое условие контактной выносливости [sн]£1,23[sн2] – выполняется.
Коэффициент КНβ для симметричного расположения колес относительно опор принимаем равным: КНβ=1,08 [1, табл. 3.5,с. 39,]
Принимаем для косозубых колес коэффициент ширины венца по межосевому расстоянию ψbа = b/aw = 0.3 [1, с. 33].
Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев:

где для косозубых колес Ка = 43 [1, с.32]
ТII – вращающий момент на валу колеса 2.
Ближайшее значение межосевого расстояния по ГОСТ 2185-66
Нормальный модуль зацепления принимаем по следующей рекомендации:
Принимаем по ГОСТ 9563-60: mn = 2 мм [1, с.36]
Примем предварительно угол наклона зубьев b = 15 о и определим числа зубьев шестерни и колеса [1, с.36]:
Источник
Коэффициент полезного действия цепных муфт
УДК 621.855
коэффициент полезного действия цепных муфт[1]
На основе данных кинематического и силового исследований привода с цепными муфтами существующих и новых конструкций оценены потери энергии в кинематических парах и получены зависимости КПД от конструктивных и эксплуатационных параметров муфт.
Ключевые слова: цепная муфта, коэффициент полезного действия, мощность.
Коэффициент полезного действия (КПД) цепных муфт – важный показатель совершенства их конструкции. Он, как известно, обусловлен потерей механической энергии, определяемой мощностью потерь на трение в кинематических парах. Поэтому по КПД можно прогнозировать ресурс муфт, зависящий от износа их элементов: цепи и звездочек. Заметим, что наряду с износостойкостью к основным показателям работоспособности рассматриваемых муфт относится сопротивление усталости применяемых цепей, причем усталостные поломки наблюдаются в муфтах, используемых, как правило, в быстроходном приводе. В свою очередь, КПД зависит от многих факторов: конструктивного исполнения муфты, типа цепи, условий работы (прежде всего смещение осей соединяемых валов и способ смазки) и т. п. Очевидно, существуют значения конструктивных и эксплуатационных параметров, соответствующие максимуму КПД (или минимуму потерь энергии).
Следовательно, КПД является интегральным критерием качества, определяющим область применения муфты того или иного типа. Типы муфт, КПД которых оценивается в настоящей статье, рассмотрены в литературе 2. Основой для данной работы являются результаты кинематического [4] и силового [5] исследований.
На базе нижеизложенной методики на кафедре «Машиностроительные технологии и оборудование» был разработан и реализован на ЭВМ автоматизированный расчет КПД цепных муфт [6], позволяющий получать необходимые для конструктора данные, которые дадут возможность на стадии проектирования привода машин правильно выбрать тип муфты и нормировать точность монтажа соединяемых ею узлов.
КПД муфты, как и любого устройства, можно оценить, зная мощность потерь на трение [5]:

где 




здесь 
Потери энергии в муфтах обусловлены главным образом относительными перемещениями деталей, определяемыми смещениями осей валов и крутильными колебаниями в приводе [7]. При радиальном смещении осей соединяемых валов мощность потерь на трение в шарнирах цепи

где 

Момент сил трения в j-м шарнире

где f2 – коэффициент трения скольжения внутри шарнира; dв – диаметр валика; Fc m – среднее значение силы прижатия валика к втулке.
Согласно результатам силового расчета, для цепной муфты с однорядной цепью (МЦО) [1]

где 

С учетом действия центробежных сил, развиваемых звеньями цепи,

где Fси – натяжение цепи, обусловленное силами инерции, 
Средняя угловая скорость смежных звеньев цепи

здесь 



С учетом приведенных выражений окончательно получим

Мощность потерь на трение между роликами и втулками

где 

Проведя преобразования, аналогичные рассмотренным, будем иметь

где f‘ – коэффициент трения между роликом и втулкой; dвт, d1 – диаметры втулки и ролика.
Мощность потерь на трение между роликами и зубьями полумуфт

где Fnm – среднее значение давления зуба звездочки на ролик; 
Принимая во внимание результаты силового и кинематического исследований МЦО, окончательно получим

где k – коэффициент трения качения ролика по зубу.
При угловом смещении δ осей валов мощность потерь на трение между зубьями полумуфт и шарнирами цепи

где f´ – коэффициент трения между роликом и втулкой или роликом и зубом (берется меньшее значение коэффициента).
В МЦО возможны одновременные радиальное и угловое смещения звездочек. Поэтому суммарная мощность потерь на трение

Видно, что потери мощности в муфте зависят как от нагрузки, так и от угловой скорости (влияние центробежных сил на натяжение цепи). Причем это влияние рекомендуется учитывать в тех случаях, когда

В цепной муфте с промежуточным валом (МЦПВ) возможно лишь угловое смещение полумуфт и промежуточного вала, причем

Муфты типов МЦД и МЦПКС по величине потерь мощности занимают промежуточное положение между МЦПВ и МЦО (таблица).
Источник
Определение общего КПД привода
КПД привода определяется по формуле [1, с.4]:

где ηМ – КПД муфты, принимаем ηМ=0.98;
ηЗП – КПД закрытой передачи, принимаем ηЗП=0,97;
ηОП – КПД открытой передачи, принимаем ηОП=0.95;
ηП – КПД, учитывающий потери на трение в подшипниках, ηП=0.99 [1,табл.1.1,с.5]. Тогда:
Определение угловых скоростей валов. Расчет мощностей и крутящих моментов на валах I, II и III.
Определим угловые скорости w1, w2 и w3:


Найдем значения мощностей на валах. Мощность на валу III:

где TIII – крутящий момент на валу III. TIII=2480 Нм (по условию).

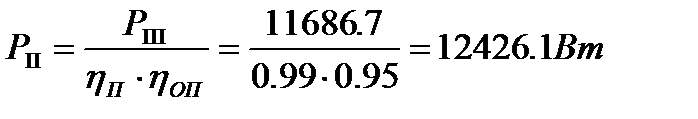

Определим требуемую мощность электродвигателя:
Далее вычислим моменты на валах привода:



Результаты энергокинематического расчета сведем в таблицу 1.1.
Таблица 1.1.Результаты энергокинематического расчета
| № вала | u | n, об/мин. | w, с -1 | Т, Нм | Р, Вт |
| 4.6 | 94.2 | 137.4 | 12939.8 | ||
| 195.6 | 20.5 | 606.2 | 12426.1 | ||
| 4.4 | |||||
| 4.7 | 11686.7 |
Расчет цилиндрической косозубой передачи.
Проектировочный расчет передачи по контактной выносливости.
По условию твердость шестерен НВ1=290. Выберем сталь 40ХН, термическая обработка – улучшение [1,стр. 34,табл.3.3].
Так как в задании нет особых требований к твердости зубчатых колес, выберем материал со средним механическими характеристиками – сталь 40Х; термическая обработка – улучшение, твердость HB=290 МПа.
Допускаемые контактные напряжения:

где 

КHL – коэффициент долговечности. При числе циклов нагружения больше базового, принимаем КHL = 1 для шестерни и колеса [с. 33].
[SH] — коэффициент безопасности, [SH] = 1.2 [1, с. 33].
Для косозубых колес расчетное допускаемое напряжение равно:

Тогда расчетное допускаемое контактное напряжение

Требуемое условие контактной выносливости [sн]£1,23[sн2] – выполняется.
Коэффициент КНβ для симметричного расположения колес относительно опор принимаем равным: КНβ=1,08 [1, табл. 3.5,с. 39,]
Принимаем для косозубых колес коэффициент ширины венца по межосевому расстоянию ψbа = b/aw = 0.3 [1, с. 33].
Межосевое расстояние из условия контактной выносливости активных поверхностей зубьев:

где для косозубых колес Ка = 43 [1, с.32]
ТII – вращающий момент на валу колеса 2.
Ближайшее значение межосевого расстояния по ГОСТ 2185-66
Нормальный модуль зацепления принимаем по следующей рекомендации:
Принимаем по ГОСТ 9563-60: mn = 2 мм [1, с.36]
Примем предварительно угол наклона зубьев b = 15 о и определим числа зубьев шестерни и колеса [1, с.36]:
Источник
Определение КПД привода



Общий КПД привода определяется как произведение КПД отдельных передач привода.
Например, для привода с двухступенчатым червячно-цилиндрическим редуктором общий КПД определяется по формуле
где hрп = 0,96 ─ КПД ременной передачи;
hзп = 0,98 ─ КПД цилиндрической зубчатой передачи;
hчп = 0,8 ─ КПД червячной передачи;
hвп = 0,85 – КПД волновой передачи;
hк = 0,96 ─ КПД конической передачи;
hп = 0,99 ─ КПД пары подшипников.
Определение требуемой мощности двигателя, Pэд.
Требуемая мощность двигателя, Pэд определяется по формуле


где, Тн ─ момент нагрузки на распределительном кулачковом валу или на выходном валу привода, Нм, задано в ТЗ;
Рэд ─ мощность электродвигателя, Вт.
x — коэффициент запаса, учитывающий динамические нагрузки в момент разгона.
По расчетному значению Рэд производится выбор электродвигателя, по табл.2.1. Техническую характеристику выбранного электродвигателя занести в таблицу 2.2.
Источник
Раздел 20. Минимизация массы и стоимости электромеханического привода
Снижение веса и габарита машин при одновременном увеличении надежности, долговечности и улучшение их качественных показателей являются важнейшими условиями дальнейшего прогресса в машиностроении. В связи с этим повышаются требования к ресурсосбережению, массогабаритным и эргономическим характеристикам.
Цель раздела — определение по главному параметру редуктора и электродвигателя их массы, стоимости на этапе технического проектирования для заданной схемы привода средств механизации пищевых машин. Дело в том, что для нахождения варианта с минимальной стоимостью привода достаточно сравнения по стоимости электродвигателей с различной частотой вращения и редукторов с различными передаточными числами, так как стоимости рамы, муфты, ременной или цепной передачи и других элементов для конкретного привода машины составляют примерно равную величину.
Проектирование начинают с ознакомления с техническим заданием (ТЗ) на проект. ТЗ на проектирование машины проектная организация получает от заказчика, где перечислены основные требования.
Задание на курсовой проект можно рассматривать как часть реального ТЗ.
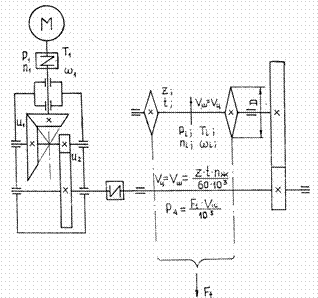
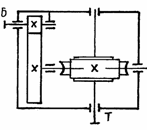
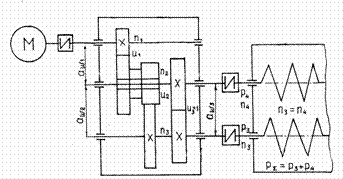
Исходные данные (рис.1 и 2). F t – окружная сила в Н на барабане ленточного или на звездочке цепного конвейера; v – скорость движения ленты или цепи в м/ c ; D б – диаметр барабана в мм; z ЗВ – число зубьев и рЗВ – шаг тяговой цепи. Для рис. 3 и 4. ТВ – вращающий момент в Нм и n C – частота вращения рабочего органа. Указывается режим работы привода и планируемый срок службы (ресурс).
Кинематический расчет привода
Двигатель является преобразователем электрической энергии в механическую и одним из основных элементов машинного агрегата. Для электромеханических приводов рекомендуются трехфазные асинхронные короткозамкнутые двигатели серии 4А. Эти двигатели универсальны, поэтому применяются в различных условиях эксплуатации. Они имеют закрытое и обдуваемое исполнение.
Двигатели серии 4А применяются для приводов установок, имеющих слабоизменяющуюся нагрузку при длительном режиме работы. Например, в приводах средств малой механизации, конвейеров, пищевых машин, грузоподъемных устройствах легкого и среднего режимов работы. Технические данные этих двигателей приведены в разделе справочные данные.
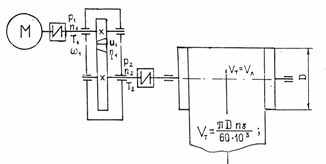
Учитывая относительно высокие пусковые плотности электродвигателей серии 4АС, целесообразно для механизмов с временем пуска до 3 с и числом включений до 120 в час.
Для машин циклического действия, работающих в повторно – кратковременном режиме менее 600 с, применяются электродвигатели серии 4МТ, например, в кранах, подъемниках, штабелерах и т.д.
Требуемая мощность привода механизма подъема груза в кВт
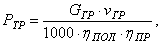
где G ГР – вес номинального поднимаемого груза механизма подъема в Н; v ГР – скорость груза в м/ c ;
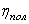
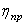
Для машин непрерывного действия требуемая мощность привода будет (схема 1 и 2)
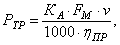
где КА – коэффициент внешней динамики;
F m – тяговое усилие конвейера для усредненной производительности в период установившегося движения в Н;
v – скорость тягового органа в м/ c .
Мощность привода при заданном усредненном моменте на валу рабочего органа в кВт (рис. 3 и 4).
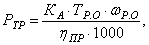
здесь Тр .о – крутящий момент в период установившегося движения для усредненной производительности;
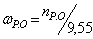
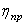
Общий коэффициент полезного действия (КПД) привода
а) для привода ленточного конвейера (ЛК) (рис. 1)
где 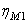
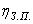
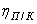
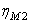
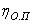
б) для привода пластинчатого конвейера (ПК) (рис. 2)
в) для привода двухвинтового пресса для отжима влаги из каныги свиней, мелкого и крупного рогатого скота (рис. 3)
здесь 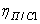
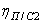
г) для привода двухвинтовых питающих шнеков волчка (рис. 4)
здесь 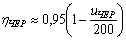
Тип передачи или устройства
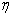
Зубчатая цилиндрическая закрытая
Зубчатая коническая закрытая
Червячная закрытая пара при
Подшипники качения (одна пара)
Подшипники скольжения (одна пара)
Далее по табл. 4 (справочные данные) подбирают электродвигатель с мощностью РЭ, кВт и частотой вращения ротора n Э , мин -1 ближайшими к РТР. При подборе РЭ допускается перегрузка двигателя до 8% при постоянной и до 12% при переменной нагрузке.
Для поиска оптимального варианта привода необходимо знать пределы передаточных чисел редуктора, освоенные передовыми странами мира (табл. 2).
u P = 8…40 при 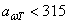
и 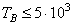
u P = 8…50 при 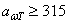
и 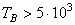
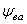
б) с раздвоенной тихоходной
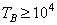
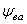
с внешним зацеплением Ц2С
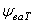
Двухсту-пенчатый соосный с
внутренним зацеплением Ц2Свн
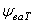
Уточнение передаточных чисел привода
Общее передаточное число привода
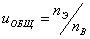
Допустим, привод, кроме редуктора, имеет открытую (ременную, цепную или зубчатую) передачу. Обычно ременная передача ставится до редуктора. Передаточное число ременной передачи подбирается таким образом, чтобы диаметр ведомого шкива был меньше или равен 1,2 d 2Т диаметру колеса тихоходной ступени ( 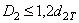
С другой стороны, 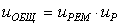
Определение мощности валов для привода пластинчатого конвейера (рис. 2) в кВт
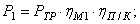
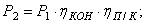
5. Частота вращения валов, мин -1
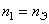
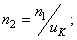
Крутящие моменты на валах в Нм
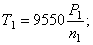
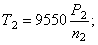
Поиск оптимального варианта привода при заданной схеме
Оптимальный вариант с электродвигателями n С = 3000; 1500; 1000 и 750, берется по результатам вычислений для всех вариантов.
Если расчет зубчатой передачи ведется по методу эквивалентных циклов, то коэффициенты долговечности определяются 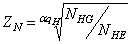
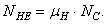
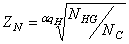
На основе обработки статистических данных для определения массы электродвигателя трехфазного переменного тока с короткозамкнутым ротором типа 4А предлагается следующая формула:
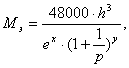
где 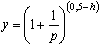
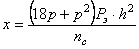
h -высота электродвигателя от основания до оси вращения в метрах;
е = 2,71 – основание натурального логарифма;
р – число полюсов электродвигателя;
nc – синхронная частота вращения двигателя, об /мин;
N э — мощность электродвигателя в кВт.
Для определения стоимости электродвигателя в У.Е. предлагается следующее выражение:
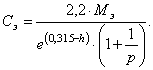
Масса редуктора определяется по нижеследующей формуле в кг
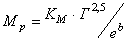
здесь КМ — коэффициент массы, зависящий от типа редуктора (таблица 3);
Г – главный параметр редуктора в метрах ( а w — межосевое расстояние цилиндрических и червячных редукторов,
d e 2— внешний делительный диаметр конического колеса);
е = 2,71 – основания натурального логарифма;
b – комплексный параметр, зависящий от типа редуктора;
КТ – коэффициент, учитывающий твердости ведущего зубчатого колеса:
б) по развернутой схеме с одной раздвоенной ступенью
3. Двухступенчатый коническо-цилиндрический
4.Трехступенчатый цилиндрический развернутый
Стоимость редуктора в У.Е. определяется по формуле:
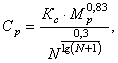
где КС – коэффициент стоимости, зависящий от термообработки зубчатых колес (таблица 4);
N – годовая программа, шт./год.
Значение КС при термообработке
и Н 1 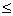
H1 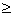
Сравнительная оценка привода ленточного конвейера, состоящего из электродвигателя, ременной передачи и редуктора Ц2С.
И с х о д н ы е д а н н ы е: ТНТ = 1900 Нм – расчетный момент на выходе редуктора; n =30 об/мин. – частота вращения на выходе; 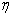
Значение 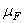
Требуемая мощность электродвигателя
В первом варианте материал зубчатых колес быстроходной ступени сталь 40ХН. Термообработка шестерни – улучшение НВ270, 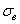
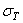
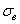
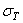
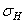
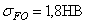
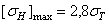
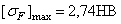
Для тихоходной ступени при рассматриваемом варианте тот же материал. Термообработка шестерни – закалка ТВЧ сквозная с охватом впадины при 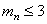
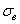
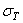
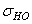
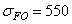
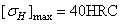
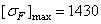
Во втором варианте для шестерни быстроходной ступени термообработка – закалка ТВЧ, а для колеса – улучшение. Для тихоходной ступени при u Р = 40 материал шестерни сталь 25 ХГТ, термообработка – цементация с последующей закалкой. НRC60, 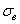
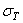
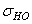
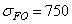
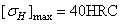
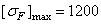
Для остальных случаев материал колес — сталь 40ХН. Термообработка шестерни и колеса – закалка ТВЧ с вышеприведенной характеристикой. Остальные данные сведены в таблицу. Здесь расчеты проведены с использованием метода эквивалентных циклов при определении коэффициентов долговечности KHL и KFL.
Синхронная частота э/ д – n С
Частота вращения валов, об /мин
Число циклов нагружения зубчатых колес
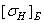
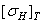
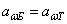
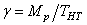
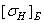
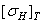
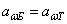
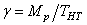
Из таблицы 5 видно, что параметры редуктора со вторым вариантом термообработки являются лучшими.
Минимальная суммарная масса для заданной схемы привода соответствует минимальной стоимости, поэтому достаточно ограничиться определением массы привода. Однако для сравнения различных вариантов привода по конструкции требуется определение минимальной стоимости и разработка ряда критериев. Здесь для каждого варианта редуктора предусмотрен индивидуальный чугунный корпус с определенными размерами, в отличие от общего корпуса с равным межцентровым расстоянием для передаточного числа от 8 до 40 завода – изготовителя.
1. При заданной кинематической схеме привода решающими управляющими параметрами являются:
а) оптимальное распределение передаточных чисел по ступеням редуктора;
б) материалы зубчатых колес ступеней и их термообработка;
в) коэффициенты ширины колес ступеней;
2. В качестве обобщенного критерия оптимизации привода можно принять минимальную суммарную массу электродвигателя с редуктором при обеспечении его надежности и требуемой долговечности.
3. Параметр технического уровня 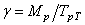
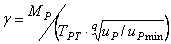
4. Если 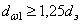
Выбор наиболее целесообразного типа редуктора и открытой передачи привода
Номенклатура показателей редукторов, мотор — редукторов и вариаторов для оценки технической характеристики и качества изделия установлена по стандарту ГОСТ 4. 124-84. Как было указано во 2– ой главе, показатели состоят из шести групп .
Необходимо отметить, что такие конструктивные показатели, как удельная масса 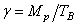
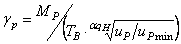
где МР – масса редуктора в кг ;
ТВ – крутящий момент на выходе редуктора в Н.м.;
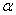
q Н — показатель ветви кривой контактной выносливости ( qН = 6 – для зубчатых редукторов; qН = 8 – для червячных редукторов);
u р – передаточное число рассматриваемого редуктора;
u р min – минимальное передаточное число редуктора из сравниваемого ряда.
Дело в том, что в российских каталогах указана марка редуктора с постоянным крутящим моментом при различных передаточных числах. При этом корпус редуктора, подшипники валов остаются неизменными. Вообще при постоянном типоразмере корпуса целесообразно указывать различные крутящие моменты в зависимости от общего передаточного числа редуктора или по крайней мере при постоянном моменте на выходе разумно применять четыре типоразмера корпуса с различными межцентровыми расстояниями, что приведено в предыдущем параграфе.
Полный средний срок службы привода по ГОСТ 27.002 – 89 должен соответствовать сроку службы машины или быть кратными для замены машинного агрегата после отработки запланированного ресурса.
Очень важным эргономическим показателем является корректированный уровень звуковой мощности – L ра , который по санитарным нормам не должен превышать 85 дБА для внутрицехового оборудования. О вредности производственного шума свидетельствует тот факт, что в США за последние десятилетия от 6 млн. до 16 млн. рабочих получили те или иные повреждения органов слуха из-за вредного действия шума на организм человека.
В настоящее время в США разработаны нормы, согласно стандарту О S НА рабочий не должен подвергаться воздействию шума свыше 90 дбА более 8 часов в день, 94 дбА – более 4 часов и 115 дБа – более 15 минут.
Источниками шума у конвейеров являются приводные агрегаты и роликоопоры . Так, например, у ленточного конвейера с движением тягового органа по сплошному гладкому настилу при скорости 0,635 м/ с возникает шум 65 дБа , а при работе с той же скоростью на роликоопорах шум составляет 75 дБа . Безусловно, уровень шума зависит от скорости тягового органа , например, роликовый конвейер с приводной лентой создает шум при скорости 0,61 м/с в пределах 74 дБа , а при скорости 0,35 м/с – 70 дБа . Установленная зависимость уровня шума от скорости тягового органа изменяется по логарифмической шкале.
Из всех видов редукторов наибольшее распространение получили редукторы с цилиндрическими эвольвентными зубчатыми колесами, благодаря высокому К ПД, надежности и долговечности, большому диапазону передаваемой мощности.
Однако зубчатые передачи не сглаживают динамические нагрузки, очень чувствительны к точности сборки и характеризуются по сравнению с червячными и ременными передачами большей интенсивностью шума и виброактивностью при износе.
Так, например, редукторы типа Ц2У-315К создают уровень шума 106 дБа , а редукторы типа Ц2Н – 500К – 116дБа, что намного превышает допустимый предел для закрытых помещений. В этой связи для приводов с редукторами Ц2У, Ц 2 , Ц3У, КЦ1 и КЦ2, МП2 предусматриваются звукоизолирующие кожухи, амортизаторы и т.д. Всероссийский научно-исследовательский и конструкторско-экспериментальный институт продовольственного машиностроения (ВНИКЭИ Продмаш ) для привода пищевых машин и внутрицеховых машин и внутрицеховых средств механизации рекомендует червячные редукторы различной конструкции, несмотря на низкий К ПД, малый срок службы, необходимость частой регулировки червячной пары в процессе эксплуатации.
Однако применение червячного редуктора и ременной передачи не дают избавления от всех проблем. Червячная передача, передавая вращение между скрещивающими валами, по сравнению с зубчатыми цилиндрическими передачами имеет следующие недостатки:
1) повышенная стоимость при изготовлении колес из цветных металлов;
2) большие потери на трение (в три — четыре, чем у эвольвентной цилиндрической передачи);
3) большие эксплутационные расходы;
4) возможность заедания при нарушении пространственного положения червячной пары;
5) малый срок службы по сравнению с зубчатыми передачами.
6) ограниченная передаваемая мощность
Коническая передача с круговыми зубьями применяются при пересекающихся осях под углом 90 0 . По сравнению с цилиндрическими конические зубчатые передачи имеют большую массу и габаритные размеры, сложнее в изготовлении. Кроме того при монтаже необходимо точная фиксация осевого положения конического зубчатого колеса. Несмотря на указанные недостатки, данная передача широко используется при необходимости по условиям компоновки.
Большое распространение в складском оборудовании и внутрицеховых машинах непрерывного транспорта получили передачи с гибкой связью. Плоскопленочные ременные, клиноременные и зубчатоременные передачи используются в основном там, где необходимо обеспечить плавность и бесшумность работы, минимальную виброактивность привода. В некоторых случаях обеспечиваются значительные межосевые расстояния при отсутствии возможности удовлетворить достаточно точное расположение узлов агрегата.
Существенными недостатками ременных передач являются большие потери на трение и низкая долговечность ремней, большие нагрузки на валы.
Размеры цепных передач и потери на трение значительно меньше, чем в ременных, однако по плавности и виброактивности , они уступают ременным и зубчатым передачам. Поэтому они применяются в качестве тихоходной передачи при значительных межцентровых расстояниях, например, в приводах роликовых конвейеров.
Для выбора наиболее целесообразного типа редуктора и открытой передачи рекомендуется сравнение различных схем привода между собой по массе, стоимости с учетом долговечности и надежности, по эргономическим и экономическим характеристикам, а также по эксплутационным расходам.
Эффективность использования энергии характеризуется коэффициентом полезного действия (табл.6).
Затраты энергии на преодоление сил трения и других потерь предлагается определить по следующей зависимости в У.Е.:
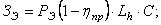
где РЭ – мощность электродвигателя в кВт;
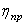
L h – срок службы привода в часах;
Источник
Эффективность гидравлической муфты Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Угловая скорость турбины: 14 Радиан в секунду —> 14 Радиан в секунду Конверсия не требуется
Угловая скорость насоса: 16 Радиан в секунду —> 16 Радиан в секунду Конверсия не требуется
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
0.875 —> Конверсия не требуется
6 Гидравлическая муфта Калькуляторы
Эффективность гидравлической муфты формула
Эффективность гидромуфты = Угловая скорость турбины/Угловая скорость насоса
η = ωt/ωp
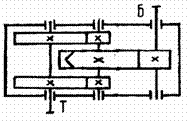
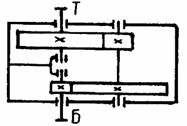
Что такое гидравлическая муфта?
Гидравлическая (или гидравлическая) муфта — это устройство, которое используется для передачи мощности от одного вала к другому через жидкую среду. У него нет механического соединения или контакта лицом к лицу.
задание КПД пары подшипников качения КПД соединительной муфты КПД цилиндричеко
Работа добавлена на сайт samzan.net: 2015-07-05
Поможем написать учебную работу
Если у вас возникли сложности с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой — мы готовы помочь.
Предоплата всего
от 25%
Подписываем
договор
26
- Выбор электродвигателя, разбивка общего передаточного отношения по ступеням, кинематический и силовой расчет
Так как мощность и частота вращения на выходном валу редуктора нам известна, то для определения требуемой мощности электродвигателя необходимо определить общее значение КПД. Общее значение КПД определяется, как произведение КПД отдельных передач, подшипников и муфт. [1.I. табл. 2.1] (см. задание).
— КПД пары подшипников качения
— КПД соединительной муфты
— КПД цилиндричекой передачи
— КПД червячной передачи
— КПД цепной передачи
Требуемая мощность электродвигателя Ртр, кВт;
Выбираем предварительное передаточное число ступеней привода по
табл 5.5[2]
червячной передачи
цилиндрической передачи
Определим требуемую частоту вращения вала электродвигателя:
где -требуемая частота вращения приводного вала рабочей машины;
=74202=2960мин-1
По каталогу [1 табл. 5.1] принимает асинхронный электродвигатель переменного трехфазного тока, закрытый обдуваемый ГОСТ 19523 – 81:
Тип электродвигателя: 4А132М2;
Мощность электродвигателя: ;
Синхронная частота вращения: ;
Скольжение: S=2.3%
Асинхронная частота вращения:
Уточним передаточное число зубчатой передачи;
uц=
Тогда передаточное число редуктора составит:
;
Погрешность передаточного отношения:
Мощности на валах :
Определим частоты вращения валов :
Определяем крутящие моменты передаваемые валами Ті, Нм;
Определенные мощности на валах , частоты вращения и моменты сводим в таблицу 1.
Таблица 1.
|
Эл.двиг. |
1 |
2 |
3(вых) |
|
|
Р, кВт |
8,2972 |
8,0499 |
7,7303 |
6 |
|
Т, Н.м |
27,034 |
26,2289 |
49,881 |
774,3243 |
|
n, мин-1 |
2931 |
2931 |
1480 |
74 |
3.Расчёт передач.
3.1 Расчёт цилиндрической косозубой передачи.
3.1.1 Выбор материала и расчёт допускаемых напряжений.
Материалы зубчатых колес и допускаемые напряжения.
Для изготовления шестерни и колеса быстроходной передачи редуктора (индекс б) принимаем сталь 40Х, термообработка- улучшение:
для шестерни: твёрдость HB1=280, предел выносливости =980МПа,предел текучести =680 МПа.
для колеса: твёрдость HB2=250, предел выносливости =850МПа,предел текучести =550 МПа.
Допустимые контактные напряжения для шестерни и колеса определяются по формуле:
где-предел контактной выносливости
-коэффициент долговечности
Sн = коэффициент безопасности. Для улучшенной стали принимают Sн=1.1
по реком.[1]
По табл.9.8[1]для улучшенной стали предел контактной выносливости
=2НВ+70
где НВ твёрдость материала
для шестерни: =2280+70=630 МПа.
для колеса: =2250+70=570 МПа.
Коэффициент долговечности:
;
где -базовое число циклов перемены напряжений;
-эквивалентное число циклов перемены напряжений за весь срок службы передачи.
По граф.9.11[1] для материала шестерни =22,0106, для материала колеса=16,5106 циклов.
Число циклов перемены напряжений за весь срок службы:
где n-частота вращения колеса;
с-число зацеплений зуба за один оборот колеса;
— отношение нагрузки на i-том режиме к максимальному;
— относительная продолжительность i –го режима работы;
Lh— число часов работы передачи;
где -срок службы привода в годах;
Кг— годовой коэффициент использования;
Кс— суточный коэффициент использования.
Lh=3652470,350,85=18242,7ч.
=602931118242,7(0,2+0,630,4+0,330,4)=95,3465107
===48,145107
Коэффициент долговечности:
=
=
Допускаемые контактные напряжения
1=0,9МПа
2=0,9МПа
По рекомендации [1] для косозубой быстроходной передачи расчетноё значение допускаемого напряжения:
[σн]б=МПа
При этом должно выполняться условие:
[σн]б<1.25min.
где min – меньшее из значений 1 и 2.
[σн]б=410,448МПа<1.25393.977=492.471МПа
Условие соблюдается.
Допускаемые напряжения изгиба
Допускаемое напряжение при изгибе для шестерен и колес определяем по формуле:
где — пределы выносливости зубьев при изгибе [2 табл. 4.1.4]
SF = 1,75 –минимальный коэффициент безопасности [1 стр. 152]
KFL – коэффициент долговечности ;
KFC – коэффициент, учитывающий влияние двустороннего приложения нагрузки; при односторонней нагрузке KFС=1;
, но не менее 1;
где m − показатель степени:
m = 6 (HB<350)
NFО – базовое число циклов напряжений ,
NFО = [ 4, стр. 33];
NFE – эквивалентное число циклов напряжений .
Предел выносливости зубьев
(улучшение)
для шестерни: МПа;
для колеса: МПа;
NFE=
;
Так как и > NFО , то KFL1 и KFL2 принимаем равное 1;
Допускаемое напряжение изгиба
МПа;
МПа;
3.1.2Проектировочный расчет.
Межосевое расстояние:
,
где — числовой коэффициент (для косозубых передач) [1.II стр. 109];
uц — передаточное число передачи ;
крутящий момент на колесе;
— коэффициент ширины венца выбирался по [табл. 6.8 1.I] принимаем =0,25
KHβ — коэффициент, учитывающий неравномерность распределения нагрузки по длине зуба.
По табл.3.1[1] предварительно принимаем Кнβ=1,08
=430(1,98+1)мм.
Принимаем стандартное значение =80мм.
Принимаем предварительно:
По рекомендации [1] принимаем предварительный угол наклона зубьев .
-число зубьев шестерни Z’=26.
Определим модуль зацепления m’ , мм.
мм.
И округляем его до ближайшего значения mn,мм в соответствии с ГОСТ (табл.4.2.2) [2].
По таблице принимаем mn=2мм.
Суммарное число зубьев передачи определяем по формуле:
.
Полученное значение округляем до ближайшего целого числа , принимаем =77.
Определим действительный угол наклона зуба:
-точность расчёта 4 знака после запятой
,
,
Число зубьев шестерни определяем по формуле:
округляем до ближайшего целого числа()
Принимаем =26.
Число зубьев зубчатого колеса:
Фактическое передаточное число:
.
Отклонение фактического передаточного числа от заданного:
.
Допускается отклонение до 4% .Данное требование выполняется.
Ширина зубчатого венца колеса:
мм.
Принимаем b2=20мм.
Ширина зубчатого венца шестерни:
мм.
Принимаем b1=25 мм.
Определим диаметры шестерни и колеса.
Делительный:
;
мм;
мм;
Впадин зубьев:
;
мм;
мм;
Вершин зубьев:
;
мм;
мм;
Поверка межосевого расстояния:
мм;
Межосевое расстояние совпала с принятым ранее следовательно смещения не будет.
Окружная скорость в зацеплении рассчитываем по формуле:
;
м/с;
По табл 4.2.14.[2] принимаем 8-ю степень точности передачи.
Окружной модуль:
3.1.3 Проверочный расчет передачи.
Условие контактной прочности зубьев:
,
где Кн -коэффициент нагрузки.
Кн=,
Где — коэффициент учитывающий неравномерность распределения нагрузки между зубьями. По табл.4.2.11.[2] .=1,1.
-коэффициент динамической нагрузки. По табл.4.2.8.[2] =1,15
Принимаем=1,08 по табл.3.5[1].
;
Мпа;
Недогрузка:
Так как допускается перегрузка до 5% , то контактная прочность зубьев обеспечена.
Условие прочности зубьев на изгиб:
,
где -коэффициент учитывающий угол наклона зубьев.
-коэффициент формы зуба.
-коэффициент нагрузки.
-окружная сила в зацеплении.
,
где -коэффициент учитывающий неравномерность распределения нагрузки между зубьями; =1,3 по табл.4.2.11[2].
-коэффициент учитывающий неравномерность распределения нагрузки по длине зуба. По рис.4.2.3[2] принимаем =1,08.
-коэффициент динамической нагрузки. По табл.4.2.8.[2].принимаем =1,3.
Для косозубых передач:
=1-=1-15,74/140=0,8875;
=1,31,08 1,3=1,8252.
Эквивалентное число зубьев колёс:
;
; ;
При числе зубьев , , при , по реком.[2]
Н.
Расчёт напряжений изгиба проводится для того колеса, для которого меньшее значение имеет отношение :
Для шестерни: =
Для колеса: = — меньшее.
Расчёт проводим для колеса:
МПа;
<[]2=250 МПа;
Условие прочности на изгиб выполняется.
3.1.4 Определение сил в зацеплении.
Окружные силы:
Н.
Радиальные силы:
Н. Н.
Осевые силы:
Н.
3.2 Расчёт червячной передачи.
3.2.1 Выбор материала и определение допускаемых напряжений.
Определим ориентировочное значение скорости скольжения зубьев;
м/с.
Для изготовления червяка по рекомендации [1] применяем сталь 40Х с закалкой твёрдостью >45HRCэ, пределом прочности =1000 МПа, пределом текучести =700 МПа.
Для изготовления червячного колеса по рекомендации [1] пир скорости скольжения =6.11 м/с, используем безоловянистую бронзу БрАЖ9-4Л, способ отливки в кокиль, пределом прочности =392 МПа, пределом текучести =196 МПа.
Допускаемые контактные напряжения:
где — коэффициент учитывающий износ материала колеса [2] табл.4.2.15
— коэффициент долговечности.
при принимают ZN=1.
Здесь =107-базовое число циклов.
=60n2сLh;
=60
так как 107 то принимаем ZN=1;
По табл. 4.2.15. принимаем =0,88.
Получаем
МПа.
Допускаемые напряжения изгиба.
где — коэффициент долговечности.
-основное допускаемое напряжение изгиба.
Для бронзы:
.
Коэффициент долговечности определяем по формуле:
:
при < то KFL=1;
где =106-базовое число циклов
-эквивалентное число циклов перемены напряжений за весь срок службы передачи по формуле:
=60n2сLh;
т.к 35,46949107>106 то KFL=1.
Получаем
МПа.
Допускаемые напряжения при перегрузках:
Контактные:
МПа.
Изгибные:
МПа.
3.2.2. Геометрический расчёт.
По табл.12.1[1] при uч=20 принимаем число заходов червяка z1=2.
Число зубьев червячного колеса:
Z2=Z1 Uч=220=40
Предварительно принимаем коэффициент диаметра червяка q’= 10.0.
Межосевое расстояние:
;
где K-коэффициент нагрузки .По рекомендациям [1] предварительно принимаем К=1,1.
= мм.
Принимаем стандартное значение aw=125 мм.
Определяем модуль:
.00 мм.
Принимаем стандартный модуль m=5.00 мм .
Коэффициент смещения:
мм.
Основные размеры червяка:
делительный диаметр червяка:
мм;
диаметр начальной окружности:
мм;
диаметр вершин зубьев:
мм;
диаметр впадин зубьев:
мм;
длина нарезаемой части червяка при х=0 и z1=2 определяем по табл.12.11[1];
мм.
С учётом увеличения длины нарезаемой части червяка для шлифуемых червяков принимаем b1=100 мм.
Угол подъёма винтовой линии:
;
Основные размеры венца червячного колеса:
делительный диаметр:
мм.
диаметр впадин зубьев:
мм.
диаметр вершин зубьев:
мм.
наибольший диаметр колеса:
мм;
Принимаем =217.5 мм.
ширина зубчатого венца при z1=2;
мм;
Принимаем b2=45 мм.
Окружная скорость червяка:
м/с;
Скорость скольжения зубьев:
м/с;
Назначаем 7-ю степень точности передачи.
3.2.3.Проверочный расчёт.
Условие контактной прочности зубьев:
;
где коэффициент нагрузки К равен:
,
где -коэффициент концентрации нагрузки.
-коэффициент, учитывающий динамическую нагрузку. По табл.12.10[1]
принимаем =1.1
где -коэффициент деформации червяка. По табл.12.9[1] принимаем =86;
y-коэффициент характера изменения нагрузки. При незначительных колебаниях нагрузки принимаем y=0.6;
;
Отсюда получаем:
;
МПа;
Перегрузка:
Так как допускается перегрузка до 5%, то контактная прочность зубьев обеспечена.
Условие прочности зубьев на изгиб:
;
где YF-коэффициент формы зуба. Определяется в зависимости от эквивалентного числа зубьев червячного колеса:
.
По таблице 9.10[1] принимаем YF=1.51.
МПа;
Прочность зубьев на изгиб обеспечена.
Определим КПД червячной передачи:
;
где -угол трения. По табл.12.6[1] принимаем =1.4.
.
3.2.4. Проверочный расчёт червячной передачи при перегрузках.
Проведём проверку прочности зубьев при перегрузках.
Условие контактной прочности при перегрузках:
;
где коэффициент перегрузки.
;
Контактная прочность зубьев при перегрузках обеспечена.
Условие прочности зубьев на изгиб при перегрузках:
;
;
Прочность зубьев на изгиб при перегрузках обеспечена.
3.2.5. Силы в зацеплении.
Определим силы действующие в зацеплении:
окружные:
Н;
Н;
осевые:
Н;
Н;
Радиальные:
,
где -угол профиля. =20;
Н;
4.Предварительный расчёт диаметров валов.
Предварительный расчёт валов заключается в определении диаметров участков валов.
Для этого используем расчетную формулу.
,
где
Т – крутящий момент на валу, Нм;
[]-допускаемое напряжение на кручение ; принимают []=15…35МПа.
4.1.Расчёт входного вала.
Для изготовления вала используем сталь 40Х термообработка –улучшение, предел выносливости =1000 МПа, предел текучести =700 МПа. Для входного вала принимаем []=20 МПа.
Принимаем dв1=20мм, а диметр вала под подшипником принимаем dп=25 мм. Планируем изготовить вал за одно целое с шестерней. Остальные диаметры вала определяются при конструировании.
4.2.Расчёт промежуточного вала.
Для изготовления вала используем сталь 40Х с закалкой, предел выносливости =1000 МПа, предел текучести =700 МПа. Для промежуточного вала принимаем []=20 МПа.
Принимаем dв2=30мм, а диметр вала под подшипником принимаем dп=25 мм. Остальные диаметры вала определяются при конструировании.
4.3.Расчёт выходного вала.
Для изготовления вала используем сталь 40Х термообработка –улучшение, предел выносливости =800 МПа, предел текучести =550 МПа. Для выходного вала принимаем []=30 МПа.
Диаметр выходного конца вала:
Принимаем dв3=55мм, а диметр вала под подшипником принимаем dп=50 мм. Остальные диаметры вала определяются при конструировании.
5.Выбор и проверочный расчёт муфт.
Для соединения вала электродвигателя с ведущим валом редуктора используется упругая втулочно-пальцевая муфта (МУВП) (ГОСТ 21424-5), состоящая из полумуфты, в которой жестко закреплены стальные пальцы, несущие на себе упругие втулки, входящие в отверстие второй полумуфты. Муфта достаточно чувствительна к смещению валов, хотя и допускает радиальные их смещения в пределах 0,3…0,5мм, угловое – до 1,50 и значительное осевое – до 5мм.
На втором выходном конце вала редуктора установлена компенщирующая зубчатая муфта (по ГОСТ 5006-94), позволяющая соединять валы, нагруженные большими крутящими моментами при различной комбинации радиальных, угловых и осевых смещений валов. Муфта представляет собой видоизменённую компенсирующую зубчатую муфту с обоймой, имеющую подвижную и неподвижную полумуфты.
Муфты выбираются по величине расчетного момента ТР и диаметру соединяемых валов:
ТР=k∙ТН,
где ТН — номинальный вращающий момент,
k — коэффициент, учитывающий режим работы К=1,5 [1 табл. 17.1].
5.1.1.Выбор муфты на входящем валу.
Упругая втулочно-пальцевая муфта (МУВП).
Расчетный момент Тр=1,5∙26.2289=39.343 Нм.
Диаметр соединяемого вала d=38мм. Для передачи такого момента и соединения валов указанных диаметров выбираем муфту со следующими параметрами [1 табл. 17.8]:
-допускаемый момент (Т)=250НМ
-диаметр посадочного отверстия d=38мм;
-посадочный диаметр на вал редуктора d=35мм;
-наибольший диаметр муфты D=120мм;
-длина муфты L=165мм;
-длина полумуфт L=80мм;
-диаметр окружности расположение пальцев D0=100мм;
-количество пальцев z=6;
-диаметр пальца под втулкой dп=14мм;
-длина резиновой втулки Lвт=28мм.
-длина пальца Lп=33мм.
-наружный диаметр втулки dвт=27мм.
-длина втулки Lвт=28мм.
-диаметр ступицы dст=70мм.
5.1.2.Проверочный расчёт муфты.
Условие прочности втулки на смятие :
где [σсм]-допускаемое напряжение на смятие для резины [σсм]=1,8…2МПа;
Условие прочности втулок выполняется.
Условие прочности пальца на изгиб
где
[σи] -допустимое напряжение при изгибе пальцев,
Принимаем [σи] =80 МПа;
Условие прочности выполняется. Муфта работоспособна.
5.2.1.Выбор муфты на выходном валу.
Зубчатая муфта.
Расчетный момент Тр=1,5∙774,324=1161,486 Нм.
Для передачи такого вращающего момента необходимо использовать зубчатую муфту со следующими параметрами (ГОСТ 5004-94):
-допускаемый вращающий момент (Т)=1400Нм;
-наружный диаметр муфты D=185мм;
-диаметр ступиц полумуфт D1=125мм;
-наибольшая длина муфты L=145мм;
-модуль зубьев m=2.5;
-число зубьев z=38;
-длина полумуфт l=70 мм.
5.2.2.Проверочный расчёт муфты.
Данная муфта предназначена для передачи крутящих моментов до 1400 Нм и проверки по допускаемым напряжениям не требует.
Работоспособность оценивается по условию износостойкости:
-допускаемое давление.
=2,538=95мм.
условие выполняется.
6.Расчёт валов редуктора по эквивалентному моменту.
Сперва необходимо определить изгибающие, крутящие и эквивалентные моменты, действующие в сечениях валов, для чего составляем расчётные схемы.
6.1.Расчётные схемы валов.
6.1.1Расчётная схема входного вала.
Исходные данные к расчёту:
Ft1=970.97H; Fr1=367.178 H; Fa1=273.669 H; T1=26.229 Hм; d1=54.026мм;
L1=126; L2=35мм; L3=35мм;
Определим нагрузку на вал от муфты:
;
Рассмотрим плоскость ХY.
Определим составляющие радиальных нагрузок подшипников:
;
;
;
;
;
Проверка:
Реакции определены верно.
Изгибающие моменты относительно оси Z в сечениях1…4.
Рассмотрим плоскость XZ:
Определим составляющие радиальных нагрузок подшипников:
;
;
;
;
;
Проверка:
Реакции определены верно.
Изгибающие моменты относительно оси Y в сечениях1…4.
Суммарные изгибающие моменты:
;
Крутящие моменты:
Эквивалентные моменты:
;
Суммарные радиальные нагрузки подшипников:
;
6.1.2.Расчётная схема промежуточного вала.
Исходные данные к расчёту:
Ft2=970.97H; Fr2=367.178 H; Fa2=273.669 H; T2=49.881 Hм; d2=105.974мм;
Ft3=1995.24H; Fr3=2818.3 H; Fa3=7743.24 H; d3=50мм;
L1=80; L2=82мм; L3=130мм;
Рассмотрим плоскость ХY.
Определим составляющие радиальных нагрузок подшипников:
;
;
;
;
Проверка:
Реакции определены верно.
Изгибающие моменты относительно оси Z в сечениях1…4.
Рассмотрим плоскость XZ:
Определим составляющие радиальных нагрузок подшипников:
;
;
;
;
;
Проверка:
Реакции определены верно.
Изгибающие моменты относительно оси Y в сечениях1…4.
Суммарные изгибающие моменты:
;
Крутящие моменты:
Эквивалентные моменты:
;
Суммарные радиальные нагрузки подшипников:
;
6.1.3Расчётная схема выходного вала.
Исходные данные к расчёту:
Ft4=7743.24H; Fr4=2818.3 H; Fa4=1995.24 H; T3=774.324 Hм; d4=200мм;
L1=75; L2=75мм; L3=70мм;
Определим нагрузку на вал от муфты:
;
Рассмотрим плоскость ХY.
Определим составляющие радиальных нагрузок подшипников:
;
;
;
;
;
Проверка:
Реакции определены верно.
Изгибающие моменты относительно оси Z в сечениях1…4.
Рассмотрим плоскость XZ:
Определим составляющие радиальных нагрузок подшипников:
;
;
;
;
;
Проверка:
Реакции определены верно.
Изгибающие моменты относительно оси Y в сечениях1…4.
Суммарные изгибающие моменты:
;
Крутящие моменты:
Эквивалентные моменты:
;
Суммарные радиальные нагрузки подшипников:
;