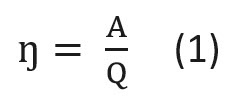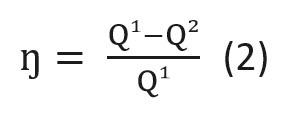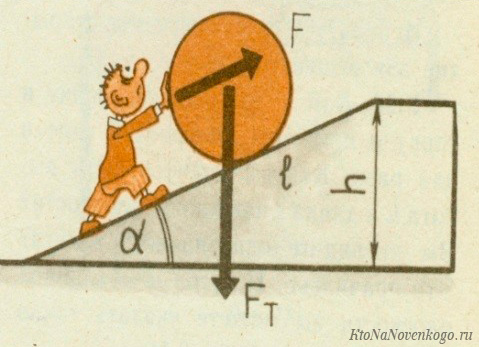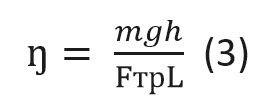п.1. Полезная работа и затраченная работа
Полезной называется работа по подъёму грузов или преодолению какого-либо сопротивления.
Затраченной (полной) называется работа, совершённая приложенной силой.
Примеры полной и полезной работы
Затраченная работа равна сумме:
- полезной работы;
- работы против силы трения в различных частях механизма;
- работы по перемещению различных составных элементов механизма.
Поэтому всегда (A_text{полезная}lt A_text{затраченная})
п.2. КПД механизма
Коэффициент полезного действия механизма – это отношение его полезной работы к затраченной работе. $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%} $$
Поскольку в реальных механизмах всегда (A_text{п}lt A_text{з}), $$ frac{A_text{п}}{A_text{з}}lt 1. $$
Следовательно КПД реальных механизмов (etalt 100text{%}).
Только в идеальном механизме, в котором нет потерь на трение, и все составные элементы не имеют веса, (A_text{п}=A_text{з}) и (eta=100text{%}).
КПД никогда не может быть выше (100text{%}).
КПД реальных механизмов можно увеличить за счет снижения трение в подвижных узлах и уменьшения веса всех составных элементов конструкции.
Для этого нужны новые смазочные вещества и лёгкие, но прочные конструкционные материалы.
п.3. Задачи
Задача 1. По наклонной плоскости поднимают груз массой 50 кг, прикладывая к нему силу 250 Н, направленную вдоль плоскости. Чему равен КПД плоскости, если её длина 10 м, а высота 3 м?
Дано:
(m=50 text{кг})
(gapprox 10 text{м/с}^2)
(F=250 text{Н})
(L=10 text{м})
(h=3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза begin{gather*} A_text{п}=mgh. end{gather*} Затраченная работа на перемещение груза вдоль наклонной плоскости begin{gather*} A_text{з}=FL. end{gather*} КПД плоскости: begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{FL}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{50cdot 10cdot 3}{250cdot 10}cdot 100text{%}=60text{%} end{gather*} Ответ: 60%
Задача 2. С помощью подвижного блока поднимают груз массой 200 кг, прикладывая силу 1200 Н. Чему равен КПД блока?
Дано:
(m=200 text{кг})
(gapprox 10 text{м/с}^2)
(F=1200 text{Н})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза и проигрыш в расстоянии. Т.е. при работе нужно вытянуть трос длиной (2h). Затраченная работа: begin{gather*} A_text{з}=Fcdot 2h. end{gather*} КПД блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh}{2Fh}cdot 100text{%}=frac{mg}{2F}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{200cdot 10}{2cdot 1200}cdot 100text{%}approx 83,3text{%} end{gather*} Ответ: 83,3%
Задача 3. Груз массой 245 кг с помощью рычага равномерно подняли на высоту 6 см. При этом к длинному плечу рычага была приложена сила 500 Н, а точка приложения силы опустилась на 30 см. Найдите КПД рычага.
Дано:
(m=245 text{кг})
(gapprox 10 text{м/с}^2)
(h_2=6 text{см}=0,6 text{м})
(F_1=500 text{Н})
(h_1=30 text{см}=0,3 text{м})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию длинного плеча рычага: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД рычага begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{245cdot 10cdot 0,06}{500cdot 0,3}cdot 100text{%}=frac{147}{150}cdot 100text{%}=98text{%} end{gather*} Ответ: 98%
Задача 4. Чему равен КПД гидравлической машины, если для равномерного подъема груза массой 1,2 т к меньшему поршню прикладывают силу 160 Н? Площади поршней равны 5 см2 и 500 см2.
Дано:
(m=1,2 text{т}=1200 text{кг})
(gapprox 10 text{м/с}^2)
(F_1=160 text{Н})
(S_1=5 text{см}^2=5cdot 10^{-4} text{м}^2)
(S_2=500 text{см}^2=5cdot 10^{-2} text{м}^2)
__________________
(eta-?)
При опускании малого поршня на высоту (h_1) из малого в большой цилиндр вытекает объем жидкости равный $$ V=S_1h_1=S_2h_2Rightarrow frac{h_2}{h_1}=frac{S_1}{S_2} $$ Полезная работа по подъему груза на высоту (h_2): begin{gather*} A_text{п}=mgh_2. end{gather*} Затраченная работа по опусканию поршня малого цилиндра: begin{gather*} A_text{з}=F_1h_1. end{gather*} КПД гидравлической машины begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{mgh_2}{F_1h_1}cdot 100text{%}=frac{mgS_1}{F_1S_2}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{1200cdot 10cdot 5cdot 10^{-4}}{160cdot 5cdot 10^{-2}}cdot 100text{%}=frac{600}{800}cdot 100text{%}=75text{%} end{gather*} Ответ: 75%
Задача 5*. Груз массой 12 кг поднимают с помощью подвижного блока массой 3 кг. Чему равен КПД блока?
Дано:
(M=12 text{кг})
(m=3 text{кг})
__________________
(eta-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Подвижный блок дает выигрыш в силе в 2 раза. Поэтому достаточно приложить силу, равную половине суммы весов груза и блока: begin{gather*} F=frac 12(M+m)g end{gather*} При этом будет проигрыш в расстоянии. Потребуется вытянуть трос длиной (2h). Затраченная работа, приложенная к тросу: begin{gather*} A_text{з}=Fcdot 2h=frac 12(M+m)gcdot 2h=(M+m)gh. end{gather*} КПД подвижного блока begin{gather*} eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Mgh}{(M+m)gh}cdot 100text{%}=frac{M}{M+m}cdot 100text{%} end{gather*} Получаем: begin{gather*} eta=frac{12}{12+3}cdot 100text{%}=80text{%} end{gather*} Ответ: 80%
Задача 6. Сколько воды можно поднять из колодца глубиной 36 м за 1 ч, если мощность электродвигателя равна 5 кВт, КПД всей установки равно 70%?
Дано:
(N=5 text{кВт}=5cdot 10^3 text{Вт})
(eta=70text{%}=0,7)
(h=36 text{м})
(t=1 text{ч}=3600 text{с})
(gapprox 10 text{м/с}^2)
__________________
(m-?)
Полезная работа по подъему груза на высоту (h): begin{gather*} A_text{п}=Mgh. end{gather*} Затраченная работа электродвигателя: begin{gather*} A_text{з}=Nt. end{gather*} КПД установки begin{gather*} eta=frac{A_text{п}}{A_text{з}}=frac{mgh}{Nt} end{gather*} Масса воды begin{gather*} m=frac{eta Nt}{gh} end{gather*} Получаем: begin{gather*} m=frac{0,7cdot 5cdot 10^3cdot 3600}{10cdot 36}=35cdot 10^3 (text{кг})=35 text{т} end{gather*} Ответ: 35 т
Задача 7*. КПД подвижного блока при подъеме первого груза равен 80%, а при подъеме второго груза – 90%. Масса какого груза больше и во сколько раз? Трением в блоке можно пренебречь.
Дано:
(eta_1=80text{%}=0,8)
(eta_2=90text{%}=0,9)
__________________
(frac{M_2}{M_1}-?)
КПД подвижного блока массой (m), с помощью которого поднимают груз массой (M) begin{gather*} eta=frac{M}{M+m} end{gather*} (см. Задачу 5 выше). Масса груза begin{gather*} eta(M+m)=MRightarrow eta m=(1-eta)MRightarrow M=frac{eta}{1-eta}m end{gather*} Получаем: begin{gather*} M_1=frac{0,8}{1-0,8}m=4m,\[6pt] M_2=frac{0,9}{1-0,9}m=9m end{gather*} Масса второго груза больше.
Отношение масс begin{gather*} frac{M_2}{M_1}=frac{9m}{4m}=2,25 (text{раз}) end{gather*} Ответ: масса второго груза больше в 2,25 раз
п.4. Лабораторная работа №13. Определение КПД наклонной плоскости
Цель работы
Научиться проводить измерения и рассчитывать КПД простого механизма на примере наклонной плоскости. Исследовать зависимость КПД наклонной плоскости от высоты.
Теоретические сведения
Работа по подъему тела весом (P) вертикально на высоту (h) (из точки C в точку B): $$ A_text{CB}=Ph $$
Работа по перемещению того же тела силой (F), направленной вдоль наклонной плоскости длиной (L) (из точки A в точку B): $$ A_text{AB}=FL $$
В обоих случаях тело перемещается с нулевого уровня AC, где (h_0=0), на уровень с высотой (h) в точку B. Работа сторонних сил в этом случае равна изменению потенциальной энергии тела: $$ A=A_text{CB}=A_text{AB}=Delta E_p $$
Получаем уравнение для идеальной наклонной плоскости (без трения): $$ Ph=FL $$
При наличии трения получаем неравенство: $$ Phlt FL $$
Полезная и затраченная работа для наклонной плоскости: $$ A_text{п}=Ph, A_text{з}=FL $$
КПД наклонной плоскости: $$ eta=frac{A_text{п}}{A_text{з}}cdot 100text{%}=frac{Ph}{FL}cdot 100text{%} $$
Затраченная работа равна сумме полезной работы и работы по преодолению силы трения: $$ A_text{з}=A_text{п}+F_text{тр}L $$
Откуда сила трения равна: $$ F_text{тр}=frac{A_text{з}-A_text{п}}{L}=frac{FL-Ph}{L}=F-Pfrac hL $$
Вес (P) и сила (F) определяются в работе с помощью динамометра с ценой деления (d=0,1 text{Н}).
Абсолютная погрешность прямых измерений $$ Delta_F=Delta_P=frac d2=0,05 text{Н}. $$
Сила (F) определяется в серии из пяти опытов с вычислением средних величин.
Высота наклонной плоскости (h) и длина наклонной плоскости (L) определяются с помощью мерной ленты с ценой деления (d=5 text{мм}). Абсолютная погрешность (Delta_L=2,5 text{мм}).
Относительные погрешности измерений вычисляются как обычно.
Относительная погрешность расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L $$
Абсолютная погрешность расчета КПД: $$ Delta_eta=etacdot delta_eta $$
Приборы и материалы
Доска длиной от 70 см, штатив с муфтой и лапкой, брусок массой не менее 300 г, мерная лента, динамометр.
Ход работы
1. Измерьте мерной лентой длину доски (L).
2. Определите вес бруска (P) с помощью динамометра.
3. Соберите наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L3.)
4. Положите брусок на наклонную плоскость, прикрепите к нему динамометр и равномерно тяните по наклонной плоскости. Следите, чтобы динамометр располагался параллельно наклонной плоскости. Запишите измеренное значение (F). Повторите измерение (F) в серии из пяти опытов.
5. Соберите новую наклонную плоскость: закрепите один конец доски в лапке штатива на высоте около (h=frac L4). Перейдите на шаг 4 и повторите серию опытов для определения (F).
6. Рассчитайте КПД для двух исследованных наклонных плоскостей. Найдите относительные и абсолютные погрешности расчетов КПД.
7. Для каждой из наклонных плоскостей укажите величину полезной и затраченной работы, найдите силу трения.
8. Сделайте выводы о зависимости силы трения и КПД от высоты наклонной плоскости.
Результаты измерений и вычислений
Длина наклонной плоскости (доски) begin{gather*} L=80 text{см}=800 text{мм},\[7pt] Delta_L=2,5 text{мм},\[6pt] delta_L=frac{Delta_L}{L}=frac{2,5}{800}approx 0,0031=0,31text{%} end{gather*}
Вес бруска begin{gather*} P=4,4 text{Н},\[7pt] Delta_P=0,05 text{Н},\[6pt] delta_P=frac{Delta_P}{P}=frac{0,05}{4,4}approx 0,0011=1,1text{%} end{gather*}
1. Наклонная плоскость высотой (h=27 text{см})
Высота наклонной плоскости begin{gather*} h=27 text{см}=270 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{270}approx 0,0093=0,93text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,9 | 2,8 | 3,0 | 2,7 | 2,8 | 14,2 |
| $$ Delta_F, H $$ | 0,06 | 0,04 | 0,16 | 0,14 | 0,04 | 0,44 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{14,2}{5}=2,84 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,44}{5}approx 0,09 (text{Н}),\[6pt] F=(2,84pm 0,09) text{Н},\[7pt] delta_F=frac{0,09}{2,84}approx 0,032=3,2text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,27=1,188 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,84cdot 0,8=2,272 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,84-4,4cdot frac{0,27}{0,8}approx 1,36 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{1,188}{2,272}approx 0,523=52,3text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,032+0,011+0,0093+0,0031=0,0554approx 0,056=5,6text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,523cdot 0,056approx 0,029=2,9text{%} $$
Окончательно получаем: $$ eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%} $$
2. Наклонная плоскость высотой (h=20 text{см})
Высота наклонной плоскости begin{gather*} h=20 text{см}=200 text{мм},\[7pt] Delta_h=2,5 text{мм},\[6pt] delta_h=frac{Delta_h}{h}=frac{2,5}{200}approx 0,013=1,3text{%} end{gather*}
Определение силы тяги (F) в серии опытов
| № опыта | 1 | 2 | 3 | 4 | 5 | Сумма |
| $$ F, H $$ | 2,4 | 2,6 | 2,5 | 2,6 | 2,5 | 12,6 |
| $$ Delta_F, H $$ | 0,12 | 0,08 | 0,02 | 0,08 | 0,02 | 0,32 |
begin{gather*} F_text{ср}=frac{sum F_i}{5}=frac{12,6}{5}=2,52 (text{Н}),\[6pt] Delta_{Ftext{ср}}=frac{sum Delta_{Fi}}{5}=frac{0,32}{5}approx 0,06 (text{Н}),\[6pt] F=(2,52pm 0,06) text{Н},\[7pt] delta_F=frac{0,06}{2,52}approx 0,024=2,4text{%} end{gather*}
Полезная работа: $$ A_text{П}=Ph=4,4cdot 0,2=0,88 (text{Дж}) $$
Затраченная работа: $$ A_text{З}=FL=2,52cdot 0,8=2,016 (text{Дж}) $$
Сила трения: $$ F_text{тр}=F-Pfrac hL=2,52-4,4cdot frac{0,2}{0,8}approx 1,42 (text{Н}) $$
КПД наклонной плоскости: $$ eta=frac{A_text{П}}{A_text{З}}=frac{0,88}{2,016}approx 0,437=43,7text{%} $$
Погрешности расчета КПД: $$ delta_eta=delta_F+delta_P+delta_h+delta_L=0,024+0,011+0,013+0,0031=0,0511approx 0,052=5,2text{%} $$
При расчете (delta_eta) использовали округление с избытком. $$ Delta_eta=0,437cdot 0,052approx 0,023=2,3text{%} $$
Окончательно получаем: $$ eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%} $$
Выводы
На основании полученных результатов можно сделать следующие выводы.
В работе проводился расчет КПД наклонной плоскости постоянной длины, но разной высоты.
Для высоты около (h=frac L3):
- полезная и затраченная работы: (A_text{П}=1,188 (text{Дж}), A_text{З}=2,272 (text{Дж}))
- сила трения: (F_text{тр}=1,36 (text{Н}))
- КПД: (eta=(52,3pm 2,9)text{%}, delta_eta=5,6text{%})
Для высоты около (h=frac L4):
- полезная и затраченная работы: (A_text{П}=0,88 (text{Дж}), A_text{З}=2,016 (text{Дж}))
- сила трения: (F_text{тр}=1,42 (text{Н}))
- КПД: (eta=(43,7pm 2,3)text{%}, delta_eta=5,2text{%})
Таким образом, с уменьшением высоты:
- сила трения растет;
- КПД наклонной плоскости падает.
Все задачи, поставленные перед исследованием, успешно выполнены.
В данном разделе вы уже познакомились с устройством и принципом работы двух простых механизмов: рычага и блока. Используя эти механизмы, мы совершаем какую-то работу.
До этого мы рассматривали идеализированные условия. Учитывали только следующие величины: приложенная к механизму сила, вес поднимаемого тела, плечи сил рычага.
Мы не учитывали ни силу трения между деталями механизмов, ни веса самого рычага, ни веса веревки в блоке, с помощью которой мы поднимаем груз. Если в лабораторных условиях эти величины могут показаться незначительными, то, например, вес каната в блоке подъемного крана уже сложно назвать незначительной величиной.
Следовательно, и работу таких механизмов тогда нужно рассчитывать по-другому. Для этого в физике разделяют работу на полную и полезную, вводят понятие коэффициента полезного действия (КПД) механизма. На данном уроке мы познакомимся с этими величинами и рассмотрим решение задач с использованием КПД.
Затраченная и полезная работы
Введем новые определения. Какую работу называют полезной, какую — полной?
Полная (затраченная) работа ($A_з$) — это работа, совершенная приложенной силой.
Полезная работа ($A_п$) — это работа по поднятию груза или преодолению какого-либо сопротивления.
В идеальных условиях (какие мы рассматривали в прошлых уроках) полная работа будет равна полезной. Но на практике между этими величинами есть разница.
На практике совершенная с помощью механизма полная работа всегда несколько больше полезной работы:
$A_п < A_з$, или $frac{A_п}{A_з} < 1$.
Почему при применении механизмов для подъема грузов и преодоления какого-либо сопротивления полезная работа не равна полной?
Например, при использовании подвижного блока (рисунок 1) мы будем дополнительно совершать работу по поднятию самого блока, веревки, ее креплений, а также по преодолению силы трения в оси блока.
КПД механизма
Что такое коэффициент полезного действия механизма?
Коэффициент полезного действия механизма (КПД) — это отношение полезной работы к полной работе:
$КПД = frac{A_п}{A_з}$.
КПД выражают в процентах и обозначают греческой буквой $eta$ (“эта”):
$eta = frac{A_п}{A_з} cdot 100%$.
Из этого определения следует, что КПД механизма всегда будет меньше $100%$.
Ученые и инженеры при конструировании механизмов всегда стремятся увеличить их КПД.
Как можно увеличить коэффициент полезного действия?
Первое, что для этого делают — стремятся уменьшить вес механизмов и трение в их осях.
В ходе истории и научно-технического прогресса коэффициент полезного действия механизмов постепенно возрастал:
- парового двигателя — $1−8%$;
- бензинового двигателя — $20−25%$;
- электрического двигателя — $90−95%$.
Как вы видите, на данный момент современные технологии обеспечивают достаточно высокий уровень КПД.
Примеры задач
Задача №1
Для поднятия груза массой $150 space кг$ используют рычаг. Груз подняли на высоту $h_1 = 0.15 space м$, приложив к длинному плечу рычага силу в $320 space Н$. При этом точка приложения этой силы опустилась на $h_2 =0.8 space м$. Рассчитайте коэффициент полезного действия рычага.
Дано:
$m = 150 space кг$
$h_1 = 0.15 space м$
$h_2 = 0.8 space м$
$F = 320 space Н$
$g = 9.8 frac{Н}{кг}$
$eta — ?$
Показать решение и ответ
Скрыть
Решение:
Запишем формулу для нахождения КПД:
$eta = frac{A_п}{A_з} cdot 100%$.
Полная (затраченная) работа будет определяться приложенной силой:
$A_з = Fh_2 = 320 space Н cdot 0.8 space м = 256 space Дж$.
Полезная работа будет определяться работой по подъему груза весом $P = gm$ на высоту $h_1$:
$A_п = Ph_1 = gmh_1 = 9.8 frac{Н}{кг} cdot 150 space кг cdot 0.15 space м = 220.5 space Дж$.
Тогда:
$eta = frac{220.5 space Дж}{256 space Дж} cdot 100% approx 0.86 cdot 100% = 80%$.
Ответ: $eta = 80%$.
Задача №2
Используя неподвижный блок рабочий поднял груз массой $80 space кг$ на высоту $7 space м$ (рисунок 2). Найдите полную работу, совершенную рабочим, если КПД этого механизма $75%$.
Дано:
$m = 80 space кг$
$h = 7 space м$
$eta = 75%$
$g = 9.8 frac{Н}{кг}$
$A_з — ?$
Показать решение ответ
Скрыть
Решение:
Запишем формулу для нахождения КПД:
$eta = frac{A_п}{A_з} cdot 100%$.
Выразим из нее полную (затраченную) работу:
$A_з = frac{A_п cdot 100%}{eta}$.
Полезная работа — это работа по подъему груза:
$A_п = Ph = gmh = 9.8 frac{Н}{кг} cdot 80 space кг cdot 7 space м = 5488 space Дж$.
Найдем полную работу:
$A_з = frac{A_п}{eta} cdot 100%= frac{5488 space Дж}{75%} cdot 100%= frac{5488 space Дж}{0.75} approx 7300 space Дж = 7.3 space кДж$.
Ответ: $A_з = 7.3 space кДж$.
Простые механизмы. КПД простых механизмов
1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.
Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.
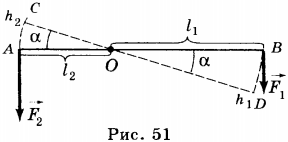
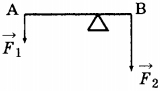
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой ( F_1 ), равной весу груза. Действуя на длинный конец рычага с силой ( F_2 ), человек поднимает груз. При этом сила ( F_1 ) стремится повернуть рычаг по часовой стрелке, а груз ( F_2 ) — против часовой стрелки.
Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы ( F_1 ) является расстояние ОА ( (l_1) ), плечом силы ( F_2 ) — расстояние ОВ ( (l_2) ).
Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. ( F_1l_1=F_2l_2 ). Произведение силы, действующей на рычаг, и её плеча называют моментом силы: ( Fl=M ). Соответственно, если рычаг находится в равновесии, то ( M_1=M_2 ).
Условие равновесия рычага можно записать по-другому:( frac{F_1}{F_2}=frac{l_2}{l_1} ). Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.
Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.
3. При подъеме груза работа силы, действующей на груз, равна ( A_1=F_1h_1 ), работа силы, приложенной к другому концу рычага, равна ( A_2=F_2h_2 ). Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и ( frac{AO}{BO}=frac{AC}{BD} ) или ( frac{l_1}{l_2}=frac{h_1}{h_2} ). Поскольку ( F_1l_1=F_2l_2 ), то ( F_1h_1=F_2h_2 ), т.е. ( A_1=2 ). Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.
4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).
Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.
Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: ( P=F ). Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.
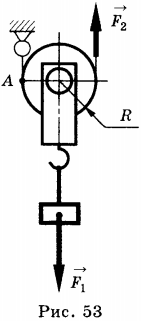
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.
В этом случае точкой вращения блока является точка А (см. рис. 52).
Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: ( P=2F ). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: ( F=P/2 ).
Измерив расстояние ( h_1 ), которое проходит груз, и расстояние ( h_2 ), на которое перемещается конец троса, можно обнаружить, что расстояние ( h_2=2h_1 ). Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа ( Ph_1=Fh_2 ), т.е. ( A_1=2 ). Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.
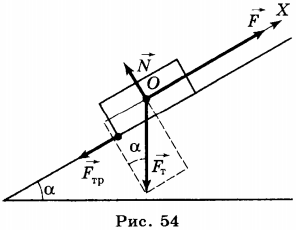
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).
Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу ( P ). Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную ( F=Psinalpha ), т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: ( mathbf{КПД}=A_п/A_сcdot 100 % ), где ( A_п ) — полезная работа, ( A_п=mgh ); ( A_с ) — совершённая работа при перемещении ящика вдоль наклонной плоскости, ( A_c=Fl ), где ( F ) — приложенная сила, ( l ) — длина наклонной плоскости.
Содержание
- ПРИМЕРЫ ЗАДАНИЙ
- Часть 1
- Часть 2
- Ответы
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо ( l_1 )?
1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м
2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.
Чему равна сила ( F_1 ), если рычаг находится в равновесии?
1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н
3. Рычаг находится в равновесии под действием двух сил. Сила ( F_1 ) = 6 Н. Чему равна сила ( F_2 ), если длина рычага 50 см, а плечо силы ( F_1 ) равно 30 см?
1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н
4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью
1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости
5. С помощью неподвижного блока в отсутствие трения силе
1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш
6. С помощью подвижного блока в отсутствие трения
1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза
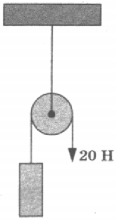
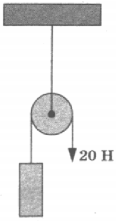
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна
1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг
8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость
1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза
9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?
1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м
10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?
1) 160%
2) 62,5%
3) 16%
4) 6,25%
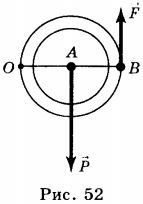
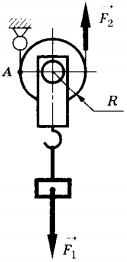
11. Груз поднимают с помощью подвижного блока радиусом ( R ) (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы ( vec{F}_1 ) относительно точки A
Б) плечо силы ( vec{F}_2 ) относительно точки A
B) момент силы ( vec{F}_1 ) относительно точки A
ФОРМУЛЫ
1) ( F_1R )
2) ( 2F_1R )
3) ( frac{F_1}{R} )
4) ( R )
5) ( 2R )
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.
Часть 2
13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.
Ответы
Простые механизмы. КПД простых механизмов
2.7 (53.16%) 38 votes
Инфоурок
›
Физика
›Презентации›Презентация по физике на тему»КПД простых механизмов».(7 класс)
Скачать материал

Скачать материал


- Сейчас обучается 42 человека из 27 регионов


- Сейчас обучается 110 человек из 46 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
КПД простых механизмов.
-
2 слайд
Законы механики держат в узде инженеров и изобретателей, чтобы они не обещали себе и другим невозможные вещи»
Леонардо да Винчи
-
3 слайд
Коэффициент полезного действия
механизма. -
4 слайд
Сегодня на уроке:
1.Узнаем формулу коэффициента полезного действия
2.Сравним КПД простых механизмов
3.Определим КПД наклонной плоскости -
5 слайд
Рабочему надо загрузить бочку с мёдом в кузов грузовой автомашины. Чтобы просто поднять её, надо приложить очень большую силу — силу, равную силе тяжести (весу) бочки. Такую силу рабочий приложить не может.
Как ему поступить? -
6 слайд
…тогда он кладет две доски на край кузова и вкатывает бочку по образовавшейся наклонной плоскости, прикладывая силу, значительно меньшую, чем вес бочки!
-
7 слайд
Тот или иной механизм нужен, в конечном итоге, для совершения работы.
При подъеме груза мы преодолеваем силу трения. (При подъеме груза мы преодолеваем силу тяжести веревки, силу трения, силу тяжести других приспособлений.)Полезная работа Ап — необходимая нам работа.
Работа по преодолению силы тяжести:
A = mgh
Затраченная на подъем работа оказывается всегда больше полезной.
Характеристика механизма, определяющая какую долю полезная работа составляет от полной, называется коэффициентом полезного действия — КПД -
-
9 слайд
Предмет исследования:
наклонная плоскость
Цель исследования:
рассчитать КПД при подъеме тела по наклонной плоскости.
Задачи исследования:
— Рассчитать полезную работу.
— Рассчитать затраченную работу.
— Сравнить полезную и затраченную работу.
— Рассчитать КПД при подъеме тела по наклонной плоскости. -
10 слайд
Лабораторная работа: «Определение КПД при подъёме тела по наклонной плоскости».
-
11 слайд
Наклонная плоскость применяется для перемещения тяжелых предметов на более высокий уровень без их непосредственного поднятия.
пандусы,
эскалаторы,
обычные лестницы,
конвейеры.
Если нужно поднять груз на высоту, всегда легче воспользоваться пологим подъемом, чем крутым: чем положе уклон, тем легче выполнить эту работу. -
12 слайд
Та тяжесть будет двигаться всего
труднее, которая будет
подниматься по линии менее
наклонной.Леонардо Да Винчи
-
13 слайд
Примеры наклонной плоскости
Горные дороги вьются пологим «серпантином» -
-
15 слайд
Очень остроумно использована наклонная плоскость на Красноярской ГЭС, где вместо шлюзов действует судовозная камера, движущаяся по наклонной эстакаде. Для ее передвижения необходимо тяговое усилие в 4000 кН.
-
16 слайд
Северное чудо – Соловецская крепость
Монастыри в древности служили важными опорными пунктами
Применялись простейшие подъемные механизмы и устройства, известные с давних пор: вороты — ручные и приводимые в движение лошадьми; блоки; полиспасты и, конечно, бревна-рычаги.
Соловецкая крепость единственное в своем роде явление русской архитектуры -
17 слайд
Соловецкая крепость
-
18 слайд
КПД простых механизмов.
-
19 слайд
Как увеличить КПД?
Вес рычага?
Вес крючков?
Трение?Вес блока?
Вес верёвок?
Трение?
Трение между телом и плоскостью?
Наклонная плоскость
Блок
Рычаг -
20 слайд
Уменьшение силы тяжести
Использование материалов с меньшей плотностью, уменьшение объёма деталей (использование полых деталей с рёбрами жёсткости) -
21 слайд
Пути повышения коэффициента полезного действия.
уменьшение силы трения
Уменьшение силы трения
F тр.=μN
μ- коэффициент трения, зависит от свойств соприкасающихся поверхностей; N- сила реакции опоры. На горизонтальной поверхности, движущейся равномерно или находящейся в состоянии покоя, равна силе тяжести N=Fтяж., F тяж.=mg. -
22 слайд
Вопрос №1.
Какое из утверждений является верным?а) На практике полная работа всегда больше полезной.
б) На практике полная работа всегда меньше полезной.
в) На практике полная работа всегда равна полезной. -
23 слайд
Вопрос№2.
С помощью простого механизма была совершена полезная работа А1, а полная работа при этом А2.
Какое из приведённых выражений определяет КПД механизма.
а) А1+А2
Б) А1/А2
В) А2/А1 -
24 слайд
Вопрос№3.
Каков КПД механизма, если полезная работа составляет одну четверть от затраченной?а)25%
Б)40%
В)75%
Г)100% -
25 слайд
Вопрос№4.
На какие действия дополнительно тратится работа при использовании простых механизмов.
а) на совершение работы по преодолению сил сопротивления среды.
Б)на совершение работы по перемещение груза.
В) на совершение работы по перемещению частей механизма. -
26 слайд
Вопрос№5.
Как можно Увеличить КПД?
а) за счёт уменьшения веса: рычага, подвижного блока, верёвок.
Б) за счёт уменьшения трения между деталями механизма.
в) за счёт уменьшения трения между механизмом и грузом.
Г) все варианты верны. -
-
28 слайд
Домашнее
задание
п.61.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 265 794 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 13.06.2022
- 298
- 3
- 13.06.2022
- 86
- 1
- 13.06.2022
- 155
- 1

- 13.06.2022
- 346
- 4
- 13.06.2022
- 253
- 5

- 13.06.2022
- 132
- 5
- 13.06.2022
- 105
- 1
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Информационные технологии в деятельности учителя физики»
-
Курс повышения квалификации «Специфика преподавания конституционного права с учетом реализации ФГОС»
-
Курс повышения квалификации «Управление финансами: как уйти от банкротства»
-
Курс профессиональной переподготовки «Организация менеджмента в туризме»
-
Курс повышения квалификации «ЕГЭ по физике: методика решения задач»
-
Курс повышения квалификации «Источники финансов»
-
Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»
-
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Метрология, стандартизация и сертификация»
-
Курс профессиональной переподготовки «Организация процесса страхования (перестрахования)»
-
Курс профессиональной переподготовки «Управление качеством»
-
Курс профессиональной переподготовки «Стандартизация и метрология»
-
Скачать материал
-
14.06.2022
1673
-
PPTX
1.8 мбайт -
160
скачиваний -
Оцените материал:
-
-
Настоящий материал опубликован пользователем Зайцева Валентина Васильевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 2 года и 4 месяца
- Подписчики: 0
- Всего просмотров: 3022
-
Всего материалов:
8
Формула КПД и как его вычислить для тепловой машины или механизма
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Эта аббревиатура вряд ли требует расшифровки: она неизвестна разве что тем, у кого в школе был «неуд» по физике.
Но для забывчивых всё же напомним, что под этим сокращением скрывается коэффициент полезного действия. Что же собой представляет эта величина?
Поговорим о ней простым и понятным языком – это может пригодиться даже в повседневной жизни.
Что такое КПД в физике и какова его формула
Для выполнения какой-либо работы необходимо затратить определённое количество энергии. Чтобы ехал велосипед, вы тратите мышечную энергию крутя педали. Чтобы двигался автомобиль, используется энергия сжигаемого топлива (бензина, солярки или газа).
Для горения лампочки требуется энергия электрического тока. Список можно продолжать до бесконечности. Точку можно поставить на солнечной энергии, благодаря которой существует жизнь на Земле.
Далее возникает логичный вопрос: а насколько эффективно расходуется эта энергия? В идеале хотелось бы, чтобы вся она шла «в дело», то есть использовалась только по прямому назначению. Но, к сожалению, на практике такого не бывает.
Затраченная энергия будет всегда больше, чем полезная работа, так как для достижения основной цели (движение, подъём груза, освещение, отопление и т.д.) часть энергии неизбежно уйдёт на неустранимые потери (преодоление силы трения, нагрев электропроводки, выброс продуктов горения в атмосферу и т.д.). Понятно, что чем меньше такие потери, тем лучше.
Критерием того, насколько эффективно работает система (устройство, агрегат, двигатель, машина и т.д.), служит показатель, получивший название коэффициент полезного действия (КПД).
Иными словами, коэффициент полезного действия показывает, какова доля полезной работы в общих энергозатратах. Математически КПД (чаще всего обозначается символом ŋ) определяется по формуле:
где A — полезная энергия (работа);
Q — энергия, затраченная на совершение полезной работы.
Понятно, что ŋ – величина безразмерная и не может быть больше единицы (да и равной единице она может быть чисто теоретически).
Выражается она в виде десятичной дроби либо в процентах (в последнем случае в формулу вставляется множитель х100).
Так, если КПД равен 0,9 (90%), то это значит, что 10% полезной мощности составили безвозвратные потери.
КПД теплового двигателя (машины)
Под тепловым двигателем понимается машина (агрегат), в которой энергия, высвобождающаяся в процессе расширения рабочего тела, преобразуется в механическую работу.
В качестве рабочего тела обычно выступает газ или газообразные вещества (пары бензина, водяной пар и т.п.).
Тепловые машины работают по замкнутому циклу. Это значит, что процесс преобразования энергии и сопутствующей теплопередачи периодически повторяется, а рабочее тело совершает круговой цикл, возвращаясь в исходное состояние.
К тепловым двигателям относятся:
- поршневые (паровые машины, двигатели внутреннего сгорания);
- роторные/турбинные (газовые или паровые турбины АЭС и ТЭЦ);
- реактивные (авиация);
- ракетные (космическая техника).
Используя положения предыдущего параграфа, КПД тепловой машины можно сформулировать как отношение полезной работы, совершённой за один цикл, к энергии (количеству теплоты), поступившей от энергоносителя (нагревателя).
Тогда формулу (1) можно преобразовать следующим образом:
где Q1 — количество теплоты, полученное двигателем от нагревателя за цикл;
Q2 — количество теплоты, отданное двигателем охладителю (холодильнику) за цикл;
Q1 – Q2 – количество теплоты, которое пошло на совершение работы.
Предположим, что Q1 = Q2, то есть на совершение полезной работы ничего не осталось – вся энергия «ушла в трубу». Тогда и КПД будет нулевым. Если же Q2 = 0, то есть вся энергия отдана полезной работе (потери отсутствуют), то коэффициент полезного действия будет равен 1.
Но это теория, на практике ни то ни другое нереалистично. В первом случае двигатель просто бесполезен, во втором – идеален, но недосягаем.
Значения КПД для различных типов тепловых двигателей приведены ниже.
Самым большим КПД обладают тепловые двигатели, работающие на основе цикла Карно (процесс назван в честь французского инженера, открывшего это явление в 1824 г.). В термодинамике оно характеризует круговой цикл, включающий в себя две стадии: расширение и сжатие рабочего тела.
Причём на протяжении обеих стадий попеременно проходят два процесса: изотермический (протекающий при постоянной температуре), и адиабатический (протекающий без теплообмена с окружающей средой). Максимальное значение КПД здесь достигается за счёт того, что тела с разной температурой не контактируют, а значит, без осуществления работы теплопередача исключается.
КПД механизма — по какой формуле вычисляют
Человек придумал разнообразные механизмы, с помощью которых можно поднимать тяжёлые грузы на определённую высоту. Так, для подъёма ведра с водой из колодца изобрели ворот, для подъёма автомобиля – домкрат. При помощи лебёдки и наклонной плоскости египтяне построили свои грандиозные пирамиды.
Пользуясь этими приспособлениями, человек редко вспоминает об их КПД. В качестве примера рассмотрим этот показатель для наклонной плоскости.
Принцип расчёта КПД остаётся неизменным: нужно найти отношение полезной работы ко всей затраченной энергии. То есть опять-таки используем общую формулу (1), сделав соответствующие преобразования.
Предположим, тело массой m нужно поднять (точнее затолкать или затянуть) на высоту h. При постоянной скорости подъёма полезная работа будет равна произведению силы тяжести (mg) на высоту (h).
Затраченная работа определяется произволением силы толчка или тяги F на длину наклонной плоскости L. Заметим, что толчковое (тяговое) усилие идёт на преодоление силы трения Fтр.
Таким образом, КПД такого простейшего механизма можно посчитать по формуле:
Несложный анализ показывает, что коэффициент полезного действия наклонной плоскости обратно пропорционален силе трения и длине аппарели. Последняя, в свою очередь, зависит от угла наклона: чем он больше, тем короче аппарель.
Как можно увеличить КПД
Современная наука постоянно ищет пути повышения коэффициента полезной модности двигателей и отдельных механизмов, внедряя новые технические решения и технологические инновации.
Чем выше будет КПД, тем экономичней будет двигатель, тем больше энергоресурсов удастся сберечь.
Тепловой двигатель
Из формулы (2) следует, что для увеличения КПД есть два пути: а) повышение температуры нагревателя; б) понижение температуры холодильника. Оба пути малоперспективны.
Нагреватель нельзя разогревать до бесконечности, так как любой материал имеет предел жаропрочности. Холодильником почти всегда служит окружающая среда, а внедрение в систему дополнительного теплообменника (например, баллона с жидким азотом) нецелесообразно: это резко увеличит вес, габариты и стоимость двигателя.
Установлено, что на коэффициент полезного действия не влияют характеристики рабочего тела. Что же остаётся?
А остаётся немало практически реализуемых способов, таких как уменьшение трения в механических узлах, минимизация теплопотерь путём достижения максимально полного сгорания топлива, создание обтекаемых форм для снижения лобового сопоставления (воздуха или воды) и т.д.
Учитывая, что в механике хорошим показателем на сегодняшний день считается КПД 30-40%, учёным и практикам есть над чем работать.
Наклонная плоскость
Из формулы (3) следует, что для повышения КПД нужно снижать силу трения (прежде всего, путём создания гладких соприкасающихся поверхностей) и увеличивать угол наклона. Но! При крутом уклоне силёнок для поднятия тяжёлого груза может и не хватить.
В заключение отметим, что в электротехнике ситуация с КПД обстоит гораздо лучше (показатель в 95% для электродвигателя – норма). На то есть объективные причины, объяснение которых выходит за рамки рассматриваемой темы.