1. Определения
2. Инвариантность
размерности многообразия
3. Край топологическго
многообразия
4. Инвариантность
края многообразия
Понятие
многообразия является одним из важнейших
в математике. Интересно, что, в сущности,
это понятие, а также понятия размерности
и края встречаются уже у Евклида. Начнем
цитатой из Евклида («Начала», Книга I):
Определения.
-
Точка
есть то, что не имеет частей. -
Линия
же — длина без ширины. -
Края
же линии — точки.
……………………………………………
5.
Поверхность есть то, что имеет только
длину и ширину.
6.
Края же поверхности – линии.
Точки,
линии и поверхности — все это примеры
многообразий. Фактически, многообразие
— это такое топологическое пространство,
в окрестности каждой точки которого
можно ввести систему координат. Для
более точного определения нам понадобится
одно весьма специфическое топологическое
свойство — локальная евклидовость.
Пусть п
—
неотрицательное целое число. Через
будем обозначать замкнутое полупространство
в евклидовом n-мерном
пространстве
,
состоящее из точек, первая координата
которых неотрицательна (рис.1):
.
Заметим,
что
состоит из одной точки.
Определение.
Топологическое пространство X
называется
локально
евклидовым размерности n,
если
всякая его точка х0
обладает
окрестностью U,
гомеоморфной n-мерному
евклидову пространству
или полупространству (рис.2). Таким
образом, в окрестности U
точки
х0
можно
ввести систему координат, в которой
положение точек, близких к х0,
будет
описываться n
параметрами.
Допуская вольность речи, можно сказать,
что вблизи точки х0
пространство
X
«имеет
n
измерений».
Поскольку n-мерное
евклидово пространство гомеоморфно
открытому евклидову шару:
,
то
в приведенном определении вместо
и
можно говорить об
открытом
шаре и полушаре или просто об открытом
множестве в
.
Примеры.
1.
Топологическое пространство является
локально евклидовым размерности 0
в том и только в том случае, если оно
дискретно.
-
Числовая
прямая
,
окружность
,
луч [0, +),
интервал [0,1), отрезок [0,1] являются
одномерными локально евклидовыми. -
Локально
евклидовыми размерности п
являются
сами пространство
и
полупространство
,
произвольные их открытые подмножества,
п-мерная
сфера
и n-мерный
шар
,
а также n-мерное
проективное пространство. -
Любое
открытое подмножество n-мерного
локально евклидова топологического
пространства само является n-мерным
локально евклидовым.
Рис.
1
Рис.
2
Локальная
евклидовость —
очень сильное требование, но само по
себе оно не гарантирует выполнения
других довольно естественных топологических
свойств. Приведем пример, который
показывает, что локально
евклидово пространство может не быть
хаусдорфовым.
Пример.
Рассмотрим
множество X
на
плоскости, состоящее из всех точек оси
абсцисс и еще одной точки – например,
точки с координатами (0;1):
{(0,1)}
(здесь
={(x,y)
y
= 0}). Введем в X
топологическую
структуру: объявим открытыми те
множества
в X,
образы которых при проекции
:
X
множества
X
на соь абсцисс открыты в
.
В этой топологии пространство X
локально евклидово размерности 1,
поскольку его можно покрыть двумя
открытыми множествами, гомеоморфными
числовой прямой:
X=
(X{(0;0)}).
В
то же время пространство X
не
хаусдорфово: точки (0;0) и (0;1) не обладают
в нем непересекающимися окрестностями.
Действительно, пусть U
и
V
–
произвольные окрестности этих точек.
Тогда
и
-окрестности
точки 0.
Поскольку
множества
и
заведомо
имеют общие точки, отличные от 0, а
прообраз любой такой точки должен
содержаться в
,
то
и
.
В
следующем основном определении нам
будет удобно воспользоваться термином
«евклидово множество»: открытое множество
в n-мерном
локально евклидовом пространстве
назовем евклидовым,
если
оно гомеоморфно открытому множеству в
полупространстве
,
(т.е. пересечению с
открытого
множества в
).
Основное
определение.
Топологическое
пространство X
называется n-мерным
топологическим многообразием, если
оно:
a)
локально евклидово размерности n;
б
)
хаусдорфово;
в)
обладает покрытием, состоящим из не
более чем счетного числа евклидовых
открытых множеств.
Условие
в)
означает, что пространство X
не
слишком велико. Часто его заменяют
другими условиями: так называемыми
сепарабельностью или второй аксиомой
счетности. Условие в)
автоматически выполнено, например, для
компактных локально евклидовых
пространств. Без доказательства отметим,
что оно гарантирует метризуемость
пространства X
и
даже вложимость его в евклидово
пространство достаточно большой
размерности. В дальнейшем мы часто будем
называть топологические многообразия
просто многообразиями.
Примеры.
1.
Всякое
не более чем счетное дискретное
пространство является нульмерным
топологическим многообразием. В то же
время несчетное дискретное пространство
(например, множество вещественных чисел,
наделенное дискретной топологией)
топологическим многообразием не
является. Для него выполнены условия
а)
и б)
определения, но не выполнено условие
в):
всякое евклидово открытое множество в
дискретном пространстве состоит из
одной точки, и в силу несчетности
пространства никакой счетный набор
таких множеств покрытия не образует.
-
Пространство
,
полупространство
,
их открытые
подмножества, сфера
,
шар
− все являются n-мерными
топологическими многообразиями. То,
что они локально евклидовы, мы уже
отмечали. Хаусдорфовость их очевидна.
Наконец, что касается их евклидовых
покрытий, то Яд,
и
их открытые подмножества сами образуют
одноэлементные такие покрытия, а сфера
и
шар
могут
быть покрыты двумя евклидовыми
множествами: дополнениями «северного
полюса» и «южного полюса» соответственно. -
Открытое
множество в n-мерном
топологическом многообразии само
является n-мерным
топологическим многообразием.
Компоненты
топологических многообразий. Поскольку
всякое многообразие локально евклидово,
то оно очевидным образом локально
линейно связно.
Теорема
1. а)
Компоненты
топологического многообразия являются
одновременно его линейно связными
компонентами.
б)
Компоненты
п-мерного
многообразия открыты в нем и, следовательно,
являются п-мерными
многообразиями.
Следующая
теорема ограничивает возможное число
компонент.
Теорема
2. Многообразие
X
состоит из не более чем счетного числа
компонент. Компактное многообразие
имеет лишь конечное число компонент.
Доказательство.
По определению, X
можно
покрыть счетным числом евклидовых
открытых множеств: X=
.
Каждое из открытых множеств
,
будучи евклидовым, имеет, самое большее,
счетное число компонент. Поскольку
объединение счетного числа не более
чем счетных множеств счетно, то мы
получаем, что X
можно
покрыть счетным числом связных множеств:
X=.
Далее,
так как каждая компонента пространства
X
содержит
по крайней мере одно из множеств
,
причем разные компоненты, очевидно,
содержат разные множества, то компонент
не может быть больше, чем множеств
;
т. е. число компонент не более чем счетно.
Пусть
теперь многообразие X
компактно.
Поскольку его компоненты образуют,
очевидно, открытое покрытие пространства
X,
то
X
можно,
в силу компактности, покрыть конечным
числом компонент. С другой стороны, в
таком подпокрытии должны участвовать
все компоненты. Следовательно, их число
конечно.
Информация
без доказательства. Существуют связные
(заведомо некомпактные) локально
евклидовы хаусдорфовы пространства,
не являющиеся многообразиями (они не
допускают счетного покрытия открытыми
евклидовыми множествами).
Инвариантность
размерности многообразия.
Остановимся подробнее на понятии
размерности
многообразия.
Вполне осмысленным является вопрос:
может
ли многообразие размерности п
быть одновременно
многообразием размерности m
при
mn?
Ответ
на него отрицательный. Таким образом,
размерность многообразия является его
топологическим инвариантом. Для
доказательства надо заметить, что в
противном случае мы нашли бы у некоторой
точки многообразия окрестность,
гомеоморфную одновременно открытому
множеству в
и
открытому множеству в
.
Это невозможно в силу следующей теоремы.
Брауэра, которую также называют «теоремой
об инвариантности области». Она
утверждает, что свойство множества в
евклидовом пространстве быть областью
топологически инвариантно, другими
словами— это топологическое свойство.
Теорема
3 (Брауэра об инвариантности области).
Если
множества А
и В
в евклидовом пространстве
гомеоморфны
и множество А
открыто, то и множество В
открыто.
Следствие.
Евклидовы
пространства разных размерностей
негомеоморфны: если mn,
то
.
Теорема
Брауэра бессодержательна при n
=
0 и несложно доказывается при n
=
1. Уже при n
=
2, а тем более при n
3 ее доказательство представляет
значительные трудности, хотя и может
быть сделано совершенно элементарным.
Доказательство
следствия.
Пусть, для определенности, т
< п.
Положим,
в условиях теоремы 3, A=
и В
=
.
Тогда теорема 3 утверждает, что
открыто в
.
Край
топологического многообразия.
Точка х0
в
n-мерном
многообразии называется внутренней,
если
она
обладает
окрестностью, гомеоморфной евклидову
пространству
(не путать с внутренними точками множества
в топологическом пространстве!). Точка
х0
называется
краевой,
если
у нее существует окрестность U,
гомеоморфная полупространству
,
а связывающий их гомеоморфизм f
:
переводит точку х0
на
границу полупространства
(ср. рис. 21). Краевые точки многообразия
X
образуют
его край,
который
обозначается через дХ.
Многообразия,
все точки которых являются внутренними,
называются многообразиями
без края, а
многообразия, у которых есть краевые
точки, называются многообразиями
с краем. Многообразие
без края называется замкнутым,
если
оно компактно, и называется открытым,
если
у него нет компактных компонент.
Примеры.
1.
Все точки в
и
являются
внутренними. В
и
точки,
не лежащие на границе, являются
внутренними, а точки, лежащие на границе
— краевыми. Таким образом,
и
—
многообразия без края, причем
—
замкнутое, а
—
открытое, а
и
—
многообразия
с краем.
2.
Примерами двумерных многообразий без
края являются поверхности в
:
кроме сферы это тор, крендель (все это
замкнутые многообразия), однополостный
и двуполостный гиперболоиды (это открытые
многообразия) и т. п. (рис. 3).
Особо
стоит отметить выпуклые многогранные
поверхности, такие как куб, призма,
пирамида и т. д. Все они гомеоморфны
сфере и тем самым являются замкнутыми
двумерными многообразиями (рис. 4).
-
Примерами
двумерных многообразий с краем служат:
а)
замыкания различных плоских областей:
кроме круга это кольцо, круг с дырами
и т. п. (рис. 5); б)
замыкания различных открытых множеств
в двумерных многообразиях без края:
«сфера с дырами», «тор с дырами»,
«крендель с дырой» и т.п. (рис. 6). -
Интересным
примером двумерного многообразия с
краем в
является так называемый лист
Мёбиуса.
Он
выглядит как результат склеивания
концов перекрученной полоски бумаги
(рис.7). Лист Мёбиуса — простейшая
односторонняя
поверхность.
Что это значит? Обычно у поверхности
две стороны: вы можете покрасить одну
сторону, скажем, в синий цвет, а другую
— в красный, так, что цвета нигде не
будут граничить друг с другом. Начав
же красить с любого места лист Мёбиуса,
вы непременно закрасите его целиком —
«со всех сторон»! Две стороны исходной
полоски бумаги отождествились при
склеивании.
Инвариантность
края многообразия.
Наше
определение внутренних и краевых точек
может вызвать резонный вопрос: не
может
ли внутренняя точка многообразия
одновременно являться краевой?
(Другими
словами, не может ли
многообразие
без края иметь непустой край?) Он сводится
к
вопросу
о том, существует ли
у
точки, лежащей на границе полупространства
,окрестность
в
,
гомеоморфная евклидову пространству
.
Ответ на
этот вопрос отрицательный, как легко
следует из теоремы Браэура об инвариантности
области. В частности, край замкнутого
полупространства совпадает с граничной
гиперплоскостью: д
=
.
Из
этого
следует, что край
n-мерного
многообразия с краем сам является
(n – 1)—мерным
многообразием без края.
(Без
обращения к теореме Брауэра легко
показать, что имеются только две
возможности: д
=
или
д
=
.
Во втором случае край любого n-мерного
многообразия с ним совпадал бы.)
Рис.
7
Примеры.
1.
Край отрезка состоит из двух точек –
его концов:
д
[0, 1] = {0, 1}.
-
Край
круга есть окружность: д
=
.
-
Более
общим образом, край n-мерного
шара есть (n – 1)-мерная
сфера. -
Край
листа Мёбиуса гомеоморфен окружности
.
-
Тор
является краем ограниченной им части
пространства — полнотория.
Александров
А.Д., Нецветаев Н.Ю. Геометрия. М.: Наука,
1990
Соседние файлы в папке Многообразия
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Многообра́зие — пространство, которое локально выглядит как «обычное» Евклидово пространство 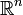
Исследования многообразий были начаты во второй половине XIX века, они естественно возникли при изучении дифференциальной геометрии и теории групп Ли. Тем не менее, первые точные определения были сделаны только в 30-х годах XX века.
Обычно рассматриваются так называемые гладкие многообразия, то есть те, на которых есть выделенный класс «гладких» функций — в таких многообразиях можно говорить о касательных векторах и касательных пространствах. Для того, чтобы измерять длины кривых и углы, нужна ещё дополнительная структура — риманова метрика.
В классической механике гладкие многообразия служат как фазовые пространства. В общей теории относительности четырёхмерные псевдоримановы многообразия используются как модель для пространства-времени.
Содержание
- 1 Топологические многообразия
- 1.1 Комментарии
- 2 Гладкие многообразия
- 3 Классификация многообразий
- 4 Дополнительные структуры
- 5 Обобщения
- 6 См. также
- 7 Литература
Топологические многообразия
n-мерное топологическое многообразие (без границы) — это хаусдорфово топологическое пространство, в котором каждая точка имеет открытую окрестность, гомеоморфную открытому подмножеству 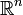
n-мерное топологическое многообразие с краем — это хаусдорфово топологическое пространство, в котором каждая точка имеет окрестность, гомеоморфную открытому подмножеству замкнутого полупространства в 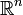
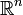
Обычно в определениях дополнительно предполагается, что многообразие либо паракомпактно (это эквивалентно метризуемости), либо, что ещё сильнее, имеет счётную базу (это эквивалентно тому, что многообразие вкладывается в Евклидово пространство конечной размерности).
Далее мы везде предполагаем, что многообразие имеет счётную базу.
Компактное связное многообразие без границы называется замкнутым, некомпактное связное многообразие называется открытым.
Комментарии
- Следует отметить, что введённое здесь понятие края вовсе не равносильно понятию относительной границы в общей топологии.
- Требование хаусдорфовости может показаться излишним; пример пространства, которое локально гомеоморфно евклидовому, но при этом не хаусдорфово, можно построить склеиванием двух копий вещественной прямой по всем точкам, кроме одной.
Гладкие многообразия
Гладкая структура, определённая ниже, обычно возникает в почти всех приложениях и при этом делает многообразие гораздо удобней в работе.
Начинаем с топологического многообразия M без границы. Назовём картой гомеоморфизм 
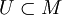
Набор карт, покрывающих всё M, называется атласом.
Если две карты 

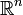
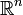
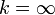
Пример: сфера может быть покрыта 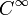
Два Ck атласа задают одну Ck-гладкую структуру, если их объединение является Ck-атласом.
Для таких многообразий можно ввести понятия касательного вектора, касательного и кокасательного пространств и расслоений.
Для заданной C1-гладкой структуры можно найти 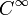
Не каждое топологическое многообразие допускает гладкую структуру. Примеры таких «шершавых» многообразий появляются уже в размерности четыре. Также существуют примеры топологических многообразий, которые допускают несколько различных гладких структур. Первый такой пример нестандартной гладкой структуры, так называемая сфера Милнора, был построен Милнором на семимерной сфере.
Классификация многообразий
Каждое связное одномерное многообразие без границы гомеоморфно вещественной прямой или окружности
Гомеоморфный класс замкнутой связной поверхности задаётся её Эйлеровой характеристикой и ориентируемостью. (Если ориентируемо, то это сфера с ручками, если нет, то связная сумма нескольких копий проективной плоскости)
Классификация замкнутых трёхмерных многообразий следует из гипотезы Тёрстона, которая была недавно доказана Григорием Перельманом.
Если размерность больше трёх, то классификация невозможна; более того, невозможно построить алгоритм, который определяет, является ли многообразие односвязным. Тем не менее существует классификация всех односвязанных многообразий во всех размерностях ≥ 5.
Можно также классифицировать гладкие многообразия.
- В размерностях 2 и 3 любая пара гомеоморфных многообразий является также диффеоморфной.
- В размерности 4 существуют примеры замкнутых многообразий, которые допускают бесконечное число неэквивалентных гладких структур, а открытые многообразия, как, например,
допускают континуум различных гладких структур.
- В размерностях 5 и выше любое топологическое многообразие допускает не более чем конечное число неэквивалентных гладких структур.
Дополнительные структуры
Часто гладкие многообразия оснащают дополнительными структурами. Вот список наиболее часто встречаемых дополнительных структур:
- Метрический тензор
- Симплектическая форма
- Комплексная структура
Обобщения
- Орбиобразие (англ.).
См. также
- Алгебраическое многообразие
- Аналитическое многообразие
- Граф-многообразие
Литература
- Дубровин Б. А., Новиков С. П., Фоменко А.Т Современная геометрия. Методы и приложения.
Wikimedia Foundation.
2010.
9 ноября стали известны лауреаты премии Мильнера. В этом году их было рекордное количество: всему виной физики, которые выпускают работы в коллаборациях, куда входит больше тысячи авторов. Премию по математике в этом году удостоился Ян Агол. Он получил награду в 3 миллиона долларов за свои работы по трехмерной топологии, в частности, за доказательство гипотеза Мардена.
С точки зрения топологов все задачи делятся на задачи для больших размерностей (больше четырех), экзотические (размерность четыре) и маломерные (размерность три и два). Может показаться, что «маломерность» звучит немного уничижительно. Это не так, именно маломерная, в частности, трехмерная топология является источником множества сложнейших задач современной математики. Достаточно упомянуть, что знаменитая гипотеза Пуанкаре была довольно просто доказана для всех размерностей, кроме трех — для решения задачи в ней потребовались гении Терстона и Перельмана.
Задача, которую в свое время решил Агол, является одной из таких сложных и специфических для трехмерной топологии задач. Мы не расскажем идею доказательства даже в общих чертах, но читателю все равно нужно приготовиться: понять, даже в общих чертах, доказанное Аголом утверждение непросто.
Что такое многообразие
Базовым понятием, с которым имеют дело геометры, является многообразие. Что это такое?
Представим, что составляем атлас карт. Обычно это происходит так: люди выбирают точку на местности, относительно которой будут проводить съемку (лучше — повыше) и подходящий ориентир. Дальше все объекты на карте размещаются относительно этой точки и прямой, связывающей ее с ориетиром. Говоря математически, мы выбираем точку отсчета и вводим на местности координаты.
Штука в том, что с обычного холма большую карту не нарисуешь. Поэтому рано или поздно, если мы хотим получить нормальную карту, нам придется перейти на другой холм. То есть сменить и точку отсчета и ориентир. Нарисуем новую карту. Некоторые объекты попадут в обе. Говоря математически, в наших картах появились точки, с которыми связаны две пары координат. Так как для разных нужд нам потребуются разные карты, то, следовательно, нам нужно знать правило перехода от одних координат к другим. Желательно, в виде каких-нибудь удобных формул.
Двигаясь дальше, мы, в принципе, можем составить карту всей нашей планеты (с морем возникнут проблемы, но для простоты проигнорируем их). Результатом работы станет атлас — то есть набор карт с координатами на них, и формулы, позволяющие пересчитывать координаты объектов из одной карты в другую.
Многообразие в математике — это, по сути, формализация (придуманная Гауссом и Эйлером) такого вот процесса картографирования.
Грубо говоря, оно представляет собой атлас, состоящих из карт, на каждой из которых заданы координаты. Для любой пары карт определено пересечение, на котором заданы функции перехода — те самые формулы, которые пересчитывают координаты точки в одной карте в координаты точки в другой карте. При этом, когда говорят о размерности многообразия, говорят о размерности карт. То есть о количестве координат в наборе, которых достаточно для описания точек на поверхности. В случае с нашим примером таких координат две, значит и наша Земля является двумерным многообразием.
Компактность и замкнутость
В математике в атласе карт может быть сколько угодно, хоть бесконечное множество. Если в каждом атласе можно выбрать конечное число карт, которые покрывают все многообразие, то такое многообразие называется компактным. Еще одним важным свойством является понятие замкнутости многообразия. Его можно пояснить на примере: возьмем интервал на прямой 0 < x < 1. И возьмем последовательность точек xn = 1/n, лежащих в нашем интервале. Пределом этой последовательности является точка 0, которая нашему интервалу не принадлежит. Так вот, интервал — это не замкнутое множество. А вот отрезок — уже замкнутое.
Если для любой последовательности предельная точка в многообразии лежит, то такое многообразие называется замкнутым. Из компактности следует замкнутость, но не наоборот. Пример замкнутого, но не компактного множества — обычная числовая прямая.
Компактность — очень сильное свойство. Теорема Уитни говорит, что, если есть заданное атласом многообразие, то его можно реализовать в виде поверхности в достаточно большой размерности. То есть, грубо говоря, склеить из наших карт «глобус» (пусть и многомерный). Если у нас был на руках компактный атлас, то полученная поверхность будет замкнутой и ограниченной (то есть ее можно будет запихнуть внутрь шара достаточно большого радиуса).
Теперь осталось определить понятие края. Говорят, что у многообразия есть край, если карты делятся на две категории — одни устроены как пространства (двумерные плоскости в нашем примере), а другие — как полупространства (то есть полуплоскоти). Например, Внутренность круга x2 + y2 ≤ 1 является замкнутым многообразием с краем.
Классификация двумерных многообразий
Рассмотрим компактные многообразия без края, которые можно представить в виде поверхности в трехмерном пространстве. Последнее требование может показаться странным, но мы накладываем его, чтобы избежать необходимости вводить понятие ориентируемости. Представим себе, что эти поверхности сделаны из резины — нам разрешается их деформировать, а также разрезать и склеивать разрезы (правда только так же, как мы разрезали — переклеивать куски из одного места в другое нельзя). Такой выбор операций не случаен — с их помощью поверхность можно привести к некоторому каноническому виду.
Канонический вид в это случае выглядит очень просто. Представим, что у нас есть два тора (тор — поверхность обычного бублика). Вырежем в боку каждого бублика по круглой дырочке и склеим края. Математики скажут, что получилась поверхность с двумя ручками. Аналогичным образом можно приклеивать еще торы. Добавив в список сферу, как поверхность с нулевым числом ручек — что, разумеется, правда, ручек у сферы нет — мы получим полный список компактных ориентируемых двумерных поверхностей без края. Этот факт известен с середины XIX века. Если нам нужны поверхности с краем (но все еще компактные), то, оказывается, ситуация не сильно сложнее — надо взять компактное многообразие и прорезать в нем дырки. Края дырок и будут краями.
Укротимые многообразия
А что делать, если мы отказываемся, например, от замкнутости. Легко представить, например, что мы выкинули из поверхности одну единственную точку. Поверхность перестала быть замкнутой (и, следовательно, компактной) : действительно, возьмем последовательность, сходящуюся к выкинутой точке. Ее предел в поверхности не содержится. Но эта поверхность может быть реализована как кусок компактной поверхности.
Есть ли некомпактные двумерные многообразия, которые не являются подмножествами компактных ориентируемых? Конечно! И такой пример легко привести. Вспомним, что все поверхности у нас характеризуются числом ручек. Но число это всегда конечно. Теперь возьмем плоскость и приклеим к ней бесконечное количество торов, уходящее вдаль. Может такая поверхность быть подмножеством компактной? Нет, ведь в этом случае у компактной поверхности окажется бесконечное число ручек, а это невозможно.
Поверхности, которые можно «засунуть» в компактное многообразие, называются укротимыми. Пример нашего многообразия с бесконечным числом ручек, соответственно, неукротим и даже имеет собственное имя — Лохнесское чудовище (можно представить себе ручки, как кольца торчащего из воды чудовища бесконечной длины).
Гиперболическая геометрия
Гиперболическая геометрия — это современное название для геометрии, основу которой заложил Николай Лобачевский. Если коротко, то история такова: в «Началах» Евклида была сформулирована аксиоматика планиметрии. И все аксиомы были простые, кроме одной. Она не давала покоя математикам на протяжении нескольких тысяч лет — ее все пытались вывести из остальных как следствие.
В XIX веке эта пятая аксиома была известна в следующей, эквивалентной оригинальной формулировке: через каждую точку, не лежащую на данной прямой, проходит прямая, параллельная данной, притом только одна. Лобачевский отказался от этой аксиомы и построил непротиворечивую геометрию, которая получила его имя (впрочем, над созданием геометрии трудилось множество ученых того времени).
В геометрии Лобачевского через точку, не лежащую на прямой, можно провести бесконечное множество прямых, параллельных данной. Но это не единственное ее удивительное свойство: если с помощью таких прямых нарисовать треугольник, сумма его углов будет меньше 180 градусов. Грубо говоря, две прямые в геометрии Лобачевского, выпущенные под первоначальным углом a, «разбегаются» сильнее, чем прямые в привычном нам пространстве.
Гиперболическое многообразие — это многообразие, у которого каждая карта в атласе представляет собой пространство Лобачевского, правда, возможно, высокой размерности.
Теорема Агола
В 1974 году Альберт Марден предположил, вот что. Возьмем гиперболическое трехмерное многообразие. Как можно узнать, что оно ручное, то есть, что его можно представить как подмножество в компактном многообразии с краем? Есть несколько естественных условий. Например, оно должно быть полным, то есть «прямые» в геометрии Лобачевского должны продолжаться бесконечно далеко. Это свойство всегда выполнено на компактных многообразиях. Кроме этого надо наложить условие на фундаментальную группу (это довольно непростая вещь, о ней поговорим при случае в следующий раз).
Марден предположил, что эти условия являются и достаточными. Спустя 30 лет, в 2004 году Ян Агол доказал этот факт. Строго математически он формулируется так: всякое полное гиперболическое 3-многообразие с конечно порожденной фундаментальной группой гомеоморфно внутренности некоторого компактного многообразия, возможно, с краем.
Анатолий Фоменко — известный российский математик и художник. В своих произведениях он опирается на математические концепции, визуализируя их часто довольно парадоксальным образом. Первый опыт иллюстрации он получил, оформляя книгу «Гомотопическая топология». В 1990 году Американское Математическое Общество издало альбом «Mathematical Impressions», включающую 84 работы Фоменко (из которых 23 выполнены в цвете) с пояснениями и комментариями.
Андрей Коняев



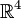 допускают континуум различных гладких структур.
допускают континуум различных гладких структур.