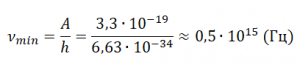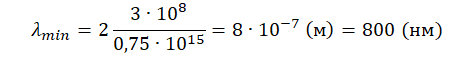Введение
Возьмем металлическую пластинку и направим на нее луч света. При этом электроны будут покидать поверхность пластинки, то есть свет выбивает электроны из вещества.
Если мы будем уменьшать частоту излучения, в какой-то момент электроны перестанут покидать металл. Возникает вопрос: почему так?
Еще один вопрос: если увеличивать интенсивность света, будет вырываться больше электронов с прежней энергией или столько же электронов с большей энергией? С помощью модели света как электромагнитной волны на эти вопросы ответить нельзя.
Есть другая модель – квантовая, предложенная Планком. Мы с ней уже знакомы, она предполагает, что излучение дискретно. Энергия излучается и поглощается отдельными порциями – квантами. С ее помощью мы и будем объяснять явление фотоэффекта.
Уравнение Эйнштейна
Если считать свет потоком частиц – квантов, то становится понятно: один квант поглощается одним электроном. Логично предположить, что сколько квантов поглотилось, столько электронов подверглись воздействию. Квант световой энергии передается электрону (см. рис. 1).
Рис. 1. Поглощение электроном кванта световой энергии
И если кванта световой энергии для выхода электрона недостаточно, электрон не выбивается, а остается в металле. Если энергии достаточно, лишняя энергия передаётся электрону в виде кинетической энергии его движения после выхода из металла (см. рис. 2).
Рис. 2. Условие выхода электрона из металла
Квант
По определению, квант – это неделимая порция какой-либо величины в физике. Мы сегодня рассматриваем кванты, то есть порции, световой энергии. Мы говорим, например, что энергия фотона равна одному кванту (одной порции, равной ).
Часто «квант» употребляется в значении неделимой порции излучения, в том же значении, что и «фотон». Тогда имеет смысл говорить об энергии одного кванта излучения. Мы будем употреблять слово «квант» в обоих значениях в зависимости от контекста, как нам удобно выражать мысли.
Эта закономерность отражена в уравнении Эйнштейна для фотоэффекта, которое выглядит так:
– это работа выхода – минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Квант энергии света расходуется на совершение работы выхода
и на сообщение электрону кинетической энергии. По сути, уравнение Эйнштейна является реализацией закона сохранения энергии.
Почему мы рассматриваем металлы
Мы сегодня говорим о выбивании светом электронов с поверхности металла. А что если будет другое вещество, не металл? Давайте рассмотрим, что будет, если свет будет падать на диэлектрик. Ничего нового: квант энергии так же поглотится электроном (см. рис. 3).
Рис. 3. Поглощение кванта электроном
Однако в диэлектрике нет свободных электронов, они входят в состав атомов, и, чтобы электрон покинул атом, нужна энергия намного большая, чем энергия фотона видимого света (см. рис. 4).
Рис. 4. Поглощение намного большей энергии электроном для его выхода из атома
Если мы будем облучать полупроводник, то энергия фотона может пойти на разрушение ковалентной связи между атомами (см. рис. 5), вследствие чего образуется пара электрон – дырка. Что это такое, вы можете вспомнить, обратившись к урокам об электрическом токе в полупроводниках.
Рис. 5. Разрушение ковалентной связи
В металлах, помимо электронов на атомных орбитах, как в диэлектриках, есть свободные электроны, и они могут покинуть поверхность металла. Для этого им нужно преодолеть притяжение кристаллической решетки, которая состоит из положительно заряженных ионов (см. рис. 6).
Рис. 6. Покидание поверхности металла свободным электроном
Выбивание именно таких электронов под действием света мы сегодня и изучаем.
Теперь понятно, почему возникает порог. Чтобы электрон покинул поверхность металла, нужен один фотон с достаточной для этого энергией. Много фотонов с малой энергией электрон не выбьют.
Этот пример подобен примеру с собакой, которая пытается перепрыгнуть через двухметровый забор. Ей для этого нужно прыгнуть один раз на высоту два метра. Если она будет прыгать на один метр хоть целый день, забор она не перепрыгнет, независимо от суммарной затраченной энергии.
Еще один пример: невысоко расположенная ветка, на которой висят яблоки. Попробуем камнем сбить яблоко. Чтобы яблоко оторвалось, нужно совершить работу по разрыву черенка. При энергии камня, меньшей, чем эта работа, яблоко не оторвется. Если энергия камня будет как раз достаточна для отрыва яблока, оно упадёт сразу под веткой (см. рис. 7).
Рис. 7. Энергия камня достаточна для отрыва яблока
Если будем бросать камни сильнее, с большей энергией, то яблоки будут не просто падать, а отлетать от ветки. Избыточная энергия камня, оставшаяся после разрыва черенка, перейдет в кинетическую энергию яблока.
При фотоэффекте наблюдаются те же процессы, только вместо камня – фотон с энергией , а вместо яблок – электроны (см. рис. 8).
Рис. 8. Пример фотоэффекта
Яблоко может быть спелым, тогда для отрыва его черенка требуется меньшая работа, чем когда яблоко еще не созрело. Работа выхода электрона зависит от материала и состояния поверхности: какой-то материал лучше держит электроны, а от какого-то оторвать электрон легче (см. рис. 9).
Рис. 9. Красная граница фотоэффекта для некоторых веществ
Работу выхода можно определить экспериментально: можно освещать материал светом с разной энергией фотонов и заметить, при какой энергии фотонов фотоэффект начинает протекать (см. рис. 10).
Рис. 10. Экспериментальное определение работы выхода
С этим всё понятно: количество электронов, покинувших металл, определяется количеством попавших на него фотонов, а кинетическая энергия электрона, если он вообще покинет материал, определяется энергией одного фотона.
Но не можем же мы сосчитать количество фотонов. И непосредственно энергию одного фотона измерять мы не будем. Эти параметры можно вычислить, а измеряем мы интенсивность света, частоту, длину волны.
Энергия одного кванта излучения определяется частотой, . Для каждого вещества фотоэффект наблюдается лишь в том случае, если частота
света больше некоторого минимального значения
, потому что кванта энергии должно хватить на совершение работы выхода:
.
Предельную частоту и соответствующую ей длину волны max называют красной границей фотоэффекта.
Красная граница фотоэффекта
Красной границей фотоэффекта называется минимальная частота и соответствующая ей максимальная длина волны, при которой наблюдается фотоэффект. Почему она так называется – красная граница?
Если мы возьмем свет такой частоты, при которой будет наблюдаться фотоэффект, и будем ее уменьшать, мы будем по оси частоты смещаться влево, пока не дойдем до предела, при котором фотоэффект прекратится. Можно поставить рядом ось длин волн.
Если мы будем так же смещаться в видимом спектре, то мы будем двигаться к красному свету, который является граничным для нашего глаза. Свет меньших частот или бόльших длин волн мы уже не видим. Граница видимости соответствует красному цвету.
Для фотоэффекта предельная частота не обязательно соответствует красному цвету, но по аналогии называется красной границей (см. рис. 11).
Рис. 11. Красная граница фотоэффекта и граница спектра видимого света
Как найти красную границу фотоэффекта?
Запишем уравнение Эйнштейна для этого случая. Т. к. энергии такого кванта хватает только на то, чтобы выбить электрон, и на его разгон энергии уже нет (см. рис. 12), составляющая будет равна нулю:
,
– красная граница фотоэффекта.
Рис. 12. Зависимость кинетической энергии фотоэлектрона от частоты падающего света
Частота или длина волны, соответствующие красной границе фотоэффекта, зависят от вещества и определяются величиной работы выхода электрона из данного вещества (см. рис. 13).
Рис. 13. Зависимость частоты (длины волны) от вещества
Суммарная энергия квантов в световом потоке, падающем на металл, – это интенсивность света. Если мы изменяем интенсивность света данной частоты, то это значит, что мы изменяем количество фотонов, а значит, и количество фотоэлектронов. Скорость каждого выбитого из металла электрона от интенсивности света не зависит.
Задача
Красная граница фотоэффекта для калия . Какую максимальную скорость могут иметь фотоэлектроны, вылетающие с поверхности калиевого фотокатода при облучении его светом с диной волны
?
Анализ условия.
Решение
Применим к данной задаче уравнение Эйнштейна для фотоэффекта и выражение для красной границы. В задаче заданы значения длин волн, поэтому сразу перейдем от частот к длинам волн по формуле . Запишем:
Получили систему уравнений, решив которую, найдем максимальную скорость электрона. Получим ответ около 580 км/с.
Математическая часть решения задачи
Подставим выражение для работы выхода из второго уравнения в первое:
Выразим отсюда искомую скорость:
Вычислим:
Как мы можем использовать фотоэффект на практике?
Свет сообщает электрону энергию и выбивает его из металла (см. рис. 14).
Рис. 14. Выход электрона из металла
Что это нам дает? Электрон мы можем зарегистрировать. Если есть свободные электроны, то можно создать электрическое поле, которое заставит их двигаться и создаст электрический ток (см. рис. 15).
Рис. 15. Возникновение электрического тока
Что делать с ним дальше – задача электроники; мы можем ток измерить, преобразовать, передать на расстояние и т. д. Главное, что энергия света передалась электрону, свет преобразовался в электричество.
А это значит, что можно сделать датчик света, который определял бы его наличие по наличию фотоэффекта, его интенсивность по количеству фотоэлектронов.
Такие устройства – это фотоэлементы, в которых световой поток управляет электрическим током или преобразуется в электрическую энергию. Фотоэлементы находят множество применений в быту и в технике. Например, они считывают информацию, записанную на звуковой дорожке кинопленки, обнаруживают проход безбилетника в метро (при пересечении невидимого луча прекращается ток в фотоэлементе (см. рис. 16)), замечают задымление в помещении и т. п.
Рис. 16. Принцип турникетов в метро
Мы рассмотрели один случай – что происходит при передаче электрону энергии фотона – электрон покидает вещество. Но в общем случае он может покинуть атом вещества и стать свободным носителем заряда внутри вещества (это явление называется внутренним фотоэффектом) (см. рис. 17).
Рис. 17. Внутренний фотоэффект
Излучение можно использовать как информационный сигнал. К примеру, пульт дистанционного управления телевизором посылает управляющие сигналы в виде инфракрасного (невидимого для наших глаз) излучения (см. рис. 18), которое воспринимается фотоэлементом на передней панели телевизора.
Рис. 18. Инфракрасное излучение
Невидимые электромагнитные сигналы пульта ведут себя так же, как видимый свет. Вы можете убедиться в этом, попытавшись переключать каналы, направляя пульт не на телевизор, а на его изображение в зеркале.
Электрон покидает атом, становится свободным, и в цепи начинает течь фототок. Он и осуществляет нужные переключения в электрической цепи телевизора.
При поглощении энергии света электронами может возникнуть ЭДС, что используется в солнечных батареях, а это еще одно очень перспективное применение фотоэффекта.
На этом наш урок окончен. Спасибо за внимание!
Список литературы
- Соколович Ю.А., Богданова Г.С. Физика: Справочник с примерами решения задач. – 2-е издание, передел. – X.: Веста: Издательство «Ранок», 2005. – 464 с.
- Касьянов В.А. Физика 11 кл. учебник для общеобразоват. учреждений. – 4-е изд. – М.: Дрофа, 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «fmclass.ru» (Источник)
- Интернет-портал объединения учителей физики Санкт-Петербурга (Источник)
- Интернет-портал Единой коллекции ЦОР (Источник)
Домашнее задание
- Что такое красная граница фотоэффекта? Как ее определить по известной работе выхода?
- Что такое внутренний фотоэффект?
- Что такое квант?
Физика, 11 класс
Урок 22. Фотоэффект
Перечень вопросов, рассматриваемых на уроке:
- предмет и задачи квантовой физики;
- гипотеза М. Планка о квантах;
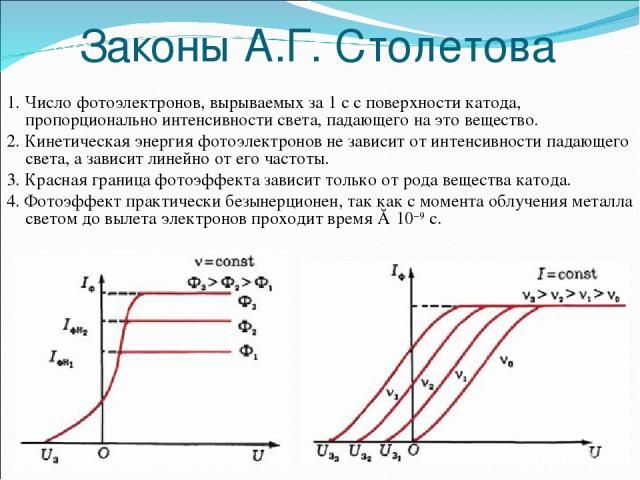
- опыты А.Г. Столетова;
- определение фотоэффекта, кванта, тока насыщения, задерживающего напряжения, работы выхода, красной границы фотоэффекта;
- уравнение Эйнштейна для фотоэффекта;
- законы фотоэффекта.
Глоссарий по теме:
Квантовая физика — раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Фотоэффект – это вырывание электронов из вещества под действием света.
Квант — (от лат. quantum — «сколько») — неделимая порция какой-либо величины в физике.
Ток насыщения — некоторое предельное значение силы фототока.
Задерживающее напряжение — минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл. которую нужно сообщить электрону, для того чтобы он мог преодолеть силы, удерживающие его внутри металла.
Красная граница фотоэффекта – это минимальная частота или максимальная длина волны света излучения, при которой еще возможен внешний фотоэффект.
Основная и дополнительная литература по теме урока:
1. Мякишев Г. Я., Буховцев Б. Б., Чаругин В. М. Физика. 11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2017. – С. 259 – 267.
2. Рымкевич А. П. Сборник задач по физике. 10-11 класс.- М.:Дрофа,2009. – С. 153 – 158.
3. Элементарный учебник физики. Учебное пособие в 3 т./под редакцией академика Ландсберга Г. С.: Т.3. Колебания и волны. Оптика. Атомная и ядерная физика. – 12-е изд. – М.: ФИЗМАТЛИТ, 2001. С. 422 – 429.
4. Тульчинский М. Е. Качественные задачи по физике в средней школе. Пособие для учителей. Изд. 4-е, переработ. и доп. М. «Просвещение», 1972. С. 157.
Теоретический материал для самостоятельного изучения
В начале 20-го века в физике произошла величайшая революция. Попытки объяснить наблюдаемые на опытах закономерности распределения энергии в спектрах теплового излучения оказались несостоятельными. Законы электромагнетизма Максвелла неожиданно «забастовали». Противоречия между опытом и практикой были разрешены немецким физиком Максом Планком.
Гипотеза Макса Планка: атомы испускают электромагнитную энергию не непрерывно, а отдельными порциями – квантами. Энергия Е каждой порции прямо пропорциональна частоте ν излучения света: E = hν.
Коэффициент пропорциональности получил название постоянной Планка, и она равна:
h = 6,63 ∙ 10-34 Дж∙с.
После открытия Планка начала развиваться самая современная и глубокая физическая теория – квантовая физика.
Квантовая физика — раздел теоретической физики, в котором изучаются квантово-механические и квантово-полевые системы и законы их движения.
Поведение всех микрочастиц подчиняется квантовым законам. Но впервые квантовые свойства материи были обнаружены именно при исследовании излучения и поглощения света.
В 1886 году немецкий физик Густав Людвиг Герц обнаружил явление электризации металлов при их освещении.
Явление вырывания электронов из вещества под действием света называется внешним фотоэлектрическим эффектом.
Законы фотоэффекта были установлены в 1888 году профессором московского университета Александром Григорьевичем Столетовым.
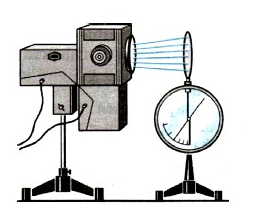
Схема установки для изучения законов фотоэффекта
Первый закон фотоэффекта: фототок насыщения — максимальное число фотоэлектронов, вырываемых из вещества за единицу времени, — прямо пропорционален интенсивности падающего излучения.
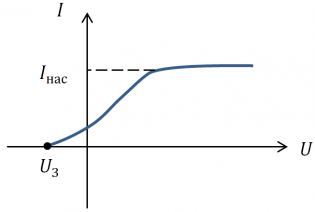
Зависимость силы тока от приложенного напряжения
Увеличение интенсивности света означает увеличение числа падающих фотонов, которые выбивают с поверхности металла больше электронов.
Второй закон фотоэффекта: максимальная кинетическая энергия фотоэлектронов не зависит от интенсивности падающего излучения и линейно возрастает с увеличением частоты падающего излучения.
Третий закон фотоэффекта: для каждого вещества существует граничная частота такая, что излучение меньшей частоты не вызывает фотоэффекта, какой бы ни была интенсивность падающего излучения. Эта минимальная частота излучения называется красной границей фотоэффекта.
hνmin = Aв
где Ав – работа выхода электронов;
h – постоянная Планка;
νmin — частота излучения, соответствующая красной границе фотоэффекта;
с – скорость света;
λкр – длина волны, соответствующая красной границе.
Фотоэффект практически безынерционен: фототок возникает одновременно с освещением катода с точностью до одной миллиардной доли секунды.
Работа выхода – это минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Для большинства веществ фотоэффект возникает только под действием ультрафиолетового облучения. Однако некоторые металлы, например, литий, натрий и калий, испускают электроны и при облучении видимым светом.
Известно, что фототоком можно управлять, подавая на металлические пластины различные напряжения. Если на систему подать небольшое напряжение обратной полярности, «затрудняющее» вылет электронов, то ток уменьшится, так как фотоэлектронам, кроме работы выхода, придется совершать дополнительную работу против сил электрического поля.
Задерживающее напряжение — минимальное обратное напряжение между анодом и катодом, при котором фототок равен нулю.
Задерживающее напряжение
Максимальная кинетическая энергия электронов выражается через задерживающее напряжение:
где 
Е – заряд электрона;

Теорию фотоэффекта разработал Альберт Эйнштейн. На основе квантовых представлений Эйнштейн объяснил фотоэффект. Электрон внутри металла после поглощения одного фотона получает порцию энергии и стремится вылететь за пределы кристаллической решетки, т.е. покинуть поверхность твердого тела. При этом часть полученной энергии он израсходует на совершение работы по преодолению сил, удерживающих его внутри вещества. Остаток энергии будет равен кинетической энергии:
В 1921 году Альберт Эйнштейн стал обладателем Нобелевской премии, которая, согласно официальной формулировке, была вручена «за заслуги перед теоретической физикой и особенно за открытие закона фотоэлектрического эффекта».
Если фотоэффект сопровождается вылетом электронов с поверхности вещества, то его называют внешним фотоэффектом или фотоэлектронной эмиссией, а вылетающие электроны — фотоэлектронами. Если фотоэффект не сопровождается вылетом электронов с поверхности вещества, то его называют внутренним.
Примеры и разбор решения заданий
1. Монохроматический свет с длиной волны λ падает на поверхность металла, вызывая фотоэффект. Фотоэлектроны тормозятся электрическим полем. Как изменятся работа выхода электронов с поверхности металла и запирающее напряжение, если уменьшить длину волны падающего света?
Для каждой величины определите соответствующий характер изменения:
1) увеличится
2) уменьшится
3) не изменится
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
|
Работа выхода |
Запирающее напряжение |
Решение:
Работа выхода — это характеристика металла, следовательно, работа выхода не изменится при изменении длины волны падающего света.
Запирающее напряжение — это такое минимальное напряжение, при котором фотоэлектроны перестают вылетать из металла. Оно определяется из уравнения:
Следовательно, при уменьшении длины волны падающего света, запирающее напряжение увеличивается.
Ответ:
|
Работа выхода |
Запирающее напряжение |
|
не изменится |
увеличится |
2. Красная граница фотоэффекта для вещества фотокатода λ0 = 290 нм. При облучении катода светом с длиной волны λ фототок прекращается при напряжении между анодом и катодом U = 1,5 В. Определите длину волны λ.
Решение.
Запишем уравнение для фотоэффекта через длину волны:
Условие связи красной границы фотоэффекта и работы выхода:
Запишем выражение для запирающего напряжения – условие равенства максимальной кинетической энергии электрона и изменения его потенциальной энергии при перемещении в электростатическом поле:
Решая систему уравнений (1), (2), (3), получаем формулу для вычисления длины волны λ:
Подставляя численные значения, получаем: λ ≈ 215 нм.
Ответ: λ ≈ 215 нм.
Начало теории электромагнитной природы света заложил Максвелл, который заметил сходство в скоростях распространения электромагнитных и световых волн. Но согласно электродинамической теории Максвелла любое тело, излучающее электромагнитные волны, должно в итоге остынуть до абсолютного нуля. В действительности этого не происходит. Противоречия между теорией и опытными наблюдениями были разрешены в начале XX века, вскоре после того, как был открыт фотоэффект.
Что такое фотоэффект
Фотоэффект — испускание электронов из вещества под действием падающего на него света.
Александр Столетов
Явление фотоэффекта было открыто в 1887 году Генрихом Герцем. Фотоэффект также был подробно изучен русским физиком Александром Столетовым в период с 1888 до 1890 годы. Этому явлению он посвятил 6 научных работ.
Для наблюдения фотоэффекта нужно провести опыт. Для этого понадобится электрометр и подсоединенная к нему пластинка из цинка (см. рисунок ниже). Если дать пластинке положительный заряд, то при ее освещении электрической дугой скорость разрядки электрометра не изменится. Но если цинковую пластинку зарядить отрицательно, то свет от дуги заставить электрометр разрядиться очень быстро.
Наблюдаемое во время этого эксперимента явление имеет простое объяснение. Свет вырывает электроны с поверхности цинковой пластинки. Если она имеет отрицательный заряд, электроны отталкиваются от нее, что приводит к полному разряжению электрометра. Причем при повышении интенсивности освещения скорость разрядки увеличивается, ровно, как и наоборот: при уменьшении интенсивности освещения электрометр разряжается медленно. Если же зарядить пластинку положительно, то электроны, которые вырываются светом, притягиваются к ней. Поэтому они оседают на ней, не изменяя заряд электрометра.
Если между световым пучком и отрицательно заряженной пластиной поставить лист стекла, пластинка перестанет терять электроны независимо от интенсивности излучения. Это связано с тем, что стекло задерживает ультрафиолетовое излучение. Отсюда можно сделать следующий вывод:
Явление фотоэффекта может вызвать только ультрафиолетовый участок спектра.
Волновая теория света не может объяснить, почему электроны могут вырываться только под действием ультрафиолета. Ведь даже при большой амплитуде и силе волн электроны остаются на месте, когда, казалось бы, они должны непременно быть вырванными.
Законы фотоэффекта
Чтобы получить более полное представление о фотоэффекте, выясним, от чего зависит количество электронов, вырванных светом с поверхности вещества, а также, от чего зависит их скорость, или кинетическая энергия. Выяснить все это нам помогут эксперименты.
Первый закон фотоэффекта
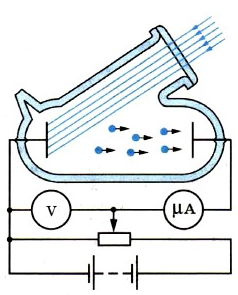
Возьмем стеклянный баллон и выкачаем из него воздух (смотрите рисунок выше). Затем поместим в него два электрода. На электроды подадим напряжение и будем регулировать его с помощью потенциометра и измерять при помощи вольтметра.
В верхней части нашего баллона есть небольшое кварцевое окошко, которое пропускает весь свет, в том числе ультрафиолетовый. Через него падает свет на один из электродов (в нашем случае на левый электрод, к которому присоединен отрицательный полюс батареи). Мы увидим, что под действием света этот электрод начнет испускать электроны, которые при движении в электрическом поле будут создавать электрический ток. Вырванные электроны будут направляться ко второму электроду. Но если напряжение небольшое, второго электрода достигнут не все электроны. Если интенсивность излучения сохранить, но увеличить между электродами разность потенциалов, то сила тока будет увеличиваться. Но как только она достигнет некоторого максимального значения, рост силы тока при дальнейшем увеличении напряжения прекратится. Максимальное значение силы тока будем называть током насыщения.
Ток насыщения — максимальное значение силы тока, также называемое предельным значением силы фототока.
Ток насыщения обозначается как Iн. Единица измерения — А (Кл/с). Численно величина равна отношению суммарному заряду вырванных электронов в единицу времени:
Iн=qt
Если же мы начнем изменять интенсивность излучения, то сможем заметить, что фототок насыщения также начинается меняться. Если интенсивность излучения ослабить, максимальное значение силы тока уменьшится. Если интенсивность светового потока увеличить, ток насыщения примет большее значение. Отсюда можно сделать вывод, который называют первым законом фотоэффекта.
Первый закон фотоэффекта:
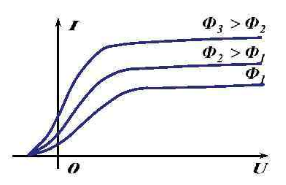
Число электронов, вырываемых светом с поверхности металла за 1 с, прямо пропорционально поглощаемой за это время энергии световой волны. Иными словами, фототок насыщения прямо пропорционален падающему световому потоку Ф.
Второй закон фотоэффекта
Теперь произведем измерения кинетической энергии, то есть, скорости вырывания электронов. Взгляните на график, представленный ниже. Видно, что сила фототока выше нуля даже при нулевом напряжении. Это говорит о том, что даже при нулевой разности потенциалов часть электронов достигает второго электрода.
Если мы поменяем полярность батареи, то будем наблюдать уменьшение силы тока. Если подать на электроды некоторое значение напряжения, равное Uз, сила тока станет равно нулю. Это значит, что электрическое поле тормозит вырванные электроны, останавливает их, а затем возвращает на тот же электрод.
Напряжение, равное Uз, называют задерживающим напряжением. Оно зависит зависит от максимальной кинетической энергии электронов, которые вырываются под действием света. Измеряя задерживающее напряжение и применяя теорему о кинетической, можно найти максимальное значение кинетической энергии электронов. Оно будет равно:
mv22=eUз
Опыт показывает, что при изменении интенсивности света (плотности потока излучения) задерживающее напряжение не меняется. Значит, не меняется кинетическая энергия электронов. С точки зрения волновой теории света этот факт непонятен. Ведь чем больше интенсивность света, тем большие силы действуют на электроны со стороны электромагнитного поля световой волны и тем большая энергия, казалось бы, должна передаваться электронам. Но экспериментальным путем мы обнаруживаем, что кинетическая энергия вырываемых светом электронов зависит только от частоты света. Отсюда мы можем сделать вывод, являющийся вторым законом фотоэффекта.
Второй закон фотоэффекта:
Максимальная кинетическая энергия фотоэлектронов линейно растет с частотой света и не зависит от его интенсивности.
Причем, если частота света меньше определенной для данного вещества минимальной частоты νmin, фотоэффект наблюдаться не будет.
Теория фотоэффекта
Все попытки объяснить явление фотоэффекта электродинамической теорией Максвелла, согласно которой свет — это электромагнитная волна, непрерывно распределенная в пространстве, оказались тщетными. Нельзя было понять, почему энергия фотоэлектронов определяется только частотой света и почему свет способен вырывать электроны лишь при достаточно малой длине волны.
В попытках объяснить это явление физик Макс Планк предложил, что атомы испускают электромагнитную энергию отдельными порциями — квантами, или фотонами. И энергия каждой порции прямо пропорциональна частоте излучения:
E=hν
h — коэффициент пропорциональности, который получил название постоянной Планка. Она равна 6,63∙10–34 Дж∙с.
Пример №1. Определите энергию фотона, соответствующую длине волны λ = 5∙10–7 м.
Энергия фотона равна:
E=hν
Выразим частоту фотона через скорость света:
ν=cλ
Следовательно:
Идею Планка продолжил развивать Эйнштейн, которому удалось дать объяснение фотоэффекту в 1905 году. В экспериментальных законах фотоэффекта Эйнштейн увидел убедительное доказательство того, что свет имеет прерывистую структуру и поглощается отдельными порциями. Причем энергия Е каждой порции излучения, по его расчетам, полностью соответствовала гипотезе Планка.
Из того, что свет излучается порциями, еще не вытекает вывода о прерывистости структуры самого света. Ведь и воду продают в бутылках, но отсюда не следует, что вода состоит из неделимых частиц. Лишь фотоэффект позволил доказать прерывистую структуру света: излученная порция световой энергии Е = hν сохраняет свою индивидуальность и в дальнейшем. Поглотиться может только вся порция целиком.
Кинетическую энергию фотоэлектрона можно найти, используя закон сохранения энергии. Энергия порции света hν идет на совершение работы выхода А и на сообщение электрону кинетической энергии. Отсюда:
hν=A+mv22
Работа выхода — минимальная энергия, которую надо сообщить электрону, чтобы он покинул металл.
Полученное выражение объясняет основные факты, касающиеся фотоэффекта. Интенсивность света, по Эйнштейну, пропорциональна числу квантов (порций) энергии hν в пучке света и поэтому определяет количество вырванных электронов. Скорость же электронов согласно зависит только от частоты света и работы выхода, которая определяется типом металла и состоянием его поверхности. От интенсивности освещения кинетическая энергия фотоэлектронов не зависит.
Для каждого вещества фотоэффект наблюдается лишь при освещении его светом с минимальной частотой волны νmin. Это объясняется тем, что для вырывания электрона без сообщения ему скорости нужно выполнять как минимум работу выхода. Поэтому энергия кванта должна быть больше этой работы:
hν>A
Предельную частоту νmin называют красной границей фотоэффекта. При этой частоте фотоэффект уже наблюдается.
Красная граница фотоэффекта равна:
νmin=Ah
Минимальной частоте, при которой возможен фотоэффект для данного вещества, соответствует максимальная длина волны, которая также носит название красной границы фотоэффекта. Это такая длина волны, при которой фотоэффект еще наблюдается. Обозначается она как λmах или λкр.
Максимальная длина волны, при которой еще наблюдается фотоэффект, равна:
λmax=hcA
Работа выхода А определяется родом вещества. Поэтому и предельная частота vmin фотоэффекта (красная граница) для разных веществ различна. Отсюда вытекает еще один закон фотоэффекта.
Третий закон фотоэффекта:
Для каждого вещества существует максимальная длина волны, при которой фотоэффект еще наблюдается. При больших длинах волн фотоэффекта нет.
Вспомните опыт, который мы описали в самом начале. Когда между цинковой пластинкой и световым пучком мы поставили зеркало, фотоэффект был прекращен. Это связано с тем, что красная граница для цинка определяется величиной λmах = 3,7 ∙ 10-7 м. Эта длина волны соответствует ультрафиолетовому излучению, которое не пропускало стекло.
Пример №2. Чему равна красная граница фотоэффекта νmin, если работа выхода электрона из металла равна A = 3,3∙10–19 Дж?
Применим формулу для вычисления красной границы фотоэффекта:
Задание EF15717
При увеличении в 2 раза частоты света, падающего на поверхность металла, задерживающее напряжение для фотоэлектронов увеличилось в 3 раза. Первоначальная частота падающего света была равна 0,75 ⋅1015 Гц. Какова длина волны, соответствующая «красной границе» фотоэффекта для этого металла? Ответ записать в нм.
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Переписать формулу закона сохранения энергии применительно к опытам 1 и 2.
4.Используя формула, связывающую задерживающее напряжение и кинетическую энергию фотона, определить работу выхода.
5.Записать формулу для красной границы фотоэффекта.
6.Выполнить решение в общем виде.
7.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Частота света в опыте 1: ν1 = ν = 0,75∙1015 Гц.
• Частота света в опыте 2: ν2 = 2ν1 = 2ν Гц.
• Задерживающее напряжение в опыте 1: U1 = U В.
• Задерживающее напряжение в опыте 2: U2 = 3U1 = 3U В.
Запишем формулу закона сохранения энергии:
hν=A+mv22
Применим ее к 1 и 2 опыту, составив систему из двух уравнений:
⎧⎪⎨⎪⎩hν1=A+mv212hν2=A+mv222
Преобразуем:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+mv222
Формула, связывающая задерживающее напряжение и кинетическую энергию фотона:
mv22=eUз
Известно, что при увеличении частоты в 2 раза задерживающее напряжение увеличилось в 3 раза. Так как задерживающее напряжение прямо пропорционально кинетической энергии фотона, то она (кинетическая энергия), также увеличивается в 3 раза. Следовательно:
mv222=3mv212
Тогда:
⎧⎪⎨⎪⎩hν=A+mv2122hν=A+3mv212
Умножим первое уравнение системы на «–3» и сложим оба уравнения:
⎧⎪⎨⎪⎩−3hν=−3A−3mv2122hν=A+3mv212
−hν=−2A
Отсюда работа выхода равна:
A=hν2
Формула для нахождения красной границы фотоэффекта:
νmin=Ah
Формула длины волны:
λ=cν
Следовательно, длина волны для красной границы фотоэффекта:
λmin=cνmin=chA=2chhν=2cν
Ответ: 800
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17645
При исследовании зависимости кинетической энергии фотоэлектронов от частоты падающего света фотоэлемент освещался через светофильтры. В первой серии опытов использовался красный светофильтр, а во второй – жёлтый. В каждом опыте измеряли напряжение запирания.
Как изменяются длина световой волны, напряжение запирания и кинетическая энергия фотоэлектронов? Для каждой величины определите соответствующий характер её изменения:
| 1) | увеличится |
| 2) | уменьшится |
| 3) | не изменится |
Запишите в таблицу выбранные цифры для каждого ответа. Цифры в ответе могут повторяться.
Алгоритм решения
1.Определить, от чего зависит и как меняется длина световой волны.
2.Записать закон сохранения энергии, формулу зависимости кинетической энергии от напряжения запирания.
3.Используя формулы, становить, как меняется напряжение запирания и кинетическая энергия.
Решение
Длина световой волны определяется ее цветом. Красный свет имеет большую длину волны. Следовательно, во втором опыте длина световой волны уменьшится.
Закон сохранения энергии для фотоэффекта:
hν=A+mv22
Формула зависимости кинетической энергии от напряжения запирания:
mv22=eUз
Следовательно:
hν=A+eUз
Работы выхода — величина постоянная для данного вещества. Следовательно, напряжение запирания зависит только от частоты световой волны. Частота — величина обратная длине волны. Так как длина волны уменьшилась, частота увеличилась. Следовательно, увеличилось и напряжение запирания.
Поскольку напряжение запирания прямо пропорционально кинетической энергии фотонов, то эта энергия также увеличивается.
Ответ: 211
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17973
На металлическую пластинку падает монохроматическая электромагнитная волна, выбивающая электроны из пластинки. Максимальная кинетическая энергия фотоэлектронов, вылетевших из пластинки в результате фотоэффекта, составляет 3 эВ, а работа выхода из металла в 2 раза больше этой энергии. Чему равна энергия фотонов в падающей волне?
Ответ:
а) 9 эВ
б) 2 эВ
в) 3 эВ
г) 6 эВ
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу закона сохранения энергии применительно к фотоэффекту.
3.Выполнить решение в общем виде.
4.Подставить известные данные и найти искомую величину.
Решение
Запишем исходные данные:
• Максимальная кинетическая энергия выбитых электронов: Emax = 3 эВ.
• Работа выхода из металла: A = 2 Emax.
Закона сохранения энергии для фотоэффекта:
hν=A+mv22
Или:
E=A+Emax=2Emax+Emax=3Emax=3·3=9 (эВ)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 5.4k
Красная граница фотоэффекта

4
Средняя оценка: 4
Всего получено оценок: 66.
4
Средняя оценка: 4
Всего получено оценок: 66.
Фотоэффект — это выбивание из атомов вещества электронов под действием электромагнитного излучения. Как показывают опыты, излучение, необходимое для этого явления должно отвечать важному условию, называемому «красной границей фотоэффекта».
Явление фотоэффекта
Свет, хотя и является электромагнитной волной, существует только в виде порций-квантов (фотонов). Испускание или поглощение фотонов происходит только целиком. Каждый фотон несет некоторую энергию, зависящую от его частоты, равную ($h$ — постоянная Планка):
$$E=hnu$$
Явление фотоэффекта состоит в том, что электроны в атоме поглощают кванты электромагнитного излучения и приобретают дополнительную энергию, достаточную для разрыва связей с ядром. В результате электрон покидает свою орбиту и либо становится свободным электроном в веществе (внутренний фотоэффект), либо выходит из вещества в окружающее пространство (внешний фотоэффект).
Энергия, которую нужно сообщить электрону для разрыва связей с ядром, называется работой выхода $A_{вых}$. Остаток энергии фотона перейдет в кинетическую энергию выбитого электрона. Этот механизм описывается уравнением, выведенным в 1905 г. А. Эйнштейном:
$$hnu=A_{вых}+{m_ev^2over 2}$$
Красная граница фотоэффекта
Получим из приведенной формулы частоту, необходимую для наблюдения фотоэффекта:
$$nu={1over h}(A_{вых}+{m_ev^2over 2})$$
Важно отметить, что, поскольку работа выхода $A_{вых}$ и масса электрона $m_e$ имеют некоторое положительное значение, а скорость электрона $v$ не может быть отрицательной, то и частота $nu$ будет иметь некоторое значение больше нуля. Минимальное значение будет достигаться, если $v=0$:
$$nu_{min}={A_{вых}over h}$$
Частота $nu_{min}$ называется «красной границей фотоэффекта», а приведенное соотношение — это формула красной границы фотоэффекта. Если фотон имеет частоту ниже, то его энергии недостаточно для разрыва связей электрона с ядром, фотоэффект с таким фотоном невозможен.
Термин «красная граница» был введен А. Столетовым, который провел наиболее глубокие исследования фотоэффекта в конце XIX в. Третий закон Столетова гласит, что для каждого вещества есть некоторая минимальная частота фотонов, ниже которой фотоэффект исчезает.
Именно красной границей фотоэффекта определяется использование красного освещения при печати фотографий в первой половине XX в. и ранее. Красная граница фотоэффекта материалов того времени лежала в желтой области видимого света. Поэтому фотопластинки проявлялись при красном освещении. В дальнейшем стали использоваться материалы с меньшей работой выхода, красная граница фотоэффекта для них переместилась в инфракрасную область, и проявлять их было необходимо уже в полной темноте.
Что мы узнали?
Красная граница фотоэффекта — это минимальная частота, при которой наблюдается фотоэффект. Если частота излучения меньше, то энергии фотонов не хватает для совершения работы выхода, и фотоэффект исчезает.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 66.
А какая ваша оценка?
Одним из интереснейших квантовых эффектов, рассматриваемых в курсе школьной физики, является фотоэлектрический эффект или фотоэффект. Фотоэффект — явление взаимодействия света с веществом, в результате которого энергия фотонов передаётся электронам вещества.
Рис. 1. Фотоэффект
Облучаем поверхность вещества. Энергия каждого фотона равна . Фотон, попадающий внутрь вещества, поглощается электроном, который, в свою очередь, приобретает дополнительную энергию. Вырываясь из поверхности вещества, электрон теряет часть энергии (взаимодействуя с ионами вещества) и, становясь свободным (когда электрон перестаёт взаимодействовать с веществом), улетает в пространство.
С точки зрения зрения закона сохранения энергии, можно получить уравнение Эйнштейна:
(1)
- где
Работа выхода электрона () — минимальная энергия, которую необходимо передать электрону, чтобы он «выбрался» на поверхность. Если энергия фотона равна точно энергии выхода, то электрон, «выйдя» на поверхность, там и останавливается, т.е. после выхода электрона, его кинетическая энергия численно равна нулю. Тогда уравнение Эйнштейна примет вид:
(2)
- где
Красная граница фотоэффекта () — частота излучения (фотона), ниже которой фотоэффект не происходит.
Аналогично можно ввести:
(3)
- где
Вывод: задачи на фотоэффект вводятся именно этим словом. Единственное, что мы можем использовать при этом, — уравнение Эйнштейна (1).