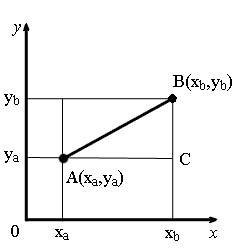Как найти кратчайшее расстояние между точками - Исправление недочетов и поиск решений вместе с Examum.ru

Вывод формулы для вычисления расстояния между двумя точками на плоскости

Из точек A и B опустим перпендикуляры на оси координат.

Рассмотрим прямоугольный треугольник ∆ABC. Катеты этого треугольника равны:

AC = x_b — x_a;

BC = y_b — y_a.

Воспользовавшись теоремой Пифагора, вычислим длину отрезка AB:

AB = √AC² + BC².

Подставив в это выражение длины отрезков AC и BC, выраженные через координаты точек A и B, получим формулу для вычисления расстояния между точками на плоскости.

Формула для вычисления расстояния между двумя точками в пространстве выводится аналогично.

Источник

Но полёт самолета — очень дорогое удовольствие. Зачем же они делают такой крюк, если можно было бы пролететь
более коротким маршрутом, соответствующим на карте прямой?

Всё дело в том, что понятие кратчайшего расстояния неразрывно связано с той поверхностью, по которой оно измеряется.
Как уже отмечалось, любая плоская карта представляет земную поверхность с искажениями. Давайте рассмотрим соответствующие
траектории на глобусе. И вот только теперь можно судить о длине обсуждаемых маршрутов.

Чтобы найти кратчайшее расстояние между двумя точками на сфере, необходимо провести через них большую окружность.
Это окружность, образованная пересечением сферы с плоскостью, проходящей через центр сферы и наши точки.
Минимальная из двух дуг большой окружности, соединяющая точки, и только она является кратчайшим расстоянием
на сфере между ними. В математике линию, отвечающую минимальному расстоянию между двумя точками, называют
геодезической на рассматриваемой поверхности.

Источник

Things You Should Know

Jot down the coordinates that you’re measuring the distance between.
Plug these coordinates into the distance formula: ${sqrt (}(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2})$ .
Solve the formula by squaring the differences of the x and y values, adding these differences together, and finding the square root of the remaining sum.

Steps

1
Take the coordinates of two points you want to find the distance between. Call one point Point 1 (x1,y1) and make the other Point 2 (x2,y2). It does not terribly matter which point is which, as long as you keep the labels (1 and 2) consistent throughout the problem.^[1]
- x1 is the horizontal coordinate (along the x axis) of Point 1, and x2 is the horizontal coordinate of Point 2. y1 is the vertical coordinate (along the y axis) of Point 1, and y2 is the vertical coordinate of Point 2.
- For an example, take the points (3,2) and (7,8). If (3,2) is (x1,y1), then (7,8) is (x2,y2).
2

Know the distance formula. This formula finds the length of a line that stretches between two points: Point 1 and Point 2. The linear distance is the square root of the square of the horizontal distance plus the square of the vertical distance between two points.^[2] More simply put, it is the square root of: $(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}$

Advertisement
3
Find the horizontal and vertical distance between the points. First, subtract y2 — y1 to find the vertical distance. Then, subtract x2 — x1 to find the horizontal distance. Don’t worry if the subtraction yields negative numbers. The next step is to square these values, and squaring always results in a positive number.^[3]
- Find the distance along the y-axis. For the example points (3,2) and (7,8), in which (3,2) is Point 1 and (7,8) is Point 2: (y2 — y1) = 8 — 2 = 6. This means that there are six units of distance on the y-axis between these two points.
- Find the distance along the x-axis. For the same example points (3,2) and (7,8): (x2 — x1) = 7 — 3 = 4. This means that there are four units of distance separating the two points on the x-axis.
4

Square both values. This means that you will square the x-axis distance (x2 — x1), and that you will separately square the y-axis distance (y2 — y1).
5

Add the squared values together. This will give you the square of the diagonal, linear distance between your two points. In the example of the points (3,2) and (7,8), the square of (8 — 2) is 36, and the square of (7 — 3) is 16. 36 + 16 = 52.
6
Take the square root of the equation. This is the final step in the equation. The linear distance between the two points is the square root of the sum of the squared values of the x-axis distance and the y-axis distance.^[4]
- To carry on the example: the distance between (3,2) and (7,8) is sqrt (52), or approximately 7.21 units.

Calculator, Practice Problems, and Answers

Add New Question

Question

How do I find the horizontal distance between (3, 4) and (8, 4)?

Subtract 3 from 8 since both are at 4 on the y axis. So distance is: 8-3=5.
Question

What is the distance from the x-axis to (7,-2)?

This is an ambiguous question. I will assume you mean the shortest distance. Then, your second point will be (7,0) because the line that goes through (7,0) and (7,-2) is perpendicular to the x-axis. So your answer is 2.
Question

What is the distance between (2, 3) and (-8,12)?

Using the distance formula shown in the above article, find the horizontal distance between the two points by subtracting (-8) from 2, which is 10. Then find the vertical distance between the points by subtracting 12 from 3, which is -9. We then add together the squares of those two distances: 3² + (-9)² = 9 + 81 = 90. Find the square root of that sum: √90 = 9.49. That’s the distance (in «units») between the two points.

See more answers

Ask a Question

200 characters left

Include your email address to get a message when this question is answered.

Submit

It doesn’t matter if you get a negative number after subtracting y2 — y1 or x2 — x1. Because the difference is then squared, you will always get a positive distance in your answer.^[5]

Thanks for submitting a tip for review!

About This Article

Article SummaryX

To find the distance between two points on a line, take the coordinates of the two points. Label one as Point 1, with the coordinates x1 and y1, and label the other Point 2, with the coordinates x2 and y2. Plug these values into the distance formula, which is the square of X2 minus X1 plus the square of Y2 minus Y1, then the square root of that result. To see the distance formula written out, read on!

Did this summary help you?

Thanks to all authors for creating a page that has been read 866,608 times.

Did this article help you?

Источник

Простейшие расстояния на плоскости

Расстояние – это длина, на которую объекты удалены друг от друга.

Чтобы измерить длину или расстояние используют различные измерительные приборы: линейку, рулетку, ленты и даже лазерные дальномеры. Все они показывают, как далеко находится один объект до другого. Длина всегда измеряется в определенных величинах: миллиметрах, сантиметрах, дециметрах, метрах, километрах.

РАССТОЯНИЕ МЕЖДУ ТОЧКАМИ:

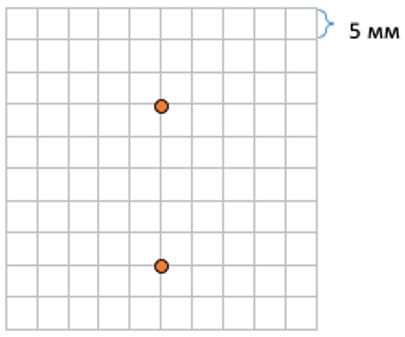
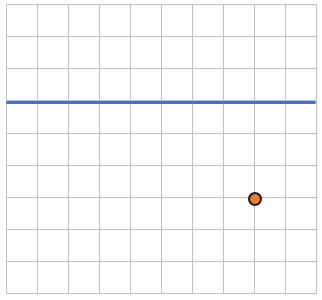
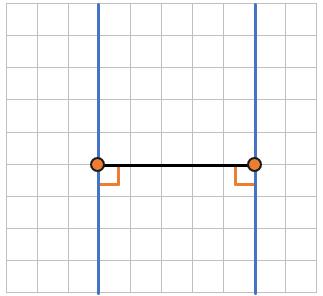
1. Представим тетрадный лист в клетку. Мы знаем, что длина и ширина каждой клетки равна 5 мм или половине сантиметра (5мм х 5мм). Попробуем найти расстояние между двумя точками:

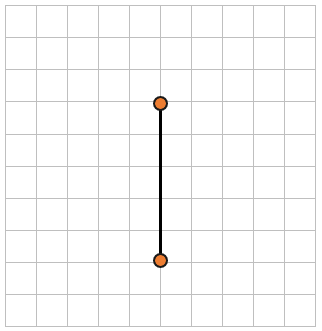
Проведем отрезок между этими точками. Этот отрезок проходит 5 клеток. Каждая клетка = 5 мм.

Значит расстояние между точками равно длине отрезка, заключенного между ними:

(5мм bullet 5 = 25мм).

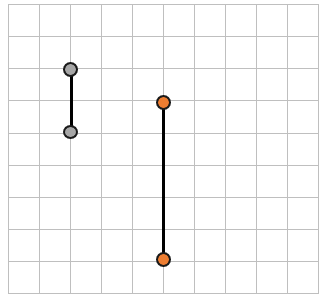
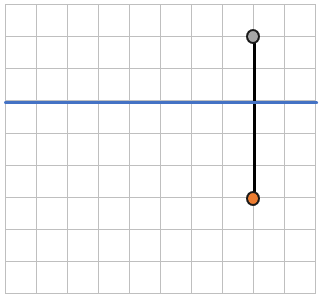
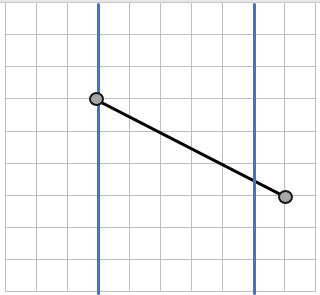
2. Добавим еще две точки на наш лист в клетку и посчитаем расстояние между ними:

Расстояние между этими двумя точками (5мм bullet 2 = 10мм). Теперь мы можем сравнить расстояния до разных точек, зная их длину:

(25мм > 10мм)

Значит расстояние между оранжевыми точками больше, чем расстояние между серыми.

РАССТОЯНИЕ МЕЖДУ ТОЧКОЙ И ПРЯМОЙ:

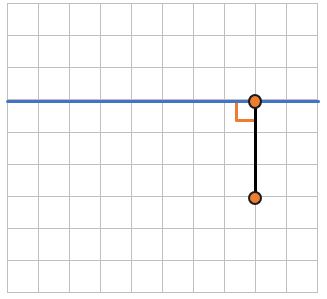
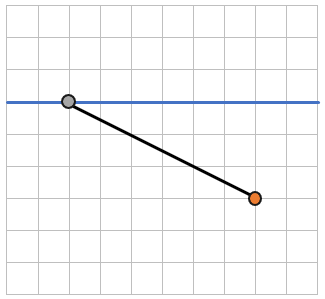
Теперь рассмотрим на клетчатой бумаге, клетки которой равны 1см х 1 см точку и прямую линию:

Найдем расстояние между точкой и прямой. Таким расстоянием будет являться наикратчайшее расстояние.

Наикратчайшее расстояние – это перпендикуляр, проведенный между двумя точками.

Это значит, что расстоянием между точкой и прямой будет длина перпендикуляра между ними.

Перпендикуляр – это отрезок, проходящий под прямым углом к чему-либо.

Теперь если мы посчитаем длину перпендикуляра – найдем расстояние между прямой и точкой:

(1см bullet 3 = 3см)

Длины каких отрезков НЕ будут являться расстоянием между прямой и точкой:

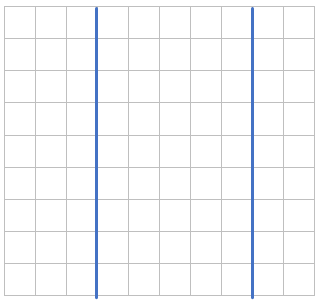
РАССТОЯНИЕ МЕЖДУ ПАРАЛЛЕЛЬНЫМИ ПРЯМЫМИ:

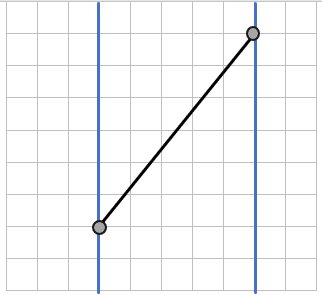
Длина любого перпендикуляра между двумя параллельными прямыми везде одинакова, поэтому, чтобы найти расстояние между параллельными прямыми, можно взять любой перпендикуляр между ними и измерить его длину:

Проведем перпендикуляр между прямыми:

Длина перпендикуляра между прямыми будет равна

расстоянию между ними, т.к. перпендикуляр – кратчайшее расстояние:

(1см bullet 5 = 5см)

Длины каких отрезков НЕ будут являться расстоянием между параллельными прямыми:

Источник

Загрузить PDF

Представьте расстояние между двумя точками в виде отрезка прямой линии, соединяющего эти точки. Длину этого отрезка можно найти по формуле: √ $(x2-x1)^{2}+(y2-y1)^{2}$ .

Шаги

1
Определите координаты двух точек, расстояние между которыми вы хотите вычислить. Обозначим их Точка 1 (x1,y1) и Точка 2 (x2,y2). Неважно, как именно вы обозначите точки, главное, не перепутать их координаты при расчетах.^[1]
- x1 − это горизонтальная координата (вдоль оси x) Точки 1, а x2 − горизонтальная координата Точки 2. Соответственно, y1 − вертикальная координата (вдоль оси y) Точки 1, и y2 − вертикальная координата Точки 2.
- Возьмем, например, точки (3,2) и (7,8). Если мы примем, что (3,2) − это (x1,y1), тогда (7,8) − это (x2,y2).
2

Ознакомьтесь с формулой для вычисления расстояния. Эта формула позволяет найти длину прямого отрезка, соединяющего две точки, Точку 1 и Точку 2. Длина этого отрезка равна квадратному корню от суммы квадратов расстояний между точками по горизонтали и вертикали. Проще говоря, это квадратный корень из $(x2-x1)^{2}+(y2-y1)^{2}$ .^[2]
3
Найдите, чему равны расстояния между точками по горизонтали и вертикали. Расстояние по вертикали найдем в виде разности y2 — y1. Соответственно, расстояние по горизонтали составит x2 — x1. Не волнуйтесь, если в результате вычитания вы получите отрицательное значение. Следующим шагом будет возведение найденных расстояний в квадрат, что в любом случае даст положительное целое число.^[3]
- Найдите расстояние вдоль оси y. Для нашего примера с точками (3,2) и (7,8), где координаты (3,2) соответствуют Точке 1, а координаты (7,8) − Точке 2, находим: (y2 — y1) = 8 — 2 = 6. Это значит, что расстояние между нашими точками по оси y равно шести единицам длины.
- Найдите расстояние вдоль оси x. Для нашего примера с точками (3,2) и (7,8) получаем: (x2 — x1) = 7 — 3 = 4. Это значит, что по оси x наши точки разделяет расстояние, равное четырем единицам длины.
4

Возведите оба значения в квадрат. Необходимо по отдельности возвести в квадрат расстояние вдоль оси x, равное (x2 — x1), и расстояние вдоль оси y, составляющее (y2 — y1):
5

Сложите полученные значения. В результате вы найдете квадрат диагонали, то есть расстояния между двумя точками. В нашем примере для точек с координатами (3,2) и (7,8) находим: (7 — 3) в квадрате равно 36, и (8 — 2) в квадрате равно 16. Складывая, получаем 36 + 16 = 52.
6
Извлеките квадратный корень из найденной величины. Это последний шаг. Расстояние между двумя точками равно квадратному корню от суммы квадратов расстояний вдоль оси x и вдоль оси y.^[4]
- Для нашего примера находим: расстояние между точками (3,2) и (7,8) равно корню квадратному из 52, то есть примерно 7,21 единицы длины.
Реклама

Советы

Не страшно, если в результате вычитания y2 — y1 или x2 — x1 у вас получилось отрицательное значение. Поскольку затем разность возводится в квадрат, расстояние все равно будет равно положительному числу.

Об этой статье

Эту страницу просматривали 89 479 раз.

Была ли эта статья полезной?

Источник