Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.
Задача
Дан ориентированный граф (G = (V, E)), а также вершина (s).
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — количество рёбер в нём.
BFS
BFS — breadth-first search, или же поиск в ширину.
Этот алгоритм позволяет решать следующую задачу.
Алгоритм работает следующим образом.
- Создадим массив (dist) расстояний. Изначально (dist[s] = 0) (поскольку расстояний от вершины до самой себя равно (0)) и (dist[v] = infty) для (v neq s).
- Создадим очередь (q). Изначально в (q) добавим вершину (s).
- Пока очередь (q) непуста, делаем следующее:
- Извлекаем вершину (v) из очереди.
- Рассматриваем все рёбра ((v, u) in E). Для каждого такого ребра пытаемся сделать релаксацию: если (dist[v] + 1 < dist[u]), то мы делаем присвоение (dist[u] = dist[v] + 1) и добавляем вершину (u) в очередь.
Визуализации:
-
https://visualgo.net/mn/dfsbfs
-
https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visualize/
Интуитивное понимание алгоритма
Можно представить, что мы поджигаем вершину (s). Каждый шаг алгоритма — это распространение огня на соседние вершины. Понятно, что огонь доберётся до вершины по кратчайшему пути.
Заметьте, что этот алгоритм очень похож на DFS — достаточно заменить очередь на стек и поиск в ширину станет поиском в глубину. Действительно, оба алгоритма при обработке вершины просто записывают всех непосещенных соседей, в которые из неё есть ребро, в структуру данных, и после этого выбирает следующую вершину для обработки в структуре данных. В DFS это стек (благодаря рекурсии), поэтому мы сначала записываем соседа, идем в обрабатываем его полностью, а потом начинаем обрабатывать следующего соседа. В BFS это очередь, поэтому мы кидаем сразу всех соседей, а потом начинаем обрабатывать вообще другую вершину — ту непосещенную, которую мы положили в очередь раньше всего.
Оба алгоритма позволяют обойти граф целиком — посетить каждую вершину ровно один раз. Поэтому они оба подходят для таких задач как: * поиск компонент связности * проверка графа на двудольность * построение остова
Реализация на C++
n — количество вершин в графе; adj — список смежности
vector<int> bfs(int s) {
// длина любого кратчайшего пути не превосходит n - 1,
// поэтому n - достаточное значение для "бесконечности";
// после работы алгоритма dist[v] = n, если v недостижима из s
vector<int> dist(n, n);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
return dist;
}Свойства кратчайших путей
Обозначение: (d(v)) — длина кратчайшего пути от (s) до (v).
Лемма 1. > Пусть ((u, v) in E), тогда (d(v) leq d(u) + 1).
Действительно, существует путь из (s) в (u) длины (d(u)), а также есть ребро ((u, v)), следовательно, существует путь из (s) в (v) длины (d(u) + 1). А значит кратчайший путь из (s) в (v) имеет длину не более (d(u) + 1),
Лемма 2. > Рассмотрим кратчайший путь от (s) до (v). Обозначим его как (u_1, u_2, dots u_k) ((u_1 = s) и (u_k = v), а также (k = d(v) + 1)).
> Тогда (forall (i < k): d(u_i) + 1 = d(u_{i + 1})).
Действительно, пусть для какого-то (i < k) это не так. Тогда, используя лемму 1, имеем: (d(u_i) + 1 > d(u_{i + 1})). Тогда мы можем заменить первые (i + 1) вершин пути на вершины из кратчайшего пути из (s) в (u_{i + 1}). Полученный путь стал короче, но мы рассматривали кратчайший путь — противоречие.
Корректность
Утверждение. > 1. Расстояния до тех вершин, которые были добавлены в очередь, посчитаны корректно. > 2. Вершины лежат в очереди в порядке неубывания расстояния, притом разность между кратчайшими расстояними до вершин в очереди не превосходит (1).
Докажем это по индукции по количеству итераций алгоритма (итерация — извлечение вершины из очереди и дальнейшая релаксация).
База очевидна.
Переход. Сначала докажем первую часть. Предположим, что (dist[v] + 1 < dist[u]), но (dist[v] + 1) — некорректное расстояние до вершины (u), то есть (dist[v] + 1 neq d(u)). Тогда по лемме 1: (d(u) < dist[v] + 1). Рассмотрим предпоследнюю вершину (w) на кратчайшем пути от (s) до (u). Тогда по лемме 2: (d(w) + 1 = d(u)). Следовательно, (d(w) + 1 < dist[v] + 1) и (d(w) < dist[v]). Но тогда по предположению индукции (w) была извлечена раньше (v), следовательно, при релаксации из неё в очередь должна была быть добавлена вершина (u) с уже корректным расстоянием. Противоречие.
Теперь докажем вторую часть. По предположению индукции в очереди лежали некоторые вершины (u_1, u_2, dots u_k), для которых выполнялось следующее: (dist[u_1] leq dist[u_2] leq dots leq dist[u_k]) и (dist[u_k] — dist[u_1] leq 1). Мы извлекли вершину (v = u_1) и могли добавить в конец очереди какие-то вершины с расстоянием (dist[v] + 1). Если (k = 1), то утверждение очевидно. В противном случае имеем (dist[u_k] — dist[u_1] leq 1 leftrightarrow dist[u_k] — dist[v] leq 1 leftrightarrow dist[u_k] leq dist[v] + 1), то есть упорядоченность сохранилась. Осталось показать, что ((dist[v] + 1) — dist[u_2] leq 1), но это равносильно (dist[v] leq dist[u_2]), что, как мы знаем, верно.
Время работы
Из доказанного следует, что каждая достижимая из (s) вершина будет добавлена в очередь ровно (1) раз, недостижимые вершины добавлены не будут. Каждое ребро, соединяющее достижимые вершины, будет рассмотрено ровно (2) раза. Таким образом, алгоритм работает за (O(V+ E)) времени, при условии, что граф хранится в виде списка смежности.
Неориентированные графы
Если дан неориентированный граф, его можно рассматривать как ориентированный граф с двумя обратными друг другу ориентированными рёбрами.
Восстановление пути
Пусть теперь заданы 2 вершины (s) и (t), и необходимо не только найти длину кратчайшего пути из (s) в (t), но и восстановить какой-нибудь из кратчайших путей между ними. Всё ещё можно воспользоваться алгоритмом BFS, но необходимо ещё и поддерживать массив предков (p), в котором для каждой вершины будет храниться предыдущая вершина на кратчайшем пути.
Поддерживать этот массив просто: при релаксации нужно просто запоминать, из какой вершины мы прорелаксировали в данную. Также будем считать, что (p[s] = -1): у стартовой вершины предок — некоторая несуществующая вершина.
Восстановление пути делается с конца. Мы знаем последнюю вершину пути — это (t). Далее, мы сводим задачу к меньшей, переходя к нахождению пути из (s) в (p[t]).
Реализация BFS с восстановлением пути
// теперь bfs принимает 2 вершины, между которыми ищется пути
// bfs возвращает кратчайший путь из s в t, или же пустой vector, если пути нет
vector<int> bfs(int s, int t) {
vector<int> dist(n, n);
vector<int> p(n, -1);
dist[s] = 0;
queue<int> q;
q.push(s);
while (!q.empty()) {
int v = q.front();
q.pop();
for (int u : adj[v]) {
if (dist[u] > dist[v] + 1) {
p[u] = v;
dist[u] = dist[v] + 1;
q.push(u);
}
}
}
// если пути не существует, возвращаем пустой vector
if (dist[t] == n) {
return {};
}
vector<int> path;
while (t != -1) {
path.push_back(t);
t = p[t];
}
// путь был рассмотрен в обратном порядке, поэтому его нужно перевернуть
reverse(path.begin(), path.end());
return path;
}Проверка принадлежности вершины кратчайшему пути
Дан ориентированный граф (G), найти все вершины, которые принадлежат хотя бы одному кратчайшему пути из (s) в (t).
Запустим из вершины (s) в графе (G) BFS — найдём расстояния (d_1). Построим транспонированный граф (G^T) — граф, в котором каждое ребро заменено на противоположное. Запустим из вершины (t) в графе (G^T) BFS — найдём расстояния (d_2).
Теперь очевидно, что (v) принадлежит хотя бы одному кратчайшему пути из (s) в (t) тогда и только тогда, когда (d_1(v) + d_2(v) = d_1(t)) — это значит, что есть путь из (s) в (v) длины (d_1(v)), а затем есть путь из (v) в (t) длины (d_2(v)), и их суммарная длина совпадает с длиной кратчайшего пути из (s) в (t).
Кратчайший цикл в ориентированном графе
Найти цикл минимальной длины в ориентированном графе.
Попытаемся из каждой вершины найти кратчайший цикл, проходящий через неё, с помощью BFS. Это делается аналогично обычному BFS: мы должны найти расстояний от вершины до самой себя, при этом не считая, что оно равно (0).
Итого, у нас (|V|) запусков BFS, и каждый запуск работает за (O(|V| + |E|)). Тогда общее время работы составляет (O(|V|^2 + |V| |E|)). Если инициализировать массив (dist) единожды, а после каждого запуска BFS возвращать исходные значения только для достижимых вершин, решение будет работать за (O(|V||E|)).
Задача
Дан взвешенный ориентированный граф (G = (V, E)), а также вершина (s). Длина ребра ((u, v)) равна (w(u, v)). Длины всех рёбер неотрицательные.
Найти длину кратчайшего пути от (s) до каждой из вершин графа. Длина пути — сумма длин рёбер в нём.
Алгоритм Дейкстры
Алгоритм Дейкстры решает приведённую выше задачу. Он работает следующим образом.
- Создать массив (dist) расстояний. Изначально (dist[s] = 0) и (dist[v] = infty) для (v neq s).
- Создать булёв массив (used), (used[v] = 0) для всех вершин (v) — в нём мы будем отмечать, совершалась ли релаксация из вершины.
- Пока существует вершина (v) такая, что (used[v] = 0) и (dist[v] neq infty), притом, если таких вершин несколько, то (v) — вершина с минимальным (dist[v]), делать следующее:
- Пометить, что мы совершали релаксацию из вершины (v), то есть присвоить (used[v] = 1).
- Рассматриваем все рёбра ((v, u) in E). Для каждого ребра пытаемся сделать релаксацию: если (dist[v] + w(v, u) < dist[u]), присвоить (dist[u] = dist[v] + w(v, u)).
Иными словами, алгоритм на каждом шаге находит вершину, до которой расстояние сейчас минимально и из которой ещё не была произведена релаксация, и делает её.
Посчитаем, за сколько работает алгоритм. Мы (V) раз ищем вершину минимальным (dist), поиск минимума у нас линейный за (O(V)), отсюда (O(V^2)). Обработка ребер у нас происходит суммарно за (O(E)), потому что на каждое ребро мы тратим (O(1)) действий. Так мы находим финальную асимптотику: (O(V^2 + E)).
Реализация на C++
Рёбра будем хранить как pair<int, int>, где первое число пары — куда оно ведёт; а второе — длина ребра.
// INF - infinity - бесконечность
const long long INF = (long long) 1e18 + 1;
vector<long long> dijkstra(int s) {
vector<long long> dist(n, INF);
dist[s] = 0;
vector<bool> used(n);
while (true) {
// находим вершину, из которой будем релаксировать
int v = -1;
for (int i = 0; i < n; i++) {
if (!used[i] && (v == -1 || dist[i] < dist[v])) {
v = i;
}
}
// если не нашли подходящую вершину, прекращаем работу алгоритма
if (v == -1) {
break;
}
for (auto &e : adj[v]) {
int u = e.first;
int len = e.second;
if (dist[u] > dist[v] + len) {
dist[u] = dist[v] + len;
}
}
}
return dist;
}Восстановление пути
Восстановление пути в алгоритме Дейкстры делается аналогично восстановлению пути в BFS (и любой динамике).
Дейкстра на сете
Искать вершину с минимальным (dist) можно гораздо быстрее, используя такую структуру данных как очередь с приоритетом. Нам нужно хранить пары ((dist, index)) и уметь делать такие операции: * Извлечь минимум (чтобы обработать новую вершину) * Удалить вершину по индексу (чтобы уменьшить (dist) до какого-то соседа) * Добавить новую вершину (чтобы уменьшить (dist) до какого-то соседа)
Для этого используют, например, кучу или сет. Удобно помимо сета хранить сам массив dist, который его дублирует, но хранит элементы по порядку. Тогда, чтобы заменить значение ((dist_1, u)) на ((dist_2, u)), нужно удалить из сета значение ((dist[u], u)), сделать (dist[u] = dist_2;) и добавить в сет ((dist[u], u)).
Данный алгоритм будет работать за (V O(log V)) извлечений минимума и (O(E log V)) операций уменьшения расстояния до вершины (может быть сделано после каждого ребра). Поэтому алгоритм работает за (O(E log V)).
Заметьте, что этот алгоритм не лучше и не хуже, чем без сета, который работает за (O(V^2 + E)). Ведь если (E = O(V^2)) (граф почти полный), то Дейкстра без сета работает быстрее, а если, наример, (E = O(V)), то Дейкстра на сете работает быстрее. Учитывайте это, когда выбираете алгоритм.
Алгоритм Дейкстры. Разбор Задач
Время на прочтение
7 мин
Количество просмотров 36K
Поиск оптимального пути в графе. Такая задача встречается довольно часто и в повседневной жизни, и в мире технологий. Справиться с такими вызовами помогает подход, который должен быть в арсенале каждого программиста — алгоритм Дейкстры.
Если вы хотите найти ответить на вопросы, чем этот алгоритм лучше BFS (поиска в ширину), при каких условиях алгоритм применим, и какие теоретические и практические задачи можно с его помощью решать, читайте далее.
Введение
Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах, и призван искать кратчайшие пути между заданной вершиной и всеми остальными вершинами в графе.
Как правило, граф обозначают как набор вершин и рёбер где число рёбер может быть задано
, а вершин числом
Для каждого ребра в графе задан неотрицательный вес , а также вершина, из которой осуществляется поиск оптимальных путей.
Алгоритм Дейкстры может найти кратчайший путь между вершинами и
в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение «бесконечность» для пары несвязанных вершин.
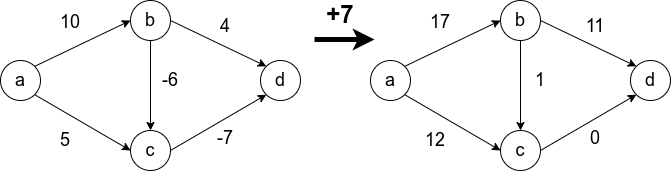
Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут. На рисунке видно, что в первом случае оптимальный путь между и
(сумма рёбер на пути наименьшая) изменяется при такой манипуляции. В оригинале путь проходит через
, а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через
Как ведёт себя алгоритм Дейкстры на исходном графе, мы разберём, когда выпишем алгоритм. Но для начала зададимся другим вопросом: «почему не применить поиск в ширину для нашего графа?». Известно, что метод BFS находит оптимальный путь от произвольной вершины в ориентированном графе до любой другой вершины, но это справедливо только для рёбер с единичным весом.
Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины рёбрами длины
, то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.
Чтобы этого избежать предлагается использовать алгоритм Дейкстры. Опишем его:
Инициализация:
Основный цикл алгоритма:
- Пока все вершины не исследованы (или формально
), повторяем:
В итоге исполнения этого алгоритма, массив будет содержать все оптимальные пути, исходящие из
.
Примеры работы
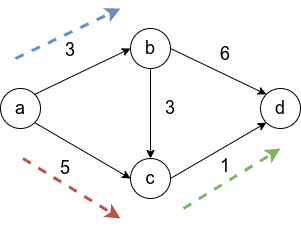
Рассмотрим граф выше, в нём будем искать пути от до всего остального.
Первый шаг алгоритма определит, что кратчайший путь до проходит по направлению синей стрелки и зафиксирует кратчайший путь. Второй шаг рассмотрит, все возможные варианты
и окажется, что оптимальный вариант двигаться вдоль красной стрелки, поскольку
меньше, чем
и
Добавляется длина кратчайшего пути до
. И наконец, третьим шагом, когда три вершины
уже лежат в
, остается рассмотреть только два ребра и выбрать, лежащее вдоль зеленой стрелки.
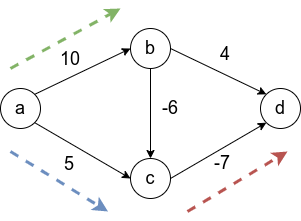
Теперь рассмотрим граф с отрицательными весами, упомянутый выше. Напомню, алгоритм Дейкстры на таком графе может работать некорректно.
Первым шагом отбирается ребро вдоль синей стрелки, поскольку это ребро наименьшего веса из исходной вершины. Затем выбирается ребро Это зафиксирует навсегда неверный путь от
к
, в то время как оптимальный путь проходит через центр с отрицательным весом. Последним шагом, будет добавлена вершина
.
Оценка сложности алгоритма
К этому моменту мы разобрали сам алгоритм, ограничения, накладываемые на его работу и ряд примеров его применения. Давайте упомянем какова вычислительная сложность этого алгоритма, поскольку это пригодится нам для решения задач, ради которых затевалась эта статья.
Базовый подход, основанный на циклах, предполагает проход по всем рёбрам каждого узла, что приводит к сложности .
Эффективная реализация предполагает использование кучи. Об этой структуре данных можно сказать коротко: она позволяет выполнять две операции за логарифмическое время. Первая операция — получение узла в дереве, с наименьшим ключом, и, вторая операция, вставка нового узла в дерево с новым ключом.
Что еще можно сказать о куче:
- это сбалансированное бинарное дерево,
- ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.
Интересную задачу с использованием куч я разбирал ранее в этом посте.
Используя кучу в алгоритме Дейкстры, где в качестве ключей используются расстояния от вершины в неисследованной части графа (в алгоритме это ), до ближайшей вершины в уже покрытом (это множество вершин
), можно сократить вычислительную сложность до
Доказательство справедливости этих оценок я оставляю за пределами этой статьи.
Далее перейдём к разбору задач!
Задача №1
Будем называть узким местом пути в графе ребро максимальной длины в этом пути. Путём с минимальным узким местом назовём такой путь между вершинами и
, что не существует другого пути
, чьё узкое место меньше по длине. Требуется построить алгоритм, который вычисляет путь с минимальным узким местом для двух данных вершин в графе. Асимптотическая сложность такого алгоритма должна быть
Решение
По условию задачи ребро с большим весом трактуется как узкое место. Вес в этом случае можно воспринимать как цену за проход по ребру. В результате решения задачи хотелось бы получить алгоритм, способный строить маршруты между узлами так, чтобы, если мы захотим провести любой другой путь, он будет содержать более тяжелые рёбра.
В случае классической задачи, поиска пути минимальной длины между двумя вершинами графа, мы поддерживаем в каждой посещенной алгоритмом вершине графа минимальную длину пути до этой вершины. Здесь стоит оговориться, что будем именовать множество посещенными вершинами, а
часть графа, для которой еще нужно найти величину пути или узкого места.
В отличии от классического алгоритма, решение этой задачи должно поддерживать величину актуального узкого места пути, приводящего в вершину . А при добавлении новой вершины из
, мы должны смотреть не увеличивает ли ребро
величину узкого места пути, которое теперь приводит в
.
Если ребро увеличивает узкое место, то лучше рассмотреть вершину
, ребро
до которой легче
. Поиск неувеличивающих узкое место ребёр нужно осуществлять не только среди соседей определенного узла
, но и среди всех
, поскольку отдавая предпочтение вершине, путь в которую имеет наименьшее узкое место в данный момент, мы гарантируем, что мы не ухудшаем ситуацию для других вершин.
Последнее можно проиллюстрировать примером: если путь, оканчивающийся в вершине имеет узкое место величины
, и есть вершина
с ребром
веса
, и
с ребром
веса
, то предпочтение отдаётся
, алгоритм даст верный результат в обоих случая, если существует
веса
или веса
.
В результате разбора выше, предлагается руководствоваться следующей формулой при выборе очередной вершины из непосещенных и обновлении величин, которые мы поддерживаем.
Стоит пояснить, что поиск по осуществляется, только для существующих связей
а
это вес ребра
.
Задача №2
Предлагается решить более практическую задачу. Пусть городов, между ними существуют пути, заданные массивом
edges[i] = [city_a, city_b, distance_ab], а также дано целое число mileage.
Требуется найти такой город из данных, из которого можно добраться до наименьшего числа городов не превысив mileage.
Стоит отметить, что граф неориентированый, т.е. по пути между городами можно двигаться в обе стороны, а длина пути между городами a и c может быть получена как сумма длин путей a -> b и b -> c, если есть маршрут a -> b -> c
Решение
С решением данной проблемы нам поможет алгоритм Дейкстры и описанная выше реализация с помощью кучи. Поставщиком этой структуры данных станет библиотека heapq в Python.
Будем использовать алгоритм Дейкстры для того, чтобы подсчитать количество соседних городов, расстояние до которых меньше mileage, для каждого из городов. Соберем количества соседей в в одном месте и найдем минимум из них.
Поскольку наш граф неориентированный, то из любой его вершины можно добраться до произвольной вершины
. Будем использовать алгоритм Дейкстры для того, чтобы для каждого из городов в графе построить кратчайшие пути до всех остальных городов, мы это уже умеем делать в теории. И чтобы, оптимизировать этот процесс, будем в его течении сразу отвергать пути, которые превышают
mileage, а не делать постфактум, когда все пути получены.
Давайте опишем функцию решения:
def least_reachable_city(n, edges, mileage):
"""
входные параметры:
n --- количество городов,
edges --- тройки (a, b, distance_ab),
mileage --- максимально допустимое расстояние между городами
для соседства
"""
# заполняем список смежности (adjacency list), в нашем случае это
# словарь, в котором ключи это города, а значения --- пары
# (<другой_город>, <расстояние_до_него>)
graph = {}
for u, v, w in edges:
if graph.get(u, None) is None:
graph[u] = [(v, w)]
else:
graph[u].append((v, w))
if graph.get(v, None) is None:
graph[v] = [(u, w)]
else:
graph[v].append((u, w))
# локально объявим функцию, которая будет считать кратчайшие пути в
# графе от вершины, до всех вершин, удовлетворяющих условию
def num_reachable_neighbors(city):
# создаем кучу, из одного элемента с парой, задающей нулевую
# длину пути до самого исходного города
heap = [(0, city)]
# и массив, содержащий города и кратчайшие
# расстояния до них от исходного
distances = {}
# затем, пока куча не пуста, извлекаем ближайший
# от посещенных городов город
while heap:
currDist, neighb = heapq.heappop(heap)
# если кратчайшее ребро ведет к городу, где мы уже знаем
# оптимальный маршрут, то завершаем итерацию
if neighb in distances:
continue
# в остальных случаях, и если сосед не является отправным
# городом, мы добавляем новую запись в массив кратчайших расстояний
if neighb != city:
distances[neighb] = currDist
# обрабатываем всех смежных городов с соседом, добавляя их в кучу
# но только если: а) до них еще не известен кратчайший маршрут и б) путь до них через neighb не выходит за пределы mileage
for node, d in graph[neighb]:
if node in distances:
continue
if currDist + d <= mileage:
heapq.heappush(heap, (currDist + d, node))
# возвращаем количество городов, прошедших проверку
return len(distances)
# выполним поиск соседей для каждого из городов
cities_neighbors = {num_reachable_neighbors(city): city for city in range(n)}
# вернём номер города, у которого наименьшее число соседей
# в пределах досигаемости
return cities_neighbors[min(cities_neighbors)]
В функции выше, в комментариях, подробно описывается, как метод Дейкстры, реализованный на куче позволяет найти расстояния до всех городов, в пределах `mileage`. Основную сложность для понимания предстваляет цикл, работающий с кучей.
Заключение
Алгоритм Дейкстры это мощный инструмент в мире работы с графами, область применения его крайне широка. С его помощью можно оценить даже целесообразность добавления новой ветки метро, новой дороги или маршрута в компьютерной сети. Он прост в исполнении и интуитивно понятен, как другие жадные (greedy) алгоритмы. Вычислительная сложность решений задач с его помощью зачастую не выше . При некоторых условиях может достигать линейной сложности (существует алгоритм линейной сложности, решающий первую задачу, при условии, что граф неориентированный).
Стоит еще раз отметить, что алгоритм не работает, когда в графе существуют отрицательные веса. Для этого существует подход динамического программирования — алгоритм Беллмана – Форда, что может послужить темой другой статьи. Несмотря на это, алгоритм Дейкстры является представителем идеального баланса простоты и мощи, для решения прикладных задач.
Статья подготовлена в преддверии старта курса «Алгоритмы для разработчиков». Узнать о курсе подробнее, а также зарегистрироваться на бесплатный демоурок можно по ссылке.
Информация
[1] Условия задач взяты из книги «Algorithms Illuminated: Part 2: Graph Algorithms and Data Structures» от Tim Roughgarden,
[2] и с сайта leetcode.com.
[3] Решения авторские.
Improve Article
Save Article
Like Article
Improve Article
Save Article
Like Article
Prerequisites:
- BFS for a Graph
- Dictionaries in Python
In this article, we will be looking at how to build an undirected graph and then find the shortest path between two nodes/vertex of that graph easily using dictionaries in Python Language.
Building a Graph using Dictionaries
Approach: The idea is to store the adjacency list into the dictionaries, which helps to store the graph in any format not only in the form of the integers. Here we have used characters as a reference on those places any custom objects can also be used.
Below is the implementation of the above approach:
Python3
from collections import defaultdict
def build_graph():
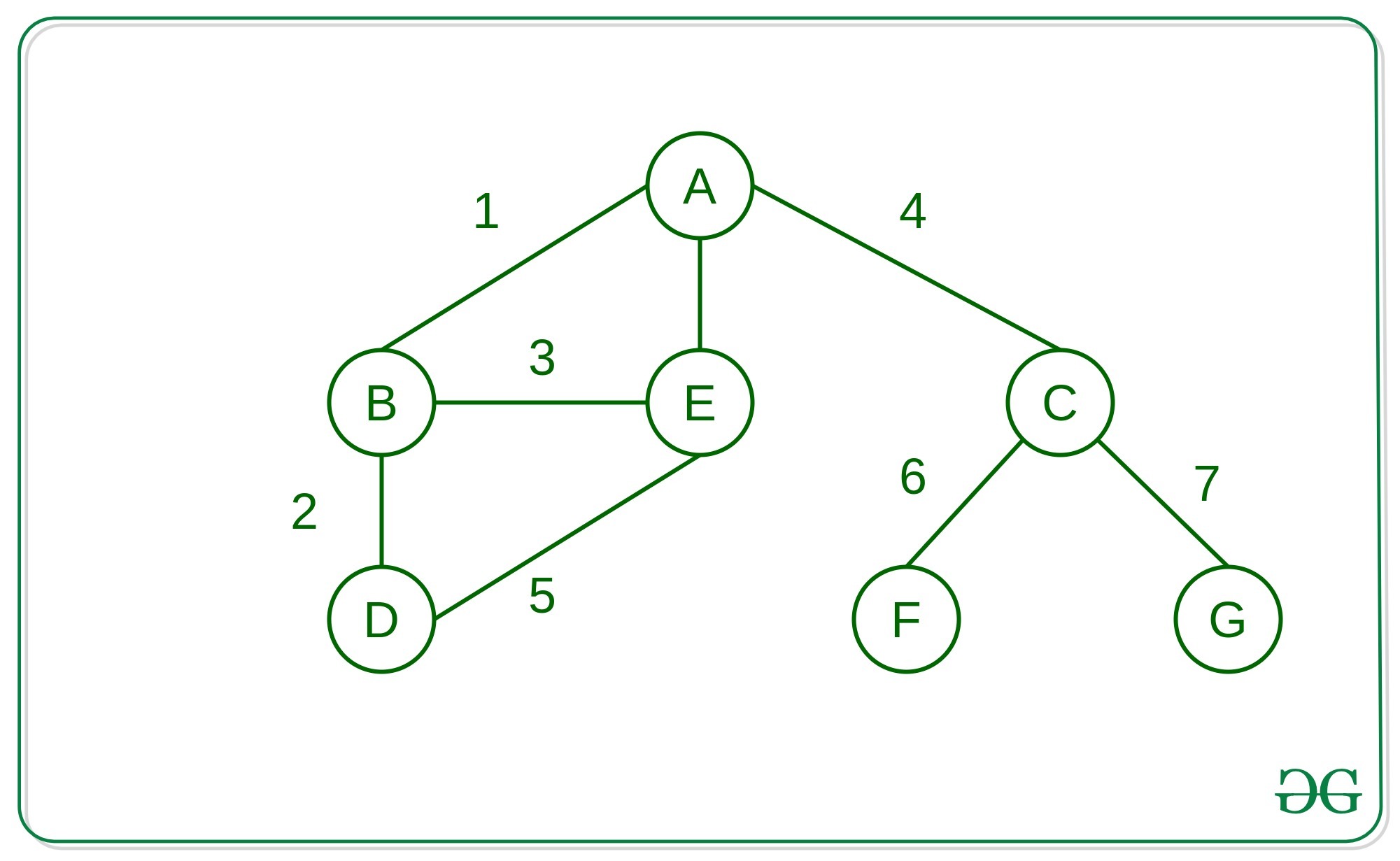
edges = [
["A", "B"], ["A", "E"],
["A", "C"], ["B", "D"],
["B", "E"], ["C", "F"],
["C", "G"], ["D", "E"]
]
graph = defaultdict(list)
for edge in edges:
a, b = edge[0], edge[1]
graph[a].append(b)
graph[b].append(a)
return graph
if __name__ == "__main__":
graph = build_graph()
print(graph)
Output:
{
'G': ['C'],
'F': ['C'],
'E': ['A', 'B', 'D'],
'A': ['B', 'E', 'C'],
'B': ['A', 'D', 'E'],
'D': ['B', 'E'],
'C': ['A', 'F', 'G']
}
Shortest Path between two nodes of graph
Approach: The idea is to use queue and visit every adjacent node of the starting nodes that traverses the graph in Breadth-First Search manner to find the shortest path between two nodes of the graph.
Below is the implementation of the above approach:
Python3
def BFS_SP(graph, start, goal):
explored = []
queue = [[start]]
if start == goal:
print("Same Node")
return
while queue:
path = queue.pop(0)
node = path[-1]
if node not in explored:
neighbours = graph[node]
for neighbour in neighbours:
new_path = list(path)
new_path.append(neighbour)
queue.append(new_path)
if neighbour == goal:
print("Shortest path = ", *new_path)
return
explored.append(node)
print("So sorry, but a connecting"
"path doesn't exist :(")
return
if __name__ == "__main__":
graph = {'A': ['B', 'E', 'C'],
'B': ['A', 'D', 'E'],
'C': ['A', 'F', 'G'],
'D': ['B', 'E'],
'E': ['A', 'B', 'D'],
'F': ['C'],
'G': ['C']}
BFS_SP(graph, 'A', 'D')
Output:
Shortest path = A B D
Last Updated :
15 Dec, 2021
Like Article
Save Article
Алгоритм поиска кратчайших путей на неориентированном графе.
-
(2 задачи, время выполнения — почти пара)
Решить задачу поиска кратчайших путей.
(Презентация ИССЛЕДОВАНЕ ОПЕРАЦИЙ)
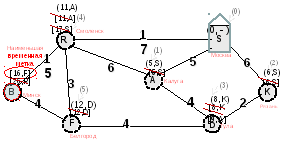
Алгоритм.
Начало.
1) В стартовой вершине Sставим (0,-) –ВЕЧНАЯ МЕТКА (Она читается
0 «из ниоткуда»).
2)Из стартовой вершины мы рассылаем ВО
все соседние ВЕРШИНЫ ВРЕМЕННЫЕ МЕТКИ
«метастазы» — в них ставится сумма 0 (из
позиции (0,-)) и расстояния до стартовой
вершины S.
Все временные метки, чтобы их отличать
от вечных пишутся в круглых скобках.
Повторяем до исчерпания вершин – пока
все вершины не заимеют вечные метки
а)На каждом этапе из всех имеющихся в
графе к настоящему моменту временных
меток выбирается лучшая – меньшая. Она
объявляется вечной. (При оформлении
такую метку надо зачеркнуть и написать
над ней точно такую же, но уже в круглых
скобках).
б)Только новорождённая временная метка
Образец оформления
Образец ответа
Сетевое планирование. Ребро-работа.
-
(СПУ1) Рассчитать минимальное время
выполнения проекта.
Сетевое планирование. Представление узел-работа.
-
(СПУ2): чтобы не производить сложных
расчетов – заменим в предыдущем условии
ВСЕ веса на их разности с 10, взятые по
модулю(таким образом все веса
положительны). Перейдём в представление
УЗЕЛ-РАБОТА. (построить граф на весь
лист, предварительно повернув его
альбомно) Пользуясь 10ти компонентным
представлением отразить сведения о
работе (название, центр-длительность,
времена начала-окончания в углах. Запасы
в серединах сторон. По одной из этих
задач построить график Ганта. Задача
обязательна по дисциплине управление
проектами.
Теория сетевого планирования.
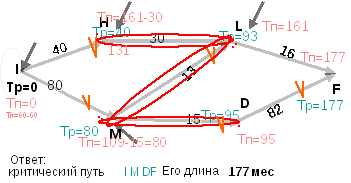
Расчёт длиннейшего — критического пути
(задача сетевого планирования) ведется
в идеологии предшествующего примера,
с небольшой разницей –
-
ПРВЫЙ ПРОХОД Метка Тр=0 ставится в левой
стартовой вершине проекта. Рассчитываются
любые вершины, которым предшествуют
только уже рассчитанные вершины (и
никакие более). В каждой вершине
суммируется время предшествующей
вершины и длина работы, от неё отделяющее.
Среди всех таких сумм мы находим
максимум, мотивировка которого в том,
что, для того чтобы состоялось событие
и могли стартовать работы исходящие
из вершины должны закончится все
входящие в неё работы. Четкую структуру
слоёв в ГРАФЕ ПРОЕКТА на первый взгляд
обычно выделить не удаётся (хотя можно
выделить слои по этапам расчёта). Расчет
ведется до тех пор, пока не будут
рассчитаны все вершины. -
Критический путь восстанавливается
с концевой вершины по меткам (галочкам).
Он сам и его длина (Тр концевой вершины)
пишется в ответ. -
ОБРАТНЫЙ ПРОХОД. На концевой вершине
копируется значение стоящей в ней
метки Тр=.. в Тп=.. Это позднее время
наступления события. Рассчитываются
поздние времена наступления событий.
Всё также как в предыдущем первом
проходе, но для расчёта должны быть
рассчитаны поздние времена Тп в
последующих вершинах. Расчет производится
на минимум: вычитается длина работы
до каждого ранее рассчитанного
последующего события из позднего
времени его наступления, худшая,т.е.
минимальная из этих разностей и есть
максимально возможное – т.е. самое
позднее время наступления события, не
приводящее к срыву максимально возможно
ранних сроков сдачи проекта, рассчитанных
в первом проходе. Критический путь не
рассчитывается галочки не ставятся. -
В третьей части для двенадцати работ
не лежащих на криическом пути и не
являющихся ни начальными ни концевыми
считаются полный, собственный, ранний
и поздний резервы времени. -
Для студентов специализации СПУ
строится график Ганта.
Соседние файлы в папке 417ПИ-Кривошеев
- #
- #
- #
- #
- #
- #
- #
Кратчайшие пути в графах. BFS. Dijkstra.
Задача
Дан ориентированный граф $G = (V, E)$, а также вершина $s$.
Найти длину кратчайшего пути от $s$ до каждой из вершин графа. Длина пути — количество рёбер в нём.
BFS
BFS — breadth-first search, или же поиск в ширину.
Этот алгоритм позволяет решать следующую задачу.
Алгоритм работает следующим образом.
- Создадим массив $dist$ расстояний. Изначально $dist[s] = 0$ (поскольку расстояний от вершины до самой себя равно $0$) и $dist[v] = infty$ для $v neq s$.
- Создадим очередь $q$. Изначально в $q$ добавим вершину $s$.
- Пока очередь $q$ непуста, делаем следующее:
- Извлекаем вершину $v$ из очереди.
- Рассматриваем все рёбра $(v, u) in E$. Для каждого такого ребра пытаемся сделать релаксацию: если $dist[v] + 1 < dist[u]$, то мы делаем присвоение $dist[u] = dist[v] + 1$ и добавляем вершину $u$ в очередь.
Визуализации:
-
https://visualgo.net/mn/dfsbfs
-
https://www.hackerearth.com/practice/algorithms/graphs/breadth-first-search/visualize/
Интуитивное понимание алгоритма
Можно представить, что мы поджигаем вершину $s$. Каждый шаг алгоритма — это распространение огня на соседние вершины. Понятно, что огонь доберётся до вершины по кратчайшему пути.
Заметьте, что этот алгоритм очень похож на DFS — достаточно заменить очередь на стек и поиск в ширину станет поиском в глубину. Действительно, оба алгоритма при обработке вершины просто записывают всех непосещенных соседей, в которые из неё есть ребро, в структуру данных, и после этого выбирает следующую вершину для обработки в структуре данных. В DFS это стек (благодаря рекурсии), поэтому мы сначала записываем соседа, идем в обрабатываем его полностью, а потом начинаем обрабатывать следующего соседа. В BFS это очередь, поэтому мы кидаем сразу всех соседей, а потом начинаем обрабатывать вообще другую вершину — ту непосещенную, которую мы положили в очередь раньше всего.
Оба алгоритма позволяют обойти граф целиком — посетить каждую вершину ровно один раз. Поэтому они оба подходят для таких задач как:
- поиск компонент связности
- проверка графа на двудольность
- построение остова
Реализация на C++
n — количество вершин в графе; adj — список смежности
vector<int> bfs(int s) { // длина любого кратчайшего пути не превосходит n - 1, // поэтому n - достаточное значение для "бесконечности"; // после работы алгоритма dist[v] = n, если v недостижима из s vector<int> dist(n, n); dist[s] = 0; queue<int> q; q.push(s); while (!q.empty()) { int v = q.front(); q.pop(); for (int u : adj[v]) { if (dist[u] > dist[v] + 1) { dist[u] = dist[v] + 1; q.push(u); } } } return dist; }
Свойства кратчайших путей
Обозначение: $d(v)$ — длина кратчайшего пути от $s$ до $v$.
Лемма 1.
Пусть $(u, v) in E$, тогда $d(v) leq d(u) + 1$.
Действительно, существует путь из $s$ в $u$ длины $d(u)$, а также есть ребро $(u, v)$, следовательно, существует путь из $s$ в $v$ длины $d(u) + 1$. А значит кратчайший путь из $s$ в $v$ имеет длину не более $d(u) + 1$,
Лемма 2.
Рассмотрим кратчайший путь от $s$ до $v$. Обозначим его как $u_1, u_2, dots u_k$ ($u_1 = s$ и $u_k = v$, а также $k = d(v) + 1$).
Тогда $forall (i < k): d(u_i) + 1 = d(u_{i + 1})$.
Действительно, пусть для какого-то $i < k$ это не так. Тогда, используя лемму 1, имеем: $d(u_i) + 1 > d(u_{i + 1})$. Тогда мы можем заменить первые $i + 1$ вершин пути на вершины из кратчайшего пути из $s$ в $u_{i + 1}$. Полученный путь стал короче, но мы рассматривали кратчайший путь — противоречие.
Корректность
Утверждение.
- Расстояния до тех вершин, которые были добавлены в очередь, посчитаны корректно.
- Вершины лежат в очереди в порядке неубывания расстояния, притом разность между кратчайшими расстояними до вершин в очереди не превосходит $1$.
Докажем это по индукции по количеству итераций алгоритма (итерация — извлечение вершины из очереди и дальнейшая релаксация).
База очевидна.
Переход. Сначала докажем первую часть. Предположим, что $dist[v] + 1 < dist[u]$, но $dist[v] + 1$ — некорректное расстояние до вершины $u$, то есть $dist[v] + 1 neq d(u)$. Тогда по лемме 1: $d(u) < dist[v] + 1$. Рассмотрим предпоследнюю вершину $w$ на кратчайшем пути от $s$ до $u$. Тогда по лемме 2: $d(w) + 1 = d(u)$. Следовательно, $d(w) + 1 < dist[v] + 1$ и $d(w) < dist[v]$. Но тогда по предположению индукции $w$ была извлечена раньше $v$, следовательно, при релаксации из неё в очередь должна была быть добавлена вершина $u$ с уже корректным расстоянием. Противоречие.
Теперь докажем вторую часть. По предположению индукции в очереди лежали некоторые вершины $u_1, u_2, dots u_k$, для которых выполнялось следующее: $dist[u_1] leq dist[u_2] leq dots leq dist[u_k]$ и $dist[u_k] — dist[u_1] leq 1$. Мы извлекли вершину $v = u_1$ и могли добавить в конец очереди какие-то вершины с расстоянием $dist[v] + 1$. Если $k = 1$, то утверждение очевидно. В противном случае имеем $dist[u_k] — dist[u_1] leq 1 leftrightarrow dist[u_k] — dist[v] leq 1 leftrightarrow dist[u_k] leq dist[v] + 1$, то есть упорядоченность сохранилась. Осталось показать, что $(dist[v] + 1) — dist[u_2] leq 1$, но это равносильно $dist[v] leq dist[u_2]$, что, как мы знаем, верно.
Время работы
Из доказанного следует, что каждая достижимая из $s$ вершина будет добавлена в очередь ровно $1$ раз, недостижимые вершины добавлены не будут. Каждое ребро, соединяющее достижимые вершины, будет рассмотрено ровно $2$ раза. Таким образом, алгоритм работает за $O(V+ E)$ времени, при условии, что граф хранится в виде списка смежности.
Неориентированные графы
Если дан неориентированный граф, его можно рассматривать как ориентированный граф с двумя обратными друг другу ориентированными рёбрами.
Восстановление пути
Пусть теперь заданы 2 вершины $s$ и $t$, и необходимо не только найти длину кратчайшего пути из $s$ в $t$, но и восстановить какой-нибудь из кратчайших путей между ними. Всё ещё можно воспользоваться алгоритмом BFS, но необходимо ещё и поддерживать массив предков $p$, в котором для каждой вершины будет храниться предыдущая вершина на кратчайшем пути.
Поддерживать этот массив просто: при релаксации нужно просто запоминать, из какой вершины мы прорелаксировали в данную. Также будем считать, что $p[s] = -1$: у стартовой вершины предок — некоторая несуществующая вершина.
Восстановление пути делается с конца. Мы знаем последнюю вершину пути — это $t$. Далее, мы сводим задачу к меньшей, переходя к нахождению пути из $s$ в $p[t]$.
Реализация BFS с восстановлением пути
// теперь bfs принимает 2 вершины, между которыми ищется пути // bfs возвращает кратчайший путь из s в t, или же пустой vector, если пути нет vector<int> bfs(int s, int t) { vector<int> dist(n, n); vector<int> p(n, -1); dist[s] = 0; queue<int> q; q.push(s); while (!q.empty()) { int v = q.front(); q.pop(); for (int u : adj[v]) { if (dist[u] > dist[v] + 1) { p[u] = v; dist[u] = dist[v] + 1; q.push(u); } } } // если пути не существует, возвращаем пустой vector if (dist[t] == n) { return {}; } vector<int> path; while (t != -1) { path.push_back(t); t = p[t]; } // путь был рассмотрен в обратном порядке, поэтому его нужно перевернуть reverse(path.begin(), path.end()); return path; }
Проверка принадлежности вершины кратчайшему пути
Дан ориентированный граф $G$, найти все вершины, которые принадлежат хотя бы одному кратчайшему пути из $s$ в $t$.
Запустим из вершины $s$ в графе $G$ BFS — найдём расстояния $d_1$. Построим транспонированный граф $G^T$ — граф, в котором каждое ребро заменено на противоположное. Запустим из вершины $t$ в графе $G^T$ BFS — найдём расстояния $d_2$.
Теперь очевидно, что $v$ принадлежит хотя бы одному кратчайшему пути из $s$ в $t$ тогда и только тогда, когда $d_1(v) + d_2(v) = d_1(t)$ — это значит, что есть путь из $s$ в $v$ длины $d_1(v)$, а затем есть путь из $v$ в $t$ длины $d_2(v)$, и их суммарная длина совпадает с длиной кратчайшего пути из $s$ в $t$.
Кратчайший цикл в ориентированном графе
Найти цикл минимальной длины в ориентированном графе.
Попытаемся из каждой вершины найти кратчайший цикл, проходящий через неё, с помощью BFS. Это делается аналогично обычному BFS: мы должны найти расстояний от вершины до самой себя, при этом не считая, что оно равно $0$.
Итого, у нас $|V|$ запусков BFS, и каждый запуск работает за $O(|V| + |E|)$. Тогда общее время работы составляет $O(|V|^2 + |V| |E|)$. Если инициализировать массив $dist$ единожды, а после каждого запуска BFS возвращать исходные значения только для достижимых вершин, решение будет работать за $O(|V||E|)$.
Задача
Дан взвешенный ориентированный граф $G = (V, E)$, а также вершина $s$. Длина ребра $(u, v)$ равна $w(u, v)$. Длины всех рёбер неотрицательные.
Найти длину кратчайшего пути от $s$ до каждой из вершин графа. Длина пути — сумма длин рёбер в нём.
Алгоритм Дейкстры
Алгоритм Дейкстры решает приведённую выше задачу. Он работает следующим образом.
- Создать массив $dist$ расстояний. Изначально $dist[s] = 0$ и $dist[v] = infty$ для $v neq s$.
- Создать булёв массив $used$, $used[v] = 0$ для всех вершин $v$ — в нём мы будем отмечать, совершалась ли релаксация из вершины.
- Пока существует вершина $v$ такая, что $used[v] = 0$ и $dist[v] neq infty$, притом, если таких вершин несколько, то $v$ — вершина с минимальным $dist[v]$, делать следующее:
- Пометить, что мы совершали релаксацию из вершины $v$, то есть присвоить $used[v] = 1$.
- Рассматриваем все рёбра $(v, u) in E$. Для каждого ребра пытаемся сделать релаксацию: если $dist[v] + w(v, u) < dist[u]$, присвоить $dist[u] = dist[v] + w(v, u)$.
Иными словами, алгоритм на каждом шаге находит вершину, до которой расстояние сейчас минимально и из которой ещё не была произведена релаксация, и делает её.
Посчитаем, за сколько работает алгоритм. Мы $V$ раз ищем вершину минимальным $dist$, поиск минимума у нас линейный за $O(V)$, отсюда $O(V^2)$. Обработка ребер у нас происходит суммарно за $O(E)$, потому что на каждое ребро мы тратим $O(1)$ действий. Так мы находим финальную асимптотику: $O(V^2 + E)$.
Реализация на C++
Рёбра будем хранить как pair<int, int>, где первое число пары — куда оно ведёт; а второе — длина ребра.
// INF - infinity - бесконечность const long long INF = (long long) 1e18 + 1; vector<long long> dijkstra(int s) { vector<long long> dist(n, INF); dist[s] = 0; vector<bool> used(n); while (true) { // находим вершину, из которой будем релаксировать int v = -1; for (int i = 0; i < n; i++) { if (!used[i] && (v == -1 || dist[i] < dist[v])) { v = i; } } // если не нашли подходящую вершину, прекращаем работу алгоритма if (v == -1) { break; } for (auto &e : adj[v]) { int u = e.first; int len = e.second; if (dist[u] > dist[v] + len) { dist[u] = dist[v] + len; } } } return dist; }
Восстановление пути
Восстановление пути в алгоритме Дейкстры делается аналогично восстановлению пути в BFS (и любой динамике).
Дейкстра на сете
Искать вершину с минимальным $dist$ можно гораздо быстрее, используя такую структуру данных как очередь с приоритетом. Нам нужно хранить пары $(dist, index)$ и уметь делать такие операции:
- Извлечь минимум (чтобы обработать новую вершину)
- Удалить вершину по индексу (чтобы уменьшить $dist$ до какого-то соседа)
- Добавить новую вершину (чтобы уменьшить $dist$ до какого-то соседа)
Для этого используют, например, кучу или сет. Удобно помимо сета хранить сам массив dist, который его дублирует, но хранит элементы по порядку. Тогда, чтобы заменить значение $(dist_1, u)$ на $(dist_2, u)$, нужно удалить из сета значение $(dist[u], u)$, сделать $dist[u] = dist_2;$ и добавить в сет $(dist[u], u)$.
Данный алгоритм будет работать за $V O(log V)$ извлечений минимума и $O(E log V)$ операций уменьшения расстояния до вершины (может быть сделано после каждого ребра). Поэтому алгоритм работает за $O(E log V)$.
Заметьте, что этот алгоритм не лучше и не хуже, чем без сета, который работает за $O(V^2 + E)$. Ведь если $E = O(V^2)$ (граф почти полный), то Дейкстра без сета работает быстрее, а если, наример, $E = O(V)$, то Дейкстра на сете работает быстрее. Учитывайте это, когда выбираете алгоритм.