Как найти кратчайший путь в невзвешенном графе - Исправление недочетов и поиск решений вместе с Examum.ru

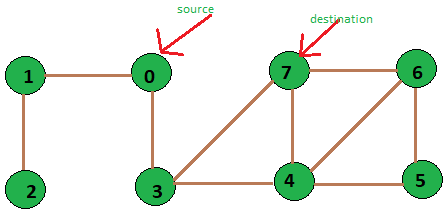
Given an unweighted graph, a source, and a destination, we need to find the shortest path from source to destination in the graph in the most optimal way.

unweighted graph of 8 vertices

Input: source vertex = 0 and destination vertex is = 7.
Output: Shortest path length is:2
        Path is::
        0 3 7

Input: source vertex is = 2 and destination vertex is = 6.
Output: Shortest path length is:5
        Path is::
        2 1 0 3 4 6

One solution is to solve in O(VE) time using Bellman–Ford. If there are no negative weight cycles, then we can solve in O(E + VLogV) time using Dijkstra’s algorithm.
Since the graph is unweighted, we can solve this problem in O(V + E) time. The idea is to use a modified version of Breadth-first search in which we keep storing the predecessor of a given vertex while doing the breadth-first search.

We first initialize an array dist[0, 1, …., v-1] such that dist[i] stores the distance of vertex i from the source vertex and array pred[0, 1, ….., v-1] such that pred[i] represents the immediate predecessor of the vertex i in the breadth-first search starting from the source.

Now we get the length of the path from source to any other vertex in O(1) time from array d, and for printing the path from source to any vertex we can use array p and that will take O(V) time in worst case as V is the size of array P. So most of the time of the algorithm is spent in doing the Breadth-first search from a given source which we know takes O(V+E) time. Thus the time complexity of our algorithm is O(V+E).

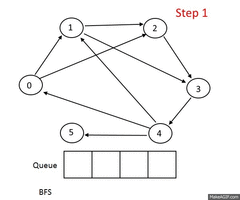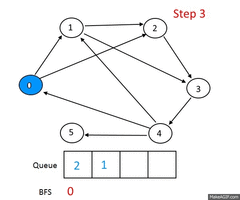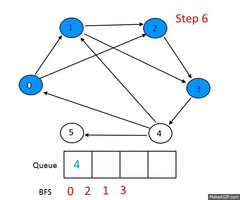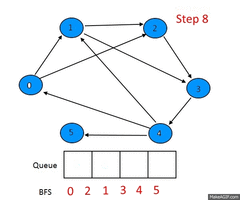
Take the following unweighted graph as an example:

Following is the complete algorithm for finding the shortest path:

Implementation:

C++

#include <bits/stdc++.h>

using namespace std;

void add_edge(vector<int> adj[], int src, int dest)

{

adj[src].push_back(dest);

adj[dest].push_back(src);

}

bool BFS(vector<int> adj[], int src, int dest, int v,

int pred[], int dist[])

{

list<int> queue;

bool visited[v];

for (int i = 0; i < v; i++) {

visited[i] = false;

dist[i] = INT_MAX;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.push_back(src);

while (!queue.empty()) {

int u = queue.front();

queue.pop_front();

for (int i = 0; i < adj[u].size(); i++) {

if (visited[adj[u][i]] == false) {

visited[adj[u][i]] = true;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.push_back(adj[u][i]);

if (adj[u][i] == dest)

return true;

}

return false;

}

void printShortestDistance(vector<int> adj[], int s,

int dest, int v)

{

int pred[v], dist[v];

if (BFS(adj, s, dest, v, pred, dist) == false) {

cout << "Given source and destination"

<< " are not connected";

return;

}

vector<int> path;

int crawl = dest;

path.push_back(crawl);

while (pred[crawl] != -1) {

path.push_back(pred[crawl]);

crawl = pred[crawl];

}

cout << "Shortest path length is : "

<< dist[dest];

cout << "nPath is::n";

for (int i = path.size() - 1; i >= 0; i--)

cout << path[i] << " ";

}

int main()

{

int v = 8;

vector<int> adj[v];

add_edge(adj, 0, 1);

add_edge(adj, 0, 3);

add_edge(adj, 1, 2);

add_edge(adj, 3, 4);

add_edge(adj, 3, 7);

add_edge(adj, 4, 5);

add_edge(adj, 4, 6);

add_edge(adj, 4, 7);

add_edge(adj, 5, 6);

add_edge(adj, 6, 7);

int source = 0, dest = 7;

printShortestDistance(adj, source, dest, v);

return 0;

}

Java

import java.util.ArrayList;

import java.util.Iterator;

import java.util.LinkedList;

public class pathUnweighted {

public static void main(String args[])

{

int v = 8;

ArrayList<ArrayList<Integer>> adj =

new ArrayList<ArrayList<Integer>>(v);

for (int i = 0; i < v; i++) {

adj.add(new ArrayList<Integer>());

}

addEdge(adj, 0, 1);

addEdge(adj, 0, 3);

addEdge(adj, 1, 2);

addEdge(adj, 3, 4);

addEdge(adj, 3, 7);

addEdge(adj, 4, 5);

addEdge(adj, 4, 6);

addEdge(adj, 4, 7);

addEdge(adj, 5, 6);

addEdge(adj, 6, 7);

int source = 0, dest = 7;

printShortestDistance(adj, source, dest, v);

}

private static void addEdge(ArrayList<ArrayList<Integer>> adj, int i, int j)

{

adj.get(i).add(j);

adj.get(j).add(i);

}

private static void printShortestDistance(

ArrayList<ArrayList<Integer>> adj,

int s, int dest, int v)

{

int pred[] = new int[v];

int dist[] = new int[v];

if (BFS(adj, s, dest, v, pred, dist) == false) {

System.out.println("Given source and destination" +

"are not connected");

return;

}

LinkedList<Integer> path = new LinkedList<Integer>();

int crawl = dest;

path.add(crawl);

while (pred[crawl] != -1) {

path.add(pred[crawl]);

crawl = pred[crawl];

}

System.out.println("Shortest path length is: " + dist[dest]);

System.out.println("Path is ::");

for (int i = path.size() - 1; i >= 0; i--) {

System.out.print(path.get(i) + " ");

}

private static boolean BFS(ArrayList<ArrayList<Integer>> adj, int src,

int dest, int v, int pred[], int dist[])

{

LinkedList<Integer> queue = new LinkedList<Integer>();

boolean visited[] = new boolean[v];

for (int i = 0; i < v; i++) {

visited[i] = false;

dist[i] = Integer.MAX_VALUE;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.add(src);

while (!queue.isEmpty()) {

int u = queue.remove();

for (int i = 0; i < adj.get(u).size(); i++) {

if (visited[adj.get(u).get(i)] == false) {

visited[adj.get(u).get(i)] = true;

dist[adj.get(u).get(i)] = dist[u] + 1;

pred[adj.get(u).get(i)] = u;

queue.add(adj.get(u).get(i));

if (adj.get(u).get(i) == dest)

return true;

}

return false;

}

Python3

def add_edge(adj, src, dest):

adj[src].append(dest);

adj[dest].append(src);

def BFS(adj, src, dest, v, pred, dist):

queue = []

visited = [False for i in range(v)];

for i in range(v):

dist[i] = 1000000

pred[i] = -1;

visited[src] = True;

dist[src] = 0;

queue.append(src);

while (len(queue) != 0):

u = queue[0];

queue.pop(0);

for i in range(len(adj[u])):

if (visited[adj[u][i]] == False):

visited[adj[u][i]] = True;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.append(adj[u][i]);

if (adj[u][i] == dest):

return True;

return False;

def printShortestDistance(adj, s, dest, v):

pred=[0 for i in range(v)]

dist=[0 for i in range(v)];

if (BFS(adj, s, dest, v, pred, dist) == False):

print("Given source and destination are not connected")

path = []

crawl = dest;

path.append(crawl);

while (pred[crawl] != -1):

path.append(pred[crawl]);

crawl = pred[crawl];

print("Shortest path length is : " + str(dist[dest]), end = '')

print("nPath is : : ")

for i in range(len(path)-1, -1, -1):

print(path[i], end=' ')

if __name__=='__main__':

v = 8;

adj = [[] for i in range(v)];

add_edge(adj, 0, 1);

add_edge(adj, 0, 3);

add_edge(adj, 1, 2);

add_edge(adj, 3, 4);

add_edge(adj, 3, 7);

add_edge(adj, 4, 5);

add_edge(adj, 4, 6);

add_edge(adj, 4, 7);

add_edge(adj, 5, 6);

add_edge(adj, 6, 7);

source = 0

dest = 7;

printShortestDistance(adj, source, dest, v);

C#

using System;

using System.Collections.Generic;

class pathUnweighted{

public static void Main(String []args)

{

int v = 8;

List<List<int>> adj =

new List<List<int>>(v);

for (int i = 0; i < v; i++)

{

adj.Add(new List<int>());

}

addEdge(adj, 0, 1);

addEdge(adj, 0, 3);

addEdge(adj, 1, 2);

addEdge(adj, 3, 4);

addEdge(adj, 3, 7);

addEdge(adj, 4, 5);

addEdge(adj, 4, 6);

addEdge(adj, 4, 7);

addEdge(adj, 5, 6);

addEdge(adj, 6, 7);

int source = 0, dest = 7;

printShortestDistance(adj, source,

dest, v);

}

private static void addEdge(List<List<int>> adj,

int i, int j)

{

adj[i].Add(j);

adj[j].Add(i);

}

private static void printShortestDistance(List<List<int>> adj,

int s, int dest, int v)

{

int []pred = new int[v];

int []dist = new int[v];

if (BFS(adj, s, dest,

v, pred, dist) == false)

{

Console.WriteLine("Given source and destination" +

"are not connected");

return;

}

List<int> path = new List<int>();

int crawl = dest;

path.Add(crawl);

while (pred[crawl] != -1)

{

path.Add(pred[crawl]);

crawl = pred[crawl];

}

Console.WriteLine("Shortest path length is: " +

dist[dest]);

Console.WriteLine("Path is ::");

for (int i = path.Count - 1;

i >= 0; i--)

{

Console.Write(path[i] + " ");

}

private static bool BFS(List<List<int>> adj,

int src, int dest,

int v, int []pred,

int []dist)

{

List<int> queue = new List<int>();

bool []visited = new bool[v];

for (int i = 0; i < v; i++)

{

visited[i] = false;

dist[i] = int.MaxValue;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.Add(src);

while (queue.Count != 0)

{

int u = queue[0];

queue.RemoveAt(0);

for (int i = 0;

i < adj[u].Count; i++)

{

if (visited[adj[u][i]] == false)

{

visited[adj[u][i]] = true;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.Add(adj[u][i]);

if (adj[u][i] == dest)

return true;

}

return false;

}

Javascript

const max_value = 9007199254740992;

function add_edge(adj, src, dest){

adj[src].push(dest);

adj[dest].push(src);

}

function BFS(adj, src, dest, v, pred, dist)

{

let queue = [];

let visited = new Array(v);

for (let i = 0; i < v; i++) {

visited[i] = false;

dist[i] = max_value;

pred[i] = -1;

}

visited[src] = true;

dist[src] = 0;

queue.push(src);

while (queue.length > 0) {

let u = queue[0];

queue.shift();

for (let i = 0; i < adj[u].length; i++) {

if (visited[adj[u][i]] == false) {

visited[adj[u][i]] = true;

dist[adj[u][i]] = dist[u] + 1;

pred[adj[u][i]] = u;

queue.push(adj[u][i]);

if (adj[u][i] == dest)

return true;

}

return false;

}

function printShortestDistance(adj, s, dest, v)

{

let pred = new Array(v).fill(0);

let dist = new Array(v).fill(0);

if (BFS(adj, s, dest, v, pred, dist) == false) {

console.log("Given source and destination are not connected");

}

let path = new Array();

let crawl = dest;

path.push(crawl);

while (pred[crawl] != -1) {

path.push(pred[crawl]);

crawl = pred[crawl];

}

console.log("Shortest path length is : ", dist[dest]);

console.log("Path is::");

for (let i = path.length - 1; i >= 0; i--)

console.log(path[i]);

}

let v = 8;

let adj = new Array(v).fill(0);

for(let i = 0; i < v; i++){

adj[i] = new Array();

}

add_edge(adj, 0, 1);

add_edge(adj, 0, 3);

add_edge(adj, 1, 2);

add_edge(adj, 3, 4);

add_edge(adj, 3, 7);

add_edge(adj, 4, 5);

add_edge(adj, 4, 6);

add_edge(adj, 4, 7);

add_edge(adj, 5, 6);

add_edge(adj, 6, 7);

let source = 0;

let dest = 7;

printShortestDistance(adj, source, dest, v);

Output

Shortest path length is : 2
Path is::
0 3 7

Time Complexity : O(V + E)
Auxiliary Space: O(V)

Algorithm

Create a queue and add the starting vertex to it.

Create an array to keep track of the distances from the starting vertex to all other vertices. Initialize all distances to infinity except for the starting vertex, which should have a distance of 0.

While the queue is not empty, dequeue the next vertex.

For each neighbor of the dequeued vertex that has not been visited, set its distance to the distance of the dequeued vertex plus 1 and add it to the queue.

Repeat steps 3-4 until the queue is empty.

The distances array now contains the shortest path distances from the starting vertex to all other vertices.

Program

Python3

from collections import deque

def bfs_shortest_path(graph, start):

queue = deque([start])

distances = [float('inf')] * len(graph)

distances[start] = 0

visited = set()

while queue:

vertex = queue.popleft()

visited.add(vertex)

for neighbor in graph[vertex]:

if neighbor not in visited:

distances[neighbor] = distances[vertex] + 1

queue.append(neighbor)

return distances

graph = [[1, 2], [2, 3], [3], [4], []]

start_vertex = 0

distances = bfs_shortest_path(graph, start_vertex)

print(distances)

In the above example, the output [0, 1, 1, 2, 3] indicates that the shortest path from vertex 0 to vertex 1 is of length 1, the shortest path from vertex 0 to vertex 2 is also of length 1, and so on.

Time and Auxiliary space

The time complexity of the above BFS-based algorithm for finding the shortest path in an unweighted graph is O(V + E), where V is the number of vertices and E is the number of edges in the graph. This is because each vertex and edge is visited at most once during the BFS traversal.

The space complexity of the algorithm is also O(V + E), due to the use of the distances array to store the shortest distances from the starting vertex to all other vertices, and the visited set to keep track of visited vertices. The queue used for BFS traversal can also have a maximum size of O(V + E) in the worst case, which contributes to the space complexity.

Last Updated :
02 May, 2023

Like Article

Save Article

Источник

Поиск в ширину (англ. breadth-first search) — один из основных алгоритмов на графах, позволяющий находить все кратчайшие пути от заданной вершины и решать многие другие задачи.

Поиск в ширину также называют обходом — так же, как поиск в глубину и все другие обходы, он посещает все вершины графа по одному разу, только в другом порядке: по увеличению расстояния до начальной вершины.

#Описание алгоритма

На вход алгоритма подаётся невзвешенный граф и номер стартовой вершины $s$. Граф может быть как ориентированным, так и неориентированным — для алгоритма это не важно.

Основную идею алгоритма можно понимать как процесс «поджигания» графа: на нулевом шаге мы поджигаем вершину $s$, а на каждом следующем шаге огонь с каждой уже горящей вершины перекидывается на всех её соседей, в конечном счете поджигая весь граф.

Если моделировать этот процесс, то за каждую итерацию алгоритма будет происходить расширение «кольца огня» в ширину на единицу. Номер шага, на котором вершина $v$ начинает гореть, в точности равен длине её минимального пути из вершины $s$.

Моделировать это можно следующим образом. Создадим очередь, в которую будут помещаться горящие вершины, а также заведём булевый массив, в котором для каждой вершины будем отмечать, горит она или нет — или иными словами, была ли она уже посещена. Изначально в очередь помещается только вершина $s$, которая сразу помечается горящей.

Затем алгоритм представляет собой такой цикл: пока очередь не пуста, достать из её головы одну вершину $v$, просмотреть все рёбра, исходящие из этой вершины, и если какие-то из смежных вершин $u$ ещё не горят, поджечь их и поместить в конец очереди.

В итоге, когда очередь опустеет, мы по одному разу обойдём все достижимые из $s$ вершины, причём до каждой дойдём кратчайшим путём. Длины кратчайших путей можно посчитать, если завести для них отдельный массив $d$ и при добавлении в очередь пересчитывать по правилу $d_u = d_v + 1$. Также можно компактно сохранить дополнительную информацию для восстановления самих путей, заведя массив «предков», в котором для каждой вершины хранится номер вершины из которой мы в неё попали.

#Реализация

Если мы всё равно поддерживаем массив расстояний, то отдельный булевый массив с метками горящих вершин можно не создавать, а вместо этого просто присвоить изначальное расстояние всех вершин некоторым некоторым специальным значением (например, -1), которое будет сигнализировать а том, что эту вершину мы ещё не просмотрели.

vector<int> g[maxn];

void bfs(int s) {
    queue<int> q;
    q.push(s);
    
    vector<int> d(n, -1), p(n);
    d[s] = 0;
    
    while (!q.empty()) {
        int v = q.front();
        q.pop();
        for (int u : g[v]) {
            if (d[u] == -1) {
                q.push(u);
                d[u] = d[v] + 1;
                p[u] = v;
            }
        }
    }
}

Теперь, чтобы восстановить кратчайший путь до какой-то вершины $v$, это можно сделать через массив p:

while (v != s) {
    cout << v << endl;
    v = p[v];
}

Обратим внимание, что путь выведется в обратном порядке.

#В неявных графах

Поиск в ширину часто применяется для поиска кратчайшего пути в неявно заданных графах.

В качестве конкретного примера, пусть у нас есть булева матрица размера $n times n$, в которой помечено, свободна ли клетка с координатами $(x, y)$, и требуется найти кратчайший путь от $(x_s, y_t)$ до $(x_y, y_t)$ при условии, что за один шаг можно перемещаться в свободную соседнюю по вертикали или горизонтали клетку.

Поиск в ширину можно использовать для нахождения выхода из лабиринта

Можно сконвертировать граф в явный формат: как-нибудь пронумеровать все ячейки (например по формуле $x cdot n + y$) и для каждой посмотреть на всех её соседей, добавляя ребро в $(x pm 1, y pm 1)$, если соответствующая клетка свободна.

Такой подход будет работать за оптимальное линейное время, однако с точки зрения реализации проще адаптировать не входные данные, а сам алгоритм обхода в глубину:

bool a[N][N]; // свободна ли клетка (x, y)
int d[N][N];  // кратчайшее расстояние до (x, y)

// чтобы немного упростить код
struct cell {
    int x, y;
};

void bfs(cell s, cell t) {
    queue<cell> q;
    q.push(s);

    memset(d, -1, sizeof d);
    d[s.x][x.y] = 0;

    while (!q.empty()) {
        auto [x, y] = q.front();
        q.pop();
        // просматриваем всех соседей
        for (auto [dx, dy] : {{-1, 0}, {+1, 0}, {0, -1}, {0, +1}}) {
            // считаем координаты соседа
            int _x = x + dx, _y = y + dy;
            // и проверяем, что он свободен и не был посещен ранее
            if (a[_x][_y] && d[_x][_y] == -1) {
                d[_x][_y] = d[x][y] + 1;
                q.push_back({_x, _y});
            }
        }
    }
}

Перед запуском bfs следует убедиться, что не произойдет выход за пределы границ. Вместо того, чтобы добавлять проверки на _x < 0 || x >= n и т. п. при просмотре возможных соседей, удобно сделать следующий трюк: изначально создать матрицу a с размерностями на 2 больше, чем нужно, и на этапе чтения данных заполнять её в индексации не с нуля, а с единицы. Тогда границы матрицы всегда будут заполнены нулями (то есть помечены непроходимыми) и алгоритм никогда в них не зайдет.

#Применения и обобщения

Помимо нахождения расстояний в невзвешенном графе, обход в ширину можно использовать для многих задач, в которых работает обход в глубину, например для поиска компонент связности или проверки на двудольность.

Множественный BFS. Добавив в очередь изначально не одну, а несколько вершин, мы найдем для каждой вершины кратчайшее расстояние до одной из них.

Это полезно для задач, в которых нужно моделировать пожар, наводнение, извержение вулкана или подобные явления, в которых источник «волны» не один. Также так можно чуть быстрее находить кратчайший путь для конкретной пары вершин, запустив параллельно два обхода от каждой и остановив в тот момент, когда они встретятся.

Игры. С помощью BFS можно найти решение какой-либо задачи / игры за наименьшее число ходов, если каждое состояние системы можно представить вершиной графа, а переходы из одного состояния в другое — рёбрами графа.

В качестве (нетривиального) примера: собрать кубик Рубика за наименьшее число ходов.

Кратчайшие циклы. Чтобы найти кратчайший цикл в ориентированном невзвешенном графе, можно произвести поиск в ширину из каждой вершины. Как только в процессе обхода мы пытаемся пойти из текущей вершины по какому-то ребру в уже посещённую вершину, то это означает, что мы нашли кратчайший цикл для данной вершины, и останавливаем обход. Среди всех таких найденных циклов (по одному от каждого запуска обхода) выбираем кратчайший.

Такой алгоритм будет работать за $O(n^2)$: худшим случаем будет один большой цикл, в котором мы для каждой вершины пройдемся по всем остальным.

Ребра на кратчайшем пути. Мы можем за линейное время найти все рёбра, лежащие на каком-либо кратчайшем пути между заданной парой вершин $a$ и $b$. Для этого нужно запустить два поиска в ширину: из $a$ и из $b$.

Обозначим через $d_a$ и $d_b$ массивы кратчайших расстояний, получившиеся в результате этих обходов. Тогда каждое ребро $(u,v)$ можно проверить критерием

$$
d_a[u] + d_b[v] + 1 = d_a[b]
$$

Альтернативно, можно запустить один обход из $a$, и когда он дойдет до $b$, начать рекурсивно проходиться по всем обратным ребрам, ведущим в более близкие к $a$ вершины (то есть те, для которых $d[u] = d[v] — 1$), отдельно помечая их.

Аналогично можно найти все вершины на каком-либо кратчайшем пути.

0-1 BFS. Если веса некоторых ребер могут быть нулевыми, то кратчайшие пути искать не сильно сложнее.

Ключевое наблюдение: если от вершины $a$ до вершины $b$ можно дойти по пути, состоящему из нулевых рёбер, то кратчайшие расстояния от вершины $s$ до этих вершин совпадают.

Если в нашем графе оставить только $0$-рёбра, то он распадётся на компоненты связности, в каждой из которых ответ одинаковый. Если теперь вернуть единичные рёбра и сказать, что эти рёбра соединяют не вершины, а компоненты связности, то мы сведём задачу к обычному BFS.

Получается, запустив обход, мы можем при обработке вершины $v$, у которой есть нулевые ребра в непосещенные вершины, сразу пройтись по ним и добавить все вершины нулевой компоненты, проставив им такое же расстояние, как и у $v$.

Это можно сделать и напрямую, запустив BFS внутри BFS, однако можно заметить, что достаточно при посещении вершины просто добавлять всех её непосещенных соседей по нулевым ребрам в голову очереди, чтобы обработать их раньше, чем те, которые там уже есть. Это легко сделать, если очередь заменить деком:

vector<int> d(n, -1);
d[s] = 0;

deque<int> q;
q.push_back(s);

while (!q.empty()) {
    int v = q.front();
    q.pop_front();
    for (auto [u, w] : g[v]) {
        if (d[u] == -1) {
            d[u] = d[v] + w;
            if (w == 0)
                q.push_front(u);
            else
                q.push_back(u);
        }
    }
}

Также вместо дека можно завести две очереди: одну для нулевых ребер, а другую для единичных, в внутри цикла while сначала просматривать первую, а только потом, когда она станет пустой, вторую. Этот подход уже можно обобщить.

1-k BFS. Теперь веса рёбер принимают значения от $1$ до некоторого небольшого $k$, и всё так же требуется найти кратчайшие расстояния от вершины $s$, но уже в плане суммарного веса.

Наблюдение: максимальное кратчайшее расстояние в графе равно $(n — 1) cdot k$.

Заведём для каждого расстояния $d$ очередь $q_d$, в которой будут храниться вершины, находящиеся на расстоянии $d$ от $s$ — плюс, возможно, некоторые вершины, до которых мы уже нашли путь длины $d$ от $s$, но для которых возможно существует более короткий путь. Нам потребуется $O((n — 1) cdot k)$ очередей.

Положим изначально вершину $s$ в $q_0$, а дальше будем брать вершину из наименьшего непустого списка и класть всех её непосещенных соседей в очередь с номером $d_v + w$ и релаксировать $d_u$, не забывая при этом, что кратчайшее расстояние до неё на самом деле может быть и меньше.

int d[maxn];
d[s] = 0;

queue<int> q[maxd];
q[0].push_back(s);

for (int dist = 0; dist < maxd; dist++) {
    while (!q[dist].empty()) {
        int v = q[dist].front();
        q[dist].pop();
        // если расстояние меньше и мы уже рассмотрели эту вершину,
        // но она всё ещё лежит в более верхней очереди
        if (d[v] > dist)
            continue;
        for (auto [u, w] : g[v]) {
            if (d[u] < d[v] + w) {
                d[u] = d[v] + w;
                q[d[u]].push(u);
            }
        }
    }
}

Сложность такого алгоритма будет $O(k n + m)$, поскольку каждую вершину мы можем прорелаксировать и добавить в другую очередь не более $k$ раз, а просматривать рёбра, исходящие из вершины мы будем только когда обработаем эту вершину в самый первый раз.

На самом деле, нам так много списков не нужно. Если каждое ребро имеет вес не более $k$, то в любой момент времени не более $k$ очередей будут непустыми. Мы можем завести только $k$ списков, и вместо добавления в $(d_v + w)$-ый список использовать $(d_v+w) bmod k$.

Заметим, что алгоритм также работает когда есть общее ограничение на длину пути, а не только на вес каждого ребра. Для более общего случая, когда веса ребер могут быть любыми неотрицательными, есть алгоритм Дейкстры, который мы разберем в следующей статье.

Источник

Обход в ширину (Поиск в ширину, англ. BFS, Breadth-first search) — один из простейших алгоритмов обхода графа, являющийся основой для многих важных алгоритмов для работы с графами.

Содержание

1 Описание алгоритма
2 Анализ времени работы
3 Корректность
4 Дерево обхода в ширину
5 Реализация
6 Вариации алгоритма
- 6.1 0-1 BFS
- 6.2 1-k BFS
7 См. также
8 Источники информации

Описание алгоритма

Алгоритм BFS
посещенные вершины

Пусть задан невзвешенный ориентированный граф , в котором выделена исходная вершина . Требуется найти длину кратчайшего пути (если таковой имеется) от одной заданной вершины до другой. Частным случаем указанного графа является невзвешенный неориентированный граф, т.е. граф, в котором для каждого ребра найдется обратное, соединяющее те же вершины в другом направлении.

Для алгоритма нам потребуются очередь и множество посещенных вершин , которые изначально содержат одну вершину . На каждом шагу алгоритм берет из начала очереди вершину и добавляет все непосещенные смежные с вершины в и в конец очереди. Если очередь пуста, то алгоритм завершает работу.

Анализ времени работы

Оценим время работы для входного графа , где множество ребер представлено списком смежности. В очередь добавляются только непосещенные вершины, поэтому каждая вершина посещается не более одного раза. Операции внесения в очередь и удаления из нее требуют времени, так что общее время работы с очередью составляет операций. Для каждой вершины рассматривается не более ребер, инцидентных ей. Так как , то время, используемое на работу с ребрами, составляет . Поэтому общее время работы алгоритма поиска в ширину — .

Корректность

Утверждение:

В очереди поиска в ширину расстояние вершин до монотонно неубывает.

Докажем это утверждение индукцией по числу выполненных алгоритмом шагов.

Введем дополнительный инвариант: у любых двух вершин из очереди, расстояние до отличается не более чем на .

База: изначально очередь содержит только одну вершину .

Переход: пусть после итерации в очереди вершин с расстоянием и вершин с расстоянием .

Рассмотрим итерацию. Из очереди достаем вершину , с расстоянием . Пусть у есть непосещенных смежных вершин. Тогда, после их добавления, в очереди находится вершин с расстоянием и, после них, вершин с расстоянием .

Оба инварианта сохранились, после любого шага алгоритма элементы в очереди неубывают.

Теорема:

Алгоритм поиска в ширину в невзвешенном графе находит длины кратчайших путей до всех достижимых вершин.

Доказательство:

Допустим, что это не так. Выберем из вершин, для которых кратчайшие пути от найдены некорректно, ту, настоящее расстояние до которой минимально. Пусть это вершина , и она имеет своим предком в дереве обхода в ширину , а предок в кратчайшем пути до — вершина .

Так как — предок в кратчайшем пути, то , и расстояние до найдено верно, . Значит, .

Так как — предок в дереве обхода в ширину, то .

Расстояние до найдено некорректно, поэтому . Подставляя сюда два последних равенства, получаем , то есть, . Из ранее доказанной леммы следует, что в этом случае вершина попала в очередь и была обработана раньше, чем . Но она соединена с , значит, не может быть предком в дереве обхода в ширину, мы пришли к противоречию, следовательно, найденные расстояния до всех вершин являются кратчайшими.

Дерево обхода в ширину

Поиск в ширину также может построить дерево поиска в ширину. Изначально оно состоит из одного корня . Когда мы добавляем непосещенную вершину в очередь, то добавляем ее и ребро, по которому мы до нее дошли, в дерево. Поскольку каждая вершина может быть посещена не более одного раза, она имеет не более одного родителя. После окончания работы алгоритма для каждой достижимой из вершины путь в дереве поиска в ширину соответствует кратчайшему пути от до в .

Реализация

Предложенная ниже функция возвращает кратчайшее расстояние между двумя вершинами.

— исходная вершина
— конечная вершина
— граф, состоящий из списка вершин и списка смежности . Вершины нумеруются целыми числами.
— очередь.
В поле хранится расстояние от до .

int BFS(G: (V, E), source: int, destination: int):
    d = int[|V|]
    fill(d, )
    d[source] = 0
    Q = 
    Q.push(source)
    while Q  
        u = Q.pop()
        for v: (u, v) in E
            if d[v] == 
                d[v] = d[u] + 1
                Q.push(v)
    return d[destination]

Если требуется найти расстояние лишь между двумя вершинами, из функции можно выйти, как только будет установлено значение .
Еще одна оптимизация может быть проведена при помощи метода meet-in-the-middle.

Вариации алгоритма

0-1 BFS

Пусть в графе разрешены ребра веса и , необходимо найти кратчайший путь между двумя вершинами. Для решения данной задачи модифицируем приведенный выше алгоритм следующим образом:

Вместо очереди будем использовать дек (или можно даже steque). Если рассматриваемое ее ребро имеет вес , то будем добавлять вершину в начало, а иначе в конец. После этого добавления, дополнительный введенный инвариант в доказательстве расположения элементов в деке в порядке неубывания продолжает выполняться, поэтому порядок в деке сохраняется. И, соответственно, релаксируем расстояние до всех смежных вершин и, при успешной релаксации, добавляем их в дек.

Таким образом, в начале дека всегда будет вершина, расстояние до которой меньше либо равно расстоянию до остальных вершин дека, и инвариант расположения элементов в деке в порядке неубывания сохраняется. Значит, алгоритм корректен на том же основании, что и обычный BFS. Очевидно, что каждая вершина войдет в дек не более двух раз, значит, асимптотика у данного алгоритма та же, что и у обычного BFS.

1-k BFS

Пусть в графе разрешены ребра целочисленного веса из отрезка , необходимо найти кратчайший путь между двумя вершинами. Представим ребро веса как последовательность ребер (где — новые вершины). Применим данную операцию ко всем ребрам графа . Получим граф, состоящий (в худшем случае) из ребер и вершин. Для нахождения кратчайшего пути следует запустить BFS на новом графе. Данный алгоритм будет иметь асимптотику .

См. также

Обход в глубину, цвета вершин
Алгоритм Дейкстры
Теория графов

Источники информации

Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459. — ISBN 5-8489-0857-4
MAXimal :: algo :: Поиск в ширину
Wikipedia — Breadth-first search
Wikipedia — Поиск в ширину
Визуализатор алгоритма

Источник

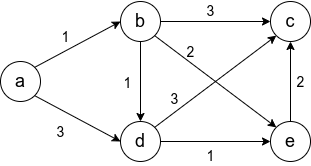
Рассмотрим следующую
задачу. В графе Г выделены две вершины:
b (начальная)
и e (конечная).
Требуется найти все пути минимальной
длины из b в
e (если
e достижима
из b)
либо установить недостижимость. Для
решения этой задачи используется очень
эффективный волновой алгоритм. Допустим,
что по дугам графа может распространяться
сигнал, причем по каждой дуге сигнал
проходит за единицу времени. Выпустим
в начальный 51 момент сигнал из вершины
b,
будем последовательно отмечать

вершины, до которых
сигнал дойдет за 1,2,3,… единиц времени
пока не будет отмечена вершина e.
Остается отметить дуги, которые сигнал
прошел по пути от b
к e.
При этом если в некоторый момент сигналу
распространяться некуда, а вершина e
не помечена, то она недостижима из b.
С помощью этого подхода можно решить
близкую задачу: найти длины кратчайших
путей от вершины b
до всех вершин
графа. Волновой алгоритм тем самым
состоит из двух этапов. Прямой ход
позволяет найти длину кратчайшего пути
(далее расстояние) от b
до e
(или до всех вершин
графа), обратный ход позволяет восстановить
пути. Прямой ход. На каждом шаге алгоритма
вершины графа делятся на два подмножества
– помеченных и не помеченных, причем
на каждом шаге некоторые вершины
переходят в класс помеченных. Пометками
являются текущие состояния счетчика
k.
Также на каждом шаге формируется
множество вершин – фронт волны (ФВ).

Шаг 0. k:=0,
ФВ:={b}.

Шаг 1. Вершины из множества
ФВ пометить числом k.

Шаг 2. Если {eÎФВ
или ФВ=Æ} то прямой ход завершен

иначе шаг 3.

Шаг 3. ФВ:={uÎV:
u не
помечена, $vÎФВ:
(v,u)ÎE},
k:=
k+1.

Переход к шагу 1.

Если вершина e
имеет пометку
(ke),
то реализуем обратный

ход. На каждом шаге
строится множество вершин «Возврат»
(В) и

отмечается некоторое
семейство дуг.

Шаг 4. k:=k
e, В:={e}.

Шаг 5. k:=k
–1; отметить дуги,
ведущие из вершин с пометкой

k,
в вершины, принадлежащие множеству В;
В:={множество

начальных вершин
отмеченных дуг}.

Шаг 6. Если k=0
то конец иначе переход к шагу 5.

По окончании работы
алгоритма подграф, образованный

отмеченными дугами и
соответствующими вершинами, содержит

все нужные кратчайшие
пути.

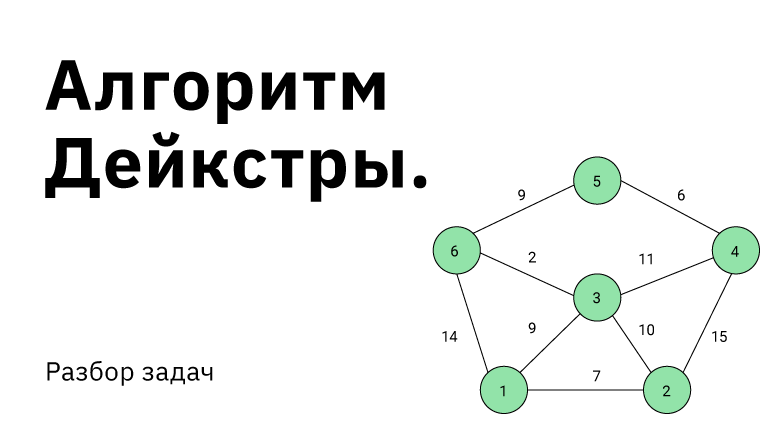
23.Взвешенный граф. Нахождение кратчайшего пути между двумя заданными вершинами во взвешенном ориентированном графе. Алгоритм Дейкстры.

Взвешенный (другое название:
размеченный) граф (или орграф) — это
граф (орграф), некоторым элементам
которого (вершинам, ребрам или дугам)
сопоставлены числа. Наиболее часто
встречаются графы с помеченными ребрами.
Числа-пометки носят различные названия:
вес, длина,стоимость.

Замечание: Обычный (не взвешенный)
граф можно интерпретировать как
взвешенный, все ребра которого имеют
одинаковый вес 1.

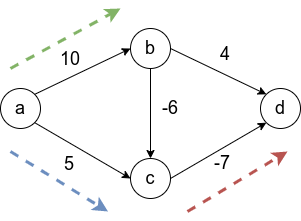
Длина пути во взвешенном (связном) графе
— это сумма длин (весов) тех ребер, из
которых состоит путь. Расстояние между
вершинами — это, как и прежде, длина
кратчайшего пути. Например, расстояние
от вершины a до вершины d во взвешенном
графе.

Путем в орграфе называется последовательность
вершин v1,v2,…,vn, для которой

существуют дуги (v1,v2)(v2,v3)… (vn-1,vn). Длина
пути — количество дуг,

составляющих путь. Если граф является
взвешенным, то длина пути определяется

как сумма весов дуг.

Алгоритм Дейкстры решает задачу о
кратчайших путях из одной вершины для
взвешенного ориентированного графа G
= (V, E) с исходной вершиной s, в
котором веса

всех рёбер неотрицательны ((u,
v) ≥ 0 для всех (u, v)
E).

Формальное объяснение В процессе
работы алгоритма Дейкстры поддерживается
множество S

V, состоящее из вершин v, для которых
δ(s, v) уже найдено. Алгоритм выбирает
вершину u
VS с наименьшим d[u], добавляет
u к множеству S и производит
релаксацию всех рёбер, выходящих из u,
после чего цикл повторяется. Вершины,
не лежащие в S , хранятся в очереди
Q с приоритетами, определяемыми
значениями функции d. Предполагается,
что граф задан с помощью списков смежных
вершин.

Не формальное объяснение

Каждой вершине из V сопоставим метку
— минимальное известное расстояние от
этой вершины до a. Алгоритм работает
пошагово — на каждом шаге он «посещает»
одну вершину и пытается уменьшать метки.
Работа алгоритма завершается, когда
все вершины посещены.

Инициализация. Метка самой вершины
a полагается равной 0, метки
остальных вершин — бесконечности. Это
отражает то, что расстояния от a до
других вершин пока неизвестны. Все
вершины графа помечаются как непосещенные.

Шаг алгоритма. Если все вершины
посещены, алгоритм завершается. В
противном случае из еще не посещенных
вершин выбирается вершина u, имеющая
минимальную метку. Мы рассматриваем
всевозможные маршруты, в которых u
является предпоследним пунктом. Вершины,
соединенные с вершиной u ребрами,
назовем соседями этой вершины. Для
каждого соседа рассмотрим новую длину
пути, равную сумме текущей метки u
и длины ребра, соединяющего u с этим
соседом. Если полученная длина меньше
метки соседа, заменим метку этой длиной.
Рассмотрев всех соседей, пометим вершину
u как посещенную и повторим шаг.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Алгоритм Дейкстры. Разбор Задач

Время на прочтение
7 мин

Количество просмотров 36K

Поиск оптимального пути в графе. Такая задача встречается довольно часто и в повседневной жизни, и в мире технологий. Справиться с такими вызовами помогает подход, который должен быть в арсенале каждого программиста — алгоритм Дейкстры.

Если вы хотите найти ответить на вопросы, чем этот алгоритм лучше BFS (поиска в ширину), при каких условиях алгоритм применим, и какие теоретические и практические задачи можно с его помощью решать, читайте далее.

Введение

Алгоритм Дейкстры работает на ориентированных (с некоторыми дополнениями и на неориентированных) графах, и призван искать кратчайшие пути между заданной вершиной и всеми остальными вершинами в графе.

Как правило, граф обозначают как набор вершин и рёбер где число рёбер может быть задано , а вершин числом

Для каждого ребра в графе задан неотрицательный вес , а также вершина, из которой осуществляется поиск оптимальных путей.

Алгоритм Дейкстры может найти кратчайший путь между вершинами и в графе, только если существует хотя бы один путь между этими вершинами. Если это условие не выполняется, то алгоритм отработает корректно, вернув значение «бесконечность» для пары несвязанных вершин.

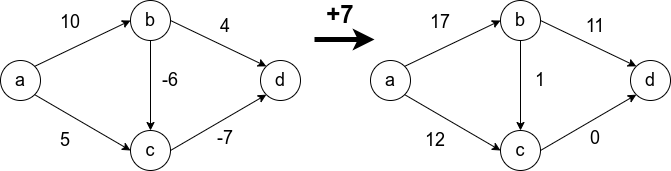
Условие неотрицательности весов рёбер крайне важно и от него нельзя просто избавиться. Не получится свести задачу к решаемой алгоритмом Дейкстры, прибавив наибольший по модулю вес ко всем рёбрам. Это может изменить оптимальный маршрут. На рисунке видно, что в первом случае оптимальный путь между и (сумма рёбер на пути наименьшая) изменяется при такой манипуляции. В оригинале путь проходит через , а после добавления семёрки ко всем рёбрам, оптимальный путь проходит через

Как ведёт себя алгоритм Дейкстры на исходном графе, мы разберём, когда выпишем алгоритм. Но для начала зададимся другим вопросом: «почему не применить поиск в ширину для нашего графа?». Известно, что метод BFS находит оптимальный путь от произвольной вершины в ориентированном графе до любой другой вершины, но это справедливо только для рёбер с единичным весом.

Свести задачу к решаемой BFS можно, но если заменить все рёбра неединичной длины рёбрами длины , то граф очень разрастётся, и это приведёт к огромному числу действий при вычислении оптимального маршрута.

Чтобы этого избежать предлагается использовать алгоритм Дейкстры. Опишем его:

Инициализация:

Основный цикл алгоритма:

Пока все вершины не исследованы (или формально ), повторяем:

В итоге исполнения этого алгоритма, массив будет содержать все оптимальные пути, исходящие из .

Примеры работы

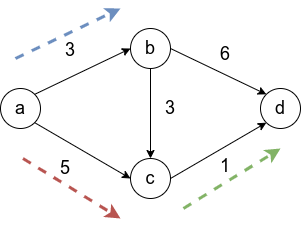
Рассмотрим граф выше, в нём будем искать пути от до всего остального.

Первый шаг алгоритма определит, что кратчайший путь до проходит по направлению синей стрелки и зафиксирует кратчайший путь. Второй шаг рассмотрит, все возможные варианты $inline A[v] + l_{vw}$ и окажется, что оптимальный вариант двигаться вдоль красной стрелки, поскольку меньше, чем и Добавляется длина кратчайшего пути до . И наконец, третьим шагом, когда три вершины уже лежат в , остается рассмотреть только два ребра и выбрать, лежащее вдоль зеленой стрелки.

Теперь рассмотрим граф с отрицательными весами, упомянутый выше. Напомню, алгоритм Дейкстры на таком графе может работать некорректно.

Первым шагом отбирается ребро вдоль синей стрелки, поскольку это ребро наименьшего веса из исходной вершины. Затем выбирается ребро Это зафиксирует навсегда неверный путь от к , в то время как оптимальный путь проходит через центр с отрицательным весом. Последним шагом, будет добавлена вершина .

Оценка сложности алгоритма

К этому моменту мы разобрали сам алгоритм, ограничения, накладываемые на его работу и ряд примеров его применения. Давайте упомянем какова вычислительная сложность этого алгоритма, поскольку это пригодится нам для решения задач, ради которых затевалась эта статья.
Базовый подход, основанный на циклах, предполагает проход по всем рёбрам каждого узла, что приводит к сложности .

Эффективная реализация предполагает использование кучи. Об этой структуре данных можно сказать коротко: она позволяет выполнять две операции за логарифмическое время. Первая операция — получение узла в дереве, с наименьшим ключом, и, вторая операция, вставка нового узла в дерево с новым ключом.

Что еще можно сказать о куче:

это сбалансированное бинарное дерево,
ключ текущего узла всегда меньше, либо равен ключей дочерних узлов.

Интересную задачу с использованием куч я разбирал ранее в этом посте.

Используя кучу в алгоритме Дейкстры, где в качестве ключей используются расстояния от вершины в неисследованной части графа (в алгоритме это ), до ближайшей вершины в уже покрытом (это множество вершин ), можно сократить вычислительную сложность до Доказательство справедливости этих оценок я оставляю за пределами этой статьи.

Далее перейдём к разбору задач!

Задача №1

Будем называть узким местом пути в графе ребро максимальной длины в этом пути. Путём с минимальным узким местом назовём такой путь между вершинами и , что не существует другого пути , чьё узкое место меньше по длине. Требуется построить алгоритм, который вычисляет путь с минимальным узким местом для двух данных вершин в графе. Асимптотическая сложность такого алгоритма должна быть

Решение

По условию задачи ребро с большим весом трактуется как узкое место. Вес в этом случае можно воспринимать как цену за проход по ребру. В результате решения задачи хотелось бы получить алгоритм, способный строить маршруты между узлами так, чтобы, если мы захотим провести любой другой путь, он будет содержать более тяжелые рёбра.

В случае классической задачи, поиска пути минимальной длины между двумя вершинами графа, мы поддерживаем в каждой посещенной алгоритмом вершине графа минимальную длину пути до этой вершины. Здесь стоит оговориться, что будем именовать множество посещенными вершинами, а V - X часть графа, для которой еще нужно найти величину пути или узкого места.

В отличии от классического алгоритма, решение этой задачи должно поддерживать величину актуального узкого места пути, приводящего в вершину v in X . А при добавлении новой вершины из V - X , мы должны смотреть не увеличивает ли ребро (v,u_1) величину узкого места пути, которое теперь приводит в u_1 .
Если ребро увеличивает узкое место, то лучше рассмотреть вершину u_2 , ребро до которой легче (v,u_1) . Поиск неувеличивающих узкое место ребёр нужно осуществлять не только среди соседей определенного узла , но и среди всех v in X , поскольку отдавая предпочтение вершине, путь в которую имеет наименьшее узкое место в данный момент, мы гарантируем, что мы не ухудшаем ситуацию для других вершин.

Последнее можно проиллюстрировать примером: если путь, оканчивающийся в вершине имеет узкое место величины , и есть вершина с ребром (p,q) веса , и с ребром (p,r) веса , то предпочтение отдаётся , алгоритм даст верный результат в обоих случая, если существует (q,r) веса или веса .

В результате разбора выше, предлагается руководствоваться следующей формулой при выборе очередной вершины из непосещенных и обновлении величин, которые мы поддерживаем.

$A(u) = min_{v in X}left(max left[A(v), wleft(v,uright)right]right), , u in V - X$

Стоит пояснить, что поиск по v in X осуществляется, только для существующих связей (v,u), а это вес ребра (v,u) .

Задача №2

Предлагается решить более практическую задачу. Пусть городов, между ними существуют пути, заданные массивом edges[i] = [city_a, city_b, distance_ab], а также дано целое число mileage.

Требуется найти такой город из данных, из которого можно добраться до наименьшего числа городов не превысив mileage.

Стоит отметить, что граф неориентированый, т.е. по пути между городами можно двигаться в обе стороны, а длина пути между городами a и c может быть получена как сумма длин путей a -> b и b -> c, если есть маршрут a -> b -> c

Решение

С решением данной проблемы нам поможет алгоритм Дейкстры и описанная выше реализация с помощью кучи. Поставщиком этой структуры данных станет библиотека heapq в Python.

Будем использовать алгоритм Дейкстры для того, чтобы подсчитать количество соседних городов, расстояние до которых меньше mileage, для каждого из городов. Соберем количества соседей в в одном месте и найдем минимум из них.

Поскольку наш граф неориентированный, то из любой его вершины можно добраться до произвольной вершины . Будем использовать алгоритм Дейкстры для того, чтобы для каждого из городов в графе построить кратчайшие пути до всех остальных городов, мы это уже умеем делать в теории. И чтобы, оптимизировать этот процесс, будем в его течении сразу отвергать пути, которые превышают mileage, а не делать постфактум, когда все пути получены.

Давайте опишем функцию решения:

def least_reachable_city(n, edges, mileage):
        """
        входные параметры:
            n --- количество городов,
            edges --- тройки (a, b, distance_ab),
            mileage --- максимально допустимое расстояние между городами 
            для соседства
        """
        # заполняем список смежности (adjacency list), в нашем случае это 
        # словарь, в котором ключи это города, а значения --- пары 
        # (<другой_город>, <расстояние_до_него>)

        graph = {}
        for u, v, w in edges:
            if graph.get(u, None) is None:
                graph[u] = [(v, w)]
            else:
                graph[u].append((v, w))
            if graph.get(v, None) is None:
                graph[v] = [(u, w)]
            else:
                graph[v].append((u, w))
        
        # локально объявим функцию, которая будет считать кратчайшие пути в 
        # графе от вершины, до всех вершин, удовлетворяющих условию
        def num_reachable_neighbors(city):
            # создаем кучу, из одного элемента с парой, задающей нулевую 
            # длину пути до самого исходного города
            heap = [(0, city)]
            # и массив, содержащий города и кратчайшие 
            # расстояния до них от исходного
            distances = {}
            # затем, пока куча не пуста, извлекаем ближайший 
            # от посещенных городов город
            while heap:
                currDist, neighb = heapq.heappop(heap)
                # если кратчайшее ребро ведет к городу, где мы уже знаем 
                # оптимальный маршрут, то завершаем итерацию
                if neighb in distances:
                    continue
                # в остальных случаях, и если сосед не является отправным 
                # городом, мы добавляем новую запись в массив кратчайших расстояний
                if neighb != city:    
                    distances[neighb] = currDist
                # обрабатываем всех смежных городов с соседом, добавляя их в кучу 
                # но только если: а) до них еще не известен кратчайший маршрут и б) путь до них через neighb не выходит за пределы mileage
                for node, d in graph[neighb]:
                    if node in distances:
                        continue
                    if currDist + d <= mileage:
                        heapq.heappush(heap, (currDist + d, node))
            # возвращаем количество городов, прошедших проверку
            return len(distances)
        
        # выполним поиск соседей для каждого из городов
        cities_neighbors = {num_reachable_neighbors(city): city for city in range(n)}
        # вернём номер города, у которого наименьшее число соседей
        # в пределах досигаемости
        return cities_neighbors[min(cities_neighbors)]

В функции выше, в комментариях, подробно описывается, как метод Дейкстры, реализованный на куче позволяет найти расстояния до всех городов, в пределах `mileage`. Основную сложность для понимания предстваляет цикл, работающий с кучей.

Заключение

Алгоритм Дейкстры это мощный инструмент в мире работы с графами, область применения его крайне широка. С его помощью можно оценить даже целесообразность добавления новой ветки метро, новой дороги или маршрута в компьютерной сети. Он прост в исполнении и интуитивно понятен, как другие жадные (greedy) алгоритмы. Вычислительная сложность решений задач с его помощью зачастую не выше . При некоторых условиях может достигать линейной сложности (существует алгоритм линейной сложности, решающий первую задачу, при условии, что граф неориентированный).

Стоит еще раз отметить, что алгоритм не работает, когда в графе существуют отрицательные веса. Для этого существует подход динамического программирования — алгоритм Беллмана – Форда, что может послужить темой другой статьи. Несмотря на это, алгоритм Дейкстры является представителем идеального баланса простоты и мощи, для решения прикладных задач.

Статья подготовлена в преддверии старта курса «Алгоритмы для разработчиков». Узнать о курсе подробнее, а также зарегистрироваться на бесплатный демоурок можно по ссылке.

Информация

[1] Условия задач взяты из книги «Algorithms Illuminated: Part 2: Graph Algorithms and Data Structures» от Tim Roughgarden,
[2] и с сайта leetcode.com.
[3] Решения авторские.

Источник