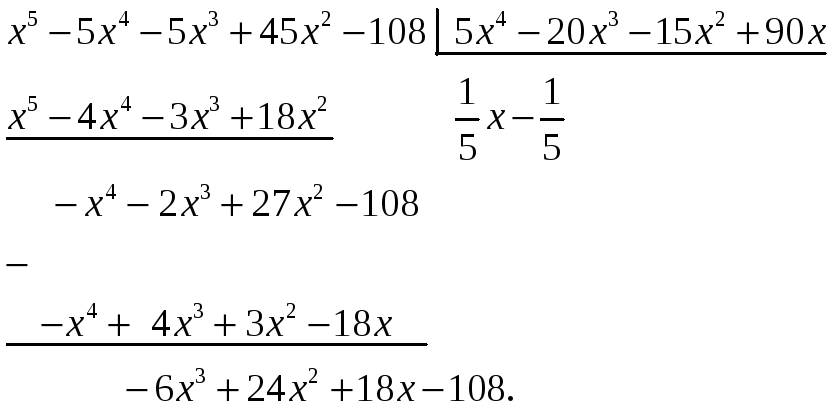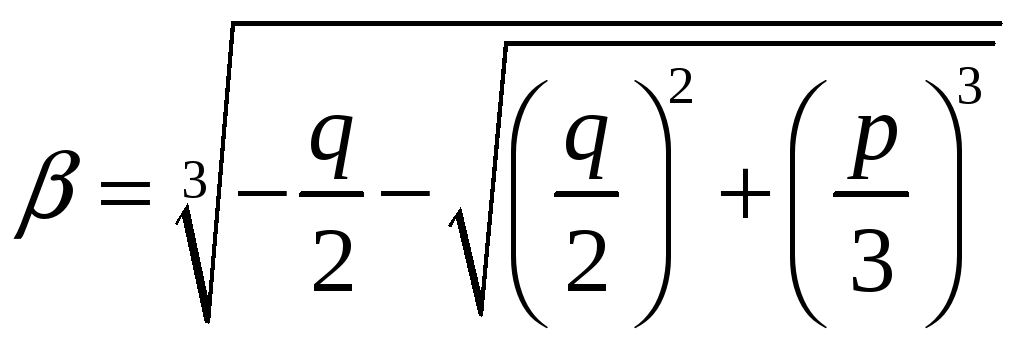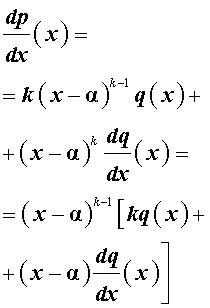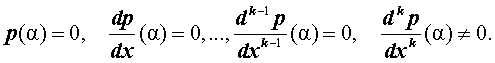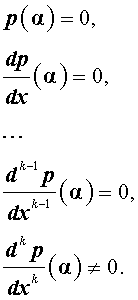Как найти кратность корня для многочлена - Исправление недочетов и поиск решений вместе с Examum.ru

Если при значении

многочлен

принимает значение
,
то число

называется корнем этого многочлена.

Число

является корнем многочлена тогда и
только тогда, когда

делится на
,
т.е.
.
Если при этом

делится на
,
но уже не делится на
,
то

называется
-кратным
корнем многочлена
.
Корни кратности

называются простыми корнями многочлена.

Чтобы проверить, будет ли число

корнем многочлена

и какой кратности, можно воспользоваться
схемой Горнера. Сначала

делится на
,
затем, если остаток равен нулю, полученное
частное делится снова на

и т.д. до получения ненулевого остатка.

Пример 1. Проверить, является ли
число

корнем многочлена

и найти кратность.

Решение. Деление на

осуществляем по схеме Горнера

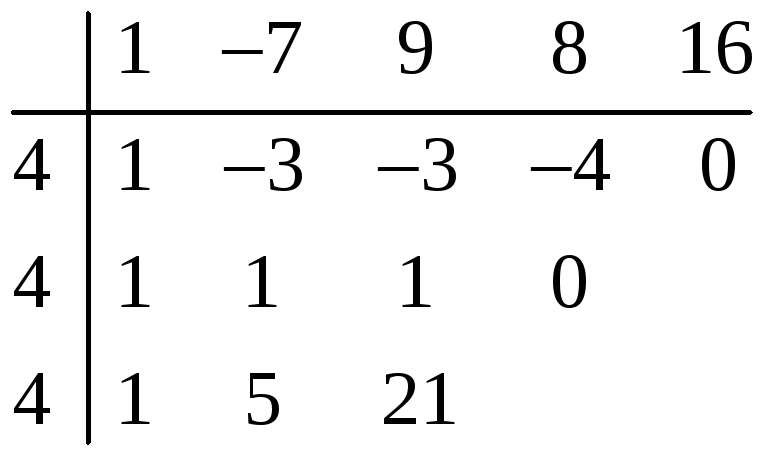
— корень кратности 2.

Пусть

— все различные корни многочлена

с кратностями, равными соответственно

— старший коэффициент
.
Тогда
.Корень
многочлена кратности

является корнем кратности

для его производной. Поэтому
,
где

— многочлен, уже не имеющий

своими корнями. Отсюда н.о.д. многочленов

и

равен
.

Следовательно, многочлен

имеет числа

простыми корнями.

Теперь для отыскания всех корней
многочлена

достаточно найти все корни многочлена
.
Это бывает сделать проще, так как степень

меньше степени
,
когда
.
Построение многочлена

называется отделением кратных корней
многочлена
.

Пример 2. Отделить кратные корни
многочлена
.

Решение.
.
Находим
.
Для этого делим с остатком

на
:

делится на остаток
.
Поэтому
.
Искомый многочлен, отделяющий кратные
корни
,
равен
.

Заметим, что в примере 2 все корни

легко вычислить.

Литература:
— § 22,
— § 9.4;

— № 555-559, 563-566, 569, 570, 585.

§ 3. Вычисление корней многочлена.

Задача вычисления корней некоторого
многочлена часто возникает в практике.
Согласно основной теореме алгебры, все
корни произвольного многочлена

с коэффициентами из числового поля

содержатся в поле комплексных чисел
.
Однако не существует какого-либо
универсального метода вычисления этих
корней. Метод решения этой задачи зависит
от степени многочлена и числового поля
.
Мы перечислим лишь самые основные методы
решения задачи вычисления корней
многочлена.

Корни многочленов 3-й и 4-й степени.

Если
,
то для отыскания всех корней многочлена

необходимо решить уравнение

(1)

Разделим обе части (1) на
.
В результате получим уравнение

(2)

имеющее те же корни, что и уравнение
(1). Сделаем теперь замену неизвестного
.
Эту замену проще всего осуществить,
представляя многочлен

по степеням

с помощью схемы Горнера (§
1) и делая затем замену
.
В результате замены получим уравнение

(3)

Корни уравнения (3) находятся по формуле
Кардано

где,
,

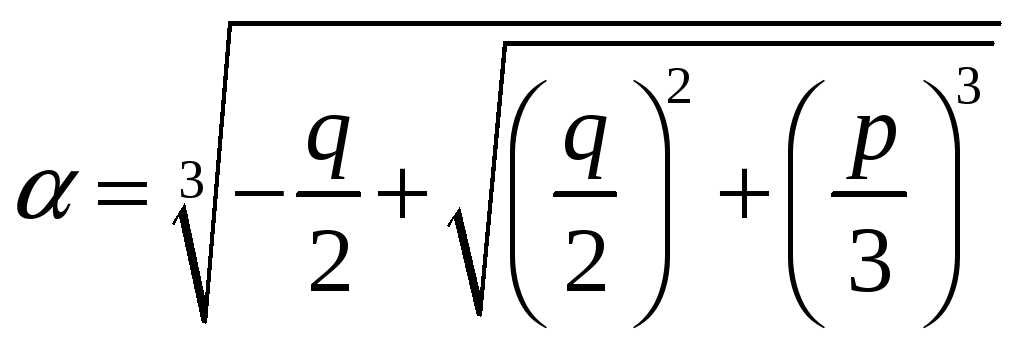
(корни извлекаются в поле комплексных
чисел
).
Применяя эту формулу, нужно для каждого
их трех значений

брать то значение
,
для которого выполняется условие

(такое значение всегда существует).

Если

— все корни уравнения (3), то

— все корни уравнения (1) и многочлена
.

Пример 1. Найти корни многочлена
.

Решение. Разложим многочлен

по степеням
.
Полагая
,
получим уравнение
.
Его корни находятся по формуле
,
где

или
.
Значениями корня

являются числа
.
Соответствующие им значения второго
корня

Отсюда
.
Корни многочлена
,
.

Если

— многочлен 4-й степени, то для вычисления
его корней достаточно иметь способ
вычисления всех корней уравнения вида

(4)

Способ Феррари решения уравнения (4)
состоит в следующем.

Левую часть (4) представляют в виде

, (5)

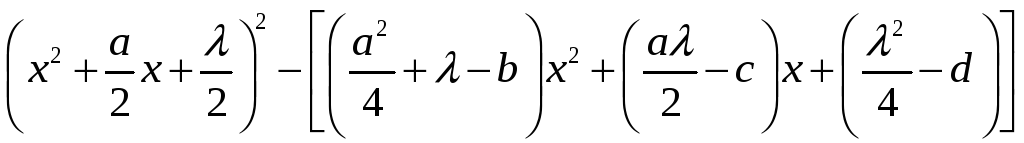
а затем подбирают

так, чтобы выражение в квадратных скобках
стало квадратом двучлена первой степени.
Для этого необходимо и достаточно
выполнение условия

, (6)

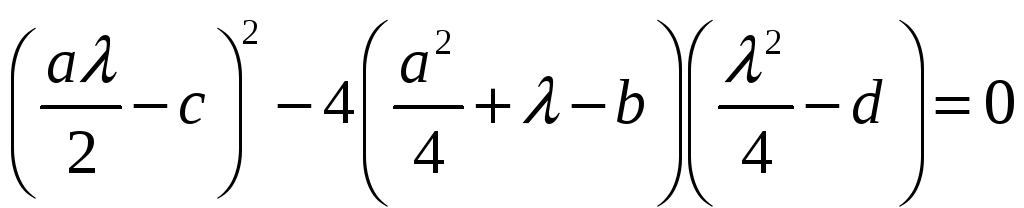
из которого следует, что

является корнем вспомогательного
кубического уравнения (6). Теперь находим
какой-нибудь один корень

и, подставляя его значение в (5), разлагаем
левую часть (4) как разность квадратов
на множители. Задача вычисления корней
сведена теперь к решению двух квадратных
уравнений.

Пример 2. Найти корни многочлена
.

Решение. Составим уравнение

(7)

Представим левую часть (7) в виде

(8)

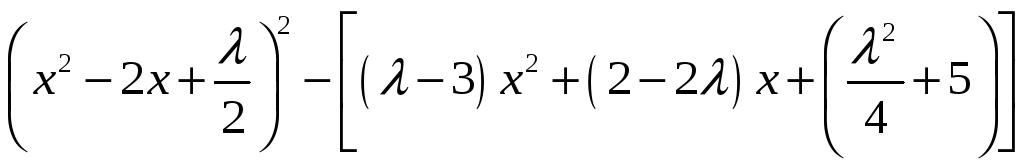
Подберем

так, чтобы дискриминант квадратного
трехчлена в квадратных скобках был
равен нулю:

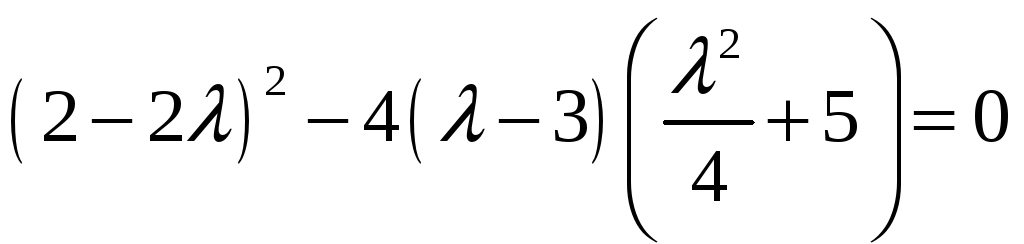
или

Можно заметить, что 4 — один из корней
этого уравнения. Тогда подставим

в (8) и уравнение (7) примет вид:

или

Отсюда, решая уравнения

и
,
получим корни нашего многочлена

Литература:

— § 38,

— № 167, 173, 174.

2. Рациональные корни
многочленов с рациональными коэффициентами.

Многочлен

имеет те же корни, что и многочлен

с целыми коэффициентами, полученный из

умножением на общее кратное знаменателей
всех коэффициентов
.

Если несократимая дробь

является корнем многочлена

с целыми коэффициентами, то выполняются
следующие условия:

1)

— делитель числа
;

2)

— делитель числа
;

3) для любого целого числа

число

является делителем числа
.

Поэтому все рациональные корни многочлена

(если они существуют) нужно искать среди
несократимых дробей, удовлетворяющих
условиям 1, 2, 3.

Если
,
то все рациональные корни

являются целыми числами.

Пример. Найти рациональные корни
многочлена

и определить их кратность.

Решение. Если

— несократимая дробь, является корнем
,
то

делит 12, а

делит 2. Все делители 12:
,
а делители 2: 1,2.

Зафиксируем
.
Тогда по (3) условию
.
В качестве

возьмем

и
.
Тогда

и
.
.
.
Числа 1 и -1 не являются корнями. Если
число

— корень, то

и
.
Такому условию удовлетворяют -2, 4. С
помощью схемы Горнера выясняем, что
число -2 является корнем кратности 2.

Далее, зафиксируем
.
Тогда

и

().
Проверять надо лишь

взаимно простые с
,
т.е.,
.
Среди этих чисел условию ()
удовлетворяют -1, 3. Проверяя по схеме
Горнера дроби

и

выясняем, что корнем является
.
Итак,

— простой корень,

— корень кратности 2.

Литература:

— § 57,

— § 11, 3,

— № 649-651.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Кратные корни многочленов

Пусть p(x) – многочлен степени n , а q(x) – многочлен степени n – k , где n и k – натуральные числа, удовлетворяющие неравенству .

Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство

p(x) = (x – α) k q (x) ,

(1)

Утверждение 1 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда оно является корнем производной этого многочлена кратности k – 1 .

Доказательство . Взяв производную от обеих частей формулы (1), получаем

Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.

Из утверждения 1 вытекает следующее

Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:

Определить кратность корня x0 многочлена f(x).

Третья производная:
f»'(x) = 60x 2 — 120x + 42
f»'(2) = 60*2 2 — 120*2 + 42 = 240 — 240 + 42 = 42, не равно нулю => кратность равна количеству найденных производных.

Ответ: 3

Метод второй: схема Горнера:

1	-5	7	-2	4	-8
2	1	-3	1	0	4	0
2	1	-1	-1	-2	0
2	1	1	1	0
2	1	3	7
2	1

Как видно из схемы Горнера количество нулей равно 3, следовательно и кратность равна 3. Схема Горнера метод намного удобнее, если x₀ — число больше 2, производными считать труднее.

Кратные корни многочлена

При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.

Определение. Пусть задан многочлен $fleft(xright) in Pleft[xright]$ ($Pleft[xright]$ — множество всех многочленов от буквы $x$ над полем $P$) и $alpha$, где $alpha$ — корень многочлена $fleft(xright)$. Элемент $alpha$ назовем $k$-кратным ($k in mathbb $, $k>1$) корнем многочлена, если имеет место следующее представление: $$fleft(xright)=left(x-alpharight)^k f_left(xright),, f_left(alpharight) ne 0.$$

Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),, f_left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.

Часто условие $f_left(alpharight) ne 0$ заменяют на $f_left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.

Процесс нахождения кратности корня

Пусть задан многочлен $fleft(xright) in Pleft[xright]$ и его корень $alpha$ ( $deg fleft(xright) > 0$). Рассмотрим задачу о нахождении кратности корня $alpha$.

Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_left(xright).$$ Тогда, если $alpha$ не является корнем $f_left(xright)$ ($f_left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_left(xright)$, где $deg f_left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.

Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.

Примеры решения задач

Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.

Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.

$1$	$-3$	$0$	$4$
$2$	$1$	$-1$	$-2$	$0$
$2$	$1$	$1$	$0$
$2$	$1$	$3$

Из таблицы видно, что многочлен $f(x)$ поделился на $left(x-2right)^2$ без остатка, а на $left(x-2right)^3$ — нет. Получаем, что $2$ — двукратный корень многочлена $f(x)$.

Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_left(xright),$$где $f_(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_left(xright),$$где $g_(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_(x)(x-alpha)g_(x)=left(x-alpharight)^3f_(x)g_(x).$$Так как $f_(alpha) ne 0$ и $g_(alpha) ne 0$, то $f_(alpha)g_(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_(x)g_(x)=h_(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_(x),$$ где $h_(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.

Для решении задачи воспользуемся алгоритмом Горнера.

$1$	$5$	$10$	$10$	$5$	$1$
$-1$	$1$	$4$	$6$	$4$	$1$	$0$
$-1$	$1$	$3$	$3$	$1$	$0$
$-1$	$1$	$2$	$1$	$0$
$-1$	$1$	$1$	$0$
$-1$	$1$	$0$

Из таблицы видно, что многочлен пятой степени $f(x)$ поделился на $left(x+1right)^5$ без остатка. Получаем, что $-1$ — корень пятой кратности.

По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_(x),, f_(2) ne 0.$$С другой стороны, в нашем случае: $$f_(x)=x^2+x-6=(x-2)(x+3),, f_(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_(x),$$ $f_(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.

Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.

Источник

Задание:

Определить кратность корня x₀ многочлена f(x)

f(x) = x⁵ — 5x⁴ + 7x³ — 2x² + 4x — 8, x₀ = 2;

Решение:

Метод первый: производными

f(2) = 2⁵ — 5*2⁴ + 7*2³ — 2*2² + 4*2 — 8 = 32 — 80 + 56 — 8 + 8 — 8 = 88 — 80 — 8 = 0

Первая производная:
f'(x) = 5x⁴ — 20x³ + 21x² — 4x + 4
f'(2) = 5 * 2⁴ — 20*2³ + 21*2² — 4*2 + 4 = 80 — 160 + 84 — 8 + 4 = 164 — 160 — 8 + 4 = 0

Вторая производная:
f»(x) = 20x³ — 60x² + 42x — 4
f»(2) = 20 * 2³ — 60*2² + 42*2 — 4 = 160 — 240 + 84 — 4 = 244 — 244 = 0

Третья производная:
f»'(x) = 60x² — 120x + 42
f»'(2) = 60*2² — 120*2 + 42 = 240 — 240 + 42 = 42, не равно нулю => кратность равна количеству найденных производных.

Ответ: 3

Метод второй: схема Горнера:

	1	-5	7	-2	4	-8
2	1	-3	1	0	4	0
2	1	-1	-1	-2	0
2	1	1	1	0
2	1	3	7
2	1

Ответ: 3

Источник

Кратные корни многочленов

Определение . Число α называют корнем кратности k многочлена p(x) , если справедливо равенство

p(x) = (x – α) k q (x) ,

(1)

Доказательство . Взяв производную от обеих частей формулы (1), получаем

Поскольку выражение, стоящее в квадратных скобках, при x = α не обращается в нуль, то утверждение 1 доказано.

Из утверждения 1 вытекает следующее

Утверждение 2 . Число α является корнем кратности k многочлена p(x) тогда и тогда, когда выполнены равенства:

Задача . Найти все значения параметра m , при которых многочлен

имеет корень кратности 2 .

Решение . Воспользовавшись утверждением 2, получаем

Кратные корни многочлена

При рассмотрении вопроса о корнях многочлена, особо выделяют понятие кратных корней.

Принято рассматривать понятие кратного корня для $k>1$. Если же $fleft(xright)$ можно представить следующим образом: $$fleft(xright)=left(x-alpharight) f_<1>left(xright),, f_<1>left(alpharight) ne 0,$$ то $alpha$ называется простым (однократным) корнем многочлена$fleft(xright)$. Если для $fleft(xright)$ имеет место следующее равенство: $$fleft(xright)=left(x-alpharight)^2 f_<1>left(xright),, f_<1>left(alpharight) ne 0,$$ то $alpha$ называется двукратным корнем многочлена $fleft(xright)$. Аналогично, существуют корни трехкратные, четырехкратные и так далее.

Часто условие $f_<1>left(alpharight) ne 0$ заменяют на $f_<1>left(xright),barvdots,(x-alpha)$. Эквивалентность этих условий вытекает из следствий теоремы Безу. Тогда, набор условий, что $f(x),vdots,left(x-alpharight)^k$, но $f(x),barvdots,left(x-alpharight)^$ эквивалентен тому, что $alpha$ — $k$-кратный корень многочлена $f(x)$.

Процесс нахождения кратности корня

Так как $alpha$ — корень $fleft(xright)$, то имеет место следующее представление: $$fleft(xright)=left(x-alpharight)f_<1>left(xright).$$ Тогда, если $alpha$ не является корнем $f_<1>left(xright)$ ($f_<1>left(alpharight) ne 0$), то, по определению, $alpha$ — простой корень многочлена $fleft(xright)$. В противном случае, $alpha$ — $k$-кратный ($k in mathbb $, $k > 1 $) корень $fleft(xright)$. Задача сводится к нахождению $k-1$, то есть к нахождению кратности корня $f_<1>left(xright)$, где $deg f_<1>left(xright) = deg fleft(xright) — 1$. Учитывая, что $deg fleft(xright) > 0$, то повторение такого алгоритма решает задачу. Для этого используется алгоритм Горнера.

Стоит упомянуть, что иногда удобней пользоваться критерием кратности корня.

Примеры решения задач

Пусть задан многочлен $fleft(xright)=x^3-3x^2+4$. Определить, является ли $2$ корнем многочлена $f(x)$. В случае положительного ответа найти его кратность.

Для решении задачи воспользуемся алгоритмом Горнера. Стоит обратить внимание на то, что хоть и слагаемое вида $a_<1>x^1$ отсутствует в записи, но нулевой коэффициент необходимо не забыть занести в таблицу.

$1$	$-3$	$0$	$4$
$2$	$1$	$-1$	$-2$	$0$
$2$	$1$	$1$	$0$
$2$	$1$	$3$

Так как $alpha$ — двукратный корень многочлена $f(x)$, то $f(x)$ представим в следующем виде: $$fleft(xright)=left(x-alpharight)^2 f_<1>left(xright),$$где $f_<1>(alpha) ne 0$. Аналогично, $g(x)$ можно представить следующим образом: $$gleft(xright)=left(x-alpharight) g_<1>left(xright),$$где $g_<1>(alpha) ne 0$. Тогда, $$f(x)g(x)=left(x-alpharight)^2f_<1>(x)(x-alpha)g_<1>(x)=left(x-alpharight)^3f_<1>(x)g_<1>(x).$$Так как $f_<1>(alpha) ne 0$ и $g_<1>(alpha) ne 0$, то $f_<1>(alpha)g_<1>(alpha)ne0$. Обозначим $f(x)g(x)=h(x)$, $f_<1>(x)g_<1>(x)=h_<1>(x)$, тогда перепишем выражение многочлена $f(x)g(x)$ следующим образом: $$h(x)=left(x-alpharight)^3h_<1>(x),$$ где $h_<1>(alpha)ne0$. Тогда по определению $alpha$ — корень $f(x)g(x)$ третьей кратности.

Для решении задачи воспользуемся алгоритмом Горнера.

$1$	$5$	$10$	$10$	$5$	$1$
$-1$	$1$	$4$	$6$	$4$	$1$	$0$
$-1$	$1$	$3$	$3$	$1$	$0$
$-1$	$1$	$2$	$1$	$0$
$-1$	$1$	$1$	$0$
$-1$	$1$	$0$

По определению, для того, что бы $2$ была корнем второй кратности, необходимо что бы имело место следующее представление: $$f(x)=left(x-2right)^2f_<1>(x),, f_<1>(2) ne 0.$$С другой стороны, в нашем случае: $$f_<1>(x)=x^2+x-6=(x-2)(x+3),, f_<1>(2)=0.$$ Получаем, что $2$ не корень второй кратности. Тогда найдем его кратность. Выразим $f(x)$ подставив $f_<1>(x)=(x-2)(x+3)$:$$f(x)=left(x-2right)^3(x+3)=left(x-2right)^3f_<2>(x),$$ $f_<2>(2)=(2+3)=5ne0$. Значит, по определению, $2$ — корень многочлена $f(x)$ третьей кратности.

Представим исходный многочлен следующим образом: $$f(x)=x^4(x^4-8x^3+10x^2-1).$$
Обозначим $f_<1>(x)=x^4-8x^3+10x^2-1$. Легко убедиться, что $f_<1>(0)=-1ne0$. Получаем, что, по определению кратного корня, $0$ — корень многочлена $f(x)$ четвертой кратности.

Как определить кратность корня для уравнения

Разделы

Дополнительно

Алгебраическим уравнением степени $n$ с одной неизвестной $x$ называется уравнение вида

$P_n(x) = a_0 x^n + a_1 x^ + cdots + a_n = 0 (a_0 neq 0)$ (1)

(т. е. уравнение $f(x) = 0$, в левой части которого стоит ц. р. ф степени $n$ от $х$).

Для алгебраических уравнений принято ставить задачу отыскания всех (вообще говоря, комплексных) корней уравнения. Так как корнями уравнения (1) являются нули (корни) многочлена в его левой части, то можно использовать сведения о целых рациональных функциях и их корнях. Утверждение формулируются применительно к уравнению (1) следующим образом:

1) Каждое уравнение степени $n$ имеет по меньшей мере один корень в комплексной области. Если каждый корень учитывать с его кратностью, т. е. считать за столько корней, какова его кратность, то число корней уравнения равно его степени $n$. При этом говорят, что $x = alpha$ — корень кратности $k$, если левая часть уравнения делится на $(x — alpha)^k$ нацело, но не делится нацело на $(x — alpha)^$.

2) Если уравнение (1) имеет комплексный (мнимый) корень $x = sigma + i tau$, то и комплексно сопряженное число $bar <х>= sigma — i tau$ является корнем уравнения (кратности обоих сопряженных корней одинаковы).

На протяжении столетий главной задачей алгебры было указание правил решения алгебраических уравнений. С древности известны формулы для решения уравнений первой и второй степени. Итальянскими математиками эпохи Возрождения (Кардано, Тарталья, Феррари) были найдены формулы для решения уравнений третьей и четвертой степени (они громоздки и не имеют большого практического значения). Попытки решения «в радикалах» (т. е. с применением действия извлечения корня) уравнений степени выше четвертой были в общем случае безуспешны. Уже в XIX веке в работах Руффини, Абеля и Галуа было установлено, что не только для корней общего уравнения степени выше четвертой не может быть дано формул, выражающих их в радикалах, но и что корни многих конкретных уравнений с числовыми (например, целыми) коэффициентами не могут быть выражены через радикалы из рациональных чисел.

источники:

Кратные корни многочлена

http://earthz.ru/science/Chislo-i-kratnost-kornej

Источник