Как найти края на изображении

В статье представлены четыре самых распространённых алгоритма обнаружения контуров.

Первые два, а именно алгоритм трассировки квадратов и трассировка окрестностей Мура, просты в реализации, а потому часто применяются для определения контура заданного паттерна. К сожалению, у обоих алгоритмов есть несколько слабых мест, что приводит к невозможности обнаружения контура большого класса паттернов из-за их особого вида смежности.

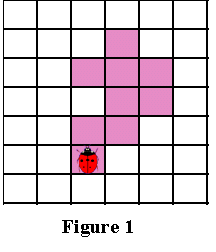
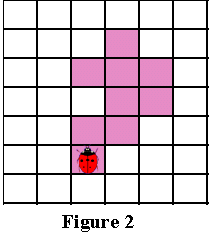
Данные алгоритмы будут игнорировать все «дырки» в паттерне. Например, если у нас есть паттерн, подобный показанному на Рисунке 1, то обнаруженный алгоритмами контур будет похож на показанный на Рисунке 2 (синими пикселями обозначен контур). В некоторых областях применения это вполне допустимо, но в других областях, например, в распознавании символов, требуется обнаружение внутренних частей паттерна для нахождения всех пробелов, отличающих конкретный символ. (На Рисунке 3 показан «полный» контур паттерна.)

Следовательно, для получения полного контура сначала необходимо использовать алгоритм «поиска дырок», определяющий отверстия в заданном паттерне, а затем применить к каждому отверстию алгоритм обнаружения контуров.

Что такое связность

В цифровых изображениях с двоичными значениями пиксель может иметь одно из следующих значений: 1 — когда является частью паттерна, или 0 — когда является частью фона, т.е. градации серого отсутствуют. (Мы будем считать, что пиксели со значением 1 чёрные, а со значением 0 — белые).

Для идентификации объектов в цифровом паттерне нам нужно находить группы чёрных пикселей, «связанных» друг с другом. Другими словами, объектами в заданном цифровом паттерне являются связные компоненты этого паттерна.

В общем случае, связная компонента — это множество чёрных пикселей P, такое, что для каждой пары пикселей p_i и p_j в P существует последовательность пикселей p_i, …, p_j, такая, что:

a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и

b) каждые 2 пикселя, находящиеся в последовательности рядом, являются «соседями».

Возникает важный вопрос: когда мы можем сказать, что 2 пикселя являются «соседями»? Поскольку мы используем квадратные пиксели, ответ на предыдущий вопрос нетривиален по следующей причине: в квадратной тесселяции пиксели имеют общее или ребро, или вершину, или не имеют ничего общего. У каждого пикселя есть 8 пикселей, имеющих с ним общую вершину; такие пиксели составляют «окрестность Мура» данного пикселя. Должны ли мы считать «соседями» пиксели, имеющие только одну общую вершину? Или чтобы считаться «соседями», два пикселя должны иметь общее ребро?

Так возникают два вида связности, а именно: 4-связность и 8-связность.

4-связность

Когда мы можем сказать, что заданное множество чёрных пикселей является 4-связным? Во-первых, нужно определить понятие 4-соседа (также называемого прямым соседом):

Определение 4-соседа: пиксель Q является 4-соседом заданного пикселя P, если Q и P имеют общее ребро. 4-соседи пикселя P (обозначенные как P2, P4, P6 и P8), показаны на Рисунке 2 ниже.

Определение 4-связной компоненты: множество чёрных пикселей P является 4-связной компонентой, если для каждой пары пикселей p_i и p_j в P существует последовательность пикселей p_i, …, p_j, такая, что:

a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и

b) каждые два пикселя, которые находятся рядом в последовательности, являются 4-соседями

Примеры 4-связных паттернов

На схемах ниже показаны примеры 4-связных паттернов:

8-связность

Когда можно сказать, что заданное множество чёрных пикселей 8-связное? Во-первых, нам нужно определить понятие 8-соседа (также называемого непрямым соседом):

Определение 8-соседа: пиксель Q является 8-соседом (или просто соседом) заданного пикселя P, если Q и P имеют общее ребро или вершину. 8-соседи заданного пикселя P составляют окрестность Мура этого пикселя.

Определение 8-связной компоненты: множество чёрных пикселей P является 8-связной компонентой (или просто связной компонентой), если для каждой пары пикселей p_i и p_j в P существует последовательность пикселей p_i, …, p_j, такая, что:

a) все пиксели в последовательности находятся во множестве P, т.е. являются чёрными, и

b) каждые два пикселя, которые находятся рядом в этой последовательности, являются 8-соседями

Примечание: все 4-связные паттерны являются 8-связными, т.е. 4-связные паттерны являются подмножеством множества 8-связных паттернов. С другой стороны, 8-связный паттерн может и не являться 4-связным.

Пример 8-связного паттерна

На схеме ниже показан паттерн, являющийся 8-связным, но не 4-связным:

Пример паттерна, не являющегося 8-связным:

На схеме ниже показан пример паттерна, не являющийся 8-связным, т.е. составленный из более чем одной связной компоненты (на схеме показаны три связные компоненты):

Алгоритм трассировки квадратов

Идея

Лежащая в основе алгоритма трассировки квадратов идея очень проста; это можно связать с тем фактом, что алгоритм стал одной из первых попыток обнаружения контура двоичного паттерна.

Чтобы понять, как он работает, нужно немного воображения…

Допустим, у нас есть цифровой паттерн, например, группа из чёрных пикселей на фоне из белых пикселей, т.е. на сетке; находим чёрный пиксель и объявляем его нашим «начальным» пикселем. (Нахождение «начального» пикселя можно реализовать множеством разных способов; мы начнём с левого нижнего угла сетки, будем сканировать каждый столбец пикселей снизу вверх, от самого левого столбца и до самого правого, пока не натолкнёмся на чёрный пиксель. Его мы и объявим «начальным«.)

Теперь представьте, что вы — божья коровка, стоящая на начальном пикселе, как это показано на показанном ниже Рисунке 1. Чтобы получить контур паттерна, вам необходимо сделать следующее:

каждый раз, когда вы оказываетесь на чёрном пикселе, поворачивайте налево, и

Чёрные пиксели, которые вы обошли, будут являться контуром паттерна.

Важным аспектом алгоритма трассировки квадратов является «чувство направления». Повороты влево и вправо выполняются относительно текущего расположения, которое зависит от того, каким образом вы попали на текущий пиксель. Следовательно, чтобы делать правильные ходы, необходимо отслеживать своё направление.

Алгоритм

Ниже представлено формальное описание алгоритма трассировки квадратов:

Входящие данные: квадратная тесселяция, T, содержащая связную компоненту P чёрных ячеек.

Выходные данные: ряд B (b₁, b₂ ,…, b_k) пикселей границы, т.е. контур.

Начало

• Задаём B как пустое множество.
• Сканируем снизу вверх и слева вправо ячейки T, пока не будет найден чёрный пиксель s из P.
• Вставляем s в B.
• Делаем текущий пиксель p начальным пикселем s.
• Поворачиваем влево, т.е. переходим в соседний пиксель слева от p.
• Обновляем p, т.е. он становится текущим пикселем.
• Пока p не равно s, выполняем

  Если текущий пиксель p является чёрным

  • вставляем p в B и поворачиваем влево (переходим в соседний пиксель слева от p).
  • Обновляем p, т.е. он становится текущим пикселем.

  иначе

  • поворачиваем вправо (переходим в соседний пиксель справа от p).
  • Обновляем p, т.е. он становится текущим пикселем.

  Завершение цикла «Пока»

Конец

Примечание: понятия «влево» и «вправо» следует рассматривать не относительно страницы или читателя, а относительно направления входа в «текущий» пиксель во время выполнения сканирования.

Демонстрация

Ниже показана анимированная демонстрация того, как алгоритм трассировки квадратов обнаруживает контур паттерна. Не забывайте, что божья коровка движется по пикселям; замечайте, как меняется её направление при поворотах влево и вправо. Повороты влево и вправо выполняются относительно текущего направления в пикселе, т.е. ориентации божьей коровки.

Анализ

Оказывается, что возможности алгоритма трассировки квадратов очень ограничены. Он неспособен обнаруживать контуры большого семейства паттернов, которые часто возникают в реальных областях применения.

В основном это связано с тем, что повороты влево и вправо не учитывают пиксели, расположенные «по
диагонали» от текущего пикселя.

Давайте рассмотрим различные паттерны с разной связностью и увидим, почему терпит неудачу алгоритм трассировки квадратов. Кроме того, мы изучим способы усовершенствования возможностей алгоритма и заставим его работать хотя бы с паттернами, имеющими особый вид связности.

Критерий останова

Одна из слабостей алгоритма заключается в выборе критерия останова. Другими словами, когда алгоритм прекращает своё выполнение?

В исходном описании алгоритма трассировки квадратов условием завершения является попадание в начальный пиксель во второй раз. Оказывается, что если алгоритм зависит от такого критерия, то он не сможет обнаружить контуры большого семейства паттернов.

Ниже показана анимированная демонстрация с объяснением того, как алгоритму не удаётся обнаружить точный контур паттерна из-за выбора плохого критерия останова:

Как видите, усовершенствование критерия останова может стать хорошим началом для улучшения результативности алгоритма в целом. Существует две эффективные альтернативы для имеющегося критерия останова:

a) Останавливаться, только посетив начальный пиксель n раз, где n не меньше 2, ИЛИ

b) Останавливаться после попадания в начальный пиксель во второй раз точно так же, как мы попали в него изначально.

Этот критерий был предложен Джейкобом Элиософфом, поэтому мы будем называть его критерием останова Джейкоба.

Смена критерия останова в общем случае улучшает результативность алгоритма трассировки квадратов, но не позволяет преодолеть другие слабые места, которые он имеет в случае паттернов с особыми видами связности.

Square Tracing Algorithm неспособен обнаружить контур семейства паттернов со связностью 8, которые НЕ имеют связности 4.

Ниже показана анимированная демонстрация того, как алгоритму трассировки квадратов (с критерием останова Джейкоба) не удаётся обнаружить правильный контур паттерна со связностью 8 без связности 4:

Этот алгоритм совершенно бесполезен?

Если вы прочитали представленный выше анализ, то наверно думаете, что алгоритму трассировки квадратов не удаётся обнаружить контуры большинства паттернов. Но оказывается. что существует особое семейство паттернов, у которого полностью правильно обнаруживается контур алгоритмом трассировки квадратов.

Пусть P — множество чёрных пикселей со связностью 4 на сетке. Пусть белые пиксели сетки, т.е. фоновые пиксели W тоже имеют связность 4. Оказывается, что при таких условиях паттерна и его фона можно доказать, что алгоритм трассировки квадратов (с критерием останова Джейкоба) всегда успешно будет справляться с определением контура.

Ниже представлено доказательство, что в случае, когда и паттерн, и пиксели фона имеют связанность 4, алгоритм трассировки квадратов будет правильно определять контур при использовании критерия останова Джейкоба.

Доказательство
Дано: паттерн P такой, что все пиксели паттерна (т.е. чёрные) и пиксели фона (т.е. белые) W имеют связность 4.

Первое наблюдение

Так как множество белых пикселей W имеет связность 4, это значит, что в паттерне не может быть никаких «дыр» (выражаясь неформально, «дырами» мы называем группы белых пикселей, полностью окружённые чёрными пикселями паттерна).

Наличие любой «дыры» в паттерне приведёт к отделению группы белых пикселей от остальных белых пикселей; при этом множество белых пикселей теряет связность 4.

На Рисунке 2 и Рисунке 3 ниже показано два вида «дыр«, которые могут возникнуть в паттерне со связностью 4:

Второе наблюдение

Любые два чёрных пикселя паттерна ОБЯЗАНЫ иметь одну общую сторону.

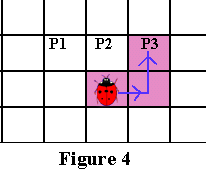
Допустим, два чёрных пикселя имеют только одну общую вершину. Тогда, чтобы удовлетворить свойству 4-связности паттерна, должен существовать путь, соединяющий эти два пикселя так, что каждые два соседних пикселя на этом пути имеют связность 4. Но это даст нам паттерн, похожий на Рисунок 3. Другими словами, это приведёт к разделению белых пикселей. На Рисунке 4 ниже показан типичный паттерн, удовлетворяющий допущению, что пиксели паттерна и фона 4-связаны, т.е. не имеют «дыр«, а каждые два чёрных пикселя имеют одну общую сторону:

Полезно представлять такие паттерны следующим образом:

Сначала рассматриваем граничные пиксели, т.е. контур паттерна. Затем если мы рассмотрим каждый граничный пиксель как имеющий 4 ребра единичной длины, то увидим, что некоторые из этих рёбер общие с соседними белыми пикселями. Мы назовём такие рёбра граничными рёбрами.

Такие граничные рёбра можно рассматривать как рёбра многоугольника. На Рисунке
5 ниже эта мысль продемонстрирована на примере многоугольника, соответствующего паттерну с Рисунка 4 выше:

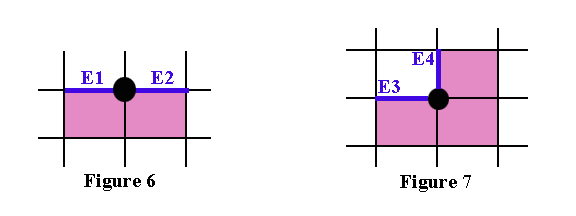
Если мы рассмотрим все возможные «конфигурации» граничных пикселей, которые могут возникать в таких паттернах, то увидим, что существует два простых случая, показанных на Рисунке 6 и Рисунке 7 ниже.

Граничные пиксели могут быть кратными этих случаев или другими расположениями, т.е. поворотами этих двух случаев. Граничные рёбра помечены синим как E1, E2, E3 и E4.

Третье наблюдение

В случае рассмотренных выше двух случаев, какой бы начальный пиксель мы не выбрали, и в каком бы направлении в него не попали, алгоритм трассировки квадратов никогда не будет «возвращаться назад» (backtrack), никогда не будет «проходить через» граничное ребро дважды (только если он не трассирует границу во второй раз) и никогда не пропустит граничное ребро. Проверьте!

Здесь нужно пояснить две концепции:

a) алгоритм «возвращается назад», когда перед трассировкой всей границы он идёт назад, чтобы посетить уже посещённый пиксель, и

b) для каждого граничного ребра существует два способа «пройти через него», а именно «внутрь» и «наружу» (где «внутрь» обозначает движение внутрь соответствующего многоугольника, а «наружу» — наружу многоугольника).

Кроме того, когда алгоритм проходит «внутрь» через одно из граничных рёбер, он пройдёт «наружу» через следующее граничное ребро, т.е. алгоритм трассировки квадратов не должен иметь возможности пройти сквозь два последовательных ребра одинаковым образом.

Последнее наблюдение

У каждого паттерна существует чётное количество граничных рёбер.

Если посмотреть на многоугольник с Рисунка 5, то можно увидеть, что:

если мы хотим начать с вершины S, отмеченной на схеме, и следовать по граничным рёбрам, пока снова не достигнем S, то заметим, что пересечём в процессе чётное количество граничных рёбер. Можно считать каждое граничное ребро «шагом» в отдельном направлении. Тогда для каждого «шага» вправо должен быть соответствующий «шаг» влево, если мы хотим вернуться в исходную позицию. То же самое относится к вертикальным «шагам». Следовательно, «шаги» должны иметь соответствующие пары и это объясняет, почему в каждом из таких паттернов будет чётное количество граничных рёбер.

Следовательно, когда алгоритм трассировки квадратов входит через начальное граничное ребро (начального пикселя) во второй раз, то он будет это делать в том же направлении, что и в первый раз.

Причина этого в том, что поскольку существует два способа прохода через граничное ребро, и алгоритм попеременно выполняет движение «внутрь» и «наружу», а граничных рёбер чётное количество, то алгоритм пройдёт через начальное граничное ребро во второй раз так же, как и в первый.

Заключение

В случае 4-связного паттерна и фона алгоритм трассировки квадратов обнаружит всю границу, т.е. контур, паттерна и прекратит работу после однократной трассировки, т.е. не будет трассировать её заново, поскольку при достижении начального граничного ребра во второй раз он войдёт в него так же, как и в первый раз. Следовательно, алгоритм трассировки квадратов с критерием останова Джейкоба будет правильно определять контру любого паттерна при условии, что и паттерн, и фон обладают 4-связностью.

Трассировка окрестностей Мура

Идея

Идея, лежащая в основе трассировки окрестностей Мура (Moore-Neighbor tracing), проста; но прежде чем объяснять её, нам нужно объяснить важное понятие: окрестности Мура пикселя.

Окрестность Мура

Окрестность Мура пикселя P — это множество из 8 пикселей, имеющих общую вершину или ребро с этим пикселем. Такие пиксели, а именно P1, P2, P3, P4, P5, P6, P7 и P8, показаны на Рисунке 1.

Окрестность Мура (Moore neighborhood, также называемая 8-соседями или indirect neighbors (непрямыми соседями)) — это важное понятие, часто упоминаемое в литературе.

Теперь мы готовы познакомиться с идеей, лежащей в основе трассировки окрестностей Мура.

Пусть существует цифровой паттерн, т.е. группа чёрных пикселей, на фоне из белых пикселей, т.е. на сетке; найдём чёрный пиксель и объявим его «начальным» пикселем. (Находить «начальный» пиксель можно разными способами, но мы, как и раньше, будем начинать с левого нижнего угла и сканировать все столбцы пикселей по порядку, пока не найдём первый чёрный пиксель, который и объявим «начальным«.)

Теперь снова представьте, что вы божья коровка, стоящая на начальном пикселе, как показано на Рисунке 2 ниже. Без потери обобщённости мы будем обнаруживать контур, двигаясь вокруг паттерна по часовой стрелке. (Неважно, какое направление мы выберем, главное — использовать его в алгоритме постоянно).

Общая идея заключается в следующем: каждый раз, когда мы попадаем в чёрный пиксель P, то возвращаемся назад, то есть к белому пикселю, в котором стояли ранее. Затем обходим пиксель P по часовой стрелке, посещая каждый пиксель в его окрестности Мура, пока не попадём в чёрный пиксель. Алгоритм завершает выполнение, когда начальный пиксель достигает начального пикселя во второй раз.

Те чёрные пиксели, которые посетил алгоритм, будут контуром паттерна.

Алгоритм

Ниже приведено формальное описание алгоритма трассировки окрестностей Мура:

Входящие данные: квадратная тесселяция T, содержащая связную компоненту P из чёрных ячеек.

Выходные данные: ряд B (b₁, b₂ ,…, b_k) граничных пикселей, т.е. контур.

Обозначим как M(a) окрестность Мура пикселя a.

Пусть p будет текущим граничным пикселем.

Пусть c будет текущим рассматриваемым пикселем, т.е. c находится в M(p).

Начало

• Задаём B как пустое множество.
• Снизу вверх и слева направо сканируем ячейки T, пока не найдём чёрный пиксель s из P.
• Вставим s в B.
• Зададим в качестве текущей граничной точки p точку s, т.е. p=s
• Вернёмся назад, т.е. перейдём к пикселю, из которого мы пришли в s.
• Зададим в качестве c следующий по часовой стрелке пиксель в M(p).
• Пока c не равно s, выполняем
  • если c — чёрный
    • Вставляем c в B
    • задаём p=c
    • возвращаемся назад (перемещаем текущий пиксель c в пиксель, из которого попали в p)

    иначе

    • перемещаем текущий пиксель c в следующий по часовой стрелке пиксель в M(p)

    Конец цикла «Пока»

Конец

Демонстрация

Ниже показана анимированная демонстрация того, как трассировка окрестностей Мура выполняет обнаружение контура паттерна. (Мы решили трассировать контур по часовой стрелке.)

Анализ

Основная слабость трассировки окрестностей Мура заключается в выборе критерия останова.

В исходном описании алгоритма для трассировки окрестностей Мура критерием останова является попадание в начальный пиксель во второй раз. Аналогично алгоритму трассировки квадратов, оказывается, что трассировка окрестностей Мура при использовании такого критерия не может обнаруживать контуры большого семейства паттернов.

Ниже показана анимированная демонстрация, объясняющая, почему алгоритму не удаётся найти точный контур паттерна из-за выбора плохого критерия останова:

Как видите, усовершенствование критерия останова может стать хорошим началом для улучшения результативности трассировки в целом. Для критерия останова есть две эффективные альтернативы, аналогичные критерию останова Джейкоба.

Использование критерия Джейкоба значительно улучшает результативность трассировки окрестностей Мура, делая его наилучшим алгоритмом для определения контура любого паттерна, вне зависимости от его связности.

Причина этого в основном заключается в том, что для поиска следующего граничного пикселя алгоритм проверяет всю окрестность Мура граничного пикселя. В отличие от алгоритма трассировки квадратов, который делает повороты только влево и вправо и упускает пиксели «по диагонали», трассировка окрестностей Мура всегда будет способна обнаружить внешнюю границу любой связной компоненты. Причина заключается в следующем: для любого 8-связного (или просто связного) паттерна следующий граничный пиксель лежит в пределах окрестности Мура текущего граничного пикселя. Поскольку трассировка окрестностей Мура проверяет каждый из пикселей в окрестности Мура текущего граничного пикселя, она обязана обнаружить следующий граничный пиксель.

Когда трассировка окрестностей Мура достигает начального пикселя во второй раз точно так же, как она сделала это в первый раз, то это значит, что был обнаружен полный внешний контур паттерна, и если не остановить алгоритм, то он заново будет обнаруживать тот же контур.

Радиальная развёртка

Алгоритм радиальной развёртки (Radial Sweep) — это алгоритм обнаружения контура, рассматриваемый в некоторых книгах. Несмотря на сложное название, лежащая в его основе идея очень проста. На самом деле, оказывается, что алгоритм радиальной развёртки идентичен трассировке окрестностей Мура. Можно задаться вопросом: «Зачем же вообще мы его упоминаем?».

Трассировка окрестностей Мура выполняет поиск в окрестности Мура текущего граничного пикселя в определённом направлении (мы выбрали направление по часовой стрелке), пока не найдёт чёрный пиксель. Затем она объявляет этот пиксель текущим граничным пикселем и продолжает работу.

Алгоритм радиальной развёртки выполняет то же самое. С другой стороны, он обеспечивает интересный способ поиска следующего чёрного пикселя в окрестности Мура заданного граничного пикселя.

Способ основан на следующей идее:

каждый раз, когда мы находим новый граничный пиксель, делаем его текущим пикселем P, и рисуем воображаемый отрезок прямой, соединяющий P с предыдущим граничным пикселем. Затем поворачиваем отрезок относительно P по часовой стрелке, пока он не натолкнётся на чёрный пиксель в окрестности Мура пикселя P. Поворот отрезка идентичен проверке каждого пикселя в окрестности Мура P.

Мы создали анимированную демонстрацию того, как работает алгоритм радиальной развёртки и чем он похож на трассировку окрестностей Мура.

А когда же останавливается алгоритм радиальной развёртки?

Давайте объясним поведение алгоритма при использовании следующих критериев останова…

Критерий останова 1

Пусть алгоритм радиальной развёртки завершает работу тогда, когда посетит начальный пиксель во второй раз.

Ниже представлена анимированная демонстрация, из которой понятно, почему правильно будет сменить критерий останова.

Стоит упомянуть также то, что при использовании этого критерия останова в обоих алгоритмах результативность алгоритма радиальной развёртки идентична трассировке окрестностей Мура.

В алгоритме трассировки квадратов и в трассировке окрестностей Мура мы выяснили, что использование критерия останова Джейкоба значительно улучшает результативность обоих алгоритмов.

Критерий останова Джейкоба требует, чтобы алгоритм прекращал выполнение при посещении начального пикселя во второй раз в том же направлении, что и в первый раз.

К сожалению, мы не можем использовать в алгоритме радиальной развёртки критерий останова Джейкоба. Причина заключается в том, что алгоритм радиальной развёртки не определяет понятия «направления», в котором он попадает в граничный пиксель. Другими словами, непонятно «направление», в котором алгоритм попал в граничный пиксель (и его определение нетривиально).

Следовательно, нам нужно предложить другой критерий останова, который не зависит от направления попадания в определённый пиксель, способный улучшить результативность алгоритма радиальной развёртки…

Критерий останова 2

Допустим, что каждый раз, когда алгоритм обнаруживает новый граничный пиксель P_i, он вставляется в ряд граничных пикселей: P₁, P₂, P₃, …, P_i; и объявляется текущим граничным пикселем. (P₁ мы будем считать начальным пикселем). Это значит, что мы знаем предыдущий граничный пиксель P_i-1 каждого текущего граничного пикселя P_i . (Что касается начального пикселя, то мы будем предполагать, что P₀ является воображаемым пикселем, неэквивалентным ни одному из пикселей на сетке, который стоит перед начальным пикселем в ряду граничных пикселей).

С учётом представленных выше допущений мы можем определить критерий останова следующим образом:

Алгоритм прекращает выполнение, когда:

a) текущий граничный пиксель P_i уже ранее встречался как пиксель P_j (где j < i ) в ряду граничных пикселей, И

b) P_i-1 =  P_j-1.

Другими словами, алгоритм завершает выполнение тогда, когда он посещает граничный пиксель P во второй раз, если граничный пиксель до P (в ряду граничных пикселей) во второй раз является тем же пикселем, который был до P, когда P был посещён в первый раз.

Если условие критерия останова удовлетворено и алгоритм не завершает работу, то алгоритм радиальной развёртки будет продолжать обнаруживать ту же границу во второй раз.

Результативность алгоритма радиальной развёртки с этим критерием останова схоже с результативностью трассировки окрестностей Мура с критерием останова Джейкоба.

Алгоритм Тео Павлидиса

Идея

Этот алгоритм — один из самых последних алгоритмов обнаружения контуров, предложенный Тео Павлидисом. Он привёл его в своей книге 1982 года Algorithms for Graphics and Image Processing (глава 7, раздел 5). Он не так прост, как алгоритм трассировки квадратов или трассировка окрестностей Мура, но не так уж и сложен (это свойственно большинству алгоритмов обнаружения контуров).

Этот алгоритм мы будем объяснять не так, как это сделано в его книге. Наш подход легче воспринимается и он даёт представление об общей идее, лежащей в основе алгоритма.

Без утери обобщённости мы решили обходить контур по часовой стрелке, чтобы соответствовать порядку всех других алгоритмов, представленных в статье. С другой стороны, Павлидис выбрал направление против часовой стрелки. На результативность алгоритма это никак не повлияет. Единственное отличие заключается в относительном направлении движений, которые мы будем делать при обходе контура.

Теперь перейдём к идее…

Допустим, у нас есть цифровой паттерн, т.е. группа чёрных пикселей на фоне из белых пикселей, т.е. на сетке; находим чёрный пиксель и объявляем его «начальным» пикселем. Искать «начальный» пиксель можно различными способами, например, изложенным выше.

Для нахождения начального пикселя пользоваться этим способом необязательно. Вместо этого мы выберем начальный пиксель, удовлетворяющий следующим ограничениям, накладываемым на выбор начального пикселя алгоритмом Павлидиса:

Важное ограничение направления, в котором мы входим в начальный пиксель

На самом деле можно выбрать ЛЮБОЙ чёрный граничный пиксель в качестве начального при таком условии: если вы изначально стоите на нём, левый соседний пиксель НЕ чёрный. Другими словами, нужно входить в начальный пиксель в таком направлении, чтобы левый соседний пиксель был белым («левый» здесь берётся относительно направления, в котором мы входим в начальный пиксель).

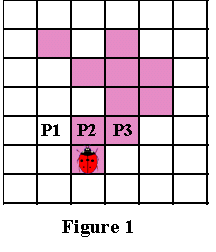
Теперь представим, что вы божья коровка, стоящая на начальном пикселе, как это показано на Рисунке 1 ниже. В процессе выполнения алгоритма нас будут интересовать только три пикселя, находящиеся перед вами, т.е. P1, P2 и P3, показанные на Рисунке 1. (Мы обозначим как P2 пиксель перед вами, P1 — это пиксель слева от P2, а P3 — пиксель справа от P2).

Как и в алгоритме трассировки квадратов, самое важное в алгоритме Павлидиса — это «чувство направления». Повороты влево и вправо выполняются относительно текущей позиции, которая зависит от того, как вы вошли в текущий пиксель. Следовательно, чтобы делать правильные ходы, важно отслеживать текущую ориентацию. Но как бы вы ни были расположены, пиксели P1, P2 и P3 определяются описанным выше образом.

Имея эту информацию, мы готовы к объяснению алгоритма…

Каждый раз, когда вы стоите на текущем граничном пикселе (который сначала является начальным пикселем), делаем следующее:

Во-первых, проверяем пиксель P1. Если P1 чёрный, тогда объявляем P1 текущим граничным пикселем и перемещаемся на один шаг вперёд, а затем делаем шаг влево, чтобы оказаться на P1 (порядок ходов очень важен).

На Рисунке 2 ниже показан этот случай. Путь, по которому нужно попасть в P1, показан синим.

И только если P1 белый, переходим к проверке P2…

Если P2 чёрный, то объявляем P2 текущим граничным пикселем и двигаемся на шаг вперёд, чтобы оказаться на P2. Этот случай показан на Рисунке 3 ниже. Путь, по которому нужно двигаться на P2, показан синим.

Только если и P1, и P2 белые, переходим к проверке P3…

Если P3 чёрный, то объявляем P3 текущим граничным пикселем и двигаемся на один шаг вправо, а затем на один шаг влево, как показано на Рисунке 4 ниже.

Вот и всё! Три простых правила для трёх простых случаев. Как видите, важно отслеживать своё направление при поворотах, потому что все ходы делаются относительно текущей ориентации. Но кажется, мы что-то забыли? Что если все три пикселя перед нами белые? Тогда мы поворачиваемся (стоя на текущем граничном пикселе) на 90 градусов по часовой стрелке, чтобы увидеть перед собой новый набор из трёх пикселей. Затем мы выполняем ту же проверку для этих новых пикселей. У вас может всё равно остаться вопрос: что если все эти три пикселя будут белыми?! Тогда снова поворачиваемся на 90 градусов по часовой стрелке, стоя на том же пикселе. Прежде чем проверить всю окрестность Мура пикселя, можно повернуться три раза (каждый раз на 90 градусов по часовой стрелке).

Если мы повернёмся три раза, так и не найдя чёрных пикселей, то это значит, что мы стоим на изолированном пикселе, не соединённом ни с каким другим чёрным пикселем. Именно поэтому алгоритм позволяет повернуться три раза, а потом завершает своё выполнение.

Ещё один аспект: Когда алгоритм завершает выполнение?

Алгоритм завершает работу в двух случаях:

a) как сказано выше. алгоритм позволяет повернуться три раза (каждый раз на 90 градусов по часовой стрелке), после его завершает выполнение и объявляет пиксель изолированным, ИЛИ

b) когда текущий граничный пиксель является начальным пикселем, алгоритм завершает выполнение, «объявляя», что обнаружил контур паттерна.

Алгоритм

Ниже представлено формальное описание алгоритма Павлидиса:

Входящие данные: квадратная тесселяция T, содержащая связную компоненту P чёрных ячеек.

Выходные данные: ряд B (b₁, b₂ ,…, b_k) граничных пикселей, т.е. контур.

Определения:

• Обозначим как p текущий граничный пиксель, т.е. пиксель, на котором мы стоим.
• Определим P1, P2 и P3 следующим образом: (см. также Рисунок 1 выше)
• P2 — это пиксель перед вами, соседний с тем, на котором вы стоите, т.е. с пикселем p.
• P1 — левый пиксель, соседний с P2.
• P3 — правый пиксель, соседний с P2.
• Определим «шаг» в заданном направлении как перемещение на расстояние одного пикселя в этом направлении.

Начало

• Задаём B как пустое множество.
• Сканируем ячейки T снизу вверх и слева направо, пока не будет найден чёрный начальный пиксель s из P (см. выше важное ограничение относительно направления, в котором мы попадаем в начальный пиксель)
• Вставляем s в B.
• Задаём текущий пиксель p в качестве начального пикселя s.
• Повторяем следующее:
  Если пиксель P1 чёрный
  • Вставляем P1 в B
  • Обновляем p=P1
  • Движемся на один шаг вперёд, а затем делаем шаг влево

  иначе если P2 чёрный

  • Вставляем P2 в B
  • Обновляем p=P2
  • Перемещаемся на один шаг вперёд (см. выше Рисунок 3)

  иначе если P3 чёрный

  • Вставляем P3 в B
  • Обновляем p=P3
  • Делаем один шаг вправо, обновляем позицию и перемещаемся влево (см. выше Рисунок 4)

  иначе если мы уже трижды повернулись на 90 градусов по часовой стрелке, находясь в одном пикселе p

  • завершаем выполнение программы и объявляем p изолированным пикселем

  иначе

  • поворачиваемся на 90 градусов по часовой стрелке, стоя на текущем пикселе p

  Пока p=s  (Завершаем цикл повтора)

Конец

Демонстрация

Ниже показана анимированная демонстрация того, как алгоритм Павлидиса обнаруживает контур заданного паттерна. Не забывайте, что мы ходим по пикселям; замечайте, как меняется ориентация при поворотах влево или вправо. Чтобы объяснить алгоритм как можно подробнее, мы включили в него все возможные случаи.

Анализ

Если вы считаете, что алгоритм Павлидиса идеален для обнаружения контуров паттернов, то вам стоит изменить своё мнение…

Этот алгоритм действительно немного сложнее, чем, допустим трассировка окрестностей Мура, в которой нет особых случаев, требующих отдельной обработки, однако ему не удастся определить контуры большого семейства паттернов, имеющее определённый вид связности.

Алгоритм очень хорошо работает на 4-связных паттернах. Его проблема возникает при трассировке некоторых 8-связных паттернов, не являющихся 4-связными. Ниже показана анимированная демонстрация того, как алгоритму Павлидиса не удаётся обнаружить правильный контур 8-связного паттерна (не являющегося 4-связным) — он пропускает большую часть границы.

Существует два простых способа изменения алгоритма для значительного улучшения его результативности.

a) Заменить критерий останова

Вместо того, чтобы завершать алгоритм, когда он посещает начальный пиксель во второй раз, можно завершать его, когда он посетит начальный пиксель в третий или даже четвёртый раз. Это улучшит общую результативность алгоритма.

ИЛИ

b) Добраться до источника проблемы, а именно, до выбора начального пикселя

Существует важное ограничение касательно направления, в котором выполняется вход в начальный пиксель. По сути, нужно войти в начальный пиксель так, чтобы когда ты стоишь на нём, пиксель слева от тебя является белым. Причина введения этого ограничения такова: поскольку мы всегда рассматриваем три пикселя перед нами в определённом порядке, в некоторых паттернах мы будем пропускать граничный пиксель, лежащий непосредственно слева от начального пикселя.

Мы рискуем пропустить не только левый соседний пиксель от начального пикселя, но и пиксель непосредственно под ним (как продемонстрировано в анализе). Кроме того, в некоторых паттернах будет пропущен пиксель, соответствующий пикселю R на Рисунке 5 ниже. Следовательно, мы предполагаем, что в начальный пиксель нужно попадать в таком направлении, чтобы пиксели, соответствующие пикселям L, W и R, показанным на Рисунке 5 ниже, были белыми.

В таком случае паттерны наподобие показанного в демонстрации будут обнаруживаться правильно и результативность алгоритма Павлидиса значительно улучшится. С другой стороны, поиск начального пикселя, удовлетворяющего таким требованиям, может быть сложной задачей, и во многих случаях такого пикселя найти будет невозможно. В этом случае следует использовать альтернативный способ улучшения алгоритма Павлидиса, а именно завершение алгоритма после посещения начальной точки в третий раз.

Canny Edge Detection — это термин, обозначающий границу объекта на изображении. Мы узнаем о нем, используя технику обнаружения краев OpenCV Canny Edge Detection.

Синтаксис

Синтаксис функции обнаружения краев:

 
edges = cv2.Canny('/path/to/img', minVal, maxVal, apertureSize, L2gradient) 

Параметры

• /path/to/img: путь к файлу изображения (обязательно);
• minVal: минимальный градиент интенсивности (обязательно);
• maxVal: максимальный градиент интенсивности (обязательно);
• aperture: это необязательный аргумент;
• L2gradient: его значение по умолчанию равно false. Если значение равно true, Canny() использует более затратное в вычислительном отношении уравнение для обнаружения ребер, что обеспечивает большую точность за счет ресурсов.

Пример 1

 
import cv2 
img = cv2.imread(r'C:UsersDEVANSH SHARMAcat_16x9.jpg') 
edges = cv2.Canny(img, 100, 200) 
 
cv2.imshow("Edge Detected Image", edges) 
cv2.imshow("Original Image", img) 
cv2.waitKey(0)  # waits until a key is pressed 
cv2.destroyAllWindows()  # destroys the window showing image 

Выход:

Пример: обнаружение границ в реальном времени

 
# import libraries of python OpenCV   
import cv2 
 
# import Numpy by alias name np 
import numpy as np 
 
# capture frames from a camera  
cap = cv2.VideoCapture(0) 
 
# loop runs if capturing has been initialized  
while(1): 
 
    # reads frames from a camera  
    ret, frame = cap.read() 
 
    # converting BGR to HSV  
    hsv = cv2.cvtColor(frame, cv2.COLOR_BGR2HSV) 
    # define range of red color in HSV  
    lower_red = np.array([30, 150, 50]) 
    upper_red = np.array([255, 255, 180]) 
 
    # create a red HSV colour boundary and   
    # threshold HSV image  
    mask = cv2.inRange(hsv, lower_red, upper_red) 
 
    # Bitwise-AND mask and original image  
    res = cv2.bitwise_and(frame, frame, mask=mask) 
 
    # Display an original image  
    cv2.imshow('Original', frame) 
 
    # discovers edges in the input image image and  
    # marks them in the output map edges  
    edges = cv2.Canny(frame, 100, 200) 
 
    # Display edges in a frame  
    cv2.imshow('Edges', edges) 
 
    # Wait for Esc key to stop  
    k = cv2.waitKey(5) & 0xFF 
    if k == 27: 
        break 
 
# Close the window  
cap.release() 
 
# De-allocate any associated memory usage  
cv2.destroyAllWindows() 

Выход:

Обнаружение края включает в себя множество математических методов, направленных на определение точек на цифровом изображении на у которого яркость изображения резко изменяется или, более формально, имеет неоднородности. Точки, в которых яркость изображения резко изменяется, обычно объединяются в набор изогнутых линейных сегментов, называемых краями. Та же проблема обнаружения разрывов в одномерных сигналах известна как обнаружение ступенек, а проблема обнаружения разрывов сигнала во времени известна как обнаружение изменений. Обнаружение краев — фундаментальный инструмент в обработке изображений, машинном зрении и компьютерном зрении, особенно в областях обнаружения признаков и извлечение признаков.

Содержание

• 1 Мотивации
• 2 Свойства кромки
• 3 Простая модель кромки
• 4 Почему это нетривиальная задача
• 5 Подходы
  • 5.1 Кэнни
  • 5.2 Другие методы первого порядка
  • 5.3 Установление пороговых значений и связывание
  • 5.4 Утончение кромок
  • 5.5 Подходы второго порядка
    • 5.5.1 Дифференциальный
  • 5.6 На основе фазового согласования
  • 5.7 На основе физики
  • 5.8 Субпиксель
• 6 См. Также
• 7 Ссылки
• 8 Дополнительная литература

Мотивации

Обнаружение резких краев применительно к фотографии

Цель обнаружения резких изменений в изображении Яркость предназначена для фиксации важных событий и изменений свойств мира. Можно показать, что при довольно общих предположениях для модели формирования изображения неоднородности яркости изображения, вероятно, будут соответствовать:

• разрывам по глубине,
• разрывам ориентации поверхности,
• изменениям в свойствах материала и
• вариациях освещения сцены.

В идеальном случае результат применения детектора края к изображению может привести к набору соединенных кривых, которые указывают границы объектов, границы маркировок на поверхности, а также кривых, соответствующих неоднородностям ориентации поверхности. Таким образом, применение алгоритма обнаружения краев к изображению может значительно уменьшить объем данных, подлежащих обработке, и, следовательно, может отфильтровать информацию, которая может рассматриваться как менее актуальная, при сохранении важных структурных свойств изображения. Таким образом, если этап обнаружения краев успешен, последующая задача интерпретации информационного содержания исходного изображения может быть существенно упрощена. Однако не всегда удается получить такие идеальные края из реальных изображений средней сложности.

Края, извлеченные из нетривиальных изображений, часто страдают из-за фрагментации, что означает, что краевые кривые не связаны, отсутствуют краевые сегменты, а также ложные края, не соответствующие интересным явлениям на изображении, что усложняет последующую задачу интерпретации данных изображения.

Обнаружение края является одним из основных этапов обработки изображения, анализа изображения, распознавания образов изображения и методов компьютерного зрения.

Свойства краев

Края, извлеченные из двумерного изображения трехмерной сцены, могут быть классифицированы как зависящие от точки обзора или независимые от точки обзора. Край, не зависящий от точки обзора, обычно отражает присущие трехмерным объектам свойства, такие как маркировка поверхности и форма поверхности. Край, зависимый от точки обзора, может изменяться при изменении точки обзора и обычно отражает геометрию сцены, например, объекты, перекрывающие друг друга.

Типичный край может быть, например, границей между блоком красного цвета и блоком желтого цвета. Напротив, линия line (как может быть извлечена детектором гребня ) может представлять собой небольшое количество пикселей другого цвета на в остальном неизменный фон. Поэтому для линии обычно может быть по одному краю с каждой стороны линии.

Простая модель кромки

Хотя в определенной литературе рассматривается обнаружение идеальных кромок ступенек, кромки, полученные из естественных изображений, обычно вовсе не являются идеальными кромками ступенек. Вместо этого они обычно подвержены одному или нескольким из следующих эффектов:

• размытие фокуса, вызванное конечной глубиной резкости и конечной функцией размытия точки .
• полутеневым размытием вызванные тенями, создаваемыми источниками света ненулевого радиуса.
• затенение на гладком объекте

Ряд исследователей использовали сглаженный по Гауссу край ступени (функция ошибок) как простейшее расширение идеального ступенчатая модель края для моделирования эффектов размытия краев в практических приложениях. Таким образом, одномерное изображение f { displaystyle f}, у которого ровно один край находится в точке x = 0 { displaystyle x = 0}, может быть моделируется как:

f (x) = I r — I ℓ 2 (erf ⁡ (x 2 σ) + 1) + I ℓ. { displaystyle f (x) = { frac {I_ {r} -I _ { ell}} {2}} left ( operatorname {erf} left ({ frac {x} {{ sqrt {2 }} sigma}} right) +1 right) + I _ { ell}.}

Слева от края интенсивность I ℓ = lim x → — ∞ f (x) { displaystyle I _ { ell} = lim _ {x rightarrow — infty} f (x)}, а справа от края это I r = lim x → ∞ е (Икс) { Displaystyle I_ {г} = lim _ {х rightarrow infty} f (x)}. Параметр масштаба σ { displaystyle sigma}называется масштабом размытия края. В идеале этот масштабный параметр следует регулировать в зависимости от качества изображения, чтобы избежать разрушения истинных краев изображения.

Почему это нетривиальная задача

Чтобы проиллюстрировать, почему обнаружение краев не является Тривиальная задача, рассмотрим задачу обнаружения ребер в следующем одномерном сигнале. Здесь мы можем интуитивно сказать, что должна быть граница между 4-м и 5-м пикселями.

Если бы разница в яркости была меньше между 4-м и 5-м пикселями и если бы разница в яркости между соседними соседними пикселями была больше, она бы не Так же легко сказать, что в соответствующей области должен быть край. Более того, можно утверждать, что в этом случае имеется несколько ребер.

Следовательно, чтобы твердо установить конкретный порог того, насколько большим должно быть изменение интенсивности между двумя соседними пикселями Сказать, что между этими пикселями должна быть граница, не всегда просто. Действительно, это одна из причин, по которой обнаружение краев может быть нетривиальной проблемой, если только объекты в сцене не являются особенно простыми и условиями освещения можно хорошо управлять (см., Например, края, извлеченные из изображения с девушкой выше.).

Подходы

Существует множество методов обнаружения границ, но большинство из них можно сгруппировать в две категории: на основе поиска и на основе перехода через ноль. Основанные на поиске методы обнаруживают края, сначала вычисляя меру силы края, обычно выражение производной первого порядка, такое как величина градиента, а затем ищут локальные направленные максимумы величины градиента с использованием вычисленной оценки локальной ориентации края, обычно в направлении градиента. Методы на основе пересечения нуля ищут пересечения нуля в выражении производной второго порядка, вычисленном на основе изображения, чтобы найти края, обычно пересечения нуля лапласиана или нулевого -кроссинг нелинейного дифференциального выражения. В качестве этапа предварительной обработки для обнаружения границ почти всегда применяется этап сглаживания, обычно сглаживание по Гауссу (см. Также шумоподавление ).

Опубликованные методы обнаружения краев в основном различаются типами применяемых сглаживающих фильтров и способом вычисления показателей силы края. Поскольку многие методы обнаружения краев основаны на вычислении градиентов изображения, они также различаются типами фильтров, используемых для вычисления оценок градиента в направлениях x и y.

Обзор ряда различных методов обнаружения краев можно найти в (Ziou and Tabbone 1998); см. также статьи энциклопедии об обнаружении краев в Энциклопедии математики и Энциклопедии компьютерных наук и инженерии.

Кэнни

Джон Кэнни рассмотрел математическую проблему получения оптимального сглаживающего фильтра с учетом критериев обнаружения, локализация и минимизация множественных откликов на одном ребре. Он показал, что оптимальный фильтр с учетом этих предположений представляет собой сумму четырех экспоненциальных членов. Он также показал, что этот фильтр хорошо аппроксимируется производными первого порядка от гауссианов. Кэнни также ввел понятие не максимального подавления, что означает, что с учетом фильтров предварительного сглаживания краевые точки определяются как точки, в которых величина градиента принимает локальный максимум в направлении градиента. Поиск пересечения нуля второй производной вдоль направления градиента был впервые предложен Хараликом. Менее чем за два десятилетия потребовалось найти современное геометрическое вариационное значение этого оператора, которое связывает его с детектором границ Марра – Хилдрета (пересечение нуля лапласиана). Это наблюдение было представлено Роном Киммелем и.

Хотя его работа была проделана на заре компьютерного зрения, детектор края Canny (включая его варианты) является по-прежнему современный детектор кромок. Детекторы фронтов, которые работают лучше, чем Canny, обычно требуют большего времени вычислений или большего количества параметров.

Детектор Кэнни-Дерише был получен на основе тех же математических критериев, что и детектор края Кэнни, хотя начинался с дискретной точки обзора и затем приводил к набору рекурсивных фильтров для сглаживания изображения вместо фильтров Гаусса.

Описанный ниже дифференциальный детектор края может рассматриваться как переформулировка метода Кэнни с точки зрения дифференциальных инвариантов, вычисленных из представления пространства масштаба, что дает ряд преимуществ в терминах теоретического анализа и субпиксельной реализации. В этом аспекте было показано, что фильтр Лог Габора является хорошим выбором для извлечения границ в естественных сценах.

Другие методы первого порядка

Можно использовать различные операторы градиента. применяется для оценки градиентов изображения из входного изображения или его сглаженной версии. Самый простой подход — использовать центральные разности:

L x (x, y) = — 1 2 L (x — 1, y) + 0 ⋅ L (x, y) + 1 2 ⋅ L (x + 1, y) L Y (x, y) = — 1 2 L (x, y — 1) + 0 ⋅ L (x, y) + 1 2 ⋅ L (x, y + 1), { displaystyle { begin { выровнено} L_ {x} (x, y) = — { frac {1} {2}} L (x-1, y) +0 cdot L (x, y) + { frac {1} { 2}} cdot L (x + 1, y) \ [8pt] L_ {y} (x, y) = — { frac {1} {2}} L (x, y-1) +0 cdot L (x, y) + { frac {1} {2}} cdot L (x, y + 1), end {align}}}

, соответствующий применению следующих масок фильтра к данные изображения:

L x = [+ 1/2 0 — 1/2] L и L y = [+ 1/2 0 — 1/2] L. { Displaystyle L_ {x} = { begin {bmatrix} + 1/2 0 -1 / 2 end {bmatrix}} L quad { text {and}} quad L_ {y} = { begin {bmatrix } +1/2 \ 0 \ — 1/2 end {bmatrix}} L.}

Хорошо известный и более ранний оператор Собеля основан на следующих фильтрах:

L x = [+ 1 0 — 1 + 2 0 — 2 + 1 0 — 1] L и L y = [+ 1 + 2 + 1 0 0 0 — 1 — 2 — 1] L. { displaystyle L_ {x} = { begin {bmatrix} + 1 0 -1 \ + 2 0 -2 \ + 1 0 -1 end {bmatrix}} L quad { text {and}} quad L_ { y} = { begin {bmatrix} + 1 + 2 + 1 \ 0 0 0 \ — 1 -2 -1 end {bmatrix}} L.}

Учитывая такие оценки производных изображений первого порядка, величина градиента затем вычисляется как:

| ∇ L | = L x 2 + L y 2 { displaystyle | nabla L | = { sqrt {L_ {x} ^ {2} + L_ {y} ^ {2}}}}

, а ориентация градиента может быть оценивается как

θ = atan2 ⁡ (L y, L x). { displaystyle theta = operatorname {atan2} (L_ {y}, L_ {x}).}

Другие операторы разности первого порядка для оценки градиента изображения были предложены в операторе Prewitt, Робертс кросс, Кайяли оператор и.

Можно расширить размерность фильтров, чтобы избежать проблемы распознавания края в изображении с низким SNR. Стоимость этой операции — потеря разрешения. Примеры: Extended Prewitt 7×7.

Установление пороговых значений и связывание

После того, как мы вычислили меру силы кромок (обычно величину градиента), следующим этапом является применение порога, чтобы решить, присутствуют ли кромки или нет в точка изображения. Чем ниже порог, тем больше краев будет обнаружено, и результат будет все более восприимчивым к шуму и обнаружению краев нерелевантных элементов изображения. И наоборот, высокий порог может привести к пропуску тонких краев или к фрагментированным краям.

Если край применяется только к изображению с градиентной величиной, результирующие края обычно будут толстыми, и потребуется постобработка некоторого типа утончения краев. Однако для краев, обнаруженных не с максимальным подавлением, краевые кривые тонкие по определению, и краевые пиксели могут быть связаны в краевой многоугольник с помощью процедуры связывания краев (отслеживания краев). На дискретной сетке этап подавления без максимума может быть реализован путем оценки направления градиента с использованием производных первого порядка, затем округления направления градиента до кратных 45 градусов и, наконец, сравнения значений величины градиента в оцененном градиенте. направление.

Обычно используемый подход к решению проблемы соответствующих пороговых значений для пороговой обработки заключается в использовании пороговой обработки с гистерезисом. Этот метод использует несколько пороговых значений для поиска краев. Мы начинаем с использования верхнего порога, чтобы найти начало ребра. Когда у нас есть начальная точка, мы затем отслеживаем путь края через изображение пиксель за пикселем, отмечая край всякий раз, когда мы превышаем нижний порог. Мы перестаем отмечать край только тогда, когда значение падает ниже нашего нижнего порога. Этот подход делает предположение, что края, вероятно, будут в виде непрерывных кривых, и позволяет нам проследить слабый участок края, который мы видели ранее, не имея в виду, что каждый зашумленный пиксель в изображении отмечен как край. Тем не менее, у нас есть проблема выбора подходящих параметров пороговой обработки, и подходящие значения пороговой обработки могут варьироваться в зависимости от изображения.

Утончение краев

Утончение краев — это метод, используемый для удаления нежелательных ложных точек на краях изображения. Этот метод используется после того, как изображение было отфильтровано на наличие шума (с использованием медианы, фильтра Гаусса и т. Д.), Был применен оператор края (например, описанные выше, canny или sobel) для обнаружения краев и после того, как края были сглажены. используя соответствующее пороговое значение. Это удаляет все нежелательные точки и, если применяется аккуратно, приводит к краевым элементам толщиной в один пиксель.

Преимущества:

1. Четкие и тонкие края приводят к большей эффективности распознавания объектов.
2. Если преобразования Хафа используются для обнаружения линий и эллипсов, тогда утонение может дать гораздо лучшие результаты.
3. Если край оказывается границей области, то утончение может легко дать параметры изображения, такие как периметр, без особой алгебры.

Для этого используется много популярных алгоритмов, один это описано ниже:

1. Выберите тип подключения, например 8, 6 или 4.
2. Предпочтительно подключение 8, когда учитываются все непосредственные пиксели, окружающие конкретный пиксель.
3. Удалите точки с севера, юга, востока и запада.
4. Делайте это за несколько проходов, т.е. после северного прохода используйте одно и то же полуобработанное изображение на других проходах и т. Д.
5. Удалить точка, если:. Точка не имеет соседей на севере (если вы находитесь на северном проходе и соответствующих направлениях для других проходов).. Точка не является концом линии.. Точка изолирована.. Удаление точек никоим образом не приведет к отключению ее соседей.
6. В противном случае оставьте точку.

Количество проходов в направлении следует выбирать в соответствии с уровнем желаемой точности.

Подходы второго порядка

Вместо этого некоторые операторы обнаружения края основаны на производных второго порядка интенсивности. Это по существу отражает скорость изменения градиента интенсивности. Таким образом, в идеальном непрерывном случае обнаружение переходов через нуль во второй производной фиксирует локальные максимумы градиента.

Ранний оператор Марра – Хилдрета основан на обнаружении нулевых переходов оператора Лапласа, применяемого к сглаженному по Гауссу изображению. Однако можно показать, что этот оператор также возвращает ложные края, соответствующие локальным минимумам величины градиента. Более того, этот оператор даст плохую локализацию на изогнутых краях. Следовательно, этот оператор сегодня представляет в основном исторический интерес.

Дифференциальный

Более усовершенствованный подход к обнаружению границ второго порядка, который автоматически обнаруживает края с точностью до субпикселей, использует следующий дифференциальный подход обнаружения переходов через нуль производной второго порядка по направлению в направление градиента:

Следуя дифференциально-геометрическому способу выражения требования не максимального подавления, предложенному Линдебергом, давайте введем в каждой точке изображения локальную систему координат (u, v) { displaystyle (u, v)}с направлением v { displaystyle v}, параллельным направлению градиента. Предполагая, что изображение было предварительно сглажено с помощью сглаживания по Гауссу и представления в пространстве масштаба L (x, y; t) { displaystyle L (x, y; t)}в масштабе t { displaystyle t}был вычислен, мы можем потребовать, чтобы величина градиента представления пространства шкалы была равна первому порядку производная по направлению в v { displaystyle v}-направлении L v { displaystyle L_ {v}}, должна иметь производную по направлению первого порядка в v { displaystyle v}-направление, равное нулю

∂ v (L v) = 0 { displaystyle partial _ {v} (L_ {v}) = 0}

, а производная второго порядка в v { displaystyle v}-направлении L v { displaystyle L_ {v}}должна быть отрицательное, т. е.

∂ vv (L v) ≤ 0. { displaystyle partial _ {vv} (L_ {v}) leq 0.}

Записывается как явное выражение в терминах локального частичного производные L x, L y,…, L yyy { displaystyle L_ {x}, L_ {y}, ldots, L_ {yyy}}, это определение ребра можно выразить как кривые перехода через нуль дифференциального инварианта

L v 2 L vv Знак равно L Икс 2 L ХХ + 2 L Икс L Y L ху + L Y 2 L YY = 0, { Displaystyle L_ {v} ^ {2} L_ {vv} = L_ {x} ^ {2} , L_ {xx} +2 , L_ {x} , L_ {y} , L_ {xy} + L_ {y} ^ {2} , L_ {yy} = 0,}

, которые удовлетворяют знаку — условие на следующий дифференциальный инвариант

L v 3 L vvv = L x 3 L xxx + 3 L x 2 L y L xxy + 3 L x L y 2 L xyy + L y 3 L yyy ≤ 0 { displaystyle L_ {v} ^ {3} L_ {vvv} = L_ {x} ^ {3} , L_ {xxx} +3 , L_ {x} ^ {2} , L_ {y} , L_ {xxy} +3 , L_ {x} , L_ {y} ^ {2} , L_ {xyy} + L_ {y} ^ {3} , L_ {yyy} leq 0}где L x, L y,…, L yyy { displaystyle L_ {x}, L_ {y}, ldots, L_ {yyy}}

обозначают частные производные, вычисленные из представления масштабного пространства L { displaystyle L}, полученное путем сглаживания исходного изображения с помощью ядра Гаусса. Таким образом, края будут автоматически получены как непрерывные кривые с субпиксельной точностью. К этим дифференциальным и субпиксельным краевым сегментам также может применяться пороговая обработка гистерезиса.

На практике приближения производной первого порядка могут быть вычислены по центральным разностям, как описано выше, в то время как производные второго порядка могут быть вычислены из представления масштабного пространства L { displaystyle L}согласно:

L xx (x, y) = L (x — 1, y) — 2 L (x, y) + L (x + 1, y), L xy (x, y) = 1 4 (L (x — 1, y — 1) — L (x — 1, y + 1) — L (x + 1, y — 1) + L (x + 1, y + 1)), L yy (x, y) = L (x, y — 1) — 2 L (x, y) + L (x, y + 1). { Displaystyle { begin {align} L_ {xx} (x, y) = L (x-1, y) -2L (x, y) + L (x + 1, y), \ [6pt] L_ {xy} (x, y) = { frac {1} {4}} (L (x-1, y-1) -L (x-1, y + 1) -L (x + 1, y-1) + L (x + 1, y + 1)), \ [6pt] L_ {yy} (x, y) = L (x, y-1) -2L (x, y) + L (x, y + 1). end {align}}}

соответствует следующим маскам фильтра:

L xx = [1-2 1] L и L xy = [- 1/4 0 1 / 4 0 0 0 1/4 0 — 1/4] L и L yy = [1 — 2 1] L. { displaystyle L_ {xx} = { begin {bmatrix} 1 -2 1 end {bmatrix}} L quad { text {and}} quad L_ {xy} = { begin {bmatrix} -1 / 4 0 1 / 4 \ 0 0 0 \ 1/4 0 -1 / 4 end {bmatrix}} L quad { text {and}} quad L_ {yy} = { begin {bmatrix} 1 \ — 2 \ 1 end {bmatrix}} L.}

Производные высшего порядка для знакового условия третьего порядка могут быть получены аналогичным образом.

На основе фазового согласования

Последние разработки в методах обнаружения краев используют подход частотной области для поиска местоположений краев. Фазовая конгруэнтность (также известная как фазовая когерентность) пытается найти места на изображении, где все синусоиды в частотной области находятся в фазе. Эти местоположения обычно будут соответствовать местоположению воспринимаемого края, независимо от того, представлен ли край большим изменением интенсивности в пространственной области. Ключевым преимуществом этого метода является то, что он хорошо реагирует на полосы Маха и позволяет избежать ложных срабатываний, которые обычно встречаются вокруг. Кромка крыши — это прерывность первого порядка, производная от профиля уровня серого.

На основе физики

Улучшение характеристик изображения (Собор Святого Павла, Лондон) с использованием Преобразование фазового растяжения (PST). На левой панели показано исходное изображение, а на правой панели показаны обнаруженные особенности с использованием PST.

преобразование фазового растяжения или PST — это основанный на физике вычислительный подход к обработке сигналов и изображений. Одна из его утилит предназначена для обнаружения и классификации признаков. PST является побочным продуктом исследования дисперсионного преобразования Фурье во времени. PST преобразует изображение, имитируя распространение через дифракционную среду со спроектированным 3D-дисперсионным свойством (показателем преломления). Работа основана на симметрии профиля дисперсии и может быть понята в терминах дисперсионных собственных функций или мод растяжения. PST выполняет те же функции, что и фазово-контрастная микроскопия, но для цифровых изображений. PST также применим к цифровым изображениям, а также к временным данным, временным рядам.

Субпиксель

Для повышения точности обнаружения границ было предложено несколько методов субпикселей, в том числе методы аппроксимации кривой, основанные на моменте, методы реконструкции и эффекты частичной площади. Эти методы имеют разные характеристики. Методы аппроксимации кривых просты в вычислительном отношении, но на них легко влияет шум. Моментные методы используют подход, основанный на интегралах, для уменьшения эффекта шума, но в некоторых случаях могут потребоваться дополнительные вычисления. Реконструктивные методы используют горизонтальные градиенты или вертикальные градиенты, чтобы построить кривую и найти пик кривой как край субпикселя. Методы эффекта частичной площади основаны на гипотезе о том, что значение каждого пикселя зависит от площади по обе стороны от края внутри этого пикселя, что дает точную индивидуальную оценку для каждого пикселя края. Было показано, что некоторые варианты метода, основанного на моментах, являются наиболее точными для изолированных краев.

Обнаружение краев на ангиографическом изображении. Слева обнаружение краев выполняется на уровне пикселей. Справа: обнаружение края субпикселя точно определяет край внутри пикселя

См. Также

• Свертка # Приложения
• Обнаружение признаков (компьютерное зрение) для других детекторов низкоуровневых признаков
• Производные изображения
• Фильтр Габора
• Уменьшение шума изображения
• Оператор Кирша для обнаружения кромок в направлениях компаса
• Обнаружение гребней для взаимосвязи между детекторами кромок и детекторами гребней
• Фильтр Лог Габора
• Преобразование растяжения фазы

Литература

1. ^Умбау, Скотт Э (2010). Цифровая обработка и анализ изображений: приложения человеческого и компьютерного зрения с CVIPtools (2-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4398-0205-2 .
2. ^H.G. Барроу и Дж. М. Тененбаум (1981) «Интерпретация линейных рисунков как трехмерных поверхностей», Искусственный интеллект, том 17, выпуски 1–3, страницы 75–116.
3. ^ Линдеберг, Тони (2001) [1994], Энциклопедия математики, EMS Press
4. ^ T. Линдеберг (1998) «Обнаружение краев и обнаружение выступов с автоматическим выбором шкалы», Международный журнал компьютерного зрения, 30, 2, страницы 117–154.
5. ^W. Чжан и Ф. Бергхольм (1997) «Оценка многомасштабного размытия и классификация типов краев для анализа сцены «, Международный журнал компьютерного зрения, том 24, выпуск 3, страницы: 219–250.
6. ^Д. Зиу и С. Таббоун (1998) «Методы обнаружения краев: обзор », Международный журнал распознавания образов и анализа изображений, 8 (4): 537–559, 1998
7. ^J. М. Парк и Я. Лу (2008) «Обнаружение краев в полутоновых, цветных и дальних изображениях», в Энциклопедии информатики и инженерии Б. В. Ва (редактор), doi 10.1002 / 9780470050118.ecse603
8. ^J. Кэнни (1986) «Вычислительный подход к обнаружению границ », IEEE Transactions on Pattern Analysis and Machine Intelligence, vol 8, pages 679–714.
9. ^Р. Харалик, (1984) «Цифровые ступеньки от пересечения нуля производных второго направления », IEEE Transactions on Pattern Analysis and Machine Intelligence, 6 (1): 58–68.
10. ^Р. Киммел и А. Bruckstein (2003) «О регуляризованных лапласовских пересечениях нуля и других оптимальных краевых интеграторах», Международный журнал компьютерного зрения, 53 (3) страницы 225–243.
11. ^Шапиро Л. Г. и Стокман Г. С. (2001) Компьютерное зрение. Лондон и др.: Прентис Холл, стр. 326.
12. ^Р. Deriche (1987) Использование критериев Кэнни для получения рекурсивно реализованного оптимального детектора края, Int. J. Computer Vision, том 1, страницы 167–187.
13. ^Сильвен Фишер, Рафаэль Редондо, Лоран Перрине, Габриэль Кристобаль. Скудная аппроксимация изображений, вдохновленная функциональной архитектурой основных визуальных областей. Журнал EURASIP о достижениях в обработке сигналов, специальный выпуск о восприятии изображений, 2007 г.
14. ^Dim, Jules R.; Такамура, Тамио (11 декабря 2013 г.). «Альтернативный подход к классификации спутникового облака: приложение с граничным градиентом». Успехи в метеорологии. 2013 : 1–8. DOI : 10.1155 / 2013/584816. ISSN 1687-9309.
15. ^Т. Линдеберг (1993) «Аппроксимации дискретной производной со свойствами масштабного пространства: основа для низкоуровневого выделения признаков», J. of Mathematical Imaging and Vision, 3 (4), страницы 349–376.
16. ^T. Pajdla и V. Hlavac (1993) «Поверхностные неоднородности в изображениях диапазона » в Proc IEEE 4th Int. Конф. Comput. Видение, стр. 524–528.
17. ^М. Х. Асгари и Б. Джалали, «Обнаружение краев цифровых изображений с использованием дисперсионного фазового растяжения», Международный журнал биомедицинской визуализации, Vol. 2015 г., ID статьи 687819, стр. 1–6 (2015).
18. ^М. Х. Асгари и Б. Джалали, «Обнаружение краев изображения на основе физики «, Глобальный симпозиум по обработке сигналов и информации IEEE (GlobalSIP 2014), статья: WdBD-L.1, Атланта, декабрь 2014 г.
19. ^Б. Джалали и А. Махджубфар, «Настройка широкополосных сигналов с помощью фотонного аппаратного ускорителя «, Труды IEEE, Vol. 2015. Т. 103, № 7. С. 1071–1086.
20. ^Ghosal, S.; Мехрота, Р. (1993-01-01). «Операторы ортогонального момента для обнаружения субпиксельного края». Распознавание образов. 26 (2): 295–306. doi : 10.1016 / 0031-3203 (93) 90038-X.
21. ^ Кристиан, Джон (2017-01-01). «Точная локализация планетарных конечностей для навигации космических аппаратов на основе изображений». Журнал космических аппаратов и ракет. 54 (3): 708–730. Bibcode : 2017JSpRo..54..708C. doi : 10.2514 / 1.A33692.
22. ^Трухильо-Пино, Агустин; Криссиан, Карл; Алеман-Флорес, Мигель; Сантана-Седрес, Даниэль (1 января 2013 г.). «Точное расположение края субпикселя на основе эффекта частичной площади». Вычисления изображений и зрения. 31 (1): 72–90. doi : 10.1016 / j.imavis.2012.10.005. hdl : 10553/43474.

Дополнительная литература

• Линдеберг, Тони (2001) [1994], Энциклопедия математики, EMS Press
• Запись об обнаружении краев в Энциклопедии компьютерных наук и инженерии
• Обнаружение краев с использованием FPGA
• Обнаружение линейных сегментов A-contrario с помощью кода и онлайн-демонстрация
• Обнаружение краев с использованием MATLAB
• Определение границ субпикселей с использованием Matlab

С точки зрения
распознавания и анализа объектов на
изображении наиболее информативными
являются не значения яркостей объектов,
а характеристики их границ – контуров.
Другими словами, основная информация
заключена не в яркости отдельных
областей, а в их очертаниях. Задача
выделения контуров состоит в построении
изображения именно границ объектов и
очертаний однородных областей.

Как правило, граница
предмета на фотографии отображается
перепадом яркости между двумя сравнительно
однотонными областями. Но перепад
яркости может быть вызван также текстурой
предмета, тенями, бликами, перепадами
освещенности, и т.п.

Будем называть
контуром изображения совокупность его
пикселов, в окрестности которых
наблюдается скачкообразное изменение
функции яркости. Так как при цифровой
обработке изображение представлено
как функция целочисленных аргументов,
то контуры представляются линиями
шириной, как минимум, в один пиксел. Если
исходное изображение, кроме областей
постоянной яркости, содержит участки
с плавно меняющейся яркостью, то
непрерывность контурных линий не
гарантируется. С другой стороны, если
на “кусочно-постоянном” изображении
присутствует шум, то могут быть обнаружены
“лишние” контуры в точках, которые не
являются границами областей.

При разработке
алгоритмов выделения контуров нужно
учитывать указанные особенности
поведения контурных линий. Специальная
дополнительная обработка выделенных
контуров позволяет устранять разрывы
и подавлять ложные контурные линии.

Процедура построения
бинарного изображения границ объектов
обычно складывается из двух последовательных
операций: выделения контуров и их
пороговой обработки.

Исходное изображение
подвергается линейной или нелинейной
обработке, с реакцией на перепады
яркости. В результате этой операции
формируется изображение, функция яркости
которого существенно отличается от
нуля только в областях резких изменений
яркости изображения. Пороговой обработкой
из этого изображения формируется
контурный объект. Выбор порога на втором
этапе должен производиться из следующих
соображений. При слишком высоком пороге
могут появиться разрывы контуров, а
слабые перепады яркости не будут
обнаружены. При слишком низком пороге
из-за шумов и неоднородности областей
могут появиться ложные контуры.

Поиск границ на
основе градиента.
Одним из наиболее простых способов
выделения границ является пространственное
дифференцирование функции яркости. Для
двумерной функции яркости A(x,
y) перепады в направлениях x и y регистрируются
частными производными 𝝏A(x,
y)/𝝏x
и 𝝏A(x,
y)/𝝏y,
которые пропорциональны скоростям
изменения яркости в соответствующих
направлениях.

Рис. 18.2.1.

Выделение перепадов
яркости иллюстрирует рис. 18.2.1. На нем
можно видеть, что подчеркивание контуров,
перпендикулярных к оси x, обеспечивает
производная 𝝏A(x,
y)/𝝏x
(рис. б), а подчеркивание контуров,
перпендикулярных к оси y, – 𝝏A(x,
y)/𝝏y
(рис. в).

В практических
задачах требуется выделять контуры,
направление которых является произвольным.
Для этих целей можно использовать модуль
градиента функции яркости

|A(x,
y)| =_,

который пропорционален
максимальной (по направлению) скорости
изменения функции яркости в данной
точке и не зависит от направления
контура. Модуль градиента в отличие от
частных производных принимает только
неотрицательные значения, поэтому на
получающемся изображении (рис. г) точки,
соответствующие контурам, имеют
повышенный уровень яркости.

Для цифровых
изображений аналогами частных производных
и модуля градиента являются разностные
функции.

Практический
пример выделения границ на фотоизображении
приведен на рис. 18.2.2. Исходное изображение
(1) является однотонным. На изображении
(2) представлен результат вычисления
вектора градиента яркости Аx,
y)
= (𝝏A/𝝏x,
𝝏A/𝝏y).
Как видно на рисунке, в точках большого
перепада яркости градиент имеет большую
длину. Отфильтровав пиксели с длиной
градиента, большей определенного порога
,
мы получим изображение границ (3).

Рис. 18.2.2.

Недостаток алгоритма —
пропуск границы с малыми перепадами
яркости и включение в число границ
деталей изображения с большими изменениями
яркости (шкурка бурундука). При зашумлении
изображения карту граничных точек будут
загрязнять и просто шум, поскольку не
учитывается, что граничные точки
соответствуют не просто перепадам
яркости, а перепадам яркости между
относительно монотонными областями.

Для снижения
влияния данного недостатка изображение
сначала подвергают сглаживающей
гауссовской фильтрации. При сглаживающей
фильтрации мелкие несущественные детали
размываются быстрее перепадов между
областями. Результат операции можно
видеть на изображении (4). Однако при
этом четко выраженные границы расплываются
в жирные линии.

Градиент яркости
в каждой точке характеризуется длиной
и направлением. Выше при поиске граничных
точек использовалась только длина
вектора. Направление градиента — это
направление максимального возрастания
функции, что позволяет использовать
процедуру подавления немаксимумов. При
этой процедуре для каждой точки
рассматривается отрезок длиной в
несколько пикселей, ориентированный
по направлению градиента и с центром в
рассматриваемом пикселе. Пиксель
считается максимальным тогда и только
тогда, когда длина градиента в нем
максимальна среди всех длин градиентов
пикселей отрезка. Граничными можно
признать все максимальные пиксели с
длинами градиента больше определенного
порога. Градиент яркости в каждой точке
перпендикулярен границе, поэтому после
подавления немаксимумов жирных линий
не остается. На каждом перпендикулярном
сечении жирной линии останется один
пиксель с максимальной длиной градиента.

Перпендикулярность
градиента яркости к границе может быть
использована для прослеживания границы,
начиная с некоторого граничного пикселя.
Такое прослеживание используется в
гистерезисной фильтрации максимальных
пикселей. Идея гистерезисной фильтрации
заключается в том, что длинный устойчивый
граничный контур, скорее всего, содержит
в себе пиксели с особенно большим
перепадом яркости, и, начиная с такого
пикселя, контур можно проследить,
переходя по граничным пикселям с меньшим
перепадом яркости.

Рис. 18.2.3.

При проведении гистерезисной
фильтрации вводят не одно, а два пороговых
значения. Меньшее ()
соответствует минимальной длине
градиента, при которой пиксель может
быть признан граничным. Большее (),
соответствует минимальной длине
градиента, при которой пиксель может
инициализировать контур. После того
как контур инициализируется в максимальном
пикселе P с
длиной градиента, большей ,
рассматриваются каждый соседний с ним
максимальный пиксель Q.
Если пиксель Q
имеет длину градиента, большую ,
и угол между векторами PQ
и (P)
близок к 90^o,
то P
добавляется к контуру, и процесс
рекурсивно переходит к Q. Его результат
для исходного изображения на рис. 18.2.2
показан на
рис. 18.2.3.

Таким образом,
алгоритм нахождения границ на основе
градиента заключается в последовательном
применении следующих операций:

— гауссовская
сглаживающая фильтрация;

— нахождение
градиента яркости в каждом пикселе;

— нахождение
максимальных пикселей;

— гистерезисная
фильтрация максимальных пикселей.

Этот алгоритм
носит названия алгоритма Кэнни и наиболее
часто применяется для нахождения границ.

Поиск границ на
основе лапласиана.
Известно, что необходимым и достаточным
условием экстремального значения первой
производной функции в произвольной
точке является равенство нулю второй
производной в этой точке, причем вторая
производная должна иметь разные знаки
по разные стороны от точки.

В двумерном варианте
аналогом второй производной является
лапласиан — скалярный оператор ^f)
= (𝝏²f/𝝏x
+ 𝝏²f/𝝏y).

Рис. 18.2.3.

Нахождение границ на
изображении с использованием лапласиана
может производиться по аналогии с
одномерным случаем: граничными признаются
точки, в которых лапласиан равен нулю
и вокруг которых он имеет разные знаки.
Оценка лапласиана при помощи линейной
фильтрации также предваряется гауссовской
сглаживающей фильтрацией, чтобы снизить
чувствительность алгоритма к шуму.
Гауссовское сглаживание и поиск
лапласиана можно осуществить одновременно,
поэтому нахождение границ при помощи
такого фильтра производится быстрее,
чем при помощи алгоритма Кэнни. Фильтр
применяется в системах, где имеет
значение и качество результата (обычно
уступает алгоритму Кэнни), и быстродействие.
Чтобы уменьшить чувствительность к
несущественным деталям, из числа
граничных точек также можно исключить
те, длина градиента в которых меньше
определенного порога (рис.
18.2.3).

Main Content

I = imread('coins.png');
imshow(I)

BW1 = edge(I,'sobel');
BW2 = edge(I,'canny');

tiledlayout(1,2)

nexttile
imshow(BW1)
title('Sobel Filter')

nexttile
imshow(BW2)
title('Canny Filter')