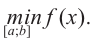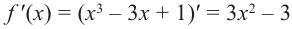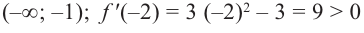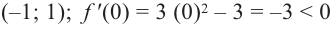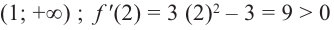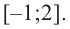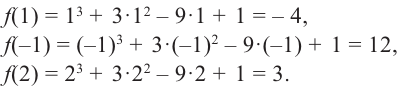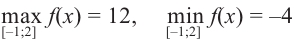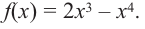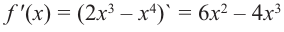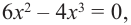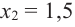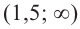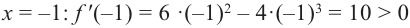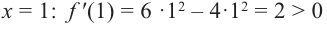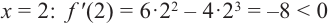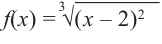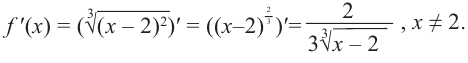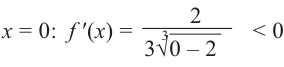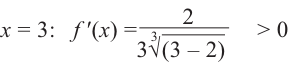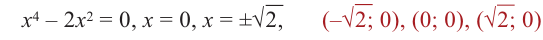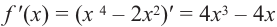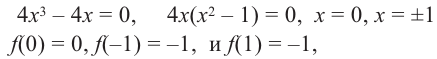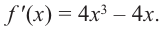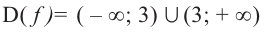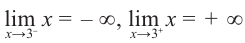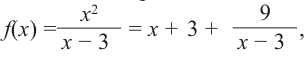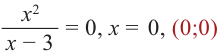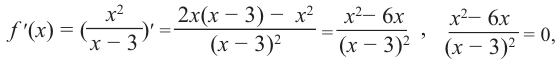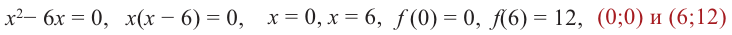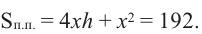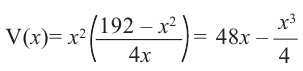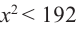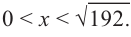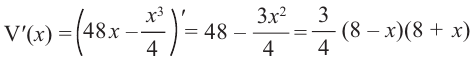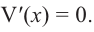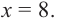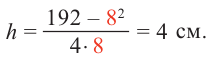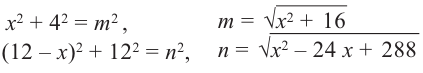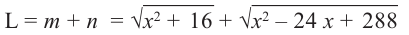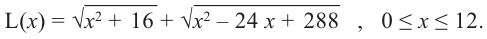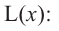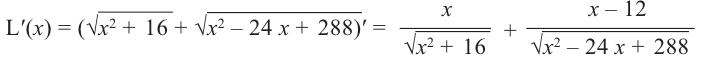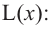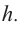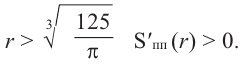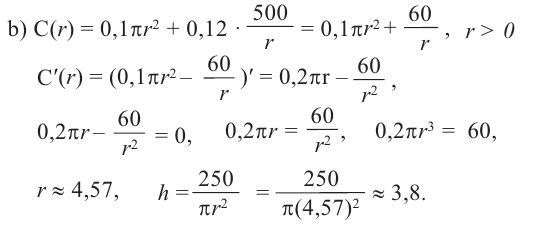Содержание:
- Критические точки и экстремумы функции
- Теорема Ферма (Необходимое условие существовании экстремумов)
- Достаточное условие существования экстремума
- Задача пример №117
- Задача пример №118
- Задача пример №119
- Задача пример №120
- Задача пример №121
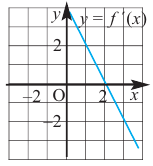
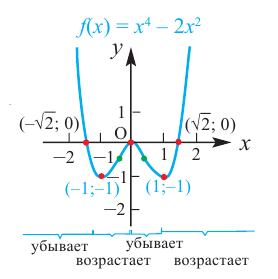
Критические точки и экстремумы функции
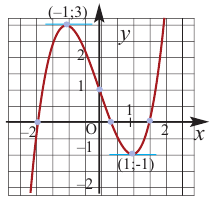
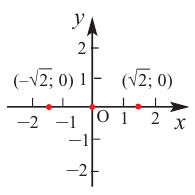
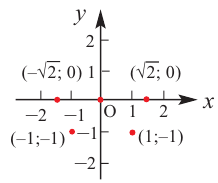
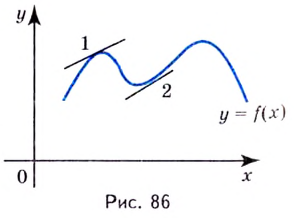
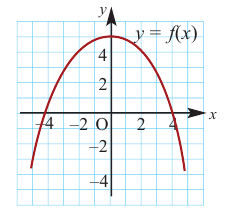
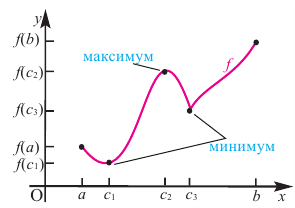
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 


2. В точках 
3. Для рассматриваемой нами функции критические точки 

По графику видно, что в точках внутреннего экстремума 

Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 

На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т.е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.

Достаточное условие существования экстремума
Пусть функция 



1 ) 


2) 


3) 


Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 



Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
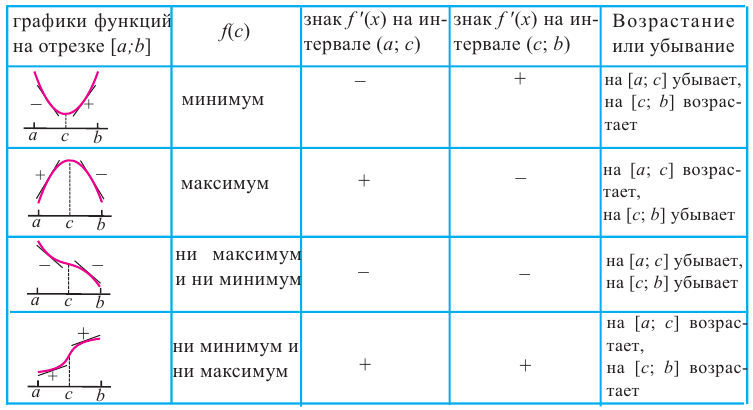
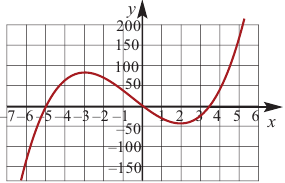
Задача пример №117
Для функции 
Решение:
Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 

Проверим знак 



Интервал 
Знак 

При 

При 

4. Используя полученные для функции 

Задача пример №118
Найдите наибольшее и наименьшее значение функции 
Решение:
Сначала найдем критические точки. Так как 



Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Задача пример №119
Найдите экстремумы функции 
Решение:
1. Производная функции:
2. Критические точки: 
3. Интервалы, на которые критические точки делят область определения функции:
Проверим знак 
Для промежутка 
Для промежутка (0; 1,5) возьмем
Для промежутка 
Интервал
Пробные точки
Знак 

Используя полученную для функции 



• Функция 

• Точка 

• Функция 
• Функция 

•
Задача пример №120
Найдите экстремумы функции
Решение:
1. Производная
2. Критические точки: для этого надо решить уравнение 



3. Промежутки, на которые критическая точка делит область определения функции: 
Определим знак 
Для 


Интервал 
Знак 
Возрастание-убывание
• Функция 

• Функция 

•
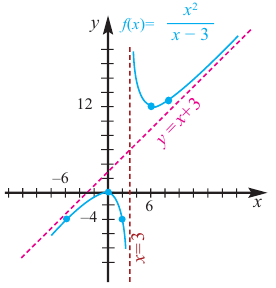
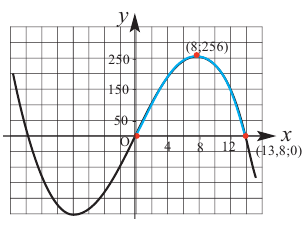
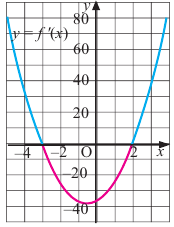
Задача пример №121
По графику функции производной 
Решение:
Производная 







Эта лекция взята из раздела решения задач по математике, там вы найдёте другие лекци по всем темам математики:
Другие темы которые вам помогут понять математику:
|
|
|
|
Лекции:
- Экстремумы функции двух переменных. Производная по направлению
- Доказательство неравенств
- Системы уравнений
- Максимальные и минимальные значения функции
- Действия с корнями
- Отрицательное биномиальное распределение
- Длина дуги кривой
- Вычислить несобственный интеграл
- Градиент функции: пример решения
- Интеграл натурального логарифма
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
Что такое исследование функции
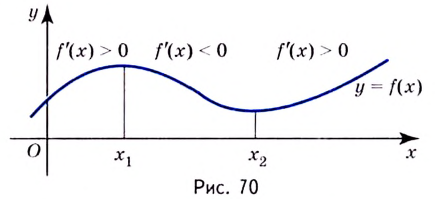
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 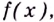
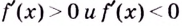
Пример:
Найдите промежутки возрастания и убывания функции
Решение:
Уравнение 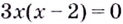
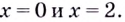
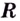
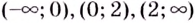
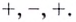
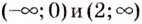
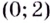
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 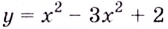
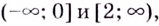
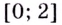
Пример:
Найдите промежутки убывания функции
Решение:
Критические точки: 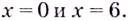
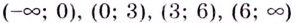
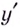
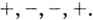
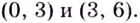
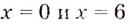
Пример:
Найдите критические точки функции 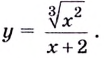
Решение:
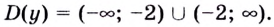
Найдём точки, в которых производная равна нулю или не существует: 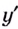
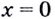
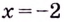

Ответ. 0 и 4.
Пример:
Докажите, что функция 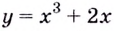
Решение:
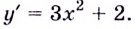
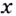
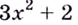
Пример:
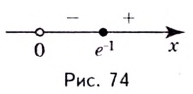
Установите, на каком промежутке функция 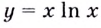
Решение:
Способ 1. 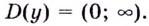
Найдём критические точки функции:
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
Следовательно, функция 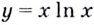
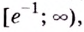
Способ 2. Решим неравенство 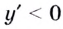
Ответ. Возрастает, если 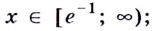
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 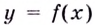
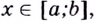
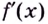
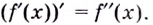
Например, найти производную 2-го порядка функции 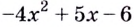
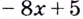
Кривая 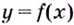
Кривая 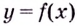
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 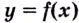
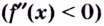
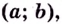
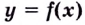
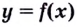
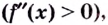
Из теоремы следует, что точками перегиба кривой 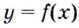
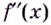
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 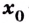
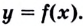
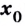
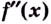
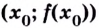
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
то кривая выпуклая; если
— кривая вогнутая;
- если производная
меняет знак при переходе через точку
то точка
является точкой перегиба кривой
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой
Решение:
1) Область определения функции:
2) Найдём вторую производную: 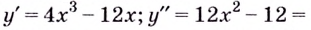
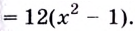
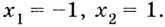
3) Разбиваем область определения на интервалы 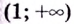
Если 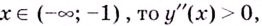
Если 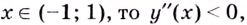
Если 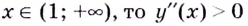
Следовательно, точки 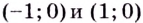
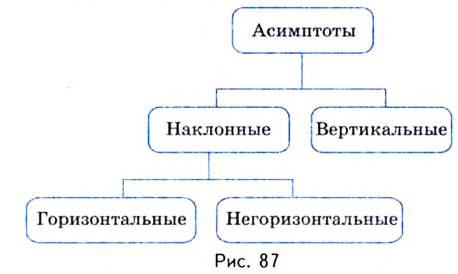
Напомним, что прямая 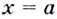
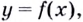
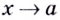
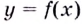
Уравнение наклонной асимптоты:
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 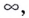
Если 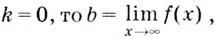
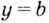
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 
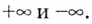
Пример №2
Найдите асимптоты кривых:
Решение:
а) 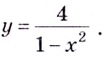
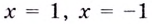
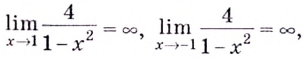
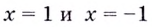
Найдём наклонную асимптоту: 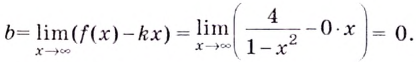
Следовательно, заданная кривая имеет три асимптоты:
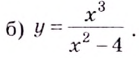
Поскольку функция не определена в точках 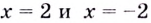
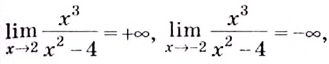
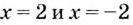
Для наклонной асимптоты
Значит прямая 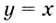
Итак, асимптоты кривой:
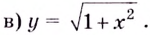
Следовательно, 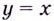
2) если 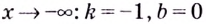

Следовательно, заданная кривая имеет две асимптоты:
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
возрастающая функция
Если для любых 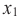
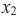
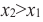
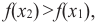
убывающая
Если для любых 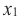
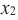
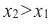
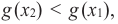
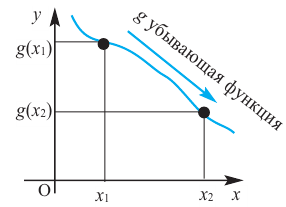
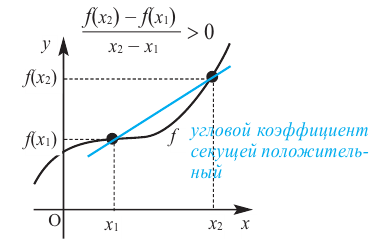
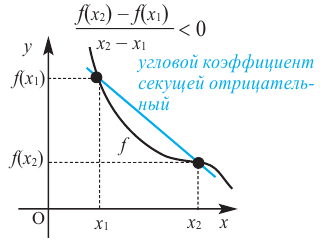
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция 
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция 
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 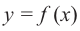
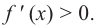
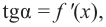
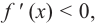
Теорема. Если функция 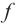
Примечание: если функция 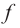
По графику функции 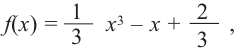
На интервалах 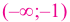
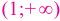
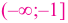
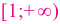
На интервале 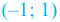
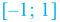
Пример №3
При помощи производной определите промежутки возрастания и убывания функции
Решение: 1. Алгебраический метод.
Найдем производную функции
Функция 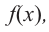
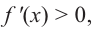
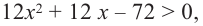
Для решения неравенства сначала надо решить соответствующее уравнение
Значит, при 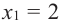
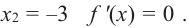
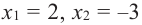
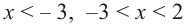
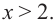
Из таблицы и непрерывности функции 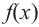
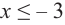
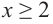
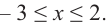
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
График производной 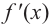
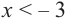
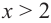
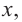
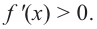
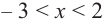
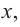
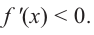
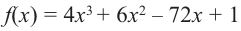
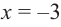
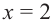
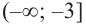
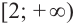
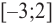
Пример №4
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 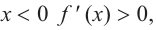
b) при 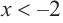
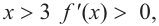
Решение:
а) при 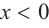
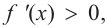
функция возрастает. При 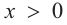
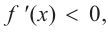
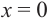
b) При 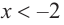
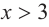
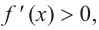
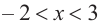
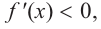
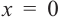
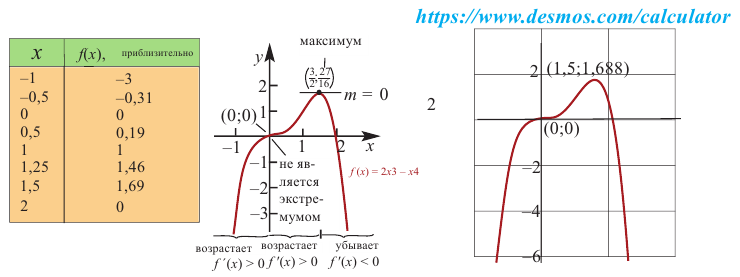
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 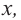
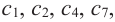
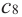
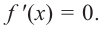
2. В точках 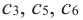
3. Для рассматриваемой нами функции критические точки 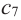
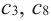
По графику видно, что в точках внутреннего экстремума(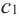
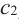
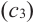
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 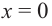
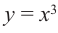
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 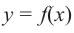
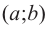
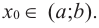
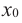
слева от точки
положительна, а справа — отрицательна, то точка
является точкой максимума.
слева от
отрицательна, а справа — положительна, то точка
является точкой минимума
с каждой стороны от точки
имеет одинаковые знаки, то точка
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 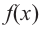
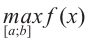
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Пример №5
Для функции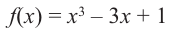
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 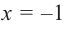
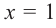
Проверим знак 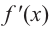
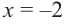
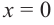
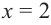

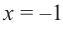
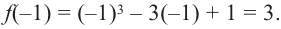
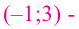
При 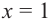
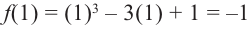
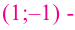
4. Используя полученные для функции 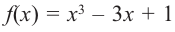
Пример №6
Найдите наибольшее и наименьшее значение функции 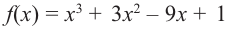
Решение: Сначала найдем критические точки.
Так как 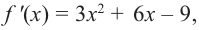
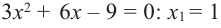
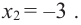
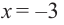
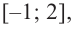
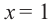
Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Пример №7
Найдите экстремумы функции
Решение: 1. Производная функции:
2. Критические точки:
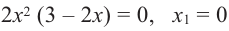
3. Интервалы, на которые критические точки делят область определения функции:
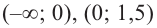
Проверим знак 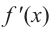
Для промежутка 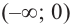
Для промежутка 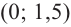
Для промежутка 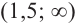
Используя полученную для функции 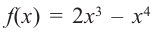
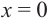
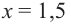
Пример №8
Найдите экстремумы функции
Решение: 1. Производная
2. Критические точки: для этого надо решить уравнение 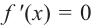
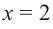
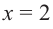
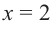
3. Промежутки, на которые критическая точка делит область определения функции: 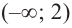
Определим знак 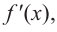
Для 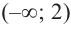
Для 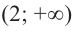
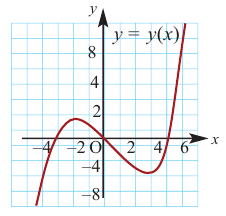
Пример №9
По графику функции производной 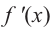
Решение:
Производная 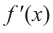
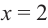
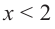
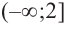
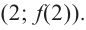
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция — многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
Пример:
Постройте график функции
1) Точки пересечения с осями координат :
2) Критические точки ( точки, в которых производная равна нулю):
значит, точки 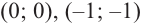
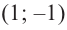
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 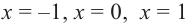
4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
Постройте график функции
1) Область определения функции:
2) Асимптоты:
Прямая 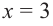
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее:
условии 
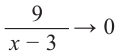
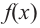
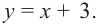
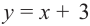
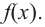
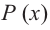
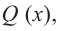
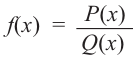
3) Точки пересечения с осями координат:
4) Критические точки:
5) Промежутки возрастания и убывания: в точке 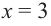
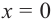
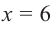
6) Построим график. Отметим на координатной плоскости точки 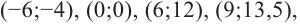
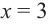
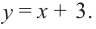
Обратите внимание! В области, близкой к точке 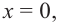
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 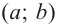
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.
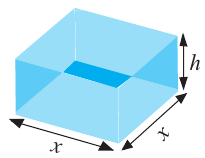
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 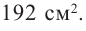
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 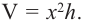
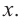
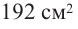
Тогда выразим 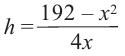
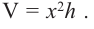
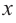
Теперь найдем область определения функции 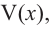
Понятно, что длина не может быть отрицательной, т. е. 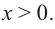
или 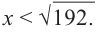
Найдем максимальное значение функции 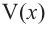
Для этого используем производную первого порядка:
При 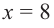
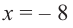
Однако. 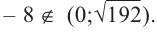
При 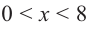
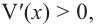
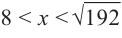
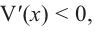
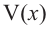
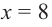
Если длина основания коробки будет 8 см, то высота будет равна
Значит, максимальный объем будет иметь коробка с размерами
Построив при помощи графкалькулятора график функции 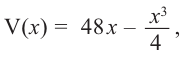
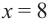
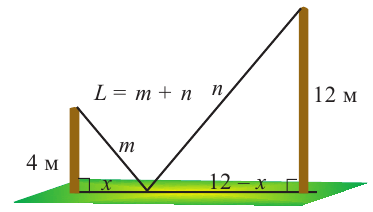
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
зависимость функции 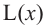
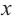
Производная функции
Найдем критические точки функции
Сравнивая значения функции 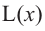
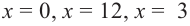
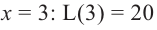
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 
4. Полученные значения объясните экспериментально.
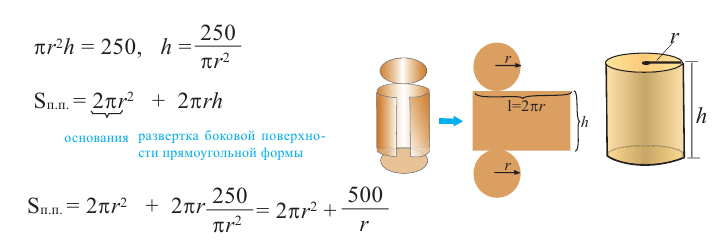
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 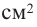
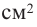
Решение: а) По условию задачи объем равен 250 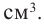
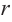
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 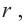
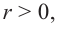
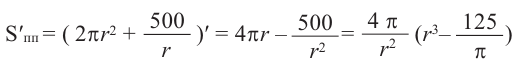
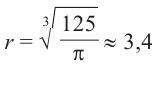
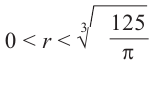
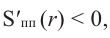
Значит,
Подставим значение 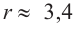
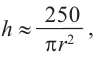
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 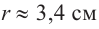
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
План урока:
Исследование функций на монотонность
Экстремумы функции
Выпуклость и вогнутость функций
Исследование функций и построение их графиков
Исследование функций на монотонность
Говоря о смысле производной, мы замечали, что у возрастающих функций она принимает положительные значения, а у убывающих – отрицательные. Убедиться в этом можно с помощью графиков. Действительно, если провести касательную к возрастающей ф-кции, то она образует с осью Ох острый угол, а потому тангенс этого угла (а он как раз равен произ-ной) окажется положительным числом:
Если же ф-кция убывает, то касательная образует с осью Ох тупой угол, чей тангенс будет отрицательным:
Рассмотрим более сложный случай, когда ф-кция на каких-то промежутках убывает, а на каких-то возрастает. В качестве примера приведем зависимость у = х2. Она является убывающей на промежутке (– ∞; 0] и возрастающей на промежутке [0; + ∞). Можно заметить, что любая касательная, проведенная на первом из этих промежутков, будет образовывать тупой угол с Ох. И наоборот, любая касательная на втором промежутке имеет острый угол:
Это означает, что произ-ная ф-кции на первом промежутке должна быть отрицательной, а на втором – положительной (сразу отметим, что граничная точка х = 0 стоит особняком, так как входит в оба промежутка). Попробуем найти произ-ную аналитически. Мы рассматриваем ф-кцию у = х2, её произ-ная равна
Действительно, произ-ная у′ = 2х принимает отрицательные значения при х∈ (– ∞;0) и оказывается положительной при х∈(0; + ∞). Заметим, что в граничной точке произ-ная равна нулю.
Это наблюдение подсказывает нам, что по знаку произ-ной можно определить, возрастает или убывает ф-кция. Однако сначала надо разобраться с тем случаем, когда произ-ная оказывается равной нулю. Рассмотрим ф-кцию у = х3. Очевидно, что она возрастает на всей числовой прямой. Значит ли это, что её произ-ная на этой прямой строго положительна? Нет, не значит. Запишем у′:
Произ-ная положительна во всех точках, кроме х = 0. При х = 0 у′ также оказывается равной нулю. Однако мы можем сказать, что у′ неотрицательна на всей числовой прямой.
Можно привести пример ф-кции
ее произ-ная равна
Сама ф-кция убывает на всей числовой прямой, а её произ-ная неположительна на ней.
Рассмотрим особый случай, когда у ф-кции произ-ная одновременно и неположительна, и неотрицательна на отрезке. Как ни сложно догадаться, это означает, что производная равна нулю. Мы помним, что нулю равна произ-ная константы:
В качестве примера приведем ф-кцию у = 2. Её произ-ная на всей числовой прямой равна нулю:
При этом ф-кция и не убывает, и не возрастает на числовой прямой:
Рассматривая все эти примеры, можно сделать вывод, что для возрастания ф-кции на промежутке достаточно, чтобы её произ-ная принимала на этом отрезке только положительные отрезки:
Аналогично можно сформулировать и достаточный признак убывания ф-кции:
Сформулированные признаки не охватывают тех ситуаций, когда произ-ная в отдельных точках промежутка обращается в ноль. Если произ-ная равна нулю на всём промежутке, то ф-кция на нем остается неизменной (как в случае с функцией у = 2). Если же производная обращается в ноль только в отдельных точках (случай у = х3 и у = х2), то эти точки оказываются граничными для промежутков возрастания и промежутков убывания функции. В этих случаях эти граничные точки добавляют в соответствующие промежутки.
Задание. Докажите, что функция
возрастает при любом значении аргумента.
Решение. Найдем произ-ную у′:
Найдем, при каких значениях х произ-ная у′ оказывается положительной. Для этого запишем неравенство:
Множитель (5х2 + 6) при любом х положителен, а потому мы можем поделить обе части неравенства на него и преобразовать его к виду
Его решениями являются промежутки (– ∞; 0) и (0; + ∞), а при х = 0 произ-ная оказывается равной нулю, то есть это граничная точка. Значит, промежутками возрастания функции являются (– ∞; 0] и [0; + ∞). Обратите внимание, что мы добавили в каждый из промежутков граничную точку х = 0. Но объединением этих промежутков является вся числовая прямая:
Получается, что ф-кция возрастает при любом х.
Теперь попытаемся найти промежутки возрастания и убывания функции
Для их нахождения определим, где произ-ная положительна, а где отрицательна. Для этого сначала найдем произ-ную:
Решим неравенство у′ > 0, при этом мы используем метод интервалов:
Отмечаем нули на координатной прямой и расставляем знаки промежутков:
Напомним, что для определения знаков промежутков можно просто выбрать на каждом из них одну точку и подставить её в неравенство. Например, на интервале х∈(– ∞; – 1) возьмем число – 2:
Итак, произ-ная положительна на промежутках (– ∞; – 1) и (0; + ∞). При х = 0 и х = 1 произ-ная обращается в ноль – это граничные точки, которые надо добавить в промежутки возрастания. То есть ф-кция возрастает на промежутках (– ∞; – 1] и [0; + ∞).
Рассматривая аналогичное неравенство у′ < 0, получаем, что произ-ная отрицательна при х∈(– 1; 0). Тогда промежутком убывания ф-кции является [– 1; 0].
Для наглядности построим график рассматриваемой нами ф-кции:
Проведенное нами действие (поиск промежутков возрастания и убывания ф-кции) называется исследованием функции на монотонность. Для его проведения необходимо вычислить производную ф-кцию у′, а потом найти, на каких промежутках она положительна или отрицательна. Если в граничных точках полученных промежутков произво-дная обращается в ноль, то эти точки следует включить в промежутки.
Экстремумы функции
Еще раз посмотрим на график рассмотренной нами ф-кции
На нем есть две особые точки: (– 1; 0) и (0; – 1). Они являются границами для промежутков возрастания и убывания. При этом значение произ-ной в этих точках оказалось равным нулю. Если мы проведем касательные к графику в этих точках, то окажется, что они являются горизонтальными линиями, то есть их угол наклона равен нулю:
Действительно, если произ-ная в точке равна нулю, то тангенс угла наклона должен быть также равен нулю. А это значит, что и сам угол равен нулю, ведь tg 0 = 0. Геометрически это означает, что касательная будет выглядеть как горизонтальная линия, которая либо параллельна оси Ох, либо совпадает с ней.
Ещё одна особенность точек (– 1; 0) и (0; – 1). Первая из них в некоторой, достаточно малой локальной области является точкой максимума функции. Действительно, если взять промежуток [– 1,5; – 0,5], то на нем именно в точке х = –1 ф-кция принимает наибольшее значение:
Аналогичную окрестность можно указать и для точки х = 0, только на ней точка (0; – 1) окажется точкой минимума функции, а не максимума:
Ни для какой другой точки на графике такую окрестность указать не удастся. Дадим более точное определение таким понятиям, как точка минимума и точка максимума функции:
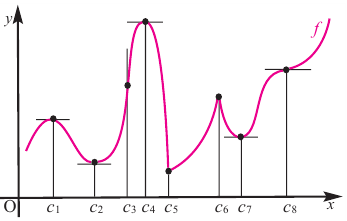
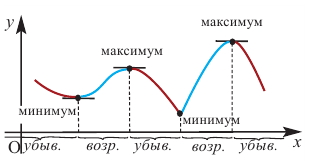
Ещё раз заметим, что в таких точках ф-кция достигает наибольшего или наименьшего значения только в определенной локальной области. Поэтому часто их называют локальными максимумами или минимумами. Пусть ф-кция задана следующим графиком:
На графике можно отметить 5 минимумов функции и 5 максимумов, причем только один максимум и минимум будут соответствовать наибольшему или наименьшему значению на всей области определения (их ещё называют глобальными максимумами и минимумами):
Грубо говоря, точки максимума соответствуют вершинам графика, а точки минимума – впадинам графика.
Для обозначения этих точек используют специальный термин – точки экстремума функции.
Довольно очевидно, что точки экстремума находятся на границе промежутков возрастания и убывания ф-кции, то есть в тех самых граничных точках. Напомним, что в этих точках произ-ная равна нулю. Однако возможен ещё один случай появления экстремума. Он связан с так называемыми негладкими ф-кциями, пример одной из которых приведен на рисунке:
На графике явно видно два экстремума функции. Однако в этих точках ф-кция меняет свое поведение резко, а не плавно. Из-за этого график кажется «зазубренным». Обратите внимание, что построить единственную касательную к графику в экстремумах не получается:
С точки зрения математического анализа это означает, что произ-ная в таких точках не существует. Заметим, что все элементарные ф-кции, а также сложные ф-кции, получаемые из нескольких элементарных, являются гладкими. Поэтому на практике в школьном курсе такие случаи почти не встречаются.
Итак, можно сформулировать признак существования экстремума:
Задание. Докажите, что у функции вида
где a, b, c, d – постоянные числа, есть не более двух экстремумов.
Решение. Чтобы найти экстремумы функции, сначала просто продифференцируем её:
Заметим, что производная является квадратичной функцией
Эта ф-кция определена при любом значении х. Это значит, что не существует таких экстремумов, в которых произ-ная не существует. Если приравнять произ-ную к нулю, то получим квадратное уравнение:
Напомним, что квадратное уравнение может иметь не более 2 различных корней. То есть у ф-кции есть не более 2 точек, в которых произ-ная обращается в ноль. Следовательно, и экстремумов у ф-кции не более двух.
Точки, в которых произ-ная обращается в ноль или не существует, называют критическими точками функции.
Заметим, что не каждая критическая точка обязательно оказывается экстремумом. Можно снова привести пример ф-кции у = х3. Она возрастает на всей области числовой прямой, то есть не имеет экстремумов. Однако ее произ-ная имеет вид у′ = 3х2, и она обращается в ноль при х = 0. В связи с этим встает вопрос – есть ли какой-то метод, позволяющий достоверно определить наличие экстремума у ф-кции? Оказывается, есть. Надо лишь проанализировать поведение производной вблизи критической точки. Если произ-ная в точке меняет знак, то она является экстремумом, а если не меняет – то не является.
Более того, можно определить, является ли экстремум точкой минимума или точкой максимума. Если произ-ная меняет знак с плюса на минус, то это точка максимума, а если с минуса на плюс – то это точка минимума.
Для примера рассмотрим ф-кцию
Попытаемся найти ее экстремумы. Для этого вычислим производную:
Найдем нули произ-ной:
Теперь отметим на координатной прямой нули ф-кции. Они разобьют числовую прямую на три промежутка. Расставим знаки производной на этих промежутках:
Знаки на промежутках можно определить, просто подставив в произ-ную одно из чисел из промежутка:
Получается, что в точке х = 0 произ-ная меняет знак с «+» на (–), а в точке х = 2 знак произ-ной не меняется. Это значит, что точка х = 0 является точкой минимума, а х = 2 – это вообще не экстремум ф-кции:
В общем случае для определения экстремумов ф-кции можно руководствоваться следующей схемой:
До этого мы рассматривали случаи, когда ф-кция была определена при любом значении аргумента. Теперь изучим ф-кцию
Ее особенностью является то, что она не определена при х = 0, так как при таком значении аргумента получается деление на ноль. Вычислим у′:
Теперь найдем нули произ-ной:
Выражение х2 + 4 при любом х не равно нулю, а потому на него можно поделить уравнение:
Теперь на числовой прямой мы должны отметить две найденные критические точки. Но также на ней следует отметить число х = 0, так как в этой точке ф-кция не определена:
Обратите внимание, что точка х = 0 НЕ является экстремумом, хотя кажется, что в ней ф-кция меняет свой знак. Дело в том, ф-кция не существует при таком значении аргумента. Это значит, что х = 0 – это асимптота графика. График ф-кции будет выглядеть примерно так:
Выпуклость и вогнутость функций
Нарисуем две немного отличающиеся друг от друга возрастающие ф-кции:
Видно, что эти графики будто выгнуты в разные стороны. Оказывается, в математике есть специальное свойство ф-кций, которое указывает на направление, в котором выгнуты их графики. Левая ф-кция является вогнутой функцией, а правая – выпуклой функцией.
Определить, выпукла или вогнута ф-кция, очень просто. Достаточно провести к графику касательную. Если она проходит выше графика, то это указывает на вогнутость функции, а если ниже, то она выпукла:
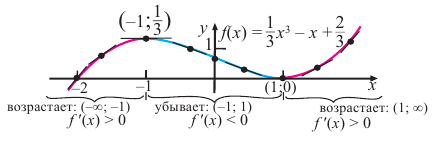
Естественно, встречаются ф-кции, которые на одном промежутке выпуклые, а на другом – вогнутые. Классическим примером является кубическая парабола у = х3. На промежутке (– ∞; 0] она вогнутая, а на промежутке [0; + ∞) она становится выпуклой. При этом в точке х = 0 она меняет свой характер. Такая точка называется точкой перегиба функции:
Ранее мы уже заметили, что точка х = 0 для ф-кции у = х3 – этой пример критической точки, которая не является экстремумом. Действительно, произ-ная ф-кции у = х3 имеет вид
и она обращается в ноль при х = 0, однако в этой точке ф-кция возрастает. Это подсказывает нам, что критические точки, в которых ф-кция НЕ меняет своего знака, являются точками перегиба. И это действительно так.
Заметим, однако, что в общем случае точка перегиба может и вовсе не являться критической точкой ф-кции. В рамках школьного курса мы не будем детально изучать выпуклость функций и точки перегиба. Отметим лишь, что для их поиска необходимо вычислять уже не только первую, но и вторую произ-ную функции.
Исследование функций и построение их графиков
Ранее мы строили графики ф-кций в основном «по точкам». То есть мы просто вычисляли значение ф-кции при различных значениях х, отмечали получившиеся точки на координатной плоскости, а потом соединяли их плавной кривой. Однако при этом можно упустить некоторые важные особенности ф-кций – наличие у них минимумов и максимумов, точки их пересечения с осями координат и т.п. Поэтому в математике используют особый алгоритм для построения графиков ф-кции, который называют «исследованием функции».
Последовательность алгоритма следующая:
- Находят область определения ф-кции. Здесь нужно учесть такие простые правила, согласно которым нельзя делить на ноль, под знаком квадратного корня не может стоять отрицательное число и т.п.
- Выясняют, является ли ф-кция четной или нечетной, периодической или непериодической.
- Находят производную ф-кции.
- Приравнивая произ-ную к нулю, находят критические точки ф-кции, промежутки ее возрастания и убывания (то есть проводят исследование на монотонность).
- Находят точку пересечения графика с осью Оу, для чего подставляют в ф-кцию х = 0. Конечно, это действие совершается только в том случае, если точка х = 0 входит в область определения ф-кции.
- Находят точку пересечения графика с горизонтальной осью Ох. Для этого надо составить уравнение у(х) = 0 и решить его. Возможна ситуация, когда решить уравнение точно не получается, тогда этот этап можно пропустить.
- Находят промежутки знакопостоянства ф-кции.
- Изучают поведение ф-кции вблизи ее особых точек. Обычно это подразумевает поиск пределов ф-кции на бесконечности или в точках, где она не определена.
- Определяют область значений ф-кции.
- С учетом всех особенностей ф-кции строят ее график.
Заметим, что у ф-кции можно также найти точки перегиба ф-кции, исследовать ее на выпуклость и вогнутость, однако в рамках программы 11 класса это не делается.
Сразу скажем, что исследование ф-кции – это трудоемкая задача. Она не очень сложная, но требует больших затрат времени и бумаги.
Для начала рассмотрим относительно простой пример ф-кции
Область ее определения – это вся числовая прямая. Ф-кция не является ни четной, ни нечетной. Доказать это на примере конкретной точки. Возьмем х = 1:
Однако у нас это условие явно не выполняется, ведь 0 ≠ 4. Если бы ф-кция была нечетной, то выполнялось бы условие
Оно также не выполняется, так как 0 ≠ – 4.
Вычислим произ-ную ф-кции:
Произ-ная также определена на всей числовой прямой. Для поиска критических точек приравняем ее к нулю:
Получили две критические точки. Отметим их на прямой и расставим знаки:
Итак, мы смогли найти точку максимума функции, равно как и ее точку минимума.
Сразу же вычислим значение ф-кции в ее экстремумах:
Для расстановки знаков возьмем по одному значению из каждого промежутка. Например, можно взять числа (– 2), 0 и 2:
Далее находим, где прямая пересекается с осью Оу, для чего подставляем в ф-кцию значение х = 0:
Получили точку (0; 2). Для нахождения точек пересечения графика с горизонтальной остью Ох надо приравнять всю ф-кцию к нулю:
Это кубическое уравнение. Решить его можно методом подбора корней и последующим делением многочлена на многочлен. Не останавливаясь на подробностях решения, укажем, что его корнями являются числа (– 2) и 1, а других корней. Убедиться в этом можно, просто подставив в уравнение эти числа.
Следующий шаг – определение промежутков знакопостоянства. Для этого надо решить неравенство у(х) > 0:
Это неравенство решается методом интервалов. Он сводится к тому, что находятся нули левой части, которые мы уже нашли – это числа (– 2) и 1. Далее они отмечаются на прямой, после чего на образовавшихся промежутках проставляются знаки:
Знаки определяем, выбирая по одной точке из каждого промежутка:
Достаточно очевидно, что при х→∞ сама ф-кция также стремится к бесконечности. Если же х→ – ∞, то и у→ – ∞.
Представим найденную нами информацию в виде таблицы. В верхней строке будем записывать промежутки и отдельные точки, а ниже – особенности ф-кции на этих промежутках (возрастает ф-кция или убывает, положительна она или отрицательна и т.п.):
В итоге график ф-кции будет иметь следующий вид:
Теперь исследуем более сложную ф-кцию
Начнем с области определения. Знаменатель дроби не может равняться нулю, а потому
Итак, аргумент ф-кции может принимать любые значение, кроме 1 и (– 1). Поэтому её область определения (она обычно обозначается как D (x)) можно записать так:
Далее проверяем ф-кцию на четность или нечетность. Напомним, что для этого надо подставить в нее вместо аргумента х аргумент (– х):
Мы получили у(х). Это означает, что ф-кция четная, а ее график симметричен относительно оси Оу.
Следующий шаг – находим произ-ную ф-кции:
Заметим, что область определения произ-ной полностью совпадает с областью определения самой ф-кции. Поэтому у ф-кции нет таких критических точек, в которых произ-ная не существует.
Теперь произ-ную можно приравнять к нулю:
Мы нашли всего одну критическую точку. Отметив ее на координатной прямой, можно выяснить, что она является точкой максимума. При этом стоит также отметить точки х = 1 и х = – 1, в которых ф-кция не определена (их ещё называют точками разрывов):
Для определения знаков произ-ной достаточно вычислить её значение в одной точке на каждом получившемся промежутке. Возьмем значения (– 2), (– 0,5), 0,5 и 2
Найдем точку пересечения графика с осью Оу, для чего подставим в ф-кцию значение х = 0:
Получили точку (0; – 1).
Далее находим точку пересечения графика с осью Ох. Для этого подставим в ф-кцию значение у = 0 и решим получившееся уравнение:
Числитель дроби в правой части при любом значении х положителен, то есть не равен нулю. Это значит, что уравнение не имеет решения. Отсюда вывод – график НЕ пересекается с осью Ох.
Следующий шаг – это определение промежутков знакопостоянства функции. Чтобы найти, при каких значениях аргумента ф-кция положительная, составим неравенство:
Это дробно-рациональное неравенство. Для его решения надо отметить на координатной прямой те значения х, при которых либо знаменатель, либо числитель обращается в ноль. Числитель при любом аргументе положителен, а нулями знаменателя являются точки х = – 1 и х = 1:
Знаки на промежутках определяем, подставляя точки из промежутков в ф-кцию:
Далее следует исследовать поведение ф-кции вблизи при х →∞ и х→ –∞. Для этого преобразуем ф-кцию, выделив целую часть:
При х→∞ число (х2 – 1) также стремится к бесконечности, а дробь
будет стремиться к единице. Аналогично можно убедиться, что при х→ – ∞ ф-кция также стремится к единице.
Все полученные данные можно удобно представить в табличном виде:
На основании этих результатов строим график:
Из рисунка видно, что область значений ф-кции имеет вид
Итак, мы узнали, что с помощью производной можно определять промежутки, на которых функция возрастает и убывает, а также находить ее минимумы и максимумы. Эти навыки помогают при решении многих практических задач, когда требуется найти такое значение некоторых параметров, при которых какая-то величина принимает максимальное или минимальное значение. Например, продавцы товара могут назначать такую цену на свою продукцию, которая принесет им максимальный доход (просто назначить как можно большую цену нельзя, так как слишком дорогой товар никто не купит). Более подробно такие задачи мы рассмотрим подобные задачи в следующих уроках.
Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 

Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 

Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
2) Найти f’ (x).
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
промежутках.
5) Сделать выводы о монотонности функции и точках ее
экстремума.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
- Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
- Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
- найти экстремальные точки функции, принадлежащие отрезку,
- найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
- выбрать из полученных значений максимальное и минимальное.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежуток монотонности функции у=х2 -8х +5
Решение: Найдем производную заданной функции: у’=2x-8
2x-8=0
х=4
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции:
Найдем нули производной:
х=-2,5
Определим знаки производной функции и изобразим на рисунке поведение функции:
Ответ: -2,5 точка min
№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc
Ответ: V=12 мc
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Ответ: 3
(схема 31)
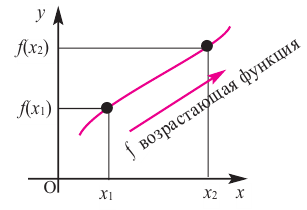
Точка x0 называется точкой максимума (минимума) функции y=f (x), если существует такая δ–окрестность точки x0, что для всех 
выполняется неравенство 
Точки максимума и минимума функции называются
точками экстремума (рис. 3.5).
Теорема 3.15 (необходимое условие существования точек экстремума функции одной переменной). Если дифференцируемая
функция y=f (x) имеет
экстремум в точке x0,
то её производная в этой точке равна
нулю или не существует
Точки, в которых производная функции
либо равна нулю, либо не
существует, называют критическими точками 1-го рода.
Критические точки, в которых производная функции равна
нулю, называются точками стационарности.
Функция y=f (x) называется возрастающей
на некотором интервале (a;b), если на этом интервале большему значению
аргумента x соответствует большее
значение переменной y, и убывающей, если большему
значению аргумента x соответствует меньшее значение
переменной y.
Для
дальнейшего исследования критические точки помещают на числовую ось, которая
делится этими точками на интервалы, после чего
поверяют выполнение следующих достаточных условий.
Теорема 3.16 (достаточное условие возрастания и убывания
функции одной переменной). Если
на некотором интервале (a;b) функция y=f (x) дифференцируема и при этом ее производная 
интервале возрастает (убывает)
Теорема 3.17 (достаточное условие существования точек экстремума функции ). Если функция y=f (x) непрерывна и
дифференцируема в некоторой δ –окрестности критической точки x0 и при переходе через нее
производная 
с минуса на плюс, то точка x0 является точкой минимума функции
Те критические
точки функции, для которых достаточное условие не выполняется, остаются просто
критическими точками 1-го рода.
Критические точки 1-го рода, в которых
производная не существует, делятся на классы:
– точки, в которых функция непрерывна, но при выполнении теоремы 3.17 имеет в этих точках «острый» экстремум (угловые
точки или точки излома) (рис. 3.6);
– точки, в которых функция непрерывна, но касательная в них к графику
функции параллельна оси 0y (угловой коэффициент такой касательной


– точки, в которых функция терпит разрыв (всегда переходят в класс
критических точек 2-го рода).
Но проведенное таким образом исследование, не дает ответ на очень важный
вопрос: как возрастает (убывает) функция – выпукло или вогнуто? Ответ на
поставленный вопрос дает дальнейшее рассмотрение функции с помощью второй
производной. Дадим ряд необходимых определений.
Функция называется выпуклой (выпуклой вверх) на некотором интервале (a;b), если касательная, проведенная к графику
функции в каждой точке этого интервала, лежит выше графика функции.
Функция называется вогнутой (выпуклой вниз) на некотором интервале (a;b), если касательная, проведенная к графику функции в каждой точке этого интервала, лежит
ниже графика функции.
Точки, отделяющие участки выпуклости от участков вогнутости функции,
называются ее точками перегиба (см. рис. 3.5).
Теорема 3.18 (необходимое
условие существования точек перегиба функции). Если дважды дифференцируемая функция y=f (x) имеет перегиб в точке x0,
то в этой точке вторая производная
равна нулю или не существует
Точки, в которых вторая производная функции либо равна нулю, либо не
существует, называют критическими точками 2-го рода.
Для дальнейшего исследования критические точки 2-го
рода помещают на числовую ось, которая делится этими точками на интервалы,
после чего поверяют выполнение следующих
достаточных условий.
Теорема 3.19 (достаточное
условие выпуклости и вогнутости
функции). Если на некотором интервале (a;b) функция y=f(x) дважды
дифференцируема и при этом ее вторая производная 
(выпукла)
Примечание. Очевидно,
что на интервале выпуклости функция имеет точку максимума, а на интервале
вогнутости – точку минимума (см. рис. 3.5).
Теорема 3.20 (достаточное условие существования точек
перегиба функции). Если функция y=f(x) непрерывна и дважды дифференцируема в некоторой окрестности критической
точки 2-го рода и при переходе через нее
вторая производная меняет знак, то данная точка
является точкой перегиба функции
Те критические точки функции, для которых достаточное условие 3.19 не
выполняется, остаются просто критическими точками 2-го рода. Критические точки
2-го рода, в которых вторая производная не существует, делятся на классы:
– точки,
в которых функция непрерывна и при выполнении теоремы 3.20 имеет в этих точках
«острый» перегиб, – в них можно провести
к графику функции бесконечное множество касательных (рис.
3.7);
– угловые точки (переходят из критических точек первого рода);
– точки, в которых функция терпит разрыв (в точках разрыва 2-го рода график функции имеет вертикальную асимптоту).
Для окончательного перечисления точек экстремума и перегиба функции
необходимо найти их ординаты, после чего выписать указанные точки двумя
координатами.
Для завершения исследования функции и построения графика необходимо
проверить наличие у нее асимптот. Напомним,
что асимптотой кривой называется прямая, расстояние до
которой от точки, лежащей на кривой, стремится к нулю при неограниченном
удалении от начала координат точки по кривой (рис. 3.8).
Асимптоты могут быть вертикальными, наклонными,
горизонтальными.
Говорят, что прямая x=a является вертикальной асимптотой графика

Например, кривая 
асимптоту x=-1, так как 
Уравнение наклонной асимптоты ищем в виде
y=kx+b (рис. 3.8).
Коэффициенты
k и b находятся
по формулам:

и 
Верно и
обратное: если существуют конечные пределы (3.41) и (3.42), то прямая y=kx+b является
наклонной асимптотой.
Если хотя бы
один из пределов (3.41) или (3.42) не существует или равен бесконечности, то
кривая y=f (x) наклонной
асимптоты не имеет.
В частности,
если k=0, то . Поэтому y=b
– уравнение горизонтальной асимптоты.
Примечание. Асимптоты графика функции y=f (x) при ∆x→+∞ и ∆x→–∞ могут быть разными. Поэтому при нахождении
пределов (3.41) и (3.42) следует отдельно рассматривать случай, когда ∆x→+∞ и когда ∆x→–∞.
Пример 3.16.
Исследовать методами дифференциального
исчисления и построить график функции 
Решение.
1. Область
определения: 
2. Исследуем функцию на непрерывность и классифицируем
ее точки разрыва. Заданная функция непрерывна всюду, кроме точки x=4. Вычислим
односторонние пределы в этой точке:

Таким образом, точка x=4 является для заданной функции точкой разрыва второго
рода, а прямая x=4 – вертикальной асимптотой графика.
3. Проведем исследование функции методами
дифференциального вычисления. Для исследования на экстремум и промежутки
монотонности вычислим первую производную:
первого рода, в которых производная равна нулю или не существует

Результаты исследования заданной функции с помощью
первой производной занесем в таблицу 3.1,
основываясь на теоремах 3.16, 3.17.
Таблица 3.1
Исследование
функции с помощью первой производной

точка минимума функции.
4. Исследуем функцию на выпуклость, вогнутость и точки
перегиба с помощью второй производной, основываясь на теоремах 3.23, 3.24:

Так как 
Остается выяснить вопрос об интервалах его выпуклости и вогнутости. Результаты
исследования занесем в следующую таблицу 3.2.
Таблица 3.2
Исследование
функции с помощью второй производной
5. Исследуем график
функции на наличие наклонных и горизонтальных асимптот, уравнение которых как
прямых линий y=kx+b.
Согласно (3.41) 

Согласно (3.42) 
Таким образом, прямая y=x+4 –
наклонная асимптота графика.
Очевидно, график заданной функции пересекает ось 0y в точке (0; –5) и, на основе обобщения
результатов всех предыдущих исследований, имеет вид, представленный на рисунке 3.9






































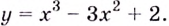
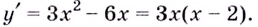
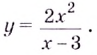
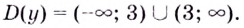
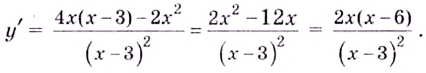
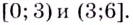
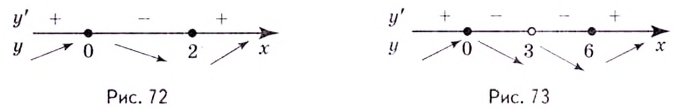
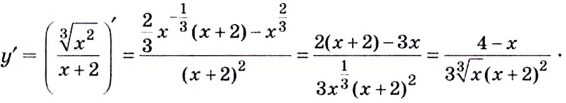
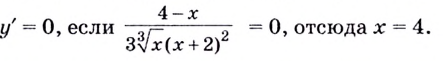
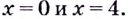
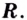
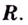
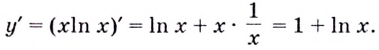
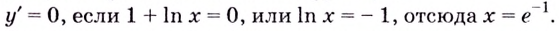
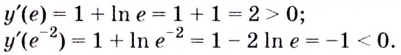
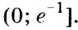
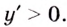
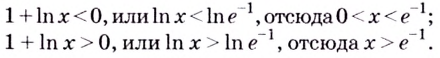
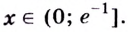
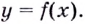
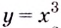
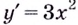
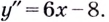
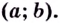
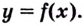
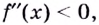 то кривая выпуклая; если
то кривая выпуклая; если 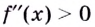 — кривая вогнутая;
— кривая вогнутая;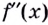 меняет знак при переходе через точку
меняет знак при переходе через точку 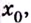 то точка
то точка 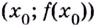 является точкой перегиба кривой
является точкой перегиба кривой 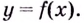
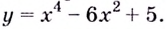
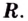
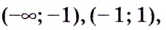
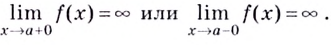
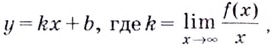
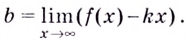
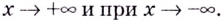
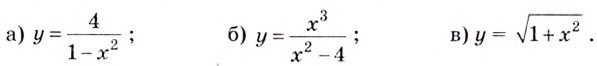
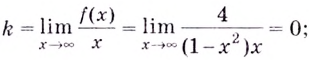
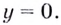
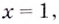
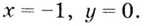
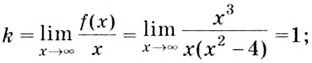
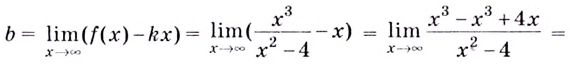
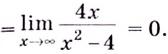
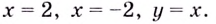
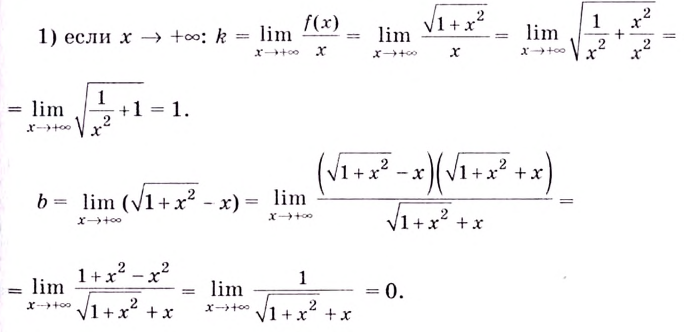
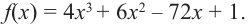
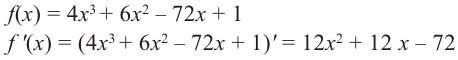
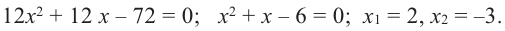

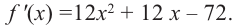
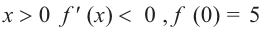
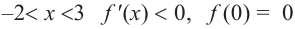
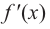 слева от точки
слева от точки 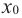 положительна, а справа — отрицательна, то точка
положительна, а справа — отрицательна, то точка 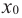 является точкой максимума.
является точкой максимума.