Как найти критическое значение манна уитни - Исправление недочетов и поиск решений вместе с Examum.ru

U-критерий Манна-Уитни (иногда называемый критерием суммы рангов Уилкоксона) используется для сравнения различий между двумя независимыми выборками, когда распределение выборки не является нормальным, а размеры выборки малы (n < 30).

Он считается непараметрическим эквивалентом двухвыборочного независимого t-критерия .

Вот несколько примеров, когда вы можете использовать U-критерий Манна-Уитни:

Вы хотите сравнить зарплату пяти выпускников университета А с зарплатой пяти выпускников университета Б. Распределение зарплаты не является нормальным.
Вы хотите узнать, различается ли потеря веса для двух групп: 12 человек, использующих диету А, и 10 человек, использующих диету Б. Потеря веса не распределяется нормально.
Вы хотите знать, отличаются ли баллы 8 учеников в классе A от результатов 7 учеников в классе B. Баллы не распределены нормально.

В каждом примере у вас есть две группы, которые вы хотите сравнить, распределение выборки не является нормальным, а размеры выборки малы.

Таким образом, U-критерий Манна-Уитни подходит, если выполняются следующие предположения.

Предположения U-критерия Манна-Уитни

Прежде чем проводить U-критерий Манна-Уитни, необходимо убедиться, что выполняются следующие четыре предположения:

Порядковая или непрерывная. Анализируемая переменная является порядковой или непрерывной. Примеры порядковых переменных включают пункты Лайкерта (например, 5-балльная шкала от «полностью не согласен» до «полностью согласен»). Примеры непрерывных переменных включают рост (измеряется в дюймах), вес (измеряется в фунтах) или экзаменационные баллы (измеряются от 0 до 100).
Независимость: все наблюдения обеих групп независимы друг от друга.
Форма: формы распределений для двух групп примерно одинаковы.

Если эти предположения соблюдены, то можно переходить к проведению U-критерия Манна-Уитни.

Как провести U-тест Манна-Уитни

Чтобы провести U-критерий Манна-Уитни, мы следуем стандартной пятиступенчатой процедуре проверки гипотез :

1. Сформулируйте гипотезы.

В большинстве случаев U-тест Манна-Уитни выполняется как двусторонний тест. Нулевая и альтернативная гипотезы записываются как:

H 0 : две популяции равны

H a : две популяции не равны

2. Определите уровень значимости для гипотезы.

Определите уровень значимости. Распространенные варианты: .01, .05 и .1.

3. Найдите тестовую статистику.

Тестовая статистика обозначается как U и является меньшей из U 1 и U 2 , как определено ниже:

U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1

U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2

где n 1 и n 2 — размеры выборки для выборки 1 и 2 соответственно, а R 1 и R 2 — сумма рангов для выборки 1 и 2 соответственно.

В приведенных ниже примерах подробно показано, как найти эту тестовую статистику.

4. Отклонить или не отклонить нулевую гипотезу.

Используя статистику теста, определите, можете ли вы отклонить или не отклонить нулевую гипотезу на основе уровня значимости и критического значения, найденных в U-таблице Манна-Уитни .

5. Интерпретируйте результаты.

Интерпретируйте результаты теста в контексте заданного вопроса.

Примеры проведения U-критерия Манна-Уитни

В следующих примерах показано, как проводить U-критерий Манна-Уитни.

Пример 1

Мы хотим знать, эффективен ли новый препарат для предотвращения приступов паники. В общей сложности 12 пациентов были случайным образом разделены на две группы по 6 человек и назначены для получения нового препарата или плацебо. Затем пациенты записывают, сколько приступов паники у них было в течение одного месяца.

Результаты показаны ниже:

| НОВЫЙ ПРЕПАРАТ | плацебо | | — | — | | 3 | 4 | | 5 | 8 | | 1 | 6 | | 4 | 2 | | 3 | 1 | | 5 | 9 |

Проведите тест Манна-Уитни U, чтобы увидеть, есть ли разница в количестве панических атак у пациентов в группе плацебо по сравнению с группой нового препарата. Используйте уровень значимости 0,05.

1. Сформулируйте гипотезы.

H 0 : две популяции равны

H a : две популяции не равны

2. Определите уровень значимости для гипотезы.

Задача говорит нам, что мы должны использовать уровень значимости 0,05.

3. Найдите тестовую статистику.

Напомним, что тестовая статистика обозначается как U и является меньшей из U 1 и U 2 , как определено ниже:

U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1

U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2

Чтобы найти R 1 и R 2 , нам нужно объединить наблюдения из обеих групп и ранжировать их в порядке от наименьшего к наибольшему:

| НОВЫЙ ПРЕПАРАТ | плацебо | | — | — | | 3 | 4 | | 5 | 8 | | 1 | 6 | | 4 | 2 | | 3 | 1 | | 5 | 9 |

Общая выборка: 1 , 1 , 2 , 3 , 3 , 4 , 4 , 5 , 5 , 6 , 8 , 9

Ранги: 1.5 , 1.5 , 3 , 4.5 , 4.5 , 6.5 , 6.5 , 8.5 , 8.5 , 10 , 11 , 12

R 1 = сумма рангов для выборки 1 = 1,5+4,5+4,5+6,5+8,5+8,5 = 34

R 2 = сумма рангов для выборки 2 = 1,5+3+6,5+10+11+12 = 44

Затем мы используем наши размеры выборки n 1 и n 2 вместе с нашей суммой рангов R 1 и R 2 , чтобы найти U 1 и U 2 .

U 1 = 6(6) + 6(6+1)/2 – 34 = 23

U2 = 6(6) + 6(6+1)/2 – 44 = 13

Наша тестовая статистика меньше U 1 и U 2 , что равно U = 13.

Примечание. Мы также можем использовать калькулятор критерия U Манна-Уитни , чтобы найти, что U = 13.

4. Отклонить или не отклонить нулевую гипотезу.

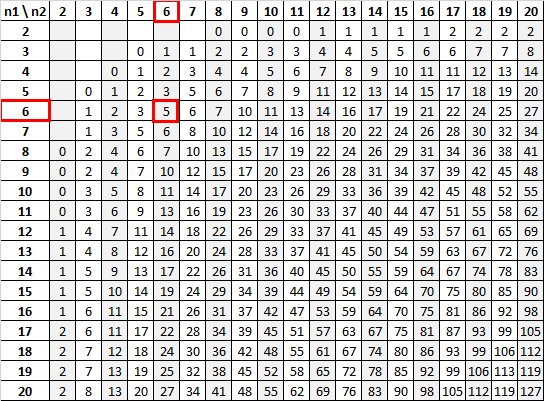
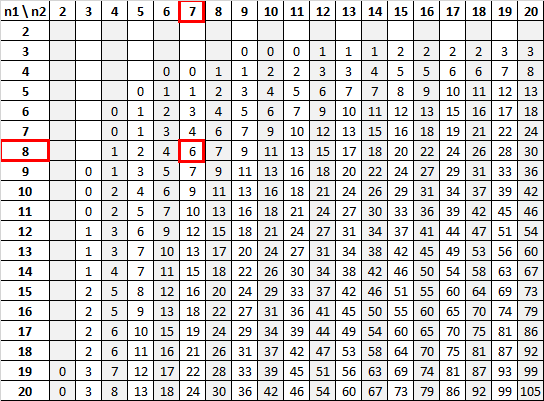
Используя n 1 = 6 и n 2 = 6 с уровнем значимости 0,05, U-таблица Манна-Уитни говорит нам, что критическое значение равно 5:

Поскольку наша тестовая статистика (13) больше нашего критического значения (5), мы не можем отвергнуть нулевую гипотезу.

5. Интерпретируйте результаты.

Поскольку нам не удалось отвергнуть нулевую гипотезу, у нас нет достаточных доказательств, чтобы сказать, что количество приступов паники, испытываемых пациентами в группе плацебо, отличается от группы, принимавшей новое лекарство.

Пример 2

Мы хотим знать, помогают ли занятия по 30 минут в день в течение одной недели учащимся лучше сдавать тест. В общей сложности 15 пациентов были случайным образом распределены в группу исследования или группу без исследования. Через неделю все студенты сдают один и тот же тест.

Результаты тестов для двух групп показаны ниже:

| ИССЛЕДОВАНИЕ | БЕЗ ИССЛЕДОВАНИЯ | | — | — | | 89 | 88 | | 92 | 93 | | 94 | 95 | | 96 | 75 | | 91 | 72 | | 99 | 80 | | 84 | 81 | | 90 |

Проведите U-критерий Манна-Уитни, чтобы увидеть, есть ли разница в результатах тестов для исследуемой группы по сравнению с группой без исследования. Используйте уровень значимости 0,01.

1. Сформулируйте гипотезы.

H 0 : две популяции равны

H a : две популяции не равны

2. Определите уровень значимости для гипотезы.

Задача говорит нам, что мы должны использовать уровень значимости 0,01.

3. Найдите тестовую статистику.

Напомним, что тестовая статистика обозначается как U и является меньшей из U 1 и U 2 , как определено ниже:

U 1 = n 1 n 2 + n 1 (n 1 +1)/2 – R 1

U 2 = n 1 n 2 + n 2 (n 2 +1)/2 – R 2

| ИССЛЕДОВАНИЕ | БЕЗ ИССЛЕДОВАНИЯ | | — | — | | 89 | 88 | | 92 | 93 | | 94 | 95 | | 96 | 75 | | 91 | 72 | | 99 | 80 | | 84 | 81 | | 90 |

Общая выборка: 72 , 75 , 80 , 81 , 84 , 88 , 89 , 90 , 91 , 92 , 93 , 94 , 95 , 96 , 99

Ранги: 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 , 11 , 12 , 13 , 14 , 15

R 1 = сумма рангов для выборки 1 = 5+7+8+9+10+12+14+15 = 80

R 2 = сумма рангов для выборки 2 = 1+2+3+4+6+11+13 = 40

Затем мы используем наши размеры выборки n 1 и n 2 вместе с нашей суммой рангов R 1 и R 2 , чтобы найти U 1 и U 2 .

U 1 = 8(7) + 8(8+1)/2 – 80 = 12

U2 = 8(7) + 7(7+1)/2 – 40 = 44

Наша тестовая статистика меньше U 1 и U 2 , что равно U = 12.

Примечание. Мы также можем использовать калькулятор критерия U Манна-Уитни , чтобы найти, что U = 12.

4. Отклонить или не отклонить нулевую гипотезу.

Используя n 1 = 8 и n 2 = 7 с уровнем значимости 0,01, U-таблица Манна-Уитни говорит нам, что критическое значение равно 6:

Поскольку наша тестовая статистика (12) больше нашего критического значения (6), мы не можем отвергнуть нулевую гипотезу.

5. Интерпретируйте результаты.

Поскольку нам не удалось отвергнуть нулевую гипотезу, у нас нет достаточных доказательств того, что результаты тестов студентов, которые учились, отличаются от результатов тестов студентов, которые не учились.

Дополнительные ресурсы

Калькулятор критерия Манна-Уитни U
Таблица U Манна-Уитни
Как выполнить U-тест Манна-Уитни в Excel
Как выполнить U-тест Манна-Уитни в R
Как выполнить U-тест Манна-Уитни в Python
Как выполнить U-тест Манна-Уитни в SPSS
Как выполнить U-тест Манна-Уитни в Stata

Источник

Допустим мы хотим сравнить уровень интеллекта детей в 7 «а» и 7 «б» классе средней общеобразовательной школы. Для сравнения двух выборок между собой воспользуемся критерием U Манна-Уитни.

Шаг 1. Занесем значения в таблицу.

7 «а»	7 «б»
ФИО Испытуемого	Баллы IQ	ФИО Испытуемого	Баллы IQ
КТИ	112	БРИ	121
ВСИ	105	ДРО	120
МНИ	109	РНА	134
АНМ	90	ВРА	119
УРА	130	ГРА	115
ВФЫ	117	ДЖА	106
РКИ	117	ВЦК	107
ТРИ	125	ЮЕР	101
ТРК	134	ЖЕН	97
ТНК	109	КОР	117

Шаг 2. Расположим все значения в один ряд (2.1) и проранжируем их (2.2).

ФИО Испытуемого	Баллы IQ (2.1)	Ранг (2.2)
РНА	134	(1+2)/2=1,5
ТРК
УРА	130	3
ТРИ	125	4
БРИ	121	5
ДРО	120	6
ВРА	119	7
ВФЫ	117	(8+9+10)/3=9
РКИ
КОР
ГРА	115	11
КТИ	112	12
ТНК	109	(13+14)/2=13,5
МНИ
ВЦК	107	15
ДЖА	106	16
ВСИ	105	17
ЮЕР	101	18
ЖЕН	97	19
АНМ	90	20

Шаг 3. Суммировать ранги значений в группе 7 «а» и в группе 7 «б»

Ранги 7 «а» = 1,5+3+4+9+9+12+13,5+13,5+17+20 = 102,5

Ранги 7 «б» = 1,5+5+6+7+9+11+15+16+18+19 = 107,5

Шаг 4. определить какая из ранговых сумм бОльшая.

Ранг 7 «а»< Ранг 7 «б» => ранговая сумма 7″б» больше

Шаг 5. Определить эмпирические значения критерия U Манна-Уитни по формуле:

$U_{emp}=(n_1 * n_2) + frac{n_x*(n_x + 1)}{2} - T_x$

,где n_1 — количество испытуемых в 1 группе; n_2 — количество испытуемых во 2 группе; T_x — большая из двух ранговых сумм; n_x — количество испытуемых в группе с бОльшей ранговой суммой.

$U_{emp}=(10 * 10) + frac{10*(10 + 1)}{2} - 107,5=100 + 55 - 107,5=47,5$

Шаг 6. По таблице определить критические значения критерия U Манна-Уитни.

$U_{kr}=23$

Шаг 7. Сравнить критические значения с эмпирическими.

23<47,5 $Rightarrow U_{kr}$ < $U_{emp}$

Шаг 8. Сделать выводы.

Источник

Подавляющее большинство психологических исследований направлены на достижение двух главных целей:

Выявить взаимосвязь между показателя. Для этого используется корреляционный анализ.
Установить различия выраженности психологических показателей в двух или более группах. В этом случае используются либо U-критерий Манна-Уитни, либо t-критерий Стъюдента.

В данной статье мы рассмотрим основные аспекты использования критерия Манна-Уитни при обработке результатов эмпирического исследования в курсовых и дипломных работах, а также магистерских диссертациях по психологии.

Содержание

Зачем нужен критерий Манна-Уитни
Расчет критерия Манна-Уитни: объяснение простыми словами
Что нужно знать про критерий Манна-Уитни на защите диплома
Ограничения критерия Манна-Уитни
«Почему вы выбрали для расчета критерий Манна-Уитни?»
Уровень статистической значимости
Пример анализа данных с помощью критерия Манна-Уитни

Зачем нужен критерий Манна-Уитни

В психологическом исследовании изучаются не результаты отдельных испытуемых, а обобщенные данные. Например, при изучении особенностей психологических параметров в двух группах изучаются средние значения в этих группах.

Напомним, что среднее (среднее арифметическое) отражает усредненный по группе показатель. Рассчитывается среднее значение следующим образом:

Суммируются показатели у всех испытуемых в группе.
Сумма делиться на число испытуемых.

Таким образом, когда мы сравниваем психологические показатели у двух испытуемых, то никакие статистические критерии не нужны. Действительно, пусть в ходе тестирования уровень личностной тревожности Иванова оказался 40 баллов, а Петрова – 50 баллов. В этом случае мы смело говорим, что Петров более тревожен, чем Иванов. Однако, если речь идет о сравнении двух групп, то ситуация усложняется.

Например, мы рассчитали средний уровень личностной тревожности в группе женщин – 58 баллов, и мужчин – 49 баллов. Так как средние значения – это статистические показатели, а не просто числа, то просто так сравнивать их нельзя. То есть, мы не можем сказать, что тревожность женщин выше, чем у мужчин. Но как же быть? Как сравнить показатели тревожности в группах мужчин и женщин?

Для этого и существуют статистические критерии анализа различий. Их расчет позволяет с определённой точностью заключить, существуют различия выраженности показателей в двух группах или нет.

Для анализа различий средних значений в двух группах используется t-критерий Стъюдента. U-критерий Манна-Уитни позволяет сравнивать не средние значения, а выраженность показателей, но в этом случае и средние значения параметров в группах будут различаться соответствующим образом.

Расчет критерия Манна-Уитни: объяснение простыми словами

В подавляющем большинство психологических исследований расчет статистических критериев в том числе и критерия Манна-Уитни производится с помощью статистических программ. Наиболее известные – это SPSS и STATISTICA. Однако несмотря на это важно в общих чертах представлять себе сущность расчета – это придаст студенту-психологу на защите диплома.

Вернёмся к нашему пример с тревожностью мужчин и женщин. Предположим у нас две группы по 10 человек. У каждого испытуемого есть определенное значение личностной тревожности. Нам нужно выяснить, различаются ли уровни тревожности в группах мужчин и женщин. Расчет критерия Манна-Уитни примерно будет проходить по следующим шагам:

Показатели тревожности в группах заносятся в таблицу ранжируются, то есть располагаются в порядке возрастания.
Далее данные по мужчинам женщинам объединяются в общий столбец (при этом они помечаются, например, разными цветом) и опять ранжируются.
А далее проводится анализ. Если данные мужчин и женщин (синие и красные числа) в основном чередуются, то различий скорее всего нет.
А вот если данные по мужчинам сгруппированы в основном вверху, где низкие показатели, а у женщин внизу, где высокие, то скорее всего различия есть.

Мы привели объяснение на пальцах. Статистические программы для расчета используют специальные алгоритмы, которые позволяют численно оценить эти пересечения данных обеих групп (синих и красных чисел) и сделать вывод о существовании или не существовании различий.

Что нужно знать про критерий Манна-Уитни на защите диплома

U-критерий Манна-Уитни – это непараметрический статистический критерий, использующийся для сравнения выраженности показателей в двух несвязных выборках.

Что такое непараметрический? Не вдаваясь в статистические тонкости, нужно понимать следующее. Параметрические статистические критерии более точные, но они предъявляют более строгие требования к данным. То есть, перед расчетом нужно все данные в группах проверять, например, на нормальность распределение. Это значит, что на графике распределения такие данные должны располагаться в виде колокола – больше всего испытуемых со средними значениями, а меньшинство имеют низкие и высокие показатели. t-критерий Стъюдента является параметрическим критерием.

Непараметрические критерии менее точные, но зато у них нет жестких требований к данным. Эти данные могут быть почти любыми.

Что значит несвязные выборки? Это означает, что группы не пресекаются, то есть в них разные испытуемые. Расчет различий в связных выборках используется, например, при выявлении эффективности тренингов, когда производятся замеры «до» и «после», а потом сравниваются. У критерия Стъюдента есть вариант для связных выборок. Критерий Манна-Уитни используется только для несвязных.

Ограничения критерия Манна-Уитни

Число испытуемых в группах при использовании критерия Манна-Уитни не должно быть больше 60 человек.
Минимальное число испытуемых – 3 человека в каждой группе.
Объем групп не должен быть строго одинаковым, но не должен сильно различаться.
Сравниваемые показатели могут быть как психологическими (тревожность, агрессивность, самооценка и пр.), так и не психологическими (успешность обучения, эффективность профессиональной деятельности и пр.)

«Почему вы выбрали для расчета критерий Манна-Уитни?»

Очень многих студентов-психологов перед защитой диплома пугает именно этот вопрос. Предлагаем в качестве основы для индивидуальных модификаций следующий ответ:

«В данной работе мы не проверяли данные на нормальность распределения, поэтому мы использовали непараметрический статистический критерий анна-Уитни, предназначенный для выявления различий показателей в двух несвязных выборках».

Важно понимать, что фактически этот вопрос означает следующее: «Почему вы выбрали критерий Манна-Уитни, а не критерий Стъюдента». Именно эти критерии наиболее часто используются для сравнительного анализа в психологических исследованиях.

Поэтому в ответе и надо указать, что на нормальность данные не проверяли, например, из-за небольшого объема групп. Поэтому решили остановиться на непараметрическом критерии.

Уровень статистической значимости

Если вы будет пользоваться для расчета критерия Манна-Уитни статистической программой, то в выдаче результатов будут присутствовать два важных показателя:

U – это, собственно, численное значение критерия. Для определения достоверности различий выраженности показателей в группах нужно сравнить полученное значение Uэмп с критическим значением из специальной таблицы – Uкр. Если Uэмп≤ Uкр, то различия выраженности показателей в группах статистически значимы.
р – уровень статистической значимости. Этот показатель присутствует при расчете всех статистических критериев и отражает степень точности вывода о наличие различий. В психологических исследованиях приняты два уровня точности:

р≤0,01 – вероятность ошибки 1%;
р≤0,05 – вероятность ошибки 5%.

Пример анализа данных с помощью критерия Манна-Уитни в дипломе по психологии

Результаты сравнительного анализа показателей жизнестойкости у молодежи и людей зрелого возраста

	Средние значения	U-критерий Манна-Уитни	Уровень статистической значимости (p)
	молодежь	люди зрелого возраста
Вовлеченность	32,9	40,9	673	0,000*
Контроль	27,2	28,3	1170,5	0,584
Принятие риска	17,9	14,4	686	0,000*
Жизнестойкость	78,0	83,6	1022,5	0,117

* — различия статистически достоверны (р≤0,05)

Анализ данных, приведенных в таблице, позволяет сделать следующие выводы:

Показатели по шкале «вовлеченность» в группе представителей старшего поколения статистически значимо выше, чем в группе представителей молодого поколения. Это означает, что люди зрелого возраста, по сравнению с молодежью, характеризуются более высокой вовлеченностью в происходящее, они в большей степени получают удовольствие от собственной деятельности. В то же время молодежь в большей степени, чем более зрелые люди, переживает чувство отвергнутости, ощущение себя «вне» жизни. Такой результат связан с психологическими особенностями возрастов: молодые люди еще не нашли своего места в жизни, что обуславливает их недостаточную вовлеченность в происходящее, в то же время зрелые люди в значительной степени укоренены в жизни, что позволяет им быть на более высоком уровне вовлеченности.

Показатели по шкале «принятие риска» в группе представителей молодежи статистически значимо выше, чем в группе представителей зрелого возраста. Это означает, что молодые люди, по сравнению с людьми зрелого возраста, характеризуются более высокой убежденностью в том, что все то, что с ним случается, способствует его развитию за счет знаний, извлекаемых из опыта, — неважно, позитивного или негативного. Молодые в больше степени, чем зрелые люди, рассматривают жизнь как способ приобретения опыта, готовы действовать в отсутствие надежных гарантий успеха, на свой страх и риск, считая стремление к простому комфорту и безопасности обедняющим жизнь личности.

Как показывают полученные данные, различия показателей жизнестойкости в группах представителей молодежи и людей зрелого возраста носят разнонаправленный характер, что в итоге предопределяет отсутствие различий в общем показателей жизнестойкости в группах испытуемых.

Итак, различия показателей жизнестойкости в группах представителей молодого поколения и людей зрелого возраста носят разнонаправленный характер: у молодежи в большей степени выражено принятие риска, а людей зрелого возраста – вовлеченность в происходящее. В итоге не выявлено различий в общем показателей жизнестойкости в группах испытуемых.

Источник

Назначение
критерия.
Данный
критерий предназначен для
оценки
достоверности различий по уровню
признака в двух независимых выборках.

Он
оценивает различие между двумя
выборками по уровню
какого-либо
признака, количественно измеренного.
Критерий является достаточно мощным
и позволяет выявить различия между
малыми
выборками,
когда объемы выборок от 3 до 60.

Чем
меньше
эмпирическое
значение критерия
,
темболее
вероятно, что различия достоверны.
Поэтому область
принятия гипотезы о существенных
различиях в уровне признака находится
слева от критического значения
,
а не справа, как в критерии
.

Ограничения
применения критерия

1. Измерение признака
должно быть произведено в шкале порядка,
интервалов или равных отношений.

2. Выборки должны
быть независимыми.

3.
Объемы обоих выборок от 3 до 60 (если же
,
то должно быть).

Гипотезы Обе выборки не различаются по уровню проявления данного признака.

Одна
выборка превосходит другую выборку по
уровню проявления данного признака.

Описание
действий

Шаг
1. Проранжировать
значения обеих выборок как одной,
приписывая меньшему значению меньший
ранг. Всего рангов получится столько,
чему равна сумма объемов двух выборок

Шаг
2. Подсчитать
сумму рангов в первой выборке
и второй выборке.
Проверить, совпадает ли общая сумма
рангов с расчетной суммой.

Шаг
3. Определить
бóльшую из двух ранговых сумм и
сформулировать гипотезы
и.

Шаг
4. Определить
значение
по формуле

где
– количество испытуемых в выборке 1;

–количество
испытуемых в выборке 2;

–бóльшая
из двух ранговых сумм;

–количество
испытуемых в группе с большей суммой
рангов;

—
номер выборки с большей суммой рангов.

Шаг
5. Определить
критическое значение
по таблице критических значений критерияМанна–Уитни для уровня статистической
значимости(или);
меньшее значениеищем в верхней строке, а большее значение— в левом столбце.

Шаг
6. Строим ось
значимости, на которой отмечаем
критическое значение
и эмпирическое значение.Чем меньше
значения
,
тем достоверность различий выше.

Если
,
то гипотеза «о сходстве»отклоняется на уровне значимости 0,05 (с
ошибкой 5%) и с достоверностью 0,95
принимается альтернативная гипотеза
о значимости различий в уровне проявления
признака.

Если
же
,
то говорят, что нет оснований для
отклонения гипотезыо сходстве уровней проявления признака
в двух выборках.

Область
принятия Область принятия

гипотезы
о различии
выборок гипотезы
осходстве
выборок

по
уровню признака по
уровню признака

Если
гипотеза «о сходстве»
по критерию

отклоняется на уровне значимости 0,05 (с
ошибкой 5%), то она отвергается и на уровне
значимости 0,01.

3. Задача на применение критерия Манна-Уитни

Задача.
У студентов физического и психологического
факультетов университета измерялся
уровень
невербального
интеллекта.

В
таблице приведены значения показателя
невербального интеллекта у 14 студентов
физического и 12 студентов психологического
факультетов.

Студенты — физики	Студенты — психологи
Номер испытуемого	Показатель невербального интеллекта	Номер испытуемого	Показатель невербального интеллекта
1	111	1	113
2	104	2	107
3	107	3	123
4	90	4	122
5	115	5	117
6	107	6	112
7	106	7	105
8	107	8	108
9	95	9	111
10	116	10	114
11	127	11	102
12	115	12	104
13	102
14	99

Можно ли
утверждать, что одна из выборок превосходит
другую по уровню невербального интеллекта?

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник