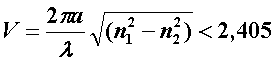Как найти критическую частоту

From Wikipedia, the free encyclopedia

In telecommunication, the term critical frequency has the following meanings:^[1]

• In radio propagation by way of the ionosphere, the limiting frequency at or below which a wave component is reflected by, and above which it penetrates through, an ionospheric layer.
• At near vertical incidence, the limiting frequency at or below which incidence, the wave component is reflected by, and above which it penetrates through, an ionospheric layer.

Critical Frequency changes with time of day, atmospheric conditions and angle of fire of the radio waves by antenna.

The existence of the critical frequency is the result of electron limitation, i.e., the inadequacy of the existing number of free electrons to support reflection at higher frequencies.

In signal processing the critical frequency it is also another name for the Nyquist frequency.

Critical frequency is the highest magnitude of frequency above which the waves penetrate the ionosphere and below which the waves are reflected back from the ionosphere.
It is denoted by «f_c«.
Its value is not fixed and it depends upon the electron density of the ionosphere.

Equations[edit]

Critical Frequency as a Function of Electron Density[edit]

Critical frequency can be computed with the electron density given by:

where N_max is maximum electron density per m³ and f_c is in Hz.^[2]

Critical Frequency as a Function of Maximum Usable Frequency Formula[edit]

Critical frequency can be computed by:

where MUF is maximum usable frequency and is the angle of incidence^[2]

Relationship with Plasma Frequency[edit]

The dependence of critical frequency with respect with electron density can be related through plasma oscillation concept particularly the ‘Cold’ Electrons mechanism.

Using the electron charge , electron mass and permittivity of free space gives,

and solving for the frequency,

Relationship with Index of Refraction[edit]

The index of refraction has the formula which shows dependence in wavelength.^[3] The result that the force due to the polarization field in an ionized gas of low concentration is canceled by the effect of collisions between ions and electrons is re‐established in a simple manner that clearly displays the physical basis for the effect. Because of this cancellation the Sellmeyer formula, determines the relation between the electron number density, N, and the index of refraction, n, in the ionosphere when collisions are neglected.^[4]

.

Using the default values for electron charge , permittivity of free space and electron mass , and changing angular velocity with respect to frequency this yields to

and solving for the refraction index n,

Critical Frequency and F layer of the Ionosphere[edit]

• All long-distance HF Radio Communications use HF Radio signals that are obliquely incident on the ionosphere, If the HF frequency is above Critical Frequency, the radio signals are passing through the ionosphere at an angle instead of head-on.^[5]
• The Critical Frequency is changing continuously and the F layer of the Ionosphere is mostly responsible for the reflection of radio waves back to Earth,
• The other layers(D) interact in other ways — absorption of frequency and during the day, the D Layers forms, and the F layer splits into F1 and F2 layers.
• Because of changing the Ionosphere during day and night, during daytime higher frequency bands under critical Frequency work best, but during nighttime the lower frequency bands work best.
• The D layer is present during the day and it is a good absorber of radio waves, increasing losses, Higher frequencies are absorbed less, so higher frequencies tends to perform better during daytime.
• The actual F2-Layer Critical Frequency Map link which refreshes every five minutes can be seen in this website http://www.spacew.com/www/fof2.html
• The Ionosphere and the Practical Maximum Usable Frequencies (MUFs) Map link which refreshes every five minutes can be seen in this website http://www.sws.bom.gov.au/HF_Systems/6/9/1

See also[edit]

• High Frequency
• High Frequency Active Auroral Research Program
• High Frequency Internet Protocol
• Low frequency
• Radio propagation
• Space weather

References[edit]

 This article incorporates public domain material from Federal Standard 1037C. General Services Administration. (in support of MIL-STD-188).

Страница 4 из 32

 РАСЧЕТ КРИТИЧЕСКИХ ЧАСТОТ В ВОЛНОВОДЕ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
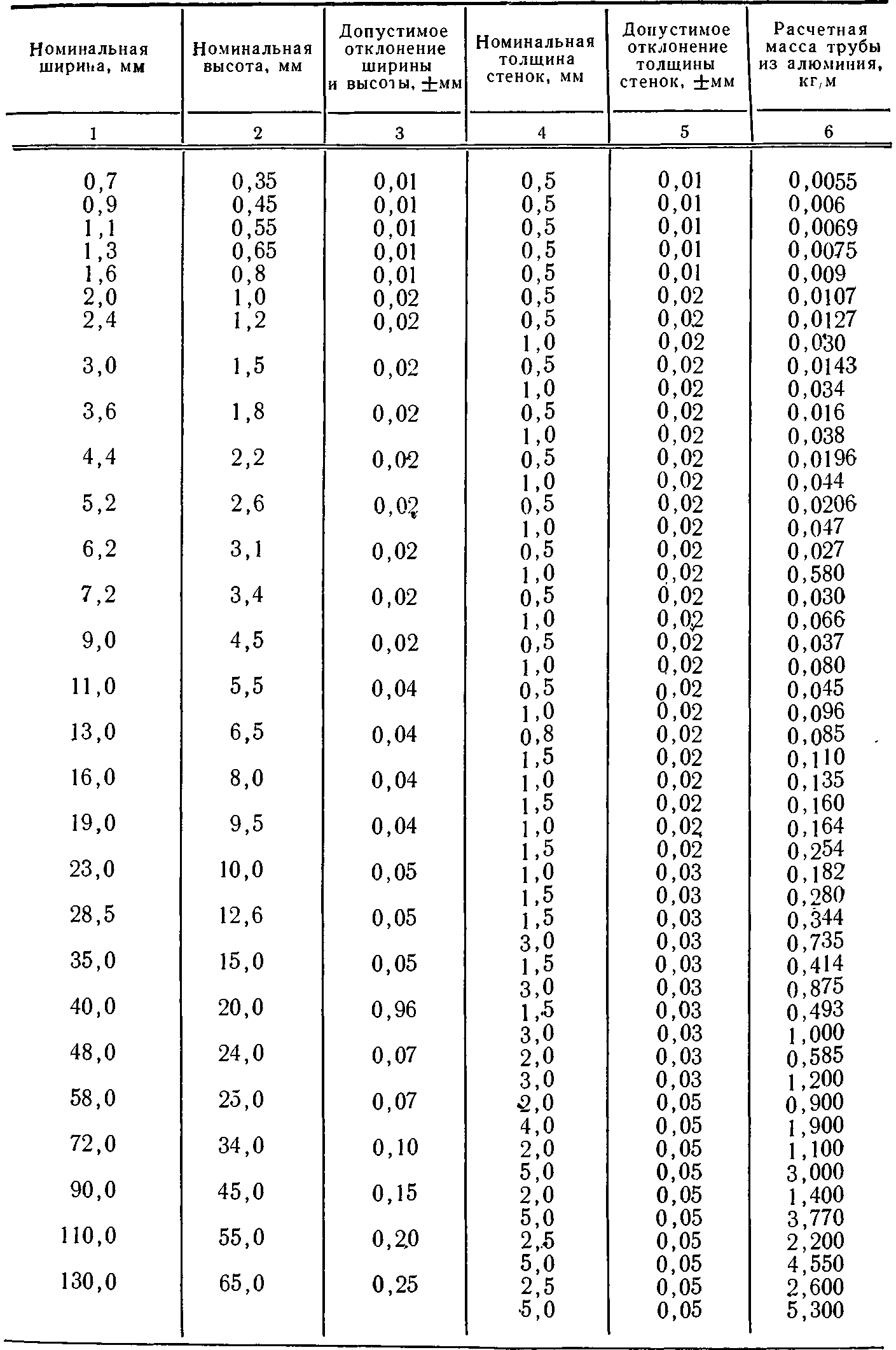
Критическая частота и длина волны волновода прямоугольного сечения могут быть определены по формулам (2.12) и (2.13). Эти формулы показывают, что чем больше индексы т и п, т. е. чем сложнее поле, тем выше критическая частота. Для разных значений т и п критические частоты для магнитных и электрических волн будут различными. При одинаковых значениях т и п для волн Е и Н критические частоты будут одинаковыми. Это является особенностью волноводов прямоугольного сечения.
В табл. 2.1 приведены расчетные формулы для определения критических длин и частот некоторых типов магнитных и электрических волн. Формулы для расчета критической частоты относятся к волноводу, который заполнен воздухом. При заполнении волновода другим диэлектриком в этих формулах вместо скорости света с следует подставлять значение скорости распространения электромагнитных волн в безграничном диэлектрике.
В табл. 2.2 в качестве примера приведены значения критических длин волн и критических частот для двух стандартных сечений волноводов.

Таблица 2.1
Формулы для расчета критических длин волн и частот волновода прямоугольного сечения

Таблица 2.2

Критические длины волн и частот для некоторых стандартных сечений волноводов

Для характеристики диапазонов волн, в пределах которых распространяются те или иные типы волн, часто строят так называемую диаграмму типов волн. Диаграмма строится для конкретного сечения волновода. На рис. 2.6 показана диаграмма для волновода сечением 48X24 мм². На этой диаграмме вдоль шкалы длин волн нанесены диапазоны, в пределах которых типы волн, указанные в табл. 2.1, распространяются в идеальном волноводе без затухания. Диаграмма типов волн, как показано на рис. 2.6, может быть разбита на три области.
В первой области λ>λ01, и ни один тип волны не может распространяться по волноводу. Во второй области λ20≤λ≤λ10, в волноводе может распространяться только один тип волны — H10. Данная область является областью основной волны в волноводе. Третья область характеризуется распространением в волноводе высших типов волн. В пределах этой области в волноводе может одновременно распространяться несколько типов волн.

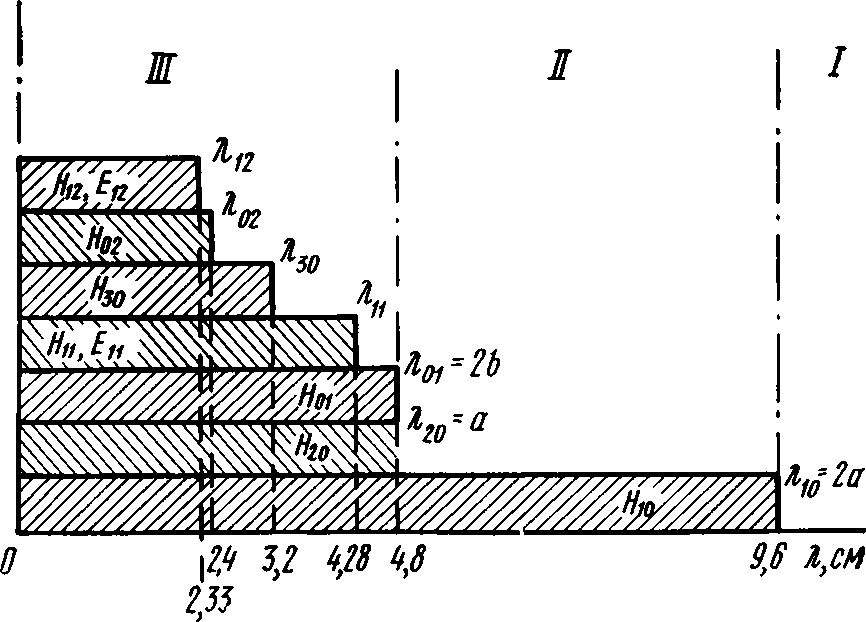
Рис. 2.6. Диаграмма типов волн в прямоугольном волноводе сечением 48×24 мм

В практике использования волноводов обычно стараются избегать одновременной передачи энергии несколькими типами волн, поскольку при этом могут иметь место нежелательные интерференционные явления, приводящие к значительной потере энергии. Кроме того, одновременное получение режима согласованной нагрузки для нескольких типов волн весьма затруднительно. Поэтому передачу энергии по волноводу ведут обычно на одном типе волны, как правило, используя основную волну. Во избежание передачи энергии волнами высших типов достаточно выбрать соответствующим образом размеры волновода.
Как видно из диаграммы типов волн (см. рис. 2.6), для того чтобы по волноводу распространялся только один тип волн, необходимо следующее условие:
a<λ<2a; λ≥2b.                                        (2.30)
Из этого условия следует, что больший размер прямоугольного волновода должен составлять, по крайней мере, половину длины волны. С другой стороны, для того чтобы исключить первую из волн типа Н высшего порядка, этот размер необходимо сделать меньше длины наикратчайшей из передаваемых волн. Учитывая указанные соображения, принимают отношение сторон b/а для прямоугольных волноводов равным примерно 1:2.
В тех случаях, когда не стремятся получить наибольшую мощность и минимальное затухание, а решающее значение имеет получение минимальных габаритов, размер b уменьшают и отношение h/a может быть значительно меньше 0,5.
Таблица 2.3
Рекомендуемые размеры волноводов прямоугольного сечения

Окончание табл. 2.3

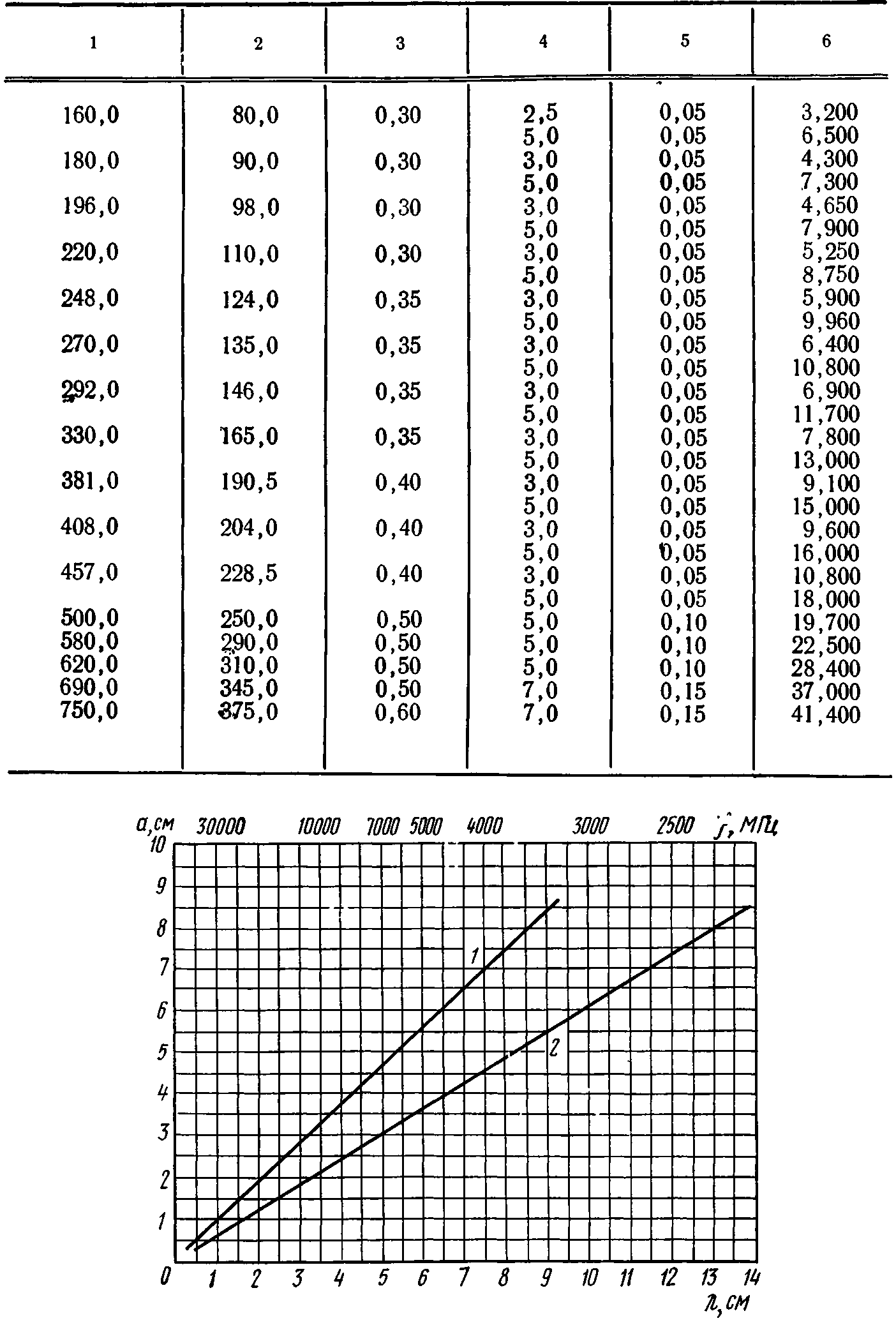
Рис. 2.7. Соотношение между размерами прямоугольных волноводов и рабочей длиной волны

Соотношение между размерами и рабочей длиной волны для прямоугольных волноводов показано на рис. 2.7. Две прямые линии с различным наклоном представляют соответственно верхние (прямая 1) и нижние (прямая 2) значения длин волн, в пределах которых целесообразно применять любой выбранный прямоугольный волновод поперечного размера а.
Рекомендуемые размеры волноводов прямоугольного сечения даны в табл. 2.3.

Международная электротехническая комиссия (МЭК) рекомендует размеры волноводов, приведенные в табл. 2.4. Наименования типов волноводов содержат цифру, которая выражает приблизительно среднюю частоту рекомендуемого диапазона частот. За единицу принимается 100 МГц. Так, например, МЭК-100 означает прямоугольный волновод, рассчитанный на среднюю частоту 10 ГГц.
Значения максимального затухания в табл. 2.4 даны для меди. Для других материалов рекомендуются следующие поправочные коэффициенты: 0,97 для серебра; 1,25 для алюминия; 1,19 для золота и 1,92 для латуни 70/30.

Таблица 2.4
Волноводы прямоугольного сечения, рекомендуемые МЭК

1. Критические частоты волноводных мод

Согласно
дисперсионным уравнениям (3.6) или (3.7),
продольное волновое число жестко связано
с поперечным волновым числом
и волновым числом среды, заполняющей
волноводИз (3.7) следует, что в зависимости от
того, какое из чисел окажется больше (или),
продольное волновое число может быть
либо вещественным, либо мнимым. Это
наглядно видно из рис. 3.2, где на числовой
оси отложено конкретное число.
В данном случае для первых двух мод– вещественное число, а для всех других
– мнимое. Если зафиксировать форму и
размеры поперечного сечения волновода
(а, следовательно, и все),
а также,
и изменять частоту, то из (3.7) нетрудно
видеть, что для каждой моды существует
частота, ниже которой продольное волновое
числостановится
мнимым. Эта частота называется критической
частотой данной моды. Ее легко найти из
(3.7), приравниваянулю:

(3.0)

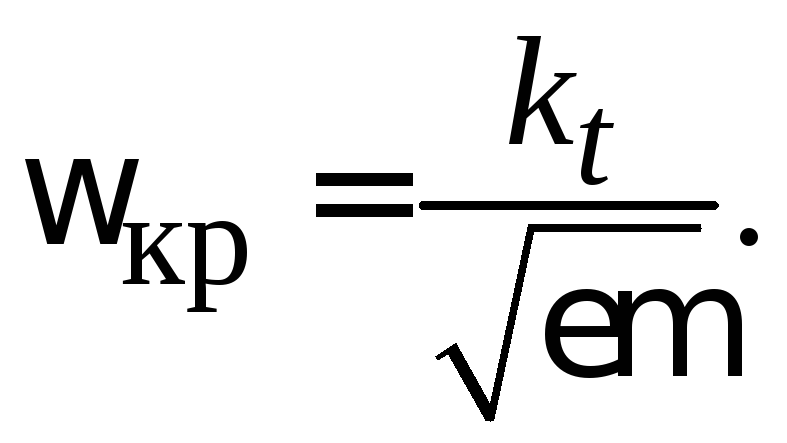
Таким
образом, критическая частота тем выше,
чем выше порядок моды и чем меньше
поперечные размеры волновода и меньше
и.
Волна основного типа имеет наименьшую
критическую частоту. Наряду с понятием
критической частоты используется
понятие, критической длины волны:

(3.0)

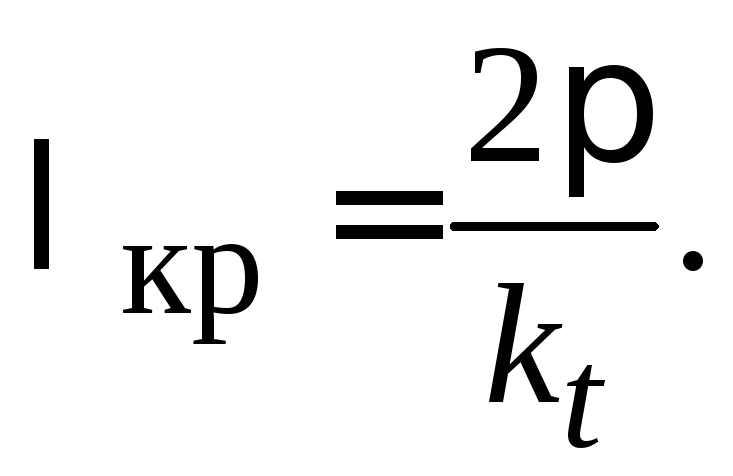
1. Поля мод на частотах выше и ниже критической

Поведение
одной и той же моды на частотах выше и
ниже критической, совершенно различно.
При
продольное волновое числовещественно, и мнимый экспоненциальный
множительвходящий в выражения (3.10), свидетельствует
о распространении волны вдоль волновода.
Модуль экспоненты не зависит отz(он равен единице), а ее фаза меняется в
зависимости отzпо линейному закону:Таким образом, в этом случае поля (3.10)
представляют собой незатухающие волны,
бегущие по волноводу в направлениях +zили –z(распространяющиеся волны). Если жето продольное волновое число– мнимая величина и экспонента в формулах
(3.10) – является вещественной функциейгде.
Фаза полей вдоль волновода не меняется,
а амплитуды либо экспоненциально
убывают, либо экспоненциально возрастают
в зависимости отz(рис. 3.3). Экспоненциальное убывание
(возрастание) будет тем круче, чем больше.
Такие «волны» называются не
распространяющимися волнами, они не
переносят мощность вдоль волновода.

Распространяющиеся
волны переносят мощность по волноводу,
ибо их поперечные компоненты поляиявляются синфазными.

1. Длина волны и фазовая скорость в волноводе

Для
распространяющихся волн вводится
понятие длины волны в волноводе
и фазовой скоростис учетом (3.12) формулы для них имеют вид:

(3.0)

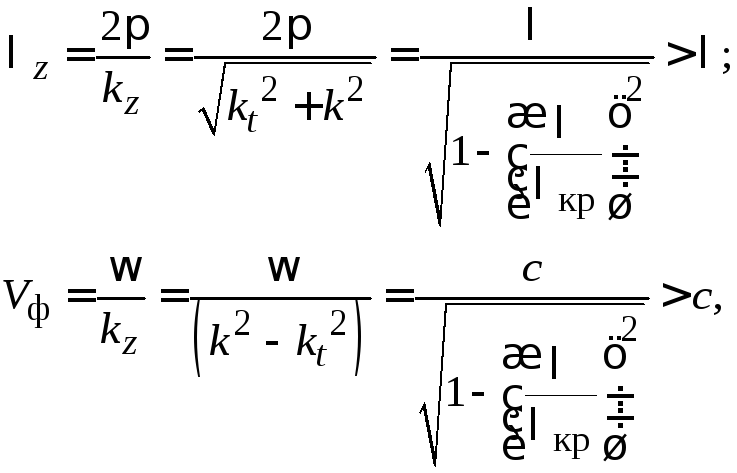
где
– длина волны в среде с проницаемостямии,
заполняющей волновод;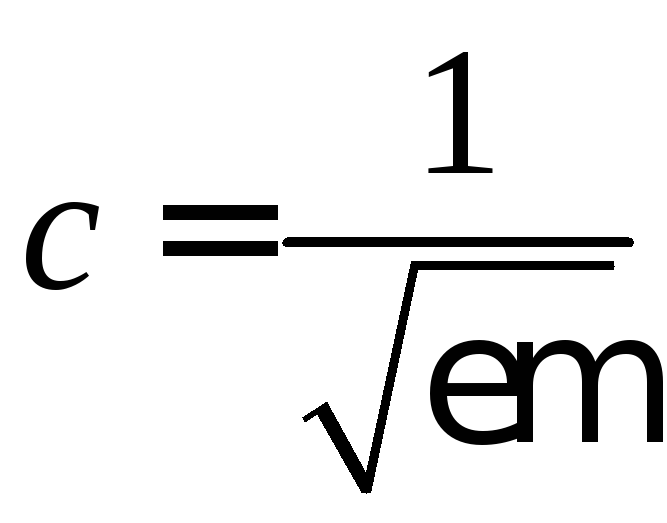– скорость света в среде, заполняющей
волновод.

Из
формул (3.13) следует, что в волноводе
длина волны
всегда больше длины волны в свободном
пространствеа фазовая скоростьбольше скорости света в свободном
пространстве(рис. 3.4).

1. Волна основного типа прямоугольного волновода h01

Решение
мембранного уравнения (3.5) в прямоугольном
волноводе дляН-волн (3.9) позволяет
найти:

1)
мембранную функцию с точностью до
амплитудного множителя С:

(3.0)

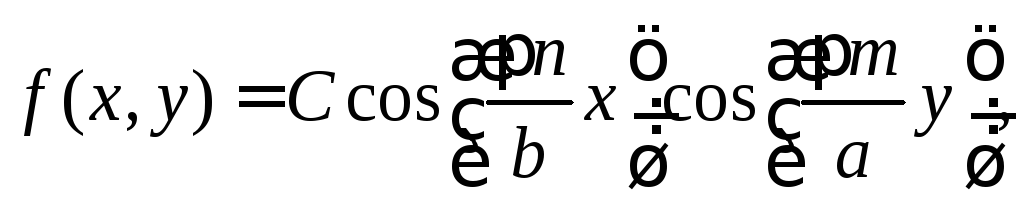
где
– поперечные размеры волновода
(рис. 3.1);– декартовые координаты поперечного
сечения прямоугольного волновода;

2)
поперечные волновые числа

(3.0)

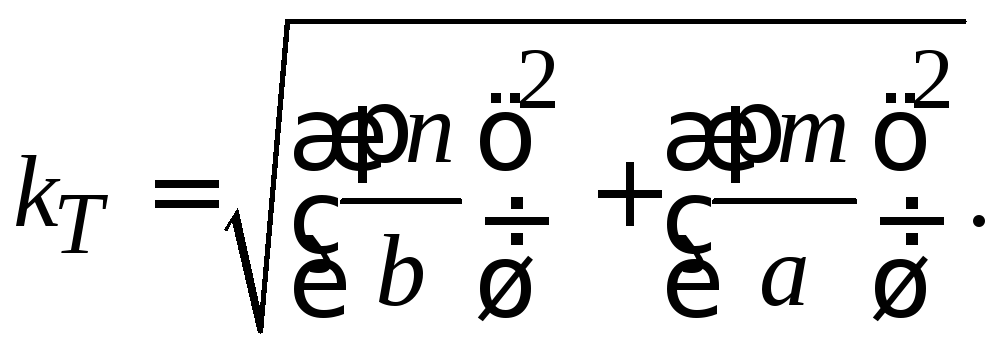
Так
как
,
то наименьшее поперечное волновое число
получается притогда для основного типа поля из (3.7),
(3.11)–(3.15) легко найти:

поперечное
волновое число (3.0)

критическую
длину волны (3.0)

критическую
частоту 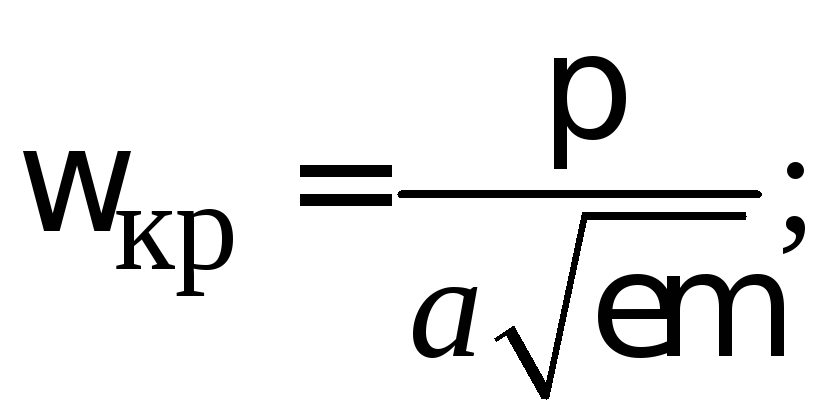(3.0)

длину
волны в волноводе 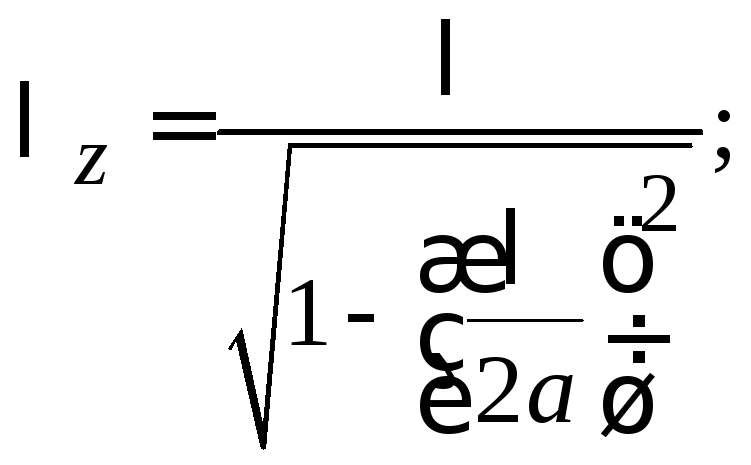(3.0)

фазовую
скорость в волноводе 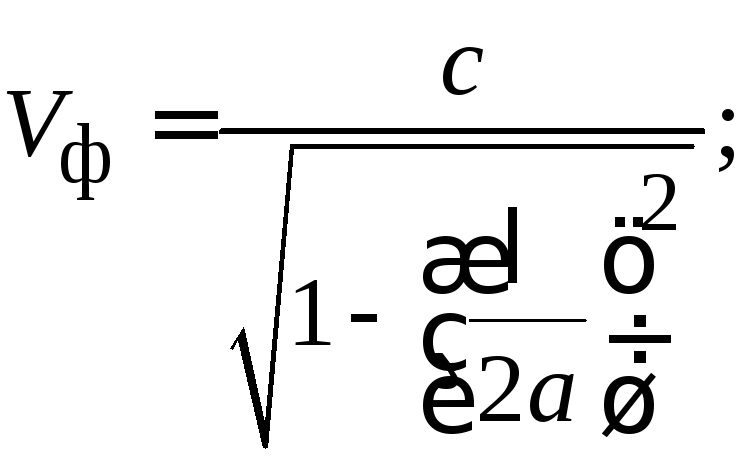(3.0)

продольное
волновое число 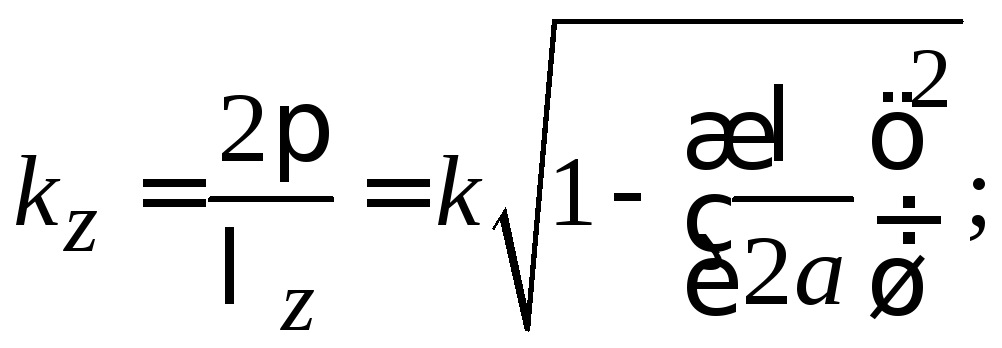(3.0)

мембранную
функцию 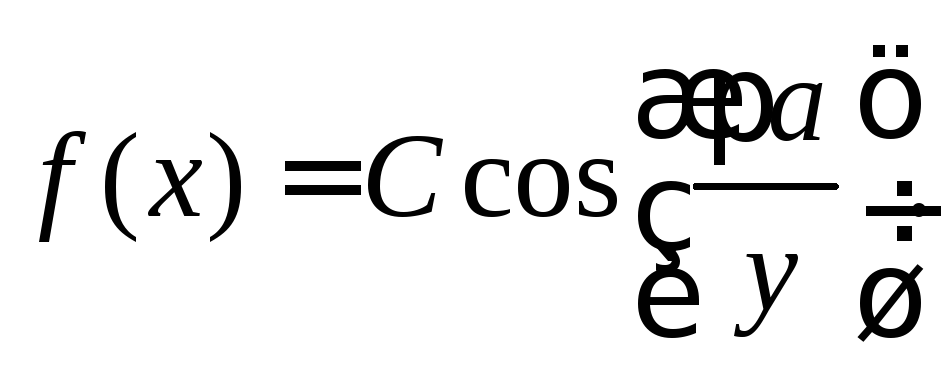(3.0)

Подстановка
(3.16)–(3.22) в уравнения (3.10) для полей
позволяет определить векторы напряженностей
электрического и магнитного поля волны
основного типа
в прямоугольном волноводе:

(3.0)

(3.0)

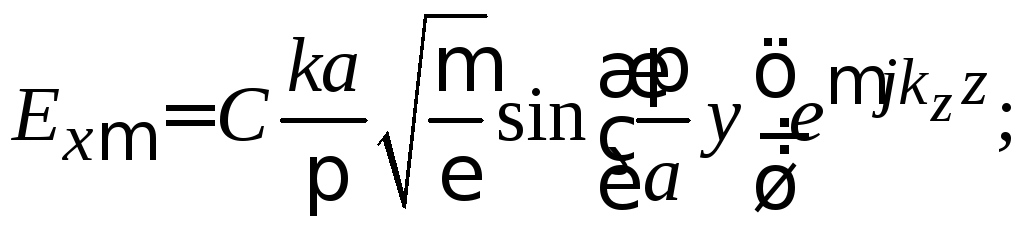
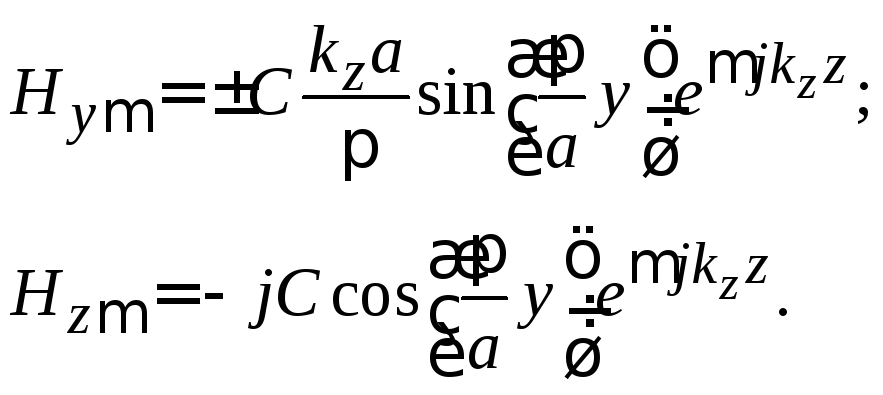
Обычно
для сравнения собственных функций
волновода между собой производится их
нормировка. Нормированные собственные
функции удобнее использовать в
электродинамических расчетах устройств
СВЧ. Вводится понятие нормы N:

(3.0)

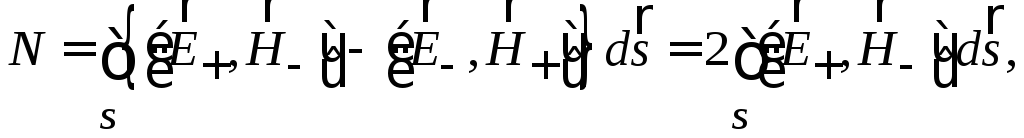
где
S– поперечное сечение волновода;

Подстановка
(3.23), (3.24) в (3.25) позволяет взять интеграл
и через норму определить амплитудный
коэффициент С:

(3.0)

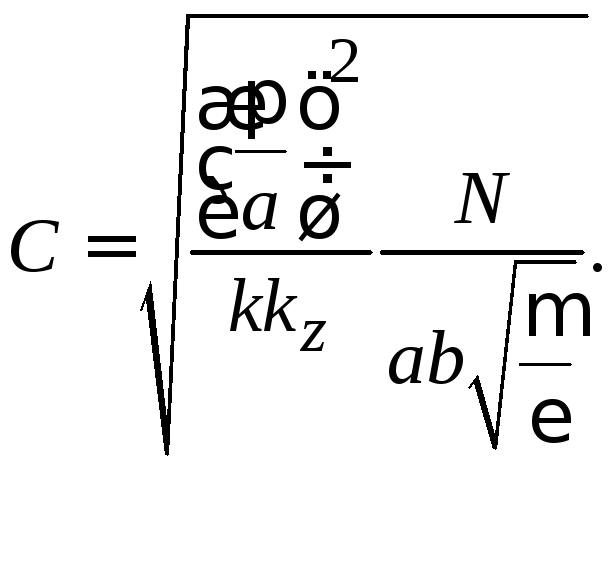
Подстановка
(3.26) в (3.23), (3.24) определяет нормированную
собственную функцию основного типа
прямоугольного волновода
:

(3.0)

(3.0)

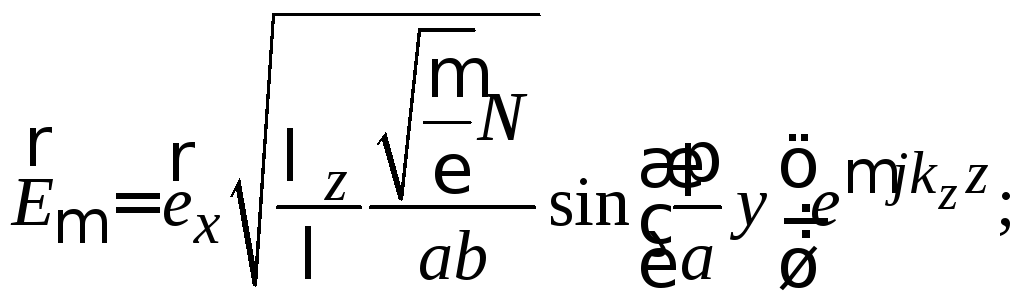
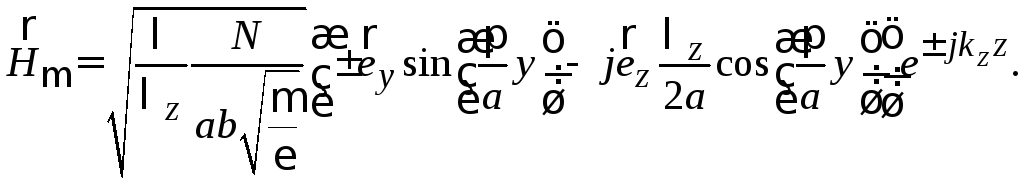
Введение
нормированных собственных функций
открывает возможность сокращенного
описания волнового режима в волноводе:
вместо подробной записи полей всех
имеющихся мод как функции координат
достаточно указать только их амплитуды.
Выбор величины нормы Nпроизволен, и чаще всего величина не
выбирается, а просто фиксируется как
константа, имеющая размерность мощности.
При определении мощности, переносимой
полем волновода, как правило, выбирают
величинуN = 1Вт.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В телекоммуникациях термин критическая частота имеет следующие значения:

• В распространении радиоволн через ионосферу, предельная частота, на которой или ниже которой отражается волновой компонент, а выше которого он проникает сквозь ионосферный слой.
• При падении, близком к вертикальному, предельной частоте, при которой или ниже этого падения, волновой компонент отражается от ионосферного слоя, а выше которого он проходит сквозь ионосферный слой.

Критично Частота меняется в зависимости от времени суток, атмосферных условий и угла распространения радиоволн антенной.

Существование критической частоты является результатом ограничения электронов, то есть недостаточности существующего количества свободных электронов для поддержки отражения на более высоких частотах.

В обработке сигналов критическая частота это также другое название для частоты Найквиста.

Критическая частота — это наибольшая величина частоты, выше которой волны проникают в ионосферу и ниже волны отражаются от ионосферы. Он обозначается как «f c ». Его значение не фиксировано и зависит от электронной плотности ионосферы.

Содержание

• 1 Уравнения
  • 1.1 Критическая частота как функция плотности электронов
  • 1.2 Критическая частота как функция от максимальной полезной частоты Формула
• 2 Связь с частотой плазмы
• 3 Связь с индексом рефракции
• 4 Критическая частота и слой F ионосферы
• 5 См. также
• 6 Ссылки

Уравнения

Критическая частота как функция плотности электронов

Критическая частоту можно вычислить с помощью электронной плотности, заданной по формуле:

fc = 9 N max { displaystyle f _ { text {c}} = 9 { sqrt {N _ { text {max}}}}}

где N max — максимальная концентрация электронов на метр, а f c в Гц.

Критическая частота как функция формулы максимальной полезной частоты

Критическую частоту можно вычислить следующим образом:

fc = MUF / sec θ { displaystyle f _ { text {c}} = MUF / sec theta}

, где MUF — максимальная используемая частота и θ { displaystyle theta}— угол падения

Взаимосвязь с плазмой F. Requency

Зависимость критической частоты от плотности электронов может быть связана с помощью концепции плазменных колебаний, в частности механизма «холодных» электронов.

ω pe = урожденная 2 м * ε 0, [рад / с] { displaystyle omega _ { mathrm {pe}} = { sqrt { frac {n _ { mathrm {e}} e ^ { 2}} {m ^ {*} varepsilon _ {0}}}}, left [ mathrm {rad / s} right]}

Использование заряда электрона e = 1.602 ⋅ 10 — 19 кулонов { displaystyle e = 1.602 cdot 10 ^ {- 19} кулонов}, масса электрона m ∗ = 9.10938356 ⋅ 10 — 31 килограмм { displaystyle m ^ { *} = 9,10938356 cdot 10 ^ {- 31} килограмм}и диэлектрическая проницаемость свободного пространства ϵ o = 8,854187817 ⋅ 10 — 12 A 2 с 4 м — 3 кг — 1 { displaystyle epsilon _ {o} = 8.854187817 cdot 10 ^ {- 12} A ^ {2} s ^ {4} m ^ {- 3} кг ^ {- 1}}дает,

ω pe = 2 π f = 56,415 ne { displaystyle omega _ { mathrm {pe}} = 2 pi f = 56,415 { sqrt {n_ {e}}}}

и решение для частоты

fc = 8,979 N max ≈ 9 N max { displaystyle f _ { text {c}} = 8,979 { sqrt {N _ { text {max}}}} приблизительно 9 { sqrt { N _ { text {max}}}}}

Взаимосвязь с показателем преломления

Показатель преломления имеет формулу n = cv { d isplaystyle n = { frac {c} {v}}}, который показывает зависимость в длине волны. Результат, заключающийся в том, что сила, обусловленная поляризационным полем в ионизированном газе с низкой концентрацией, компенсируется эффектом столкновений между ионами и электронами, восстанавливается простым способом, который ясно показывает физическую основу эффекта. Из-за этой отмены формула Селлмейера определяет соотношение между плотностью электронов N и показателем преломления n в ионосфере при столкновениях пренебрегают.

n 2 — 1 = — N e 2 ϵ om ω 2 { displaystyle n ^ {2} -1 = { frac {-Ne ^ {2}} { epsilon _ {o} m omega ^ {2}}}.

Использование значений по умолчанию для заряда электрона e { displaystyle e}, диэлектрической проницаемости свободного пространства и массы электрона ϵ o { displaystyle epsilon _ {o}}, и изменение угловой скорости ω { displaystyle omega}относительно частоты f { displaystyle f}это дает

n 2-1 = 3182,607 N (2 π f) 2 { displaystyle n ^ {2} -1 = { frac {3182.607N} {(2 pi f) ^ {2} }}}

и решение для показателя преломления n,

n = 1 — 80,616 N f 2 ≈ 1 — 81 N f 2 { displaystyle n = { sqrt {1 — { frac {80,616N } {f ^ {2}}}}} приблизительно { sqrt {1 — { frac {81N} {f ^ {2}}}}}

Критическая частота и слой F ионосферы

• Все дальние ВЧ R В adio Communications используются ВЧ-радиосигналы, которые падают на ионосферу под углом. Если ВЧ-частота выше критической частоты, радиосигналы проходят через ионосферу под углом, а не в лоб.
• Критическая частота — это изменяется непрерывно, и слой F ионосферы в основном отвечает за отражение радиоволн обратно на Землю,
• другие слои (D) взаимодействуют другими способами — поглощение частоты, а в течение дня D-слои формируется, а слой F разделяется на слои F1 и F2.
• Из-за изменения ионосферы днем ​​и ночью, днем ​​более высокие полосы частот в критической частоте работают лучше всего, но в ночное время лучше всего работают более низкие полосы частот.
• Слой D присутствует в течение дня и хорошо поглощает радиоволны, увеличивая потери. Более высокие частоты поглощаются меньше, поэтому более высокие частоты имеют тенденцию работать лучше в дневное время.
• фактическая ссылка на карту критических частот уровня F2 который обновляется каждые пять минут, можно увидеть на этом веб-сайте http://www.spacew.com/www/fof2.html
• Ссылка на карту ионосферы и практических максимальных используемых частот (МПЧ), которая обновляется каждые пять минут можно увидеть на этом веб-сайте http://www.sws.bom.gov.au/HF_Systems/6/9/1

См. также

Ссылки

Эта статья включает материалы общественного достояния из Администрации общих служб документ: «Федеральный стандарт 1037C».(в поддержку MIL-STD-188 )

Условием существования направляемой моды является экспоненциальное убывание её поля в оболочке вдоль координаты r, причём степень уменьшения напряжённости с ростом r определяется значением n, уменьшение которого приводит к перераспределению поля в оболочку ОВ – появлению вытекающих волн. При n=0 происходит качественное изменение волнового процесса, заключающегося в невозможности существования направляемой моды. Этот режим называется критическим, в связи с чем очень важно определение условий его возникновения, что можно осуществить подстановкой в последнее уравнение значения n=0, в результате чего правые части уравнений обращаются в бесконечность и для Е и Н мод будет справедливо условие [7]

I₀`(cr)=0, (3.3.1)

которое определяет границы их возникновения или исчезновения.

Последнее уравнение имеет бесчисленное множество решений, поэтому, обозначив положительный корень через p_0m, а также используя выражения для c и n, мы получим

.

Введём величину, которая носит название нормированной частоты

(3.3.2)

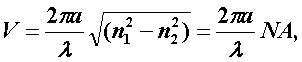
где а – радиус сердцевины волокна.

Это один из важнейших обобщающих параметров, используемых для оценки свойств ОВ, который связывает его структурные параметры и длину световой волны, распространяемой в волокне.

С увеличением радиуса сердцевины волокна величина V растет, а с увеличением длины волны уменьшается. В табл. 3.1. приведены соотношения нормированной частоты, длины волны и радиуса сердцевины при различных значениях коэффициента преломления оболочки (n₁=1,51) [11].

Таблица 3.1 – Соотношения для нормированной частоты

Одномодовый режим реализуется, если нормированная частота V≤2,405.Чем меньше разность ∆n=n₁—n₂, тем при большем радиусе световода обеспечивается одномодовый режим.

В этом случае:

(3.3.3)

и при n=0 для каждого из корней имеет место критическое значение нормированной частоты:

P_0m = c_кр а = V_0m, где m = 1,2,3,…M, а

p₀₁ = 2,405; p₀₂ = 5,520; p₀₃ = 8,654 и т. д.

Если для некоторой симметричной моды нормированная частота больше её критического значения (V>V_0m), то она распространяется в ОВ, в противном случае – нет. Так, при 2,405<V<5,520 в ОВ распространяются моды Е₀₁ и Н₀₁, а при 5,520<V<8,654 к ним добавляются моды Е₀₂ и Н₀₂ и т.д., в то время как неравенство V<2,405 указывает на отсутствие симметричных мод.

Последняя формула позволяет определить значения критических длин волн l_0m^кр для симметричных волн в виде [2]

, (3.3.4)

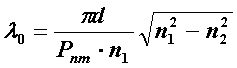
или, переходя к частоте,

. (3.3.5)

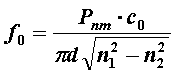
Очевидно, что для распространяющейся моды должно выполняться условие l<l_0m^кр, то есть V>V_0m, в противном случае этой моды нет.

В отличие от симметричных мод несимметричные имеют все шесть составляющих векторов электромагнитного поля и их невозможно разделить на электрические и магнитные. Критическая нормированная частота в этом случае определяется выражением [7]

V_nm = p_nm, n = 1, 2, 3 … N; m = 1, 2, 3, … M, (3.3.6)

где p_nm – положительный корень соответствующего трансцендентного уравнения, который характеризует тип волны (моду) и может быть определен из таблицы 3.2 [11]

Таблица 3.2 – Значения корней трансцендентного уравнения

Среди направляемых мод особое положение занимает мода НЕ₁₁, у которой критическое значение нормированной частоты n = 0. Это основная (фундаментальная) мода ступенчатого ОВ, так как она распространяется при любой частоте и структурных параметрах волокна. С точки зрения геометрической оптики, она образуется лучом, вводимым вдоль оси волокна, так как только характеристики такого луча не зависят от условий отражения на границе «сердцевина – оболочка». Выбирая параметры ОВ, можно получить режим распространения только этой моды, что реализуется при условии

. (3.3.7)