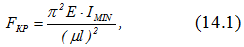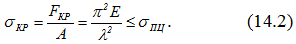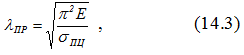Критическая нагрузка
Критическая нагрузка – это нагрузка, превышение которой вызывает потерю устойчивости прямолинейной формы равновесия стержня. Критическую нагрузку обозначают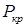 
. Можно утверждать, что достижение сжимающей нагрузкой критического значения равносильно разрушению стержня, так как неустойчивая прямолинейная форма равновесия неминуемо будет утрачена (стержень изогнется), что, приведет к практически неограниченному росту напряжений.
При потере устойчивости при превышении критической нагрузки прямолинейная ось стержня искривляется. Форма потери устойчивости — конфигурация изогнутой оси стержня. Форма потери устойчивости зависит от условий закрепления стержня и места приложения сжимающей нагрузки по его длине.
Критическая
нагрузка это нагрузка, соответствующая
началу возникновения в грунте зон
сдвигов и окончанию фазы уплотнения,
когда под краем нагрузки возникают
между касательными и нормальными
напряжениями соотношения, приводящие
грунт (сначала у ребер подошвы фундамента)
в предельное напряженное состояние.
Эту нагрузку называют начальной
критической нагрузкой. Она совершенно
безопасна в основаниях сооружений, так
как до ее достижения грунт всегда будет
находиться в фазе уплотнения.
Начальная
критическая нагрузка характеризует
пределы применимости теории
линейно-деформируемой среды.
Начальная
критическая нагрузка характеризует
пределы применимости теории
линейно-деформируемой среды. Если
давление на грунт не превышает эту
нагрузку, то ни в одной точке грунтового
массива касательное напряжение не
превосходит предельное. При превышении
же этой нагрузки в грунте происходит
формирование зон предельного состояния.
Начальным критическим
давлением на основание называется то
значение давления, при котором в грунте
основания возникают области предельного
напряженного состояния. При давлениях
меньших начальных критических значений
во всех точках основания (рис. 6.5)
напряженные состояния допредельные,
что совершенно безопасно для оснований
сооружений. В этом случае до достижения
начального критического давления грунт
находится в фазе уплотнения (см. рис.
6.6) и подход к ее определению демонстрируется
для полосовой нагрузки на грунт. На рис.
8.5 представлены ее реальная и расчетные
схемы.
Рис. 8.5. Реальная
(а) и расчетные (б, в, г) схемы к определению
начального критического давления
Для нахождения
начального критического давления
значения главных напряжений σ1 и σ3
определяются с учетом приложенной
нагрузки Р = Р0— q и соответственно веса
грунта.
Вертикальное
сжимающее напряжение (давление) от
собственного веса грунта в точке М (см.
рис. 8.5,в), лежащей на глубине z от подошвы
фундамента, определяется из выражения
(8.18)
Полные главные
напряжения в грунте на глубине :
(8.19)
(8.20)
На площадках
сдвига, когда грунт от действия нагрузки
находится в конце среза уплотнения,
имеет место предельное равновесие:
(8.21)
Тогда, подставив
(8.19) и (8.20) в (8.21), получим уравнение кривой,
соответствующей границе пластической
зоны грунта:
(8.22)
Выражение (8.22)
можно рассматривать как уравнение
границы области, проходящей через точку
М (см. рис. 8.5,в), на контуре которой при
действии под подошвой фундамента
давления Р имеет место состояние
предельного равновесия. Координаты
точек этой границы определяются
неизвестными z и α.
Решая уравнение
(8.22) относительно z, получим:
(8.23)
Приравняв первую
производную этого выражения по α нулю,
находим максимальную глубину границы
этой области zmax, где площадка скольжения
получает опасный наклон к горизонту:
(8.24)
Из уравнения (8.24)
следует, что при z = zmax, cosα = sinφ или α =
π/2-φ
(8.25)
Тогда, подставляя
(8.25) в формулу (8.24), получаем выражение
для низкой точки сдвига грунта (zmax) в
следующем виде:
(8.26)
Решая это относительно
Р = Рсr найдем такое значение критического
давления, при котором область предельного
равновесия развивается на заданную
глубину zmах:
(8.27)
Исходя из условия,
что начальное критическое давление
соответствует отсутствию пластических
деформаций во всех точках основания,
т.е. zmax = 0, имеем
формула (8.28)
Это и есть формула
для определения начального критического
давления на грунт основания. Формула
(8.28) (при с = 0) была получена Н.П. Пузыревским
(1923) и, как правило, называется его именем.
Практика показывает, что фундамент,
спроектированный таким образом, что
давление под его подошвой не превышало
бы начального критического давления,
будет иметь экономически невыгодные
размеры.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Лабораторная работа №14 по испытанию на устойчивость прямого стального стержня при его продольном изгибе.
Цель работы – исследовать явление потери устойчивости прямолинейной формы равновесия при осевом сжатии, проверить опытным путем справедливость формулы Эйлера.
Основные сведения
У стержней, длина которых значительно больше поперечных размеров, при определенной величине осевой сжимающей силы происходит искривление оси. Это явление носит название продольного изгиба. Переход прямолинейной формы равновесия в криволинейную называется потерей устойчивости.
Сжимающая сила, при которой прямолинейная форма равновесия перестает быть устойчивой, называется критической. Ее можно определить по формуле Эйлера
где Е – модуль продольной упругости материала;
l – длина стержня;
Imin – минимальный момент инерции сечения;
μ – коэффициент приведения длины, который зависит от способов закрепления концов стержня.
Формула Эйлера применима лишь в том случае, если потеря устойчивости стержня происходит при напряжениях, меньших предела пропорциональности σпц, т.е. когда справедлив закон Гука
Здесь А – площадь поперечного сечения;
λ=μ∙l/imin – гибкость стержня;
– минимальный радиус инерции сечения.
Предельная гибкость, начиная с которой можно использовать формулу Эйлера, определяется по формуле
зависит лишь от физико-механических свойств и является постоянной для данного материала.
Так, например, для стали Ст.З λпр = 100, для древесины λпр = 110, для чугуна λпр = 80, для дюралюминия λпр = 60.
Стержни, у которых λ > λпр, называются стержнями большой гибкости.
При меньших значениях гибкости (стержни средней гибкости) критические напряжения σкр > σпц определяются по эмпирическим формулам или соответствующим им таблицам (графикам). Например, формула Ясинского для определения критических напряжений имеет вид
σкр = a – bλ, (14.4)
где a и b – эмпирические коэффициенты.
Например, для стали Ст.3 a = 310 МПа, b = 1,14 МПа, для древесины (сосна) a = 28,7 МПа, b = 0,19 МПа.
Эмпирические формулы, особенно для древесины, дают лишь приближенный результат.
Для стержней малой гибкости, у которых σкр, подсчитанные по формуле Ясинского, получаются больше, чем опасные (предельные) напряжения, принимают:
σкр = σт – для пластичных материалов;
σкр = σпч – для хрупких материалов.
Порядок выполнения и обработка результатов
Опыты по исследованию устойчивости сжатых стержней производятся либо на испытательных машинах малой мощности (Р-5 и других), либо на специальных установках, например, СМ-20.
На испытательных машинах величина критической силы определяется непосредственно по шкале динамометра.
На установке СМ-20 (рис. 14.1) нагружение производится с помощью винтовой пары (подъемный винт-гайка) через тарированную пружину; величина нагрузки определяется по осадке пружины δ, которая пропорциональна сжимающей силе:
F = С · δ,
где С – жесткость пружины, определяется из тарировочного графика.
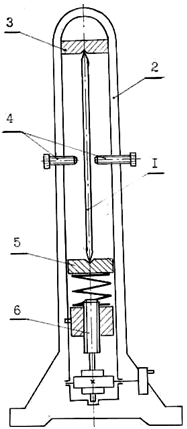
Рис. 14.1. Схема установки СМ-20:
1 – образец; 2 – корпус; 3 – верхняя опора;
4 – ограничительные упоры;
5 – нижняя опора; 6 –силовое устройство
Установка СМ-20 позволяет определить критическую силу для стержня с шарнирно опертыми концами (μ = 1).
Порядок проведения испытаний и обработки результатов следующий.
- Измеряем длину и размеры поперечного сечения образца, определяем геометрические характеристики сечения и гибкость стержня (Imin, A, imin, λ).
- Сравниваем значения λ и λпр, выясняем, по какой формуле следует определять критическую силу.
- Вычисляем теоретическое значение критической силы.
- Устанавливаем стержень на опорах установки.
- Упоры при помощи винтов устанавливаем примерно на одинаковых расстояниях (2 – З мм) от испытуемого образца.
- Производим нагружение стержня путем плавного и медленного вращения маховика по часовой стрелке, с возрастанием нагрузки нужно непрерывно следить за поведением образца.
Если при F < Fкр слегка изогнуть стержень рукой и отпустить, после некоторых колебаний он вновь выпрямится (устойчива прямолинейная форма равновесия).
С увеличением нагрузки частота собственных колебаний уменьшается, и при критической нагрузке она равна нулю.
При достижении нагрузкой критического значения стержень слегка искривляется и касается одного из упоров. Если изогнутый стержень руками вернуть в исходное прямолинейное положение и отпустить, он вновь искривится, т.е. прямолинейная форма перестала быть устойчивой. - Снимаем отсчет по шкале осадки пружины δ и заносим его в журнал испытаний, разгружаем образец вращением маховика против часовой стрелки.
- Определяем по паспорту установки коэффициент жесткости пружины С.
- Вычисляем опытное значение критической силы
Fкр оп= С · δ. - Сравниваем величины Fкр оп и Fкр т, определяем процент расхождения и делаем соответствующие выводы.
Контрольные вопросы
- Какой изгиб называется продольным?
- Что понимается под критической силой?
- От чего зависит величина критической силы?
- Когда применима формула Эйлера?
- Что такое коэффициент приведения длины и чему он равен при различных случаях закрепления концов сжатых стержней?
- Как определяется критическое напряжение, если формула Эйлера неприменима?
- Чему равна гибкость стержня?
- Как определить предельную гибкость?
- Как опытным путем определить значение критической нагрузки?
Определение ударной вязкости >
Краткая теория >
Примеры решения задач >
Расчет потери устойчивости по методу эффективной ширины или методу приведенного напряжения основан на определении критической нагрузки системы, в дальнейшем называемой LBA (линейный расчет потери устойчивости). В этой статье объясняется аналитический расчет критического коэффициента нагрузки, а также использование метода конечных элементов (МКЭ).
Критические факторы нагрузки, связанные с напряжением
[1] предоставляет следующее уравнение (гл. 10, уравнение 10.6) для чисто аналитического определения коэффициента критической нагрузки на изгибающуюся панель:
Формула 1
1αcr = 1 ψx4 · αcr,x 1 ψz4 · αcr,z 1 ψx4 · αcr,x 1 ψz4 · αcr,z2 1 — ψx2 · αcr,x2 1 — ψz2 · αcr,z2 1αcr,τ21/2
Как видите, отношения напряжений, а также коэффициенты критических нагрузок определяются отдельно для отдельных компонентов напряжения или должны быть известны. Коэффициенты критической нагрузки можно определить путем пересчета критических напряжений потери устойчивости пластины. Это определение уже объяснялось в этой технической статье .
Таким образом, для отдельных компонентов напряжения получаются следующие соотношения:
Формула 2
αcr,x = σcr,p,xσx,Edαcr,z = σcr,p,zσz,Edαcr,τ = τcr,pτEd
Этот метод особенно подходит для неупругих или продольно-жестких пластин потери устойчивости, для которых применяются соответствующие значения потери устойчивости из [2] или [3] .
Расчет с использованием конечного элемента An
Если имеется сильно усиленная пластина потери устойчивости с продольными и поперечными ребрами жесткости, для определения критической нагрузки на всю конструкцию следует использовать расчет методом конечных элементов. В качестве основы следует применить модель поверхности и учесть все граничные условия (например, опоры на краях, геометрическое положение и нагрузку на ребро жесткости, а также граничные напряжения). Для определения в соответствии с LBA применяется поведение упругого материала. В следующем примере показано моделирование продольно усиленной пластины потери устойчивости в программе RFEM.
Дополнительный модуль RF-STABILITY используется для определения критического коэффициента нагрузки. При выборе формы колебаний необходимо учитывать общий сбой системы.
1-й Собственная форма в этом примере показывает глобальную потерю устойчивости и поэтому должна рассматриваться как решающая. Однако в некоторых случаях при проектировании могут быть использованы более высокие формы колебаний. Таким образом, коэффициент критической нагрузки может быть рассчитан для всех составляющих напряжения, а также отдельно (только одна составляющая напряжения на случай нагружения).
Автономная программа PLATE-BUCKLING позволяет выполнить полный расчет потери устойчивости с использованием метода приведенных напряжений, включая автоматическое определение собственных значений для каждого компонента напряжения.
Коэффициент критической нагрузки при расчете потери устойчивости
Теперь можно либо определить отдельные коэффициенты критической нагрузки, либо аналитически рассчитать общий коэффициент критической нагрузки, используя уравнение. 10.6, приведенные в [1] , или использовать их непосредственно из расчета МКЭ. В некоторых случаях аналитическое решение можно рассматривать как консервативное. Таким образом, PLATE-BUCKLING предоставляет следующие возможности.
