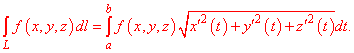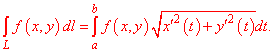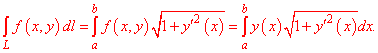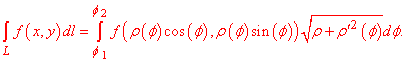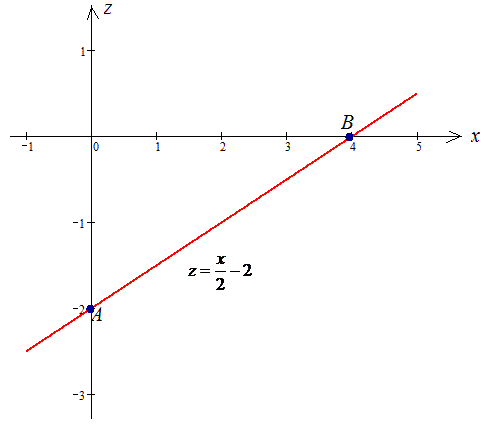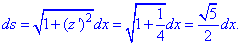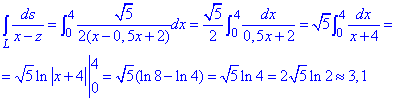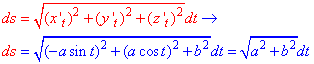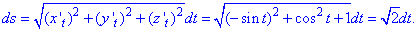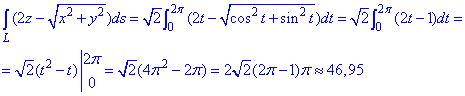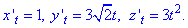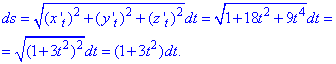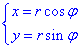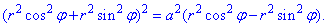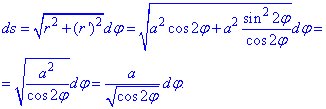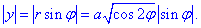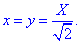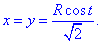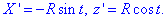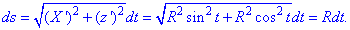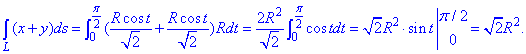Как найти криволинейный интеграл по прямой

Определенные интегралы в случаях когда интегрирование проводится не вдоль отрезка, а некоторой кривой (на плоскости или в пространстве) называются криволинейными. Различают криволинейные интегралы І и ІІ рода.

Формулы криволинейного интегралу первого рода

Пусть в пространстве (на плоскости) задано параметрическое уравнение гладкой кривой f (x, y, z)
x=x(t), y=y(t), z=z(t).
tє[a, b].
Каждая из функций непрерывна на промежутке интегрирования.
Функция f(x, y, z)=0 описывает кривую в пространстве.
В таком случае криволинейный интеграл первого рода равен интегралу за параметром от функции умноженной на корень квадратный из суммы квадратов производных координат за параметром

Для случая кривой на плоскости формула неопределенного интегралу I роду упрощается

Когда кривая интегрирования задана явно y=y(x), формула перехода к определенному интегралу имеет вид

Пусть функция задана полярными координатами rho=rho(phi), phi₁<phi<phi₂. Тогда криволинейный интеграл первого рода вдоль кривой вычисляется по формуле

На этом все формулы, что Вам нужны для вычисления интегралов, однако без готовых ответов трудно представить их приложение, поєтому перейдем к практической части.

Примеры подобрано из учебной программы для студентов ЛНУ им. И. Франко. Они охватывают широкий класс заданий, которые непременно встретите на контрольной работе и экзаменах. Поэтому внимательно разберите ответы к примерам и выучите приведенные наверху формулы вічисления криволинейных интегралов.

Пример 1.7 Вычислить криволинейный интеграл 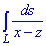вдоль дуги L — отрезок прямой z=x/2-2, что соединяет точки A(0;- 2) и B(4;0) в плоскости xOz.
Решение: Построим графически прямую и нанесем на нее точки ограничивающие дугу

За видом видим, что необходимо вычислить криволинейный интеграл I рода.
z=x/2-2, z’=1/2.
Подынтегральная функция примет значение
1/(x-z)=1/(x -(x/2-2))=1/(0,5x+2).
Найдем дифференциал дуги заданной кривой по формуле

Подставляем и находим криволинейный интеграл

Неопределенный интеграл сводится к логарифму, который не имеет особенностей (гладкая функция) на промежутке интегрирования.

Пример 1.10 Вычислить криволинейный интеграл вдоль дуги L:
, где L — дуга кривой x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
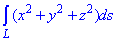
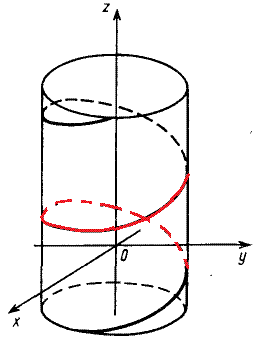
Решение: Параметрическая кривая x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi] описывает часть винтовой линии.
Ее график на цилиндрической поверхности имеет вид.

Часть винтовой линии, которая отвечает промежутку [0;2pi] изображена красным цветом.
Подынтегральная функция равна x²+y²+z².
Нужно вычислить криволинейный интеграл I рода.
Находим производные координат по параметру
x’_t=a*sin(t), y’_t=a*sin(t), z’_t=b.
Дальше вычисляем дифференциал дуги параметрически заданной кривой согласно формуле:

Формулы дифференциалу дуги в декартовой, полярной и пространственной системах координат приведены в теоретическом материале и поэтому здесь на них задерживаться не будем.
Интегрированием вычисляем криволинейный интеграл

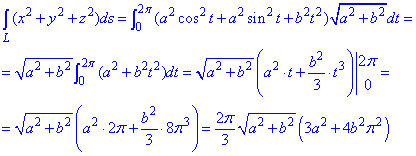
Интеграл не сложен в плане расчетов.

Пример 1.12 Вычислить криволинейный интеграл 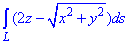вдоль дуги L, где L — дуга кривой x=cos(t), y=sin(t), z=t [0;2pi].
Решение: Имеем идентичное уравнение x=cos(t), y=sin(t), z=t — винтовой линии.

Для вычисления криволинейного интеграла I рода находим производные координат
x’_t=-sin(t), y’_t=cos(t), z’_t=1.
Подставляем их в дифференциал дуги винтовой линии:

Превращаем подінтегральную функцию и находим криволинейный интеграл

Пример 1.14 Вычислить криволинейный интеграл int(x+y, dS)
вдоль дуги L — дуга кривой x=t, , z=t^₃, [0;1].
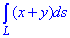
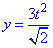
Решение: Прежде чем вычислить криволинейный интеграл I рода находим производные за параметром.

Подставляем их в формулу дифференциала дуги:

Определенный интеграл вычисляем в указанных пределах

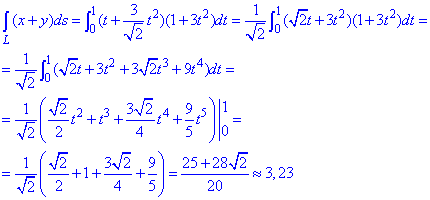
Под интегралом раскрыли скобки и применили простые формулы интегрирования.

Пример 1.18 Вычислить криволинейный интеграл int (1/x²+y²+z²,ds)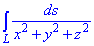
вдоль дуги кривой L:
x=a*cos(t), y=a*sin(t), z=b*t, t[0;2pi].
Решение: Интегрировать опять придется вдоль винтовой линии.

Производные за параметром имеют вид
x’_t=-a*sin(t), y’_t=a*sin(t), z’_t=b.
Вычисляем дифференциал дуги кривой:

Дальше превращаем криволинейный интеграл к определенному и находим его значение

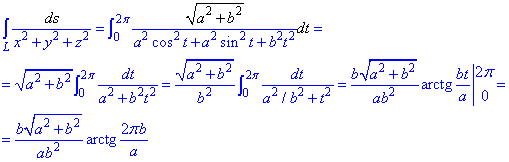
При интегрировании будем иметь арктангенс.
В результате вычислений получили компактную формулу через параметры формы цилиндра.

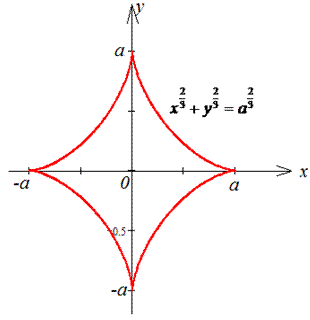
Пример 1.20 Вычислить криволинейный интеграл int(x^4/3+y^4/3,ds) вдоль дуги L:
дуга астроиды x^2/3+y^2/3=a^2/3.
Решение: Запишем параметрическое уравнение астроиды:
x=a*cos³(t), y=a*sin³(t), где t[0;2pi].
График астроиды в декартовой системе координат имеет вид

Для вычисления криволинейного интеграла I рода вычисляем производные за параметром
x’_t=-3a*cos²(t)*sin(t), y’_t=3a*cos(t)*sin²(t).
и подставляем в дифференциал дуги астроиды:

Криволинейный интеграл 1 рода находим методом замены переменной

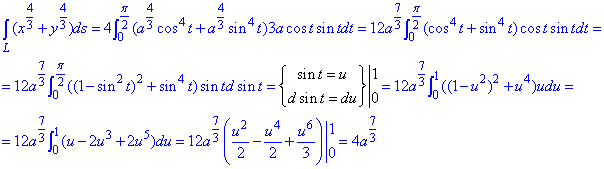
Это позволяет перейти к простому понятному виду подынтегральной функции.

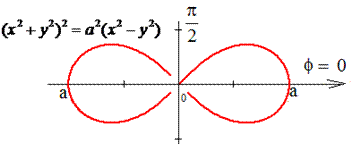
Пример 1.21 Вычислить криволинейный интеграл 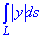вдоль дуги лемнискаты (x²+y²)²=a²(x²-y²).
Решение: Для лемнискаты раньше рассматривали интегралы на нахождение площади.

Запишем уравнение лемнискаты в полярной системе координат, используя превращение координат:

Тогда из уравнения дуги

выражаем радиус-вектор и вычисляем производную за углом

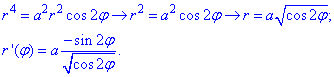
Найдем дифференциал дуги по формуле:

Запишем подынтегральную функцию:

Вычисляем криволинейный интеграл первого роду как 4 интеграла по 1 четверти

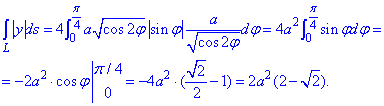
Синус в первой четверти положителен, поэтому модуль опускаем.

Пример 1.25 Вычислить криволинейный интеграл вдоль дуги L:
, где L — четверть круга x²+y²+z²=R², y=x что лежит в первом октанте.
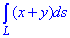
Решение: Имеем сферу x²+y²+z²=R² и плоскость y=x, которая ее пересекает.
График дуги в пространстве имеет вид как на рисунку

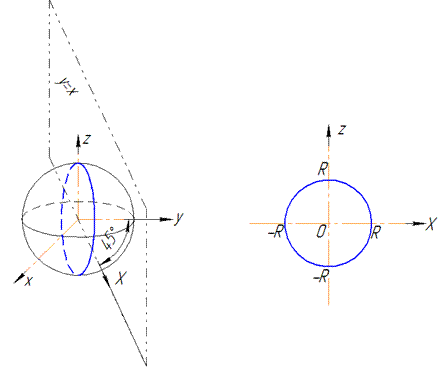
В сечении получим круг, который проектируется на плоскость y=x уравнением X²+z²=R², где
Такие манипуляции необходимы, чтобы параметризовать круг
Параметрическое уравнение круга:
x=R*cos(t), z=R*sin(t) и t[0;Pi/2] (I октант).
Тогда переменные выражаются зависимостью

Вычисляем производные

затем находим дифференциал дуги:

Подставляем все в интеграл и выполняем вычисление

Как Вы могли убедиться, ничего сложного в нахождении криволинейных интегралов первого рода нет. В теории известны формулы как переходить от криволинейных к определенным интегралам, ими и воспользовались. Сами же интегралы не сложны, да и кривые на практике подбираются таким образом, чтобы Вы с ними долго не возились на практических занятиях.
Все сводится к умению интегрировать, что в свою очередь требует знания таблицы основных интегралов.



3. Криволинейные интегралы

И чтобы у вас сразу отлегло от сердца: криволинейные интегралы – это всего лишь однократные интегралы. Они похожи на «обычные» определённые интегралы.
Уже из самого названия нетрудно догадаться, что путём интегрирования криволинейных интегралов являются кривые линии (в общем случае).

Итак, паркет вашей комнаты – это координатная плоскость , в углу стоИт
эльф ось , а сверху «зависло» расправленное одеяло, заданное функцией .

Возьмите в руки мел и начертите на полу под одеялом произвольную кривую . Как вариант, у неё могут быть углы  – такая линия называется кусочно-гладкой. Можно изобразить даже ломаную. ВажнА спрямляемость и непрерывность пути интегрирования. Теперь суть:

Представьте, что от одеяла осталась всего лишь нитка, лежащая над кривой . Вертикальная поверхность, расположенная между кривой «эль» на полу и этой «ниткой» представляет собой фрагмент криволинейного цилиндра. …Получилась такая стоячая изогнутая ширма. …Представили? Отлично!

3.1. Криволинейный интеграл первого рода

имеет вид  и по модулю* равен площади   данной «ширмы» (фрагмента криволинейного цилиндра).

* Если график   целиком или бОльшей частью расположен ниже плоскости , то площадь получится со знаком «минус».

В частности, если подынтегральная функция задаёт плоскость , то криволинейный интеграл равен площади «ленты» единичной высоты, а также и длине самой линии интегрирования: .
…Чего только не придумаешь, чтобы не делать чертежей

Значок  называют дифференциалом дуги кривой . Во многих источниках его обозначают через , но, на мой взгляд, это не слишком удачный выбор.

Если на плоскости  вместо кривой начертить отрезок прямой, то получится не что иное, как плоская криволинейная трапеция, параллельная оси . Соответствующий интеграл хоть и каламбурно, но с полным правом можно назвать «прямолинейным», и это двоюродный брат определённого интеграла.

3.1.1. Как вычислить криволинейный интеграл 1-го рода?

2.6.2. Центр тяжести тела

| Оглавление |



Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Содержание:

1. Криволинейный интеграл
2. Вычисление криволинеиного интеграла
3. Криволинейный интеграл второго рода

Криволинейный интеграл

Используя понятие длины кривой, а также формулы для ее вычисления при различных способах задания кривой, можно ввести понятие интеграла вдоль спрямляемой (в частности, гладкой или кусочно гладкой) кривой так же, как вдоль прямолинейного отрезка.

Пусть на плоскости с прямоугольной декартовой системой координат имеется непрерывная спрямляемая кривая (рис. 5.1),

в точках которой задана действительная функция Выберем разбиение кривой с точками деления Длины элементарных дуг обозначим через а максимальную их этих длин — через Возьмем на каждой дуге по точке

Отметим, что подобное разбиение можно построить и в случае замкнутой кривой, если за точку совпадающую в этом случае с взять любую точку кривой а остальные точки расположить в соответствии с выбранным направлением на этой замкнутой кривой.

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Составим сумму вида

которую называют интегральной суммой функции вдоль кривой

Пусть существует предел интегральных сумм (5.1) при не зависящий ни от выбора разбиения кривой от выбора точек на элементарных дугах, т.е. для любого числа существует такое число что для любого разбиения кривой с параметром при любом выборе точек на дугах выполняется неравенство

Такой предел называют криволинейным интегралом первого рода (иногда — первого типа) вдоль кривой (или дуги) и обозначают

Итак,

Отметим, что в определении криволинейного интеграла первого рода направление обхода кривой не играет никакой роли, так как от выбора направления не зависит интегральная сумма.

Пусть, например, кривая не замкнута, а обозначает ту же кривую, но с противоположным направлением обхода (от к если исходным является направление от к ). Тогда можно записать

Аналогично можно ввести понятие интеграла вдоль пространственной кривой. Пусть на пространственной кривой задана функция (рис. 5.2).

Как и в плоском случае, проведем разбиение кривой точками на элементарные дуги На каждой дуге выберем точку

Составив интегральную сумму и перейдя к пределу при получим значение интеграла вдоль пространственной кривой

где — длина элементарной дуги — максимальная из длин

Возможно вам будут полезны данные страницы:

Вычисление криволинеиного интеграла

Если плоская кривая спрямляема, можно ввести натуральный параметр этой кривой. В этом случае положение точки на кривой будет определяться длиной дуги кривой от начальной точки до точки Пусть кривая задана параметрическими уравнениями

где — длина кривой Тогда функцию определенную на кривой можно рассматривать как сложную функцию натурального параметра

Выберем разбиение кривой и точки на элементарных дугах этого разбиения. Составим соответствующую интегральную сумму. Пусть есть значение натурального параметра для точки а — значение натурального параметра для точки Тогда длины элементарных дуг можно записать в виде а интегральную сумму представить следующим образом:

Правая часть равенства есть интегральная сумма, соответствующая определенному интегралу от функции по отрезку Переход к пределу в обеих интегральных суммах выполняется при одном условии

Поэтому

причем существование одного из интегралов в этом равенстве означает существование и другого. Выявленная связь позволяет получить условия существования криволинейного интеграла первого рода.

Если кривая спрямляема, а функция непрерывна на этой кривой (часто говорят — непрерывна вдоль кривой то сложная функция непрерывна на отрезке так как функции и параметрического представления кривой являются непрерывными на отрезке Следовательно, интеграл в правой части (5.6) существует [VI]. Резюмируя, можем сформулировать следующую теорему.

Теорема 5.1. Если кривая спрямляема (в частности, является кусочно гладкой), а функция непрерывна вдоль этой кривой, то криволинейный интеграл первого рода от функции вдоль кривой существует.

Итак, криволинейный интеграл первого рода можно свести к определенному интегралу с помощью формулы (5.6). Однако эта формула с практической точки зрения не очень удобна, поскольку в качестве параметра кривой далеко не всегда (а точнее, редко) выбирают натуральный параметр.

Пусть кривая задана произвольными параметрическими уравнениями

где функции и непрерывны вместе со своими производными и на отрезке Тогда кривая спрямляема и для нее определен натуральный параметр Натуральный параметр можно отсчитывать от любого конца кривой и в данном случае отсчет удобно вести от начальной точки кривой, соответствующей значению Тогда возрастанию параметра будет соответствовать возрастание параметра а для дифференциала длины дуги плоской кривой будет выполняться равенство

При этом значение соответствует точке и значению а значение точке и значению В определенном интеграле в равенстве (5.6) справа можно выполнить замену переменного, переходя от натурального параметра s к параметру В результате указанное равенство преобразуется к виду

Таким образом, для вычисления криволинейного интеграла первого рода следует заменить в подынтегральной функции переменные и их выражениями через параметр а дифференциал — дифференциалом длины дуги, выразив его через параметр Оговоренное выше согласование параметра и натурального параметра означает, что в определенном интеграле в (5.9) справа нижний предел интегрирования меньше верхнего т.е.

Если плоская кривая является графиком функции то в качестве параметра кривой естественно выбрать абсциссу точки кривой. При этом формула (5.9) приобретает вид

Аналогично при задании кривой функцией в виде получаем

Пусть кривая задана в полярной системе координат уравнением Тогда, учитывая формулы связи декартовых и полярных координат, а также выражение для дифференциала длины дуги в полярных координатах

находим

Примеры с решением

Пример 1.

Вычислим криволинейный интеграл первого рода где — дуга параболы заключенная между точками В данном случае

и в соответствии с (5.10)

Пример 2.

Найдем криволинейный интеграл первого рода вдоль кривой заданной параметрическими уравнениями

В соответствии с (5.8) имеем

Кроме того, Следовательно, используя (5.9), получаем

Пример 3.

Вычислим криволинейный интеграл первого рода от функции вдоль замкнутой кривой заданной уравнением (астроиды).

Для вычисления интеграла необходимо кривую задать параметрическими уравнениями. Астроиду можно описать следующим образом:

Находим и Следовательно, Отметим, что правая часть последнего равенства обращается в нуль в четырех точках, соответствующих значениям

т.е. астроида является кусочно гладкой кривой.

Переходя от криволинейного интеграла к определенному, получаем

Функция под знаком определенного интеграла справа является периодической с периодом Поэтому интеграл по отрезку можно заменить учетверенным интегралом по отрезку Таким образом,

Пример 4.

Найдем криволинейный интеграл первого рода от функции вдоль отрезка прямой, соединяющего точки Уравнение этой прямой имеет вид и для вычисления криволинейного интеграла можно использовать формулу (5.10). В данном случае Используя в определенном интеграле замену переменного получаем

Пример 5.

Пусть — правый лепесток лемнискаты Бернулли, который в полярных координатах описывается уравнением Вычислим вдоль криволинейный интеграл от функции

Так как и

Учитывая, что в данном случае и используя (5.12), находим

Условия существования криволинейного интеграла переносятся и на пространственный случай. Если пространственная кривая задана параметрическими уравнениями

где функции и и непрерывны на отрезке вместе со своими производными, а функция пределена и непрерывна на кривой то криволинейный интеграл от функции вдоль кривой существует, причем

Пример 6.

Вычислим криволинейный интеграл первого рода вдоль пространственной кривой заданной параметрическими уравнениями

Предварительно находим

Далее в соответствии с формулой (5.13) получаем

В заключение отметим следующее. Так как криволинейный интеграл первого рода, согласно формуле (5.6), фактически есть определенный интеграл, на него переносятся основные свойства определенного интеграла: линейность, аддитивность, оценка интеграла по модулю (модуль интеграла не превосходит интеграла от модуля функции), теорема о среднем. Последняя позволяет ввести понятие среднего значения функции вдоль кривой под которым понимают отношение криволинейного интеграла от вдоль к длине кривой

В то же время понятия верхнего и нижнего пределов интегрирования, присущие определенному интегралу, не имеют аналогов для криволинейного интеграла, а известное свойство определенного интеграла менять знак, когда верхний и нижний пределы меняются местами, не распространяется на криволинейный интеграл первого рода.

Криволинейный интеграл второго рода

Пусть на плоскости задана кривая и на этой кривой — непрерывные функции и Разобьем кривую точками на элементарных дуги и выберем на каждой дуге точку (см. рис. 5.1). Обозначим через координаты точки Кроме того, обозначим через проекции векторов на координатные оси и Составим интегральные суммы

вдоль кривой для функции по переменному и для функции по переменному По-прежнему через обозначим максимальную из длин элементарных дуг

Если существуют пределы интегральных сумм (5.26) при не зависящие ни от разбиения кривой на элементарные дуги, ни от выбора точек на этих дугах, то эти пределы называют криволинейными интегралами второго рода вдоль кривой от функции по переменному и от функции по переменному у и обозначают

Итак, по определению

В приложениях часто встречается сумма интегралов (5.27) и (5.28) от двух функций и (в частном случае эти функции могут совпадать). Такую сумму называют криволинейным интегралом второго рода общего вида и записывают под одним знаком интеграла:

К криволинейному интегралу второго рода приводит задача вычисления работы силы при перемещении материальной точки по криволинейному пути.

Действительно, предел в правой части формулы (5.25) можно представить в виде суммы двух пределов, каждый из которых есть криволинейный интеграл второго рода по соответствующему переменному.

Следовательно, вместо (5.25) можем записать

где и — проекции силы на координатные оси и

Отметим, что работу силы на криволинейном пути можно представить и криволинейным интегралом первого рода в виде (5.24). Это позволяет записать равенство

которое устанавливает связь между криволинеиными интегралами двух видов.

Криволинейные интегралы первого и второго рода имеют много общего. Однако у них есть и существенное различие: если первый из этих интегралов не зависит от выбора направления обхода кривой (от выбора ориентации этой кривой), то второй при изменении направления обхода на противоположное меняет знак. Это связано с тем, что в интегральной сумме интеграла первого рода значения функции умножаются на длины дуг в то время как в случае интеграла второго рода значения функции умножаются на проекции (или ) вектора на координатную ось (или ). В последнем случае изменение направления обхода приводит к изменению направления векторов и, как следствие, к изменению знака их проекций. Таким образом, для криволинейных интегралов второго рода имеем

причем из существования интегралов в правых частях этих равенств вытекает существование интегралов в левых частях, и наоборот..

Понятие криволинейного интеграла второго рода можно перенести на случай пространственной кривой. Если на кривой в пространстве заданы непрерывные функции то, как и выше, разбивая кривую на элементарные дуги с длинами можно построить интегральные суммы

и рассмотреть их пределы при стремлении к нулю величины Эти пределы, если они существуют, называют криволинейными интегралами второго рода по переменным и вдоль пространственной кривой и обозначают

В приложениях часто встречается сумма этих интегралов, которую объединяют общим знаком интеграла:

Для пространственной кривой существует аналогичная связь между криволинейными интегралами первого и второго родов:

где — векторная функция, для которой и

являются координатными функциями в прямоугольной декартовой системе координат — углы, образованные единичным вектором касательным к кривой в точке с осями и соответственно.

Криволинейный интеграл второго рода по замкнутому контуру часто обозначают специальным символом и иногда называют контурным интегралом. Для такого интеграла направление обхода контура уже нельзя задать, указав начальную и конечную точки кривой. Чтобы определить направление обхода контура, можно использовать различные способы. Например, при параметрическом задании контура в качестве направления его обхода можно выбрать то, которое соответствует возрастанию параметра кривой.

В плоском случае для простейших контуров (окружность, эллипс) направление обхода часто сравнивают с движением часовой стрелки. При этом обход контура против хода часовой стрелки (или просто против часовой стрелки) называют положительным, а обход контура по ходу часовой стрелки (по часовой стрелке) — отрицательным (рис. 5.5, а).

В приложениях зачастую контур фигурирует как граница некоторой плоской области (в этом случае контур простой). Тогда обход контура можно соотнести с этой областью: при положительном обходе контура область все время остается слева, а при отрицательном — справа (рис. 5.5, б).

Однако описанные способы указания направления обхода контура приемлемы лишь в относительно простых ситуациях. В каком смысле следует понимать обход контура на рис. 5.6

против часовой стрелки? В таких непростых ситуациях направление обхода можно задать, выбрав на контуре три различные точки и указав, в каком порядке они проходятся. Для контурных интегралов, в которых направление обхода контура задано как положительное (против часовой стрелки),иногда используют специальное обозначение если же направление обхода контура задано как отрицательное, то используют обозначение Таким образом, если — окружность, то в интеграле

предполагается обход против часовой стрелки, а в интеграле по часовой стрелке.

Пример 9.

Вычислим криволинейный интеграл второго рода

вдоль пространственной кривой заданной параметрическими уравнениями

В данном случае и Поэтому, используя формулу (5.36), находим

Пример 10.

Найдем криволинейный интеграл второго рода

вдоль параболы между ее точками и В соответствии с (5.34) имеем