Как найти кручение линии - Исправление недочетов и поиск решений вместе с Examum.ru

Содержание

Кривизна и кручение. Натуральные уравнения кривой

Краткие теоретические сведения

Кривизна кривой

Кривизной $k$ кривой в данной точке называют модуль скорости вращения касательной по отношению к длине дуги.

Регулярная дважды дифференцируемая без особых точек кривая $gamma$, заданная векторной функцией $vec{r}=vec{r}(t)$, имеет в каждой точке определенную кривизну, причем
$$
|k(t)|=frac{|vec{r’}(t)times vec{r»}(t)|}{|vec{r'(t)}|^3}.
$$

Для кривой, заданной параметрически
$$ x=x(t), ,, y=y(t), ,, z=z(t), $$
кривизна в точке $P(t=t_0)$ находится по формуле:
$$
k^2(t_0)=frac{left| begin{array}{cc}
y’ & z’ \
y»& z» \
end{array}
right|^2+left| begin{array}{cc}
z’ & x’ \
z»& x» \
end{array}
right|^2+left| begin{array}{cc}
x’ & y’ \
x» & y» \
end{array}
right|^2}{Bigl((x’)^2+(y’)^2+(z’)^2Bigr)^3},
$$
где все производные вычисляются при $t=t_0$.

Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то векторы $vec{r’}(s)$ и $vec{r»}(s)$ перпендикулярны, причем $|vec{r’}(s)|=1$. Тогда выражение для кривизны принимает вид:
$$
k(s)= |vec{r»}(s)|.
$$

Что вы скажете о кривой, которая в каждой свой точке имеет нулевую кривизну?

Для плоской кривой, лежащей в плоскости $(xy)$, кривизну можно найти по формулам:
$$
begin{array}{rl}
x=x(t), y=y(t):& k = displaystylefrac{|x’y»-x»y’|}{left((x’)^2+(y’)^2right)^{3/2}}, \
y=y(x):& k = displaystylefrac{|y»|}{left(1+(y’)^2right)^{3/2}}, \
rho=rho(varphi):& k = displaystylefrac{|rho^2+2(rho’)^2-rhorho»|}{left(rho^2+(rho’)^2right)^{3/2}}.\
end{array}
$$

Кручение

Абсолютным кручением $varkappa$ кривой называют скорость вращения соприкасающейся плоскости вокруг касательной.
$$
|varkappa (t)|=frac{|(vec{r’}(t), vec{r»}(t), vec{r»’}(t))|}{|vec{r’}(t)times vec{r»}(t)|^2}.
$$

В случае естественной параметризации
$$
|varkappa(s)|=frac{|(vec{r’}(s), vec{r»}(s), vec{r»’}(s))|}{k^2(s)}
$$

Для плоской кривой кручение равно нулю: $varkappa=0$!

Натуральные уравнения кривой

Если кривая задана естественной параметризацией $vec{r}=vec{r}(s)$, то кривизна и кручение будут являться функциями длины дуги
$$
k=k(s), quad varkappa=varkappa(s).
$$
Система этих двух соотношений называется натуральными уравнениями кривой.

Натуральные уравнения полностью определяют форму кривой, ибо связывают инварианты, которые не меняются при преобразовании координат (при изменении положения указанной кривой в пространстве относительно системы координат).

Решение задач

Задача 1 (Феденко №351)

Найдите кривизну кривой:
$$
x=a,mbox{cos}^3t,,,y=a,mbox{sin}^3t.
$$

Задача 2 (Феденко №380)

Найдите параболу $y=ax^2+bx+c$, имеющую с синусоидой $y=mbox{sin}x$ в точке $A(pi/2,1)$ общие касательную и кривизну.

Задача 3 (Феденко №405)

Составьте натуральные уравнения кривой:
$$
x=a(mbox{cos},t+t,mbox{sin},t), ,, y=a(mbox{sin},t-t,mbox{cos},t).
$$

Краткое решение задачи 3

$$
s=frac{at^2}{2}.
$$

$$
k=frac{1}{at}.
$$

$$
t=frac{1}{ak} Rightarrow s= frac{1}{2ak^2}.
$$

Натуральные уравнения:
$$
k=frac{1}{at},,,s=frac{at^2}{2}
$$
или
$$
k^2=frac{1}{2as}.
$$

Феденко записывает ответы через радиус кривизны:
$R=frac{1}{k}$.

Задача 4 (Феденко №486, №514)

Найдите кривизну и кручение, составьте натуральные уравнения кривой:
$$
x=a,mbox{ch}t, , y=a,mbox{sh}t, , z=a, t.
$$

Решение задачи 4

Задачу можно решать двумя способами:

1 способ. Найти $k(t), varkappa(t), s(t)$.

2 способ. Сначала найти выразить $t$ через $s$ и записать естественную параметризацию кривой $vec{r}=vec{r}(s)$. А далее найти $k(s)$ и $varkappa(s)$.

Воспользуемся первым способом.
begin{gather*}
vec{r}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , at},\
vec{r’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , a},\
vec{r»}(t_0)={a,mbox{ch}t, , a,mbox{sh}t, , 0}\
vec{r»’}(t_0)={a,mbox{sh}t, , a,mbox{ch}t, , 0}.
end{gather*}

$$
Rightarrow quad k^2(t) = frac{1}{4a^2mbox{ch}^4t}.
$$
$$
Rightarrow quad k(t) = frac{1}{2a,mbox{ch}^2t}.
$$

begin{equation*}
varkappa(t) = frac{ left|
begin{array}{ccc}
a,mbox{sh}t & a,mbox{ch}t & a \
a,mbox{ch}t & a,mbox{sh}t & 0 \
a,mbox{sh}t & a,mbox{ch}t & 0 \
end{array}
right|}{a^4cdot 2mbox{ch}^2t} = frac{1}{2a,mbox{ch}^2t}.
end{equation*}

В задаче №473 была та же кривая и мы получили, что
$$s=asqrt{2},mbox{sh},t.$$
Используя тождества для гиперболических функций, выразим $t$ через $s$ и подставим их в выражения для кривизны и кручения:
begin{equation*}
s=asqrt{2},mbox{sh}t=asqrt{2},sqrt{mbox{ch}^2t-1} ,, Rightarrow ,, mbox{ch}^2t=frac{s^2}{2a^2}+1 ,, Rightarrow
end{equation*}
begin{equation*}
k(s)=varkappa(s)=frac{1}{2a,mbox{ch}^2t} = frac{a}{s^2+2a^2}.
end{equation*}

Вычисления сделаны для $a>0$.

Задача 5 (Феденко №496)

Найдите функцию $f(t)$, для которой данная кривая — плоская:
$$
vec{r}(t)={a,mbox{cos}t, , a,mbox{sin}t, , f(t)}
$$

Решение задачи 5

$$
begin{array}{lll}
x=a,mbox{cos}t,, &y=a,mbox{sin}t, , &z=f(t),\
x’=-a,mbox{sin}t, , &y’=a,mbox{cos}t, , &z’=f'(t),\
x»=-a,mbox{cos}t, , &y»=-a,mbox{sin}t, , &z»=f»(t),\
x»’=a,mbox{sin}t, , &y»’=-a,mbox{cos}t, , &z»’=f»'(t).
end{array}
$$

Для плоской кривой кручение равно нулю:
begin{equation*}
varkappa(t) = left|
begin{array}{rrr}
-a,mbox{sin}t & a,mbox{cos}t & f'(t) \
-a,mbox{cos}t & -a,mbox{sin}t & f»(t) \
a,mbox{sin}t & -a,mbox{cos}t & f»'(t) \
end{array}
right| = left( f'(t) + f»'(t) right)cdot2a^2=0.
end{equation*}
begin{equation*}
f'(t)=-f»'(t) quad Rightarrow quad f(t)=c_1+c_2,mbox{sin}t+c_3,mbox{cos}t.
end{equation*}

Как найти уравнение плоскости, в которой лежит кривая?

Известно, что плоская кривая лежит в своей соприкасающейся плоскости!
Второй способ — составить уравнение плоскости по трем точкам.

Источник

Лекция 3

Формулы Френе.
Кривизна и кручение кривой в произвольной
параметризации. Винтовая линия.

Р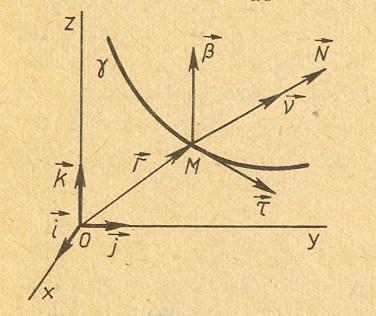ассмотрим
векторы

гладкой линии

заданной естественной параметризацией
.

1). Так как
то
(1)

2). Вектор

– единичный вектор гладкой нормали

параллелен
спрямляющей плоскости

3).
.
В (1) заменяем

и

по формулам (3) и (2). Получим

Подставим выражение

в (2).

4).
.
Дифференцируем по s:

=
.
Заменим

и

их выражениями по (3) и (4):

Формулы (3),(4),(5)
называются формулами Френе, которые
рассматривают связь между базисными
векторами сопровождающими треугольниками,
кручением и кривизной линии.

Определение 3.1.
Число

называется кручением линии

в точке М
на всей линии
.
Кручение есть функция параметра S.

Исходя из (5) и так
как
—
единичный вектор, то
.
Кручение больше 0 тогда и только тогда,
когда
и

противоположно направлены.

Геометрический
смысл кручения.

Модуль кручения
в данной точке кривой есть скорость
изменения направления функции b(S)
по отношению к естественному параметру
S.
Так как вектор b=b(S)
перпендикулярен соприкасающейся
плоскости, то абсолютная величина
кручения характеризует скорость
изменения положения соприкасающейся
плоскости по отношению к параметру S.

Если линия задана
в естественной параметризации, то
кривизна и кручение есть функция по
параметру S:

.Уравнения
такого вида называются натуральными
уравнениями кривой и характеризуют
кривую с точностью до движения, так как
если у двух кривых натуральные уравнение
совпадают, то кривые отличны только
положением в пространстве. Если у двух
кривых натуральные уравнения совпадают,
то на каждой из них существует естественная
параметризация, такая что в точках с
одинаковыми параметрами кривизна и
кручение одинаковы.

Вычислительная
формула для кручения линии заданной в
естественной параметризации.

—
продифференцируем
это равенство. Используем (5).

ыразим смешанное произведение
векторов производных:

формула
кручения (6)

Определение 3.2.
Линия называется плоской, если все её
точки принадлежат некоторой плоскости
.

Если во всех точках
гладкой плоской линии кручение равно
нулю.

Произвольная
параметризация.

Пусть кривая

задана произвольной параметризацией
своими параметрическими уравнениями:

Рассмотрим возможную
замену параметра t
на s,
причем функция s=h(t)
является допустимой заменой параметра
^-1
:
^-1

Найдем

Вектор
второй производной
параллелен
соприкасающейся плоскости, так как он
выражен через вектор

и
.

Рассмотрим векторное
произведение первой и второй производной.

Винтовая линия

Винтовая
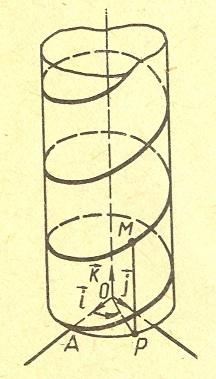
линия получена путем равномерного
вращения М
(х,у,z)

около оси Оz
и равномерного движения параллельно
оси Оz.
Является гладкой линией класса
.

Параметрические
уравнения винтовой линии:

Направляющая винтовой линии совпадает
с направляющей кругового цилиндра (ОХУ:
,
значит, винтовая линия лежит на прямом
круговом цилиндре с осью Оz.

Векторное уравнение
винтовой линии:
.

Используя формулу
,
имеем:
.
Таким образом,
.

Через М
проходит прямолинейная образующая МР
цилиндра, имеющая направляющий вектор

Так как
,
то винтовая линия пересекает все
образующие под постоянным углом (углом
между кривой и прямой называется угол
между касательной к этой кривой и данной
прямой).

Длина дуги винтовой
линии равна
.

Вектор главной
нормали:

Так как

(по формуле Френе), то

(k
– кривизна винтовой линии).

Главная нормаль
винтовой линии в точке М
есть
перпендикуляр к оси цилиндра, проведенный
через точку М,
т.к.

где Р
– проекция М
на ОХУ.
Вектор главной нормали направлен
противоположно вектору

Кручение винтовой
линии:
.
Знак кручения совпадает со знаком числа
b.

Винтовая линия
является частным случаем достаточно
широкого класса линий, называемых
кривыми Бертрана. Гладкая линия

называется кривой Бертрана, если для
нее существует другая гладкая линия

и такое отображение
,
что в каждой паре соответствующих точек
линии

и

имеют общую главную нормаль.

Соседние файлы в папке вопрос 14

Источник

From Wikipedia, the free encyclopedia

In the differential geometry of curves in three dimensions, the torsion of a curve measures how sharply it is twisting out of the osculating plane. Taken together, the curvature and the torsion of a space curve are analogous to the curvature of a plane curve. For example, they are coefficients in the system of differential equations for the Frenet frame given by the Frenet–Serret formulas.

Definition[edit]

Animation of the torsion and the corresponding rotation of the binormal vector.

Let r be a space curve parametrized by arc length s and with the unit tangent vector T. If the curvature κ of r at a certain point is not zero then the principal normal vector and the binormal vector at that point are the unit vectors

${displaystyle mathbf {N} ={frac {mathbf {T} '}{kappa }},quad mathbf {B} =mathbf {T} times mathbf {N} }$

respectively, where the prime denotes the derivative of the vector with respect to the parameter s. The torsion τ measures the speed of rotation of the binormal vector at the given point. It is found from the equation

{displaystyle mathbf {B} '=-tau mathbf {N} .}

which means

{displaystyle tau =-mathbf {N} cdot mathbf {B} '.}

As , this is equivalent to .

Remark: The derivative of the binormal vector is perpendicular to both the binormal and the tangent, hence it has to be proportional to the principal normal vector. The negative sign is simply a matter of convention: it is a byproduct of the historical development of the subject.

Geometric relevance: The torsion τ(s) measures the turnaround of the binormal vector. The larger the torsion is, the faster the binormal vector rotates around the axis given by the tangent vector (see graphical illustrations). In the animated figure the rotation of the binormal vector is clearly visible at the peaks of the torsion function.

Properties[edit]

A plane curve with non-vanishing curvature has zero torsion at all points. Conversely, if the torsion of a regular curve with non-vanishing curvature is identically zero, then this curve belongs to a fixed plane.
The curvature and the torsion of a helix are constant. Conversely, any space curve whose curvature and torsion are both constant and non-zero is a helix. The torsion is positive for a right-handed^[1] helix and is negative for a left-handed one.

Alternative description[edit]

Let r = r(t) be the parametric equation of a space curve. Assume that this is a regular parametrization and that the curvature of the curve does not vanish. Analytically, r(t) is a three times differentiable function of t with values in R³ and the vectors

are linearly independent.

Then the torsion can be computed from the following formula:

${displaystyle tau ={frac {det left({mathbf {r} ',mathbf {r} '',mathbf {r} '''}right)}{left|{mathbf {r} 'times mathbf {r} ''}right|^{2}}}={frac {left({mathbf {r} 'times mathbf {r} ''}right)cdot mathbf {r} '''}{left|{mathbf {r} 'times mathbf {r} ''}right|^{2}}}.}$

Here the primes denote the derivatives with respect to t and the cross denotes the cross product. For r = (x, y, z), the formula in components is

${displaystyle tau ={frac {x'''left(y'z''-y''z'right)+y'''left(x''z'-x'z''right)+z'''left(x'y''-x''y'right)}{left(y'z''-y''z'right)^{2}+left(x''z'-x'z''right)^{2}+left(x'y''-x''y'right)^{2}}}.}$

Notes[edit]

^ Weisstein, Eric W. «Torsion». mathworld.wolfram.com.

References[edit]

Pressley, Andrew (2001), Elementary Differential Geometry, Springer Undergraduate Mathematics Series, Springer-Verlag, ISBN 1-85233-152-6

Источник

Выведем формулы для вычисления кривизны и кручения кривой , заданной в декартовых координатах.

Теорема 1. В каждой точке регулярной кривой класса кривизна определена и неотрицательна. Если – натуральная параметризация, то . Если – произвольная регулярная параметризация, то .

Первое утверждение теоремы следует из уравнения сопровождающего репера Френе, если его возвести в квадрат и воспользоваться тем, что и .

Пусть кривая имеет произвольную регулярную параметризацию Выразим через производные по : , но . Поэтому . Продифференцируем это равенство по : и возведем в квадрат. Поскольку и , то , ч. т.д.

Если кривая плоская , то формула для кривизны примет вид . Если плоская кривая задана уравнением , то ее кривизна вычисляется по формуле .

Если на некотором интервале кривизна кривой равна нулю, то в натуральной параметризации и, значит, , где – некоторые постоянные векторы из и кривая представляет собой отрезок прямой в пространстве.

Кривизна допускает следующую геометрическую интерпретацию: пусть и – близкие точки регулярной кривой, обозначим через угол между касательными в этих точках, а через – длину дуги кривой от точки до точки . Тогда кривизна регулярной кривой в точке может быть вычислена по формуле . Действительно, если обозначить единичные касательные векторы в точках через и, то поскольку , то =

Теорема 2. В каждой точке регулярной класса кривой в , в которой кривизна , определено кручение кривой. Если – натуральная параметризация, то . Если – произвольная параметризация, то .

Если кривая задана в натуральной параметризации, то из последнего уравнения сопровождающего репера Френе находим: Здесь мы воспользовались тем, что, если , то вектор главной нормали и вычислили его производную.

Если теперь кривая взята в произвольной параметризации , то имеем следующие формулы . Подставляя их в полученную формулу для кручения (в случае натуральной параметризации) получим, . Воспользуемся, наконец, тем, что и формулой для кривизны в случае произвольной параметризации и получим нужную формулу для кручения.

Покажем, что если кручение некоторой пространственной кривой на интервале равно нулю, то кривая плоская. Действительно, если воспользоваться натуральной параметризацией, то , следовательно, бинормаль . Поскольку , то . Интегрируем и получаем, что , что и означает, что кривая, когда натуральный параметр принадлежит интервалу , находится в плоскости перпендикулярной постоянному вектору .

Две функции (где – дуга некоторой кривой в ) называются натуральными уравнениями кривой. Их задание позволяет найти кривую с точностью до движения в .

Пример. Найдем все кривые в с натуральными уравнениями Возьмем некоторую точку кривой с данными натуральными уравнениями. Можем считать, что точке отвечает значение дуги . Поскольку , то кривая плоская и можно выбрать координаты в так, чтобы бинормаль . Тогда формулы Френе можно записать как дифференциальное уравнение для двумерного вектора : . Поскольку матрица не зависит от , то решение имеет вид . Нетрудно проверить, что . Отсюда получаем, что . Далее интегрируем это уравнение и находим кривую . Если выбрать базис в плоскости следующим образом , то уравнения кривой запишутся в виде . Очевидно, что это есть окружность радиуса .