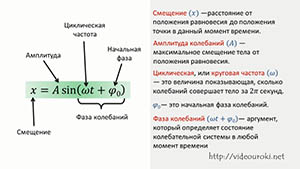
Чтобы описать колебательные процессы и отличить одни колебания от других, используют 6 характеристик. Они называются так (рис. 1):
- амплитуда,
- период,
- частота,
- циклическая частота,
- фаза,
- начальная фаза.
Рис. 1. Основные характеристики колебаний – это амплитуда, период и начальная фаза
Такие величины, как амплитуду и период, можно определить по графику колебаний.
Начальную фазу, так же, определяют по графику, с помощью интервала времени (large Delta t), на который относительно нуля сдвигается начало ближайшего периода.
Частоту и циклическую частоту вычисляют из найденного по графику периода, по формулам. Они находятся ниже в тексте этой статьи.
А фазу определяют с помощью формулы, в которую входит интересующий нас момент времени t колебаний. Читайте далее.
Что такое амплитуда
Амплитуда – это наибольшее отклонение величины от равновесия, то есть, максимальное значение колеблющейся величины.
Измеряют в тех же единицах, в которых измерена колеблющаяся величина. К примеру, когда рассматривают механические колебания, в которых изменяется координата, амплитуду измеряют в метрах.
В случае электрических колебаний, в которых изменяется заряд, ее измеряют в Кулонах. Если колеблется ток – то в Амперах, а если – напряжение, то в Вольтах.
Часто обозначают ее, приписывая к букве, обозначающей амплитуду индекс «0» снизу.
К примеру, пусть колеблется величина ( large x ). Тогда символом ( large x_{0} ) обозначают амплитуду колебаний этой величины.
Иногда для обозначения амплитуды используют большую латинскую букву A, так как это первая буква английского слова «amplitude».
С помощью графика амплитуду можно определить так (рис. 2):
Рис. 2. Амплитуда – это максимальное отклонение от горизонтальной оси либо вверх, либо вниз. Горизонтальная ось проходит через уровень нуля на оси, на которой отмечены амплитуды
Что такое период
Когда колебания повторяются точно, изменяющаяся величина принимает одни и те же значения через одинаковые кусочки времени. Такой кусочек времени называют периодом.
Обозначают его обычно большой латинской буквой «T» и измеряют в секундах.
( large T left( c right) ) – период колебаний.
Одна секунда – достаточно большой интервал времени. Поэтому, хотя период и измеряют в секундах, но для большинства колебаний он будет измеряться долями секунды.
Чтобы по графику колебаний определить период (рис. 3), нужно найти два одинаковых значения колеблющейся величины. После, провести от этих значений к оси времени пунктиры. Расстояние между пунктирами – это период колебаний.
Рис. 3. Период колебаний – это горизонтальное расстояние между двумя похожими точками на графике
Период – это время одного полного колебания.
На графике период найти удобнее одним из таких способов (рис. 4):
Рис. 4. Удобно определять период, как расстояние между двумя соседними вершинами, либо между двумя впадинами
Что такое частота
Обозначают ее с помощью греческой буквы «ню» ( large nu ).
Частота отвечает на вопрос: «Сколько полных колебаний выполняется за одну секунду?» Или же: «Сколько периодов умещается в интервал времени, равный одной секунде?».
Поэтому, размерность частоты — это единицы колебаний в секунду:
( large nu left( frac{1}{c} right) ).
Иногда в учебниках встречается такая запись ( large displaystyle nu left( c^{-1} right) ), потому, что по свойствам степени ( large displaystyle frac{1}{c} = c^{-1} ).
Начиная с 1933 года частоту указывают в Герцах в честь Генриха Рудольфа Герца. Он совершил значимые открытия в физике, изучал колебания и доказал, что существуют электромагнитные волны.
Одно колебание в секунду соответствует частоте в 1 Герц.
[ large displaystyle boxed{ frac{ 1 text{колебание}}{1 text{секунда}} = 1 text{Гц} }]
Чтобы с помощью графика определить частоту, нужно на оси времени определить период. А затем посчитать частоту по такой формуле:
[ large boxed{ nu = frac{1}{T} }]
Существует еще один способ определить частоту с помощью графика колеблющейся величины. Нужно отмерить на графике интервал времени, равный одной секунде, и сосчитать количество периодов колебаний, уместившихся в этот интервал (рис. 5).
Рис. 5. На графике частота – это количество периодов, уместившихся в одну секунду
Что такое циклическая частота
Колебательное движение и движение по окружности имеют много общего – это повторяющиеся движения. Одному полному обороту соответствует угол (large 2pi) радиан. Поэтому, кроме интервала времени 1 секунда, физики используют интервал времени, равный (large 2pi) секунд.
Число полных колебаний для такого интервала времени, называется циклической частотой и обозначается греческой буквой «омега»:
( large displaystyle omega left( frac{text{рад}}{c} right) )
Примечание: Величину ( large omega ) так же называют круговой частотой, а еще — угловой скоростью (ссылка).
Циклическая частота отвечает на вопрос: «Сколько полных колебаний выполняется за (large 2pi) секунд?» Или же: «Сколько периодов умещается в интервал времени, равный (large 2pi) секунд?».
Обычная ( large nu ) и циклическая ( large omega ) частота колебаний связаны формулой:
[ large boxed{ omega = 2pi cdot nu }]
Слева в формуле количество колебаний измеряется в радианах на секунду, а справа – в Герцах.
Чтобы с помощью графика колебаний определить величину ( large omega ), нужно сначала найти период T.
Затем, воспользоваться формулой ( large displaystyle nu = frac{1}{T} ) и вычислить частоту ( large nu ).
И только после этого, с помощью формулы ( large omega = 2pi cdot nu ) посчитать циклическую ( large omega ) частоту.
Для грубой устной оценки можно считать, что циклическая частота превышает обычную частоту примерно в 6 раз численно.
Определить величину ( large omega ) по графику колебаний можно еще одним способом. На оси времени отметить интервал, равный (large 2pi), а затем, сосчитать количество периодов колебаний в этом интервале (рис. 6).
Рис. 6. На графике циклическая (круговая) частота – это количество периодов, уместившихся в 2 пи секунд
Что такое начальная фаза и как определить ее по графику колебаний
Отклоним качели на некоторый угол от равновесия и будем удерживать их в таком положении. Когда мы отпустим их, качели начнут раскачиваться. А старт колебаний произойдет из угла, на который мы их отклонили.
Такой, начальный угол отклонения, называют начальной фазой колебаний. Обозначим этот угол (рис. 7) какой-нибудь греческой буквой, например, (large varphi_{0} ).
(large varphi_{0} left(text{рад} right) ) — начальная фаза, измеряется в радианах (или градусах).
Начальная фаза колебаний – это угол, на который мы отклонили качели, перед тем, как их отпустить. Из этого угла начнется колебательный процесс.
Рис. 7. Угол отклонения качелей перед началом колебаний
Рассмотрим теперь, как величина (large varphi_{0} ) влияет на график колебаний (рис. 8). Для удобства будем считать, что мы рассматриваем колебания, которые происходят по закону синуса.
Кривая, обозначенная черным на рисунке, начинает период колебаний из точки t = 0. Эта кривая является «чистым», не сдвинутым синусом. Для нее величину начальной фазы (large varphi_{0} ) принимаем равной нулю.
Рис. 8. Вертикальное положение стартовой точки в момент времени t = 0 и сдвиг графика по горизонтали определяется начальной фазой
Вторая кривая на рисунке обозначена красным цветом. Начало ее периода сдвинуто вправо относительно точки t = 0. Поэтому, для красной кривой, начавшей новый период колебаний спустя время (large Delta t), начальный угол (large varphi_{0} ) будет отличаться от нулевого значения.
Определим угол (large varphi_{0} ) с помощью графика колебаний.
Обратим внимание (рис. 
Как вычислить начальный угол по интервалу смещения
Алгоритм нахождения начального угла состоит из нескольких несложных шагов.
- Сначала определим интервал времени, обозначенный синими стрелками на рисунке. На осях большинства графиков располагают цифры, по которым это можно сделать. Как видно из рис. 8, этот интервал (large Delta t) равен 1 сек.
- Затем определим период. Для этого отметим одно полное колебание на красной кривой. Колебание началось в точке t = 1, а закончилось в точке t =5. Взяв разность между этими двумя точками времени, получим значение периода.
[large T = 5 – 1 = 4 left( text{сек} right)]
Из графика следует, что период T = 4 сек.
- Рассчитаем теперь, какую долю периода составляет интервал времени (large Delta t). Для этого составим такую дробь (large displaystyle frac{Delta t }{T} ):
[large frac{Delta t }{T} = frac{1}{4} ]
Полученное значение дроби означает, что красная кривая сдвинута относительно точки t = 0 и черной кривой на четверть периода.
- Нам известно, что одно полное колебание — один полный оборот (цикл), синус (или косинус) совершает, проходя каждый раз угол (large 2pi ). Найдем теперь, как связана найденная доля периода с углом (large 2pi ) полного цикла.
Для этого используем формулу:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large displaystyle frac{1}{4} cdot 2pi = frac{pi }{2} =varphi_{0} )
Значит, интервалу (large Delta t) соответствует угол (large displaystyle frac{pi }{2} ) – это начальная фаза для красной кривой на рисунке.
- В заключение обратим внимание на следующее. Начало ближайшего к точке t = 0 периода красной кривой сдвинуто вправо. То есть, кривая запаздывает относительно «чистого» синуса.
Чтобы обозначить запаздывание, будем использовать знак «минус» для начального угла:
[large varphi_{0} = — frac{pi }{2} ]
Примечание: Если на кривой колебаний начало ближайшего периода лежит левее точки t = 0, то в таком случае, угол (large displaystyle frac{pi }{2} ) имеет знак «плюс».
Для не сдвинутого влево, либо вправо, синуса или косинуса, начальная фаза нулевая (large varphi_{0} = 0 ).
Для синуса или косинуса, сдвинутого влево по графику и опережающего обычную функцию, начальная фаза берется со знаком «+».
А если функция сдвинута вправо и запаздывает относительно обычной функции, величину (large varphi_{0} ) записываем со знаком «-».
Примечания:
- Физики начинают отсчет времени из точки 0. Поэтому, время в задачах будет величиной не отрицательной.
- На графике колебаний начальная фаза ( varphi_{0}) влияет на вертикальный сдвиг точки, из которой стартует колебательный процесс. Значит, можно для простоты сказать, что колебания имеют начальную точку.
Благодаря таким допущениям график колебаний при решении большинства задач можно изображать, начиная из окрестности нуля и преимущественно в правой полуплоскости.
Что такое фаза колебаний
Рассмотрим еще раз обыкновенные детские качели (рис. 9) и угол их отклонения от положения равновесия. С течением времени этот угол изменяется, то есть, он зависит от времени.
Рис. 9. Угол отклонения от равновесия – фаза, изменяется в процессе колебаний
В процессе колебаний изменяется угол отклонения от равновесия. Этот изменяющийся угол называют фазой колебаний и обозначают (varphi).
Различия между фазой и начальной фазой
Существуют два угла отклонения от равновесия – начальный, он задается перед началом колебаний и, угол, изменяющийся во время колебаний.
Первый угол называют начальной ( varphi_{0}) фазой (рис. 10а), она считается неизменной величиной. А второй угол – просто ( varphi) фазой (рис. 10б) – это величина переменная.
Рис. 10. Перед началом колебаний задаем начальную фазу — начальный угол отклонения от равновесия. А угол, который изменяется во время колебаний, называют фазой
Как на графике колебаний отметить фазу
На графике колебаний фаза (large varphi) выглядит, как точка на кривой. С течением времени эта точка сдвигается (бежит) по графику слева направо (рис. 11). То есть, в разные моменты времени она будет находиться на различных участках кривой.
На рисунке отмечены две крупные красные точки, они соответствуют фазам колебаний в моменты времени t1 и t2.
Рис. 11. На графике колебаний фаза – это точка, скользящая по кривой. В различные моменты времени она находится в разных положениях на графике
А начальная фаза на графике колебаний выглядит, как место, в котором находится точка, лежащая на кривой колебаний, в момент времени t=0. На рисунке дополнительно присутствует одна мелкая красная точка, она соответствует начальной фазе колебаний.
Как определить фазу с помощью формулы
Пусть нам известны величины (large omega) — циклическая частота и (large varphi_{0}) — начальная фаза. Во время колебаний эти величины не изменяются, то есть, являются константами.
Время колебаний t будет величиной переменной.
Фазу (large varphi), соответствующую любому интересующему нас моменту t времени, можно определить из такого уравнения:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
Левая и правая части этого уравнения имеют размерность угла (т. е. измеряются в радианах, или градусах). А подставляя вместо символа t в это уравнение интересующие нас значения времени, можно получать соответствующие им значения фазы.
Что такое разность фаз
Обычно понятие разности фаз применяют, когда сравнивают два колебательных процесса между собой.
Рассмотрим два колебательных процесса (рис. 12). Каждый имеет свою начальную фазу.
Обозначим их:
( large varphi_{01}) – для первого процесса и,
( large varphi_{02}) – для второго процесса.
Рис. 12. Для двух колебаний можно ввести понятие разности фаз
Определим разность фаз между первым и вторым колебательными процессами:
[large boxed{ Delta varphi = varphi_{01} — varphi_{02} }]
Величина (large Delta varphi ) показывает, на сколько отличаются фазы двух колебаний, она называется разностью фаз.
Как связаны характеристики колебаний — формулы
Движение по окружности и колебательное движение имеют определенную схожесть, так как эти виды движения могут быть периодическими.
Поэтому, основные формулы, применимые для движения по окружности, подойдут так же, для описания колебательного движения.
- Связь между периодом, количеством колебаний и общим временем колебательного процесса:
[large boxed{ T cdot N = t }]
( large T left( c right) ) – время одного полного колебания (период колебаний);
( large N left( text{шт} right) ) – количество полных колебаний;
( large t left( c right) ) – общее время для нескольких колебаний;
- Период и частота колебаний связаны так:
[large boxed{ T = frac{1}{nu} }]
(large nu left( text{Гц} right) ) – частота колебаний.
- Количество и частота колебаний связаны формулой:
[large boxed{ N = nu cdot t}]
- Связь между частотой и циклической частотой колебаний:
[large boxed{ nu cdot 2pi = omega }]
(large displaystyle omega left( frac{text{рад}}{c} right) ) – циклическая (круговая) частота колебаний.
- Фаза и циклическая частота колебаний связаны так:
[large boxed{ varphi = omega cdot t + varphi_{0} }]
(large varphi_{0} left( text{рад} right) ) — начальная фаза;
(large varphi left( text{рад} right) ) – фаза (угол) в выбранный момент времени t;
- Между фазой и количеством колебаний связь описана так:
[large boxed{ varphi = N cdot 2pi }]
- Интервал времени (large Delta t ) (сдвигом) и начальная фаза колебаний связаны:
[large boxed{ frac{Delta t }{T} cdot 2pi = varphi_{0} }]
(large Delta t left( c right) ) — интервал времени, на который относительно точки t=0 сдвинуто начало ближайшего периода.
Циклическая частота колебаний, теория и онлайн калькуляторы
Циклическая частота колебаний
Определение
Мерой колебательного движения служит циклическая (или угловая, или круговая) частотой колебаний.
Это скалярная физическая величина.
Циклическая частота при гармонических колебаниях
Пусть колебания совершает материальная точка. При этом материальная точка через равные промежутки времени проходит через одно и то же положение.
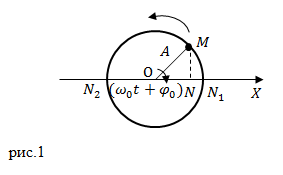
Самыми простыми колебаниями являются гармонические колебания. Рассмотрим следующую кинематическую модель. Точка M с постоянной по модулю скоростью ($v$) движется по окружности радиуса A. В этом случае ее угловую скорость обозначим ${omega }_0$, эта скорость постоянна (рис.1).
Проекция точки $M$ на диаметр окружности (точка $N$), на ось X, выполняет колебания от $N_1$ до $N_2 $и обратно. Такое колебание N ,будет гармоническим. Для описания колебания точки N необходимо записать координату точки N, как функцию от времени ($t$). Пусть при $t=0$ радиус OM образует с осью X угол ${varphi }_0$. Через некоторый промежуток времени этот угол изменится на величину ${omega }_0t$ и будет равен ${omega }_0t+{varphi }_0$, тогда:
[x=A{cos left({omega }_0t+{varphi }_0right) }left(1right).]
Выражение (1) является аналитической формой записи гармонического колебания точки N по диаметру $N_1N_2$.
Обратимся к выражению (1). Величина $A$ — это максимальное отклонение точки, совершающей колебания, от положения равновесия (точки О — центра окружности), называется амплитудой колебаний.
Параметр ${omega }_0$ — циклическая частота колебаний. $varphi =({omega }_0t+{varphi }_0$) — фаза колебаний; ${varphi }_0$ — начальная фаза колебаний.
Циклическую частоту гармонических колебаний можно определить как частную производную от фазы колебаний по времени:
[{omega }_0=frac{?varphi }{partial t}=dot{varphi }left(2right).]
При ${varphi }_0=0$, уравнение колебаний (1) преобразуется к виду:
[x=A{cos left({omega }_0tright) }left(3right).]
Если начальная фаза колебаний равна ${varphi }_0=frac{pi }{2}$ , то получим уравнение колебаний в виде:
[x=A{{rm s}in left({omega }_0tright) }left(4right).]
Выражения (3) и (4) показывают, что при гармонических колебаниях абсцисса $x$ — это функция синус или косинус от времени. При графическом изображении гармонических колебаний получается косинусоида или синусоида. Форма кривой определена амплитудой колебаний и величиной циклической частоты. Положение кривой зависит от начальной фазы.
Циклическую частоту колебаний можно выразить через период (T) колебаний:
[{omega }_0=frac{2pi }{T}left(5right).]
Циклическую частоту с частотой $?$$?$ свяжем выражением:
[{omega }_0=2pi nu left(6right).]
Единицей измерения циклической частоты в Международной системе единиц (СИ) является радиан, деленный на секунду:
[left[{omega }_0right]=frac{рад}{с}.]
Размерность циклической частоты:
[{dim left({omega }_0right)=frac{1}{t}, }]
где $t$ — время.
Частные случаи формул для вычисления циклической частоты
Груз на пружине (пружинный маятник — идеальная модель) совершает гармонические колебания с круговой частотой равной:
[{omega }_0=sqrt{frac{k}{m}}left(7right),]
$k$ — коэффициент упругости пружины; $m$ — масса груза на пружине.
Малые колебания физического маятника будут приблизительно гармоническими колебаниями с циклической частотой равной:
[{omega }_0=sqrt{frac{mga}{J}}left(8right),]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника.
Примером физического маятника является математический маятник. Круговая частота его колебаний равна:
[{omega }_0=sqrt{frac{g}{l}}left(9right),]
где $l$ — длина подвеса.
Угловая частота затухающих колебаний находится как:
[omega =sqrt{{omega }^2_0-{delta }^2}left(10right),]
где $delta $ — коэффициент затухания; в случае с затуханием колебаний ${omega }_0$ называют собственной угловой частотой колебаний.
Примеры задач с решением
Пример 1
Задание: Чему равна циклическая частота гармонических колебаний, если максимальная скорость материальной точки равна ${dot{x}}_{max}=10 frac{см}{с}$, а ее максимальное ускорение ${ddot{x}}_{max}=100 frac{см}{с^2}$?
Решение: Основой решения задачи станет уравнение гармонических колебаний точки, так как из условий, очевидно, что они происходят по оси X:
[x=A{cos left({omega }_0t+{varphi }_0right) }left(1.1right).]
Скорость колебаний найдем, используя уравнение (1.1) и кинематическую связь координаты $x$ и соответствующей компоненты скорости:
[v_x=frac{dx}{dt}=-A{omega }_0left({sin left({omega }_0t+{varphi }_0right) }right)left(1.2right).]
Максимальное значение скорости (амплитуда скорости) равна:
[v_{max}={dot{x}}_{max}=Aщ_0 left(1.3right).]
Ускорение точки вычислим как:
[a_x==frac{dv_x}{dt}=-A{{omega }_0}^2left({cos left({omega }_0t+{varphi }_0right) }right)left(1.4right),]
из (1.4):
[a_{max}={ddot{x}}_{max}=A{{omega }_0}^2(1.5).]
Из формулы (1.3) выразим амплитуду, подставим ее в (1.5), получим циклическую частоту:
[{dot{x}}_{max}=A{omega }_0to A=frac{{dot{x}}_{max}}{{omega }_0};; {ddot{x}}_{max}=A{щ_0}^2=frac{{dot{x}}_{max}}{щ_0}{щ_0}^2to щ_0=frac{{ddot{x}}_{max}}{{dot{x}}_{max}}.]
Вычислим циклическую частоту:
[щ_0=frac{100}{10}=10(frac{рад}{с}).]
Ответ: $щ_0=10frac{{rm рад}}{{rm с}}$
Пример 2
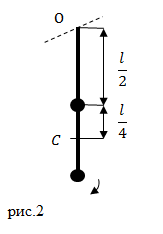
Задание: На длинном невесомом стержне закреплены два груза одинаковой массы. Один груз находится на середине стержня, другой на его конце (рис.2). Система совершает колебания около горизонтальной оси, проходящей через свободный конец стрежня. Какова циклическая частота колебаний? Длина стержня равна $l$.
Решение: Основой для решения задачи является формула нахождения частоты колебаний физического маятника:
[{omega }_0=sqrt{frac{mga}{J}}left(2.1right),]
где $J$ — момент инерции маятника относительно оси вращения; $a$ — расстояние между центром масс маятника и точкой подвеса; $m$ — масса маятника. Масса маятника по условию задачи состоит из масс двух одинаковых шариков (масса одного шарика $frac{m}{2}$). В нашем случае расстояние $a$ равно расстоянию между точками O и C (см. рис.2):
[a=frac{3}{4}l left(2.2right).]
Найдем момент инерции системы из двух точечных масс. Относительно центра масс (если ось вращения провести через точку C), момент инерции системы ($J_0$) равен:
[J_0=2cdot frac{m}{2}cdot frac{l^2}{16}=frac{ml^2}{16}left(2.3right).]
Момент инерции нашей системы относительно оси, проходящей через точку О найдем по теореме Штейнера:
[J=J_0+m{(frac{3}{4}l )}^2=frac{ml^2}{16}+frac{m9l^2}{16}=frac{5}{8}ml^2left(2.4right).]
Подставим правые части выражение (2.2) и (2.4) в (2.1) вместо соответствующих величин:
[{omega }_0=sqrt{frac{mgfrac{3}{4}l }{frac{5}{8}ml^2}}=sqrt{frac{6g}{5l}}.]
Ответ: ${omega }_0=sqrt{frac{6g}{5l}}$
Читать дальше: амплитуда скорости груза.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Циклическая частота колебаний

4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
Любые колебательные процессы в Природе (в том числе и непериодические) могут быть представлены в виде бесконечной суммы простых гармонических колебаний. Поэтому в первую очередь изучаются гармонические колебания. Рассмотрим такую характеристику этих колебаний, как циклическая частота.
Период и частота гармонических колебаний
Впервые гармоническими колебаниями заинтересовались еще античные философы, изучая вопросы музыкальной гармонии. Поэтому простейшие колебания, происходящие по закону круговых функций (синуса или косинуса), называются гармоническими.
Формула гармонических колебаний:
$$x=Asin(omega t+varphi)$$
Как можно видеть из графика колебаний (а также из изучения круговых функций в математическом анализе), функции эти регулярно повторяют свои значения. Более того, регулярно повторяется форма графика колебаний. Это свойство функции называется периодичностью. То есть, функция, обладающая периодичностью, имеет равные значения на промежутках, равных своему периоду.
Период обозначается латинской буквой $T$. Однако, физический и математический подход к измерению периода немного различен.
В математике в качестве аргумента круговой функции рассматривается угол поворота вектора, образующего ее, и этот угол удобно измерять в радианах (каждый радиан равен дуге, имеющей длину радиуса). В радианах измеряется и период круговой функции. Для простого синуса или косинуса $T = 2pi$.
В физике угол поворота менее важен, нередко такой угол даже невозможно указать (например, для колебаний пружинного маятника). Поэтому в физике период измеряется в единицах времени – секундах. Дополнительно это дает возможность ввести специальную характеристику, позволяющую определить «скорость» колебаний – частоту (обозначается греческой буквой $nu$ («ню»).
Если период показывает, за сколько времени совершается одно колебание, то частота показывает, сколько колебаний совершается за одну секунду:
$$nu= {1over T}$$
Частота измеряется в колебаниях в секунду или Герцах (Гц). Один герц – это одно колебание в секунду.
Круговая частота
Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.
Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:
$$T = {2pi over omega}$$
В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:
$$T = {2pi over omega}={1over nu}$$
Или, после упрощений:
$$omega = 2pi nu$$
Таким образом, параметр $omega$ в $2pi$ раз больше частоты колебаний. Поскольку в одном круге $2pi$ радиан, то параметр $omega$ называется «круговой» или «циклической» частотой.
Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.
Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.
Что мы узнали?
Круговая (циклическая) частота – это важный параметр гармонического колебания, удобный в математической обработке функций. Круговая частота обозначает количество радиан, прошедших гармонической функцией за единицу времени. Она прямо пропорциональна обычной частоте.
Тест по теме
Доска почёта

Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4.6
Средняя оценка: 4.6
Всего получено оценок: 207.
А какая ваша оценка?
Обновлено: 27.05.2023
Любые колебательные процессы в Природе (в том числе и непериодические) могут быть представлены в виде бесконечной суммы простых гармонических колебаний. Поэтому в первую очередь изучаются гармонические колебания. Рассмотрим такую характеристику этих колебаний, как циклическая частота.
Период и частота гармонических колебаний
Впервые гармоническими колебаниями заинтересовались еще античные философы, изучая вопросы музыкальной гармонии. Поэтому простейшие колебания, происходящие по закону круговых функций (синуса или косинуса), называются гармоническими.
Формула гармонических колебаний:
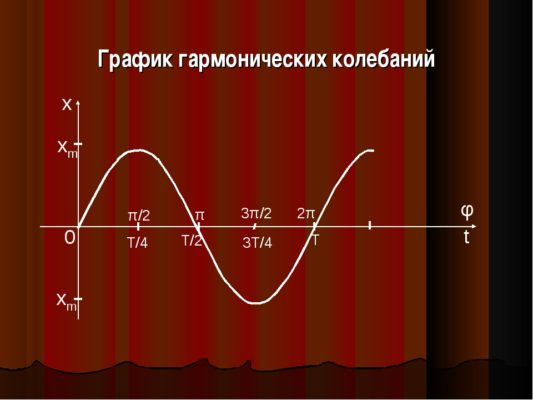
Рис. 1. График гармонических колебаний.
Как можно видеть из графика колебаний (а также из изучения круговых функций в математическом анализе), функции эти регулярно повторяют свои значения. Более того, регулярно повторяется форма графика колебаний. Это свойство функции называется периодичностью. То есть, функция, обладающая периодичностью, имеет равные значения на промежутках, равных своему периоду.
Период обозначается латинской буквой $T$. Однако, физический и математический подход к измерению периода немного различен.
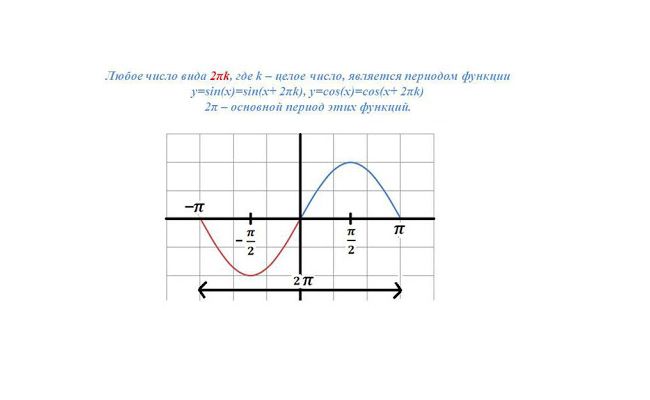
В математике в качестве аргумента круговой функции рассматривается угол поворота вектора, образующего ее, и этот угол удобно измерять в радианах (каждый радиан равен дуге, имеющей длину радиуса). В радианах измеряется и период круговой функции. Для простого синуса или косинуса $T = 2pi$.
Рис. 2. Период синуса и косинуса.
Если период показывает, за сколько времени совершается одно колебание, то частота показывает, сколько колебаний совершается за одну секунду:
Частота измеряется в колебаниях в секунду или Герцах (Гц). Один герц – это одно колебание в секунду.
Круговая частота
Как видим, физический и математический подход к описанию периода функций несколько отличаются, и возникает вопрос их связи.
Из приведенной выше формулы гармонических колебаний можно видеть, что она имеет период:
В эту формулу входит параметр $omega$, который обратно пропорционален периоду. При сравнении этой формулы с формулой частоты можно получить:
Или, после упрощений:
Физический смысл частоты – это количество колебаний, происходящих в системе за единицу времени, а физический смысл круговой частоты – это количество радиан, проходящих функцией, описывающей систему, за единицу времени.
Рис. 3. Круговая (циклическая) частота.
Таким образом, удобный и наглядный параметр частоты может быть легко преобразован для вида, удобного в математических преобразованиях.
Что мы узнали?
Круговая (циклическая) частота – это важный параметр гармонического колебания, удобный в математической обработке функций. Круговая частота обозначает количество радиан, прошедших гармонической функцией за единицу времени. Она прямо пропорциональна обычной частоте.
Единица измерения периода в системе СИ – секунда.
На графике колебаний период определяется как промежуток времени. через который система возвращается в то же состояние, в котором она находилась в начальный момент времени, который выбирается произвольно (рис.1).
Рис.1. Определение по графику периода колебаний.
Единица измерения частоты в системе СИ – 1 Герц (Гц).
Циклическая частота – это число колебаний, совершаемых телом за секунд:
Единица измерения циклической частоты в системе СИ — рад/с.
Частота и циклическая частота связаны между собой формулой:
Примеры решения задач
| Задание | Определить частоту колебаний железнодорожных вагонов, если период их вертикального колебания равен 0,5 с. |
| Решение | Частота колебаний – это величина, обратная периоду: |
Гц
| Задание | Маятник совершает 9 колебаний за 18 с. Определить период и частоту колебаний. Записать уравнение гармонических колебаний и построить график колебаний маятника, если амплитуда равна 10 см. |
| Решение | Частота колебаний определяется формулой: |
Гц
В данном случае:
| Задание | Период колебаний крыльев шмеля 5 мс, а частота колебаний крыльев комара 600 Гц. Определить, какое насекомое и на сколько больше сделает взмахов крыльями при полете за 1 минуту. |
| Решение | Определим частоту колебаний крыльев шмеля: |
С другой стороны, частота:
Приравняв правые части равенств, найдем число взмахов крыльями, которое сделает шмель за время :
Число взмахов крыльями, которое сделает комар за время , найдем непосредственно из формулы:
мин .
На уроке рассматривается простейший вид колебательного движения — гармонические колебания. Рассматриваются основные характеристики колебательного движения: амплитуда, период (частота) и фаза колебаний.
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобретя в каталоге.
Получите невероятные возможности
Конспект урока «Гармонические колебания. Амплитуда, период и частота колебательного движения»
В рамках прошлой темы говорилось о новом виде механического движения – колебательном движении.
Механическое колебательное движение —это движение, при котором состояния тела с течением времени повторяются, причем тело проходит через положение устойчивого равновесия поочередно в противоположных направлениях.
Если колебания происходят в системе только под действием внутренних сил, то такие колебания называют свободными.
Колебательной системой называют такую физическую систему, в которой при отклонении от положения равновесия возникают и существуют колебания.
Маятник – это твердое тело, совершающее под действием приложенных сил колебания около неподвижной точки или вокруг оси.
В рамках данной темы будет рассмотрен простейший вид колебательного движения — гармонические колебания.
Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
Смещение от положения равновесия при гармонических колебаниях описывается уравнениями вида:
Эти уравнения называют кинематическим законом гармонического движения.
Покажем, что гармонические колебания действительно подчиняются закону синуса или косинуса. Для этого рассмотрим следующую установку.
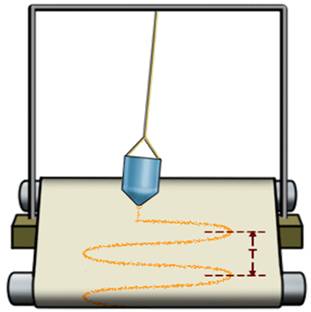
Возьмем нитяной маятник, а в качестве груза к нему выберем небольшой массивный сосуд с маленьким отверстием снизу и насыплем в него песок.А под полученную систему положим длинную бумажную ленту.
Если ленту перемещать с постоянной скоростью в направлении, перпендикулярном плоскости колебаний, то на ней останется волнообразная дорожка из песка, каждая точка которой соответствует положению колеблющегося груза в тот момент, когда он проходил над ней. Из опыта видно, что след, который оставляет песок на листе бумаги, есть некая кривая.
Она называется синусоидой. Из курса математики старших классов вы узнаете о том, что аналогичные графики имеют функции типа
Значит, графически зависимость смещения колеблющейся точки от времени изображается синусоидой или косинусоидой.
Через точки, соответствующие положению равновесия маятника, проведена ось времени t, а перпендикулярно ей — ось смещения икс. График дает возможность приблизительно определить координату груза в любой момент времени.
Теперь разберемся с величинами, входящими в уравнение колебательного движения.
Смещение — величина, характеризующая положение колеблющейся точки в некоторый момент времени относительно положения равновесия и измеряемая расстоянием от положения равновесия до положения точки в данный момент времени.
Амплитуда колебаний — максимальное смещение тела от положения равновесия.
Циклическая, или круговая частота, показывающая, сколько колебаний совершает тело за 2p секунд.
j0 — это начальная фаза колебаний.
Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
Период колебаний обычно обозначается буквой Т и в системе СИ измеряется в секундах.
Число колебаний в единицу времени называется частотой колебаний. Обозначается частота буквой ν. За единицу частоты принято одно колебание в секунду. Эта единица названа в честь немецкого ученого Генриха Герца.
Период колебания и частота колебаний связаны следующей зависимостью:
Т.е. частота — это величина обратная периоду и равная числу полных колебаний, совершаемых за 1 секунду.
Циклическая частота также связана с периодом колебаний или частотой. Эту связь математически можно записать в следующем виде:
Таким образом, любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
При совершении телом гармонических колебаний не только его координата, но и такие величины, как сила, ускорение, скорость, тоже изменяются по закону синуса или косинуса.
Это следует из известных вам законов и формул, в которых указанные величины попарно связаны прямо пропорциональной зависимостью, например законом Гука или вторым законом Ньютона. Из этих формул видно, что сила и ускорение достигают наибольших значений, когда колеблющееся тело находится в крайних положениях, где смещение наиболее велико, и равны нулю, когда тело проходит через положение равновесия.
Что же касается скорости, то она, наоборот, в крайних положениях равна нулю, а при прохождении телом положения равновесия достигает наибольшего значения.
Колебания, практически близкие к гармоническим, совершает тяжелый шарик, подвешенный на легкой и малорастяжимой нити, длина которой значительно больше диаметра шарика. Такую колебательную систему называют математическим маятником.
Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
Также гармонические колебания может совершать груз подвешенный на пружине, совершающий колебания в вертикальной плоскости. Такую колебательную систему называют пружинным маятником — это система, состоящая из материальной точки массой m и пружины.
Основные выводы:
– Гармонические колебания — это колебания, при которых смещение колеблющейся точки от положения равновесия изменяется с течением времени по закону синуса или косинуса.
– Любое колебательное движение характеризуется амплитудой, частотой (или периодом) и фазой колебаний.
– Амплитуда колебаний — максимальное смещение тела от положения равновесия.
– Промежуток времени, в течение которого тело совершает одно полное колебание, называется периодом колебаний.
– Число колебаний в единицу времени называется частотой колебаний.
– Фаза колебаний — это аргумент периодической функции, который при заданной амплитуде колебаний определяет состояние колебательной системы в любой момент времени.
– Математический и пружинный маятники — это простейшие идеализированные колебательные системы, подчиняющиеся закону синуса или косинуса.
– Математический маятник — это материальная точка, подвешенная на невесомой нерастяжимой нити, прикрепленной к подвесу и находящейся в поле силы тяжести.
– Пружинный маятник — это система, состоящая из материальной точки массой m и пружины, которая совершает колебания в вертикальной плоскости.
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Амплитуда колебаний (лат. amplitude — величина) — это наибольшее отклонение колеблющегося тела от положения равновесия.
Для маятника это максимальное расстояние, на которое удаляется шарик от своего положения равновесия (рисунок ниже). Для колебаний с малыми амплитудами за такое расстояние можно принимать как длину дуги 01 или 02, так и длины этих отрезков.
Амплитуда колебаний измеряется в единицах длины — метрах, сантиметрах и т. д. На графике колебаний амплитуда определяется как максимальная (по модулю) ордината синусоидальной кривой, (см. рис. ниже).
Период колебаний.
Период колебаний — это наименьший промежуток времени, через который система, совершающая колебания, снова возвращается в то же состояние, в котором она находилась в начальный момент времени, выбранный произвольно.
Другими словами, период колебаний (Т) — это время, за которое совершается одно полное колебание. Например, на рисунке ниже это время, за которое грузик маятника перемещается из крайней правой точки через точку равновесия О в крайнюю левую точку и обратно через точку О снова в крайнюю правую.
За полный период колебаний, таким образом, тело проходит путь, равный четырем амплитудам. Период колебаний измеряется в единицах времени — секундах, минутах и т. д. Период колебаний может быть определен по известному графику колебаний, (см. рис. ниже).
Частота колебаний.
Частота колебаний — это число колебаний, совершаемых за единицу времени, например, за 1 с.
Единица частоты в СИ названа герцем (Гц) в честь немецкого физика Г. Герца (1857-1894). Если частота колебаний (v) равна 1 Гц, то это значит, что за каждую секунду совершается одно колебание. Частота и период колебаний связаны соотношениями:
.
В теории колебаний пользуются также понятием циклической, или круговой частоты ω. Она связана с обычной частотой v и периодом колебаний Т соотношениями:
.
Циклическая частота — это число колебаний, совершаемых за 2π секунд.
Читайте также:
- Рекомендации по уходу за сухими волосами кратко
- Россия при первых романовых перемены в государственном устройстве 7 класс кратко
- Советская модель социализма кратко
- Подходы к оценке поведенческой нормы и девиации кратко
- Итоговая документация по контролю в менеджменте кратко
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Гармоническими называют колебания, в которых интересующий нас параметр изменяется во времени по тригонометрическому закону (синус или косинус).
$z=z_mcos (omega_0 t+alpha) (1),$ где:
- $z_m$ — является амплитудой колебаний;
- $(omega_0 t+alpha)$ – фаза колебаний;
- $alpha $ — служит начальной фазой колебаний (фаза колебаний в момент времени, который считают начальным ($t=0$));
- $omega_0$ — обозначение циклической (или круговой) частоты процесса.
Колебания играют важную роль в разных физических процессах. Среди множества колебаний гармонические колебания занимают особое место, поскольку:
- они считаются наиболее простыми для математического описания;
- любое периодическое движение можно разложить на составляющие, которые можно считать гармоническими компонентами рассматриваемого колебательного движения.
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Рассмотрим колебательное движение материальной точки.
Кинематическая модель гармонических колебаний
Пусть материальная точка $A$ равномерно движется по окружности (рис.1). Угловую скорость ее движения обозначим $omega_0=const$. Радиус окружности равен $R$.
Рисунок 1. Точка движется по окружности. Автор24 — интернет-биржа студенческих работ
Проектируя место наше точки в момент времени $t$ (рис.1) на ось $OZ$ мы получим точку $Z$, которая находится на расстоянии $z$ от начала координат (точки $O$). С течением времени (в ходе перемещения материальной точки $A$ по окружности) точка $Z$ будет совершать колебания от положения $Z_1$ до положения $Z_2$ и в обратную сторону.
Рассматриваемое колебание точки $Z$ будет гармоническим. Для его описания достаточно записать закон изменения расстояния $z$ (координаты $z$) от начала координат (точки $O$) в зависимости от времени, то есть получить функцию $z(t)$.
«Частота гармонических колебаний» 👇
Будем считать, что при $t=0$ радиус $ОA$ составляет угол $alpha$ с осью $OZ$. Через время $t$ данный угол изменится на величину $omega_0 t$. Из прямоугольного треугольника $OZA$ мы получим:
$z(t)=Rcos (omega_0 t+alpha)=z_mcos (omega_0 t+alpha) (2).$
Выражение (2) описывает гармонические колебания точки $A$ по оси $OZ$.
Параметр $R=z_m$ в данном случае – это наибольшее отклонение точки, выполняющей колебания от положения равновесия (точки $O$), данный параметр носит название амплитуды колебаний.
Угловая скорость вращения точки по окружности в данной модели будет играть роль циклической частоты колебаний.
- При начальной фазе колебаний равной нулю $(alpha=0),$ имеем $z(t)= z_mcos (omega_0 t );$
- При $alpha=frac{pi}{2}$ мы получим, что $z(t)= z_msin (omega_0 t ).$
Мы видим, что при гармонических колебаниях координата $z$ является функцией синуса или косинуса, зависящей от времени.
Гармонические колебания часто изображают в виде графиков. При этом по горизонтальной оси откладывают время, на вертикальной оси — координату. Получают периодическую кривую (синусоиду или косинусоиду). При этом форма кривой зависит только от амплитуды и круговой частоты гармонических колебаний. Положение данной кривой определяет начальная фаза колебаний.
Период колебаний и круговая частота
Синус (косинус) является периодической функцией, следовательно, рассматриваемое нами движение является периодическим. Период этих тригонометрических функций составляет $T=2pi$. Это означает, что по истечении времени $T$ точка, выполняющая колебания приходит в свое исходное положение, сохраняя свое направление движения. $T$ называют периодом колебаний.
Период колебаний и круговая частота колебаний связаны выражением:
$omega_0=frac{2pi}{T}(3).$
Частота колебаний
Кроме циклической частоты при описании колебаний используют линейную частоту (или просто частоту), обозначаемую $nu$.
Линейная частота является величиной обратной периоду колебаний:
$nu=frac{1}{T}(4)$.
Она измеряется в герцах (Гц), тогда как единицей измерения циклической частоты является обратная секунда.
Определение 1
Частотой (линейной частотой) называют физическую величину, которая служит характеристикой периодического процесса, равную числу колебаний (повторений) за единицу времени.
$nu=frac{n}{t}(5),$
где $n$ — количество колебаний (повторений процесса); $t$ — время наблюдения.
Линейная частота связана с круговой частотой формулой:
$nu=frac{omega_0}{2pi}(6).$
Формулы циклической частоты для гармонических осцилляторов
Классическими примерами гармонических осцилляторов в механике являются:
- груз на упругой пружине (пружинный маятник);
- математический маятник;
- физический маятник (твердое тело, выполняющее колебания (качания) относительно неподвижной горизонтальной оси, которая проходит через точку, не совпадающую с его центром масс);
- электрический $LC$ контур.
Допустим, что осцилляторы совершают свободные (без действия внешних сил) колебания при отсутствии трения.
Груз на пружине выполняет колебания с циклической частотой равной:
$omega_0=sqrt{frac{k}{m}}(7),$
где $k$ — коэффициент упругости пружины; $m$- масса тела, подвешенного к пружине.
Круговая частота малых колебаний физического маятника равна:
$omega_0=sqrt{frac{mga}{I}}(8),$
где $m$ — масса маятника; $a$ — расстояние от центра масс, до точки подвеса маятника; $I$ — момент инерции маятника.
Математический маятник — это частный случай физического маятника. У этого маятника массу считают сосредоточенной в одной точке — центре его центре масс. Чаще всего в качестве математического маятника рассматривают шарик, который выполняет колебания на длинной нити.
Циклическая частота колебаний математического маятника равна:
$omega_0=sqrt{frac{g}{l}}(9),$
где $l$ — длина нити.
Классическим примером осциллятора, который может выполнять свободные незатухающие гармонические электромагнитные колебания является идеальный электрический контур, состоящий из конденсатора и катушки индуктивности.
Циклическая частота данных колебаний определяется выражением:
$omega_0=frac{1}{sqrt{LC}}(10)$,
где $C$ — емкость конденсатора; $L$ — индуктивность катушки.
Из приведенных выше формул мы видим, что частота свободных колебаний без учета трения зависит только от свойств самих осцилляторов.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме