Как найти круговую орбиту

From Wikipedia, the free encyclopedia

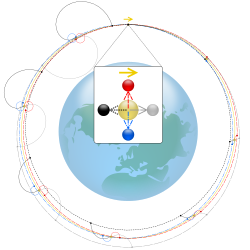
A circular orbit is an orbit with a fixed distance around the barycenter; that is, in the shape of a circle.

Listed below is a circular orbit in astrodynamics or celestial mechanics under standard assumptions. Here the centripetal force is the gravitational force, and the axis mentioned above is the line through the center of the central mass perpendicular to the plane of motion.

In this case, not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.

Circular acceleration[edit]

Transverse acceleration (perpendicular to velocity) causes change in direction. If it is constant in magnitude and changing in direction with the velocity, circular motion ensues. Taking two derivatives of the particle’s coordinates with respect to time gives the centripetal acceleration

where:

The formula is dimensionless, describing a ratio true for all units of measure applied uniformly across the formula. If the numerical value of is measured in meters per second per second, then the numerical values for will be in meters per second, in meters, and in radians per second.

Velocity[edit]

The speed (or the magnitude of velocity) relative to the central object is constant:^[1]: 30

where:

Equation of motion[edit]

The orbit equation in polar coordinates, which in general gives r in terms of θ, reduces to:^{[clarification needed][citation needed]}

where:

• is specific angular momentum of the orbiting body.

This is because

Angular speed and orbital period[edit]

Hence the orbital period () can be computed as:^[1]: 28

Compare two proportional quantities, the free-fall time (time to fall to a point mass from rest)

(17.7% of the orbital period in a circular orbit)

and the time to fall to a point mass in a radial parabolic orbit

(7.5% of the orbital period in a circular orbit)

The fact that the formulas only differ by a constant factor is a priori clear from dimensional analysis.^{[citation needed]}

Energy[edit]

The specific orbital energy () is negative, and

Thus the virial theorem^[1]: 72 applies even without taking a time-average:^{[citation needed]}

• the kinetic energy of the system is equal to the absolute value of the total energy
• the potential energy of the system is equal to twice the total energy

The escape velocity from any distance is √2 times the speed in a circular orbit at that distance: the kinetic energy is twice as much, hence the total energy is zero.^{[citation needed]}

Delta-v to reach a circular orbit[edit]

Maneuvering into a large circular orbit, e.g. a geostationary orbit, requires a larger delta-v than an escape orbit, although the latter implies getting arbitrarily far away and having more energy than needed for the orbital speed of the circular orbit. It is also a matter of maneuvering into the orbit. See also Hohmann transfer orbit.

Orbital velocity in general relativity[edit]

In Schwarzschild metric, the orbital velocity for a circular orbit with radius is given by the following formula:

where is the Schwarzschild radius of the central body.

Derivation[edit]

For the sake of convenience, the derivation will be written in units in which .

The four-velocity of a body on a circular orbit is given by:

( is constant on a circular orbit, and the coordinates can be chosen so that ). The dot above a variable denotes derivation with respect to proper time .

For a massive particle, the components of the four-velocity satisfy the following equation:

We use the geodesic equation:

The only nontrivial equation is the one for . It gives:

From this, we get:

Substituting this into the equation for a massive particle gives:

Hence:

Assume we have an observer at radius , who is not moving with respect to the central body, that is, their four-velocity is proportional to the vector . The normalization condition implies that it is equal to:

The dot product of the four-velocities of the observer and the orbiting body equals the gamma factor for the orbiting body relative to the observer, hence:

This gives the velocity:

Or, in SI units:

See also[edit]

• Elliptic orbit
• List of orbits
• Two-body problem

References[edit]

2014-05-30   

Определите радиус r орбиты спутника Земли, который все время находится над одной и той же точкой земной поверхности.

Решение:

Орбита, по которой должен двигаться спутник, находится в плоскости, проходящей через земной экватор. В противном случае широта, на которой находится спутник, будет меняться. Кроме того, орбита должна быть круговой, так как по эллиптической орбите спутник, в отличие от Земли, вращается неравномерно. Таким образом, надо найти радиус r круговой орбиты в плоскости экватора с периодом обращения спутника Т = 24 ч. Из уравнения движения спутника получаем

$v^{2}/r=GM/r^{2}$,

где v -скорость движения спутника, М — масса Земли, G — гравитационная постоянная. Замечая, что $g=GM/R^{2}_{З}$, получаем для периода обращения

$T=2 pi frac{r}{v}=2 pi sqrt{frac{r^{3}}{ R^{2}_{З}g}}$

Из этого выражения легко находим радиус орбиты спутника

$r=R_{З} left ( frac{gT^{2}}{4 pi^{2} R_{З}}right )^{1/3}=6,4R_{З}=42,24 cdot 10^{2} км$

Круговая орбита изображена в верхнем левом квадранте этой диаграммы, где гравитационная потенциальная яма центральной массы показывает потенциальную энергию, а кинетическую энергию орбитальной скорости отображается красным. Высота кинетической энергии остается постоянной на протяжении всей круговой орбиты с постоянной скоростью.

A круговая орбита — это орбита с фиксированным расстоянием вокруг барицентра, то есть в форма круга.

Перечисленная ниже круговая орбита в астродинамике или небесной механике при стандартных допущениях. Здесь центростремительная сила — это сила тяжести, а упомянутая выше ось — это линия, проходящая через центр центральной массы, перпендикулярную плоскости движения.

В этом случае не только расстояние, но также скорость, угловая скорость, потенциальная и кинетическая энергия постоянны. Нет периапсиса или апоапсиса. У этой орбиты нет радиального варианта.

Содержание

• 1 Круговое ускорение
• 2 Скорость
• 3 Уравнение движения
• 4 Угловая скорость и период обращения
• 5 Энергия
• 6 Дельта-v для достижения круговой орбиты
• 7 Орбитальная скорость в общей теории относительности
  • 7.1 Вывод
• 8 См. Также
• 9 Ссылки

Круговое ускорение

Поперечное ускорение (перпендикулярно скорости) вызывает изменение направление. Если он постоянен по величине и изменяется по направлению со скоростью, следует круговое движение. Взяв две производные от координат частицы по времени, получаем центростремительное ускорение

a = v 2 r = ω 2 r { displaystyle a , = { frac {v ^ {2}} {r} } , = { omega ^ {2}} {r}}

где:

Формула безразмерная, описывающая соотношение, истинное для всех единиц измерения, применяемых единообразно по формуле. Если числовое значение a { displaystyle mathbf {a}}измеряется в метрах в секунду в секунду, то числовые значения для v { displaystyle v ,}будет в метрах в секунду, r { displaystyle r ,}в метрах и ω { displaystyle omega }в радианах в секунду.

Скорость

Скорость (или величина скорости) относительно центрального объекта постоянна:

v = GM r = μ r { displaystyle v = { sqrt {GM ! over {r}}} = { sqrt { mu over {r}}}}

где:

Уравнение движения

Уравнение орбиты в полярных координатах, которое в целом дает r в терминах θ, сокращается до:

r = h 2 μ { displaystyle r = {{h ^ {2}} over { mu}}}

где:

• h = rv { displaystyle h = rv}— удельный угловой момент вращающегося тела.

Это потому, что μ = rv 2 { displaystyle mu = rv ^ {2}}

Угловая скорость и период обращения

ω 2 r 3 = μ { displaystyle omega ^ {2} r ^ {3} = mu}

Следовательно, период обращения (T { displaystyle T , !}) можно вычислить как:

T = 2 π r 3 μ { displaystyle T = 2 pi { sqrt {r ^ {3 } over { mu}}}}

Сравните две пропорциональные величины, время свободного падения (время, чтобы упасть в точечную массу из состояния покоя)

T ff = π 2 2 r 3 μ { displaystyle T_ {ff} = { frac { pi} {2 { sqrt {2}}}} { sqrt {r ^ {3} over { mu}}}}(17,7% периода обращения по круговой орбите)

и время падения до точечной массы на радиальной параболической орбите

T par = 2 3 r 3 μ { displaystyle T_ { par} = { frac { sqrt {2}} {3}} { sqrt {r ^ {3} over { mu}}}}(7,5% орбитального периода в круговая орбита)

Тот факт, что формулы различаются только на постоянный коэффициент, априори очевиден из анализа размеров.

Энергия

удельная орбитальная энергия (ϵ { displaystyle epsilon ,}) отрицательно, а

ϵ = — v 2 2 { displaystyle epsilon = — {v ^ {2} over {2}}}

ϵ = — μ 2 r { displaystyle epsilon = — { mu over {2r}}}

Таким образом теорема вириала применяется даже без усреднения по времени:

• кинетическая энергия системы равна абсолютному значению полной энергии
• потенциальная энергия системы равна равна удвоенной полной энергии

убегающая скорость с любого расстояния в √2 раза больше скорости на круговой орбите на этом расстоянии: кинетическая энергия в два раза больше, следовательно, полная энергия равна нулю.

Дельта-v для выхода на круговую орбиту

Маневрирование на большую круговую орбиту, например геостационарная орбита требует большей delta-v, чем орбита ухода, хотя последняя подразумевает удаление произвольно далеко и наличие большей энергии, чем необходимо для орбитальная скорость круговой орбиты. Это также вопрос выхода на орбиту. См. Также переходная орбита Хомана.

Орбитальная скорость в общей теории относительности

В метрике Шварцшильда орбитальная скорость для круговой орбиты с радиусом r { displaystyle r}задается следующей формулой:

v = GM r — r S { displaystyle v = { sqrt { frac {GM} {r-r_ {S}}}}}

где r S = 2 GM c 2 { displaystyle scriptstyle r_ {S} = { frac {2GM} {c ^ {2}}}}— радиус Шварцшильда центрального тело.

Деривация

Для удобства деривация будет записана в единицах, в которых c = G = 1 { displaystyle scriptstyle c = G = 1}.

четырехскоростная тела на круговой орбите определяется как:

u μ = (t ˙, 0, 0, ϕ ˙) { displaystyle u ^ { mu} = ({ dot {t}}, 0,0, { dot { phi}})}

(r { displaystyle scriptstyle r}постоянно на круговой орбите, и координаты могут быть выбрано так, чтобы θ = π 2 { displaystyle scriptstyle theta = { frac { pi} {2}}}). Точка над переменной обозначает вывод относительно собственного времени τ { displaystyle scriptstyle tau}.

Для массивной частицы компоненты четырехскоростной удовлетворяют следующему уравнению:

(1-2 M r) t ˙ 2 — r 2 ϕ ˙ 2 = 1 { displaystyle left (1 — { frac {2M} {r}} right) { dot {t}} ^ {2} -r ^ {2} { dot { phi}} ^ {2} = 1}

Мы используем уравнение геодезических:

x ¨ μ + Γ ν σ μ x ˙ ν x ˙ σ Знак равно 0 { displaystyle { ddot {x}} ^ { mu} + Gamma _ { nu sigma} ^ { mu} { dot {x}} ^ { nu} { dot {x} } ^ { sigma} = 0}

Единственное нетривиальное уравнение — это уравнение для μ = r { displaystyle scriptstyle mu = r}. Это дает:

M r 2 (1-2 M r) t ˙ 2 — r (1-2 M r) ϕ ˙ 2 = 0 { displaystyle { frac {M} {r ^ {2}}} left (1 — { frac {2M} {r}} right) { dot {t}} ^ {2} -r left (1 — { frac {2M} {r}} right) { dot { phi}} ^ {2} = 0}

Отсюда получаем:

ϕ ˙ 2 = M r 3 t ˙ 2 { displaystyle { dot { phi}} ^ {2 } = { frac {M} {r ^ {3}}} { dot {t}} ^ {2}}

Подставляя это в уравнение для массивной частицы, получаем:

(1-2 M r) T ˙ 2 — M rt ˙ 2 = 1 { displaystyle left (1 — { frac {2M} {r}} right) { dot {t}} ^ {2} — { frac {M } {r}} { dot {t}} ^ {2} = 1}

Следовательно:

t ˙ 2 = rr — 3 M { displaystyle { dot {t}} ^ {2} = { frac {r} {r-3M}}}

Предположим, у нас есть наблюдатель в радиусе r { displaystyle scriptstyle r}, который не движется относительно центральной тела, то есть их четырехскоростная пропорциональна вектору ∂ t { displaystyle scriptstyle partial _ {t}}. Условие нормализации подразумевает, что оно равно:

v μ = (rr — 2 M, 0, 0, 0) { displaystyle v ^ { mu} = left ({ sqrt { frac {r}) {r-2M}}}, 0,0,0 right)}

Скалярное произведение четырех скоростей наблюдателя и движущегося по орбите тела равно гамма-фактору относительного наблюдателю, следовательно:

γ = g μ ν u μ v ν = (1-2 M r) rr — 3 M rr — 2 M = r — 2 M r — 3 M { displaystyle gamma = g_ { mu nu} u ^ { mu} v ^ { nu} = left (1 — { frac {2M} {r}} right) { sqrt { frac {r} {r-3M }}} { sqrt { frac {r} {r-2M}}} = { sqrt { frac {r-2M} {r-3M}}}}

Это дает скорость :

v = M r — 2 M { displaystyle v = { sqrt { frac {M} {r-2M}}}}

Или, в единицах СИ:

v = GM r — r S { displaystyle v = { sqrt { frac {GM} {r-r_ {S}}}}}

См. также

• Эллиптическая орбита
• Список орбит
• Задача двух тел

Ссылки