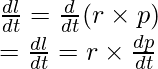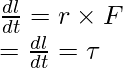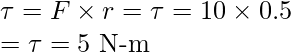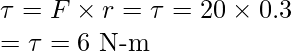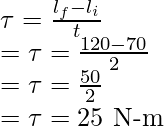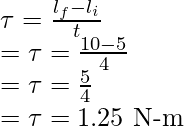Ниже два калькулятора, которые переводят мощность в момент силы (или крутящий момент) и наоборот для заданной угловой скорости. Формулы под калькулятором.
Момент силы и мощность
Угловая скорость, оборотов в минуту
Точность вычисления
Знаков после запятой: 3
Мощность и момент силы
Угловая скорость, оборотов в минуту
Точность вычисления
Знаков после запятой: 2
Несколько формул/
Для мощности:
где P — мощность (Ватты или килоВатты), τ — крутящий момент (Ньютон-метр), ω — угловая скорость (радиан в секунду), а точка обозначает скалярное произведение.
Для момента силы:
Угловая скорость в калькуляторе задается в оборотах в минуту, приведение ее к радианам в секунду тривиально:
так как один оборот это радиан.
Мощность, достигаемая системой, которая равномерно вращается вокруг определенной оси в заданный период времени, равна произведению крутящего момента на угловую скорость. Угловая скорость и крутящий момент обратно пропорциональны друг другу.
Угловая скорость — это векторное выражение движения вращения, которое показывает, насколько быстро вещество может вращаться или вращаться по сравнению с другой точкой. Крутящий момент можно объяснить как измерение силы, отвечающей за вращение вещества вокруг оси.
Проще говоря, значение угловой скорости равно скорость вращения вещества вокруг оси или изменение углового смещения между двумя телами.
Размерная формула для угловой скорости: M ^ 0L ^ 0T ^ — ^ 1, где M обозначается как масса вещества, L обозначается как длина вещества, а T обозначается как время, затраченное на вещество.
Единицей СИ для угловой скорости является радиан в секунду (рад/с). Точка компаса для угловой скорости находится прямо перпендикулярно плоскости вращения. Размерная формула для крутящего момента: ML^2T^-^2.
Единицей СИ для крутящего момента является ньютон-метр. Термин крутящий момент, как момент силы, сила, сила вращения, который зависит от границ исследования.
Крутящий момент равен угловой скорости?
Угловая скорость представлена с помощью греческой буквы омега (омега), а крутящий момент — с помощью тау.
Нет, крутящий момент и угловая скорость — это разные термины. Термин крутящий момент является мерой кратчайшей силы. Крутящий момент относится к силе силы, вызывающей изменение движения при вращении материи. Смысл угловой скорости — это скорость вращения вещества, вращения вокруг оси или изменения углового смещения между двумя телами.
При определенном вращении материи вокруг оси каждая точка материи имеет одинаковую угловую скорость. Но точки, большие от оси вращения, движутся с несколькими тангенциальными скоростями, чем точки, расположенные ближе к оси вращения.
Другим термином для угловой скорости является вектор угловой частоты и скорость вращения.
Кредит изображения — Википедия
Зависит ли крутящий момент от угловой скорости?
Если значение крутящего момента увеличивается, то значение угловой скорости уменьшается, а если значение крутящего момента уменьшается, то значение угловой скорости увеличивается.
Крутящий момент физических свойств зависит от угловой скорости. Угловая скорость или угловая скорость обратно пропорциональны физическому свойству крутящего момента. Крутящий момент для материи, которая вращается в движении, может быть выражен как отношение мощности к угловой скорости.
Какая связь между крутящим моментом и угловой скоростью?
Крутящий момент прямо пропорционален мощности. Означает, что значение крутящего момента увеличивается, тогда значение мощности также увеличивается, а когда значение уменьшается, в этом случае значение мощности также уменьшается.
Связь между крутящим моментом и угловой скоростью косвенно пропорциональна друг другу, это означает, что если значение крутящего момента увеличивается, то значение угловой скорости уменьшается таким же образом, если значение крутящего момента уменьшается, значение угловой скорости увеличивается.
Крутящий момент — это циклическая идентичность кратчайшей силы. С другой стороны, скорость используется для оценки расстояния, пройденного за определенное время. Для вращающегося объекта крутящий момент может быть выражен как пропорция физического свойства мощности и физического свойства угловой скорости.
Формула для крутящего момента и угловой скорости или угловой скорости: —
Формула для крутящего момента и угловой скорости или угловой скорости:
Крутящий момент = frac{Мощность}{Скорость}
тау = гидроразрыва {P} { омега}
Вывод формулы для крутящего момента и угловой скорости или угловой скорости:
Вывод формулы для крутящего момента и угловой скорости или угловой скорости:
tau обозначается как Torque.
P обозначается как мощностью
omega обозначается как угловая скорость или угловая скорость.
В соответствии с преобразованием приведенного выше уравнения можно оценить значение угловой скорости или крутящего момента. Соблюдая уравнение, можно легко записать соотношение между крутящим моментом и мощностью или соотношение между крутящим моментом и угловой скоростью.
Как найти угловую скорость по крутящему моменту?
Крутящий момент — это не энергия. Крутящий момент — это векторное выражение. Направление вектора крутящего момента зависит от направления силы на оси.
Для случая движения вращения, чтобы объяснить взаимосвязь между мощностью и крутящим моментом, ассимилируйте линейный эквивалент. Линейное смещение можно объяснить как; расстояние, пройденное в окружении, если оборот и оценивается произведением радиуса и пройденного угла.
Линейное расстояние можно записать как произведение времени и линейной скорости.
Выражение для линейного расстояния:
Линейное расстояние = Радиус times Угловая скорость times Время
Крутящий момент можно объяснить как измерение силы, отвечающей за вращение вещества вокруг оси.
Крутящий момент = Сила время Радиус
Форс-мажор = frac{Крутящий момент}{Радиус}
Мощность = frac{Сила times Linear Distance}{Время}
Мощность = frac{frac{Крутящий момент}}{Радиус} times Угловая скорость times Time}{Time}
Мощность = крутящий момент х угловая скорость
Крутящий момент = frac{Мощность}{Угловая скорость}
Таким образом, угловая скорость может быть оценена по крутящему моменту.
График угловой скорости и крутящего момента:
На графике углов и крутящих моментов в вертикальной части нанесен крутящий момент, а в горизонтальной — угловая скорость..
Постановка задачи с решением:-1
Мальчик играет со своей игрушкой. Когда мальчик крутил свою игрушку в этот раз, он приложил к своей игрушке мощность около 15 Вт. Теперь игрушка начинает вращаться со скоростью 12 радиан в секунду.
Теперь оцените величину крутящего момента.
Решение:-
Данные данные,
Мощность (P) = 15 Вт.
Угловая скорость ( омега) = 12 радиан в секунду
Необходимо рассчитать значение крутящего момента (тау) =?
Мы знаем,
Формула для крутящего момента и угловой скорости или угловой скорости:
Крутящий момент = frac{Мощность}{Скорость}
тау = гидроразрыва {P} { омега}
Где,
tau обозначается как Torque.
P обозначается как мощность
омега обозначается как угловая скорость или угловая скорость
Итак, ставим значение и получаем,
тау = гидроразрыва {15} {12}
тау = 1.25 Ньютон-метр
Мальчик играет со своей игрушкой. Когда мальчик крутил свою игрушку в этот раз, он приложил к своей игрушке мощность около 15 Вт. Теперь игрушка начинает вращаться со скоростью 12 радиан в секунду.
Итак, величина крутящего момента составляет 1.25 ньютон-метра.
Постановка задачи с решением:-2
Грузовик едет из Калькутты в Мумбаи. Когда колесо грузовика вращается в это время, мощность, подаваемая на колесо, составляет около 20 Вт. Теперь колесо грузовика начинает вращаться со скоростью 15 радиан в секунду.
Теперь оцените величину крутящего момента.
Решение:-
Данные данные,
Мощность (P) = 20 Вт.
Угловая скорость ( омега) = 15 радиан в секунду
Необходимо рассчитать значение крутящего момента (тау) =?
Мы знаем,
Формула для крутящего момента и угловой скорости или угловой скорости:
Крутящий момент = frac{Мощность}{Скорость}
тау = гидроразрыва {P} { омега}
Где,
tau обозначается как Torque.
P обозначается как мощность
омега обозначается как угловая скорость или угловая скорость
Итак, ставим значение и получаем,
тау = гидроразрыва {20} {15}
тау = 1.33 Ньютон-метр
Грузовик едет из Калькутты в Мумбаи. Когда колесо грузовика вращается в это время, мощность, подаваемая на колесо, составляет около 20 Вт. Теперь колесо грузовика начинает вращаться со скоростью 15 радиан в секунду.
Итак, величина крутящего момента составляет 1.33 ньютон-метра.
Вывод:
Сила вокруг оси обратно пропорциональна скорости или угловой скорости. Увеличивает значение крутящего момента скорости, а уменьшает значение крутящего момента скорости, увеличивает.
For a rigid body, motion is generally both rotational and translation. If the body is fixed at one point, the motion is usually rotational. It is known that force is needed to change the translatory state of the body and to provide it with linear acceleration. Torque and angular momentum are rotational equivalents of force and momentum. These entities help us change the rotational state of the body. Torques and angular momentum are very useful and are encountered almost everywhere in daily life. The power of the engine and motors is measured by torque. So, while studying any rigid body, it is essential to understand the concepts of torque and angular momentum. Let’s look at these concepts in detail.
Torque
Torque is analogous to the force in the case of rotational motion. Consider an example of a door. The position of the door is fixed, it can only rotate around its axis. Then what causes the door to rotate? Force is required, but the force applied to the hinge of the door does not work. So, it is not the force alone, the position to which it is applied matters too.
In rotational motion, the analogous force is torque. This is also called the moment of force. This causes angular acceleration in the body, which means forcing to change the rotational state of the body. Let a particle P be located far from the origin at a point whose position vector is given by . If the force F is acting on the particle, the moment of force is given by,
Since the cross-product is involved, it is a vector quantity. The magnitude of the torque is given by,
Here, “r” is the magnitude of the position vector, and θ is the angle between the position vector and force. In the formula, the part “rsinθ” is the perpendicular distance of the force from the axis of the rigid body.
Dimensions of torque are given by ML2T-2. These are also dimensions of energy but, these quantities should not be confused as similar. They are very different quantities.The unit of torque is N-m.
Angular Momentum of Particle
It has been mentioned that torque is analogous to force. In the same way, angular momentum is analogous to linear momentum. This is also a vector product similar to its counterpart torque. Consider a particle P with the linear momentum “p” and a position vector with respect to the origin O. The angular momentum of the particle is denoted by “L”,
L = r × p
The magnitude of angular momentum will be given by,
L = rpsinθ
Where r and p are the magnitudes of the position vector and linear momentum respectively. The angle θ is the angle between the position vector and the linear momentum. Here also “rsin(θ)” is the perpendicular angle between the momentum and the position vector.
Relationship between Angular Momentum and Torque
The relationship between the angular momentum and torque is similar to the relationship between the force and the momentum. Force is the change in momentum of the particle. Similarly, torque is the change in angular momentum of the particle. Differentiating the formula for the angular momentum,
Applying the product rule for differentiation,
Now, is the velocity of the particle, but since it is in the same direction as the momentum,
r x = 0
So, now the equation becomes,
represents the force F,
Thus, this proves that the rate of change of angular momentum is given by torque.
Sample Problems
Question 1: Find out the torque on the door if a force of 10N is applied on the door 0.5m from the hinge.
Answer:
Torque is given by,
Where r is the perpendicular distance of the force from the rotational axis.
Given: r = 0.5m and F = 10N.
Plugging the values in the equation,
Question 2: Find out the torque on the door if a force of 20N is applied on the door 0.3m from the hinge.
Answer:
Torque is given by,
Where r is the perpendicular distance of the force from the rotational axis.
Given: r = 0.3m and F = 20N.
Plugging the values in the equation,
Question 3: A body is revolving around an axis in a circular motion with a radius of 0.1m, the momentum of the body is given by 50 Kgm/s. Find the angular momentum of the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Given: r = 0.3m and p = 50Kgm/s.
Plugging the values in the equation,
l = r xp
⇒l =0.3 × 50
⇒l = 15
Question 4: A body is revolving around an axis in a circular motion with a radius of 0.2m, the momentum of the body is given by 70 Kg/s. Find the angular momentum of the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Given: r = 0.2m and p =70 Kg/s.
Plugging the values in the equation,
l = r × p
⇒l =0.2 × 70
⇒l = 14
Question 5: A body is revolving around an axis in a circular motion with a radius of 0.2m, the momentum of the body is given by 70 Kg/s. A torque is applied on the body for 2 seconds and the momentum becomes 120Kgm/s. Find the torque applied to the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Rate of Change in angular momentum gives us the torque.
Initial angular momentum
li = 0. 2 × 70
li = 14
Final angular momentum
li = 0. 2 × 120
li = 24
Rate of change of angular momentum =
Question 6: A body is revolving around an axis in a circular motion with a radius of 0.1m, the momentum of the body is given by 50 Kgm/s. A torque is applied on the body for 4 seconds and the momentum becomes 100Kgm/s. Find the torque applied to the body.
Answer:
Angular momentum of a body is given by,
l = r × p
Where r is the perpendicular distance of the force from the rotational axis and p is the linear momentum.
Rate of Change in angular momentum gives us the torque.
Initial angular momentum
li = 0. 1 × 50
li = 5
Final angular momentum
li = 0. 1 × 100
li = 10
Rate of change of angular momentum =
Last Updated :
14 Jul, 2021
Like Article
Save Article
Крутящий
момент на рабочем валу машины определяется
по формуле
,
где
Т
– крутящий момент, Нм;
Р
– мощность, кВт;
n
–
частота вращения, мин-1.
Переходя
от рабочего вала машины к следующему
валу привода (например к тихоходному
валу редуктора), крутящий момент
определится
,
где
Ттр
– крутящий момент на тихоходном валу
редуктора; Тм
– крутящий момент на рабочем валу
машины; uп
– передаточное число передачи от
рабочего вала машины к тихоходному валу
редуктора;
—
КПД передачи.
Определяем
крутящие моменты на валах
Проверка:
Определяем
частоты вращения валов привода
и
угловые скорости валов
Раздел 2. Выбор материалов и определение допускаемых напряжений
2.1 Выбор материалов и термообработки шестерен
В
производственных условиях при
проектировании и изготовлении редукторов
выбор материалов и назначение термической
обработки производится на базе опыта
конструкторов и технологов. Рекомендации
по применению марок стали для изготовления
различных деталей приведены в работе
[1].
В
курсовом проектировании при выборе
марок стали и термической обработки
для шестерен и колес можно руководствоваться
табл.4.
Для
лучшей приработки зубьев твердость
шестерни рекомендуется назначать больше
твердости колеса для прямозубых передач
на 10-15
единиц по шкале НВ.
Для косозубых передач твердость шестерни
должна быть еще больше на 50-70НВ
(для улучшения несущей способности
передачи).
Для
передач, к размерам которых не предъявляют
высоких требований, следует применять
дешевые марки сталей типа 40,
40Х.
Для колес открытых передач большого
диаметра (D500
мм)
применить стальное литье (35Л,
40Л, 45Л, 40ГЛ,
термообработка – нормализация, улучшение)
в паре с кованной шестерней из стали
соответствующей марки.
Таблица
4
Предпочтительные
марки сталей
|
Термическая |
Твердость |
Диаметр |
||||
|
любой |
315 |
200 |
125 |
80 |
||
|
Ширина |
||||||
|
любой |
200 |
125 |
80 |
50 |
||
|
Нормализация, |
НВ
НВ
НВ |
45 — — |
45 35ХМ — |
45 45Х 35ХМ |
45 45 40Х |
45 45 45 |
|
Объемная |
НRC |
— |
— |
35ХМ |
35ХМ |
35ХМ |
|
Поверхностная |
НRC |
— |
— |
35ХМ |
35ХМ |
35ХМ |
|
ТВЧ |
НRC |
— |
— |
50ХМ |
50ХМ |
50ХМ |
|
Цементация |
НRC |
— |
— |
20ХН2М |
20ХН2М |
20ХН2М |
|
Нитроцементация |
НRC |
— |
— |
25ХГТ |
25ХГТ |
25ХГТ |
|
Азотирование |
НRC |
— |
— |
40ХН2МА |
40ХН2МА |
40ХН2МА |
|
В |
По
рекомендациям [1] принимаем следующие
марки сталей: для шестерни сталь 35ХМ
твердостью 35-45
HRC
(объемная закалка);
для колеса сталь 40Х
твердостью 270-300
НВ (улучшение).
Средние твердости зубьев шестерни и
колеса определятся
По
графику 1 находим
Рис.1.
График соотношения твердостей, выраженных
в единицах HB
и HRC.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В прошлой публикации мы начали рассчитывать требуемые характеристики привода дельта-робота и нашли максимальную требуемую скорость вращения. Здесь рассмотрим задачу силового анализа, то есть найдём максимальный требуемый крутящий момент. Помимо этого, получим зависимости для поиска угловых ускорений входных звеньев при известных положении, скорости и ускорении выходного звена. Немного поговорим о факторах, влияющих на точность позиционирования. В конце затронем вопрос выбора комплектующих, после чего можно будет уже полностью погружаться в процесс проектирования, имея на руках все необходимые нам данные.
Важно отметить, что данная статья тесно связана с предыдущей, и, не ознакомившись с ней, трудно будет уловить суть происходящего здесь.
Список обозначений
– крутящие моменты первого, второго и третьего рычагов соответственно;
– составляющие приложенной к исполнительному звену силы по осям ;
– матрица Якоби;
– приведённая к точке V масса каретки (подвижной платформы);
– приведённые к точке V массы рычагов механизма;
– момент инерции i-го звена относительно мгновенной оси вращения;
– масса i-го звена;
– угловая скорость i-го звена относительно мгновенной оси вращения;
– линейная скорость мгновенной оси вращения i-го звена;
– линейная скорость точки приведения A;
– масса каретки;
– момент инерции рычага (никакого отношения к матрице Якоби это не имеет);
– первый, второй и третий элементы i-ой строки транспонированной матрицы Якоби;
– максимальный крутящий момент i-го рычага.
Итак, основная идея силового расчёта схожа с основной идеей задачи о поиске максимальной скорости. Сначала необходимо задать массив точек, равномерно распределённых по рабочей зоне. Далее в каждой точке выполняется алгоритм расчёта, который должен определить максимальные крутящие моменты приводов, удовлетворяющий заданному состоянию механизма. Последним шагом происходит поиск максимального момента среди всех полученных значений.
Крутящий момент — это характеристика показывающая усилие, которое привод способен развивать. Говоря совсем простым языком, эта силовая характеристика, показывающая, насколько большое усилие торможения привод способен преодолеть, чтобы вращаться, или какое усилие он способен развивать при полной остановке, но во включенном состоянии. Стоит ещё уточнить, что момент привода, а точнее двигателя, почти всегда зависит от частоты вращения. То есть, если мы перестанем его тормозить, он может начать вращаться быстрее.
Почему вообще, привод (или двигатель), который будет вращать рычаги дельта-робота, должен обладать моментом? Дело в том, что для того, чтобы начать вращать рычаг с какой-то скоростью, это звено нужно сначала разогнать, то есть придать ему ускорение. А чтобы обеспечить ускорение, нужна сила или вращающий момент (для вращательного движения). Например, если мы возьмём тяжелое и длинное бревно, но мы не можем сразу начать крутить его со скоростью, скажем, 60 оборотов в минуту. Сначала мы будем медленно раскручивать его, а вот, когда раскрутим, тогда момента уже почти к нему прикладывать и не надо – бревно будет крутиться по инерции. Без сил трения оно будет вращаться вечно (если очень грубо).
Дельта-робот – высокоскоростной механизм. Его рычаги не только должны вращаться с большой скоростью – они должны и набирать эту скорость быстро. А значит, нам потребуется придать им и высокий, в сравнении с «медленными» механизмами, крутящий момент. Помимо рычагов, у дельта-робота есть ещё и подвижная платформа, которая, прежде всего, и должна быстро перемещаться. Ведь вращаем мы рычаги лишь чтобы передать усилие на неё. На платформе расположено какое-то исполнительное устройство, которое имеет кукую-то массу. Чтобы быстро разогнать эту массу, нам, опять же, через кинематические цепи всех плеч требуется передать ей усилие, а оно зарождается в приводе.
Подводя итого, можно сказать, что из-за инерционности, то есть наличия массы, для тела, двигающегося поступательно с ускорением, и момента инерции, для тела, которое ускорено вращается, нам и требуется привод с каким-то, подходящим нам, крутящим моментом.
Помимо этого, дельта-робот может перемещать своё исполнительное звено достаточно медленно и без значительного ускорения, но выполнять при этом какую-то силовую операцию, например, нажимать на что-то. В этом случае сила нажатия также передаётся на приводы через кинематические цепи механизма и пересчитывается в крутящие моменты.
Решить задачу силового расчёта можно двумя (а может и больше) методами.
Что можно сказать о первом?
Он основывается на принципе Д’Аламбера, согласно которому звено механизма можно рассматривать, как неподвижное, то есть находящиеся в равновесии, если ко всем внешним силам, действующим на него, добавить силы инерции. На практике силы инерции сосредотачивают в центре масс звеньев и, считают, что на тело действует результирующая сила – главный вектор инерции и результирующий момент – главный момент сил инерции. Вот, кстати, хорошая книжка по всем вопросам конструирования машин, где об этом доступно рассказывается.
Механизм при таком подходе разбивается на группы, а к группам прикладываются силы реакции от оставшихся частей механизма.
Я это делал, и скажу я вам – это сложно, долго и сделать безошибочно очень затруднительно.
Решаешь ты такой себе решаешь, а потом получаешь что-то вроде этого:
Поэтому, я не буду тратить здесь на это время, а сразу перейду к более простому и быстрому методу.
Второй метод представляет собой сущую магию. Если не в даваться в подробности, которые описаны тут, то можно сказать, что:
где – крутящие моменты первого, второго и третьего рычагов соответственно;
– составляющие приложенной к исполнительному звену силы по осям
;
– матрица Якоби.
Как составить матрицу Якоби сказано в предыдущей статье. Это, оказывается, не сложно.
В случае, когда мы хотим найти максимальный крутящий момент привода при выполнении роботом какой-то медленной технологической операции, например, смене инструмента, мы можем указать конкретную область, в которой задать массив точек для анализа, и конкретный вектор силы.
Пример
На видео я измеряю примерную силу, необходимую для смены рабочего органа (Nozzle-а), так называемого, вакуумного пинцета расстановщика электронных компонентов.
Можно, например, при помощи обычных весов также получить примерное значение силы, необходимое для гравировки или сверления печатных плат:
«Снять» эти данные можно с какого-нибудь промышленного станочка.
Запустив расчётный алгоритм в каждой точке, можно найти максимальное значение, крутящего момента, возникающего в приводе при таком режиме работы.
Пример алгоритма в MATLAB
%Задаём область для анализа
X = 40;
Y = 40;
Z = -380;
a = 30;
b = 30;
c = 10;
F = 3;
%Флаг необходимости рассматривания наихудшего направления
worDir = 0;
F_vect = [3; 2; 1];
Mmax = 0;
%Плотность точек
dotDensity = 30;
%Рабочая зона
WZ_D = 320;
WZ_d = 100;
WZ_H = 150;
WZ_Z = -390;
WZ_h = 50;
%Переменная, показывающая необходимость дополнительного
addSeg = 0;
vmax = 1000;
R_l = 170;
R_r = 320;
OQ = 77.9423;
VM = 23.094;
cos120 = cosd(120);
sin120 = sind(120);
cos240 = cosd(240);
sin240 = sind(240);
%Проверяем, находится ли заданная область в рабочей зоне
%Задаём точки для проверки
CP_X = [X, X+a, X+a, X, X, X, X+a, X+a];
CP_Y = [Y, Y, Y+b, Y+b, Y+b, Y, Y, Y+b];
CP_Z = [Z, Z, Z, Z, Z+c, Z+c, Z+c, Z+c];
%Находим индексы точек, попадающих в цилиндрическую область
inCil = CP_X.^2+CP_Y.^2 <= (WZ_D/2)^2;
%Находим инексы точек попадающих
%1 Только в цилиндрическую РЗ
if addSeg == 0
inDopSeg = (CP_Z >= WZ_Z) & (CP_Z <= (WZ_Z+WZ_H));
end
%В цилиндрическую РЗ и усечённый конус
if addSeg == 1
z0 = WZ_Z - WZ_h*(WZ_D/2)/((WZ_D-WZ_d)/2);
a2_c2 = ((WZ_D/2)/(WZ_Z-z0))^2;
inDopSeg = CP_X.^2 + CP_Y.^2 <= a2_c2*(CP_Z-z0).^2;
end
%В цилиндрическую РЗ и в часть сферы
if addSeg == 2
inDopSeg = (CP_X.^2 + CP_Y.^2 + (CP_Z-(WZ_Z-WZ_h+WZ_d/2)).^2 <= (WZ_d/2)^2)|(CP_Z > WZ_Z);
end
%Формируем индексы точек, удовлетворяющих всем условиям
inWZ = inCil & inDopSeg;
CP_XX = CP_X(inWZ);
%Если все точки вошли в рабочую зону
if size(CP_X, 2) == size(CP_XX, 2)
%Формируем массив точек для анализа
x = linspace(X, X+a, dotDensity);
y = linspace(Y, Y+b, dotDensity);
z = linspace(Z, Z+c, dotDensity);
[X, Y, Z] = meshgrid(x, y, z);
TestPointsX = reshape(X, [1, size(X, 1)^3, 1]);
TestPointsY = reshape(Y, [1, size(Y, 1)^3, 1]);
TestPointsZ = reshape(Z, [1, size(Z, 1)^3, 1]);
% %Тестовая отрисовка точек
% hold('on');
% plot3(aTestPointsX, TestPointsY, TestPointsZ, '.r');
% hold('off');
%Запускаем цикл проверки в каждой точке
for k = 1:size(TestPointsX, 2)
J = [ TestPointsX(k)/(R_l*(1 - ((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)))^(1/2)*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2)), ((2*OQ - 2*VM + 2*TestPointsY(k))/(2*R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2)) - ((2*OQ - 2*VM + 2*TestPointsY(k))*((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2))/(4*R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)))^(1/2) + (1/((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2) - ((2*OQ - 2*VM + 2*TestPointsY(k))*(OQ - VM + TestPointsY(k)))/(2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)))/(1 - (OQ - VM + TestPointsY(k))^2/((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2))^(1/2), (TestPointsZ(k)/(R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2)) - (TestPointsZ(k)*((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2))/(2*R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)))^(1/2) - (TestPointsZ(k)*(OQ - VM + TestPointsY(k)))/(((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)*(1 - (OQ - VM + TestPointsY(k))^2/((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2))^(1/2));
(3^(1/2)/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2)/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2) + ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2 + 3^(1/2)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/(2*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2), ((VM - OQ + TestPointsY(k)/2 - (3^(1/2)*TestPointsX(k))/2 + 3^(1/2)*(TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2))/(2*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) + ((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) + ((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)) - 1/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)))/(1 - (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2), (TestPointsZ(k)/(R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (TestPointsZ(k)*((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(2*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) - (TestPointsZ(k)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/((1 - (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2)*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2));
((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2 + 3^(1/2)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/(2*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) - (3^(1/2)/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2)/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2), ((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2 - 3^(1/2)*(TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2))/(2*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - ((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) + ((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)) - 1/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)))/(1 - (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2), (TestPointsZ(k)/(R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (TestPointsZ(k)*((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(2*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) + (TestPointsZ(k)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/((1 - (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2)*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2))];
J = -transpose(inv(J));
%Если требуется рассмотреть наихудшее направление в каждой точке
if worDir == 1
M_max_TP = [norm(J(1, :))*F, norm(J(2, :))*F, norm(J(3, :))*F];
else
%Иначе
M_max_TP = [J(1, :)*F_vect, J(2, :)*F_vect, J(3, :)*F_vect];
end
%Находим максимальный момент среди рычагов
Mmax = max([abs(M_max_TP), Mmax]);
end
maxM = Mmax*10^(-3)
else
%Иначе
errordlg('Выбранная область не входит в рабочую зону', 'Ошибка');
endТот, кто разбирался с прошлыми алгоритмами, разберётся и с этим. Вот небольшая иллюстрация, показывающая смысл входных данных:
Гораздо интереснее случай перемещения с высоким ускорением – это основное применение дельта-робота.
Для алгоритма тогда потребуется найти приведённую к центру подвижной платформы массу механизма. В результате поискового запроса узнаем: «приведенной массой механизма называется такая условная масса, которая как бы сосредоточена в точке приведения механизма, кинетическая энергия которой равна сумме кинетических энергий всех звеньев механизма».
Приведённую к точке V массу всего механизма найдём, как сумму приведённых масс от его звеньев:
где – приведённая к точке V масса каретки (подвижной платформы);
– приведённые к точке V массы рычагов механизма.
Можно заметить, что в этом уравнении отсутствуют слагаемые, приведённой массы штанг. В связи с тем, что штанги почти всегда выполняются из лёгких композитных материалов и их моментом инерции пренебрегают, а массу считают сосредоточенной на их концах, то есть в шарнирах 🕮 🕮. Иными словами, масса (не приведённая, а обычная) каждого рычага будет складываться из массы самого рычага и массы одной штанги. Массу оставшихся трёх штанг нужно включить в массу каретки.
Теперь найдём каждое слагаемое в формуле (2). Приведённая к точке A масса в общем виде считается так:
где – момент инерции i-го звена относительно мгновенной оси вращения;
– масса i-го звена;
– угловая скорость i-го звена относительно мгновенной оси вращения;
– линейная скорость мгновенной оси вращения i-го звена;
– линейная скорость точки приведения A.
То есть, если звено, приведённую массу которого мы ищем, совершает одновременно и вращательное и поступательное движение (штанга), то в формуле приведённой массы присутствуют два слагаемых. Причём нужно для каждой расчётной точки вычислять мгновенную ось вращения, её скорость, момент инерции штанги относительно этой оси и угловую скорость. Кошмар. Если же звено только вращается (рычаг) или только двигается поступательно (платформа), имеем:
где – масса каретки;
– момент инерции рычага (никакого отношения к матрице Якоби это не имеет).
Приведённая масса механизма нам нужна для того, чтобы получить значение силы, «как бы» действующей на исполнительное звено. Действие этой силы заменяет инерционные нагрузки от всех звеньев механизма. Вычисляете она по школьной формуле:
Поскольку для каждой расчётной точки нужно вычислить максимальный крутящий момент, который достигается при максимальном значение нагружающей силы, то необходимо, чтобы приведённая масса также была максимальна. Это достигается при для конкретного значения скорости платформы
. Эту задачу мы решать уже умеем. Вообще, отношение
будет постоянным для конкретной точки при любой скорости
. Но так как у нас уже есть алгоритм, вычисляющий максимальную угловую скорость рычага при максимальной требуемой линейной скорости рабочего органа, мы будем считать именно при
.
Итак, зная размеры звеньев механизма, зная максимальную требуемую скорость исполнительного звена (не обязательно), и получив ориентировочные массоинерционные характеристики звеньев механизма, можно найти максимальную приведённую к точке V массу всего механизма.
Тут сразу можно сказать: «Стоп, а откуда брать «массоинерционные характеристики звеньев механизма»?». Есть два варианта.
Первый:
Шутка, мы ведь механизм только проектируем. Откуда у нас уже готовое «железо»?
На самом деле, для примерной оценки моссоинерционных характеристик звеньев механизма нужно сначала сделать трёхмерные модели этих звеньев. Подразумевается, что вы владеете какой-то инженерной программой для 3Д моделирования, ведь вы же собираетесь дельта-робота делать.
При построениях обязательно нужно задавать тот материал, из которого звенья будут выполнены. В случае добавления в сборку таких элементов, как двигатель, то есть элементов, имеющих внутренние полости, следует подбирать плотность материала так, чтобы итоговая масса добавляемого элемента была приблизительно равна массе его реального двойника. Не стоит забывать и о массе штанг, которые можно, например, добавить в массу других звеньев также путём изменения их плотности:
Тогда, заглянув в раздел свойств, или используя специальную команду, легко можно «вытащить» из программы любые массоинерционные характеристики:
Понятное дело, что наличия 3Д модели на данном этапе не предполагается, так как, по меньшей мере, конструкция рычага зависит от используемого привода, а мы привод тут и выбираем. Да и инерционность самого привода тут никак не учитывается. Но всё же, необходимо уже на данном этапе сформировать общие представления о будущем устройстве и примерную 3Д модель хоть как-то создать. В конечном счёте всё равно мы введём коэффициент запаса, который эти неточности компенсирует.
А теперь самое интересное. Эквивалентную силу, действующую на механизм, мы найти можем, но направление этой силы нам неизвестно. И тут на помощь, как и в прошлой статье, приходит идея о том, что произведение двух векторов (матричное уравнение (1)) достигает своего максимального значения в случае, когда вектора коллинеарные. Упрощая это до понятной формулы можно записать:
где – первый, второй и третий элементы i-ой строки транспонированной матрицы Якоби;
– максимальный крутящий момент i-го рычага.
Произведя расчёт по этой формуле для каждого из трёх приводов в каждой точке заданного массива, можно легко получить максимальный крутящий момент, который может возникнуть при работе механизма с заданным максимальным ускорением .
Выбирать привод по полученному значению следует, очевидно, «с запасом».
Алгоритм силового расчёта для ускоренных перемещений
global vmax %Максимальная требуемая скорость исполнительного звена
global Jr mk %Массоинерционных характеристики
global amax %Максимальное требуемое ускорение рабочего органа
%Задаём начальное значение
%Добавляем глобальные переменные входных и выходных данных
global WZ_D WZ_H WZ_Z WZ_d WZ_h %Рабочая зона
global addSeg %Переменная, показывающая необходимость дополнительного
%сегмента в рабочей зоне
global dotDensity %Плотность точек
%Плотность точек анализа
dotDensity = 30;
%Параметры рабочей зоны
WZ_D = 320;
WZ_d = 100;
WZ_H = 150;
WZ_Z = -390;
WZ_h = 50;
addSeg = 0;
%Максимальная требуемая скорость рабочего органа
vmax = 1000;
%Максимальное требуемое от рабочего органа ускорение
amax = 10000;
%Момент инерции рычага
Jr = 2410;
%Масса каретки
mk = 0.3;
%Размеры звеньев
R_l = 170;
R_r = 320;
OQ = 77.9423;
VM = 23.094;
%Константы
cos120 = cosd(120);
sin120 = sind(120);
cos240 = cosd(240);
sin240 = sind(240);
%Генерируем массив точек для анадлиза
[TestPointsX, TestPointsY, TestPointsZ] = genTP();
%Задаём начальные значения
Mmax = 0;
Mmin = 1e20;
%Запускаем цикл проверки в каждой точке
for k = 1:size(TestPointsX, 2)
J = [ TestPointsX(k)/(R_l*(1 - ((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)))^(1/2)*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2)), ((2*OQ - 2*VM + 2*TestPointsY(k))/(2*R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2)) - ((2*OQ - 2*VM + 2*TestPointsY(k))*((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2))/(4*R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)))^(1/2) + (1/((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2) - ((2*OQ - 2*VM + 2*TestPointsY(k))*(OQ - VM + TestPointsY(k)))/(2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)))/(1 - (OQ - VM + TestPointsY(k))^2/((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2))^(1/2), (TestPointsZ(k)/(R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(1/2)) - (TestPointsZ(k)*((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2))/(2*R_l*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((OQ - VM + TestPointsY(k))^2 + R_l^2 - R_r^2 + TestPointsX(k)^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)))^(1/2) - (TestPointsZ(k)*(OQ - VM + TestPointsY(k)))/(((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2)^(3/2)*(1 - (OQ - VM + TestPointsY(k))^2/((OQ - VM + TestPointsY(k))^2 + TestPointsZ(k)^2))^(1/2));
(3^(1/2)/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2)/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2) + ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2 + 3^(1/2)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/(2*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2), ((VM - OQ + TestPointsY(k)/2 - (3^(1/2)*TestPointsX(k))/2 + 3^(1/2)*(TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2))/(2*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) + ((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) + ((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)) - 1/(2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)))/(1 - (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2), (TestPointsZ(k)/(R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (TestPointsZ(k)*((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(2*R_l*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 + (3^(1/2)*TestPointsY(k))/2)^2 + (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) - (TestPointsZ(k)*(OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/((1 - (OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2)*((OQ - VM - TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2));
((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2 + 3^(1/2)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/(2*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) - (3^(1/2)/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (3^(1/2)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2)/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2), ((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2 - 3^(1/2)*(TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2))/(2*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - ((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)*((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(4*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) + ((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)) - 1/(2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)))/(1 - (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2), (TestPointsZ(k)/(R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(1/2)) - (TestPointsZ(k)*((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2))/(2*R_l*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2)))/(1 - ((TestPointsX(k)/2 - (3^(1/2)*TestPointsY(k))/2)^2 + (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + R_l^2 - R_r^2 + TestPointsZ(k)^2)^2/(4*R_l^2*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)))^(1/2) + (TestPointsZ(k)*(VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2))/((1 - (VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2/((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2))^(1/2)*((VM - OQ + TestPointsY(k)/2 + (3^(1/2)*TestPointsX(k))/2)^2 + TestPointsZ(k)^2)^(3/2))];
%Находим максимальные скорости входных звеньев
w_max_TP = [norm(J(1, :))*vmax, norm(J(2, :))*vmax, norm(J(3, :))*vmax];
%Вычисляем приведённую массу в точке V
m_pr = mk + Jr*(w_max_TP(1)/vmax)^2 + Jr*(w_max_TP(2)/vmax)^2 + Jr*(w_max_TP(3)/vmax)^2;
%Вычисляем силу, действующую на механизм
F = m_pr*amax*(10^(-3));
J = transpose(inv(J));
M_max_TP = [norm(J(1, :))*F, norm(J(2, :))*F, norm(J(3, :))*F];
%Находим максимальный момент среди рычагов
Mmax = max([abs(M_max_TP), Mmax]);
Mmin = min([abs(M_max_TP), Mmin]);
end
%Переводим результат в H•м
maxM = Mmax*10^(-3)
%Вычисляем неравномерность максимального крутящего момента по рабочей зоне
uneven = Mmax/MminЗдесь используется функция «genTP», генерирующая облако точек для анализа. Я давал её в предыдущей статье.
Приведённый код выдаёт два числа – максимальный найденный крутящий момент и отношение наибольшего среди всех расчётных точек максимального крутящего момента и наименьшему максимальному крутящему моменту среди опять же всех расчётных точек. Иными словами, последняя величина показывает неравномерность максимального крутящего момента по рабочей зоне. Если эта величина больше, скажем, десяти, нам следует выбрать либо другие размеры механизма, либо подобрать для последнего другую (меньших размеров) желаемую рабочую зону. Чем меньше неравномерность, тем лучше.
В приведённой мной публикации автор рассказывает об, так называемых, особых положениях и показывает, что один из видов этих особых положений находится на границе реальной рабочей зоны. Поэтому, порой, нам достаточно лишь «отодвинуть» желаемую рабочую зону от реальной, чтобы снизить неравномерность динамических характеристик.
Другой подход для определения силовых характеристик
В вкратце расскажу и о другом подходе, который позволит узнать крутящие момент, возникающие в приводах.
Не так давно была опубликована статья, в которой авторы (один из них я) дали алгоритм динамического моделирования движения робота в системе Autodesk Inventor по траектории, подготовленной в MATLAB.
Как эту траекторию подготовить и как воспользоваться модулем динамического моделирования Autodesk Inventor подробно в этой статье описано.
Кнопка для скачивания прячется тут

Её пока не добавили, но она обязательно будет.
Преимуществом такого подхода являете то, что мы можем получить любые силовые факторы, возникающие при именно том движении (заранее спланированном), которое робот и будет совершать. Можно получить и силы, действующие на привод для выбора подшипников, и силы в трёхподвижных шарнирах для того, чтобы убедиться, что они не будут перегружены.
Недостаток такого подхода очевиден – на исследуемой траектории от привода может не потребоваться столь большого усилия, которое может от него потребоваться при движении по иной, нерассмотренной нами траектории.
Задача об ускорениях
В прошлой статье был представлен алгоритм поиска зависимости угловых скоростей входных звеньев от линейной скорости и положения выходного звена. Напомню, MATLAB дифференцировал функции положения в символьном виде.
Если полученные зависимости продифференцировать ещё раз, получим как раз зависимость угловых ускорений входных звеньев от ускорения, скорости и положения выходного звена.
%Задаём символьные переменные
syms Tetta_1(t) X_V(t) Y_V(t) Z_V(t)
syms OQ VM R_l R_r F f X_0 Y_0 Z_0
syms omega_1(t) v_VX(t) v_VY(t) v_VZ(t)
syms epsilon_1 a_VX a_VY a_VZ
%Записываем решение обратной кинематической задачи в аналитическом виде
NL = sqrt(R_r^2-X_V^2);
y_M = -VM + Y_V;
y_Q = -OQ;
const_1 = y_M - y_Q;
NQ = sqrt(const_1^2 + Z_V^2);
Eq1 = Tetta_1 == 2*pi - acos((R_l^2 + NQ^2 - NL^2)/(2*R_l*NQ))...
- acos(const_1/NQ);
%Дифференцируем по времени
Eq2 = diff(Eq1, t);
%Заменяем производные на физические величины
Eq2 = subs(Eq2, [diff(Tetta_1(t), t), diff(X_V(t), t), diff(Y_V(t), t),...
diff(Z_V(t), t)], [omega_1 v_VX v_VY v_VZ ]);
%Повторяем два вышеизложенных действия для поиска углового ускорения
Eq3 = diff(Eq2, t);
Eq3 = subs(Eq3, [diff(omega_1, t), diff(v_VX(t), t), diff(v_VY(t), t),...
diff(v_VZ(t), t), diff(X_V(t), t), diff(Y_V(t), t), diff(Z_V(t), t)],...
[epsilon_1 a_VX a_VY a_VZ v_VX v_VY v_VZ])
%Выражаем через ускорение
col2 = collect(Eq3, [a_VX a_VY a_VZ])Формула, генерируемая этим скриптом, достаточно большая, но вполне работоспособная.
Если из полученного решения сделать функцию, то выглядеть она будет вот так:
%Находит решение обратной кинематической задачи для дельта-робота для
%ускорений
function [epsilon_1, epsilon_2, epsilon_3] = OZK_a(X_V, Y_V, Z_V, v_VX, v_VY, v_VZ, a_VX, a_VY, a_VZ)
%Расчёт координат точки V в системах координат, повёрнутых на 120° и 240°
%по часовой стрелке относительно основной
global R_l R_r cos120 sin120 cos240 sin240 VM OQ
X_V_120 = X_V*cos120 - Y_V*sin120;
Y_V_120 = X_V*sin120 + Y_V*cos120;
X_V_240 = X_V*cos240 - Y_V*sin240;
Y_V_240 = X_V*sin240 + Y_V*cos240;
Z_V_120 = Z_V;
Z_V_240 = Z_V;
%Расчёт векторов скоростей точки V в системах координат, повёрнутых на 120° и 240°
%по часовой стрелке относительно основной
v_VX_120 = v_VX*cos120 - v_VY*sin120;
v_VY_120 = v_VX*sin120 + v_VY*cos120;
v_VX_240 = v_VX*cos240 - v_VY*sin240;
v_VY_240 = v_VX*sin240 + v_VY*cos240;
v_VZ_120 = v_VZ;
v_VZ_240 = v_VZ;
%Расчёт векторов ускорений точки V в системах координат, повёрнутых на 120° и 240°
%по часовой стрелке относительно основной
a_VX_120 = a_VX*cos120 - a_VY*sin120;
a_VY_120 = a_VX*sin120 + a_VY*cos120;
a_VX_240 = a_VX*cos240 - a_VY*sin240;
a_VY_240 = a_VX*sin240 + a_VY*cos240;
a_VZ_120 = a_VZ;
a_VZ_240 = a_VZ;
%Расчёт угловых ускорений поворота рычагов в соответствующих системах координат
epsilon_1 = (a_VY/(Z_V^2 + (OQ - VM + Y_V)^2)^(1/2) - ((OQ - VM + Y_V)*(2*v_VY^2 + 2*v_VZ^2 + 2*a_VZ*Z_V + 2*a_VY*(OQ - VM + Y_V)))/(2*(Z_V^2 + (OQ - VM + Y_V)^2)^(3/2)) + (3*(2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))^2*(OQ - VM + Y_V))/(4*(Z_V^2 + (OQ - VM + Y_V)^2)^(5/2)) - (v_VY*(2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V)))/(Z_V^2 + (OQ - VM + Y_V)^2)^(3/2))/(1 - (OQ - VM + Y_V)^2/(Z_V^2 + (OQ - VM + Y_V)^2))^(1/2) + ((2*v_VX^2 + 2*v_VY^2 + 2*v_VZ^2 + 2*a_VX*X_V + 2*a_VZ*Z_V + 2*a_VY*(OQ - VM + Y_V))/(2*R_l*(Z_V^2 + (OQ - VM + Y_V)^2)^(1/2)) - ((2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))*(2*X_V*v_VX + 2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V)))/(2*R_l*(Z_V^2 + (OQ - VM + Y_V)^2)^(3/2)) - ((2*v_VY^2 + 2*v_VZ^2 + 2*a_VZ*Z_V + 2*a_VY*(OQ - VM + Y_V))*(X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2))/(4*R_l*(Z_V^2 + (OQ - VM + Y_V)^2)^(3/2)) + (3*(2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))^2*(X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2))/(8*R_l*(Z_V^2 + (OQ - VM + Y_V)^2)^(5/2)))/(1 - (X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2)^2/(4*R_l^2*(Z_V^2 + (OQ - VM + Y_V)^2)))^(1/2) - ((v_VY/(Z_V^2 + (OQ - VM + Y_V)^2)^(1/2) - ((2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))*(OQ - VM + Y_V))/(2*(Z_V^2 + (OQ - VM + Y_V)^2)^(3/2)))*(((2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))*(OQ - VM + Y_V)^2)/(Z_V^2 + (OQ - VM + Y_V)^2)^2 - (2*v_VY*(OQ - VM + Y_V))/(Z_V^2 + (OQ - VM + Y_V)^2)))/(2*(1 - (OQ - VM + Y_V)^2/(Z_V^2 + (OQ - VM + Y_V)^2))^(3/2)) + (((2*X_V*v_VX + 2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))/(2*R_l*(Z_V^2 + (OQ - VM + Y_V)^2)^(1/2)) - ((2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))*(X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2))/(4*R_l*(Z_V^2 + (OQ - VM + Y_V)^2)^(3/2)))*(((2*X_V*v_VX + 2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))*(X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2))/(2*R_l^2*(Z_V^2 + (OQ - VM + Y_V)^2)) - ((2*Z_V*v_VZ + 2*v_VY*(OQ - VM + Y_V))*(X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2)^2)/(4*R_l^2*(Z_V^2 + (OQ - VM + Y_V)^2)^2)))/(2*(1 - (X_V^2 + Z_V^2 + (OQ - VM + Y_V)^2 + R_l^2 - R_r^2)^2/(4*R_l^2*(Z_V^2 + (OQ - VM + Y_V)^2)))^(3/2));
epsilon_2 = (a_VY_120/(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(1/2) - ((OQ - VM + Y_V_120)*(2*v_VY_120^2 + 2*v_VZ_120^2 + 2*a_VZ_120*Z_V_120 + 2*a_VY_120*(OQ - VM + Y_V_120)))/(2*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(3/2)) + (3*(2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))^2*(OQ - VM + Y_V_120))/(4*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(5/2)) - (v_VY_120*(2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120)))/(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(3/2))/(1 - (OQ - VM + Y_V_120)^2/(Z_V_120^2 + (OQ - VM + Y_V_120)^2))^(1/2) + ((2*v_VX_120^2 + 2*v_VY_120^2 + 2*v_VZ_120^2 + 2*a_VX_120*X_V_120 + 2*a_VZ_120*Z_V_120 + 2*a_VY_120*(OQ - VM + Y_V_120))/(2*R_l*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(1/2)) - ((2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))*(2*X_V_120*v_VX_120 + 2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120)))/(2*R_l*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(3/2)) - ((2*v_VY_120^2 + 2*v_VZ_120^2 + 2*a_VZ_120*Z_V_120 + 2*a_VY_120*(OQ - VM + Y_V_120))*(X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2))/(4*R_l*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(3/2)) + (3*(2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))^2*(X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2))/(8*R_l*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(5/2)))/(1 - (X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2)^2/(4*R_l^2*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)))^(1/2) - ((v_VY_120/(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(1/2) - ((2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))*(OQ - VM + Y_V_120))/(2*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(3/2)))*(((2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))*(OQ - VM + Y_V_120)^2)/(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^2 - (2*v_VY_120*(OQ - VM + Y_V_120))/(Z_V_120^2 + (OQ - VM + Y_V_120)^2)))/(2*(1 - (OQ - VM + Y_V_120)^2/(Z_V_120^2 + (OQ - VM + Y_V_120)^2))^(3/2)) + (((2*X_V_120*v_VX_120 + 2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))/(2*R_l*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(1/2)) - ((2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))*(X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2))/(4*R_l*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^(3/2)))*(((2*X_V_120*v_VX_120 + 2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))*(X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2))/(2*R_l^2*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)) - ((2*Z_V_120*v_VZ_120 + 2*v_VY_120*(OQ - VM + Y_V_120))*(X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2)^2)/(4*R_l^2*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)^2)))/(2*(1 - (X_V_120^2 + Z_V_120^2 + (OQ - VM + Y_V_120)^2 + R_l^2 - R_r^2)^2/(4*R_l^2*(Z_V_120^2 + (OQ - VM + Y_V_120)^2)))^(3/2));
epsilon_3 = (a_VY_240/(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(1/2) - ((OQ - VM + Y_V_240)*(2*v_VY_240^2 + 2*v_VZ_240^2 + 2*a_VZ_240*Z_V_240 + 2*a_VY_240*(OQ - VM + Y_V_240)))/(2*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(3/2)) + (3*(2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))^2*(OQ - VM + Y_V_240))/(4*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(5/2)) - (v_VY_240*(2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240)))/(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(3/2))/(1 - (OQ - VM + Y_V_240)^2/(Z_V_240^2 + (OQ - VM + Y_V_240)^2))^(1/2) + ((2*v_VX_240^2 + 2*v_VY_240^2 + 2*v_VZ_240^2 + 2*a_VX_240*X_V_240 + 2*a_VZ_240*Z_V_240 + 2*a_VY_240*(OQ - VM + Y_V_240))/(2*R_l*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(1/2)) - ((2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))*(2*X_V_240*v_VX_240 + 2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240)))/(2*R_l*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(3/2)) - ((2*v_VY_240^2 + 2*v_VZ_240^2 + 2*a_VZ_240*Z_V_240 + 2*a_VY_240*(OQ - VM + Y_V_240))*(X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2))/(4*R_l*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(3/2)) + (3*(2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))^2*(X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2))/(8*R_l*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(5/2)))/(1 - (X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2)^2/(4*R_l^2*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)))^(1/2) - ((v_VY_240/(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(1/2) - ((2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))*(OQ - VM + Y_V_240))/(2*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(3/2)))*(((2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))*(OQ - VM + Y_V_240)^2)/(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^2 - (2*v_VY_240*(OQ - VM + Y_V_240))/(Z_V_240^2 + (OQ - VM + Y_V_240)^2)))/(2*(1 - (OQ - VM + Y_V_240)^2/(Z_V_240^2 + (OQ - VM + Y_V_240)^2))^(3/2)) + (((2*X_V_240*v_VX_240 + 2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))/(2*R_l*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(1/2)) - ((2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))*(X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2))/(4*R_l*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^(3/2)))*(((2*X_V_240*v_VX_240 + 2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))*(X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2))/(2*R_l^2*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)) - ((2*Z_V_240*v_VZ_240 + 2*v_VY_240*(OQ - VM + Y_V_240))*(X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2)^2)/(4*R_l^2*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)^2)))/(2*(1 - (X_V_240^2 + Z_V_240^2 + (OQ - VM + Y_V_240)^2 + R_l^2 - R_r^2)^2/(4*R_l^2*(Z_V_240^2 + (OQ - VM + Y_V_240)^2)))^(3/2));
endВсё это может пригодиться при планировании движения или, например, при расчёте крутящего момента от ускоренного движения рычага.
Пару слов о точности
Одной из ключевых характеристик любого манипулятора выступает точность. Производители зачастую закладывают в этот показатель разный смысл. В нашем случае под точностью будем понимать величину, на которую может отклоняться реальная координата рабочего органа от заданной.
На этот показатель валяют множество факторов. Выделим три основных:
-
точность изготовления деталей робота;
-
деформации от нагрузок;
-
дискретность перемещения.
Что касается первого фактора, то тут стоит сказать том, что при изготовлении и сборке наиболее жёсткие требования предъявляются к взаимному положение всех трёх плеч и одинаковости их размеров. Ведь если, к примеру, все три рычага окажутся длиннее, чем требуется (причём «одинаково длиннее»), эту неточность легко компенсировать в программном обеспечении системы управления, изменив этот параметр на тот, что получился в реальности.
При проектировании робота следует заранее продумать, как мы будем его настраивать и как будем изготавливать. Много информации можно подчерпнуть из публикаций по конструированию и настройке ЧПУ станков. Это очень важно! Я здесь набил кучу шишек – спустил много денег на изготовление качественных деталей, но оказалось, что настроить своего дельта-робота простыми средствами (обкаткой индикатором, угломерами) я не могу, так как заранее должным образом не продумал конструкцию для этого. Может быть, я когда-нибудь напишу статью о грамотном конструировании и последующей настройке устройства на базе дельта-робота.
Для оценки деформации от нагрузок можно провести исследование в модуле анализа напряжений какой-нибудь САПР, например, Autodesk Inventor.
Для оценки деформаций в режимах медленных перемещений под действием внешней нагрузки этот метод вполне применим, если есть понимание, как такой расчёт правильно выполнять. Я тут не специалист, учить не буду.
Для перемещений с высоким ускорением можно считать, что деформации от инерционных нагрузок к моменту остановки пропадут, так как пропадёт и ускорение, их вызывающее. Тогда, в большинстве случаев, нам и не сильно важно, насколько рабочий орган отклонится от заданной траектории за счёт инерционности конструкции, так как начнёт он своё движение из заданной точки в недеформированном состоянии и закончит аналогичным образом. Но есть и исключения, например 3Д печать, с высокими скоростями и ускорениями приведёт к «перелёту» экструдера (а значит и дорожки выдавливаемого им пластика) в местах с резким изменением направления скорости. Здесь проще бороться с неточностями уже грамотной настройкой системы управления, которая будет либо снижать скорость при изменении её направления, либо программно компенсировать «перелёты» рабочего органа.
Если учесть тот факт, что в качестве источника движения очень часто выступают шаговые двигатели, то неминуемо встаёт вопрос о дискретности движения. Для оценки максимального перемещения исполнительного звена, вызванного минимальным угловым перемещением привода можно написать скрипт в пакете MATLAB, который анализирует массив точек внутри рабочей области механизма. Каждой такой точке ставится в соответствие другая точка, которая получается при изменении угловых координат всех трёх приводов на минимальный шаг. Далее между получившимися точками вычисляется расстояние. Среди всех этих расстояний ищется максимальное. Минимальный угловой шаг привода зависит от коэффициента дробления шага
, выставленного в драйвере, значения углового шага двигателя
и передаточного отношения редуктора
и вычисляется по простейшей формуле:
%Вычисляет максимальный шаг перемещения при изменении на минимальный шаг
%углов поворота всех трёх рычагов
function [dS] = find_dS(TestPointsX, TestPointsY, TestPointsZ)
global dTh_mot kd ur %Входные данные для вычисления минимального шага
%Вычисляем минимальный угловой шаг входных звеньев
dTheta = dTh_mot/(kd*ur);
%Задаём начальное значение
dS = 0;
%Запускаем цикл расчёта в каждой точке
for k = 1:size(TestPointsX, 2)
vectTheta = OZK(TestPointsX(k), TestPointsY(k), TestPointsZ(k))
V1 = PZK(vectTheta(1), vectTheta(2), vectTheta(3));
V2 = PZK(vectTheta(1)+dTheta, vectTheta(2)+dTheta, vectTheta(3)+dTheta);
dS = max([sqrt((V1(1)-V2(1))^2+(V1(2)-V2(2))^2+(V1(3)-V2(3))^2), dS]);
end
endФункция принимает на вход массив точек, в которых будет производится расчёт. Алгоритм для генерации такого массива я давал в прошлой статье, а функции для решения прямой и обратной задач кинематики я давал во второй статье этого цикла.
Выбор приводов
Чтобы выбрать привод для дельта-робота нужно сначала проанализировать, что выбирают другие инженеры в качестве источника движения этого механизма.
С промышленными моделями всё не понятно – там производители используют свои сервоприводы, которые, порой, не понятно, на каком двигателе работают, и со своими редукторами, тоже не ясно, как устроенными.
В общем, не будем с этим разбираться. Лучше посмотрим, что используют инженеры в открытых проектах. А там, почти, только шаговые двигатели.
Так как максимальная скорость вращения шагового двигателя составляет 1000-2000 об/мин, а нам для дельта-робота нужно будет максимум 100 об/мин, то сама напрашивается идея добавления к двигателю редуктора.
С шаговым двигателем всё сравнительно прозрачно. Есть различные стандарты фланца двигателя Nema 8, Nema17, Nema23, Nema42. Двигатели с одним фланцем могут быть разной длины и, соответственно, иметь разный крутящий момент. Шаговики могут быть снабжены энкодером и замкнутой системой управления. Это превращает их в сервоприводы, свободные от такой проблемы, как пропуски шагов. У двигателей может быть разное значения углового шага – обычно 0.9° и 1.8° на шаг. Есть конечно и масса других характеристик, но нас они будут мало интересовать.
Куда интереснее дела обстоят с редуктором. На AliExpress первыми лотами по запросу «редуктор nema23» выскакивают планетарные редукторы, причём последние имеются «подешевле» (погрубее) и «подороже» (более качественные и точные).
Подбираем по нужному передаточному отношению и максимальному крутящему моменту. Всё вроде бы здорово. Но обращу внимание на то, что проглядел лично я. Вот характеристики того редуктора, который я выбрал :
Здесь, как оказалось, особое внимание следует обратить на последнюю строчку. Что такою люфт ≤ 7 угловых минут? Наверное это очень мало – мы этого и не заметим.
Нет. На плече рычага 170 мм заметим:
Я «застопорил» шаговый двигатель и обнаружил люфт около 0.35 мм на плече около 170 мм. Если перевести в градусы, то это как раз около 6-и угловых минут, что и обещает производитель. Но если загнать этот люфт в алгоритм анализа дискретности перемещения вместо минимального углового шага привода, окажется, что максимальный люфт рабочего органа может составить аж 0.55 мм. А для многих приложений это много. Учитывайте это.
Так что тут стоит поискать редуктор с меньшим люфтом (скорее всего на другом принципе).
Во многих проектах можно встретить простейший ременной редуктор:
Люфта в нём не должно быть, зато может появиться неточность, связанная с растяжением ремня. Но ремней сейчас огромный выбор, и я уверен, что подходящий найдётся. Не спроста же в промышленных роботах этой решение находит своё место. Да и для тех, кому не хочется городись что-то самому, всё есть в продаже.
В общем. Конкретного ответа на вопрос, какой привод использовать для дельта-робота, я не дам. При выборе следует учитывать скоростные и силовые характеристики, наличие обратной связи. Особое внимание стоит обратить на люфт и погрешность. Мне пока больше симпатизирует (из дешёвого сегмента) ременной редуктор. Кто знает какой привод лучше по соотношению цена-характеристики – добро пожаловать в комментарии.
Когда будет следующий пост, и о чём он будет – не знаю. Надеюсь кому-то мои изыскания принесут пользу. До новых встреч.